CONTROL OF AN ASYMMETRICAL OMNI DIRECTIONAL

MOBILE ROBOT

Seyed Mohsen Safavi, Mohammad Ajoodanian, Ahmad movahedian

Mechanical Engineering Department, Isfahan University Of Technologhy (IUT) ,Isfahan,Iran

Keywords: Holonomic Omnidirectional mobile robot; Asymmetrical Structure.

Abstract: This paper describes how to control an asymmetric wheeled mobile robot with omnidirectional wheels,

considering the sample of a robot with three wheels. When flexible motion capabilities are required this

robot must be designed to meet the related requirements, namely fast and agile motions as well as robust

navigation. This paper provides an overview for the design of kinematics and dynamics of the robot, as well

as the motion and velocities equations. In addition to the above, a control method to obtain a proper control

model is explained. Simulation example is presented to demonstrate the ability of this control method. The

implementation and test of the controller on the real robot gives the results compatible with the simulation.

It was learned that the discontinuities between omnidirectional wheels’ rollers play an important role in

decreasing the accuracy of motion.

1 INTRODUCTION

Omnidirectional vehicles provide superior

maneuvering capability compared to the more

common car-like vehicles. The ability to move along

any direction, irrespective of the orientation of the

vehicle, makes it an attractive option in dynamic

environments. The annual RoboCup competition,

where teams of fully autonomous robots engage in

soccer matches, is an example of where

omnidirectional vehicles have been used in

computationally intensive dynamic environments

(Kalmár-Nagy et al., 2004) (Veloso et al., 1999)

(Kitano et al., 1998).

Among omnidirectional mobile robots, the one with

three or more wheels is more powerful. A holonomic

system is one in which the number of degrees of

freedom (DOF) is equal to the number of

coordinates needed to specify the configuration of

the system. In the field of mobile robots, the term

holonomic mobile robot is applied to the abstraction

called the robot, or base, without regard to the rigid

bodies which make up the actual mechanism. Thus,

any mobile robot with three degrees of freedom of

motion in the plane has become known as a

holonomic mobile robot (Holmberg et al., 1999).

Many different control mechanisms have been

created to achieve holonomic motion (Jung et al,.

1999) (Moore er al., 1999). In addition, these

systems have symmetric mechanisms. The

symmetric mobile robots with 3 DOF mostly have

120-degree angles between the wheels and the full

structure includes 3 actuators as well as 3 wheels

(Kalmár-Nagy et al., 2004). The control procedure

of such robots has been the subject of discussion in

several research papers. However in small robots (18

cm diameter of base) there is not enough space to

accommodate other components and the change in

angles between the wheels would partially overcome

this problem. The angle between front wheels is

140˚ and the two other angles are 110˚, which causes

asymmetric problem in robot and its control system.

The objective of this paper is to establish a real time

control strategy that could move the asymmetrical

robot to a given location with zero final velocity as

quickly as possible based on measurement of the

vehicle position and orientation.

The paper is ordered in such a way to describe the

Persia Robot system followed by the kinematics and

dynamic model of asymmetric omnidirectional robot

vehicle. Then Simulations and PD control method

are presented. The paper ends with the concluding

remarks.

120

Mohsen Safavi S., Ajoodanian M. and movahedian A. (2005).

CONTROL OF AN ASYMMETRICAL OMNI DIRECTIONAL MOBILE ROBOT.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 120-125

DOI: 10.5220/0001188501200125

 SciTePress

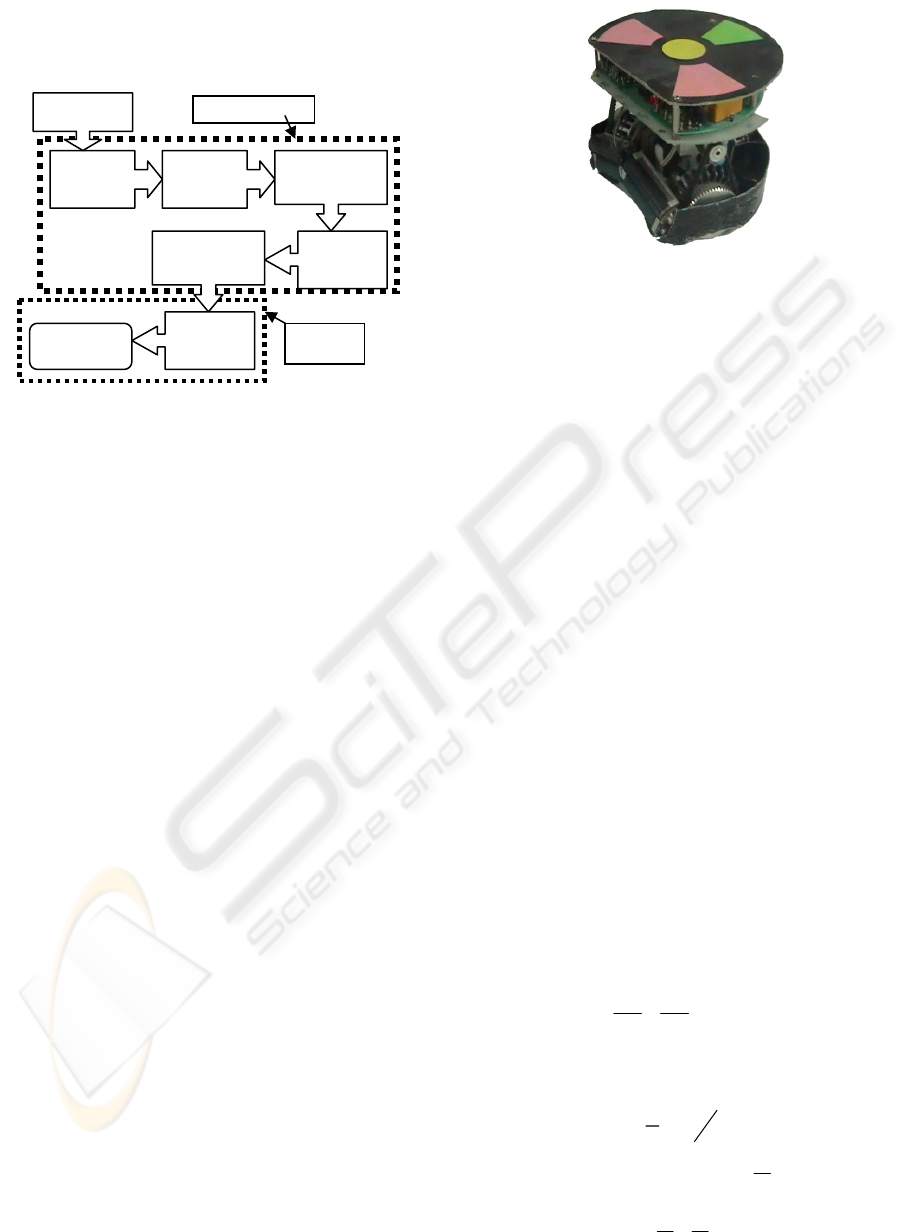
2 ROBOPERSIA SYSTEM

OVERVIEW

The complete RoboPersia system is a layered set of

subsystems which is shown in Figure 1. Figure 2

shows a photograph of the RoboPersia. An overhead

camera captures global images of the field. The

vision software processes the images to identify the

location and the velocity of robots and the ball. This

state of the field is passed to the Decision-Making

System (DMS). DMS is the highest level planner in

the system, responsible for distributing the overall

goal of the team amongst the individual robots.

DMS is responsible for the multi-robot coordination

and cooperation by selecting a role for each robot.

Some example roles include ATTACK and

DEFEND. The DMS roles and role parameters with

the field state are sent to the Role Layer which is

responsible for executing roles by selecting

behaviour for each robot. Some example behaviours

include KICK and MOVE. Behaviours and

behaviour parameters with the field state are passed

to Behaviour Layer. The Behaviour Layer attempts

to execute the desired behaviour by dedicating the

proper motion while avoiding obstacles. This layer

determines the immediate desired heading and

distance for the control layer .The Control Layer,

based on PD controller, controls the position and

head of the robots by changing the actuators duty

cycles. The feedback comes from the state of the

field

2.1 Optimizing the Omni Directional

Wheel

The holonomic and non-holonomic omnidirectional

mobile robot has been studied by using a variety of

mechanism. Several omnidirectional platforms have

been known to be realized by developing a

specialized wheel or mobile mechanisms (Holmberg

et al., 1999). These include various arrangements of

universal or omni wheels (La 1979; Carlisle 1983),

double universal wheels (Bradbury 1977), Swedish

or Mecanum wheels (Ilon 1971), chains of spherical

wheels (West and Asada 1992) or cylindrical wheels

(Hirose and Amano 1993), orthogonal wheels

(Killough and Pin 1992), ball wheels (West and

Asada 1994) and omni directional poly roller wheel

(Asama, 1995, Watanaba, 1998). All of these

mechanisms, except for some types with ball wheels,

have discontinuous wheel contact points which are a

great source of vibration; primarily because of the

changing support provided; and often additionally

because of the discontinuous changes in wheel

velocity needed to maintain smooth base motion

(Watanabe, 1998) (Williams et al., 2002) (Pin et al.,

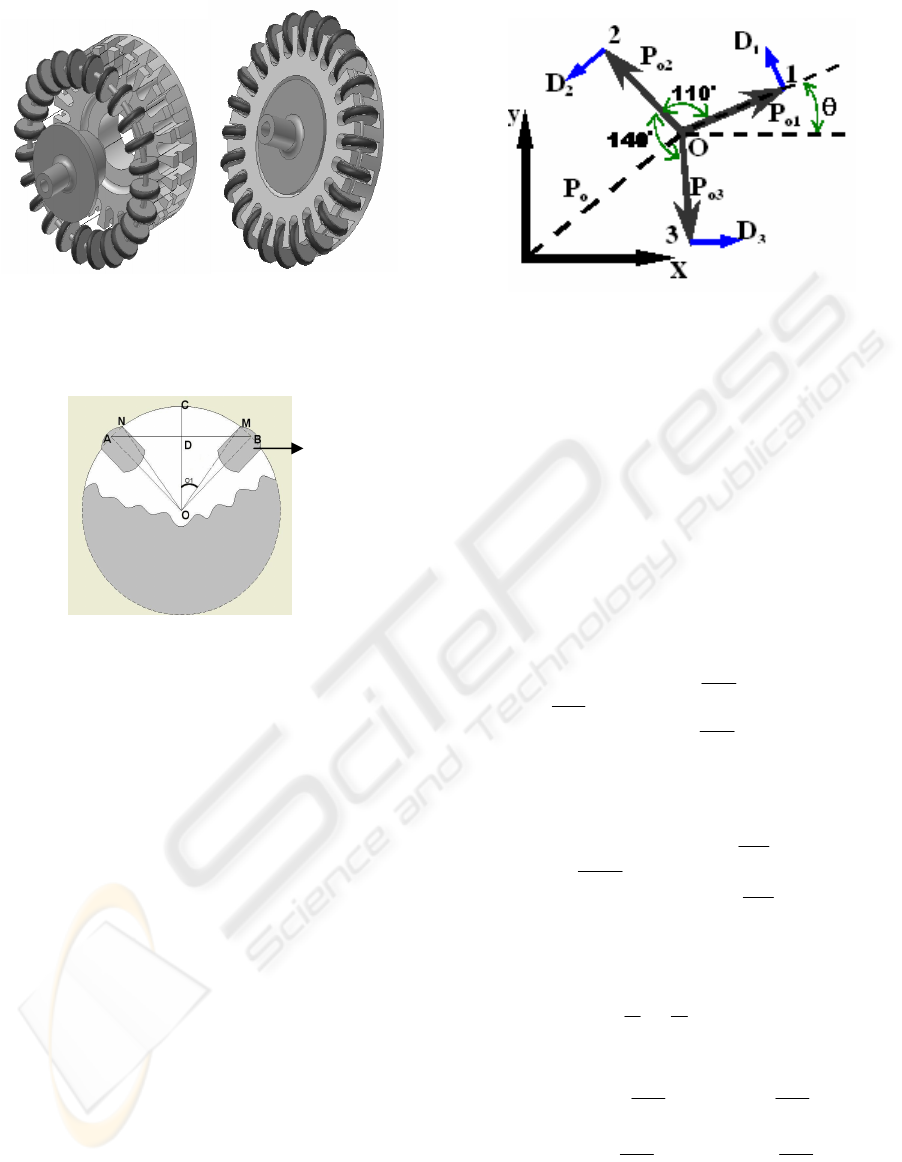
1994) (Diegel et al., 2002). In order to decrease the

vibration of the platform, the number of little rollers

was increased from 12 per wheel, which was used in

the previous design to 22 with the constant diameter

(Fig. 3). The run-out is decreased nearly 0.08-

0.1mm.It’s where the previous run out was 1mm. An

equation was derived for determining the run out,

namely to find how much a given wheel design will

bounce up and down as it rotates (run-out). The

derivation is relatively straightforward procedure by

using trigonometry, and the resulting formula is

shown below in which n is the number of the rollers

and R is radius of the wheel (Fig. 4).

(1)

BOMBOCo

∠

−

∠

1 (2)

(3)

(4)

(5)

Figure 2: RoboPersia

Figure 1: Complete RoboPersia System

Global

Vision

Decision

Making

Role Laye

Behavior

Layer

Control

Layer

Onboard

Controller

Actuato

Robo

Off Field PC

Camera

)1cos1( oRODOCoutRun

Max

−=−=−

)

BOC

=∠

BOMBOMR

2* =∠⇒=∠

)

O −=∠∴

CONTROL OF AN ASYMMETRICAL OMNI DIRECTIONAL MOBILE ROBOT

121

⎥

⎦

⎤

⎢

⎣

⎡

3 ROBOT KINEMATIC

Omni directional robots usually use special wheels,

which were described in the preceding section. The

body of each wheel is connected to the DC motor

shaft. Therefore, a robot with three omni directional

wheels can equilibrate on plane easily and follow

any trajectory. Our robot structure includes three

special omni-directional wheels for the motion

system as shown in Fig.3.

3.1 Kinematics Modeling

Using omni directional wheels, the schematic view

of robot kinematics can be shown in Fig. 5 (Kalmar-

Nagy, T., 1998), where O is the robot center of

mass, Po is defined as the vector connecting O to the

origin and D is the drive direction vector of each

wheel and θ is the angle of counter clockwise

rotation. Unitary rotation matrix, [R (

)] is defined

as:

(6)

The position vectors {P

},…,{P

}with respect to

the local coordinates centered at the robot center of

mass are given as:

(7)

(8)

(9)

Where, L is the distance of wheels from the robot

canter of mass (O).

(10)

(11)

Figure 3: The explosive view of new omni

directional wheel and Omni directional Wheel

()

[]

⎟

⎠

⎞

−

⎜

⎝

⎛

cos

sin

cos

∠

110,

21 oo

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

)

sin(

)

cos(

π11

1o2

PRP

−

∠

110,

31 oo

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−

1o3

Sin

Cos

PRP

oii

PRD

⎟

⎠

⎞

⎜

⎝

⎛

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

−

⎥

⎦

⎤

⎢

⎣

⎡

)

cos(

)

sin(

)

cos(

)

sin(

321

DDD

Rolle

Figure 4: Schematic of Omni directional.

Figure 5: Omnidirectional Robot Model, Top View.

ICINCO 2005 - ROBOTICS AND AUTOMATION

122

⎟

⎠

⎞

⎜

⎝

⎛

+−+

−−−−

−

∧

)

cos()

sin(

)

cos()

sin(

cossin

)(

θθ

3.2 Equation of motion and

velocities

Using the above notations, the wheel position and

velocity vectors can be expressed using rotation

matrix [R (

)] as:

()

ioi

=+rPR P

(12)

()

ioi

•

=+vPRP

(13)

The vector P

=(x y)

is the position of the center of

mass with respect to Cartesian coordinates. The

individual wheel velocities are

(14)

Substituting equation (13) into equation (14) results

in:

(15)

Note that the second term in the right hand side is

the tangential velocity of the wheel. This tangential

velocity could be also written as:

(16)

From the kinematics model of the robot, it is clear

that the wheel velocity is a function of linear and

angular velocities of robot center of mass, i.e.:

(17)

4 DYNAMIC EQUATIONS

Linear and angular momentum balance can be

written as;

(18)

(19)

Where

f is the magnitude of the force produced by

the ith motor, m is the mass of the robot and J is its

moment of inertia.

f =αU −βv (20)

Where

f is the magnitude of the force generated by

a wheel attached to the motor, and v (m/s) is the

velocity of the wheel. The constants α (N/V) and β

(kg/s) can readily be determined from experiment or

from motor catalogue.

Substituting equation (20) into equation (18) and

(19) yields:

(21)

(22)

This system of differential equations can be written

in the following form (Kalmár-Nagy et al., 2004):

(23)

With

(24)

And

(25)

So that the non-dimensional equations of motion

become(Kalmár-Nagy et al., 2004):

(26)

Where q(θ, t) is the control action(Kalmár-Nagy et

al., 2004):

q(θ, t) = P(θ)U(t) (27)

()

)]([

DRv

θυ

oii

DRRPDRP

)()()(

θθθυ

⋅

L DRRP )()(

θθθ

⋅⋅

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

+−+

−−−−

−

⎟

⎠

⎞

⎜

⎝

⎛

⋅

θθ

)

cos()

sin(

)

cos()

sin(

cossin

⋅⋅

∑

)( PDR mf

∑

⋅⋅

JfL

∑

=−

)()(

iii

mvU PDR

θβα

∑

=−

)(

JvUL

θβα

⎟

⎠

⎞

⎜

⎝

⎛

−=

⎟

⎠

⎞

⎜

⎝

⎛

∧

)()(

θα

⎟

⎠

⎞

⎜

⎝

⎛

)(

),(

θθ

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

CONTROL OF AN ASYMMETRICAL OMNI DIRECTIONAL MOBILE ROBOT

123

5 POSITION CONTROL AND

IMPLEMENTATION

In order to control the position and head angle of

robot a PD controller is employed. Mathematically a

PD controller can be expressed as

(28)

By increasing K

the rise time becomes faster, but on

the other hand the overshoot increases too, which is

undesired. Furthermore the stability gets worse.

Derivative control improves system performance in

two ways. Firstly, it adds positive phase angles to

increase the open-loop frequency response so as to

improve system stability and to increase close-loop

system bandwidth to increase the speed of response.

Secondly, it provides braking when the response is

getting closing to the new set point. This braking

action not only helps to reduce overshoot but also

tends to reduce steady-state error. Influence of

derivative control on the system is proportional to

, but increasing derivative feedback will slow the

system response and magnify any noise that may be

present. It is important to note that derivative control

has no influence on the accuracy of the system, but

just on the response time.

A problem that can occur with derivative control is

that in a real control system, the set point is usually

stepped up or down in discrete steps. A step change

has an infinitely positive slope, which will saturate

the derivative function. A solution to this problem is

to base the derivative control on the feedback signal

alone instead of the error because the controlled

variable can never actually change instantaneously,

even if the set point does. The effect of proportional

and derivative action is summarized in table 1.

Table 1: Controller properties

Action Rise

Time

Overshoot Stability

Increasing K

Faster Increases Gets

worse

Increasing K

Slower Decreases Improves

A digital controller is used for our purpose. For

digital filter differentiation of a function e(t) the

following technique is used. The slope of e (t) at the

t = kT is approximated to be slope of the straight line

connecting e[(k-1)T] with e(kT). Numerical

derivative of e (t) at t=kT can be written as

(29)

The z-transform of this equation yields

(30)

So the digital PD controller can be written as

(31)

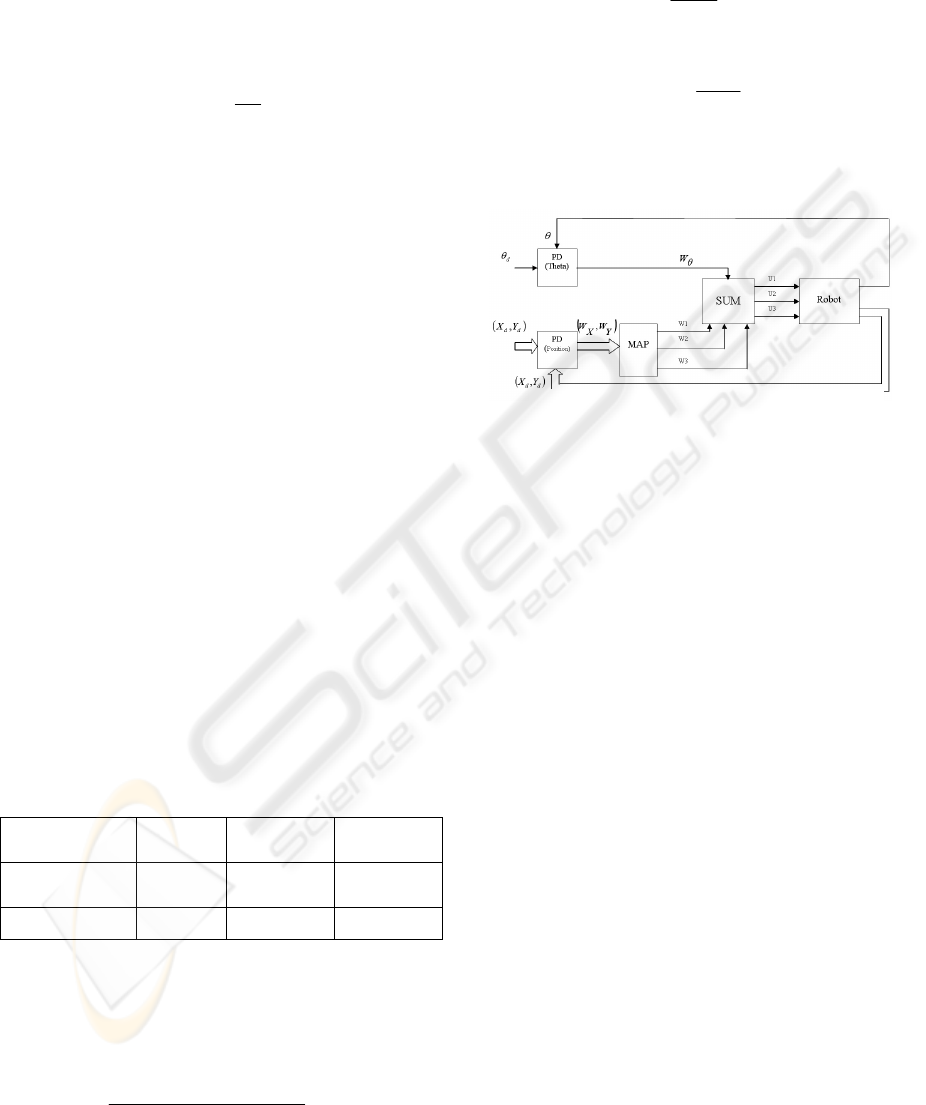
We use this equation to implement the controller. As

depicted in Fig.6, the position and the angle of the

robot is obtained by using a camera.

These measurements are compared with the desired

set-point values and the calculated errors. The

camera also gives the derivative of output values.

The error in position is fed to a digital PD (position

PD). Position PD output is applied to a limiter and

then mapped to direction of each wheel by an

appropriate function block (W1, W2, W3). Error in

robot angle is fed to another PD (head angle

PD).Head angle PD output (W

) is limited and then

added to the outputs of mapping block.

(32)

These signals determine the duty cycle of each robot

motor.

To tune the PDs, the following procedure is pursued.

The derivative action removed by setting K

=0, the

gain K

is tuned to give the desired response and K

is adjusted to damp the overshoot. The above steps

are repeated until an acceptable response is

achieved.

To demonstrate the computational efficiency and

robustness of the algorithm, simulations were

performed (with m=3kg, j=0.014 Kgm

, L=0.07m).

Position and velocity of the vehicle are assumed to

be measured 50 times per second. The inputs to the

algorithm are initial and desired positions and head

angle.

TeKK

)(

−

⎥

⎦

⎤

⎢

⎣

⎡

−

KKK

⎪

⎩

⎪

⎨

⎧

WWU

TkekTe

])1[()( −−

Figure 6: Control Diagram

ICINCO 2005 - ROBOTICS AND AUTOMATION

124

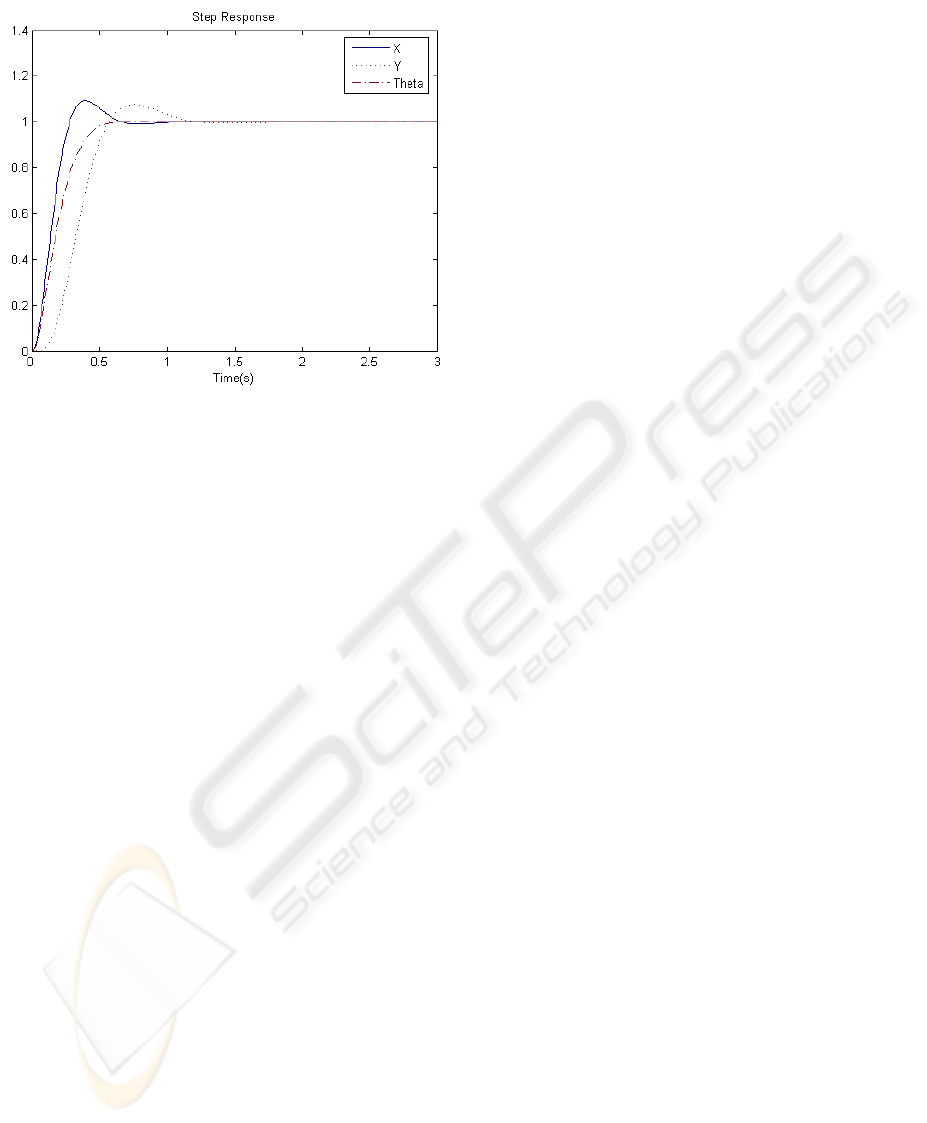
The results are shown in Fig. 7.As depicted, the

robots head angle overshoot is smaller than X

overshoot and y overshoot.

6 CONCLUSIONS

Wheeled mobile robots (WMRs) are increasingly

present in industrial and service robotics,

particularly when flexible motion capabilities are

required on reasonably smooth ground and surface

(Schraft et al., 1998). Several mobility

configurations (wheel number and type, their

location and actuation, single or multi-body

structure) can be found in the applications (Jones et

al., 1993), which can be lead to designing and

implementing an asymmetric robot.

This paper has presented a control model for a

specific kind of asymmetric omnidirectional

wheeled mobile robot. During initial modelling and

experimental works, it was supposed that

asymmetric feature could be a limitation for robot to

meet the requirements. While this is true, it was

however learned that if we derive proper control

model for robot we can overcome this limitation to

some extent. Since our objective was to model the

control of a specific kind of an asymmetric

omnidirectional wheeled mobile robot, this paper did

not develop a method for a large variety of

asymmetric robots. A control method that depends

on the angles between robot wheels, and includes

motion and velocity equations are supposed to be

developed in the future studies as extension of this

work.

REFERENCES

Tamás Kalmár-Nagy, Raffaello D’Andrea ,Pritam

Ganguly 2004. “Near-optimal dynamic trajectory

generation and control of an omnidirectional vehicle”.

Robotics and Autonomous Systems 46 (2004) 47–64

M. Veloso, E. Pagello, H. Kitano (Eds.), RoboCup-99:

Robot Soccer World Cup III, Lecture Notes in

Computer Science, 1856 Springer,New York, 2000

H. Kitano, J. Siekmann, J.G. Garbonell (Eds.), RoboCup-

97: Robot Soccer World Cup I, Vol. 139, Lecture

Notes in Computer Science 1395, Springer, New

York, 1998.

Robert Holmberg_ and Oussama Khatib,” Development of

a Holonomic Mobile Robot for Mobile Manipulation

Tasks”. FSR’99 International Conference on Field and

Service Robotics, Pittsburgh, PA, Aug. 1999

M. Jung, H. Shim, H. Kim, J. Kim, The miniature omni-

directional mobile robot OmniKity-I (OK-I),

Proceedings of the InternationalConference on

Robotics and Automation 4 (1999) 2686–2691.

K.L. Moore, N.S. Flann, Hierarchial task decomposition

approach to path planning and control for an omni-

directional autonomous mobile robot, Proceedings of

the International Symposium on Intelligent

Control/Intelligent Systems and Semiotics (1999)

302–307.

Keigo Watanabe, 1998,"Control of an Omnidirectional

Mobile Robot", 1998 Second International Conference

on Knowledge Based Intelligent Electronic System,

Adelaide Australia

Robert L. Williams, II, Member, IEEE, Brian E. Carter,

Paolo Gallina, and Giulio Rosati. Dynamic Model

With Slip for Wheeled Omnidirectional Robots. IEEE

Transactions On Robotics and Automation, VOL. 18,

NO. 3, JUNE 2002.

Francois G. Pin, Stephan M.Killough,1994."A New

Family of Omnidirectional and Holonomic Wheeled

Platforms for Mobile Robots," IEEE Trans. On

Robotics and Automation, vol 10,no.4,pp.480-

489,1994

Olaf Diegel, Aparna Badve, Glen Bright, Johan Potgieter,

Sylvester Tlale,"Improved Mecanum Wheel Design

for Omni-directional Robots",Proc. 2002 Australasian

Conference on Robotics and Automation Auckland,

November 2002.

Schraft R D, Schmierer G 1998 Serviceroboter . Springer,

Berlin

Jones J L, Flynn A M 1993 Mobile Robots: Inspiration to

Implementation. A K Petters,Wellesly, MA

)1,1,1,0

( rad

XYX ==

===

Figure 7: Step Response

CONTROL OF AN ASYMMETRICAL OMNI DIRECTIONAL MOBILE ROBOT

125