MULTIOBJECTIVE OPTIMAL DESIGN OF STRUCTURE AND

CONTROL OF A CONTINUOUSLY VARIABLE TRANSMISSION

Jaime Alvarez-Gallegos, Carlos A. Cruz-Villar

CINVESTAV-IPN. Electrical Engineering Department.

Av. IPN 2508 Col. San Pedro Zacatenco. Apdo Post. 14 740 Mexico D.F.

Edgar A. Portilla-Flores

Universidad Autonoma de Tlaxcala. Engineering and Technology Department

Calz. Apizaquito s/n Km. 15, 90300 Apizaco Tlax. Mexico

Keywords:

Mechatronic system, parametric optimal design, continuously variable transmission.

Abstract:

An approach to solve the mechatronic design problem is to formulate the problem as a multiobjective dynamic

optimization problem (MDOP), where kinematic and dynamic models of the mechanical structure and the

dynamic model of the controller are considered besides a set of constraints and a performance criteria. This

design methodology can provide a set of optimal mechanical and controller parameters so that the desired

dynamic behavior and the performance criteria are satisﬁed. In this paper a MDOP is proposed and applied to a

continuously variable transmission (CVT). Performance criteria are the mechanical efﬁciency and the minimal

controller energy. The goal attainment method and a sequential approach are used to solve the MDOP.

1 INTRODUCTION

Optimization arises by the necessity to design or to

improve systems according to the requirement un-

der which systems operate. There are several crite-

ria that can help to quantify the system performance;

however, these criteria are often in conﬂict since fre-

quently the structural objectives of design require

hard conditions for the controller. Therefore the de-

sign problem is usually considered as a multiobjec-

tive design problem in order to obtain better systems.

Recent research in the area of mechatronic systems

exposes the need of a concurrent design methodol-

ogy for mechatronic systems. This methodology must

produce mechanical, electronical and control ﬂexibil-

ity for the designed system (Zhang et al., 1999), (van

Brussel et al., 2001).

In (Li et al., 2001) a concurrent method for mecha-

tronic systems design is proposed. There, a simple

dynamic model of the mechanical structure is ob-

tained. The dynamic model obtained allows an easier

controller design which improves the dynamic perfor-

mance. However, this concurrent design concept is

based on an iterative process. This method obtains the

mechanical structure in a ﬁrst step and the controller

design in a second step, if the resulting controller de-

sign is very difﬁcult to implement, the ﬁrst step must

be done again.

The main contribution of this paper is to develop

and apply an integral methodology to formulate the

system design problem in the dynamic optimization

framework. In order to do this, the parametric optimal

design of a pinion-rack continuously variable trans-

mission (CVT) is stated as a multiobjective dynamic

optimization problem (MDOP), where both the kine-

matic and dynamic models of the mechanical struc-

ture and the dynamic model of the controllers are

jointly considered besides system performance crite-

ria. The methodology allows us to obtain a set of opti-

mal mechanical and controller parameters in only one

step, which can produce a simple system reconﬁgura-

tion.

In the multiobjective optimization framework, a

classical approach is to reduce the original problem

into an equivalent single objective problem using a

weighted sum of the original objectives. In most of

the cases, this single objective problem will be eas-

ier to solve than the original multiobjective problem.

However, the weakness of the weighted method is that

not all of the non dominated solutions can be found

unless the problem is convex (Osyczka, 1984).

On the other hand, in spite of the development of

many control strategies in the last decades, the pro-

portional, integral and derivative (PID) controller re-

mains as the most popular approach for industrial

processes control due to the adequate performance in

most of such applications. Many PID design tech-

niques have been developed; these provide a sim-

154

Alvarez-Gallegos J., A. Cruz-Villar C. and A. Portilla-Flores E. (2005).

MULTIOBJECTIVE OPTIMAL DESIGN OF STRUCTURE AND CONTROL OF A CONTINUOUSLY VARIABLE TRANSMISSION.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics, pages 154-160

DOI: 10.5220/0001185001540160

 SciTePress

ple tuning process to determinate the PID controller

gains. However, these do not provide a good control

performance in all cases.

A MDOP can be solved by converting it into a non-

linear programming (NLP) problem (Kraft, 1985),

(Goh and Teo, 1988) and using the Goal Attainment

method (Liu et al., 2003) for the resulting problem.

Two transcription methods exist for the MDOP prob-

lem: the sequential and the simultaneous methods

(Betts, 2001). In the sequential method, only the

control variables are discretized; this method is also

known as the control vector parameterization. In the

simultaneous method the state and control variables

are discretized resulting in a large-scale NLP problem

which usually requires special solution strategies.

Current research efforts in the ﬁeld of power trans-

mission of rotational propulsion systems, are dedi-

cated to obtain low energy consumption with high

mechanical efﬁciency. An alternative solution to this

problem is the so called continuously variable trans-

mission (CVT), whose transmission ratio can be con-

tinuously changed in an established range. There are

many CVT’s conﬁgurations built in industrial sys-

tems, especially in the automotive industry due to the

requirements to increase the fuel economy without

decreasing the system performance. The mechani-

cal development of CVT’s is well known and there

is little to modify regarding its basic operation prin-

ciples. However, research efforts go on with the con-

troller design and the CVT instrumentation side. Dif-

ferent CVT’s types have been used in different in-

dustrial applications; the Van Doorne belt or V-belt

CVT is the most studied mechanism (Shafai et al.,

1995), (Setlur et al., 2003). This CVT is built with

two variable radii pulleys and a chain or metal-rubber

belt. Due to its friction-drive operation principle, the

speed and torque losses of rubber V-belt are a dis-

advantage. The Toroidal Traction-drive CVT uses

the high shear strength of viscous ﬂuids to transmit

torque between an input torus and an output torus.

However, the special ﬂuid characteristic used in this

CVT becomes the manufacturing process expensive.

A pinion-rack CVT which is a traction-drive mecha-

nism is presented in (De-Silva et al., 1994), this CVT

is built-in with conventional mechanical elements as

a gear pinion, one cam and two pair of racks. The

conventional CVT manufacture is an advantage over

other existing CVT’s.

In this paper the parametric optimal design of a

pinion-rack CVT is stated as a MDOP to obtain a set

of optimal mechanical and controller parameters of

the CVT and, a higher mechanical efﬁciency and a

minimal energy controller. This paper is organized

as follows: The description and the dynamic CVT

model are presented in Section 2. The design vari-

ables, performance criteria and constraints to be used

in the parametric CVT design are established in Sec-

tion 3. Section 4 presents some optimization results

and discuss them. Section 5 presents some conclu-

sions and future work.

2 DESCRIPTION AND DYNAMIC

CVT MODEL

In order to apply the design methodology proposed

in this paper, the pinion-rack CVT presented in (De-

Silva et al., 1994) is used. The pinion-rack CVT,

changes its transmission ratio when the distance be-

tween the input and output rotation axes is changed.

This distance is called “offset” and will be denoted by

“e”. This CVT is built-in with conventional mechan-

ical elements as a gear pinion, one cam and two pair

of racks. Inside the CVT an offset mechanism is inte-

grated. This mechanism is built-in with a lead screw

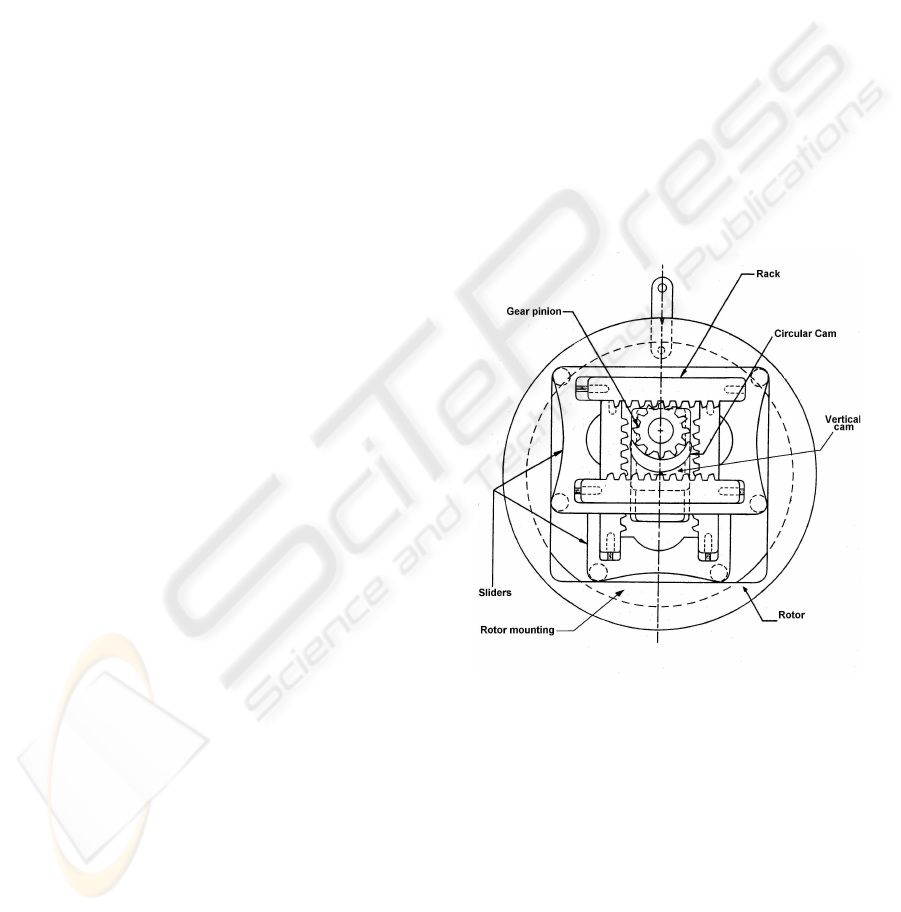
attached by a nut to the vertical transport cam. Fig. 1

depicts the main mechanical CVT components.

Figure 1: Main CVT mechanical components

The dynamic model of a pinion-rack CVT is pre-

sented in (Alvarez-Gallegos et al., 2005). Ordinary

differential equations (1), (2) and (3) describe the

CVT dynamic behavior. In equation (1): T

is the

input torque , J

is the mass moment of inertia of the

gear pinion, b

is the input shaft coefﬁcient viscous

damping, r is the gear pinion pitch circle radius, T

is the CVT load torque, J

is the mass moment of

inertia of the rotor, R is the planetary gear pitch cir-

cle radius, b

is the output shaft coefﬁcient viscous

damping and θ is the angular displacement of the ro-

tor. In equations (2) and (3): L, R

, K

and n

represent the armature circuit inductance, the circuit

MULTIOBJECTIVE OPTIMAL DESIGN OF STRUCTURE AND CONTROL OF A CONTINUOUSLY VARIABLE

TRANSMISSION

155

resistance, the back electro-motive force constant, the

motor torque constant and the gearbox gear ratio of

the DC motor, respectively. Parameters r

, λ

, b

and

denote the pitch radius, the lead angle, the viscous

damping coefﬁcient of the lead screw and the viscous

damping coefﬁcient of the offset mechanism, respec-

tively. The control signal u (t) is the input voltage to

the DC motor. J

= J

+ Mr

+ n

is the

equivalent mass moment of inertia, J

is the mass

moment of inertia of the DC motor shaft, J

is the

mass moment of inertia of the DC motor gearbox and

d = r

tan λ

, is a lead screw function. Moreover,

(t) =

arctan



tan



2Ωt −



is the rack angle

meshing. The combined mass to be translated is de-

noted by M and P =

tan φ cos θ

is the loading

on the gear pinion teeth, where φ is the pressure angle.





− T

+ J





θ (1)

−







sin θ





+ b









˙e

cos θ



+ R

i = u (t) −





˙e (2)





i −P =



M +



¨e +





˙e (3)

3 PARAMETRIC OPTIMAL

DESIGN

In order to apply the design methodology proposed in

this work, two criteria are considered. The ﬁrst cri-

terion is the mechanical CVT efﬁciency which con-

siders mechanical parameters and the second criterion

is the minimal energy controller which considers the

controller gains and the dynamic system behavior.

3.1 Performance criteria and

objective functions

The performance of a system is measured by sev-

eral criteria, one of the most used criteria is the sys-

tem efﬁciency because it reﬂects the energy loss. In

this work, the mechanical efﬁciency criterion of the

gear systems is used in the optimization methodology.

This is because the racks and the gear pinion are the

principal CVT mechanical elements .

The mathematical equation (4) for mechanical ef-

ﬁciency presented in (Spotts, 1964) is used in this

work, where µ, N

, N

, m, r

and r

represent the

coefﬁcient of sliding friction, the gear pinion teeth

number, the spur gear teeth number, the gear module,

the pitch pinion radius and the pitch spur gear radius

respectively.

η = 1 − πµ





= 1 −

πµ





(4)

In (Alvarez-Gallegos et al., 2005) the speed ratio

equation is stated by (5), where ω is the input angular

speed and Ω is the output angular speed of the CVT.

Ω

= 1 +

cos θ

(5)

Considering r

≡ r and r

≡ R, the CVT mechan-

ical efﬁciency is given by (6).

η(t) = 1 −

πµ

1 +

e cos θ

(6)

In order to maximize the mechanical CVT efﬁ-

ciency, F (·) given by (7) must be minimized.

F (·) =

1 +

e cos θ

(7)

Equation (7) can be written as (8) which is used to

state the design problem objective function.

F (·) =



2r + e cos θ

r + e cos θ



(8)

The second objective function is stated to obtain the

minimal controller energy.

3.2 Constraint functions

The design constraints for the CVT optimization

problem are proposed according to geometric and

strength conditions for the gear pinion of the CVT.

To prevent fracture of the annular portion between

the axe bore and the teeth root on the gear pinion,

the pitch circle diameter of the pinion gear must be

greater than the bore diameter by at least 2.5 times

the module (Papalambros and Wilde, 2000). Then, in

order to avoid fracture, the constraint g

must be im-

posed. To achieve a load uniform distribution on the

teeth, the face width must be 6 to 12 times the value of

the module (Norton, 1996), this is ensured with con-

straints g

and g

. To maintain the CVT transmission

ratio in the range [2r, 5r] constraints g

, g

are im-

posed. Constraint g

ensures a teeth number of the

gear pinion equal or greater than 12 (Norton, 1996). A

practical constraint requires that the gear pinion face

width must be equal or greater than 20mm, in order

to ensure that, constraint g

is imposed. To constraint

ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

156

the distance between the corner edge in the rotor and

the edge rotor, constraint g

is imposed. Finally to

ensure a practical design for the pinion gear, the pitch

circle radius must be equal or greater than 25.4mm,

then constraint g

is imposed.

On the other hand, it can be observed that J

, J

are

parameters which are function of the CVT geometry.

For this mechanical elements the mass moments of

inertia are deﬁned by

ρπm

(N + 2)

h (9)

= ρh



πr

−

max

+ mN )

−

πr



(10)

where ρ, m, N, h, e

max

, r

and r

are the mater-

ial density, the module, the teeth number of the gear

pinion, the face width, the highest offset distance be-

tween axes, the rotor radius and the bearing radius,

respectively.

3.3 Design variables

In order to propose a parameter vector for the para-

metric optimal CVT design, the standard nomencla-

ture for a gear tooth is used.

Equation (11) states a parameter called module m

for metric gears, where d is the pitch diameter and N

is the teeth number.

m =

(11)

The face width h, which is the distance measured

along the axis of the gear and the highest offset dis-

tance between axes e

max

are parameters which deﬁne

the CVT size.

The vector p

is proposed in order to carry out the

parametric optimal CVT design.

= [p

, p

]

= [N, m, h, e

max

, K

]

(12)

3.4 Optimization problem

In order to obtain the mechanical CVT parameter op-

timal values, we propose a multiobjective dynamic

optimization problem given by equations (13) to (21).

As the objective functions must be normalized to

the same scale, the corresponding factors W =

[0.4397, 1126.71]

were obtained using the algorithm

of the subsection 3.5 by minimizing each objective

function subject to constraints given by equations (14)

to (21).

min

p∈R

F (x, p, t) = [F

, F

]

(13)

where





+ x

cos θ

+ x

cos θ



subject to

˙x

sin θ

− T

−

+ b

+ J

cos θ

+ J

˙x

u (t) − (

− Rx

(14)

˙x

= x

˙x

(

− (b

−

tan φ cos θ

M +

u(t) = −p

ref

− x

) − p

ref

− x

)dt (15)

ρπp

+ 2)

(16)

ρp



3πr

−

+ p

)

− πr



(17)

A = 1 +

cos θ

(18)

d = r

tan λ

(19)

arctan

tan



t −

i

(20)

= 0.01 − p

− 2.5) ≤ 0

= 6 −

≤ 0

− 12 ≤ 0

= p

− p

≤ 0

= p

−

≤ 0 (21)

= 12 − p

≤ 0

= 0.020 − p

≤ 0

= 0.020 −

−

√

2(p

+ p

)

≤ 0

= 0.0254 − p

≤ 0

MULTIOBJECTIVE OPTIMAL DESIGN OF STRUCTURE AND CONTROL OF A CONTINUOUSLY VARIABLE

TRANSMISSION

157

3.5 Solution algorithm

The resulting problem stated by (22)-(25) is solved

using the goal attainment method, which is described

below.

Lets consider the problem of minimizing (22)

F (x, θ, t) = [F

, F

]

(22)

(x, θ, t)dt i = 1, 2

under θ and subject to:

˙x = f(x, θ, t) (23)

g(x, θ, t) ≤ 0 (24)

h(x, θ, t) = 0 (25)

x(0) = x

θ ∈ R

The gradient calculation (26) is obtained using the

sensitivity equations stated by (27).

∂F

∂θ



∂L

∂x

∂θ

(t) +

∂L

∂θ



dt (26)

∂ ˙x

∂θ

∂f

∂x

∂θ

∂f

∂θ

(27)

Formulating the MDOP in the goal attainment

framework, the resulting problem is stated in equa-

tions (28) and (29) subject to equations (23) to (25),

where ω = [w

, w

]

is the scattering vector (Osy-

czka, 1984), F

= [1, 1]

are the desired goals for

each objective function and F

(θ) and F

(θ) are the

evaluated function.

min

θ,λ

G (θ, λ)

∆

= λ (28)

subject to:

g(θ) ≤ 0

(θ) = F

(θ) − ω

λ − F

≤ 0 (29)

(θ) = F

(θ) − ω

λ − F

≤ 0

A vector θ

which contains the current parameter

values is proposed and the NLP problem given by

equations (30) and (31) is obtained, where B

is the

BFGS updated positive deﬁnite approximation of the

Hessian matrix, and the gradient calculation is ob-

tained using sensitivity equations. Hence, if γ

solves

the subproblem given by (30) and (31) and γ

= 0,

then the parameter vector θ

is an original problem

optimal solution. Otherwise, we set θ

i+1

= θ

+ γ

and with this new vector the process is done again.

min

γ∈R

j+1

QP (θ

) = G





+ ∇G





γ +

(30)

subject to

g(θ

) + ∇g





γ ≤ 0

(θ

) + ∇g





γ ≤ 0 (31)

(θ

) + ∇g





γ ≤ 0

4 OPTIMIZATION RESULTS

This section presents some optimization results when

the solution algorithm of section 3.5 is applied to

solve the problem stated in section 3.4 under the fol-

lowing conditions. The system parameters used in nu-

merical simulations were: b

= 1.1N ms/rad, b

0.05Nms/rad, r = 0.0254m, T

= 8.789Nm,

= 0Nm, λ

= 5.4271, φ = 20, M = 10Kg,

= 4.188E − 03m, K

= 63.92E − 03Nm/A,

= 63.92E − 03V s/rad, R = 10Ω, L =

0.01061H, b

= 0.015Ns/m, b

= 0.025Nms/rad

and n = ((22 ∗ 40 ∗ 33)/(9 ∗ 8 ∗ 9)). The initial con-

ditions vector was [x

(0), x

(0)]

[7.5, 0, 0, 0]

. In order to show the CVT dynamic per-

formance, for all simulations the output reference was

considered as x

ref

= 7.5 for 0 ≤ t ≤ 2; x

ref

= 7.2

for t > 2.

The goal attainment method requires the goal for

each one of the objective functions. The goal for F

was obtained by minimizing this function subject to

equations (14)-(21). The optimal solution vector p

is shown in table 1. The goal for F

was obtained

by minimizing this function subject to equations (14)-

(21). The optimal solution vector p

for this problem

is also shown in table 1.

Varying the scattering vector can produce different

non dominated solutions. In table 1, two cases are

presented; p

∗

is obtained with ω = [0.5, 0.5]

, p

∗

obtained with ω = [0.3, 0.7]

Figures 2, 3 and 4 show the mechanical CVT efﬁ-

ciency, the control CVT input and the CVT output re-

spectively, with solutions vectors p

∗

, p

and p

. The

solution p

∗

was selected because it has the same over

achievement of the proposed goal for each function.

Discussion

Solutions p

∗

and p

∗

in table 1, have an euclidean

norm closer to that one associated to the proposed de-

sired vector of goals. These results are according with

the structure and control integration approach consid-

ered in this work.

It can be observed in ﬁgure (2), that the optimal

multiobjective solution implies a low sensitivity of

the mechanical efﬁciency with respect to reference

ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

158

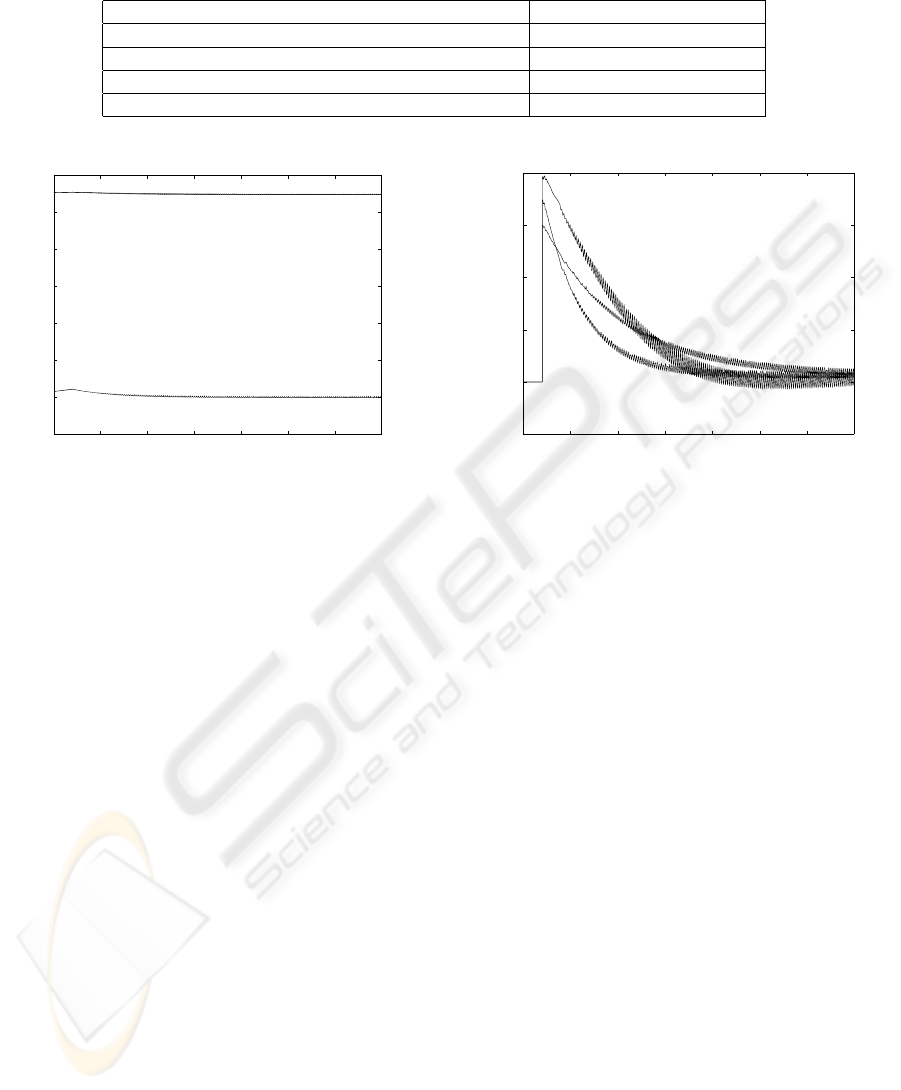
Table 1: MDOP solutions

∗

, m

∗

, h

∗

, e

∗

max

, K

∗

, K

∗

]

F (•) = [F

(•), F

(•)]

= [38.1838, 0.0017, 0.02, 0.0636, 10.000, 1.00] F (p

) = [1.0000, 3.1580]

= [12.0000, 0.0028, 0.02, 0.0880, 5.000, 0.01] F (p

) = [3.1999, 1.0000]

∗

= [33.6469, 0.0017, 0.02, 0.0631, 5.000, 0.01] F (p

∗

) = [1.2149, 1.2149]

∗

= [38.1800, 0.0017, 0.02, 0.0636, 5.001, 0.01] F (p

∗

) = [1.0786, 1.2730]

0 5 10 15 20 25 30 35

0.91

0.92

0.93

0.94

0.95

0.96

0.97

0.98

t [s]

Mechanical efficiency

Figure 2: Mechanical efﬁciency

changes. This is an advantage for CVT’s, because the

output speed requirements are usually changed.

In ﬁgure (3) it can be observed that the p

∗

vector

minimizes the initial overshoot of the control input.

This fact implies a lower mechanical system wear.

Figure (4) shows the output CVT behavior, it can be

observed that with the optimal multiobjective solution

a smoother convergence to the reference is obtained.

5 CONCLUSIONS

In this paper, we have developed a suitable parametric

optimal design methodology for mechatronic systems

where kinematic and dynamic behaviors are jointly

considered. This methodology was successfully ap-

plied to a traction-drive CVT. Results obtained lead

to a higher mechanical efﬁciency and to a minimal en-

ergy controller. The advantage of this design method-

ology is that the parametric optimal design can be

considered as a MDOP. Formulating it in the goal at-

tainment framework, new considerations for the op-

timization problem are applied to the objective func-

tions. This is a process which does not happen in a

weighted approach.

The slow CVT output convergence to the reference

shown in ﬁgure (4) is due to the small value of the lead

angle (λ

). Further work, will include this parameter

as an optimization variable.

0 5 10 15 20 25 30 35

−0.5

0.5

1.5

t [s]

Control u [V]

Figure 3: Control input

Further research includes the proposal of new de-

sign constraints. These constraints must consider

stress conditions and bounding of the state variables.

On the other hand, another objective function of the

overall mechanical efﬁciency of the CVT, includ-

ing the offset mechanism and lead screw constraints,

could be considered in the parametric optimal design.

These facts would improve the CVT response.

REFERENCES

Alvarez-Gallegos, J., Cruz-Villar, C., and Portilla-Flores,

E. (2005). Parametric optimal design of a pinion-

rack based continuously variable transmission. In

IEEE/ASME International Conference on Advanced

Intelligent Mechatronics (Accepted paper).

Betts, J. (2001). Practical Methods for Optimal Control

using Nonlinear Programming. SIAM, Philadelphia,

USA, 1st edition.

De-Silva, C., Schultz, M., and Dolejsi, E. (1994). Kine-

matic analysis and design of a continuously variable

transmission. In Mech. Mach. Theory, Vol 29, No. 1

pp. 149-167. PERGAMON Press.

Goh, C. and Teo, K. (1988). Control parametrization: a uni-

ﬁed approach to optimal control problems with gen-

eral constraints. In Automatica, Vol 24, No. 1 pp. 3-18.

Pergamon Journals Ltd.

Kraft, D. (1985). On converting optimal control problems

MULTIOBJECTIVE OPTIMAL DESIGN OF STRUCTURE AND CONTROL OF A CONTINUOUSLY VARIABLE

TRANSMISSION

159

into nonlinear programming problems. In Computa-

tional Mathematical Programming, NATO ASI Series

Vol F15, pp. 261-280. Springer-Verlag.

Li, Q., Zhang, W., and Chen, L. (2001). Design for control-a

concurrent engineering approach for mechatronic sys-

tems design. In Transactions on Mechatronics, Vol 6,

No. 2 pp. 161-168. IEEE/ASME.

Liu, G. P., Yang, J., and Whidborne, J. (2003). Multiobjec-

tive Optimisation and Control. Research Studies Press

LTD., Baldock, Hertfordshire, England, 1st edition.

Norton, R. (1996). Machine Design, An integrated ap-

proach. Prentice Hall Inc., Upper Saddle River, NJ

07458, 1st edition.

Osyczka, A. (1984). Multicriterion optimization in engi-

neering. John Wiley and Sons., 605 Third Avenue,

New York, N.Y. 10016, USA., 1st edition.

Papalambros, P. and Wilde, D. (2000). Principle of opti-

mal design. Modelling and computation. Cambridge

University Press, The Edinburg Building, Cambridge

CB2 2RU, UK, 1st edition.

Setlur, P., Wagner, J., Dawson, D., and Samuels, B. (2003).

Nonlinear control of a continuously variable transmis-

sion (cvt). In Transactions on Control Systems Tech-

nology, Vol 11, pp. 101-108. IEEE.

Shafai, E., Simons, M., Neff, U., and Geering, H. (1995).

Model of a continuously variable transmission. In

First IFAC Workshop on Advances in Automotive Con-

trol, pp. 575-593.

Spotts, M. (1964). Mechanical Design Analysis. Prentice

Hall Inc., Englewood Cliffs, N.J., 1st edition.

van Brussel, H., Sas, P., N

emeth, I., Fonseca, P. D., and

van den Braembussche, P. (2001). Towards a mecha-

tronic compiler. In Transactions on Mecatronics, Vol

6, No. 1 pp. 90-104. IEEE/ASME.

Zhang, W., Li, Q., and Guo, L. (1999). Integrated design

of a mechanical structure and control algorithm for a

programmable four-bar linkage. In Transactions on

Mechatronics, Vol 4, No. 4 pp. 354-362. IEEE/ASME.

0 5 10 15 20 25 30 35

7.15

7.2

7.25

7.3

7.35

7.4

7.45

7.5

7.55

7.6

t [s]

Output angular speed [rad/s]

Figure 4: Output CVT behavior

ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

160