
BIOPRODUCTS DRYING OPTIMAL CONTROL IN
OSCILLATING REGIMES
Renat Sadykov
Kazan State Architecture Building University, Zelenaya 1, Kazan, Russia
Dmitry Antropov
JSC “Etalon MCS”, Adoratskogo 2, Kazan, Russia
Rauf Kafiatullin
JSC “Kazanenergo” Tukaya162 ,Kazan, Russia
Keywords:
Drying, mathematical model, optimal control, automation.
Abstract: On the basis of the developed approaches and mathematical model (MM) of the bioactive products drying
block is carried out the optimization problem of the equipment choice and its operation modes in view of
deleted binary mixture an ethanol - water composition changes. The analysis of the problem with engaging
of the Pontryagin’s maximum principle has revealed optimal control structure. There is developed the
automated control system of drying installation with firmware, based on modern microprocessor technique.
The guidelines on an drying processes intensification, worked out on the basis of the internal and external
interconnected heatmasstransfer research, and the process optimal control considerably raise productivity of
drying aggregates, reduce fuel and power expenditures.
1 INTRODUCTION
Biotechnology is an effective production method of
bioactive products. Drying as a final stage of the
technological process plays an important role in the
production, since the thermal and mechanical effects
in the drying process affect the quality of the
products.
Let’s consider the drying process of irreplaceable
aminoacids (α –forms) originated in the
microbiology synthesis.
The experiments in (Yenikeev E.S., Ivanova
E.N.) have discovered that vacuum-conductive and
pseudo-liquefied drying methods don’t enable in all
cases to obtain the products of high quality as α-
aminoacids (especially treonin) have high inclination
to an agglomeration. There is the following
explanation of the agglomeration of particles in the
drying process. Binary liquid (ethanol-water 50 vol.
%) is moving out of the material being dried.
Ethanol as being more volatile component is moving
out more quickly and, therefore, an abundance of
water in the material is growing up.
As it is known from the technology of aminoacids
(Gracheva I.M., 1980) they are crystallized in
ethanol-water blend and are well dissolved in water.
Therefore crystal’s partial dilution and their
adhesion take place in the drying process.
It has been shown in (Sadykov R.A., 1988) that
the production problem of homogeneous dispersible
or powdery product might be solved by vacuum-
oscillating drying mode (Sadykov R.A., 1986,
Sadykov R.A., 1988). This process is frequentative
alternation of heating of the material in pseudo-
liquefied layer, pressure impulse drop with
subsequent vacuumization (material cooling by
pressure dumping in drying chamber) and layer
impulse jog by air supply. Material layer at jogging
strikes on special destroying elements is divided
finely and mixed up. Typical curves of the kinetic
and the termogram of the drying process based on
combined pressure drop and vacuum (CPDV) are
shown in fig.1. (U - liquid specific mole contention).
176
Sadykov R., Antropov D. and Kafiatullin R. (2005).
BIOPRODUCTS DRYING OPTIMAL CONTROL IN OSCILLATING REGIMES.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics, pages 176-181
DOI: 10.5220/0001183401760181
Copyright
c
SciTePress
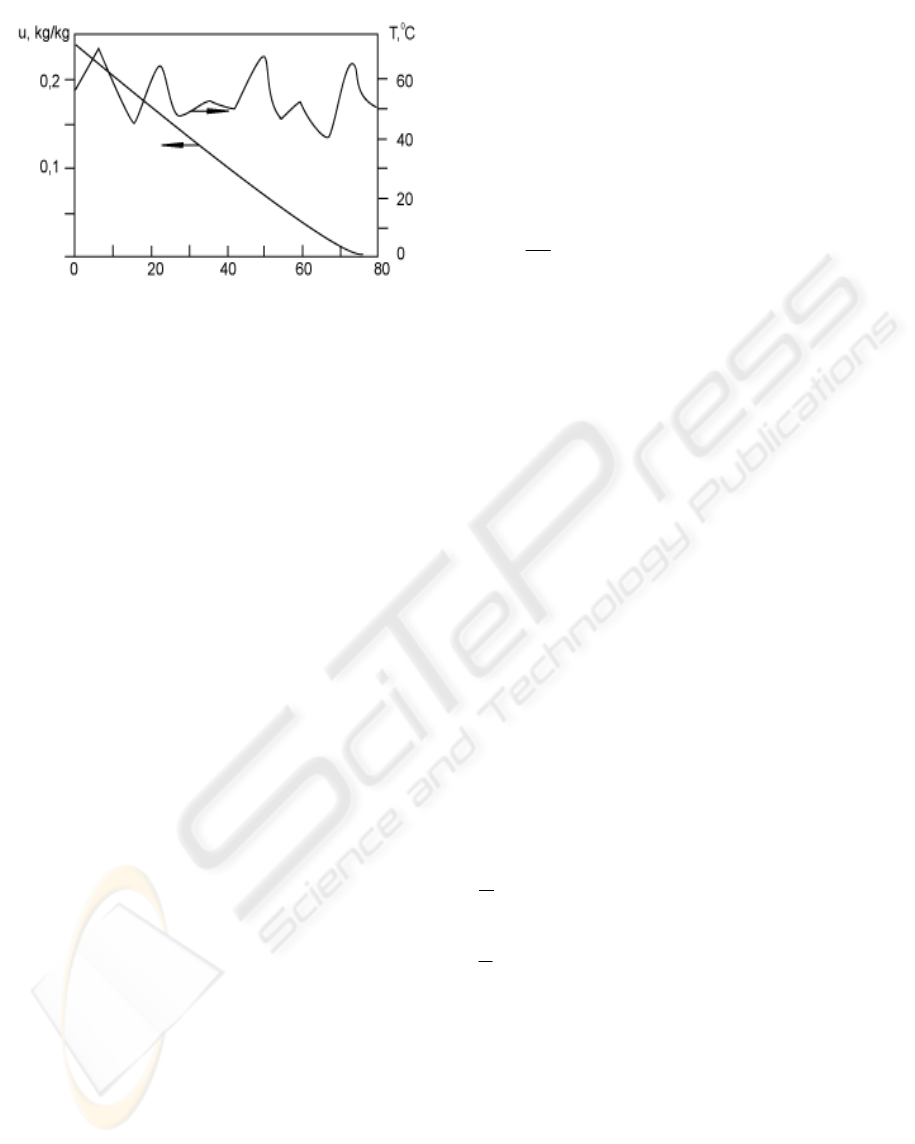
τ, min
Figure 1: Kinetic 1 and termogram 2 of L-treonin
(G=0,007 m3/s, Т
h
=86ºС, h=0,07 m, τ
h
=8 min, τ
v
=5
min)
To find out the dependence of τ
k
- CPDV drying
time aminoacids on some regime parameters it has
been carried out the complete four-factor experiment
(Ivanova E.N.). The following regressive formula
has been derived:
τ
k
= - 2007 + 8,616τ
h
+ 4,5τ
v
+ 88056G + 174,6h
+ 33,28τ
h
h – 0,0075τ
h
τ
v
– 782,76τ
h
G,
where τ
k
- kinetic time, s; τ
v
- vacuumization
time, s; G – heat carrier volume flow m
3
/s ; h – layer
thick, m; τ
h
- heating time, s. It is worth to note that
this formulation is reliable for some given regimes
of the process only. It can not be used for
formalization of the drying process in general and
for its optimization.
The full theory of the drying process for moving
off multicomponent (intersoluble partlysoluble and
interinsoluble) liquid systems (Sadykov R.A., 1989,
Sadykov R.A., 2004) is absent now and the
development of adequate mathematical models
(MM) of the process is quite actual. MM describes
moving kinetic of every component in binary liquid
blend (Sadykov R.A., 1985). The report is devoted
to an optimization of such MM.
2 DRYING PROCESS
OPTIMIZATION OF
IRREPLACEABLE
AMINOACIDS
During optimization of production process variants
of technical performance are compared among
themselves by reduced costs after CPDV
optimization regime in every variant (Golubev L.G.,
1978). The comparison was performed by criterion
minimization of the drying stage contribution to cost
price of product unit. It means profits maximization
in view of fixed productivity.
The problem of optimization CPDV regime is to
select M value and G(τ), Т
hc
(τ), z(τ) functions when
τ
∈
[0, τ
k
] and z=0 in vacuumization stage, z=1 in
heating.
00
0
1
({[ ()](1)()},
) athc Т VaIzGGTTzd
M
κ
τ
κ
τ
ββ β ββτ
++ − +− +
∫
=
(1)
М – dry aminoacid mole number; Т
hc
– heat carrier
temperature at a layer input;
Т
at
– ambient air
temperature;
0
β
- characterizes expenses
independent on regime;
a
β
- sterile air 1
3
m
cost
T
β
- cost of heating 1
3
m
air up to 1 K; V
β
- cost of
vacuumization pump work in unit time. It is
necessary to keep conditions which ensure product
none overheating, sufficiently low finite humidity,
pseudoliquified regime in heating and none
asportation aminoacids with heat carrier.
Т
at
≤ Т
h
≤ Т
h max
, Т≤Т
max
, U(τ
k
)≤U
k
,
M
min
≤M≤M
max,
G≤G
max
The detailed consideration (1) with taking into
account equations system of CPDV drying MM
(Sadykov et al., 1985) clarifies that
М=М
max
, G=
G
max
in optimal regime; to select Т
гр
(τ) and z(τ)
Pontryagin’s maximum principle is used (Pontryagin
et al., 1983).
The are set: state variables vector
),,,,(
43210
χχχχχχ
=
=(I(τ), U(τ), T(τ),
x(τ), р
c
(τ)), dual variables vector
),,,,(
43210
ξξξξξξ
=
,Pontryagin’s function
4
0
ii
i
H
ξχ
=
=
∑
&
&
and problem’s Hamiltonian
0;1
() { ()},
max
z
H
η
ττ
=
=
Th
∈
[T
at
,Т
m
],
BIOPRODUCTS DRYING OPTIMAL CONTROL IN OSCILLATING REGIMES
177

Т
h max,
T<T
max
T
m
= T≥T
max
where
Т
m
- heat carrier maximum temperature
providing accomplishment of condition :
Т<Т
max
+
2К (index h – means heating , v - vacuumization)
c
р
– specific mass heat of a heat carrier at a constant
pressure
hc
ρ
– heat carrier density at a heater input
State and dual variables must satisfy the equations:
(1 ) ,
hv
zz
χ
χχ
=+−
&& &
4
0
,
i
ii
i
i
χ
ξ
ξ
χ
=
∂
=−
∂
∑
&
&
0,4i =
(2)
and edge conditions:
τ
=0: χ
0
=0, χ
1
= U(0), χ
2
= T(0),
χ
3
= x(0), χ
4
= p
at
;
τ= τ
к
: χ
1
=U
к,
|ξ
0
| + |ξ
1
|=1, ξ
2
= ξ
3
= ξ
4
=η=0.
(3)
State variable р
с
is inserted with a view of obvious
separation of heat carrier’s pump-down stages and
vapour’s pump-down stage: during the
first stage
0xTU ===
&
&&
and during the second
stage are correct of MM equations (Sadykov et al.,
1985):
,U)xy(xU y
&
&
−=
where
y
y
– ethanol mole fraction in eliminated
vapour phase,
x – alcohol mole fraction
Dots mean time differentiation.
,
Mc)rc(V
)]T,x(p[Qc
U
µ+β−α
ρ
−=
&
;U
c
r
T
&&
=
where,
],)1(74,41)][()([
2
222111
xxTpTp
RTU
xy
−−−
−
=
µγµγα
,
T
]
dT
)T(plnd
)y1(
dT
)T(plnd
y[
RT
)T,x(p
2
2
1
1
ρ
−µ−+µ=β
.
RT
)T,x(pµ
=ρ
Q(p) – effective eviction speed
r – specific molar evaporation heat of a thin mixture
с – specific mole heat of a humid material at account
on a mole number of a dry material
µ
1
– alcohol molecular weight
µ
2
– aqua molecular weight
Then
p
c
(τ) must satisfy equations:
γ
1
– activity ratio of an alcohol fumes
γ
2
– activity ratio of an aqua fumes
Р
1
(τ) – alcohol fumes saturation pressure
Р
2
(τ) – aqua fumes saturation pressure
c
p - pressure in the drying chamber
),(
maxmax
max
max
2
h
h
h
Т
cG
UrM
T
K
TT
Т
phc
−−+
⋅
−
ρ
&
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
178

(4)
саtch ррp −=
&
(5)
Formulation (4) is relevant to the physics of process
and is derived from its MM.
Formulation (5) is supplied for substitution of an
intermittent growth (of the
р
с,
to the value of р
аt
) for
uninterrupted process while there is a material
jogging. The above make it possible to use the
theorem of Pontryagin with limits on the differential
features of
χ
&
.
The substitution is relevant because the value of
р
с
has no influence on a heating stage (it assumes that
р
с
is equal to an atmospheric pressure). Fast
approaching of the
р
с
to the р
аt
before
vacuumization is necessary.
Meanwhile due to (5) the
р
с
differs from the р
аt
in
a value less then 0,03% in 8 sec from the beginning
of the process. In (2) the
χ
&
is continuous by control
(Т
h
,z) and is continuously differential by
χ
all
over the entity of real physical limits of alternation
of
χ
except of hyper surface:
р
с
- р(х, Т)=0, (6)
where
χ
&
has ordinary discontinuity (Korn et al.,
1978). Though the left part of (6) is continuously
differential by
χ and this enables the continuity of
ξ
and Н by τ (Korn et al., 1978) on the segment [0,
τ
к
]. From the maximum’s principle it is following
that ξ
0
=const≤0. Thus
04i / =χ∂χ
∂
&
3,0=i
and
44,
c
c
p
p
ξ
ξ
∂
=−
∂
&
&
On account of the limitedness
c/c pp ∂∂
&
and the
stipulation ξ
4
(τ
к
)=0 enables ξ
4
(τ)=const=0.
Invariability of ξ
0
and ξ4 simplifies the problem.
While solving the boundary problem (2)-(3) with
every fixed τ the control is selected which enables
maximum Н from the following : a) z=0; b) z=1 и
Т
h
=Т
at
and c) z=1 и Т
h
=Т
m
.
Such simplicity of the control choice law is a result
of affine dependence
H from Т
h
and from
discontinuity of z value area.
The method of resolving the boundary problem – is
a reduction to the series of Cauchy problems
(Krylov V.I., 1977). Cauchy problems integration is
complicated by discontinuity in right-hand members
(2). The solution has extreme points therefore
special numerical method has been designed.
Its difference from prevalent methods consists in the
combination of different step of integration choice
laws - Rhunge law (problems (Krylov V.I., 1977) for
“flat” sectors and immediate estimation in extreme
points.
The prime cost of product unit minimums
discovered in such a way (for i variant of the
equipment) have been used for the comparison of
reduced costs for each variant.
i
R =
i
P +
E
i
C (7)
R - reduced costs
P – prime cost
E - normative factor recoupment of capital
investments
C – capital costs
To design industrial crystal aminoacid drying
block the best variant has been selected.
Thus the method of the CPDV drying optimal
regimes has been proposed. It is based on the MM of
the process and takes into account componentwise
contents of ethyl alcohol and aqua in aminoacids. It
can be used in design and valuation of oscillating
drying apparatus and their automated control
,)1()]()1(74,41[
2
2
1
12211
2
T
dT
dp
x
dT
dp
xxppxx
&
&
⎥
⎦
⎤
⎢
⎣
⎡
−++−−−
γγγγ
)T,x(ppc >
),( cc pQp
V
x
−
=cvp
&
),( Txppc ≤
BIOPRODUCTS DRYING OPTIMAL CONTROL IN OSCILLATING REGIMES
179
systems. The results of this work can be generalized
in the case of removal of an endless amount of thin
mixture components from drying products. It is
necessary to note that there are probable situations in
such distention when it fails to set optimal G in
advance. So
G(τ) function must be searched as
Т
d
(τ) z(τ), by solving the problem of Pontryagin’s
maximum principle.
3 AUTOMATION DRYING
PROCESS
The algorithm of automatic optimum control mode
is based on optimization model which, in turn, is
formulated on the basis of MM of drying process in
view of the technology requirements raised to an
end-product.
The automated control system model of drying
workshop is designed to allow familiarizing with the
processes proceeding in drying installation at
absence of technological object.
The laboratory-scale plant consisting of several
oscillating drying installations includes the
following technological control objects: dryer;
charging device; unloading mechanism; receiver;
condenser; hotwell.
The system emulator implements the following
functions of the automatic control and supervision:
1 Automatic control: dryer top pressure; dryer
lower part temperature; air temperature to a dryer;
air temperature from a dryer; pressure before a
receiver.
2 Remote supervision: dryer top pressure; product
temperature on an entry; product temperature on an
exit; dryer lower part temperature; air temperature to
a dryer; air consumption in a dryer; pressures before
a receiver.
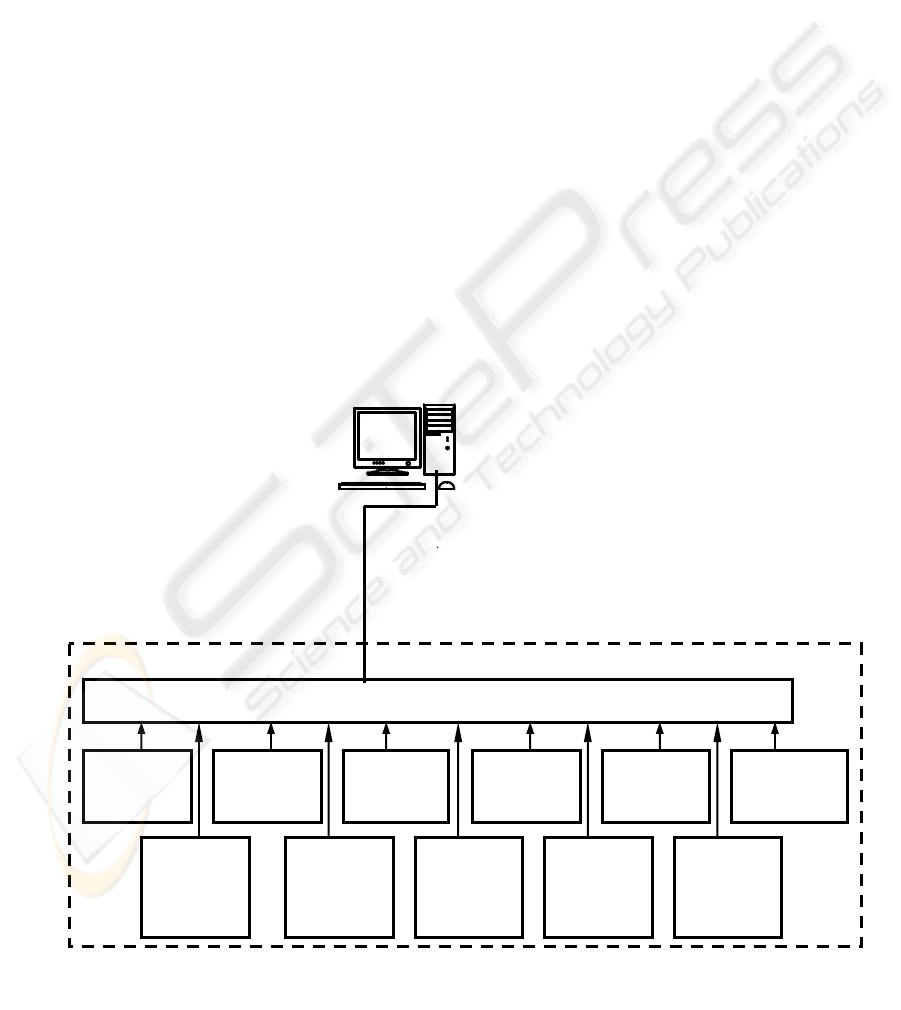
The automated control system model includes the
following levels (fig. 2): a level of sensing
transducers and actuating mechanisms; a level of
control unit (PLC); a level of the operators interface
(HMI).
In the laboratory-scale plant of the drying plant
control system the role of sensing transducers is
played by PC with program emulation of drying
installation work. The program simulates work of
field sensing transducers, emulating their current
output signals. Current signals are transferred to the
next level - on an input of the control unit.
Drying installation
actuators heat-carrier
sensor
liquid phase
structure
sensor
gas phase
structure
sensor
level of
loading
(or mass)
sensor
clearing
degree
sensor
material
humidity
sensor
relative air
humidity
sensor
drying
chamber
pressure
sensor
flow
meter
RS-485
HMI
material
temperature
sensor
PLC
Figure 2: Model of control system of the drying plant.
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
180

At this level the control logic of technological
installation is implemented. According to which
incoming data from sensing transducers and actuators
is being processed and analyzed. Generation of
control actions on the specified algorithm takes place.
The control level of the drying plant
automation system is implemented on modern
microprocessor devices. One controller with
necessary input-output modules is used for each
drying plant.
There are following modules included:
The programmed control unit with a
support of InterBus network. Implements drying
installation control algorithms.
The analog input module. Signals from pressure
and consumption sensors.
The module of signals from temperature
transmitters.
The module of discrete output signals. It is used
for management of quick-acting valves, the
ventilating fan and the vacuum pump.
One control unit with modules of input-output
provide implementation of the following functions:
• Data acquisition from sensing transducers;
• Preprocessing and normalizations of analogue
and discrete signals;
• Output of control actions on actuators;
• Management of technological installation:
data from sensing transducers level is being
processed and analyzed. Control actions on the
specified algorithms of regulating are being
generated.
The level of operator interface supplies the
operator with on-line information of a process
passing. Ensure reception of managing instructions
from the operator and transfer instructions to the
control unit. At this level functions of accumulation
and representation of the archival historical
information are implemented by SCADA-system.
In the capacity of workstations of operators are
used PC with the network InterBus interface. An
operating system established at operators stations -
Microsoft Windows. OPC Server provides data
exchange between the managing controllers and the
operators interface.
REFERENCES
Yenikeev E.S., Zolotov A.V., Karaeva G.A., and others.
Deposit copy in ОНТИТЭИ microbioindustry., №167
МБ - Д 83.
Ivanova E.N., Kapitonov N.A., Migunov V.V and others.
Deposit copy in ОНТИТЭИ microbioindustry., №168
МБ - Д 83.
Gracheva I.M., Gavrilova N.N., Ivanova L.A. Technology
of the microbial albuminous medications, aminoacids
and lipoids. - М.: Food industry, 1980. – 448pp.
Sadykov R.A., Karpov A.M., Pobedimski D.G., and
others. Design of the optimal drying technology of the
crystal aminoacids. Biotechnology, 1988, т.4, №3
340-345 pp.
Sadykov R.A., Migunov V.V, Verner Z.S., and others.
Drying method of the dispersed materials. Patent №
3788966 БИ№ 6.1986.
Sadykov R.A., Bakhtiyarov F.R., Pevzner I.L. and others.
Vacuum dryer for drying friable and lumping
materials. Patent № 1460562.БИ №11.1988.
Sadykov R.A., Migunov V.V., Karpov A.M. and another.
Study and Theoretical Modelling of the Drying of the
Aminoacids - The Products of Microbial Synthesis
Acta. Biotechnol. 5 (1985), 4, 363 -373 pp.
Sadykov R.A., Migunov V.V. Heat mass transmission at
vacuum-conductive drying of the dispersed materials.
ТОХТ. - 1989. Т XXIII, № 3, 331- 339 pp.
Sadykov R.A. Transport processes at momentary phases
contact. KSEU 2004, 176 p.
Golubev L.G., Sazhin B.S, Valashek E.R. Drying in
pharmaceutical industry. - М.: Medicine, 1978. - 272
pp.
Pontryagin, L. S., Boltyansky, V. G., Gamkrelidze, R. V.
and Mischenko, E. F., Mathematical theory of optimal
processes, Nauka, Moscow, 1983, 392 pp., (in
Russian).
Korn G., Korn T. Math’s handbook for researchers and
engineers. -М: Science, 1978.-831 pp.
Krylov V.I., Bobkov V.V., Monastyrnuii P.I..
Computational approaches - M.: Science, 1977, т.2.-
400 pp.
BIOPRODUCTS DRYING OPTIMAL CONTROL IN OSCILLATING REGIMES
181
