A New Training Algorithm for Neuro-Fuzzy Networks

Stefan Jakubek

and Nikolaus Keuth

Vienna University of Technology,

Institute for Mechanics and Mechatronics,

Gußhausstr. 27-29/E325, A-1040 Vienna, Austria

AVL List GmbH, Hans-List Platz 1, A-8020 Graz , Austria,

Abstract. In this paper a new iterative construction algorithm for local model

networks is presented. The algorithm is focussed on building models with sparsely

distributed data as they occur in engine optimization processes. The validity func-

tion of each local model is ﬁtted to the available data using statistical criteria

along with regularisation and thus allowing an arbitrary orientation and extent

in the input space. Local models are consecutively placed into those regions of

the input space where the model error is still large thus guaranteeing maximal

improvement through each new local model. The orientation and extent of each

validity function is also adapted to the available training data such that the de-

termination of the local regression parameters is a well posed problem. The reg-

ularisation of the model can be controlled in a distinct manner using only two

user-deﬁned parameters. Examples from an industrial problems illustrate the ef-

ﬁciency of the proposed algorithm.

1 Introduction

Modeling and identiﬁcation of nonlinear systems is challenging because nonlinear proc-

esses are unique in the sense that they may have an inﬁnite structural variety compared

to linear systems. A major requirement for a nonlinear system modeling algorithm is

therefore universalness in the sense that a wide class of structurally different systems

can be described.

The architecture of local model networks is capable of fulﬁlling these requirements

and can therefore be applied to tasks where a high degree of ﬂexibility is required. The

basic principles of this modeling approach have been more or less independently de-

veloped in different disciplines like neural networks, fuzzy logic, statistics and artiﬁcial

intelligence with different names such as local model networks, Takagi-Sugeno fuzzy

models or neuro-fuzzy models [1–5].

Local model networks possess a good interpretability. They interpolate local mod-

els, each valid in different operating regions, determined by so-called validity functions.

Many developments are focused on the bottleneck of the local model network which is

the determination of these subdomains or validity functions, respectively.

One important approach is Fuzzy clustering as presented in [6, 1,7, 8]. An important

issue in this ﬁeld is the interpretability of the validity functions, for example as operating

regimes. Recent developments can be found for example in [9, 10].

Jakubek S. and Keuth N. (2005).

A New Training Algorithm for Neuro-Fuzzy Networks.

In Proceedings of the 1st International Workshop on Artiﬁcial Neural Networks and Intelligent Information Processing, pages 23-34

DOI: 10.5220/0001180200230034

 SciTePress

Another development is the local linear model tree, LOLIMOT [11]. It is based

on the idea to approximate a nonlinear map with piece-wise linear local models. The

algorithm is designed such that it systematically bisects partitions of the input space.

Local models that do not ﬁt sufﬁciently well are thus replaced by two or more smaller

models in the expectation that they will ﬁt the nonlinear target function better in their

region of validity.

In the practical application that motivated this work the amount of data available

for identiﬁcation is limited and the distribution of the data in their input space is sparse

[12]. This imposes a limit on the network construction algorithm and it can lead to the

situation that many local models are built where much fewer would be sufﬁcient. Also,

the sparseness of the input data gives rise to a more or less automated regularization

that can be handled even by inexperienced users. The local model network construction

algorithm presented in this paper can be seen as a mixture of classical fuzzy clustering

techniques and the LOLIMOT construction algorithm. The present clustering algorithm

takes into account the spatial distribution of the data in the input space and the prospec-

tive shape of the target function. The extent of the local model in the input space and its

orientation are determined such that maximal statistical consistency/compliance with

the sample data is achieved along with a spatial distribution of the data that yields a

well conditioned problem.

The efﬁciency of the training algorithm is thus signiﬁcantly increased resulting in

less computational effort and fewer local models.

2 Algorithm Description

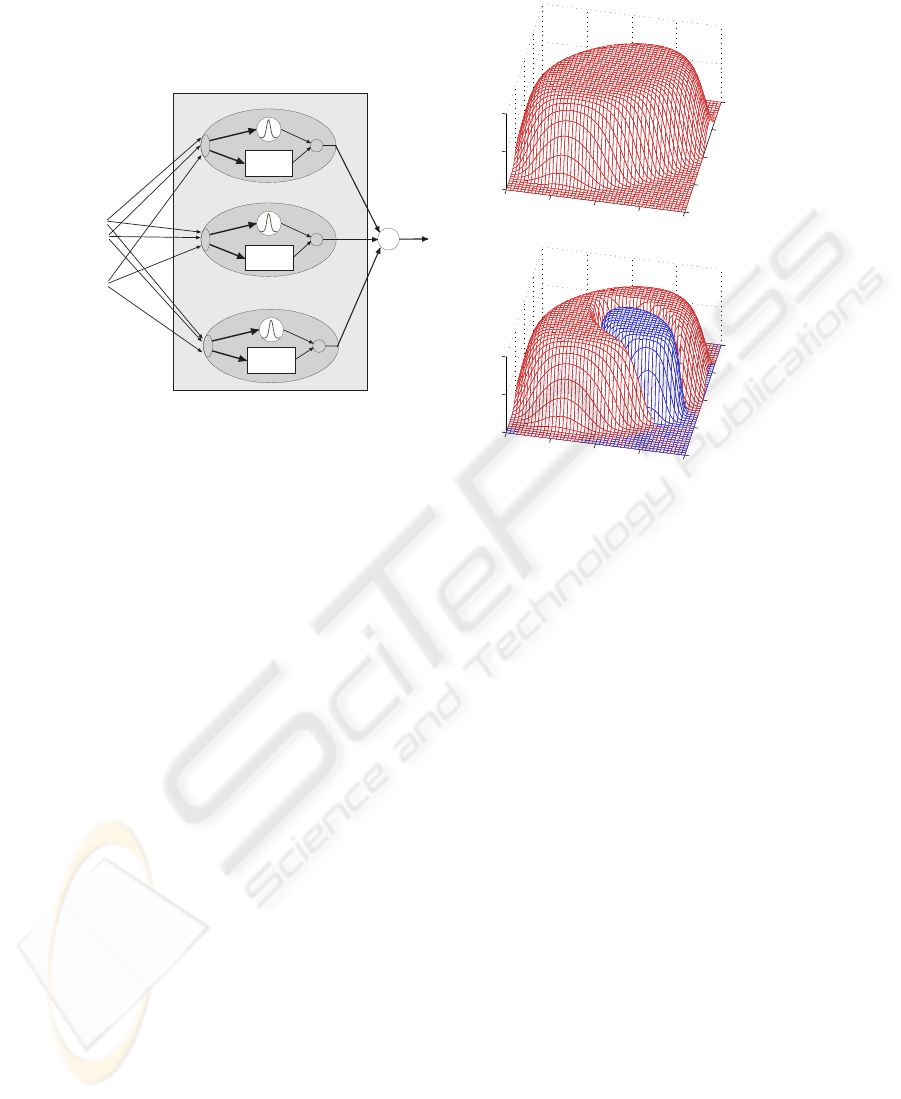
Fig. 1 illustrates the architecture of a local model network. Each local model (denoted

as LM

) takes the input vector u = [ u

. . . u

]

to compute its associated

validity function Φ

and its local estimation ˆy

of the nonlinear target function f(u).

The aggregate network output is the sum of all local model outputs ˆy

ˆy(u) =

i=1

(u)ˆy

(u, θ

) (1)

Here, θ

is a vector containing the parameters of the local model and the local model

output is generated from u and θ

The structure of the validity function Φ

was chosen as

(u) = exp



−[(u − z

)

(u − z

)]



k=i+1

(1 − Φ

(u)) (2)

The vector z

contains the location of the current local model center, A

is a sym-

metric and positive deﬁnite matrix that determines the orientation and extent of the va-

lidity function in the input space and the exponent κ

is a shape factor that determines

the ﬂatness of the validity function and thus also the degree of overlap between different

local models. In the given examples this factor was set to 4, a further discussion on the

choice of κ follows.

ˆy

Fig.1. Concept of local model networks

−0.5

0.5

1.5

−0.5

0.5

1.5

0.5

, u

)

−0.5

0.5

1.5

−0.5

0.5

1.5

0.5

, u

)

Fig.2. Shape and hierarchy of validity functions

The structure of eq. (2) shows that every validity function is initally an exponential

function with ellipsoidal contour lines. The product in (2) clips all subsequent validity

functions from this original function, see Fig. 2. This choice has the following advan-

tage: All subsequent local models are set into domains of the input space, where the

preexisting model is insufﬁcient. Eq. (2) ensures the dominance of the new local mod-

els in such domains. In Fig. 2 the situation is illustrated for a two-dimensional input

space where a small domain is clipped from an originally ellipsoidal validity function.

The structure of (2) by iteself does not guarantee that validity functions yield a

partition of unity. For that purpose the validity functions are normalized which is not

explicitly oulined here for the sake of brevity.

The overall quality of the network output is assessed either by the R

statistics or

by the R

pred

statistics as outlined in [13]. The R

pred

statistics inherently describes the

generalization quality of the model.

2.1 Training procedure

The local model network construction algorithm consists of an outer loop that deter-

mines the location, extent and orientation of each local model and a nested inner loop

that optimises the parameters of the local model:

1. Start with an initial model: The initial model can either be a global model that

covers all the available data or an ”ordinary” local model as described below.

2. Set the next local model: Find the data point with the worst output error or predic-

tion error. Choose the location of this data point as a candidate for the next local

model. Design the orientation and extent of the new model such that it meets sta-

tistical compliance criteria with the sample data in the region of its validity. This

procedure will be described in detail in the next section.

3. Compute the local model parameters and the associated statistical parameters that

are necessary for the computation of prediction intervals

4. Test for Convergence: The performance criteria R

and R

pred

for the network out-

put are computed. Once they have reached or exceeded their termination values the

algorithm stops. Also, if no further improvement can be achieved the tree construc-

tion is stopped. Otherwise the algorithm proceeds with step 2. Especially in the

case when the training data are subject to strong noise disturbance it is important

that the training algorithm is controlled by a useful regularisation factor. Otherwise,

the construction algorithm would create smaller and even smaller local models to

improve the overall ﬁt. In our case this is prevented by means of conﬁdence levels

as will be described in detail in the next section.

After the local model network construction algorithm has ﬁnished to place local

models each model undergoes a ﬁnal examination for its contribution to the overall

network output. If it turns out that a certain model does not contribute signiﬁcantly

anymore because it has been replaced by other models to a great extent it is removed.

3 Local Model Design

3.1 Local Model Structure

Every local model roughly consists of two parts: Its validity function Φ

(u) and its

model parameters θ

. The output ˆy

of a local model at a point u in the input space is

chosen as

ˆy

(u) = x

(u) · θ

. (3)

Here, x

(·) represents a row vector of regressor functions which can be chosen ar-

bitrarily. The advantage of the structure of (3) lies in the fact that ˆy

depends linearly

on the parameters θ

. Therefore, least-squares techniques can be applied for their com-

putation. It remains to determine suitable regressor functions for x

(·) which will be

outlined in section 3.3.

3.2 Determination of the validity function

In the presence of noise it is desirable that every local model should have optimal sta-

tistical signiﬁcance. The algorithm presented in the sequel takes into account both the

spatial distribution of the data and the expected shape of the target function and how

well it can be modeled by the given regressors. In practical situations both the effect of

noise and the prospective shape of the target function are unknown and the presented

clustering approach turned out to be a reliable compromise.

1. The selection of a center ”candidate” z

of a new local model is based on the

estimation error e

= y

− ˆy(u

). Here ˆy(u

) is the model output from the network

at it’s current state when i − 1 models have already been built:

ˆy(u

) =

i−1

k=1

)ˆy

, θ

) (4)

Given n data records u

for model training the new center candidate is chosen as

the data record where the output error is maximal:

i,cand

= u

with j

= arg max ||e

|| (5)

This selection ensures that a new local model is set in the area where it is needed

most.

2. Next, an initial set of neighbouring training data is chosen to compute an ”initial”

regression model. The minimum amount of data necessary for this initial model

is determined by the requirement that the regression matrix must have maximum

rank which depends both on the regressor functions and on the spatial distribution

of the data. Next, the model statistics of the regression model are computed (see

sec. 3.4) and a check is performed whether the initial data set lies within a pre-

scribed prediction interval corresponding to a conﬁdence level α. If this is not the

case the iteration terminates and the algorithm proceeds with the computation of

the parameters of the validity function. Typically, the conﬁdence level α is chosen

between 90% and 99.9%.

3. Otherwise, further training data points in the vicinity of z

i,cand

are added succes-

sively and the initial regression model together with the model statistics are adapted

to these data using recursive least squares techniques. This step is repeated as long

as α % of the selected training data lie within the prediction interval. Thus it is

ensured that the local model size and shape corresponds to the shape of the target

function and the noisyness of the data.

4. Once training data have been selected in this way their distribution in the input

space is used to determine the actual center along with the shape and extent of the

validity function.

Figures 3 and 4 give an example for a nonlinear map f(u) : IR → IR and α = 97%.

The training data are represented by dots. Figure 3 depicts an ”initial” regression model:

The center candidate was chosen as z

i,cand

= 0 for this illustrative example, all data

points in the interval u ∈ [0; 0.17] were selected for the regression. The dashed curves

represent the boundaries of the 97% prediction interval. Figure 4 depicts the ”ﬁnal” sit-

uation: Additional training data points had been added until ﬁnally about 97% of the

selected data lie within the boundaries of the 97% conﬁdence interval. The resulting

validity function which was added to the ﬁgure for clarity extends from 0.1 to 0.8 hav-

ing its maximum at 0.4. Figure 5 illustrates the ﬁnal situation for α = 99.99%. The

increased conﬁdence level α results in larger conﬁdence intervals and consequently the

validity function now has a greater extent. It can also be seen that in this example the

shape of the nonlinearity has a much greater inﬂuence on the model size than in Figure

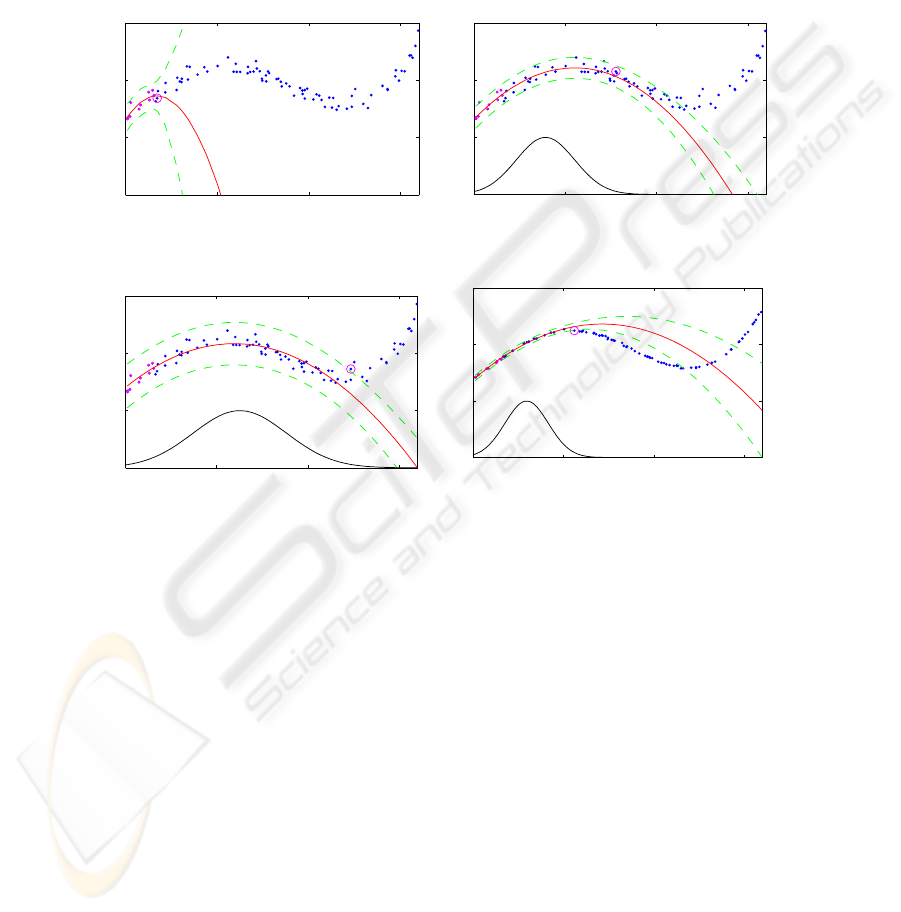
4. Figure 6 contains the same map f(x), however, the inﬂuence of noise was drasti-

cally reduced. Altough the conﬁdence level is still at 99.99% the extent of the validity

function is now signiﬁcantly smaller. From these examples it becomes obvious that the

conﬁdence level α serves as an excellent regularisation parameter that automatically

adapts the local models to the noise corruption of the training data and to the regressor

functions.

0 0.5 1 1.5

Φ(u), y, ˆy

Fig.3. Initial model with α = 97%

0 0.5 1 1.5

Φ(u), y, ˆy

Fig.4. Final local model with α = 97%

0 0.5 1 1.5

Φ(u), y, ˆy

Fig.5. Final local model with α = 99.99%

0 0.5 1 1.5

Φ(u), y, ˆy

Fig.6. Final local model with α = 99.99% and

less noise

It remains to determine the nonlinear parameters of the validity function from the

training data selected in the manner described above. Let U

sel

be a matrix containing

all these data records including the center candidate z

, i.e. every row vector of U

sel

contains the coordinate vector u

of a selected data point.

Then, the actual center is obtained by taking the center of gravity of the data in

sel

= mean(U

sel

) (6)

where mean(·) takes the mean value over every column of its argument. The actual

center is thus not the initial center candidate but the center of gravity of all chosen data

points. This has the advantage that the algorithm is less sensitive to outliers in the data

set.

The matrix A

is computed by

= γ · [cov(U

sel

)]

−1

(7)

where cov(·) denotes the empirical covariance matrix. This approach is taken from [14]

where it was applied for the design of ellipsoidal basis function networks. The principal

orientation of the new validity function is thus determined by [cov(U

sel

)]

−1

and its

extent in the input space is controlled by γ. The latter is chosen such that Φ

is still 0.9

at the data point in U

sel

which is located most remote from the new center z

. Thus, it

is ensured that there are actually enough data points available for parameter estimation.

Besides α, both γ and the shape parameter κ constitute a second means of regularisation

for the algorithm. The larger κ is chosen the smaller the overlap between single local

models will be. Thus κ directly controls the locality of the models. This does play an

important role in the determination of covariances as will be outlined later. The factor

γ is directly related to the choice of κ and just has to ensure the LS-problem is well

posed as stated earlier. Consequently, the conﬁdence level α and κ are used to tune the

training algorithm.

3.3 Computation of the local model parameters

As already mentioned earlier the output of each local model is computed through the

regression model (3). It remains to determine suitable regression functions x

(u). In

general, there is no ”optimal” solution that suits all possible nonlinear problems. The

LOLIMOT-Algorithm [11] features linear models and in the present application the

regressor functions were chosen as quadratic polynomials.

Let X denote a matrix constructed from the regression vectors of all n training data

records:

X =







)







and Q







) 0 · · · 0

0 Φ

) · · · 0

0 0 · · · Φ

)







(8)

where Q

denotes a diagonal matrix composed from the Φ

, evaluated at the training

data points. If y is a vector containing the values of the target function at the data points

then the i-th local parameter vector is given by





−1

y. (9)

3.4 Local Model Statistics

Using the abbreviation





−1

(10)

the parameter variance cov(θ) can be expressed by

cov(θ) = σ

XΘ

. (11)

with the assumption that the measurement noise at different training data points is un-

correlated E{ee

} = σ

I. It has to be mentioned that the noise covariance σ

not known in most cases and therefore has to be replaced by the empirical covariance

computed from the available data.

The variance of the local model output ˆy

) is then calculated by

cov(ˆy

(u)) = E



− ˆy

)



== σ

[1 + x(u

)Θ

XΘ

)]. (12)

The prediction interval at a point u in the input space with a signiﬁcance level of α

is given by

|ˆy(u) − y(u)|

= σ

1 + x(u)Θ

XΘ

x(u)

× t

1−

(13)

As indicated, the t-statistics have to be computed for a signiﬁcance level of α-%

with the degrees of freedom depending on both the number of training data involved

and the number of regressors.

4 Global Model Design

Apart from the local model design the interaction of all local models has to be consid-

ered in a global design. This involves the aggregation of the local model outputs as well

as global model statistics, global prediction intervals and efﬁcient ways to compute the

and R

pred

statistics.

4.1 Global Model Output

As deﬁned in (1) the global model output is a weighted sum of all local outputs. The

weights depend on the location u in the input space and are determined from the validity

functions Φ:

ˆy(u) =

i=1

(u)ˆy

(u, θ

)

As already mentioned earlier the design parameters of the validity function, κ in

particular implicitly determine the degree of overlap between the local models and thus

serve as a regularisation parameter. It is straightforward that strong overlap in general

leads to smoother function approximation.

4.2 Global Prediction Intervals

Computation of conﬁdence intervals at the global level involves two steps:

1. Computation of the covariance

2. Determination of the effective degrees of freedom at the global level for the t

statistics.

Step 1 is straightforward since the global model output is a linear combination of

the local model as given by (1). Strictly speaking, the outputs of different local models

ˆy

(u) are not independent since the underlying models all originate from the same data.

However, the shape parameter κ in (2) entails that there is only little overlap between

single local models. The statistical interdependencies between local models is therefore

neglegible, which was also veriﬁed in numerous tests.

cov(ˆy(u)) =

i=1

(u)cov(ˆy

(u)) (14)

In the above formula cov(ˆy

(u)) is taken from (12). It is noteworty that (14) does

not contain σ

directly. The covariance cov(ˆy

(u)) of every local model depends on the

model structure and on the local measurement noise. This means that (14) could also be

applied if the measurment noise varies from local model to local model, provided that

cov(ˆy

(u)) is computed correctly.

Step 2 is taken from [5] where the effective number of parameters n

eff

is deter-

mined from the trace of the so-called ”smoothing matrix”.

The remaining degrees of freedom then result to D OF = n − n

eff

and this is the

basis for the computation of the t-statistics. It is noteworthy that n

eff

is not necessarily

an integer number. During the tree construction process it sometimes happens that the

validity function of a certain local model is successively clipped away by subsequent

models so that it ﬁnally doesn’t contribute anymore to the model quality. In the present

application these models are ﬁnally removed if their n

eff,i

has dropped below 1.

5 Results

In the given example measurement data from an IC-Engine are considered. For the de-

velopment and testing of the presented algorithm measurement databases from different

engine manufacturers were used. The dimension of the input space in these databases

varies from three to eight.

The three-dimensional database will be illustrated in detail since in this case some

demonstrative graphical illustrations can be given.

In particular, the air efﬁciency A

of a valvetronic engine shall be represented as a

function of engine speed n, valve lift L

and intake closure time T

= f (n, L

, T

)

The resulting network models the map f : IR

→ IR with an accuracy of R

0.9941 and R

pred

= 0.9931 using 7 local models. In comparison, the LOLIMOT-

algorithm using the same quadratic local model structure needs 30 local models to reach

the same accuracy.

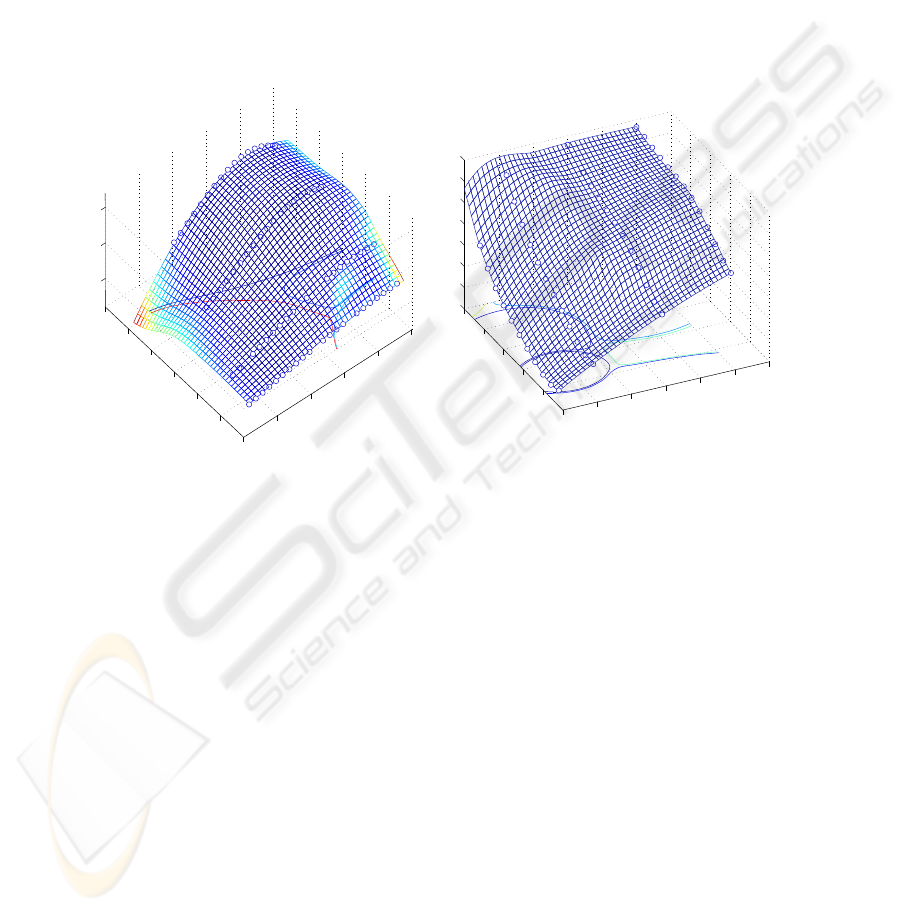
Figures 7, 8 and 9 depict the network output each with one input kept constant.

Apart from the network output the corresponding training data points are depicted and

the validity functions are represented by contour lines. Note that not all seven validity

functions are visible in the respective intersection planes. It can be seen that they are

ﬁtted to the shape of the target function in an efﬁcient way.

400

450

500

550

600

650

0.5

Fig.7. Valvetronic engine example: Model out-

put for n = 2600 =const.

1000

2000

3000

4000

5000

60001

0.1

0.2

0.3

0.4

0.5

0.6

0.7

Fig.8. Valvetronic engine example: Model

output for T

= 498 =const.

The measurement data considered in this example were also used to compare the

performance of the presented network architecture and training algorithm to that of a

perceptron network. The number of hidden neurons was chosen such that the effective

number of weights corresponds to the number of parameters in the competing local

model network. The weights of the perceptron network were optimized using standard

training algorithms in combination with different regularization techniques in order to

balance bias and variance errors. In a Monte-Carlo simulation it turned out that despite

this efforts the perceptron has particular difﬁculties interpolating the large gaps between

the individual valve lift values (cf. Fig. 7 and Fig. 10).

Altogether, 300 Perceptrons were trained in the manner described above, resulting

in the following statistical assessment: 13% of all Perceptrons had a performance supe-

rior to that of the local model network. They exceeded the R

pred

value of 0.9931 and the

interpolation behaviour was better. 13% of all Perceptrons produced a comparable per-

formance in terms of the same criteria. The remaining 74% of all 300 perceptrons were

450

500

550

600

650

1000

2000

3000

4000

5000

6000

−0.5

0.5

1.5

Fig.9. Valvetronic engine example: Model

output for L

= 6 =const.

400

500

600

700

−1

Fig.10. Valvetronic engine example: Percep-

tron output for n = 2600 =const.

outperformed by the local model network, cf. Fig. 10. In many cases the conﬁdence

interval was unacceptably large for practical applications.

6 Conclusion and Outlook

In this paper a new iterative tree construction algorithm for local model trees was pre-

sented. The validity functions of the generated model are closely ﬁtted to the available

data by allowing an arbitrary orientation and extent of the validity function of each local

model in the input space.

The regularisation of the model can be controlled by a shape factor κ which deter-

mines the overlap between local models and by a conﬁdence level α that controls the

relative size of each local model.

The application to data from internal combustion engines shows that the proposed

algorithm produces excellent results with a relatively low number of local models.

References

1. Babuska, R., Verbruggen, H.: An overview of fuzzy modeling for control. control Engineer-

ing Practice 4 (1996) 1593 – 1606

2. Johansen, T.A., Foss, B.A.: Operating regime based process modeling and identiﬁcation.

Computers and Chemical Engineering 21 (1997) 159 – 176

3. Babuska, R.: Recent Advances in Intelligent Paradigms and Applications. Springer-Verlag,

Heidelberg (2002)

4. Ren, X., Rad, A., Chan, P., Wai, L.: Identiﬁcation and control of continuous-time nonlin-

ear systems via dynamic neural networks. Industrial Electronics, IEEE Transactions on 50

(2003) 478–486

5. Nelles, O.: Nonlinear System Identiﬁcation. 1st edn. Springer Verlag (2002)

6. Bezdek, J., Tsao, E.K., Pal, N.: Fuzzy kohonen clustering networks. In: IEEE International

Conference on Fuzzy Systems, IEEE (1992) 1035 – 1043

7. Yen, J., L., W.: Application of statistical information criteria for optimal fuzzy model con-

struction. IEEE Transactions on Fuzzy Systems 6 (1998) 362 – 372

8. Gath, I., Geva, A.: Unsupervised optimal fuzzy clustering. IEEE Transactions on Pattern

Analysis and Machine Intelligence 11 (1989) 773–781

9. Abonyi, J., Babuska, R., Szeifert, F.: Modiﬁed gath-geva fuzzy clustering for identiﬁcation

of takagi-sugeno fuzzy models. In: IEEE Tarnsactions on systems, man. and Cybernetics.

Volume 32., IEEE (2002) 612–621

10. Trabelsi, A., Lafont, F., Kamoun, M., G., E.: Identiﬁcation of nonlinear multivariable systems

by adaptive fuzzy takagi-sugeno model. International Journal of Computational Cognition

(http://www.YangSky.com/yangijcc.htm) 2 (2004) 137–153

11. Nelles, O., Isermann, R.: Basis function networks for interpolation of local linear models.

In: IEEE Conference on Decision and Control (CDC). (1996) 470–475

12. Bittermann, A., Kranawetter, E., J., K., B., L., T., E., Altenstrasser, H., Koegeler, H.,

Gschweitl, K.: Emissionsauslegung des dieselmotorischen fahrzeugantriebs mittels doe und

simulationsrechnung. Motorentechnische Zeitschrift (2004)

13. Hong, X., Sharkey, P., Warwick, K.: A robust nonlinear identiﬁcation algorithm using press

statistics and forward regression. In: IEEE Transactions on Neural Networks. Volume 14.,

IEEE (2003) 454 – 458

14. Jakubek, S., Strasser, T.: Artiﬁcial neural networks for fault detection in large-scale data

acquisition systems. Engineering Applications of Artiﬁcial Intelligence 17 (2004) 233–248