WIND TURBINE ROTOR ACCELERATION: IDENTIFICATION

USING GAUSSIAN REGRESSION

W. E. Leithead

Dept of Electronic and Electrical Engineering, University of Strathclyde, Glasgow, U.K.

and

Hamilton Institute, National University of Ireland, Maynooth, Co. Kildare, Ireland

Yunong Zhang, Kian Seng Neo

Hamilton Institute, National University of Ireland, Maynooth, Co. Kildare, Ireland

Keywords: Data analysis, Gaussian regression, inde

pendent processes, fast algorithms.

Abstract: Gaussian processes prior model methods for data analysis are applied to wind turbine time series data to

identify both rotor speed and rotor acceleration from a poor measurement of rotor speed. In so doing, two

issues are addressed. Firstly, the rotor speed is extracted from a combined rotor speed and generator speed

measurement. A novel adaptation of Gaussian process regression based on two independent processes rather

than a single process is presented. Secondly, efficient algorithms for the manipulation of large matrices are

required. The Toeplitz nature of the matrices is exploited to derive novel fast algorithms for the Gaussian

process methodology that are memory efficient.

1 INTRODUCTION

Following some initial publications in the late 1990s

(e.g., Rasmussen (1996), Gibbs (1997), Mackay

(1998), Williams and Barber (1998)), interest has

grown quickly into the application of Gaussian

process prior models to data analysis; e.g. Williams

(1999), Gibbs and Mackay (2000), Sambu et al

(2000), Toshioka and Ishii (2001), Leith et al

(2002), Shi et al (2003), Solak et al (2003), Leithead

et al (2003a), Leithead et al (2003b). In this paper,

these methods are applied to wind turbine time

series data, specifically, site measurements of the

rotor speed for a commercial 1MW machine.

However, the measurement is some unknown

combination of the rotor speed and the generator

speed (scaled by the gearbox ratio) (Leithead et al,

2003b). Furthermore, the data is corrupted by

significant measurement noise. The objective of the

data analysis is to extract from the data both the

rotor speed and the rotor acceleration, an initial yet

important part of identifying the aerodynamics and

drive-train dynamics of variable speed wind turbines

(Leithead et al, 2003b). Previously, only traditional

filtering methods have been employed (Leithead et

al, 2003b).

To successfully identify the wind turbine rotor

spee

and acceleration using Gaussian process prior

models, two particular issues must be addressed.

Firstly, since the measurement is a combination of

rotor speed and generator speed, only that

contribution to the measurement due to the rotor

speed must be extracted. Secondly, since analysis

using Gaussian process prior models involves the

inversion and multiplication of N-dimensional

square matrices where N is the number of data

measurements (24,000 in this case), the matrix

manipulations must be efficient. In this paper, novel

adaptations of the Gaussian process data analysis

methodology to meet these two issues are presented

(the first in section 3 and the second in section 4)

and successfully applied to the wind turbine data (in

section 5).

E. Leithead W., Zhang Y. and Seng Neo K. (2005).

WIND TURBINE ROTOR ACCELERATION: IDENTIFICATION USING GAUSSIAN REGRESSION.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and

Control, pages 84-91

DOI: 10.5220/0001179300840091

 SciTePress

2 GAUSSIAN PROCESS PRIOR

MODELS

Gaussian process prior models and their application

to data analysis is reviewed in theis section.

Consider a smooth scalar function f(.) dependent

on the explanatory variable,

. Suppose

N measurements,

{

, of the value of the

function with additive Gaussian white measurement

noise, i.e. y

D ℜ⊆∈z

}

)y,(

=f(z

)+n

are available and denote them

by M. It is of interest here to use this data to learn

the mapping f(z) or, more precisely, to determine a

probabilistic description of f(z) on the domain, D,

containing the data. Note that this is a regression

formulation and it is assumed the explanatory

variable, z, is noise free. The probabilistic

description of the function, f(z), adopted is the

stochastic process, f

, with the E[f

], as z varies,

interpreted to be a fit to f(z). By necessity, to define

the stochastic process, f

, the probability

distributions of f

for every choice of value of

∈

are required together with the joint probability

distributions of

for every choice of finite

sample, {z

,…,z

}, from D, for all k>1. Given the

joint probability distribution for

, i=1..N, and the

joint probability distribution for n

, i=1..N, the joint

probability distribution for y

, i=1..N, is readily

obtained since the measurement noise, n

, and the

f(z

) (and so the

) are statistically independent. M

is a single event belonging to the joint probability

distribution for y

, i=1..N.

In the Bayesian probability context, the prior

belief is placed directly on the probability

distributions describing f

which are then

conditioned on the information, M, to determine the

posterior probability distributions. In particular, in

the Gaussian process prior model, it is assumed that

the prior probability distributions for the f

are all

Gaussian with zero mean (in the absence of any

evidence the value of f(z) is as likely to be positive

as negative). To complete the statistical description,

requires only a definition of the covariance function

=E[ , ], for all z

),(C

jif

and z

. The

resulting posterior probability distributions are also

Gaussian. This model is used to carry out inference

as follows.

Clearly where p(M)

acts as a normalising constant. Hence, with the

Gaussian prior assumption,

M)/p(M),f(p)M|f(p

[]

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

−∝

−

fMfp

2221

`2111

exp)|(

ΛΛ

(1)

where

, Λ

yy ],[

"=Y

is E[f

, f

], the ij

element of the covariance matrix Λ

is E[y

, y

] and

the i

element of vector Λ

is E[y

, f

]. Both Λ

and

depend on z. Applying the partitioned matrix

inversion lemma, it follows that

(

)

][ )

()

(exp|

zzzzzz

ffffMfp −Λ−−∝

−

(2)

with

, .

Therefore, the prediction from this model is that the

most likely value of f(z) is the mean,

, with

variance Λ

-1

ΛΛ=

-1

2111

ΛΛΛ−Λ=Λ

. Note that is simply a z-dependent

weighted linear combination of the measured data

points, Y, using weights

. The measurement

noise, n

-1

ΛΛ

, i=1,..N, is statistically independent of f(z

i=1,..N, and has covariance matrix B. Hence, the

covariances for the measurements, y

, are simply

E[y

] = E[ , ]+ B

; E[y

, f

] = E[ , f

] (3)

In addition, assume that the related stochastic

process,

, where and e

δ−=

δ+

/)f(ff

)(

zez

a unit basis vector, is well-defined in the limit as

0→

, i.e. all the necessary probability

distributions for a complete description exist. Denote

the derivative stochastic process, i.e. the limiting

random process, by

. When the partial derivative

of f(z) in the direction e

exists, E[ ] as z varies is

interpreted as a fit to

)(

∂

. Provided the

covariance E[

, ] is sufficiently differentiable,

it is well known (O’Hagan, 1978) that

is itself

Gaussian and that

]f[E

∂

(4)

where z

denotes the i

element of z; that is, the

expected value of the derivative stochastic process is

just the derivative of the expected value of the

stochastic process. Furthermore,

]f,f[E]f,f[E

101

zzz

∇=

∇∇=

(5)

where

Q(z

∇

) denotes the partial derivative of

Q(z

) with respect to the i

element of its first

argument, etc.

WIND TURBINE ROTOR ACCELERATION: IDENTIFICATION USING GAUSSIAN REGRESSION

The prior covariance function is generally

dependent on a few hyperparameters,

. To obtain a

model given the data, M, the hyperparameters are

adapted to maximise the likelihood, p(M|

), or

equivalently to minimize the negative log likelihood,

), where

)(

)(detlog

)(

−

θθθ

CCL

(6)

with

)( Λ=

C , the covariance matrix of the

measurements.

3 MODELS WITH TWO

GAUSSIAN PROCESSES

Suppose that the measurements are not of a single

function but of the sum of two functions with

different characteristics; that is, the measured values

are y

=f(z

)+g(z

)+n

. Now, it is of interest to use the

data to learn the mappings, f(z) and g(z), or, more

precisely, to determine a probabilistic description for

them. The probabilistic description by means of a

single stochastic process, discussed in the previous

section, is no longer adequate. Instead, a novel

probabilistic description in terms of the sum of two

independent stochastic processes, f

and g

, is

proposed below.

Since f

and g

are independent, E[FG

]=0 where

and . Let the

covariance functions for f

]f,f[

F "=

]g,g[

G "=

and g

be and

, respectively. Note that this is a different

model from one using a single stochastic process

with covariance function, (C

),(C

jif

),(C

jig

+ C

). It follows that

[]

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

YGF

GGFF

GGGG

FFFF

ΛΛ

Λ 0

TTT

(7)

with

, and

]E[

=Λ ]E[

=Λ

GGFF

BQ ΛΛ ++=

The prior joint probability distribution for F, G

and Y is Gaussian with mean zero and covariance

matrix Λ. The requirement is to obtain the posterior

probability distribution for F and G conditioned on

the data set, M, subject to the condition that they

remain independent. Of course, the posterior

probability distribution remains Gaussian. The mean

and covariance matrix for the posterior is provided

by the following theorem (Leithead et al, 2005).

Theorem 1: Given that the prior joint probability

distribution for F, G and Y is Gaussian with mean

zero and covariance matrix Λ, the posterior joint

probability distribution for [F

, G

]

conditioned on

the M, subject to the condition that they remain

independent, is Gaussian with

⎥

⎦

⎤

⎢

⎣

⎡

⎥

⎦

⎤

⎢

⎣

⎡

−−

−

−−

−

BQBQ

YQBQ

GGF

FFF

GGF

FFF

cov

mean

(8)

where

FFF

Proof. Omitted due to space limitations.

Note, since f

and g

remain independent when

conditioned on M, the prediction and covariance for

) are simply the sum of the individual

predictions and covariance values.

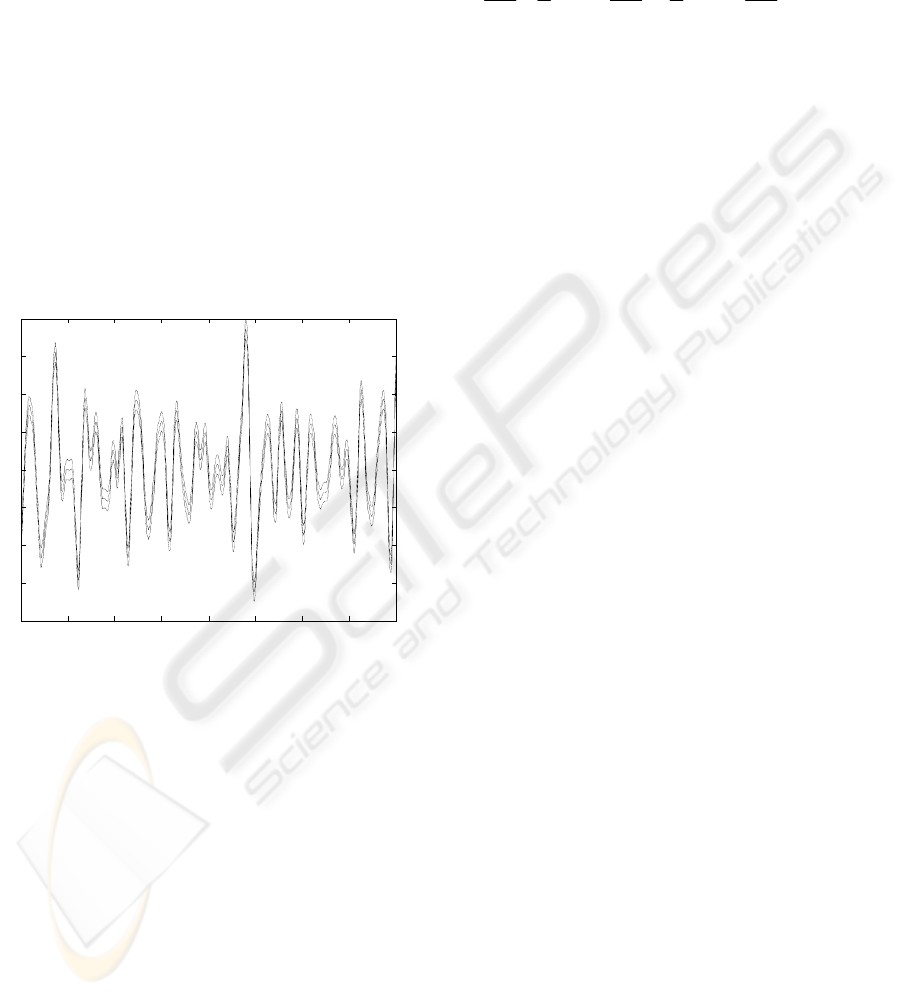
0 1 2 3 4 5 6 7 8

-4

-3

-2

-1

Data, long length-scale prediction and total error

Seconds

Figure 1: Data values (***), long length-scale component

with confidence intervals (––) and total error and

confidence interval (==)

Example: A commonly used prior covariance

function for a Gaussian process with scalar

explanatory variable is

][

)zz(exp

da −−

(9)

It ensures that measurements associated with nearby

values of the explanatory variable should have

higher correlation than more widely separated values

of the explanatory variable;

is related to the

overall mean amplitude and d inversely related to

the length-scale of the Gaussian process.

Let the covariance function for f

be (9) with

a=1.8 and d=2.5, and the covariance function for g

be (9) with a=0.95 and d=120; that is, f

has a long

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

length-scale and g

a short length-scale. In addition,

let the measurement noise be Gaussian white noise

with variance b=0.04, i.e. B

., where

is the

Kronecker delta. A set of 800 measurements at

constant interval, 0.01, for y

=f(z

)+g(z

)+n

, with the

f(z

) and g(z

) the sample values for the stochastic

processes f

and g

, respectively, is shown in figure

A prediction for the long and short length-scale

components is obtained using (8); that is, the

conditioning on the data is chosen such that as much

of the data as possible is explained by the long

length-scale component. The long length-scale

component with its confidence interval (

standard

deviations) is shown in Figure 1 and the short

length-scale component with its confidence interval

is shown in Figure 2. The prediction error for (f

2±

)

with its confidence interval is also depicted in Figure

0 1 2 3 4 5 6 7 8

-2

-1.5

-1

-0.5

0.5

1.5

Short length-scale prediction and confidence intervals

Seconds

Figure 2: Short length-scale component with confidence

intervals

In Section 5, Theorem 1 is applied to the wind

turbine measurement data to extract the contribution

due to the rotor speed and, together with (4) and (5),

to identify the rotor acceleration.

4 TOEPLITZ-BASED

EFFICIENCY IMPROVEMENT

In section 3, a novel adaptation of the Gaussian

regression methodology to support the extraction of

separate components from data is presented.

However, before that procedure can be applied to

large data sets, fast and memory efficient algorithms

are required. That requirement is addressed in this

section.

As the log likelihood, (6), is in general nonlinear

and multimodal, efficient optimisation routines

usually need gradient information,

111

−−−

∂

−

⎟

⎠

⎞

⎜

⎝

⎛

∂

Ctr

θθθ

(10)

where

denotes the i-th hyperparameter and )(

⋅

the trace operation of a matrix. Let us denote

∂

/ hereafter by

for notational convenience.

Clearly, in general, the number of operations in

solving for

and is of , whilst

the memory space to store

C , and

Cdetlog

1−

)(

1−

(see Table 1 for specific values). For large

data sets, fast algorithms, that require less memory

allocation, are required for the basic matrix

manipulations,

, and ,

when tuning the Gaussian process prior model

hyperparameters.

)(

Cdetlog

1−

)(

PCtr

−

Now consider a time series with fixed interval

between the measurements. The explanatory

variable, z, in the Gaussian process prior model is a

scalar, the time t. When the covariance function

depends on the difference in the explanatory

variable, as is almost always the case, the covariance

matrix

)(

C and its derivative matrices

are

Toeplitz; that is,

[]

110

021

201

110

)(

−

−−

−

⎥

⎦

⎤

⎢

⎣

⎡

cccc

cToeplitz

ccc

#%##

Furthermore,

)(

C is symmetric and positive

definite.

Here, the Toeplitz nature of

)(

C is exploited to

derive novel fast algorithms for the Gaussian process

methodology that require less memory allocation. It

is well-known that positive-definite Toeplitz

matrices can be elegantly manipulated in

operations. For example, Trench's algorithm

inverts

with operations, and Levinson's

algorithm solves for

with operations

(Golub & Van Loan, 1996). However, direct

application of these algorithms to Gaussian process

regression may fail even with medium-scale datasets

due to lack of memory space, see Table 1. For

example, on a Pentium-IV 3GHz 512MB-RAM PC,

)(

C 4/13

1−

WIND TURBINE ROTOR ACCELERATION: IDENTIFICATION USING GAUSSIAN REGRESSION

a MATLAB-JAVA algorithm usually fails around

because storing almost uses up the

available system memory. The solution is to adapt

the fast algorithms to use only vector-level storage.

From Table 1 that approach is theoretically able to

handle very large datasets, such as 1-million data

points, in terms of memory requirements.

7000=N

1−

Table 1: Memory/storage requirement in double precision

N Matrix Vector

1000 7.7 MB 7.6 KB

7000 373.9 MB 53.4 KB

15000 1716.6 MB 114.4 KB

20000 152.6 KB

30000 228.9 KB

50000 381.5 KB

100000 762.9 KB

1000000 7.629 MB

Two versions of fast Toeplitz-computation

algorithms are discussed and compared below;

namely, a full-matrix version and a vector-storage

version.

4.1 Full-Matrix Toeplitz

Computation

The simplest way of applying Toeplitz computation

to Gaussian process regression is to compute

directly as the basis for the other matrix

manipulations. Specifically, Trench's algorithm of

operations can be readily modified to obtain

whilst simultaneously determining as

the logarithm sum of the reflection coefficients.

Then, given

, the computation

1−

)(

1−

C Cdetlog

1−

∑∑

−

ijij

pcPCtr )(

is easily performed in

operations, where

)(

and p

are the ij-th

elements of

and P, respectively.

1−

Table 2: Accuracy and speedup of Toeplitz computation

N=1000 N=2000 N=3000

Accuracy on

Cdetlog

4.1×10

-15

3.4×10

-15

3.5×10

-15

1−

1.3×10

-12

7.0×10

-13

2.2×10

-12

)(

PCtr

−

8.1×10

-14

1.7×10

-13

5.5×10

-14

Speed up 70.45 91.64 90.84

Note that Trench's algorithm uses Durbin's

algorithm to solve Yule-Walker equations (Golub &

Van Loan, 1996). These two algorithms are

implemented separately; specifically, the matrix-free

algorithm that generates an instrumental vector and

the remaining part that generates

. The former

does not contain any matrix or matrix-related

computation/storage, and is thus able to perform

very high-dimension Toeplitz-computation. In view

of this, it is also used in Section 4.2 as a part of the

vector-storage version of Toeplitz-computation.

1−

A large number of numerical experiments are

performed to verify the correctness of the modified

algorithms and their implementation. The covariance

function is

ijji

bda

+−− ][

)zz(exp

(11)

with random hyperparameters,

, )3,0(∈a

)05.0,0(

∈

d , )3.0,0(

∈

b . The numerical stability,

accuracy and speed-up of the algorithms are

compared to the standard MATLAB matrix-

inversion routines, see Table 2 where the mean of

the relative errors and speed-up ratios are shown.

Each test is based on 100 random covariance

matrices. Trench's algorithm is sufficiently stable

for the Gaussian process context in the sense that it

can work well for

, though it is slightly

less stable than the MATLAB INV routine (the latter

can work well for

10/

−

≥ad

10/

−

≥ad

4.2 Vector-Storage Toeplitz

Computation

As discussed above, the full-matrix Toeplitz

computation works well for medium-scale

regression tasks with a speed-up of around 100.

However, the matrix-level memory allocation is still

an issue for large datasets with N greater than 7,000

such as the wind-turbine data. It follows from Table

1, that if possible, a specialized vector-level storage

version of the algorithms is attractive for specific

computation task, such as Gaussian regression for

time series.

The modified matrix-free Durbin’s algorithm, see

above, is used to compute

and Levinson’s

algorithm to compute

. The remaining

manipulation, namely

, is obtained with

the aid of the following theorem.

Cdetlog

1−

)(

PCtr

−

Theorem 2. can be computed as

)(

PCtr

−

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

∑

−

ppPCtr

2)(

ϕϕ

(12)

where P is Toeplitz with representative vector

and ],,,[

21 N

pppp "=

denotes the summation

of the elements in the

i th diagonal of .

1−

Proof. Omitted due to space limitation.

Table 3: Accuracy and run-time of Toeplitz computation.

Accuracy in the form

of mean (std)

Time

(seconds)

N=10000

1.4×10

-13

(2.0×10

-13

)

29.1 (22.5)

N=20000

2.0×10

-13

(3.7×10

-13

)

264.7

(154.2)

N=30000

1.4×10

-13

(2.1×10

-13

)

730.8

(393.3)

N=40000

2.5×10

-13

(5.6×10

-13

)

1555.3

(784.8)

N=50000

2.8×10

-13

(1.4×10

-12

)

2497.1

(1339.3)

N=60000

1.4×10

-13

(2.2×10

-13

)

3641.7

(1957.0)

Before applying them to Gaussian process

regression, a large number of numerical experiments

are also performed for the efficient and economical

vector-storage version of the Toeplitz algorithms.

Random covariance matrices are generated and

tested as in the previous subsection. Table 3 shows

the numerical accuracy and execution time of the

algorithms (the standard deviation is given in

brackets). The results substantiate the efficacy of the

vector-storage Toeplitz computation on large

datasets.

5 WIND TURBINE DATA

The measurement data for the wind turbine rotor

speed consist of a run of 600 seconds sampled at

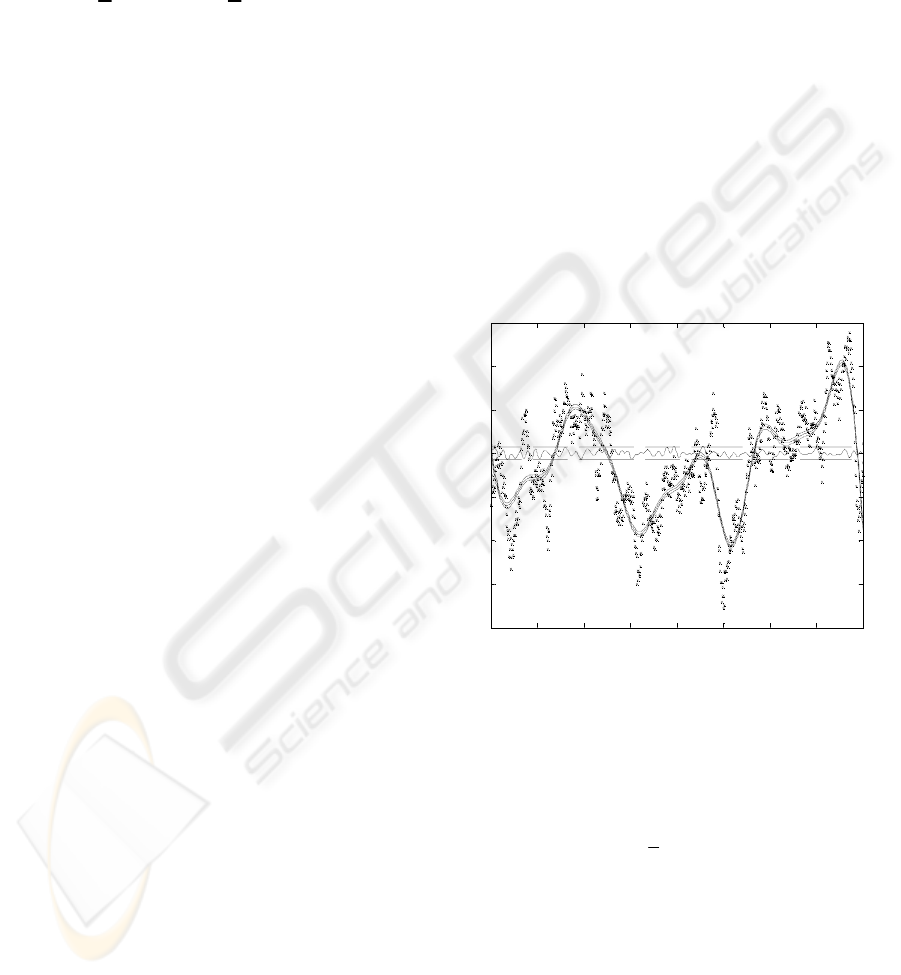
40Hz. A typical section, from 200s to 400s, is shown

in Figure 3. The data has a long length-scale

component due to variations in the aerodynamic

torque, caused by changes in the wind speed and the

pitch angle of the rotor blades, and a short length-

scale component due to the structural and electro-

mechanical dynamics of the machine. From Figure

3, these two components can be clearly seen as can

the poor quality of the data.

200 220 240 260 280 300 320 340 360 380 400

24.5

25.5

26.5

27.5

Data

Seconds

Figure 3: Rotor speed measurements from 200s to 400s

265 266 267 268 269 270 271 272 273 274 275

24.5

25.5

26.5

27.5

Long-length scale prediction and confidence intervals

Seconds

Data

Prediction

Std Dev

Figure 4: Rotor speed prediction, confidence intervals and

data from 265s to 275s

200 220 240 260 280 300 320 340 360 380 400

24.5

25.5

26.5

27.5

Long-length scale prediction and confidence intervals

Seconds

Figure 5: Rotor speed prediction with confidence intervals.

WIND TURBINE ROTOR ACCELERATION: IDENTIFICATION USING GAUSSIAN REGRESSION

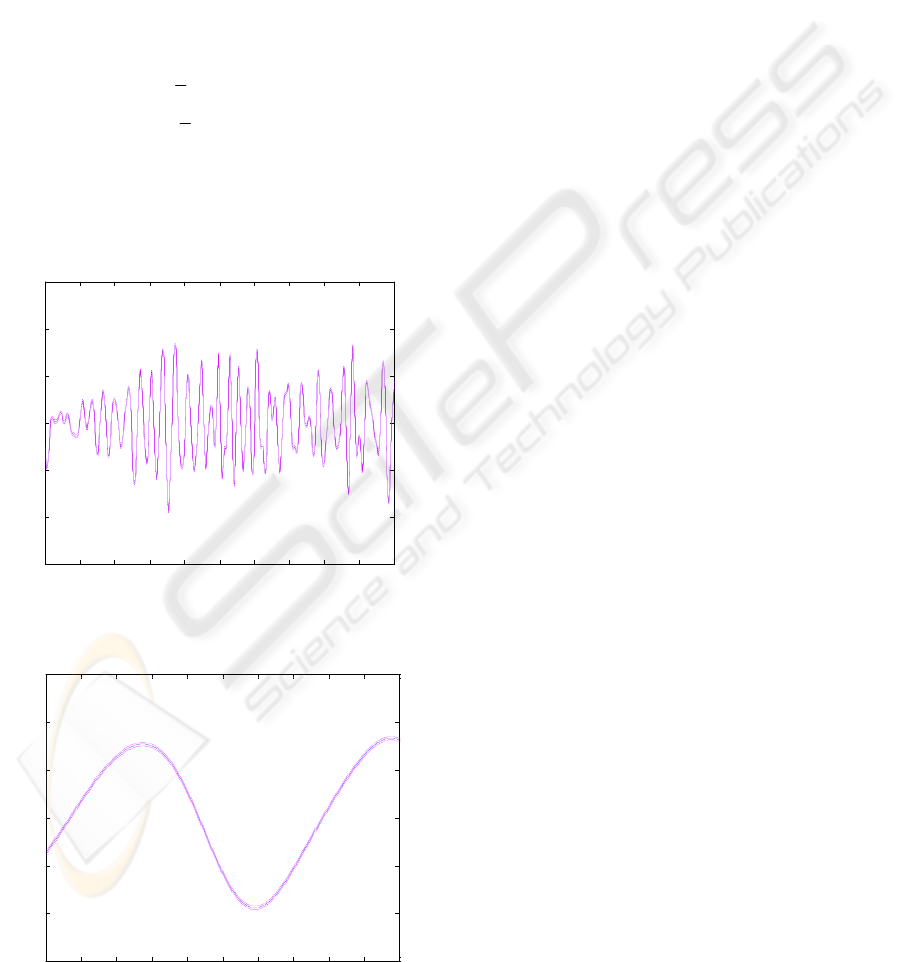
It is required to estimate the long-length-scale

component in the rotor speed. Since the structural

and electro-mechanical dynamics only induce small

oscillations in the measured values, a prediction of

the rotor speed using (8) is appropriate with f

and g

the long and short-length components respectively.

The covariance function for f

is chosen to have the

form (9) with hyperparameters a

and d

as is the

covariance function for g

with hyperparameters a

and d

. The measurement noise is assumed to be

Gaussian white noise with variance b. Hence, the

prior covariance for the measurements, y

, at time, t

are

bda

+−−+

−−=

])tt(exp[

])tt(exp[]y,y[E

jig

jif

fji

(13)

Given the data, the hyperparameters are adapted to

maximize the likelihood. Since there are 24,000 data

values, it is necessary to use the vector-storage

Toeplitz algorithms of Section 4.2.

200 220 240 260 280 300 320 340 360 380 400

-1.5

-1

-0.5

0.5

1.5

Derivative prediction with confidence intervals

Seconds

Figure 6: Derivative prediction with confidence intervals

265 266 267 268 269 270 271 272 273 274 275

-1.5

-1

-0.5

0.5

1.5

Derivative prediction with confidence intervals

Seconds

Figure 7: Derivative prediction with confidence intervals

A section, from 200s to 400s, of the prediction for

the rotor speed, i.e. the long length-scale component,

together with the confidence intervals is shown in

Figure 5 and a typical short section, from 265s to

275s, in Figure 4. From the latter, it can be seen that

the rotor speed has been successfully extracted.

However, it is not the rotor speed per se that is of

interest but its derivative. A section, from 200s to

400s, of the prediction for the derivative of the rotor

speed together with the confidence intervals is

shown in Figure 6 and a short section, from 265s to

275s, in Figure 7.

6 CONCLUSIONS

From poor quality wind turbine rotor speed

measurements, the rotor speed and acceleration are

estimated within narrow confidence intervals using

Gaussian process regression. To do so, two issues

are addressed. Firstly, the rotor speed is extracted

from a combined rotor speed and generator speed

measurement. A novel adaptation of Gaussian

process regression based on two independent

processes rather than a single process is presented.

Secondly, efficient algorithms for the manipulation

of large matrices (24,000x24,000) are required. The

Toeplitz nature of the matrices is exploited to derive

novel fast algorithms for the Gaussian process

methodology that are memory efficient.

ACKNOWLEDGEMENTS

This work was supported by Science Foundation

Ireland grant, 00/PI.1/C067, and by the EPSRC

grant, GR/M76379/01

REFERENCES

Gibbs, M. N., 1997. Bayesian Gaussian processes for

regression and classification, Ph.D. thesis, Cambridge

University.

Gibbs, M. N., and Mackay, D. J. C., 2000. Variational

Gaussian process classifiers, IEEE Transactions on

Neural Networks, Vol. 11, pp. 1458-1464.

Golub, G. H., and Van Loan, C. F. , 1996. Matrix

Computations. Baltimore: Johns Hopkins University

Press.

Leith, D. J., Leithead, W. E., Solak, E., and Murray-

Smith, R., 2002. Divide and conquer identification

using Gaussian process priors, Proceedings of the 41st

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

IEEE Conference on Decision and Control, Vol. l 1,

pp. 624-629.

Leithead, W. E., Solak, E., and Leith, D., 2003a. Direct

identification of nonlinear structure using Gaussian

process prior models, Proceedings of European

Control Conference, Cambridge.

Leithead, W. E., Hardan, F., and Leith, D. J., 2003b,

Identification of aerodynamics and drive-train

dynamics for a variable speed wind turbine,

Proceedings of European Wind Energy Conference,

Madrid.

Leithead, W. E., Kian Seng Neo, Leith, D. J., 2005.

Gaussian regression based on methods with two

stochastic processes, to be presented, IFAC, Prague,

2005.

Mackay, D. J. C., 1998. Introduction to Gaussian

processes. In Neural Networks and Machine Learning,

F: Computer and Systems Sciences (Bishop, C. M.,

Ed.), Vol. 168, pp. 133-165, Springer: Berlin,

Heidelberg.

O’Hagan, A., 1978. On curve fitting and optimal design

for regression, J. Royal Stat Soc. B, 40, pp. 1-42.

Rasmussen, C. E., 1996. Evaluation of Gaussian processes

and other methods for non-linear regression, Ph.D.

thesis, University of Toronto.

Sambu, S., Wallat, M., Graepel, T., and Obermayer, K.,

2000. Gaussian process regression: active data

selection and test point rejection, Proceedings of the

IEEE International Joint Conference on Neural

Networks, Vol. 3, pp. 241-246.

Shi, J. Q., Murray-Smith, R., and Titterington, D. M.,

2003. Bayesian regression and classification using

mixtures of multiple Gaussian processes, International

Journal of Adaptive Control and Signal Processing,

Vol. l 17, pp. 149-161.

Solak, E., Murray-Smith, R.,. Leithead, W. E., Leith, D.,

and Rasmussen, C. E., 2003. Derivative observations

in Gaussian process models of dynamic systems,

Advances in Neural Information Processing Systems,

Vol. 15, pp. 1033-1040, MIT Press.

Williams, C. K. I., 1999. Prediction with Gaussian

processes: from linear regression to linear prediction

and beyond, Learning in Graphical Models (Jordan,

M. I., Ed.), pp. 599-621.

Williams, C. K. I., and Barber, D., 1998. Bayesian

classification with Gaussian processes, IEEE

Transactions on Pattern Analysis and Machine

Intelligence, Vol. l 20, pp. 1342-1351.

Yoshioka, T., Ishii, S., 2001. Fast Gaussian process

regression using representative data, Proceedings of

International Joint Conference on Neural Networks,

Vol. l 1, pp. 132-137.

WIND TURBINE ROTOR ACCELERATION: IDENTIFICATION USING GAUSSIAN REGRESSION