ON-LINE SUPERVISED ADJUSTMENT OF THE CORRECTING

GAINS OF FRACTIONAL ORDER HOLDS

A. Bilbao-Guillerna, M. De la Sen and S. Alonso-Quesada

Instituto de Investigación y Desarrollo de Procesos, Facultad de Ciencia y Tecnología,

Universidad del País Vasco, Aptdo. 644 de Bilbao, 48080-Bilbao (Spain)

Keywords: FROH, multimodel, switching techniques.

Abstract: A discrete control using different possible discretization models of a continuous plant is presented. The

different models of the scheme are obtained from a set of different discretizations of a continuous transfer

function under a fractional-order-hold of correcting gain [1,1]

∈

− (β-FROH). The objective is to design a

supervisory scheme which is able to find the most appropriate value for the gain β in an intelligent design

framework. A tracking performance index evaluates each possible discretization and the scheme chooses the

one with the lowest value. Two different methods of adjusting this value are presented and discussed. The

first one selects it among a fixed set of possible values, while in the second one the value of

can be

updated by adding or subtracting a small quantity. Simulations are presented to show the usefulness of the

scheme.

1 INTRODUCTION

This paper deals with the problem of controlling a

known continuous plant using an appropriate

discrete controller selected from a group of possible

ones. Each possible controller is associated to a

different discretization of the plant (Alonso-Quesada

and De la Sen, 2004; Broeser, 1995; Ibeas et al.

2002; Middleton et al. 1988; Narendra and

Balakrishnan, 1995 and 1998). A fractional order

hold is used in order to generate the continuous input

from the discrete signal. The choice of the

gain

of the FROH device should be taken into account,

since the discretization zeros depend on its election

(Åström and Wittenmark, 1984; Bárcena et al.,

2000; Ishitobi, 1996). In order to find the most

appropriate discretization of the continuous plant,

two different methods are proposed. In the first one,

a set of fixed values of

are used to generate a

group of discretization models. Obviously, only one

value of

can be used at each time, but since the

plant is supposed to be known we can simulate the

behavior of all the possible discretization. A tracking

index evaluates the performance of all of them and

the system uses the one with the lowest value to

implement the FROH device and the control law. In

the second method, we only allow the system to

update the value of

to a close one. The behavior

of the current discretization is compared with the

behavior of other two possible discretizations. One

model using a gain

being slightly larger and the

other one using a

being a bit smaller. The second

method has a slower convergence to an optimum

value of

, but it avoids the transient in the output

which may occurred when

is changed a large

value. Some computer simulations about two

practical cases will be given in order to highlight the

usefulness of the proposed multi-model scheme. In

the first case, a DC motor is simulated. In the second

one, we deal with a LCR parallel circuit (Tank

circuit).

2 PROBLEM DESCRIPTION

In this paper, we are dealing with the problem of

controlling a continuous plant by using a set of

discrete controllers. Each of those controllers is

associated to a different discretization of the

continuous plant under a fractional order hold

(FROH) with a correcting gain β. The plant

continuous input signal obtained from a β-FROH

follows this equation,

266

Bilbao-Guillerna A., De la Sen M. and Alonso-Quesada S. (2005).

ON-LINE SUPERVISED ADJUSTMENT OF THE CORRECTING GAINS OF FRACTIONAL ORDER HOLDS.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 266-271

DOI: 10.5220/0001178302660271

 SciTePress

()

ut u t kT

−

⎡⎤

−

=+ −

⎢⎥

⎣⎦

(1)

for

()

kT t k T≤< + , where

T is the sampling

time,

[1,1]

∈− and ()

uukT= is the input signal

to the hold at

tkT= for each integer 0k ≥ . For

= and 1

= the zero-order-hold (ZOH) and the

first-order-hold (FOH) are obtained respectively.

The discrete transfer function of a continuous one,

()

, results to be as follows,

() ()

() () () ()

() ()

Ns Bz

Hz Z h s Gs Z h s

Ds Az

ββ

⎡⎤

=⋅= ==

⎢⎥

⎣⎦

...

bz b z b

zaz a

−

+++

(2)

where,

(1 ) 1

() 1

TsT

hs e

Ts s

−−

−

⎛⎞

−−

=− +

⎜⎟

⎝⎠

the transfer function of a β-FROH, Z the Z-transform

and the polynomial degrees,

deg( ) 0

deg( )

deg( ) 1 0

Dif

⎧

⎨

+≠

⎩

and

deg( )mB= . Moreover, 1nm=+ if

deg( ) deg( )ND< or nm

if deg( ) deg( )ND= .

Since the use of a ZOH is more common in practice

than the use of a FROH,

()

z may be calculated

just using ZOH devices in the following way,

[]

(1) ()

() () () ()

zzGs

Hz Zh s Gs Z h s

zTzs

ββ

−−

⎡⎤

=⋅+ ⋅

⎢⎥

⎣⎦

(3)

where,

()

−

is the transfer function of a

ZOH device. The following standard assumptions

are made:

1-It is assumed that both polynomials

()Ns and

()Ds are known.

2-The reference model,

mmm

BA= , is

exponentially stable, i.e. all the roots of

satisfy

≤− for some

(

]

0,1

∈ .

3-There exists a known convex and compact subset

D ⊆ℜ of the parameter space where the real

parameter vectors belong to so that for all plant

parameterization in D the polynomials A and B are

coprime.

2.1 Basic adaptive controller

The transfer function of the reference model is,

() () ()

()

() ()

BzBzAz BA

zA z AA

−

== (4)

where

()

contains the free-design reference

model zeros, ()Bz

−

is formed by the

unstable(assumed known) plant zeros and

()

z is a

polynomial including the eventual closed-loop stable

pole-zero cancellations which are introduced when

necessary to guarantee that the relative degree of the

reference model is non less than that of the closed-

loop system so that the synthesized controller is

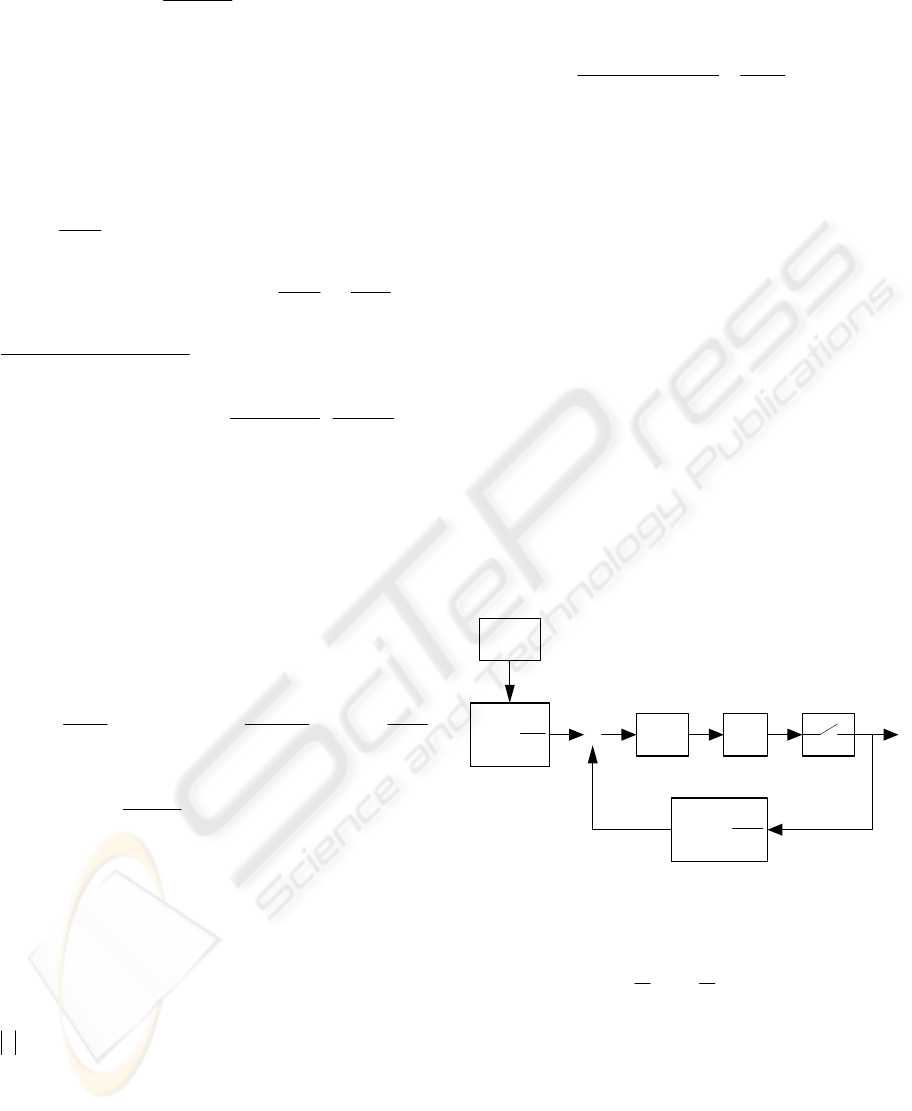
causal. A basic control scheme is displayed in figure

2. Then, we will consider the polynomials

R ,

and

(T depends only on the reference model zeros

polynomial which is of constant coefficients) where

TBA= and

R (monic),

S are the unique

solutions with degrees fulfilling

(

)

deg 2

Rni

− ,

(

)

deg 1

Si=−,

()

deg 2

An=

of the polynomial diophantine equation

01, 0kk kk k m k k k m

R BS BAA AR BS AA

+−

+= ⇔ += (5)

with

1,kkk

RBR

at every sampling instant. Figure 1

shows the control scheme.

Reference

Input

⊗

FROH G(s)

()

,ck

()yt

()ut

−

Figure 1: Basic control scheme

From (4)-(5), perfect matching is achieved through

the control signal:

,kckk

uu y

=−

(6)

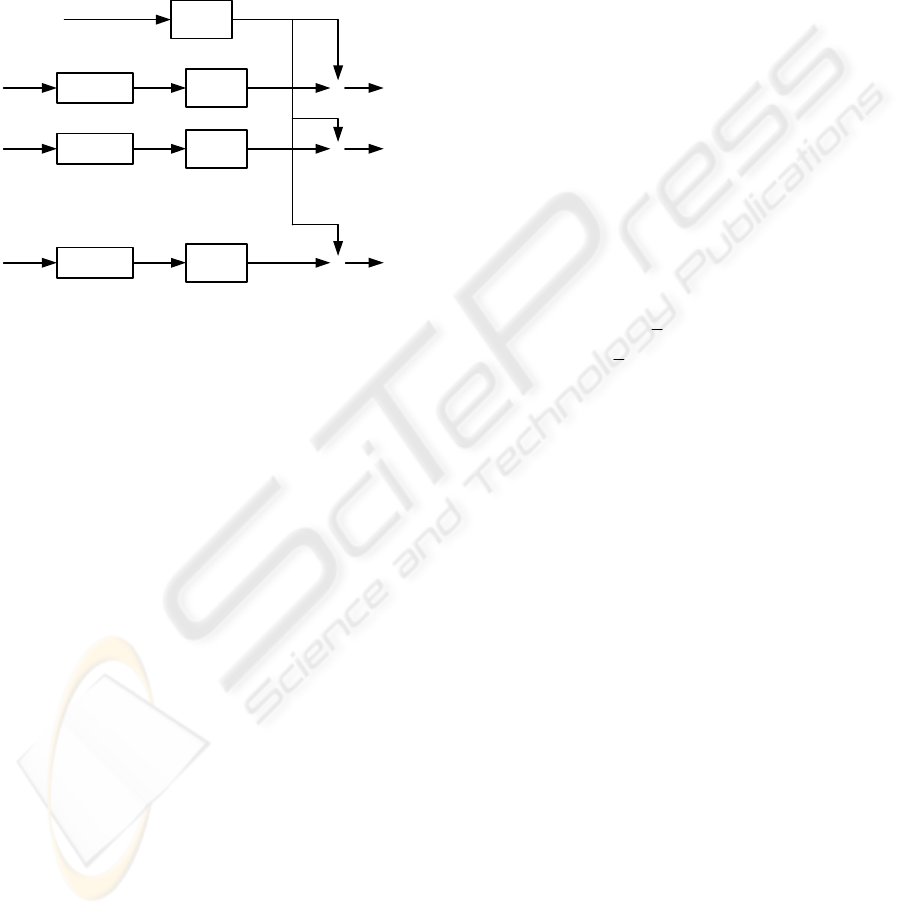
2.2 Multimodel scheme A

In order to find the most appropriate value of the

gain

, we consider a set of possible design values

of it and the corresponding discrete transfer function

is obtained,

ON-LINE SUPERVISED ADJUSTMENT OF THE CORRECTING GAINS OF FRACTIONAL ORDER HOLDS

267

()

() ()· ()

zZhsGs

⎡⎤

⎣⎦

for 1

n≤≤A (7)

where

n is the number of possible values of

and

()

is used to indicate its value for the

A model.

Once all the possible discrete transfer function are

obtained for the whole set of intended values, we can

simulate the performance of all of them when the

previous control law is applied and compared their

responses with the desired reference output.

()

()Gs

(1)

()FROH

()Gs

(2)

()FROH

()

FROH

⊗

()

1,k

2,k

()ut

()

()yt

()

()et

()

−

Figure 2: Multimodel scheme

Each plant input is generated by using the control

law (6), where the reference transfer function (4),

which should be matched, is the corresponding

FROH discretization of

()

Gs. In other words, we

have as many reference transfer functions as the

number of possible values of

we are considering.

2.3 Switching rule and identification

performance index

The objective of the supervisor is to evaluate the

tracking performance of the possible controllers

operating on the plant for the given reference model

with the aim of choosing the current controller from

the set of parallel controllers. The proposed

performance index is:

()

(1)

() ()

jkM

yyd

τττ

−

=−

∑

∫

(8)

for

n≤<A , where, (0,1]

∈ and 0M > are

design real parameters.

is a forgetting factor

which allows us to give more importance to the last

time interval.

2.4 Multimodel scheme B

In this case, instead of letting the system to choose

among any of the possible values of

, we only

allow the system to change to a close value. The

system starts with an arbitrary value and the tracking

performance is compared with the tracking

performance of two possible close values of

. One

being a bit larger and the other one a bit lower. With

this method, when we compare their responses, the

system can only choose among three possible cases.

In other words, n

is always three. However, these

three possible values are not going to be constant

and they are updated. If the system chooses one of

the two close values of

, then it becomes the

active one and the other two are chosen by adding

and subtracting a quantity to it. If the system chooses

to maintain the same value of

, then the other two

possible values are updated as well by considering

other two closer values of

. In order to explain

this method, the following algorithm describes how

it works,

a) At

sample the active value of

. Other

two values,

sup

βββ

+∆ and

inf

βββ

=−∆ are

used for simulation. Suppose that the last

switching took place at

k sample.

b) If

(1)kTkTMT+−≥ , then the tracking

performance of the three possible discretizations are

compared and the one with the lowest value of (8) is

used in the FROH device.

c) If the system chooses to maintain the same value

, first

∆

is decreased and then

sup

and

inf

are updated.

- if

1kk

ββ

then / mf

ββ

∆

=∆ (with 1mf > ) and

sup inf

kk kk

ββββββ

+∆ = −∆

d) If the system chooses another value,

∆

maintains its value and

sup

and

inf

are calculated

by adding and subtracting this value

- if

sup

1kk

ββ

= then

sup

ββ β

+∆,

inf

1kk

ββ

- if

inf

1kk

ββ

= then

sup

1kk

ββ

inf

ββ β

=−∆

Note that there are two supervisory hierarchized

levels of action of this intelligent system, namely:

The basic control: It consists of generating

via u

from (5) for each of the discrete

models integrated in the multi-model

scheme.

The choice of

: The model and gain

of the FROH is on-line selected by a

switching rule via minimization of the

supervisory performance index (8).

ICINCO 2005 - ROBOTICS AND AUTOMATION

268

3 SIMULATION RESULTS

In this section two different cases are presented in

order to show the usefulness of the proposed

scheme. The first one simulates a DC motor, while

the second one deals with a resonant circuit. In both

cases, the two different multi model methods are

used.

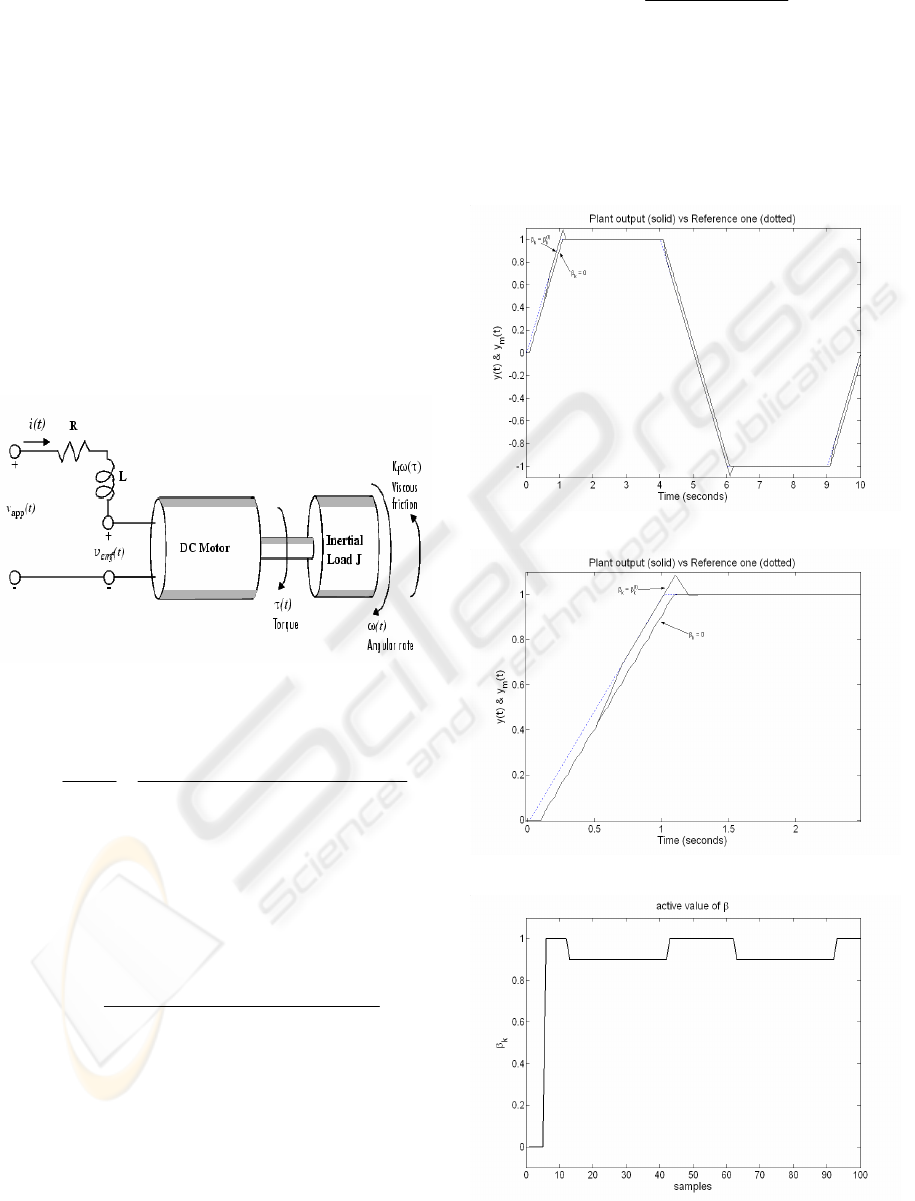
3.1 DC motor

A simple model of a DC motor driving an inertial

loads shows the angular rate of the load,

()wt , as the

output and applied voltage,

()

app

vt, as the input. The

objective is to control the angular rate by varying the

applied voltage (Krishnan, 2001). Fig 3 shows a

standard model of the DC motor.

Figure 3: DC motor model

The transfer function of a DC motor can be

described as:

()

() ( )

app

ffbm

vs LJs LK JRsRKkk

++++

The simulation is done by using the following

parameters,

0.5R =Ω, 1.5LmH= , 0.05 /

kNmA= ,

0.00025 / /

Nm rad s= , 0.0001 / /

kNmrds= ,

0.025 / /

kVrads= , which give the continuous

transfer function,

0.05

()

3.75·10 0.0001252 0.0013

−

The first simulation uses the first multimodel case.

The set of possible gains

are:

()

1( 1)/10

=− − for 121i≤≤

The sampling time is chosen 0.1s and the residence

time is 5 samples. The reference output is obtained

from the following continuous transfer function,

500000

()

200 12500

Figures 4 shows the plant output when the

value

is maintained fixed and when it is updated. The

dotted line indicates the desired reference output.

Figure 5 shows the active value of

during the

whole simulation. It is obvious that the tracking

performance is improved by selecting an appropriate

value of the gain

Figure 4 a: Plant output with method A

Figure 4 b: Plant output with method A (zoom over first

seconds)

Figure 5: active value of

with method A

ON-LINE SUPERVISED ADJUSTMENT OF THE CORRECTING GAINS OF FRACTIONAL ORDER HOLDS

269

The simulation is repeated with the second

multimodel method. Figure 6 shows the plant output

and figure 7 the on-line active value of

selecting

via switchings using (8). The initial value for

∆

0.2 and m

is 1.2.

Figure 6: Plant output with method B

Figure 7: Active value of

with method B

In this case, it takes more time to achieve a good

value of

as we do not let it to take the best one in

the first switching. One could think that this is a bad

option. However, next simulation will show that

sometimes this method have a better performance.

3.2 Resonant Circuit (Tank Circuit)

A resonant circuit is simply an LCR circuit with a

zero-pole cancellation at

0s = at the resonance

frequency (Floyd, 2003).

Figure 8: Parallel RLC circuit

Usually the effect of the resistance is small

compared to the size of the inductance and the

capacitance. This leads to highly resonant behavior.

In this work, we will consider a parallel RLC circuit

with a transfer function,

()

out

RC LC

The resonant frequency

w of a resonant circuit is

the frequency corresponding to the peak value of the

transfer function and it occurs when

wLC= .

Simulations are performed for a circuit with

parameters

100R

Ω , 2LmH

and 300CpF= .

Replacing these values, the transfer function results

to be:

2712

3.333·10

()

3.3333·10 1.667·10

The reference output is obtained from the following

continuous transfer function:

26 12

1.667·10

()

1.667·10 1.667·10

The resonant frequency is located in

205

fkHz

== . Both multi-model schemes

with the same parameters as in previous section are

simulated. The reference input is generated as the

sum of four of four sinusoidal signals of different

frequencies {0.1w

, w

, 10w

, 100w

}. It is suited

for the circuit to select the one at the resonant

frequency. Figure 9 shows the plant output in both

cases together with the reference output. In this case,

although both outputs tend to the desired one, the

second multi-model has a better transient behavior in

the first time interval. This occurs, because when we

change the value of

in a big quantity, the plant

behavior suffers a little transient as it can be shown.

However, with small changes this transient is found

to be smaller.

Figure 9: Plant outputs using method 1 and 2

ICINCO 2005 - ROBOTICS AND AUTOMATION

270

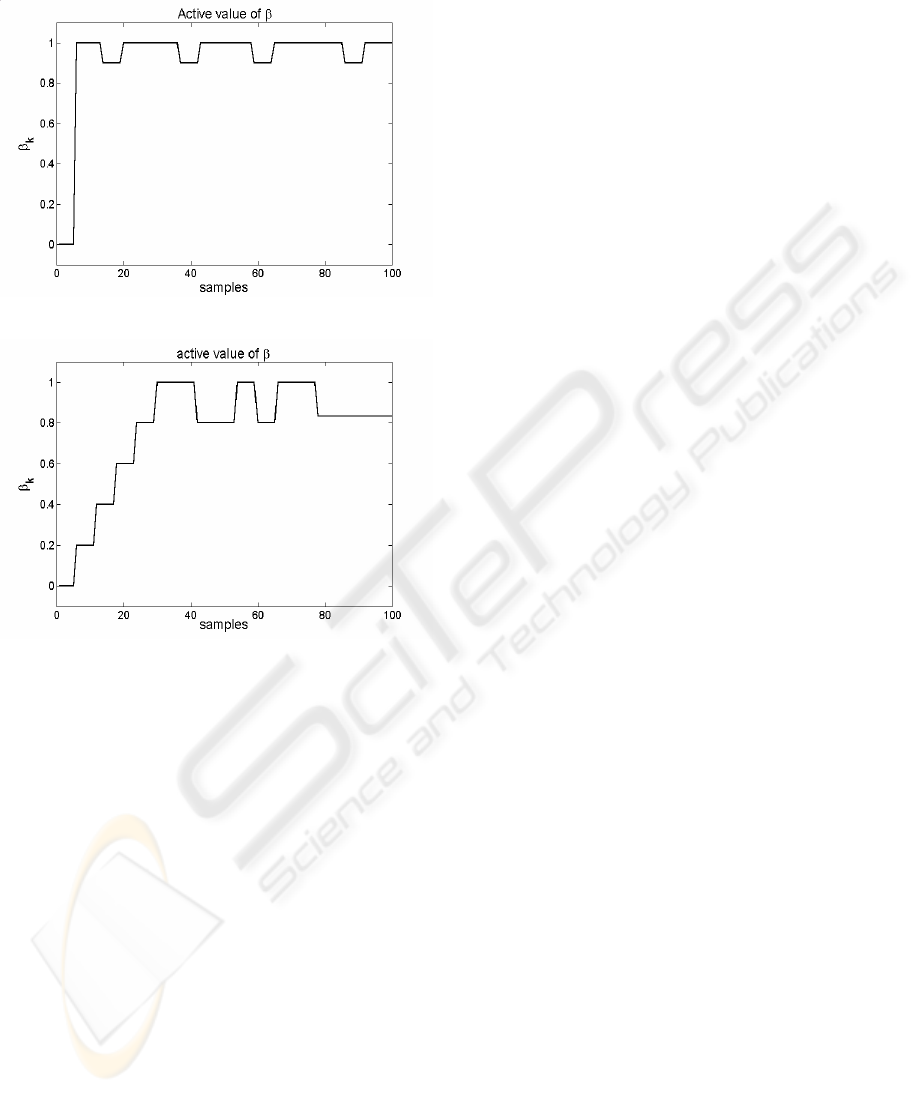
Finally, figures 10 and 11 show the active value of

in both simulations.

Figure 10: Active value of

with method 1

Figure 11: Active value of

with method 2

4 CONCLUSIONS

In this paper, a multi-model based discrete control

scheme for a continuous plant has been presented.

The different discrete models are obtained by

discretizing the continuous plant under a FROH

device. The scheme is designed to find the value of

the gain

which leads to the best tracking

performance. Two different methods have been

presented for this purpose. The first one selects the

current value of the gain among a fixed set of

possible values. The second one updates

only to a

close value, avoiding bad transients which may

occur when the changing is big. Finally, the

proposed schemes have been used in two practical

cases. Simulations showed that an appropriate

choice of the value of

leads to a good tracking

performance, even if a continuous plant is under

control by a discrete controller. Moreover, the

advantages and disadvantages of both methods have

been figured out through the simulation results.

ACKNOWLEDGEMENTS

The authors are very grateful to MEC and UPV by

partial supports through Research Grants DPI 2003-

00164 and Scholarship of A.Bilbao BES-2004-4261,

and 9/UPV 00I06.I06-15263/2003.

REFERENCES

Alonso-Quesada, S. and De la Sen, M., 2004. ‘Robust

Adaptive Control with Multiple Estimation Models for

Stabilization of a Class of Non-inversely Stable Time-

varying plants’, Asian Journal of Control, Vol. 6, Nº

1, pp. 59-73.

Åström, K.J. and Wittenmark, B., 1984. ‘Zeros of

Sampled Systems’, Automatica, 20, 31-38.

Bárcena, R., De la Sen, M. and Sagastabeitia, I., 2000

‘Improving the Stability of the Zeros of Sampled

Systems with Fractional Order Hold’, IEE Proc.

Control Theory and Applications, 147, Vol. 4, pp.456-

464.

Broeser, P.M.T., 1995. ‘A Comparison of Transfer

Functions Estimators’, IEEE Transactions on

Instrumentation and Measurement, Vol. 44, Nº 3,

pp.657-661.

Floyd, T., 2003. ’Electronic Circuits Fundamentals’,

Prentice Hall.

Ibeas, A., De la Sen, M. and Alonso-Quesada, S., 2002. ‘A

Multiestimation Scheme for Discrete Adaptive Control

which Guarantees Closed-loop Stability’, Proc. of the

WSEAS Multiconference on Systems, pp.6301-

6308.

Ishitobi, M., 1996. ‘Stability of Zeros of Sampled Systems

with Fractional Order Hold’, IEE Proc., Control

Theory and Applications, 143, pp. 296-300.

Krishnan, R., 2001. ‘Electronic Motor Drives: Modelling,

Analysis and Control. Book 1’, Prentice Hall.

Middleton, R.H., Goodwin, G.C. Hill, D.J and Mayne,

D.Q., 1988. ‘Design Issues in Adaptive Control’, IEEE

Transactions on Automatic Control, Vol. 33, Nº 1,

pp.50-58.

Narendra, K. S. and Balakrishnan, J., 1994. ‘Improving

Transient Response of Adaptive Control Systems

using Multiple Models and Switching’, IEEE

Transactions on Automatic Control, Vol. 39, No. 9,

pp. 1861-1866.

Narendra, K. S. and Balakrishnan, J., 1997 ‘Adaptive

Control Using Multiple Models”, IEEE Transactions

on Automatic Control, Vol. 42, No. 2, pp. 171-187.

ON-LINE SUPERVISED ADJUSTMENT OF THE CORRECTING GAINS OF FRACTIONAL ORDER HOLDS

271

ICINCO 2005 - ROBOTICS AND AUTOMATION

272