
EXTRAPOLATION WITH A SELF-ORGANISING
LOCALLY INTERPOLATING MAP
Controlling nonlinear Processes with ambiguous inverse Behaviour
Helge Hülsen, Sergej Fatikow
Division of Microrobotics and Control Engineering, University of Oldenburg
Uhlhornsweg 84, 26111 Oldenburg, Germany
Keywords: Associative Networks, Self-Organisation, Self-Supervised Learning, Extrapolation.
Abstract: Besides their typical classification task, Self-Organizing Maps (SOM) can be used to approximate input-
output relations. They provide an economic way of storing the essence of past data into input/output support
vector pairs. In this paper the SOLIM algorithm (Self-Organising Locally Interpolating Map) is reviewed
and an extrapolation method is introduced. This framework allows finding one inverse of a nonlinear many-
to-one mapping by exploiting the inherent neighbourhood criteria of the SOM part. Simulations show that
the performance of the mapping including the extrapolation is comparable to other algorithms.
1 INTRODUCTION
Several derivates of Self-Organizing Maps (SOM)
have been successfully applied to the control of
nonlinear, dynamic processes, which can also have
ambiguous inverse system behaviour (Barreto 2003).
A very important enhancement of the classical
SOM from Kohonen (overview in (Kohonen 2001))
has been the Local Linear Map (LLM) from Ritter et
al. (Ritter 1992) that has been further developed and
applied to various problems in robotics (Moshou
1997) and system dynamics modelling (Principe
1998)(Cho 2003). An LLM not only divides an input
space into subspaces as a standard SOM does but
assigns a local linear model to each subspace and
thus performs a mapping to an output space. By de-
scending on the error function of the local models
better estimates for these models are found. Re-
markable was the ability of the algorithm to learn a
meaningful mapping for processes with an ambigu-
ous inverse behaviour. This effect results from ap-
plying Kohonen's self-organising rule to update the
local model that has been responsible for the output
and all of its neighbours. The drawbacks of the LLM
are its discontinuities in the mapping at the transi-
tions between neighboured local models and the
strong dependency of the learning performance on
the Jacobians that define the linear models.
To solve the discontinuity problem Aupetit et al.
developed a continuous version of the LLM, the
Continuous Self-Organizing Map (CSOM) (Aupetit
1999)(Aupetit 2000), but still the mapping and the
learning was depending on the Jacobians and, in
addition, depending on interpolation parameters.
Walter followed another approach by avoiding a
discretisation of the input space and sharing the in-
fluence of each model on the output (Walter
1997)(Walter 2000). The influences are found with
help of an optimisation algorithm. On one hand this
leads to a continuous mapping, which can be opti-
mised with respect to different user-defined criteria
to resolve ambiguities. On the other hand this opti-
misation can be a relatively high computational load
for high network dimensions. Furthermore, under
certain conditions, there are problems with extrapo-
lation and the continuity of the mapping.
The Self-Organising Locally Interpolating Map
(SOLIM) from the author (Hülsen 2004a)(Hülsen
2004b) interpolates between different models with-
out any additional parameters. Learning is per-
formed in a self-supervised structure, which can be
interpreted as identification with exchanged input
and output. The main drawback of this algorithm is
the high computational effort for big networks,
which is in great part due to the extrapolation princi-
ple. In addition, extrapolation was only performed in
173
Hülsen H. and Fatikow S. (2005).
EXTRAPOLATION WITH A SELF-ORGANISING LOCALLY INTERPOLATING MAP - Controlling nonlinear Processes with ambiguous inverse
Behaviour.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and
Control, pages 173-178
DOI: 10.5220/0001177801730178
Copyright
c
SciTePress
a small area around the main mapping area. This
paper will introduce a new extrapolation algorithm
for the SOLIM.
The paper is organised as follows: In the next
section the fundaments of the SOLIM algorithm will
be explained. In section three the new extrapolation
principle will be presented in detail, followed by
simulations in section four. The paper ends with the
conclusion.
2 SOLIM: SELF-ORGANIZING
LOCALLY-INTERPOLATING
MAP
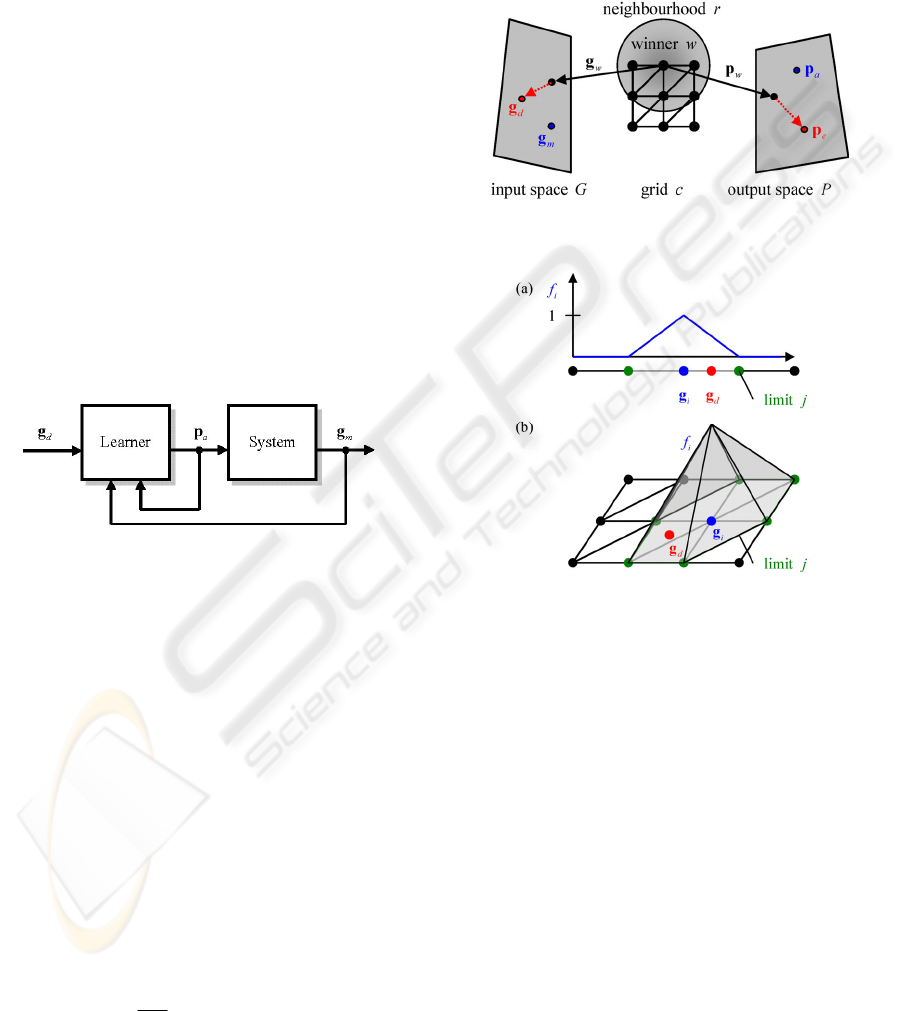
The SOLIM is a framework that shall perform two
tasks in a control context (
Figure 1):
1. Map from a desired state of a process
d
g
to
actuation parameters
a
p
to reach that state.
2. Use that pair of measured state
m
g
and actua-
tion parameters
a
p
to adapt the mapping.
Figure 1: Self-supervised learning (Barreto 2004)
2.1 Mapping
As in a standard SOM (Hagan 1996), the base of
SOLIM is a grid
c
of
N
neurons with a certain
topology (Figure 2). Each neuron
i
is connected to
an input support vector
i
G
∈g and an output sup-
port vector
i
P
∈p . To perform the mapping
GP
→
an influence weight
i
f
with respect to the input vec-
tor
d
g
is calculated for each neuron. The output
vector
a
p
is then the linear combination of all out-
put support vectors
a
i
i
i
f=⋅
∑
pp
%
, (1.1)
where the weight
i
f
is scaled down to not exceed 1
if 1
otherwise
i
k
k
f
k
f
k
i
i
f
f
f
⎧
>
⎪
∑
=
⎨
⎪
⎩
∑
%
. (1.2).
The influence weights
i
f
are measures of how close
the input vector
d
g
is to the corresponding input
support vectors
i
g
. The influence weight is 1 for
di
=
gg
and decreases to 0 at the limits of the influ-
ence range of neuron
i
(Figure 3).
Figure 2: Mapping and learning with self-organizing maps
(adopted from (Ritter 1992))
Figure 3: Influence
i
f
of neuron
i
for (a) a 1D grid in a
1D input space and (b) a 2D grid in a 2D input space
The limit
j
of an influence range is defined
solely by a selection of input support vectors
j
g
. For
the case of a 1D grid there are two limits for each
input support vector (
Figure 3(a)). When the grid is
placed in a 1D input space the limits are points, in a
2D input space the limits are lines and in a 3D input
space the limits are planes. Now considering a 2D
grid there are six limits for each input support vector
(
Figure 3(b)). When the grid is placed in a 2D input
space the limits are lines and in a 3D input space the
limits are planes again. In input spaces with higher
dimensions the limits will be hyperplanes.
A limit
j
can generally be defined by a position
vector
ij
g
and a plane normal
ij
n
, whose calculation
can be found in (Hülsen 2004b). The influence
weight
ij
f
with respect to a limit
j
is calculated
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
174
with help of the relative distance
ij
d
of the input
vector
d
g
from
i
g
in the direction to the limit plane
()
()
ij d i
ij
ij ij i
d
⋅−
=
⋅−
ngg
ngg
. (1.3)
A blending function
()
i
jij
f
bd= sets the influence to
0 for
1
ij
d > , to 1 for
0
ij
d < and defines a transition
for
01
ij
d<<, i.e. the change of the influence from
one neuron to another.
The influences to the limits
j
are then combined to
the influence of the neuron
i
on the output vector
()
min
i
ij
j
f
f= . (1.4)
Finally, it should be noted that the limits are de-
fined in a way that for a 1D grid two neurons are
responsible for the output vector, for a 2D grid three
neurons are responsible, for a 3D grid four neurons
are responsible, and so on (see also (Hülsen 2004b)).
2.2 Learning
Learning is performed in the input space
G
as well
as in the output space
P
with help of the Kohonen
learning rule (Kohonen 2001). Following the rule
not only the support vector of the "winner-neuron"
w
is updated but to a certain extent
()
,,
h
wi
r
also
the support vectors belonging to a neighbourhood
r
in the grid
c
(see Figure 2). In case of learning in
the input space the winner
w
is the neuron with the
highest influence with respect to the input vector
d
g
, which in turn serves as an attractor for
w
g
and
its neighbours
()
()
() ( 1) () ( 1)
,,
ii g gdi
hwir
νν νν
ε
−−
=+⋅ ⋅−gg gg. (1.5)
g
ε
is a learning constant that, as the neighbourhood
radius
g
r
, is decreased with time. In case of learning
in the output space the winner
w
is the neuron with
the highest influence with respect to the measured
process output
m
g
. Since the process input
a
p
be-
longs to
m
g
, it can be used to find an estimate
e
p
for
w
p
by solving (1.1) for
iw
=
p
1
e
aii
iw
w
f
f
≠
⎛⎞
=−⋅
⎜⎟
⎝⎠
∑
pp p
%
%
. (1.6)
e
p
then serves as attractor for
w
p
and its
neighbours during the Kohonen update rule
()
()
() ( 1) () ( 1)
,,
ii p pei
hwir
νν νν
ε
−−
=+⋅ ⋅−pp pp . (1.7)
The Kohonen learning rule is topology conserv-
ing, which means that support vectors of neurons
that are neighbours in the grid
c
become neighbours
in the input space and output space. This property is
an inherent criterion to resolve ambiguities in the
inverse system behaviour
GP
→ , since neighbours
in the input space map to neighbours in the output
space.
3 EXTRAPOLATION WITH
SOLIM
The main contribution of this paper is to show that
extrapolation is possible within the context of the
SOLIM-algorithm. Like the SOLIM-interpolation
the extrapolation algorithm only needs to know the
support vectors in the input and output space to per-
form a reasonably accurate extrapolation. The learn-
ing algorithm can be adapted to this enhanced map-
ping in a straight-forward manner.
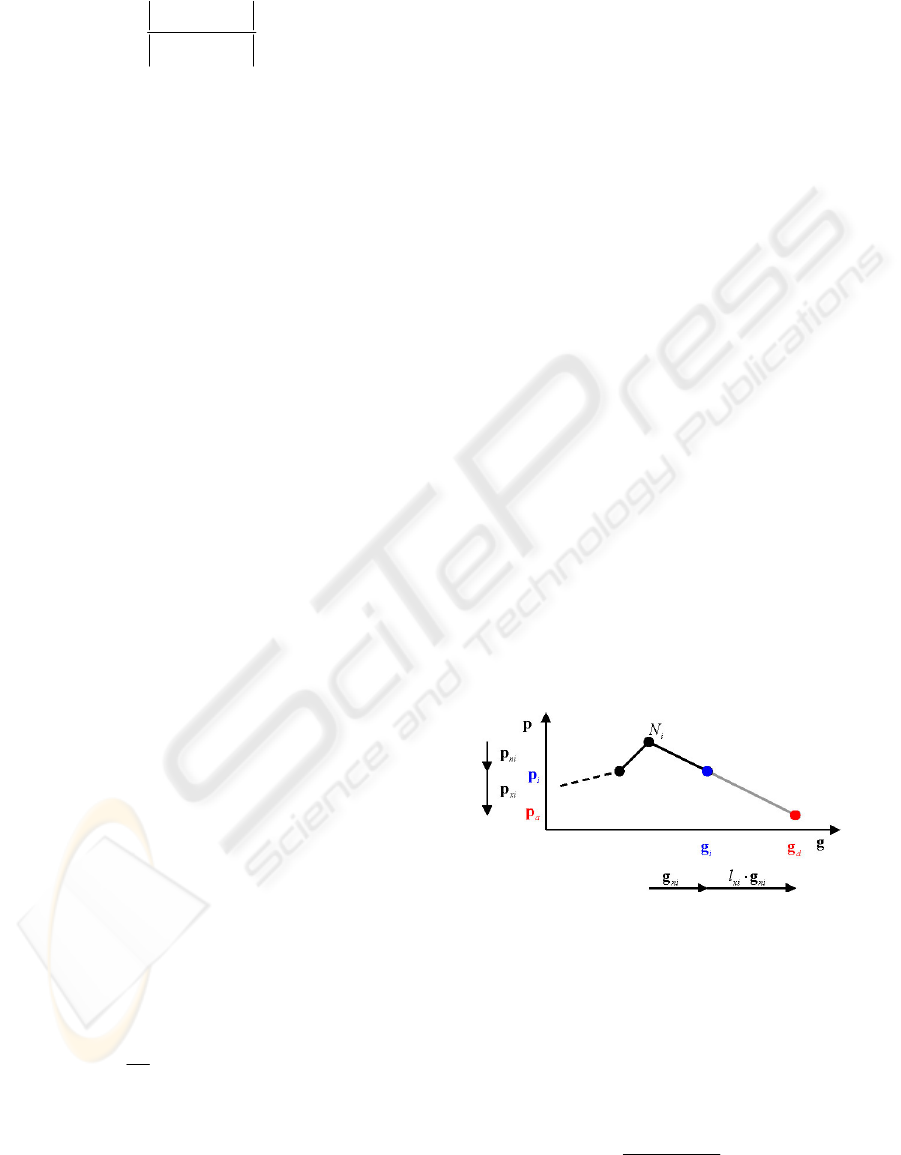
3.1 Mapping
The mapping for regions outside the grid of input
support vectors is performed by adding an extrapola-
tion component
xi
p
to each support vector
i
p
prior
to interpolating between them (Figure 4)
()
a
iixi
i
f=⋅+
∑
ppp
%
. (1.8)
Figure 4: Extrapolation component
xi
p
corresponds to
distance
x
in
i
l ⋅
g
of input vector from grid (1D grid)
The extrapolation component is computed as
x
ixin
i
l=⋅
pp
, (1.9)
where
xi
l
is a weight that defines the distance of the
input vector
d
g
from the input support vector
i
g
in
relation to
ni
g
(Figure 4, Figure 5)
()
2
d
in
i
xi
ni
l
−
=
ggg
g
. (1.10)
EXTRAPOLATION WITH A SELF-ORGANISING LOCALLY INTERPOLATING MAP - Controlling nonlinear
Processes with ambiguous inverse Behaviour
175
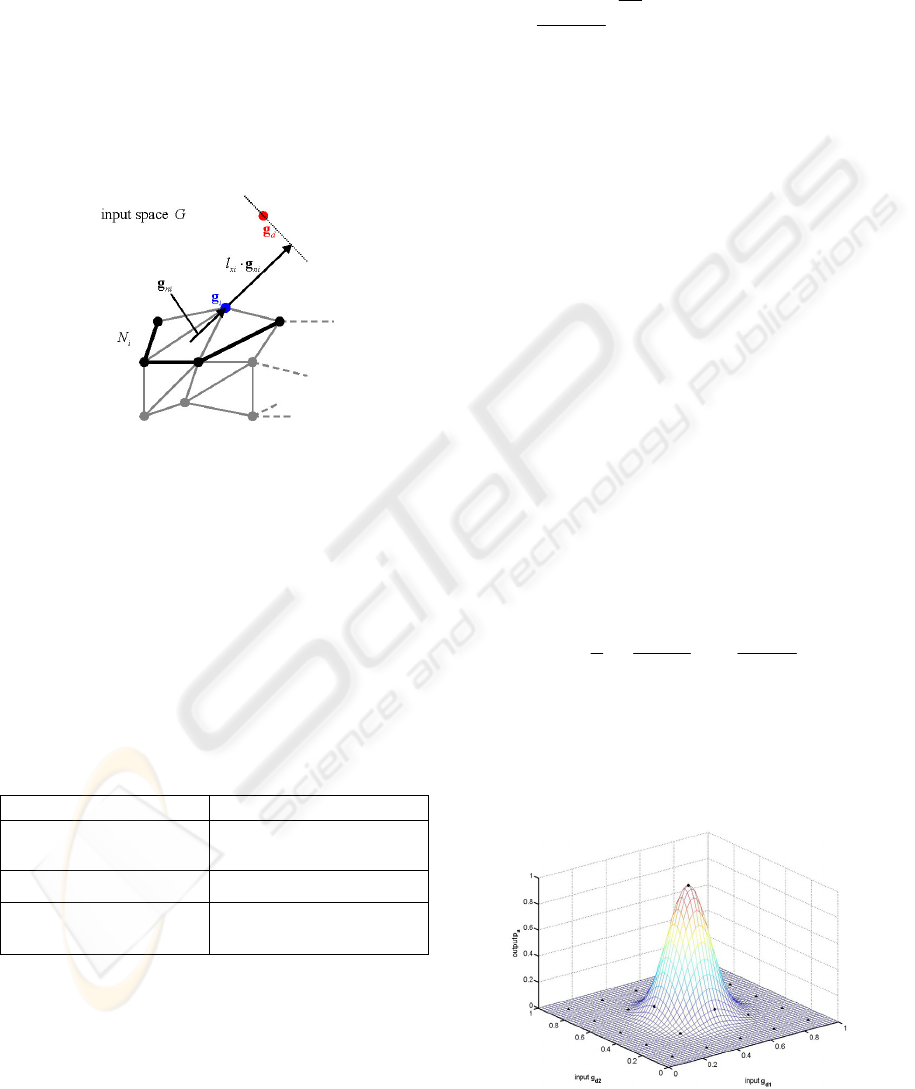
ni
g
is the mean difference vector between the input
support vector
i
g
and all input support vectors in its
limiting neighbourhood
i
N
()
i
n
iik
kN∈
=−
∑
ggg
. (1.11)
Analogously,
ni
p
is the mean difference vector be-
tween the output support vector
i
p
and all output
support vectors in its limiting neighbourhood
i
N
()
i
n
iik
kN∈
=−
∑
ppp
. (1.12)
Figure 5: Calculation of
x
in
i
l ⋅
g
in a 2D grid
The main idea behind the interpolation as well as
the extrapolation mapping is that the relation be-
tween input vector and input support vector grid is
similar to the relation between output vector and
output support vector grid (Table 1). The weights
i
f
%
and
xi
l
can therefore be applied in the input space in
the same way as in the output space. In addition,
since the calculation of the weights only depends on
the dimension of the grid
c
the mapping can be ap-
plied in both directions.
Table 1: Similarity of mapping in input and output space
input space output space
()
d
iixi
i
f≈⋅+
∑
ggg
%
()
a
iixi
i
f=⋅+
∑
ppp
%
x
ixin
i
l=⋅
gg
x
ixin
i
l=⋅
pp
()
i
n
iik
kN
∈
=−
∑
ggg
()
i
n
iik
kN
∈
=−
∑
ppp
3.2 Learning
The learning algorithm remains unchanged except
that the calculation of the estimation
e
p
for the sup-
port vector
w
p
that is most responsible for the sys-
tem output
m
g
(compare (1.6)) must take the ex-
trapolation components into account. Therefore (1.8)
must be solved for
iw
=
p
, using (1.9) and (1.12)
()
1
1
1
w
aiixi
iw
w
e
xw
xw k
kN
f
f
lk
l
≠
∈
⎛⎞
⎛⎞
−⋅+
⎜⎟
⎜⎟
⎝⎠
⎜⎟
=
+⋅
⎜⎟
+⋅
⎜⎟
⎝⎠
∑
∑
ppp
p
p
%
%
. (1.13)
It can be seen that when the extrapolation weight for
w
p
is
0
xw
l = (1.13) becomes similar to (1.6), be-
cause no extrapolation is performed.
4 SIMULATIONS
The performance of the extrapolation algorithm can
be evaluated by mapping with support vectors that
represent a 2D Gaussian bell and by learning the
inverse of a well-known function.
4.1 Mapping
For a performance measurement of the mapping 5x5
input support vectors
i
g
will be placed at the posi-
tions
{
}
,1 ,2
,
0.1,0.3,0.5,0.7,0.9
ii
gg∈ . The corre-
sponding output support vectors
i
p
will be placed at
the corresponding positions of a 2D Gaussian bell
with
0.5
µ =
and
0.1
σ
= (Figure 6)
22
,1 ,2
1
exp
2
ii
i
gµ gµ
σσ
⎛⎞
⎛⎞
−−
⎛⎞⎛⎞
⎜⎟
=−⋅ +
⎜⎟
⎜⎟⎜⎟
⎜⎟
⎜⎟
⎝⎠⎝⎠
⎝⎠
⎝⎠
p . (1.14)
For this support vector constellation the SOLIM
mapping in the range
[]
,1 ,2
,
0..
1
dd
gg∈ is shown in
Figure 7. The RMS-error of 0.043 is comparable to
other algorithms as stated in Table 2.
Figure 6: 2D Gaussian bell in the range
[]
,1 ,2
,0..1
dd
gg∈
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
176
Figure 7: SOLIM-approximation (5x5 neurons) of 2D
Gaussian bell in the range
[]
,1 ,2
,0..1
dd
gg∈
Table 2: RMS-error for approximation of 2D Gaussian
bell (
0.5
µ = ,
0.1
σ
= ) with 25 support vectors in the
range
[]
,1 ,2
,0..1
dd
gg∈ . Values from (Göppert 1997).
Algorithm RMS-error
local PSOM 0.049
RBF 0.041
CRI-SOM 0.016
SOLIM 0.043
To test the performance of the extrapolation
functions the same mapping is shown in Figure 8 for
a broader input range
[]
,1 ,2
,
0.5..1.
5
dd
gg∈− . The
extrapolation is reasonable but the error is relatively
large (RMS-error = 0.063) because the falling slope
at the borders is continued although the Gaussian
bell approaches the zero-plane. This error can be
decreased significantly by using more neurons that
better represent the slopes, e.g. by placing 7x7 neu-
rons in the same area as shown in Figure 9 (RMS-
error = 0.025).
4.2 Learning
To validate the learning algorithm one inverse of the
function
()
g
= 10 sin(p) + 1/3 sin(3p
)
⋅⋅ (1.15)
shall be learned. In Figure 10 the result after 956
learning steps can be seen, where the RMS-error is
0.1% of the input vector range
[]
1
0..10
d
g ∈− . The
development of the error can be found in Figure 11.
It can be seen that the SOLIM algorithm with the
presented extrapolation can find one inverse to a
many-to-one, non-linear function.
Figure 8: SOLIM-approximation (5x5 neurons) of 2D
Gaussian bell in the range
[]
,1 ,2
, 0.5..1.5
dd
gg∈−
Figure 9: SOLIM-approximation (7x7 neurons) of 2D
Gaussian bell in the range
[]
,1 ,2
, 0.5..1.5
dd
gg∈−
Figure 10: Linear map with 10 neurons fits to
one inverse of (1.15) after 956 iteration steps.
RMS-error: 0.1% of
d
g
-range
EXTRAPOLATION WITH A SELF-ORGANISING LOCALLY INTERPOLATING MAP - Controlling nonlinear
Processes with ambiguous inverse Behaviour
177
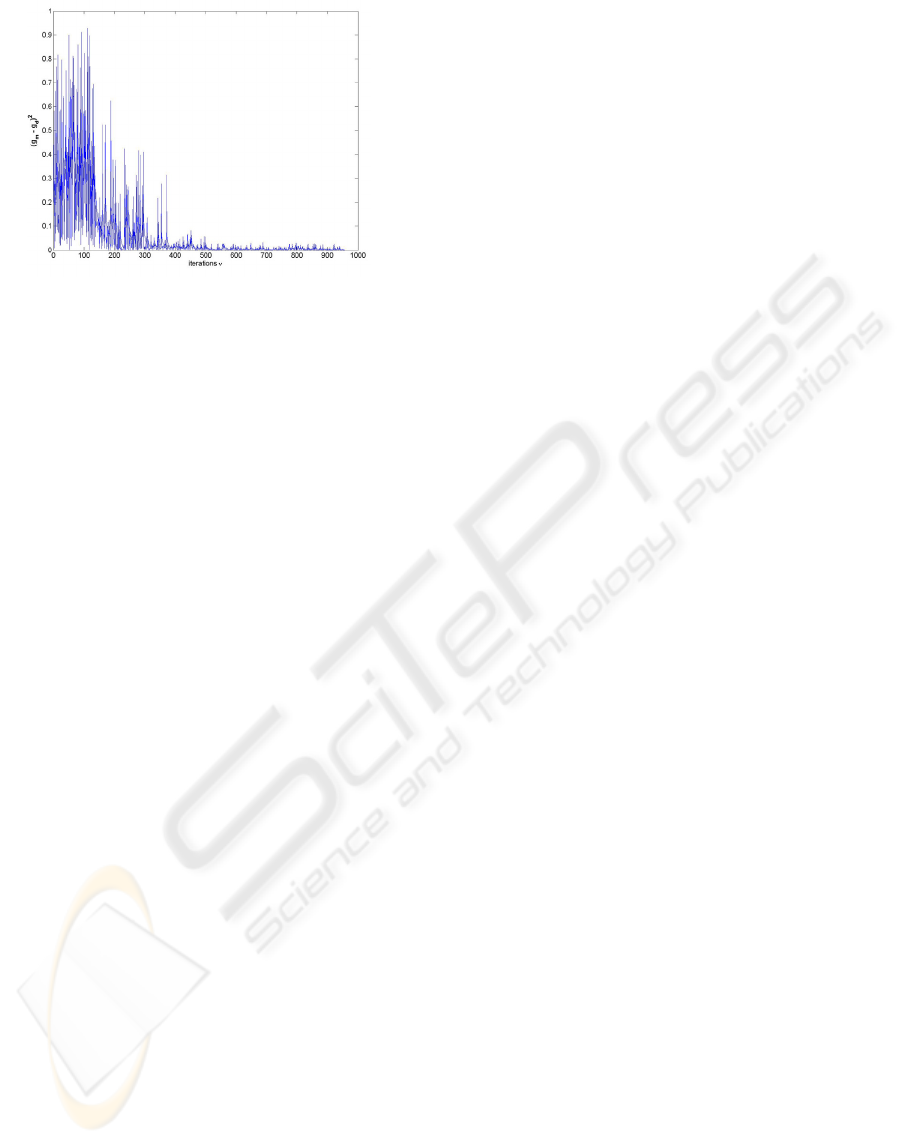
Figure 11: Development of RMS-error
5 CONCLUSION
It can be concluded that the presented algorithm has
the following properties:
• The extrapolation results from the interpolation
between the slopes at the borders, which is cal-
culated from the border support vectors and
their neighbours.
• The interpolation as well as the extrapolation
part only needs the input and output support
vectors to perform a mapping. No interpolation
factors and no local linear model matrices are
required. The price is that only 0-order continu-
ity is ensured, which mostly is sufficient.
• The mapping performance is comparable to
other algorithms (PSOM, RBF, ...).
• One mapping for ambiguous inverse system
behaviour can be found within a sufficient
number of iteration steps. Still a comparison to
other algorithms is missing since there is no
commonly accepted benchmark-system that can
be easily set up.
The following problems have not been solved yet:
• The topology is still fixed and must be known a-
priori. There exist algorithms that dynamically
build topologies and neighbourhood relation-
ships, depending on the input data "structure".
• There are still learning parameters that must be
tuned before each experiment and that partially
vary depending on time. For online training
these parameters must be varied automatically.
• The presented algorithm shall be tested in a real
application. One good demonstration is to learn
non-linear, time-variant and many-to-one mo-
tion characteristics of microrobots (Hülsen
2004a).
REFERENCES
Aupetit, M., Couturier, P., and Massotte, P. (1999). A
continuous self-organizing map using spline technique
for function approximation. In
Proc. Artificial Intelli-
gence and Control Systems (AICS'99)
, Cork, Ireland.
Aupetit, M., Couturier, P., and Massotte, P. (2000). Func-
tion approximation with continuous self-organizing
maps using neighboring influence interpolation. In
Proc. Neural Computation (NC'2000), Berlin, Ger-
many.
de A. Barreto, G., Araújo, A. F. R., and Ritter, H. J.
(2003). Self-organizing feature maps for modeling and
control of robotic manipulators.
Journal of Intelligent
and Robotic Systems
, 36(4):407-450.
de A. Barreto, G. and Araújo, A. F. R. (2004). Identifica-
tion and control of dynamical systems using the self-
organizing map.
IEEE Transactions on Neural Net-
works
, 15(5):1244-1259.
Cho, J., Principe, J. C., and Motter, M. A. (2003). A local
linear modeling paradigm with a modified counter-
propagation network. In
Proc. Int. Joint Conf. on Neu-
ral Networks
, pages 34-38, Portland, OR, U.S.A.
Hagan, M. T., Demuth, H. B., and Beale, M. (1996). Neu-
ral Network Design
. PWS Publishing Co., Boston,
MA, U.S.A.
Hülsen, H., Trüper, T., and Fatikow, S. (2004a). Control
system for the automatic handling of biological cells
with mobile microrobots. In
Proc. American Control
Conference (ACC'04)
, pages 3986-3991, Boston, MA,
U.S.A.
Hülsen, H. (2004b). Design of a fuzzy-logic-based bidirec-
tional mapping for kohonen networks. In
Proc. Int.
Symposium on Intelligent Control (ISIC'04)
, pages
425-430, Taipei, Taiwan.
Kohonen, T. (2001).
Self-Organizing Maps. Springer,
Berlin, Germany, 3. edition.
Moshou, D. and Ramon, H. (1997). Extended self-
organizing maps with local linear mappings for func-
tion approximation and system identification. In
Proc.
Workshop on Self-Organizing Maps (WSOM'97)
,
pages 181-186, Helsinki, Finland.
Principe, J. C., Wang, L., and Motter, M. A. (1998). Local
dynamic modelling with self-organizing maps and ap-
plications to nonlinear system identification and con-
trol.
Proceedings of the IEEE, 86(11):2240-2258.
Ritter, H., Martinetz, T., and Schulten, K. (1992).
Neural
Computation and Self-Organizing Maps: An Introduc-
tion
. Addison-Wesley, Reading, M.A., U.S.A.
Walter, J., Nölker, C., and Ritter, H. (2000). The PSOM
algorithm and applications. In
Proc. of Int. Symp. on
Neual Computation (NC'2000)
, pages 758-764, Berlin,
Germany.
Walter, J. (1997).
Rapid Learning in Robotics. Cuvillier
Verlag, Göttingen. http://www.techfak.uni-
bielefeld.de/ walter/.
ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL
178
