IDENTIFICATION AND PREDICTION OF MULTIPLE SHORT

RECORDS BY DYNAMIC BAYESIAN MIXTURES

Pavel Ettler

COMPUREG Plze

n, s.r.o.

P.O.Box 334, 306 34 Plze

n, Czech Republic

Miroslav K

arn

Institute of Information Theory and Automation

P.O.Box 18, 182 08 Praha 8, Czech Republic

Keywords:

System identiﬁcation, prediction, probabilistic mixtures, decision support.

Abstract:

A short data record is not suitable for proper identiﬁcation of system model which is necessary for reliable

data prediction. The idea consists in utilization of multiple similar short data records for identiﬁcation of a

dynamic Bayesian mixture. The mixture is used for prediction according to one of three methods described.

Simulated and real data examples illustrate the methods.

1 INTRODUCTION

Applicable model-based control or decision sup-

port rely on system model identiﬁed from available

data. Problem arises when data records are too short

for standard identiﬁcation procedure, especially for

higher order models. Examples of such situation can

be met in many areas including such diverse disci-

plines like analyzing treatment data in medicine or

pass scheduling for metal rolling. Typically, there ex-

ists a set of data records each consisting of several

samples mostly for several data channels. Such sim-

ilar multiple records can be grouped according to a

speciﬁc rule and processed in a way described in the

following.

Section 2 sketches basics about Bayesian mixtures

used for identiﬁcation and prediction. The idea is

demonstrated on a simple deterministic case in Sec-

tion 3. Examples for noisy and multi-dimensional

data are displayed in Section 4 while Section 5 con-

cerns real data. Conclusions 6 summarize results and

outline the future work.

2 EMPLOYING MIXTURES

External behavior of dynamic stochastic systems is

the most generally described by a probability density

function (pdf, denoted by f ) relating the current sys-

tem output y

to the current system input u

and past

observed history of data d(t − 1) = (d

, . . . , d

t−1

= (y

, u

). Such a model is rarely available di-

rectly. Instead, its version f (y

, d(t − 1), Θ) pa-

rameterized by unknown parameter Θ is assumed.

Among various parameterized models, the prominent

role is assigned to ﬁnite, normal probabilistic mix-

tures

f(y

, d(t − 1), Θ) =

c=1

(θ

c;t

, r

), (1)

where N

(ˆy, r) is normal pdf given by the mean ˆy and

covariance matrix r; θ

are regression coefﬁcients of

c-th normal pdf, called component; ψ

c;t

is regression

vector formed in a known way from u

; d(t − 1) and

≥ 0 is component weight such that

c=1

1. The unknown parameter Θ is represented by the

collection r

, θ

, α

. The prominence of mixtures

comes from their (asymptotic) universal approxima-

tion property: loosely speaking they are able to model

any stochastic dynamic system (Haykin, 1994; K

arn

et al., 2005).

Identiﬁcation of mixtures is hard but relatively well

elaborated task (Titterington et al., 1985; K

arn

y et al.,

2005) and for asymptotically valid version with con-

stant component weights can be taken as practically

solved task. For instance, the extensive Matlab tool-

box Mixtools (Nedoma et al., 2002) contains the rele-

vant implementations of such an identiﬁcation, which

estimates also number of components and structures

of respective regression vectors. The projection-based

methodology, proposed in (Andr

ysek, 2004) seems to

be the best procedure available.

Ettler P. and Kárný M. (2005).

IDENTIFICATION AND PREDICTION OF MULTIPLE SHORT RECORDS BY DYNAMIC BAYESIAN MIXTURES.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Signal Processing, Systems Modeling and

Control, pages 66-70

DOI: 10.5220/0001175400660070

 SciTePress

The system model f(y

, d(t − 1)) obtained after

“excluding” unknown parameters via identiﬁcation is

essentially predictor of the output y

. Its performance

depends weakly on overestimation of the structure of

respective regressors but it is signiﬁcantly inﬂuenced

by the assumption that the component weights are

time invariant. The assumption allows independent

jumps between active (the best describing) compo-

nents irrespectively of u

, d(t − 1). This condition is

met in some applications but in the considered tech-

nical ones is unrealistic: usually, the system is de-

scribed just by a subset (often with a single term) of

components for some period of time. Under this situa-

tion, the output prediction based on the whole mixture

is poor. This problem can be overcome by detecting

and utilizing the active components for time periods

in question.

3 BASIC IDEA

Particular short data record, which is to be processed

contains too few samples for valuable identiﬁcation.

The basic idea consists in rearrangement of data and

their identiﬁcation by a dynamic Bayesian mixture.

The mixture or its selected components are then used

for prediction.

3.1 Rearrangement of data

To illustrate the method, let us simulate a simple ex-

ample of n

= 10 one-dimensional data records each

consisting of n

= 5 samples generated by the model

= a

k−1

, (2)

where a

= 0.6, y

= 75 and k = 2, . . . , 5 is the

discrete time index.

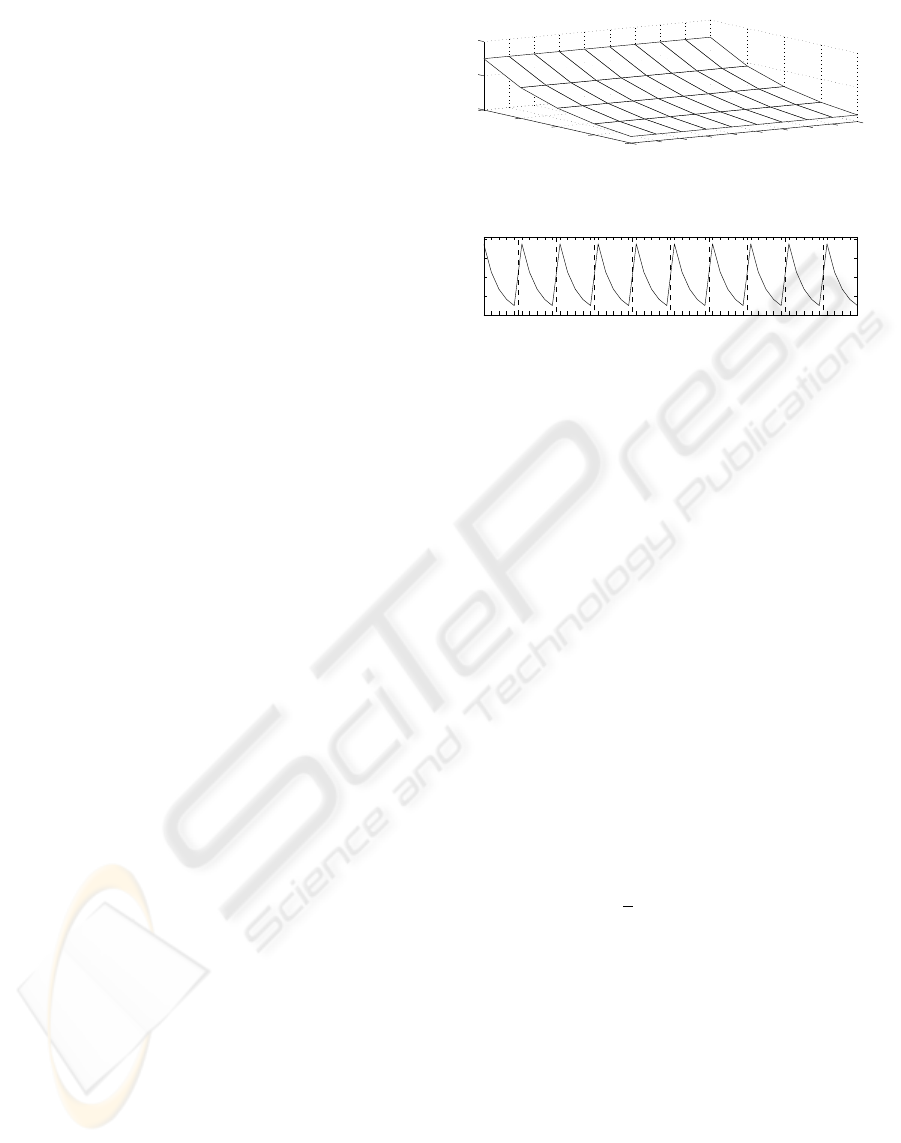
Data can be depicted by a mesh plot shown on the

upper graph of Fig. 1. For the sake of identiﬁcation

particular records can be merged into a single vector

with l = n

· n

items as shown on the lower graph

of the same ﬁgure. Then, the overall sample index is

t = 1, . . . , l.

3.2 Identiﬁcation – deterministic

case

Mixtools package (Nedoma et al., 2002) was used for

mixture identiﬁcation. For the given deterministic ex-

ample, the result came up to expectation exactly. The

mixture is composed of two components, one corre-

sponding to the model dynamics (2) and another mod-

elling transitions among records.

100

record number

Data transformation

k (sample index)

1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5 1 2 3 4 5

k (sample index)

5 10 15 20 25 30 35 40 45 50

t (overall samples index)

Figure 1: Data rearrangement. Short data records generated

by a simple model shown on the upper mesh plot are merged

into the single vector shown on the lower graph.

3.3 Prediction and evaluation

criterion

The mixture was identiﬁed in order to get valuable

prediction. One-step-ahead prediction is considered

for the sake of simplicity. For an m-order model the

prediction is accomplished for (n

− m) time instants

for a single data record ( y

c;k

means prediction by c-th

component):

p;k

c=1

c;k

, k = m + 1, . . . , n

(3)

Predictions are treated as merged original data

forming a vector y

(t), t = 1, . . . , l. To evaluate pre-

diction quality the following modiﬁed quadratic cri-

terion E

is used (subscript s stands for selected in-

stants of t for which predictions are evaluated):

t=1

− y

p;t

)

. (4)

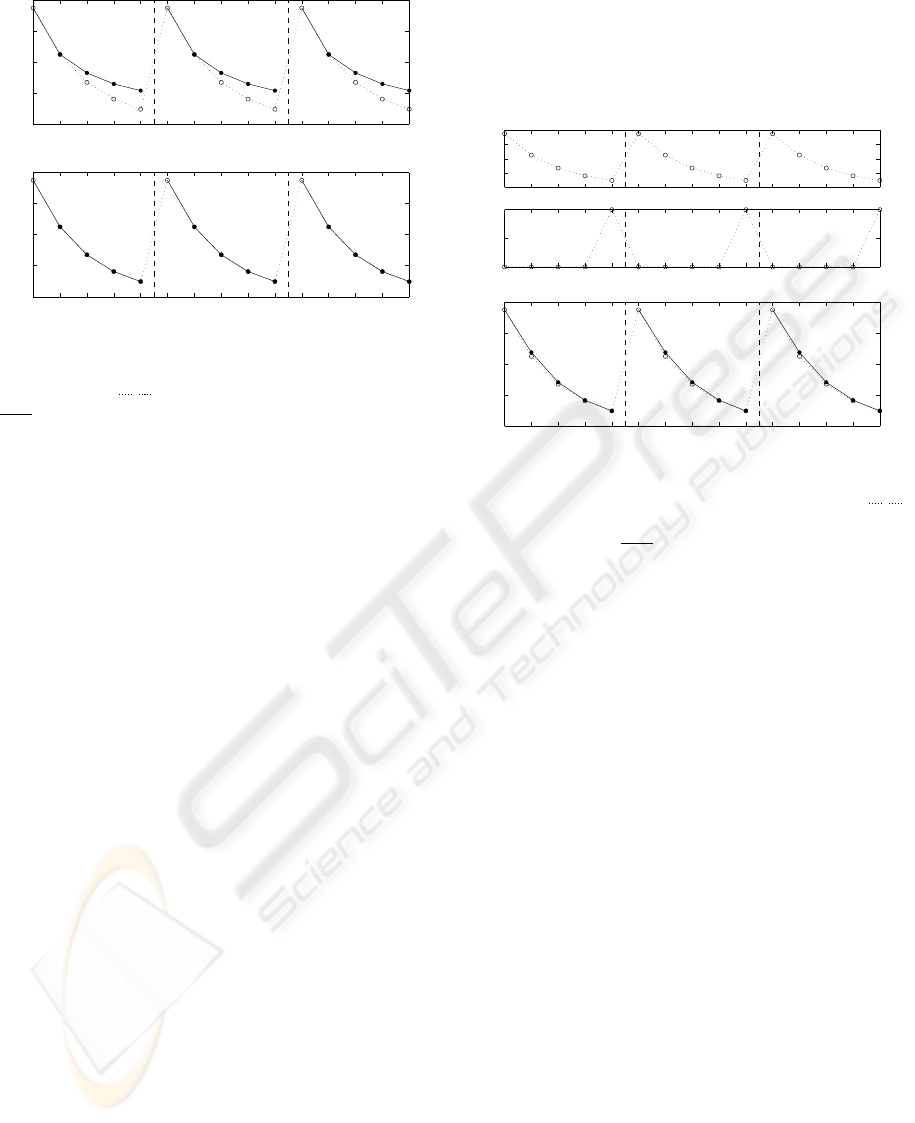
Fig. 2 shows the original data and predictions for

3 randomly chosen succeeding records. The whole

mixture, ie. both components for this case were used

for prediction on the upper graph. It is obvious that

the prediction is poor (E

= 52.9). The lower graph

shows predictions calculated from the selected com-

ponent. For this deterministic case the component

matches the model (2) exactly and thus the prediction

is perfect (E

= 0).

3.4 Component selection

Criterion for selection of components to be used for

prediction is crucial for the mentioned principle.

IDENTIFICATION AND PREDICTION OF MULTIPLE SHORT RECORDS BY DYNAMIC BAYESIAN MIXTURES

1 2 3 4 5 1 2 3 4 5 1 2 3 4 5

y: data °, prediction •

Deterministic case − all mixture components used for prediction

= 52.90

1 2 3 4 5 1 2 3 4 5 1 2 3 4 5

y: data °, prediction •

Deterministic case − selected mixture component used for prediction

= 0.00

Figure 2: Deterministic case: whole mixture vs. selected

component. Three data records put together and plotted by

the dotted line (

). Prediction plotted by the solid line (

) was omitted for starting points of records for the 1st

order model. For the upper graph whole mixture was used

for prediction while the selected component was used for

prediction shown on the lower graph.

Method A The simplest possibility is to engage just

the component the weight α

of which was identiﬁed

as the maximal one. It means practically to set the

weight to one for that component and to zero for the

others and than to use the mixture for prediction.

Method B Another possibility consists in evalua-

tion of prediction error criterion for all possible com-

binations of components to be involved. For most

realistic cases the method results in utilizing sev-

eral components instead of one. This can simply re-

ﬂect uncertainty of measurement or indicate that data

records should be split into two or more groups to al-

low approximation by a simpler mixture.

3.5 Extending data record

Method C A rather different approach consists in

extending the merged data by an additional chan-

nel x

, which indicates transitions among particular

records:



1 for the last sample in the record

0 otherwise

The situation is illustrated by two upper plots on

Fig. 3.

In this case components preserve their identiﬁed

weights α

, ie. the whole mixture is used for predic-

tion. Zero elements of x(t), which is now included in

the regression vectors ψ

c;t

(1) eliminate inﬂuence of

“transient” components on computation of y

(t). On

the other side, the ones in x(t) enable to predict tran-

sitions accordingly. The lower plot on Fig. 3 shows

the result for the deterministic case. The prediction is

not exact (E

= 1.52) but the problem of component

selection was avoided.

1 2 3 4 5 1 2 3 4 5 1 2 3 4 5

y: data °, prediction •

Extended deterministic case − all mixture components used for prediction

= 1.52

1 2 3 4 5 1 2 3 4 5 1 2 3 4 5

Extended deterministic case − transition indication added

1 2 3 4 5 1 2 3 4 5 1 2 3 4 5

0.5

Figure 3: Extended deterministic case: additional data

channel indicates transition among records. Two data (

) channels plotted on upper graphs. Whole mixture was

used for prediction (

) shown on the lower graph.

4 SIMULATED EXAMPLES

4.1 Adding noise

Increased model order and introduction of noise make

the simulation more realistic:

= a

k−1

+ a

k−2

+ c

, (5)

where a

= 0.6, a

= 0.1, c

= 4 are parameters of

the model,

k = 2, . . . , 5 and e

is the output of a random number

generator with normal distribution N (0, 1). Starting

points of records are given by

= y

+ c

, (6)

where y

= 50, c

= 50 and e

is the output of a

random number generator with uniform distribution

in the interval < 0, 1 >.

The identiﬁcation was accomplished ﬁrstly on orig-

inal merged data d(t) where d

= y

and on the ex-

tended data where d

= (y

, x

) afterwards to allow

comparison of predictions shown on Fig. 4. For the

upper plot, the original data were used for identiﬁ-

cation and the single most important component was

used for prediction (method A). The middle plot uses

the same data and multiple components (2 of 8) se-

lected according to the method B. For the lower plot,

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

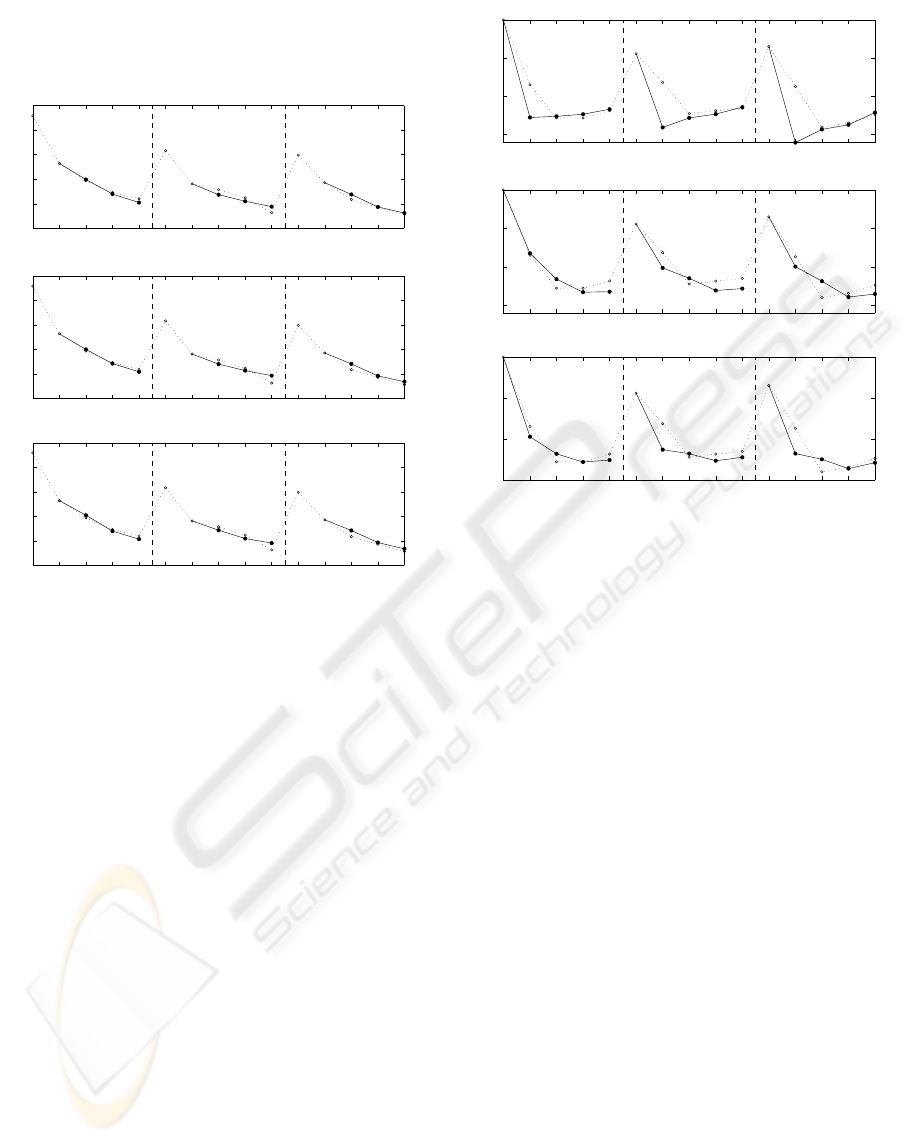
the extended data were utilized and the whole mixture

used for prediction (method C). Values of E

are very

similar for all three methods for this case.

1 2 3 4 5 1 2 3 4 5 1 2 3 4 5

100

y: data °, prediction •

Method A

= 7.69

1 2 3 4 5 1 2 3 4 5 1 2 3 4 5

100

y: data °, prediction •

Method B

= 7.38

1 2 3 4 5 1 2 3 4 5 1 2 3 4 5

100

y: data °, prediction •

Method C

= 7.40

Figure 4: Comparison of prediction methods for noisy data.

4.2 Multiple dimensions

Multiple dimensions and increased uncertainty make

the identiﬁcation more difﬁcult. Let us consider the

model

= AY

k−1

+ c

N;k

, (7)

where



1;k

2;k



, A =



0.6 0.1

0.2 −0.8



and c

= 4.

Merged data to be identiﬁed consist of a 2×l matrix

for methods A and B and 3 × l matrix for method C.

Fig. 5 compares the three methods of prediction. It

can be seen that method B is becoming favourable for

increasing uncertainty being involved.

5 REAL DATA EXAMPLE

A subset of records from a hot reversing rolling

mill was selected for a real data example. The mill

processes metal bars or slabs in several passes to pro-

duce thick strips. Thickness is not measured automat-

ically on the given mill, which makes pass scheduling

a non-trivial task.

1 2 3 4 5 1 2 3 4 5 1 2 3 4 5

−50

100

y2: data °, prediction •

Method A

= 704.06

1 2 3 4 5 1 2 3 4 5 1 2 3 4 5

−50

100

y2: data °, prediction •

Method B

= 135.31

1 2 3 4 5 1 2 3 4 5 1 2 3 4 5

−50

100

y2: data °, prediction •

Method C

= 175.46

Figure 5: Comparison of prediction methods for multidi-

mensional noisy data for channel y

Three data channels – working roll position, rolling

force and electric current of the roll drive were se-

lected for the example. Characteristic values (means

of selected parts of passes) were evaluated for 5 suc-

ceeding passes to produce 3 × 5 data matrix for a sin-

gle record. Available records for a speciﬁc material

were merged (Fig. 6) and used for identiﬁcation.

Fig. 7 shows predictions for three real data chan-

nels. The mixture was identiﬁed for the second-order

model. Method B turned out to be far most success-

ful for this case (3 of 7 components were utilized).

This conﬁrmed the trend indicated by previous exam-

ples. Direct comparison of values of the criterion (4)

would be misleading for this case because of dissimi-

lar ranges and units used for particular data channels.

Therefore Fig. 8 shows histograms of prediction er-

rors recalculated to the percentage of range of the cor-

responding data channel.

6 CONCLUSIONS

Utilization of Bayesian dynamic mixtures for identi-

ﬁcation and subsequent prediction of multiple short

data records was described. The principle was shown

on a simple deterministic case. Two methods of pre-

diction differing in number of mixture components to

be utilized and the third method relying on extension

of data were introduced and demonstrated on noisy

IDENTIFICATION AND PREDICTION OF MULTIPLE SHORT RECORDS BY DYNAMIC BAYESIAN MIXTURES

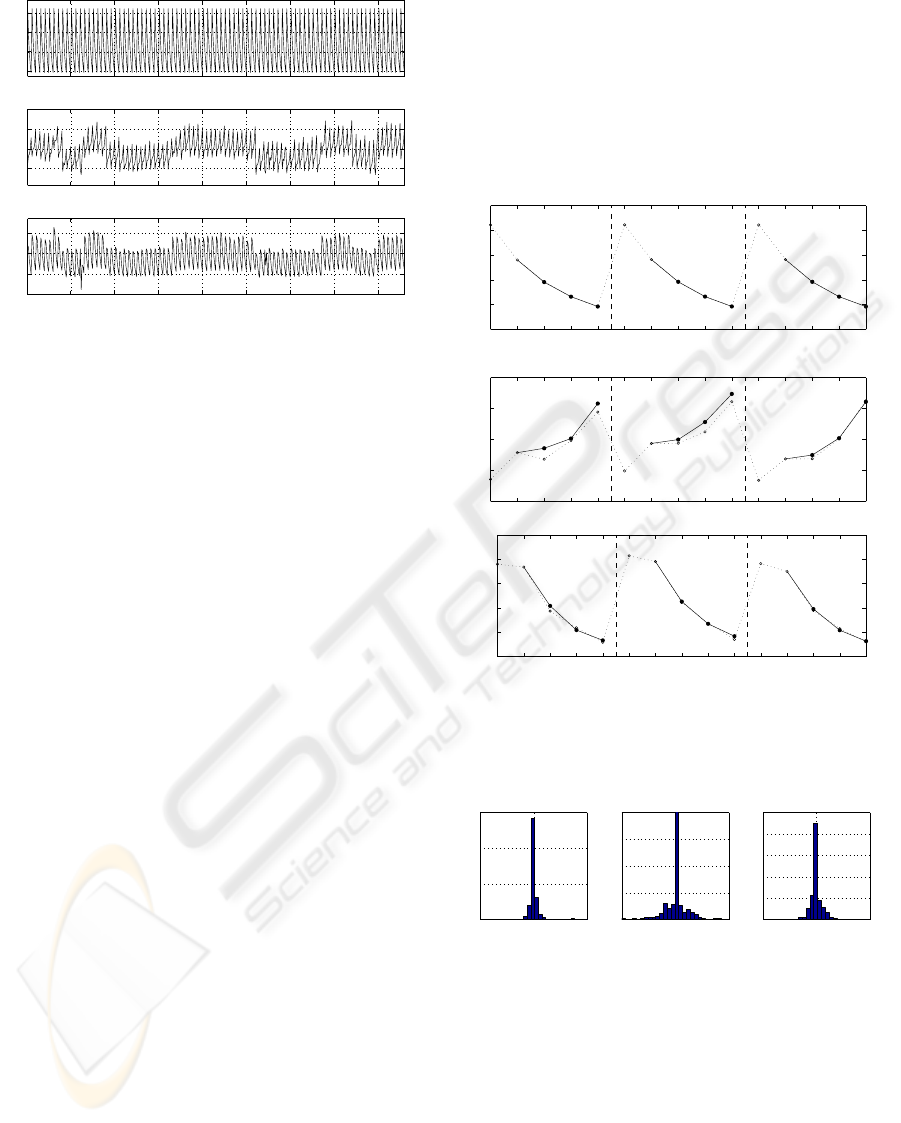
50 100 150 200 250 300 350 400

Z [mm]

Real data

50 100 150 200 250 300 350 400

F [MN]

50 100 150 200 250 300 350 400

500

1000

1500

2000

I [A]

Figure 6: Real data from a hot reversing rolling mill.

86 records of characteristic values for ﬁnal 5 passes were

merged. Three data channels were selected: Z - position of

the working roll, F - rolling force and I - electric current of

the main mill drive.

and multidimensional data respectively. A simpliﬁed

set of data records from a hot reversing rolling mill

was used for a real data example.

Experiments showed that the mixture used for pre-

diction should be composed by more than one com-

ponent (method B). The algorithm for components se-

lection will be more elaborated.

Further research will be focussed on utilization of

the idea for real multidimensional short data records.

Results should help to advance applications of the

Bayesian decision support.

ACKNOWLEDGEMENTS

The work was accomplished within the research cen-

tre DAR, supported by the grant 1M6798555601 of

the Czech Ministry of Education.

REFERENCES

Andr

ysek, J. (2004). Approximate recursive Bayesian

estimation of dynamic probabilistic mixtures. In

Andr

ysek, J., K

arn

y, M., and Krac

ık, J., editors, Mul-

tiple Participant Decision Making, pages 39–54. Ad-

vanced Knowledge International, Magill, Adelaide.

Haykin, S. (1994). Neural networks: A comprehensive

foundation. Macmillan College Publishing Company,

New York.

arn

y, M., B

ohm, J., Guy, T., Jirsa, L., Nagy, I., Nedoma,

P., and Tesa

r, L. (2005). Optimized Bayesian Dynamic

Advising: Theory and Algorithms. Springer, London.

to appear.

Nedoma, P., B

ohm, J., Guy, T. V., Jirsa, L., K

arn

y, M.,

Nagy, I., Tesa

r, L., and Andr

ysek, J. (2002). Mixtools:

User’s Guide. Technical Report 2060,

UTIA AV

CR,

Praha.

Titterington, D., Smith, A., and Makov, U. (1985). Statis-

tical Analysis of Finite Mixtures. John Wiley & Sons,

Chichester, New York, Brisbane, Toronto, Singapore.

ISBN 0 471 90763 4.

1 2 3 4 5 1 2 3 4 5 1 2 3 4 5

Best prediction • for real data °

Z [mm]

1 2 3 4 5 1 2 3 4 5 1 2 3 4 5

2.5

3.5

4.5

F [MN]

1 2 3 4 5 1 2 3 4 5 1 2 3 4 5

800

1000

1200

1400

1600

1800

I [A]

Figure 7: Prediction of real data made according to the

method B. Data taken from a hot reversing rolling mill.

−0.5 0 0.5

Relative frequency

Z %

−10 0 10

Histograms of prediction error

F %

−10 0 10

I %

Figure 8: Histograms of percentage prediction error for

three real data channels.

ICINCO 2005 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL