A STRATEGY FOR BUILDING TOPOLOGICAL MAPS THROUGH

SCENE OBSERVATION

Roger Freitas, M

ario Sarcinelli-Filho and Teodiano Bastos-Filho

Departamento de Engenharia El

etrica, Universidade Federal do Esp

ırito Santo

Vit

oria - E.S., Brazil

Jos

e Santos-Victor

Instituto de Sistemas e Rob

otica, Instituto Superior T

ecnico

Lisbon, Portugal

Keywords:

Learning, Topological Navigation, Incremental PCA, Affordances.

Abstract:

Mobile robots remain idle during signiﬁcant amounts of time in many applications, while a new task is not as-

signed to it. In this paper, we propose a framework to use such periods of inactivity to observe the surrounding

environment and learn information that can be used later on during navigation. Events like someone entering

or leaving a room, someone approaching a printer to pick a document up, etc., convey important information

about the observed space and the role played by the objects therein. Information implicitly present in the mo-

tion patterns people describe in a certain workspace is then explored, to allow the robot to infer a “meaningful”

spatial description. Such spatial representation is not driven by abstract geometrical considerations but, rather,

by the role or function associated to locations or objects (affordances) and learnt by observing people’s behav-

iour. Map building is thus bottom-up driven by the observation of human activity, and not simply a top-down

oriented geometric construction.

1 INTRODUCTION

In many applications, mobile robots remain idle for

signiﬁcant amounts of time, while a new task is not

assigned to it. Similarly, in many research labs mo-

bile robots remain inactive during extended periods

of time, while new sensorial information processing

or navigation algorithms are being tested.

The motivation of this work is to use those periods

of inactivity to observe the surrounding environment

and learn information that can be used later on during

navigation. For example, events like someone enter-

ing or leaving a room or approaching a printer to pick

a document up, convey important information about

the observed space and the role played by the objects

therein.

The development of algorithms to extract useful in-

formation from the observation of such events could

bring signiﬁcant savings in programming, while af-

fording the robot with an extended degree of ﬂexi-

bility and adaptability. In this work, we explore the

information implicitly present in the motion patterns

people describe in a certain workspace, to allow the

robot to infer a “meaningful” spatial description. In-

terestingly, such spatial representation is not driven

by abstract geometrical considerations but, rather, by

the role or function associated to locations or objects

and learnt by observing people’s behaviour.

The mobile robot we use in this work combines pe-

ripheral and foveal vision. The peripheral vision is

implemented by an omnidirectional camera that cap-

tures the attention stimuli to drive a standard, narrow

ﬁeld of view pan-tilt (perspective) camera (foveal vi-

sion).

Other research groups have used information asso-

ciated to people’s trajectories to help robot navigation.

In (Bennewitz et al., 2002) mobile robots equipped

with laser sensors are used to extract trajectories of

people moving in houses and ofﬁces. The trajectories

are estimated using the Expectation-Maximization

(EM) algorithm and the models are used to predict

human trajectories in order to improve people follow-

ing. In (Bennewitz et al., 2003) the same authors pro-

pose a method for adapting the behavior of a mobile

robot according to the activities of the people in its

surrounding. In (Kruse and Wahl, 1998) an off-board

camera-based monitoring system is proposed to help

mobile robot guidance. In (Appenzeller et al., 1997)

it is developed a system that builds topological maps

by looking at people. Their approach is based on

cooperation between Intelligent Spaces (Fukui et al.,

2003) and robots. Intelligent Spaces are environments

168

Freitas R., Sarcinelli-Filho M., Bastos-Filho T. and Santos-Victor J. (2005).

A STRATEGY FOR BUILDING TOPOLOGICAL MAPS THROUGH SCENE OBSERVATION.

In Proceedings of the Second Inter national Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 168-174

DOI: 10.5220/0001171101680174

 SciTePress

endowed with sensors like video cameras, acoustic

sensors, pressure sensors, monitors and speakers that

send information about the environment to a central

processing system. Usually, the beings present in the

environment are human beings and, in some cases, ro-

bots. From the analysis of the sensorial data, the Intel-

ligent Space can supply the “users” with necessary in-

formation to accomplish some task. For example, this

kind of environment is able to build maps and send

them to the robots, allowing them to navigate safely.

However, this approach is characterized by low scal-

ability, i.e., if the robot is supposed to navigate in a

different environment, such environment should be

structured a priori.

Our approach to this problem is to extract the mo-

tion patterns of people from the robot’s viewpoint di-

rectly, using an on-board vision system. The advan-

tage of such approach is that the robot can learn from

environments that are not structured for this purpose,

thus giving to the learning process more ﬂexibility

and scalability. However, the robot cannot observe

the entire environment at once, which is a limitation

that can be overcome by using an incremental learn-

ing strategy. Such a strategy allows the robot to ob-

serve the environment from an initial position and to

create a partial model representing the observed re-

gion. Then, starting from this initial model, the ro-

bot may change its position in the environment, and

to keep observing it from the new position. From

the new observations, the initial model could be vali-

dated, changed or enlarged.

The implementation of the incremental learning

process is based on an incremental algorithm of Prin-

cipal Component Analysis (PCA). An incremental al-

gorithm that is based on (Murakami and Kumar, 1982;

Hall et al., 1998; Arta

c et al., 2002) is here adopted.

The omnidirectional images that are captured by the

robot during the learning process will represent the

nodes of a topological map of the environment. The

incremental PCA (IPCA) algorithm allows the inte-

gration of new images (new nodes) in an online way.

This incremental approach, in conjunction with the

strategy of observing people’s movements, will give

the robot a high level of autonomy on building maps,

while extracting information that allows the percep-

tion of some functionalities associated to speciﬁc re-

gions of the environment.

Such topics are hereinafter addressed in the follow-

ing way: Section 2 describes the overall learning sys-

tem, and preliminary results are shown in Section 3.

Section 4 describes the approach to enlarge the par-

tial map created through observation, and in Section 5

some conclusions and discussions about possible de-

velopments are presented.

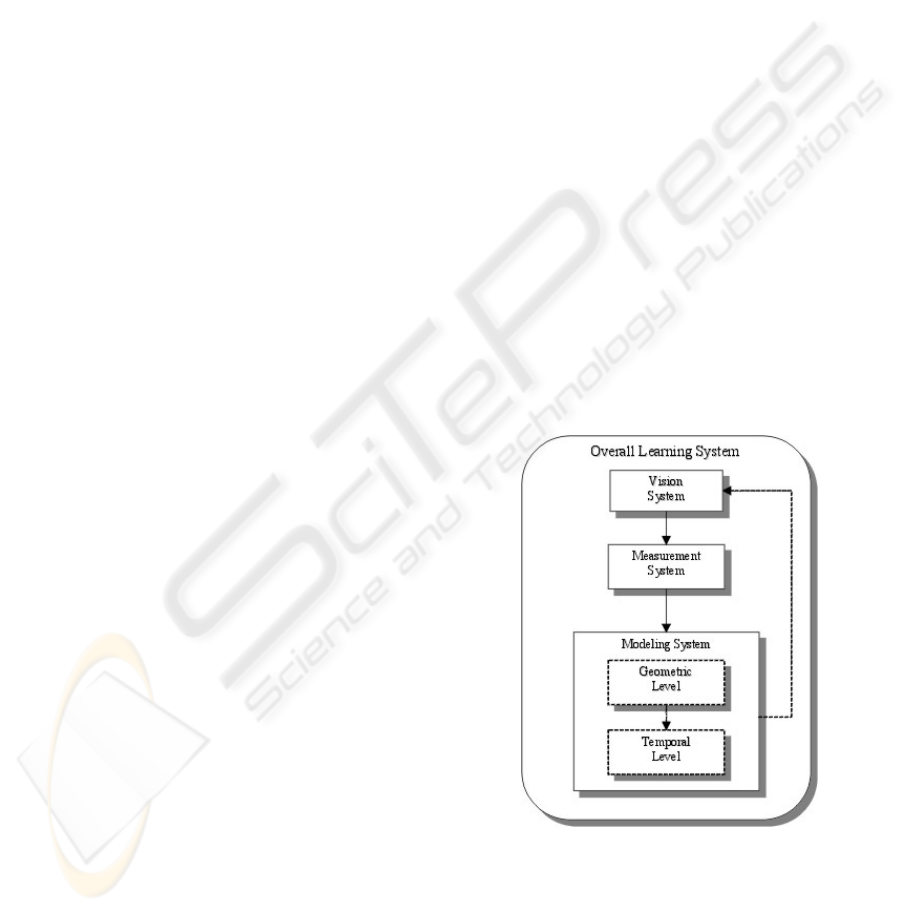
2 OVERALL LEARNING SYSTEM

Fig. 1 shows a scheme of our overall approach. The

most important subsystems, which embed increasing

level of cognition, are the vision, measurement and

modeling subsystems.

The Vision System comprises peripheral and foveal

visual capabilities. Peripheral vision is accomplished

by an omnidirectional camera and is responsible for

detecting movement. Foveal vision is accomplished

by a perspective camera that is able to execute pan and

tilt rotations, and is responsible for tracking moving

objects.

The Measurement System is responsible for trans-

forming visual information into features the robot is

trying to learn, e.g., transforming 2D image informa-

tion into trajectory points on the ﬂoor, referred to a

common coordinate frame.

The Modeling System is responsible for building

models that explain data from the measurement sys-

tem. This system operates in two different levels

of cognition, labelled geometric level and temporal

level. The geometric level modeling system outputs

strictly geometric models. The temporal level model-

ing system outputs models that incorporate concepts

like temporal analysis and appearance. Depending

on the kind of model the robot is trying to build, this

system could also drive the way the vision system op-

erates (e.g. controlling the gaze direction).

Figure 1: The Overall Learning System

In this paper, we use the scheme shown in Fig. 1 to

learn possible trajectories and interesting places in the

environment surrounding the robot. In this case, the

Measurement System is responsible for transforming

2D image information into trajectory points on the

ﬂoor. The Modeling System is responsible for build-

A STRATEGY FOR BUILDING TOPOLOGICAL MAPS THROUGH SCENE OBSERVATION

169

ing models of possible trajectories and/or ﬁnding in-

teresting places in the environment that should be in-

vestigated in more detail (low level modeling).

We assume that the robot has no prior knowledge

about the structure of the working environment. From

any position inside it, the robot should extract useful

information to navigate. In order to do that, it should

be able to detect moving objects, track these objects

and transform this information into possible trajecto-

ries (a set of positions in an external coordinate sys-

tem) to be followed. In the following subsections, we

describe in detail each one of these subsystems.

2.1 Vision System

The vision system deals with two types of visual in-

formation: peripheral and foveal (see Fig. 2). The

peripheral vision uses an omnidirectional camera to

detect interesting image events and to drive the atten-

tion of the foveal camera. The foveal vision system

is then used to track the objects of interest, using a

perspective camera with a pan-tilt platform.

2.1.1 Attention System

The attention system operates on the omnidirectional

images and detects motion of objects or people in the

robot vicinity. Other visual cues could be consid-

ered, but in the current implementation we deal ex-

clusively with motion information. Motion detection

can be easily performed by using background subtrac-

tion. Moving objects are detected by subtracting the

current image from the background image (previously

obtained). In this work, the background is modeled

using the method proposed in (Gutchess et al., 2001),

which uses a sequence of images taken from the same

place and outputs a statistical background model de-

scribing the static parts of the scene.

Fig. 3 shows an omnidirectional image taken in

the laboratory and the result of movement detection.

Once the movement is detected, a command is sent

Figure 2: The Vision System

(a)

20 40 60 80 100 120 140 160

(b)

Figure 3: Omnidirectional image captured (a), movement

detection (b).

to the pan and tilt camera to drive its gaze direction

towards the region of interest and to start tracking the

moving object. To direct the camera gaze towards the

detected target, we would need to determine the re-

quired camera pan and tilt angles. The camera pan

angle must be set to the angular position of the tar-

get in the omnidirectional image. To determine the

tilt angle, we would need to determine the distance to

the detected target. Instead, for simpliﬁcation we al-

ways use a reference tilt position that roughly points

the camera towards the observed region.

2.1.2 Tracking System

Whenever the Tracking System is activated, the At-

tention System is deactivated. We are currently us-

ing a simple tracking algorithm to illustrate the idea

of learning about the environment from observing hu-

man actions. The next step is to improve its perfor-

mance and robustness.

The current tracking routine takes two consecutive

images as the input and extracts the pixels display-

ing some change. The result is that different regions

(moving objects) in the two images are highlighted.

Then, we calculate a bounding box around the de-

tected area. The point to be tracked is the middle point

of the bottom edge of the bounding box (theoretically

a point on the ﬂoor).

While operating, the system is continuously detect-

ing regions of interest in the peripheral ﬁeld of view.

The foveal vision system then tracks these objects,

while they remain visible. If the target is not visible

anymore, the Attention System is made active again.

The measurement system described in the sequence

will integrate the information of different tracked ob-

jects into a common coordinate system, from where

more global information can be interpreted.

2.2 Measurement System

In order to estimate trajectories relative to the robot,

it is necessary to estimate the distance from the robot

to the moving object in each image acquired. Usu-

ICINCO 2005 - ROBOTICS AND AUTOMATION

170

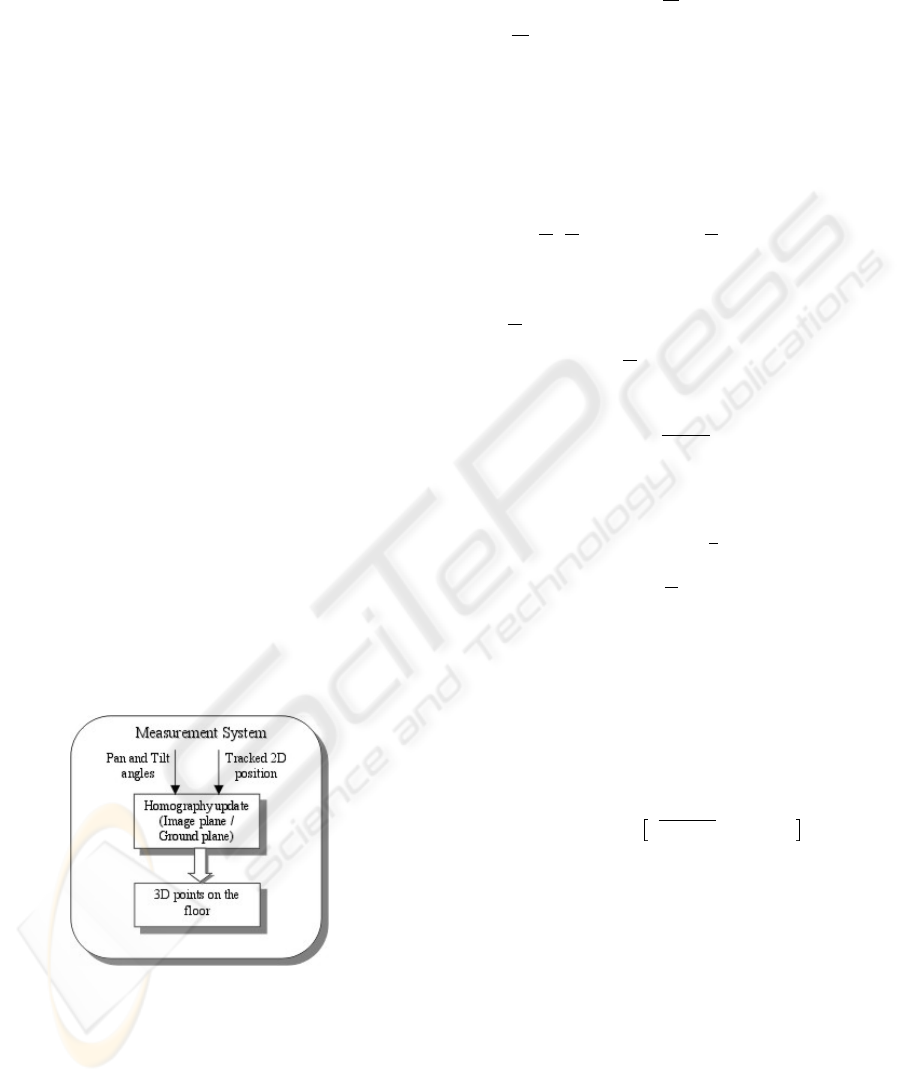
ally, this problem is solved using two or more cam-

eras set in different places and applying stereo vision

techniques.

As the robot is stationary while observing the envi-

ronment, consecutive images of a given moving ob-

ject differ only by camera rotations (pan and tilt).

Thus, stereo can not be used to reconstruct the 3D tra-

jectory of the target. The alternative used to solve this

problem is to estimate the homography H between

the ﬂoor and the image plane, i.e., to ﬁnd an a pri-

ori plane projective transformation that transforms an

image point (u,v) into a point on the ﬂoor (X,Y,1),or





= H





, (1)

where H is the 3×3 homography matrix. Initially, the

homography is estimated using a set of ground plane

points, whose 3D positions are known with respect to

some reference frame. Then, when the foveal camera

moves, the homography is updated as a function of

the performed motion. So, as the camera is tracking

the object, its pose is changing, and the same happens

to the homography between the image plane and the

ﬂoor. For this reason, we use the pan and tilt angles

to update the homography (see Fig. 4).

We assume that the intrinsic parameters of the pan-

tilt camera are known a priori, after an initial cali-

bration step. The intrinsic parameters are used to de-

compose the homography matrix into a rotation ma-

trix and a displacement vector (camera pose) relating

the camera frame to a world frame. Pan and tilt angles

generate canonical rotation matrices that multiply the

original rotation matrix, thus updating the homogra-

phy.

Figure 4: The Measurement System

In order to recover camera pose, we apply the

methodology presented in (Gracias and Santos-

Victor, 2000), which we brieﬂy describe next. The

homography, H, can be written as

H = λKL (2)

where λ is an unknown scale factor, K is the camera

intrinsic parameter matrix and L is a matrix composed

from the full (3 x 3) rotation matrix R and the trans-

lation vector t. Hence,

L =[

] , (3)

where

R is a 3x2 submatrix comprising the ﬁrst two

columns of matrix R. Due to noise in the estimation

process, homography H will not follow exactly the

structure of (2). Alternatively, using the Frobenius

norm to measure the distance between matrices, the

problem can be formulated as

λ, L =argmin

λ,L

λL − K

−1

H

frob

(4)

subject to

L = I

, where L is a 3x2 submatrix

comprising the ﬁrst two columns of L. The solution

of (4) can be found through Singular Value Decom-

position (SVD). Let UΣV

be the SVD of K

−1

Then,

L is given by

L = UV

, (5)

and

λ =

tr(Σ)

. (6)

The last column of L, namely t, can be found as

t = K

−1





, (7)

thus resulting

L =[

] . (8)

The last column of rotation matrix R can be found

by computing the cross product of the the ﬁrst two

columns. The updated rotation matrix is given by

NewR = R · R

PAN

· R

TILT

. (9)

Finally, the updated homography is then

NewH = λ · K · NewL, (10)

where

NewL =

NewR Newt

Newt = NewR · t.

We have now a way to project all tracked trajecto-

ries onto a common coordinate system associated to

the ground plane. In this global coordinate system,

the different trajectories described by moving objects

can be further analyzed and modeled, as described in

the next subsection.

2.3 Modeling System

The modeling system is responsible for building mod-

els explaining data emerging from the measurement

system. Depending on the nature of the models the

robot is building, this system can drive the way vi-

sion system operates. This system can operate in two

different levels of cognition:

A STRATEGY FOR BUILDING TOPOLOGICAL MAPS THROUGH SCENE OBSERVATION

171

• geometric level - the geometric level modeling sys-

tem outputs strictly geometric models, e.g., metric

trajectories that could be followed by the robot;

• temporal level - the temporal level modeling sys-

tem outputs models that incorporate a temporal

analysis as well as concepts like appearance, e.g.,

images representing regions of the environment can

be associated to a spacial description the robot can

use to navigate (topological maps);

2.3.1 Geometric Level

In this work, the modeling system operates on geo-

metric level, once it aims to interpret the observed

(global) trajectories onto representations that can be

used for navigation. Currently, we consider three

main uses of such data:

• the observed trajectories correspond to free (obsta-

cle free) pathways that the robot may use to move

around in the environment;

• regions where trajectories start or end might corre-

spond to some important functionality (e.g. doors,

tables, tools, etc) and should be represented in a

map;

• if many trajectories meet in a certain area, it means

that that region must correspond to some important

functionality as well.

Hence, from observation the robot can learn the lo-

cation of interesting places in the scene and the most

frequent ways to go from one point to another. Mov-

ing further, the robot also might be able to distinguish

uncommon behaviours, what could be used in surveil-

lance and monitoring tasks.

2.3.2 Temporal Level

The next step in the modeling process would be the

addition of a temporal analysis of the events that oc-

cur while the robot observes the scene. Concepts like

appearance are incorporated in the model as well. Ap-

pearance is often used to solve the problem of mo-

bile robot localization based on video images (Gaspar

et al., 2000). Rather than characterizing from strictly

known geometric features, the approach is to rely on

appearance-based methods and a temporal analysis to

enrich the model of the environment. The temporal

analysis will allow the characterization of pathways,

as well as regions where people usually stop and stay

for periods of time while engaged in some activity.

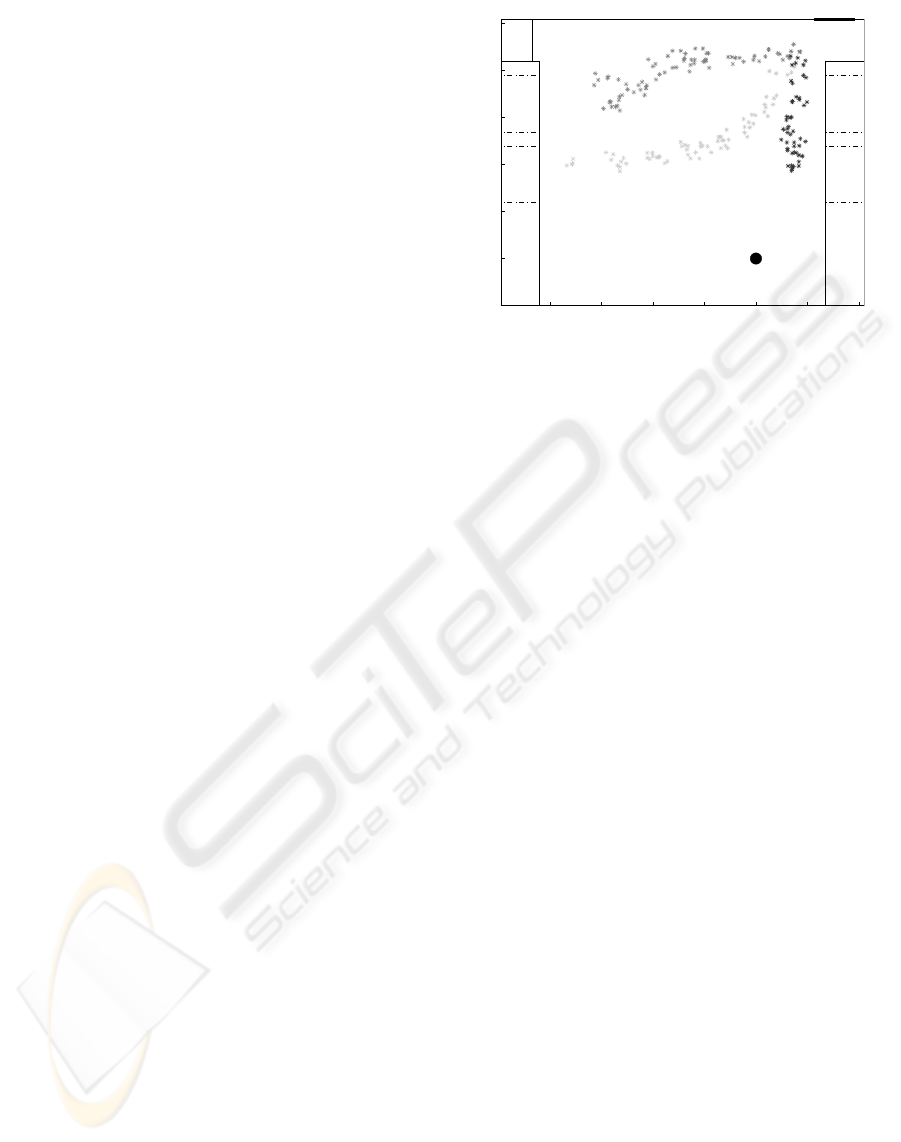
3 EXPERIMENTAL RESULTS

We performed preliminary experiments in the labora-

tory to verify the performance of the Vision, Measure-

−400 −300 −200 −100 0 100 20

−100

100

200

300

400

500

TABLE

Workstation Workstation

TABLE

Workstation Workstation

DOOR

ROBOT

Measures performed

X(cm)

Y(cm)

Figure 5: Real data measured from observing people’s

movements.

ment and Modeling systems. The robot stayed ob-

serving the laboratory while people walked by, along

different trajectories. Each trajectory was performed

and recorded separately. The positions on the ﬂoor,

measured by the system, are shown in Fig. 5.

The data generated by the Measurement System is

then interpreted by the Modeling System. When an-

alyzing the data shown in Fig. 5, the most interest-

ing point is the kind of information that can be ex-

tracted from such data. One could try, for example, to

extract models of observed trajectories. In this case,

the model could be obtained statistically (Bennewitz

et al., 2002) or deterministically. In the deterministic

case, local (e.g. splines) or global (e.g. polynomial)

models could be used.

To illustrate the idea, the trajectories shown in Fig.

6 were modeled using a linear polynomial model.

Places of interest can be detected as well (see Fig.

6). In this case, we applied a threshold on the data

shown in Fig. 5 based on the number of times a po-

sition was visited. This is done in order to ﬁlter the

data, thus discarding positions that are not frequently

visited. Then, we use a k-means algorithm to cluster

the remaining data.

By identifying these places, a strategy for modeling

and identiﬁcation can be derived, thus providing an

autonomous way of learning models for such places.

For example, as we can see in Fig. 6, three of such

places of interest appear in front of workstations in

the laboratory.

4 ENLARGING THE MAP

The experimental results obtained suggest that, from

its initial position, it is unlikely that the robot can

model correctly all the trajectories and interesting

places in the environment. This is expected to happen

ICINCO 2005 - ROBOTICS AND AUTOMATION

172

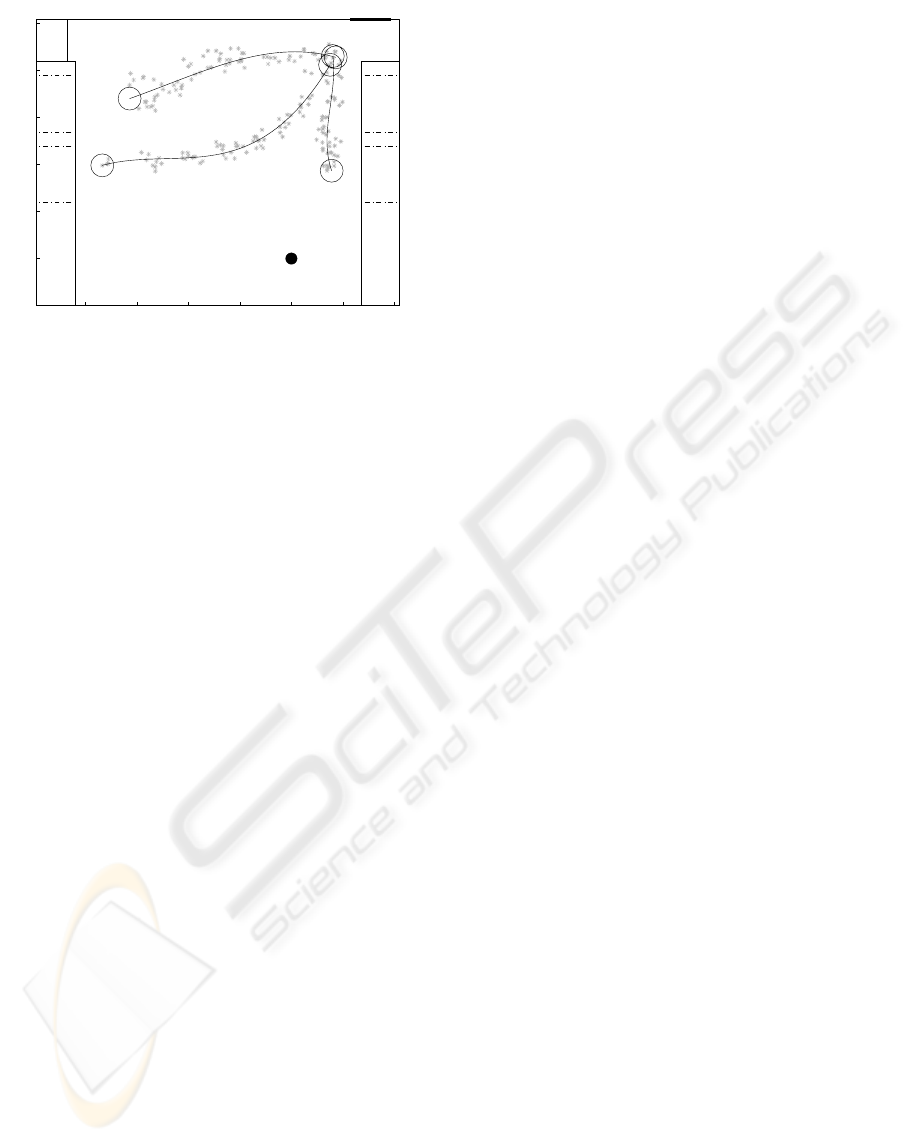
−400 −300 −200 −100 0 100 20

−100

100

200

300

400

500

TABLE

Workstation Workstation

TABLE

Workstation Workstation

DOOR

ROBOT

Modeled Trajectories & Interesting places

X(cm)

Y(cm)

Figure 6: Examples of modeled trajectories and places of

interest.

due to occlusions and the high uncertainty assigned to

distant regions.

Trajectory models based on observations made

from the robot’s initial position are highly affected

by occlusions. Besides the incorrect models, occlu-

sions can lead to a misclassiﬁcation of the regions of

the environment labelled as “interesting places.” For

example, from the viewpoint of the robot, one can de-

scribe (or model) the region where a door is placed as

a region where people usually appear and disappear.

In most cases, and if occlusions are not present, such a

description would sufﬁce to correctly distinguish the

object door from other “interesting places” in the en-

vironment. However, if occlusions are present, the

trajectory points where they occur would be incor-

rectly modelled as regions corresponding to doors.

From these considerations, it can be concluded that

it is necessary that the robot, based on the initial

model built from its initial position, changes its po-

sition in the environment and restart the observation

process, aiming to validate the current model. A strat-

egy that allows the robot to choose the new viewpoint,

given the current (and partial) metric map, should now

be developed. New measurements could then be com-

pared to the old ones through odometry readings.

Once a trajectory has been validated, the robot

could start the topological mapping. The validated

trajectory would be followed by the robot, while cap-

turing images and building the map in a incremental

way. Each image would be assigned to a map node,

representing a position in the environment. The idea

consists in representing the robot environment as a

topological map, storing a (usually large) set of land-

mark images. To speedup the comparison of the robot

views with these landmark images, it is advantageous

to use low-dimensional approximations of the space

spanned by the original image set. One example is to

use principal component analysis (PCA) that uses the

set of input images to extract an orthonormal basis (or

model) of a lower dimensional subspace (eigenspace)

that approximates the input images.

In the traditional approach to calculate these

eigenspace models, known as batch method, the ro-

bot must capture all the images needed to build the

map and then, using either eigenvalue decomposition

of the covariance matrix or singular value decompo-

sition of the data matrix, calculate the model. This

approach has some drawbacks, however. Since the

entire set of images is necessary to build the model, it

is impossible to make the robot to build a map while

visiting new positions. Update of the existing model

is only possible from scratch, which means that origi-

nal images must be kept in order to update the model,

thus requiring a lot of storage capability.

To overcome these problems, some authors (Mu-

rakami and Kumar, 1982; Hall et al., 1998) proposed

algorithms that build the eigenspace model incremen-

tally (sometimes referred to as subspace tracking in

the communications literature). The basic idea be-

hind these algorithms is to start with an initial sub-

space (described by a set of eigenvectors and asso-

ciated eigenvalues) and update the model in order to

represent new acquired data. This approach allows

the robot to perform simultaneous localization and

map building. There is no need to build the model

from scratch each time a new image is added to the

map, thus making easier to deal with dynamic envi-

ronments. Recently, Arta

c et al (Arta

c et al., 2002)

improved Hall’s algorithm (Hall et al., 1998) by sug-

gesting a way to update the low dimensional projec-

tions of the images, thus allowing to discard the image

as soon as the model has been updated. Whenever the

robot acquires a new image, the ﬁrst step consists in

determining whether or not this image is well repre-

sented by the existing subspace model. The compo-

nent of the new image that is not well represented by

the current model is added to the basis as a new vector.

Then, all vectors in the basis are “rotated” in order to

reﬂect the new energy distribution in the system. The

rotation is represented by a matrix of eigenvectors ob-

tained by the eigenvalue decomposition of a special

matrix (see (Freitas et al., 2003) for details).

Through this IPCA algorithm, it is possible to make

the transition from geometric to appearance models.

The robot will follow the metric trajectory based on

odometry, while acquiring images and building the

topological map of that trajectory incrementally.

5 CONCLUSIONS AND FUTURE

WORK

Currently, the temporal analysis modeling level is un-

der development, and experimental results will be

A STRATEGY FOR BUILDING TOPOLOGICAL MAPS THROUGH SCENE OBSERVATION

173

available soon . A further development of the mod-

eling system could consist of the addition of a Func-

tional Level. This level would be associated with the

affordances of the environment, perceived by the ro-

bot. According to Gibson (Gibson, 1979), “the af-

fordance of anything is a speciﬁc combination of the

properties of its substance and its surface taken with

reference to an animal.” In other words, the term af-

fordance can be understood as the function or role,

perceived by an observer, that an object plays in the

environment. Such functionalities are quickly per-

ceived through vision, and full tridimensional object

models are not always required so that their function-

alities in the environment could be perceived.

Even though a robot had a full tridimensional

model of the environment and information about the

movement of the objects, it wouldn’t have a human-

like scene vision. When human beings (and ani-

mals) observe a scene, they “see” several possibilities

and restrictions (Sloman, 1989), such as possibilities

of acquisition of more information through a change

in the viewpoint and possibilities of reaching a goal

through interaction with objects present in the envi-

ronment. Hence, Gibson’s affordances are closely re-

lated to these possibilities and restrictions. Once the

affordances represent a rich source of information to

understand the environment, it is important to develop

a strategy to identify and extract them from the im-

ages captured by the robot. Then, it is possible that

the observation of people while executing common

tasks reveal some affordances in the environment. For

example, one can assign to the doors of an environ-

ment the affordance “passage.” If the robot could ob-

serve people appearing and disappearing in a speciﬁc

region, it would perceive that region as an access to

such an environment.

While the robot is building the map or navigating

based on a map previously built, it is likely that the

robot faces an object or a person in its way. In order

to avoid the collision, it is necessary to develop an ob-

stacle detection algorithm and an obstacle avoidance

strategy based on information that can be extracted

from images. Besides, an environment inhabited by

people is subject to changes in its conﬁguration. If

these changes are not detected by the robot and repre-

sented in the environment model, the map would not

be a correct representation of the environment any-

more. Hence, it is also necessary to develop a method-

ology to detect changes in the environment conﬁgura-

tion.

REFERENCES

Appenzeller, G., Lee, J., and Hashimoto, H. (1997). Build-

ing topological maps by looking at people: An exam-

ple of cooperation between intelligent spaces and ro-

bots. Proceedings of the International Conference on

Intelligent Robots and Systems (IROS 1997), 3:1326–

1333.

Arta

c, M., Jogan, M., and Leonardis, A. (2002). Mobile

robot localization using an incremental eigenspace

model. Proceedings of the International Conference

on Robotics and Automation (ICRA 2002).

Bennewitz, M., Burgard, W., and Thrun, S. (2002). Using

EM to learn motion behaviors of persons with mo-

bile robots. Proceedings of the International Confer-

ence on Intelligent Robots and Systems (IROS 2002),

1:502–507.

Bennewitz, M., Burgard, W., and Thrun, S. (2003). Adapt-

ing navigation strategies using motions patterns of

people. Proceedings of the International Conference

on Robotics and Automation (ICRA 2003), 2:2000–

2005.

Freitas, R., Santos-Victor, J., Sarcinelli-Filho, M., and

Bastos-Filho, T. (2003). Performance evaluation of

incremental eigenspace models for mobile robot local-

ization. In Proc. IEEE 11th International Conference

on Advanced Robotics (ICAR 2003), pages 417–422.

Fukui, R., Morishita, H., and Sato, T. (2003). Expression

method of human locomotion records for path plan-

ning and control of human-symbiotic robot system

based on spacial existence probability model of hu-

mans. Proceedings of the International Conference

on Robotics and Automation (ICRA 2003).

Gaspar, J., Winters, N., and Santos-Victor, J. (2000).

Vision-based navigation and environmental represen-

tations with an omni-directional camera. IEEE Trans-

actions on Robotics and Automation, 16(6):890–898.

Gibson, J. J. (1979). The Ecological Approach to Visual

Perception. Houghton Mifﬂin, Boston.

Gracias, N. and Santos-Victor, J. (2000). Underwater

video mosaics as visual navigation maps. VisLab-TR

07/2000 - Computer Vision and Image Understanding,

79(1):66–91.

Gutchess, D., Trajkovi

c, M., Cohen-Solal, E., Lyons, D.,

and Jain, A. K. (2001). A background model initial-

ization algorithm for video surveillance. International

Conference on Computer Vision, 1:733–740.

Hall, P., Marshall, D., and Martin, R. (1998). Incremental

eigenanalysis for classiﬁcation. British Machine Vi-

sion Conference, 14:286–295.

Kruse, E. and Wahl, F. (1998). Camera-based monitor-

ing system for mobile robot guidance. Proceedings

of the International Conference on Intelligent Robots

and Systems (IROS 1998), 2:1248–1253.

Murakami, H. and Kumar, B. (1982). Efﬁcient calculation

of primary images from a set of images. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

4(5):511–515.

Sloman, A. (1989). On designing a visual system (towards

a gibsonian computation model of vision). Journal of

Experimental and Theoretical AI, 1(4):289–337.

ICINCO 2005 - ROBOTICS AND AUTOMATION

174