MOMENT BASED FEATURES FOR CONTENT BASED IMAGE
RETRIEVAL
Ryszard S. Chora
´
s
Institute of Telecommunications, University of Technology & Agriculture
Kaliskiego Street 7, 85-796 Bydgoszcz, Poland
Keywords:
Image databases, image feature extraction, image retrieval.
Abstract:
Content based information retrieval is now a widely investigated issue that aims at allowing users of
multimedia information systems to retrieve images coherent with a sample image. A way to achieve this goal
is the automatic computation of features such as color, texture, shape, and position of objects within images,
and the use of the features as query terms.
In this paper we describe some results of a study on similarity evaluation in image retrieval using shape,
texture, color and object orientation and relative position as content features. Images are retrieval based
on similarity of features where features of the query specification are compared with features of the image
database to determine which images match similar with the given features. Feature extraction is a crucial part
for any of such retrieval systems.
1 INTRODUCTION
Content based image retrieval (CBIR) techniques are
becoming increasingly important in multimedia infor-
mation systems. CBIR uses (M.S. Lew, 2001) an au-
tomatic indexing scheme where implicit properties of
an image can be included in the query to reduce search
time for retrieval from a large database.
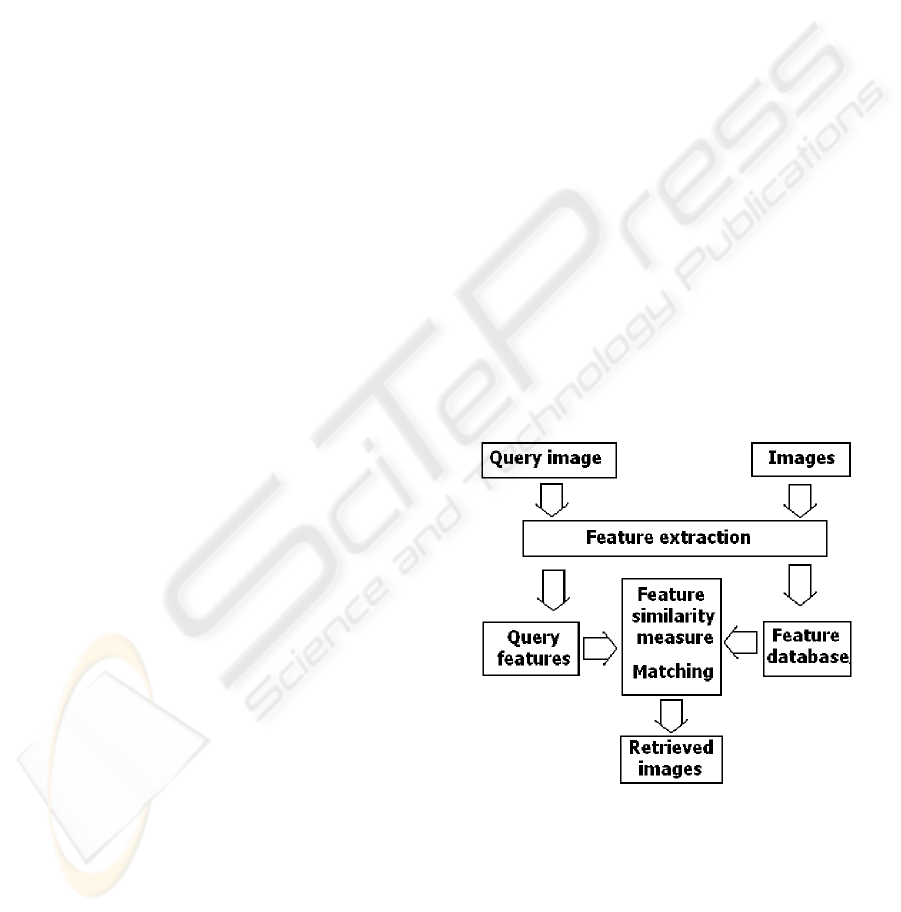
In this paper, a image retrieval method based on
the primitives of color, texture and shape moments
will be proposed. Color, texture and shapes feature
can be described by moment analysis. The basic im-
age retrieval system based on this concept is shown in
Figure 1.
For query images, we first compute ROI (Region of
Interest) and extract a set of color, texture and shape
features.
2 FEATURE EXTRACTION
2.1 Color features
Color has been the most widely used feature in CBIR
systems. We use the Y U V color model. The Y U V
Figure 1: The image retrieval process.
space is widely used in image compression and other
applications. Y represents the luminance of a color,
and U, V represent the chromaticity of a color. The
color distributions of the Y , U, and V components of
image can be represented by its color moments.
395
S. Chora
´
s R. (2005).
MOMENT BASED FEATURES FOR CONTENT BASED IMAGE RETRIEVAL.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 395-398
DOI: 10.5220/0001166303950398
Copyright
c
 SciTePress

Figure 2: Y U V components of database images(3429,3430,3431,3432)
Color moments have been successfully used in
many retrieval systems (like QBIC (M.J. Swain, D.H.
Ballard, 1991)(W. Niblack et all., 1993), especially
when the image contains just the object. The first or-
der (mean), the second (variance) and the third order
(skewness) color moments have been proved to be ef-
ficient and effective in representing color distributions
of images (M. Stricker, M. Orengo, 1995). Mathemat-
ically, the first three moments are defined
µ
c
=
1
MN
M
X
x=1
N
X
y =1
f
c
(x, y) (1)
σ
c
= (
1
MN
M
X
x=1
N
X
y =1
(f
c
(x, y) − µ
c
)
2
)
1
2
(2)
s
c
= (
1
MN
M
X
x=1
N
X
y =1
(f
c
(x, y) − µ
c
)
3
)
1
3
(3)
where f
c
(x, y) is the value of the c-th color compo-
nent of the image pixel (x, y), and M N is the number
of pixels in the image.
Since only 9 (three moments for each of the three
color components) numbers are used to represent the
color content of each image, color moments are very
compact representation compared to other color fea-
tures.
2.2 Shape features - Zernike
moments
There are two types of shape representation: the
region based and contour based methods. Contour
based are local representations and need further
processing. The region-based shape descriptor
belongs to the broad class of shape analysis tech-
niques based on moments (A. Khotanzad, 1990)(G.
Taubin, D.B. Cooper, 1991). Zernike moment (ZM)
sequence, Z
nm
is uniquely determined by the image
f(x, y) and conversely, f(x, y) is uniquely described
by Z
nm
.
Zernike introduced a set of complex polynominals,
which form a complete orthogonal set over the inte-
rior of the unit circle x
2
+ y
2
= 1. The polynominals
(A. Khotanzad, 1990) have the form
V
nm
(x, y) = V
nm
(ρ, θ) = R
nm
(ρ)e
(jmθ)
(4)
where n is a non-negative integer and m is a non
zero integer subject to the constraints n − |m| even
and |m| ≤ n, ρ is the length of vector from the origin
to the pixel (x, y) and θ the angle between vector ρ
and x axis in counter-clockwise direction.
The polar coordinates (ρ, θ) in the image domain
are related to the Cartesian coordinates (x, y) as x =
ρcos(θ) and y = ρsin(θ).
R
nm
(ρ) are the Zernike radial polynominals in (ρ, θ)
polar coordinates defined by (A. Khotanzad, 1990), as
follows :
ICINCO 2005 - ROBOTICS AND AUTOMATION
396

Table 1: Moments of color components
Image Color components Mean µ
c
Variance σ
c
Skewness s
c
3429 Y 158,23 2922,03 -0,05
3429 3429 U 148,07 341,20 -0,33
3429 V 114,74 136,63 -0,11
3430 Y 168,83 2423,25 -0,64
3430 3430 U 143,99 151,45 -0,11
3430 V 108,87 131,91 -0,01
3431 Y 182,81 2194,36 -0,80
3431 3431 U 136,60 109,34 -0,38
3431 V 115,87 119,71 0,31
3432 Y 160,64 2841,31 -0,15
3432 3432 U 134,98 377,52 0,11
3432 V 123,67 134,44 0,26
R
nm
(ρ) =
n−m
2
X
s=0
(−1)
s
[(n − s)!]ρ
n−2s
s!(
n+|m|
2
− s)!(
n−|m|
2
− s)!
(5)
Note that R
n,−m
(ρ) = R
nm
(ρ).
The polynominals of (5) are orthogonal
ZZ
x
2
+y
2
≤1
[V
nm
(x, y)]
∗
V
nm
(x, y)dxdy =
π
n + 1
δ
np
δ
mq
(6)
where δ
αβ
= 1 for α = β and δ
αβ
= 0 otherwise,
is the Kronecker symbol.
Zernike moment of order n and repetition m is
defined as (A. Khotanzad, 1990), (G. Taubin, D.B.
Cooper, 1991):
Z
nm
=
n + 1
π
ZZ
x
2
+y
2
≤1
V
∗
nm
(ρ, θ)f (x, y)dxdy (7)
where:
- f(x, y) is the continuous image intensity function
at (x, y) in Cartesian coordinates.
For a digital image the discrete approximation of
equation 7 is given as
Z
nm
=
n + 1
π
X
x
X
y
f(x, y)V
∗
nm
(ρ, θ), x
2
+y
2
≤ 1
(8)
To calculate the Zernike moments of an image
f(x, y), the image is first mapped onto the unit disk
using polar coordinates, where the center of the image
is the origin of the unit disk. Pixels falling outside the
unit disk are not used in the calculation.
We use the Zernike moments modules |Z
mn
| as the
features of shape in the recognition of pattern.
The magnitude of Zernike moments has rotational in-
variance property. An image can be better described
by a small set of its Zernike moments than any other
type of moments such as geometric moments, Legen-
dre moments, rotational moments, and complex mo-
ments in terms of mean-square error. Zernike mo-
ments do not have the properties of translation invari-
ance and scaling invariance. The way to achieve such
invariance is image translation and image normaliza-
tion before calculation of Zernike moments.
To characterize the shape we used a feature vector:
SF V = (Z
1m
, Z
2m
, . . . , Z
nm
) (9)
consisting of the Zernike moments. This vector is
used to index each shape in the database. The dis-
tance between two feature vectors is determined by
city block distance measure.
3 FUZZY MOMENTS
The centroid of the segmented image is found and
furthermore, m concentric circles are drawn with the
centroid of the image as center such that the radius ρ
j
of the jth circle.
The radial and angular fuzzy moments of the seg-
ment contained between angles α and α + θ and be-
tween circles of radius ρ
j
and ρ
j+1
are defined as fol-
lows
MOMENT BASED FEATURES FOR CONTENT BASED IMAGE RETRIEVAL
397

Ψ
ρ
j
,α
(k, p, q) =
ρ
j+1
X
ρ
j
α+θ
X
α
ρ
k
µ(F (ρ, θ))cos
p
θsin
q
θ
(10)
where k is order of the radial moments and (p + q) is
the order of the angular moments and
µ =







0 f ≤ a
2 × [
(f−a)
(c−a)
]
2
a ≤ f ≤ b
1 − 2 × [
(f−a)
(c−a)
]
2
b ≤ f ≤ c
1 x ≥ c
(11)
4 QUERY PROCESSING
The color image retrieval must be researched in the
certain color space. The YUV space is selected to
research the color image retrieval therefore we must
perform all the operations according to the Y,U,V
components.
The general algorithm for color image retrieval is as
follows:
1. Calculate the three component images of the color
image in the certain color space (i.e. YUV)
2. Calculate the color moments for each component
image
3. Calculate the Zernike moments for each compo-
nent image
4. Calculate the fuzzy moments for each component
image
5. Each component image corresponds to feature vec-
tors V
c
= [CM F V
c
, SM F V
c
, F M F V
c
] where
CM F V
c
is color moment feature vector (3 mo-
ments for each image components), and SM F V
and F M F V are respectively Zernike moments and
fuzzy moments for each image components c =
Y, U, V .
6. Feature vector for color image is
V
imag e
= [V
Y
, V
U
, V
V
]
7. Calculate the distance between each subfeature of
one image to the other images and the minimum is
selected as the feature distance between color im-
ages
8. Take the feature distance as the image similarity to
perform the color image retrieval.
Three similarity functions sim
Y
(Q, D),
sim
U
(Q, D) and sim
V
(Q, D), respectively account-
ing for YUV image components, are computed. Each
function simX(Q, D) between a database image
feature, defined by the tuple D = (d
0
, d
1
, . . . , d
n
),
and the query image feature, also defined by a tuple
Q = (q
0
, q
1
, . . . , q
n
) is computed using the cosine
similarity coefficient, defined as:
sim(Q, D) =
P
d
i
q
i
p
P
d
2
i
×
P
g
2
i
(12)
The resulting coefficients are merged to form the final
similarity function as:
sim(Q, D) = a × sim
Y
(Q, D) +
+b × sim
U
(Q, D) + c × sim
V
(Q, D) (13)
where a, b and c are weighting coefficient empirically
set.
5 CONCLUSION
Currently available large images repositories require
new and efficient methodologies for query and re-
trieval. Content based access appears to be a promis-
ing direction to increase the efficiency and accuracy
of unstructured data retrieval. We have introduced a
system for similarity evaluation based on the extrac-
tion of simple features such as color and fuzzy image
moments. We considered these features as a simple
set perceptually useful in the retrieval from thematic
databases, i.e. limited to a common semantic domain.
REFERENCES
A. Khotanzad (1990). Invariant image recognition by
zernike moments. IEEE Trans. on Patt.Anal.and
Mach. Intell., 12(5):489–497.
G. Taubin, D.B. Cooper (1991). Recognition and position-
ing of rigid objects using algebraic moment invariants.
In SPIE Conf. On Geometric Methods in Computer Vi-
sion, volume 1570, pages 175–186.
M.J. Swain, D.H. Ballard (1991). Color indexing. Interna-
tional Journal of Computer Vision, 7(1):11–32.
M.S. Lew (2001). Principles of Visual Information Re-
trieval. Springer-Varlag, London.
M. Stricker, M. Orengo (1995). Similarity of color images.
In SPIE Storage and Retrieval for Image and Video
Databases III, volume 2185, pages 381–392.
T. Gevers, A.W.M. Smeulders (1999). Colour based object
recognition. Pattern Recognition, 32:453–464.
W. Niblack et all. (1993). Querying images by content, us-
ing color, texture, and shape. SPIE Conference on
Storage and Retrieval for Image and Video Database,
1908:173–187.
ICINCO 2005 - ROBOTICS AND AUTOMATION
398