
CALCULATION OF OPTIMAL PATHS IN THE
CONFIGURATION SPACE USING ARTIFICIAL POTENTIAL
FIELDS AND A* AND D* ALGORITHMS FOR AN
ARTICULATED ROBOT. COMPARISON OF TECHNIQUES
Miguel A. Gutiérrez, Alejandro Morales
Depto. Informática y Ciencias Computación, Universidad Católica de Ávila, Ávila, Spain
Vidal Moreno, Belén Curto
Depto. Informática y Automática, Universidad de Salamanca, Salamanca, Spain
Keywords: Configuration space, Articulated robot, Potential f
ields, Path planning.
Abstract: In this paper, we use a calculation path technique based on the configuration space in the case of an
articulated robot of two degrees of freedom. We propose the use of artificial potential fields to represent the
configuration space and the use of techniques of artificial intelligence like A* and D* to search a free
collision path into the configuration space. This combination of techniques can be used in static and
dynamic environments with more than three dimensions without considering the geometry of the obstacles.
The results for this combination of techniques are presented, choosing in each case the best option for each
one of the techniques for the combination.
1 INTRODUCTION
In the design of autonomous robots, one of the tasks
on which more studies have been made is the path
planning. Different techniques like potential fields or
artificial intelligence algorithms like A* or D* have
been used.
We can use the potential field method to
calcu
late the path from the initial configuration to
the final one. One of the first works presented on the
use of potential fields in the path planning was
(Hwang 1988), where a survey of the possibilities of
this method was made. In (Melchior 2003) the
potential field method is used to represent the
environment of the robot in 2D. A risk coefficient is
assigned to each obstacle to increase the repulsion
field in the surroundings of some obstacles. The
algorithm used to search a path between two
positions of the map was A*. Also in 2D spaces, the
potential field method is used in (Prestes 2004) to
represent the surrounding of a Nomad2000 robot in
order to make easy to find paths towards the
unexplored zones of the map. In (Ge 2002)
(Kacandes 1989) (Lee 1995) the potential fields
method is proposed to find a path in dynamic
environments. For example in (Lee 1995), the
surrounding of the robot was observed in regular
intervals of time, and the space occupied by the
obstacles at the end of the interval was calculated at
the beginning of the same one. After this, a repulsion
field is generated around the space that is going to
be occupied by the obstacles and an attraction one
towards the goal. In this work, the robot is assumed
to be precise and the obstacles are supposed to be
circular. A similar exposition was made in (Ge
2002), where the speed and acceleration of the
obstacles were well-known with respect to the robot.
All these methods are proposed in 2D work spaces.
Other methods calculate potential fields without
local minima. In (Latombe 1991) (Wong 2000) the
potential field map is calculated by a road map
previously calculated by a front of waves. Potential
field method has been used in 3D spaces in (Elnagar
2002) (Yachida 1995) (Zhang 1997), for example in
the path planning for flying robots.
Another option for path planning is the use of
artificial in
telligence algorithms. In (Trovato 1996),
Karen I. Trovato makes a study of the algorithms A*
and D* in the case of a robotic arm and an
11
A. Gutiérrez M., Morales A., Moreno V. and Curto B. (2005).
CALCULATION OF OPTIMAL PATHS IN THE CONFIGURATION SPACE USING ARTIFICIAL POTENTIAL FIELDS AND A* AND D* ALGORITHMS
FOR AN ARTICULATED ROBOT. COMPARISON OF TECHNIQUES.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 11-16
DOI: 10.5220/0001165800110016
Copyright
c
SciTePress

automobile. In (Gilliard 2002) the A* algorithm is
used on a search space represented using BSP trees.
This representation depends on the geometry of the
obstacles. This makes that this technique of path
planning very difficult to use in environments with
three or more dimensions. In (Adi 2004) the A*
algorithm has been used on hierarchic maps,
dividing the search in several levels. The main map
is divided in several smaller submaps, that can as
well be divided in smaller ones, etc. The search is
made on each one of the maps separately and the
obtained paths are united to get an only path.
All the mentioned path planning techniques
work in the work space. Other works use these
techniques in the configuration space.
The idea of reducing the robot to a point in an
appropriate space was introduced by Udupa (Udupa
1997), although the term configuration space had not
been used yet. Later, Lozano-Pérez (Lozano-Pérez
1983) adopted the notion of Cspace from the
mechanics and popularised it in path planning. In
some works the Cspace is calculated by means of
geometric methods as much for obstacles as for
robots with polygonal or polyhedral convex forms
(Lozano-Pérez 1983) (Seidel 1986). Other ones have
tried to make a representation in bitmap in such a
way that “elemental blocks” can be identified and
easily transformed into the Cspace, so that combined
form the Cspace for more complicated forms
(Branicky 1991). More recent works set out to
calculate bitmap of the Cspace like the convolution
of bitmap of the workspace with the one of the robot
(Kavraki 1995) (Moreno 1997) (Blanco 1997). In
these, the sufficiently small CPU time is used in the
calculation of the Cspace to use it in the planning
task without this supposes a boosting charge. In
(Blanco 1997) the potential field without minima is
used in the configuration space. In other works, the
geometric properties of the obstacles for the
construction of the Cspace are used to reduce the
time of calculation (Helgason 2001) (Williams
2001) (Chen 1996). In (Fox 1993), Maciejewski
proposes a path planning technique based on the
geometric characteristics of the obstacles in the
configuration space. Those techniques that use the
geometric properties of the obstacles are very
difficult to be applied in environments with more
than three dimensions.
In this work, we will use a combination of these
techniques. We will represent the configuration
space of an articulated robot using the potential field
technique and we will use path search algorithms
like A* and D* for searching collision-free paths.
We will use a bitmap to represent the configuration
space. This representation allows us to use the
technique independently of the geometry of the
robot or the obstacles. The selected search
algorithms work in static and dynamic
environments, so this technique can be used in both
type of environments. In addition, the measurement
of the performance of the algorithms implemented
will be presented.
The remainder of this paper is organized as
follows: in section 2 we present the problem
statement. The different techniques used to calculate
the configuration space of the robot and its
representation with potential fields are commented.
In section 3, we present a software platform
developed to validate the path planning process.
Finally, in section 4 we present the performance of
the technique in different environments and in
section 5 the main conclusions are presented.
2 PROBLEM STATEMENT
The path calculation technique used in this paper
works in the configuration space. First, the
configuration space corresponding to the work space
of the robot is calculated. The representation of this
configuration space is made by a bitmap. This
representation allows us to work independently of
the geometry of the obstacles and the robot. The
configuration space is represented by potential
fields: attraction to the goal and repulsion from
obstacles. Using this bitmap representation, the
repulsion field of the obstacles is calculated. In order
to obtain the path from the initial configuration to
the final configuration, we will use the A* in static
environments and the D* algorithm in dynamic
environments. Both algorithms guide their search by
an heuristic function. We use the potential field to
guide the search algorithms.
The result of the search algorithm is a series of
configurations that, if they are adopted by the robot,
it will move in the workspace without colliding with
obstacles.
2.1 Calculating the Configuration
Space
To calculate the configuration space we use the
method proposed in (Moreno 1997). In this method
the Cspace is calculated like the convolution of the
function that represents the robot and other function
that represents the workspace. In the particular case
of an articulated robot with two degrees of freedom
the final expressions to calculate the obstacles in the
Cspace are:
ICINCO 2005 - ROBOTICS AND AUTOMATION
12

Figure 1: Application develope
d
ϕϕθϕθ
drdrBrACB ),(),()( 1)0(111 ⋅−=
∫
ϕϕθϕθθ
θ
drdrBrACB
∫
⋅−= ),()1,(),( )2,0(2212
where A
1
and A
2
are the subsets of the workspace
that represent the two links that form the robot and B
is the subset of the workspace occupied by the
obstacles.
Using this bitmap representation, the potential
field is calculated. To calculate the attraction force
of the potential field in one point, we use the
distance to the goal configuration. Possible functions
are: Euclidean, Manhattan, eight neighbours, etc.
This function is easy to calculate and valid in spaces
with more than three dimensions. To calculate the
repulsive force of the obstacles, we use a front of
waves that calculate the repulsive force in each point
in the surroundings of the obstacle. This force is
smaller as we move away from the obstacle.
With this method we can calculate the Cspace of
the robot in a short time, and it is easy to modify if
the robot is in a dynamic environment.
2.2 Using Potential Fields like
Heuristic Function
The A* and D* are heuristic guided algorithms. We
use the potential fields representation of the
configuration space like heuristic function to guide
the collision-free path search. The definition and
pseudocode of the algorithms can be found in
(Feigenbaum 1986) (Stentz 1994) and (Stentz 1995).
To do this, the function that chooses the best
neighbour in the A* algorithm must be modified.
The original function consists of two terms: cost
from the starting node (g) and the heuristic that
guides the search. This last term is divided in two
terms: the first is the attraction force in this point
(h
A
) and the second is the repulsive force in this
point (h
R
). The resulting function is the following
one:
f = g + h where h = h
A
+ h
R
.
In the same function in the D* algorithm, the
resulting function consists of only two terms: the
first is the attraction force in this point (h
A
) and the
second is the repulsive force in this point (h
R
).
f = h
A
+ h
R
.
Both functions can be quick and easily
calculated in any dimension spaces.
3 PROCEDURE VALIDATION
We have developed a software platform to validate
the path calculation. This application presents the
user the work space and its corresponding
configuration space. In both representations we can
see the robot, the obstacles, the calculated path, the
explored nodes and the repulsion field around the
obstacles. When the user modifies the work space,
the corresponding configuration space is
automatically recalculated and showed to the user.
We can see two different path calculations in figure
1.
3.1 Pseudocode
The pseudocode of the algorithm used may be the
following:
env = robot_environment();
cspace = cspace_from(env);
pot_cspace = repulsive_field(cspace);
result = search_alg(pot_cspace,
dist_function,data_struct);
wresult = to_workspace(result);
apply_robot(wresult);
CALCULATION OF OPTIMAL PATHS IN THE CONFIGURATION SPACE USING ARTIFICIAL POTENTIAL
FIELDS AND A* AND D* ALGORITHMS FOR AN ARTICULATED ROBOT. COMPARISON OF TECHNIQUES
13
The
robot_environment function generates a
bitmap representation of the environment of the
robot. This bitmap represents the workspace of the
robot and the calculation path technique used works
in the configuration space. The
cspace_from
function generates the Cspace. Then, the
repulsive_field function calculates the
repulsive fields of the obstacles in the configuration
space. At this time, the map for the path calculation
is ready. We use one search algorithm like A* or D*
to search a free-collision path using like heuristic
function the potential field generated before. The
path generated must be transformed for its use in the
workspace using the
to_workspace function.
Finally,
apply_robot acts in the robot to follow
the path.
4 PERFORMANCE OF THE
ALGORITHM
In this chapter, the performance of this technique is
presented. First we present the CPU time results
obtained using both algorithms in different
environments. The location and number of obstacles
and the initial and goal positions of the robot have
been generated of random way.
In the particular case of an articulated robot with
two degrees of freedom, two different free-collision
paths could be found: elbow-up and elbow-down
configurations. Those searches can be made in
parallel, so that we can choose the best solution, the
faster solution, etc. The CPU times choosing the best
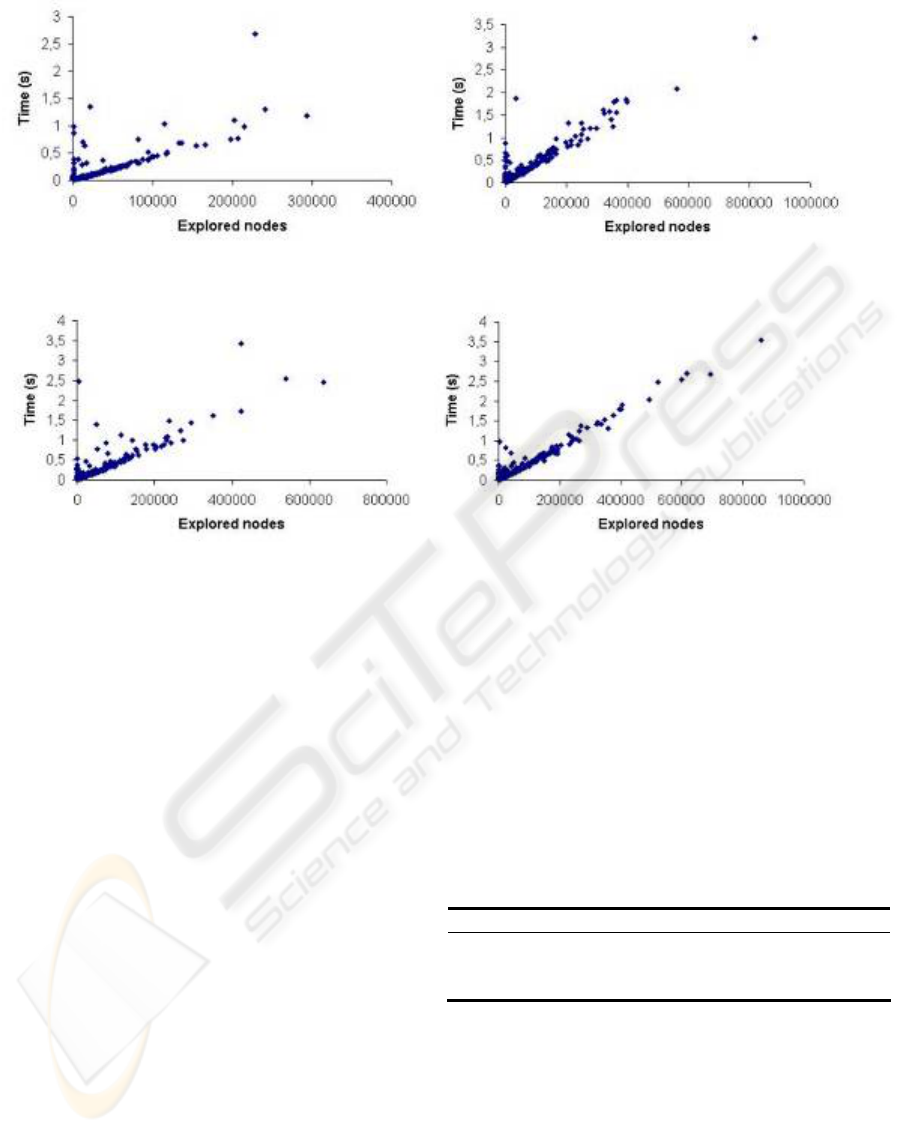
solution are listed at figure 2.
Figure 2: Different CPU time results in different environments using both search algorithms
To calculate the attraction forces in the potential
field we use the distance to the goal configuration.
We can see the results using the Euclidean,
Manhattan and 8-distance functions in the following
table.
Path length Explored nodes Time (s)
Euclidean 100,774 61894,857 0,659
Manhattan 94,833 38947,389 0,421
8-distance 105,05 45177,01 0,573
As we can observe in this table, the number of
explored nodes is quite bigger in the case of using
Euclidean distance.
The most important data structure in both
algorithms is the open list, mainly because a good
selection of the data structure has an important
repercussion in the time of calculation and in the
memory usage. We have tested the algorithms with
two different data structures: an ordered list and a
binary heap. The results obtained are listed in figure
ICINCO 2005 - ROBOTICS AND AUTOMATION
14
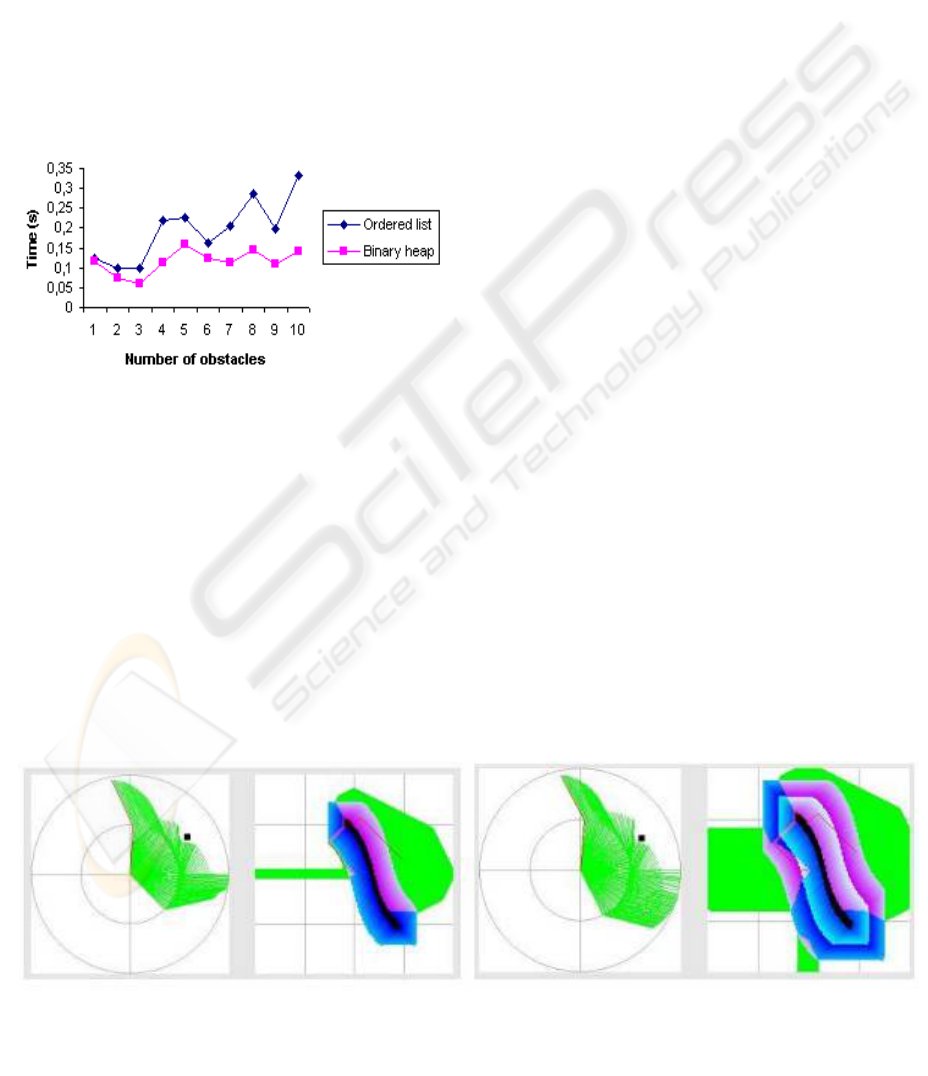
3. The results show that the use of the binary head
data structure reduces the time of computation.
A parameter to be considered when representing
the work space with potential fields is the size of the
repulsion field that separates the robot from the
obstacles. Numerous tests demonstrate that, from
certain size, to increase the size of the repulsion field
makes the number of explored nodes to find the path
grow, increasing the time used to calculate it. This
tests show that a repulsion field size over ten points
causes the increase of the number of explored nodes.
Nevertheless, in the cases of a repulsion field size
below ten points (even the no existence of repulsion
field) the number of explored nodes is very similar.
This proves the importance of using a size of
repulsion field not excessively big, since we forced
the search algorithms to give a roundup to avoid the
obstacle. An example of this can be showed in the
figure 4.
5 CONCLUSIONS
The main target of this work has been the
representation of the environment of an articulated
robot using the potential field technique and the
implementation of path search algorithms in these
environments and the measurement of its
performance.
The results demonstrate that, in static
environments, there are not important differences of
performance between search algorithms.
The search algorithms have a higher
performance if the Manhattan distance is used
instead of the Euclidean distance or 8-distance in the
calculation of the distance to the goal configuration.
It is the same if a binary heap is used to store the
open list instead of a ordered list.
The size of the repulsion field that moves away
the robot from the obstacles must not be excessively
great, since the yield of the algorithms diminishes as
this field of repulsion grows. The results show that,
although the information provided by the potential
field is not much, the implemented algorithms
search allow us to obtain the optimal way between
two configurations in a fast way.
REFERENCES
Adi, J. and Muller, M., 2004. Near optimal hierarchical
path finding. Journal of Game Development.
Blanco, F., 1997. Un nuevo enfoque en la planificación de
caminos libres de colisiones para estructuras robóticas.
PhD thesis, Universidad de Salamanca.
Branicky, M., Newman, W., 1991. Real-time
configuration space transforms for obstacle avoidance.
The International Journal of Robotics Research.
Figure 3: Different data structures for the open list in
the search algorithms
Chen, D., 1996. Developing algorithms and software for
geometric path planning problems. ACM Computers
Survey.
Elnagar, A., 2002. A heuristic approach for local path
planning in 3d environments. Robotica.
Feigenbaum, E., 1986. The Handbook of Artificial
Intelligence. Addison Wesley.
Fox, J. and Maciejewski, A., 1993. Path planning and the
topology of configuration space. IEEE Transactions
on Robotics and Automation.
Ge, S. and Cui, Y., 2002. Dynamics motion planning for
mobile robots using potential field method.
Autonomous Robots.
Gilliard, P., 2002. Real-time bsp-based path planning with
A*. Brazilian Symposium on Computer Graphics and
Figure 4: Different results using 10 points repulsion field (left) and using 20 points one (right)
CALCULATION OF OPTIMAL PATHS IN THE CONFIGURATION SPACE USING ARTIFICIAL POTENTIAL
FIELDS AND A* AND D* ALGORITHMS FOR AN ARTICULATED ROBOT. COMPARISON OF TECHNIQUES
15

Image Processing.
Helgason, R., Kennington, J. and Lewis, K., 2001. Cruise
missile mission planning: A heuristic algorithm for
automatic path generation. Journal of Heuristics.
Hwang, Y. and Ahuja, N., 1988. Robot path planning
using potential field representation. PhD Thesis.
Kacandes, P., Langen, A. and Warnecke, H., 1989. A
combined generalized potential fields / dynamic path
planning approach to collision avoidance for a mobile
autonomous robot operating in a constrained
environment. Intelligent Autonomous Systems 2, An
International Conference.
Kavraki, L., 1995. Computation of configuration space
obstacles using de fast fourier transform. IEEE
Transactions on Robotics and Automation.
Latombe, J., and Barraquand, J., 1991. Robot motion
planning: a distributed representation approach.
International Journal of Robotics Research.
Lee, B., 1995. An analytic approach to moving obstacle
avoidance using artificial potential field. Proceedings
of the International Conference on Intelligent Robots
and Systems.
Lozano-Pérez, T., 1983. Spatial planning: a configuration
space approach. IEEE Transactions on computers.
Melchior, P., Orsoni, B., Lavialle, O., Poty, A. and
Oustaloup, A., 2003. Consideration of obstacle danger
level in a path planning using a* and fast-marching
optimization: comparative study. Signal Process.
Moreno, V., Curto, B., 1997. Mathematical formalism to
perform a fast evaluation of the configuration space.
Proc. of the IEEE International Symposium on
Computational Intelligence in Robotics and
Automation.
Prestes, E., Idiart, M., Trevisan, M. and Engel, P., 2004.
Autonomous learning architecture for environmental
mapping. J. Intell. Robotics Syst.
Seidel, R., Guibas, L., 1986. Computing convolution by
reciprocal search. Proc. of the ACM Symposium
Computational Geometry.
Stentz, A., 1994. Optimal and efficient path planning for
partially-known environments. Carneige Mellon
University.
Stentz, A., 1995. The focused d* algorithm for real-time
replanning. Carneige Mellon University.
Trovato, K., 1996. A* planning in discrete configuration
spaces of autonomous systems. PhD. Thesis.
Udupa, S., 1997. Collision Detection and Avoidance in
Computer Controlled Manipulators. PhD thesis.
California Institute of Technology.
Williams, M., and Jones, D., 2001. A rapid method for
planning paths in three dimensions for a small aerial
robot. Robotica.
Wong, B., and Spetsakis, M., 2000. Scene reconstruction
and robot navigation using dynamic fields.
Autonomous Robots.
Yachida, M., Kitamura, Y. and Tanaka, T., 1995. 3d path
planning in a dynamic environment using an octree
and an artificial potential field. Proceedings of the
International Conference on Intelligent Robots and
Systems.
Zhang, Y. and Valavanis, K., 1997 A 3d potential panel
method for robot motion planning. Robotica.
ICINCO 2005 - ROBOTICS AND AUTOMATION
16
