A NEW METHOD FOR WEIGHT UPDATING IN FUZZY

COGNITIVE MAPS USING SYSTEM FEEDBACK

Theodore L. Kottas, Yiannis S. Boutalis

Department of Electrical and Computer Engineering, Democritus University of Thrace, Xanthi, Hellas (Greece)

Manolis A. Christodoulou

Department of Electronic and Computer Engineering, Technical University of Crete, Chania, Hellas

Keywords: Fuzzy Cognitive Maps, Hebbian rule, State feedback, Weight Updating.

Abstract: Fuzzy Cognitive Maps (FCMs) have found many applications in social -financial -political problems. In this

paper we propose a method of FCM operation, which can be used to represent and control any real system,

including traditional electro-mechanical systems. In the proposed approach the FCM reaches its equilibrium

point using direct feedback from the node values of the real system and the limitations imposed by the

control objectives for the node values of the system. The experts’ knowledge, which is represented in the

weights of the nodes’ interconnections, undergoes a continuous on-line adaptation based on feedback from

the real system. An algorithm for weight updating is proposed, which is based on system feedback and

which includes specially designed matrices that lead the FCM and consequently the real system associated

with it in a balanced equilibrium state. The proposed methodology is tested by simulating the operation of a

hydro-electric plant.

1 INTRODUCTION

Some problems of electrical and mechanical

engineering are placed in the fuzzy part of science

and they have been studied thoroughly enough the

last years from a good many of scientists. A large

number of different methods have occasionally been

used in order to work out this kind of problems. The

scientific community was placed under the

obligation of giving solutions to problems the

settlement of which seemed rather difficult the years

before.

Fuzzy Cognitive Maps (FCM) can model

dynamical complex systems that change with time

following nonlinear laws (Kosko, 1992). FCMs use

a symbolic representation for the description and

modeling of the system. In order to illustrate

different aspects in the behavior of the system, a

fuzzy cognitive map is consisted of nodes with each

node representing a characteristic of the system.

These nodes interact with each other showing the

dynamics of the system in study. An FCM integrates

the accumulated experience and knowledge on the

operation of the system, as a result of the method by

which it is constructed, i.e., using human experts

who know the operation of system and its behavior.

Fuzzy cognitive maps have already been used to

model behavioral systems in many different

scientific areas. For example, in political science

(Schneider, 1998), fuzzy cognitive maps were used

to represent social scientific knowledge and describe

decision-making methods (Kottas, 2003), (Zhang,

1989), (Georgopoulou, 2001). Kosko enhanced the

power of cognitive maps considering fuzzy values

for their nodes and fuzzy degrees of

interrelationships between nodes (Kosko, 1992),

(Kosko, 1997). After this pioneering work, fuzzy

cognitive maps attracted the attention of scientists in

many fields and they have been used in a variety of

different scientific problems. Fuzzy cognitive maps

have been used for planning and making decisions in

the field of international relations and political

developments (Kottas, 2003) and to model the

behavior and reactions of virtual worlds. FCMs have

been proposed as a generic system for decision

analysis (Zhang, 1989), (Zhang, 1992) and as

coordinator of distributed cooperative agents.

One open issue related to FCMs, is their

operation in close cooperation with the real system

they describe. This in turn implies that such an on-

202

L. Kottas T., S. Boutalis Y. and A. Christodoulou M. (2005).

A NEW METHOD FOR WEIGHT UPDATING IN FUZZY COGNITIVE MAPS USING SYSTEM FEEDBACK.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics, pages 202-209

DOI: 10.5220/0001163502020209

 SciTePress

line interaction with the real system might require

changes in the weight interconnections, which

reflect the experts’ knowledge about the node

interdependence. This knowledge might not be

entirely correct or perhaps, the system has

undergone to changes during its operation.

In this paper an FCM operation method is

proposed, which is in close interaction with the

system it represents. The FCM nodes are divided in

control and reference nodes, where control nodes

represent control variables of the system and

reference nodes represent either variables with

constant values or variables with desired (goal)

values. In the proposed approach, the FCM reaches

its equilibrium point using direct feedback from the

node values of the real system and the limitations

imposed by the reference nodes. The

interconnections weights are on-line adjusted during

this operation by using an extended Hebbian

updating law, which uses the system feedback and

employs two specially defined collateral matrices,

which help the FCM to adjust its weights and reach

an equilibrium point in a more realistic and balanced

way.

The paper is organized as follows: Section 2

gives a short description of FCMs and their way of

operation. Section 3 introduces the proposed

combined operation of the FCM and the real system

and presents the relevant Hebbian rule to update

interconnections weights. The proposed weight

updating method is extended in Section 3.1 to

include the specially defined placement and

calibration matrices. Section 4 gives a simulation

study of a hydro-electric power plant, where a

comparative study of the proposed method versus

the traditional approach in reaching equilibrium

points in FCM is made. The final conclusions are

given in Section 5.

2 FUZZY COGNITIVE MAPS

REPRESENTATION AND

DEVELOPMENT

Fuzzy cognitive maps approach is a hybrid modeling

methodology, exploiting characteristics of both

fuzzy logic and neural networks theories and it may

play an important role in the development of

intelligent manufacturing systems. The utilization of

existing knowledge and experience on the operation

of complex systems is the core of this modeling

approach. Experts develop fuzzy cognitive maps and

they transform their knowledge in a dynamic

cognitive map (Miao, 2001).

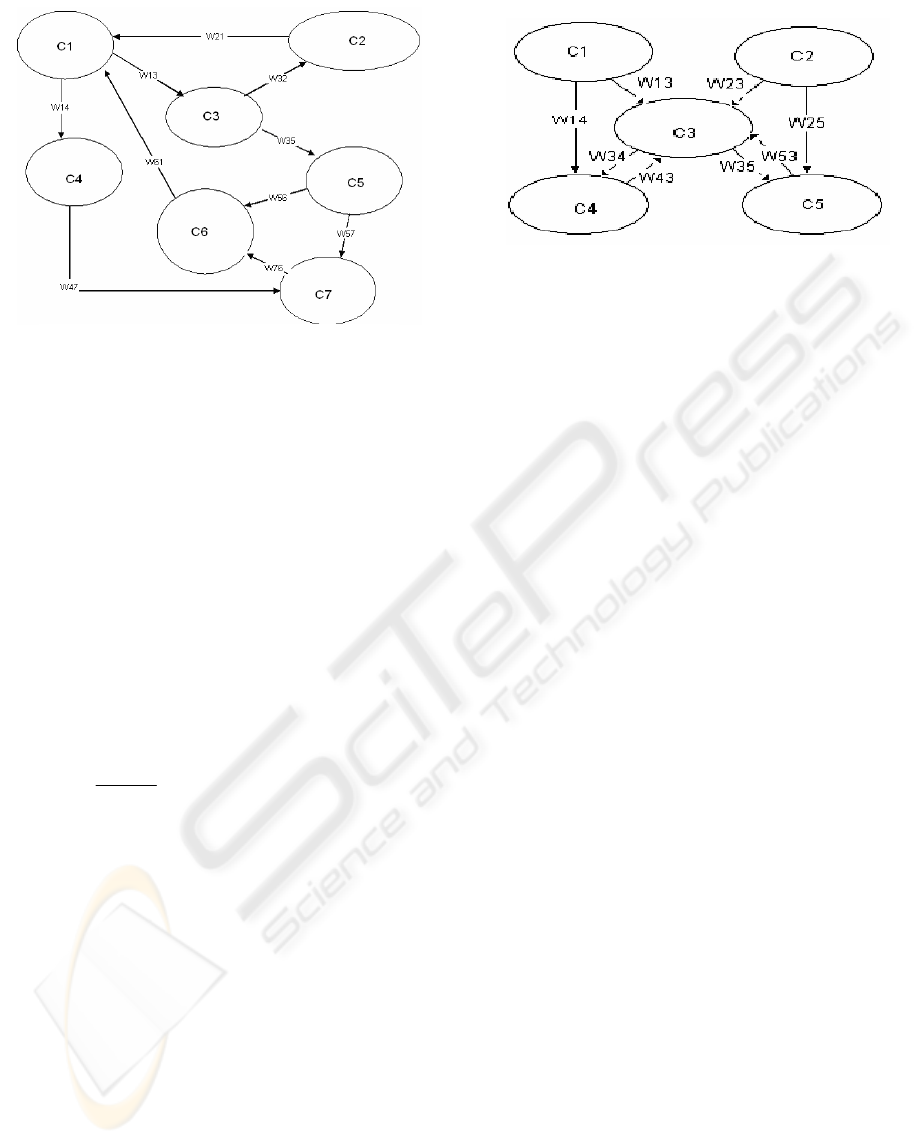
The graphical illustration of FCM is a signed

directed graph with feedback, consisting of nodes

and weighted interconnections. Nodes of the graph

stand for the nodes that are used to describe the

behavior of the system and they are connected by

signed and weighted arcs representing the causal

relationships that exist among nodes (Fig. 1). Each

node represents a characteristic of the system. In

general it stands for states, variables, events, actions,

goals, values, trends of the system which is modeled

as an FCM (Jang, 1995). Each node is

characterized by a number A

, which represents its

value and it results from the transformation of the

real value of the system's variable, for which this

node stands, in the interval [0, 1]. It must be

mentioned that all the values in the graph are fuzzy,

and so weights of the interconnections belong to the

interval [-1, 1]. With the graphical representation of

the behavioral model of the system, it becomes clear

which node of the system influences other nodes and

in which degree.

The most essential part in modeling a system

using FCMs, is the development of the fuzzy

cognitive map itself, the determination of the nodes

that best describe the system, the direction and the

grade of causality between nodes. The selection of

the different factors of the system, which must be

presented in the map, will be the result of a close-up

on system's operation behavior as been acquired by

experts. Causality is another important part in the

FCM design, it indicates whether a change in one

variable causes change in another, and it must

include the possible hidden causality that it could

exist between several nodes. The most important

element in describing the system is the

determination of which node influences which other

and in what degree. There are three possible types of

causal relationships among nodes that express the

type of influence from one node to the others. The

weight of the interconnection between node C

and

node C

denoted by W

, could be positive (W

> 0)

for positive causality or negative (W

< 0) for

negative causality or there is no relationship between

node C

, and node C

, thus W

= 0. The causal

knowledge of the dynamic behavior of the system

is stored in the structure of the map and in the

interconnections that summarize the correlation

between cause and effect. The value of each node is

influenced by the values of the connected nodes with

the corresponding causal weights and by its previous

value. So, the value A

for each node C

is calculated

by the following rule, (Jang, 1995):

A NEW METHOD FOR WEIGHT UPDATING IN FUZZY COGNITIVE MAPS USING SYSTEM FEEDBACK

203

where

, is the value of node

C at step s,

−

is the value of node

C , at step s-1,

−

is the value

of node

C at step s-1, and

W is the weight of the

interconnection between

C and

, and f is a

squashing function.

Squashing functions:

1) f = tanh(x) maps the nodes values in [-1 , 1]

−

by using c=1 we convert the

nodes values in [0 , 1]. It also called sigmoid

function. The second function is the most common

function which is used in FCM’s.

3 THE NEW METHOD FOR

WEIGHT UPDATING

In this section we will analyze the proposed method

of updating the interconnections weights of FCM

taking into account feedback node values from the

real system. Using the updated weights the FCM

reaches a new equilibrium point by means of

equation (1). Some of the new node values can be

applied as control values to the real system. One

commonly used technique for updating weights in

FCMs is the Hebbian updating rule (Kosko, 1986

a,b), (Papageorgiou, 2004). In our approach the

updating is made by using the conventional Hebbian

rule, which however, uses measurements from the

node values taken from the real system. This way

the updating of the weights reflects real changes that

have to be made in our knowledge about the system,

which is represented by the interconnection weights.

This situation is more apparent in cases where there

exist steady value nodes, which, in the real system,

are not affected by the values of the other nodes. In

this case, if the FCM convergence equation (1) is

left to operate with weight adjustments that do not

take into account the steady node values fact, then

the equilibrium point will give node values for the

above mentioned nodes, which might be different

than the steady values, which in turn implies an

unrealistic point of operation for our system.

Let us, for example, analyze an FCM having one

or more nodes with constant values. This means that

no human action can intervene, in a mechanic way

with this value. Suppose that in the FCM of Fig. 2

nodes C1 and C2 cannot change their values. The

values of these nodes derive from the system that is

examined. The table of interconnection weights for

this system is:

00 13 14 0

00 23 0 25

00 0 34 0

00 43 0 0

00 53 0 0

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

We see that columns 1 and 2 that concern nodes C1

and C2 are zero. When applying equation (1) for

node value updating we have to consider the steady

values of nodes C1 and C2 by using a companion

adjusting equation. Thus, equation (1) is now

replaced by the following two equations:

iij

sss

jij

Af AWA

=≠

−−

∑

⎛⎞

⎜⎟

⎝⎠

(1)

,1,1,

iij

s FCM s FCM s FCM

jij

Af AWA

=≠

−−

∑

⎛⎞

⎜⎟

⎝⎠

(2)

And for the steady state nodes the correction

equation is:

Figure 2: FCM with steady stea nodes

Figure 1: A simple fuzzy cognitive map

ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

204

FCM system

AA=

(3)

where

ystem

A is the node’s value, derived from the

real system. These values are either measured on-

line or are known beforehand as the steady nodes

values of the above example. In order to drive the

FCM in a realistic representation of the system and

its control actions we have to update the

interconnection weights using these measured node

values from the real system. Based on the updated

weights, equations (1) and (2) will produce a new set

of node values which represent the control actions

applied to the real system. The procedure, which is

depicted in Fig. 3, is repetitively applied during the

operation of the system. The weights that are non

zero are renewed according to the Hebbian rule:

sFCM sFCM

iij

AWA

system

=≠

⎛⎞

⎜⎟

−+

⎜⎟

⎝⎠

=−

∑

(4)

(1 )

kk sFCM

ij ij

WW appA

−

+−=

(5)

where k is the number of iteration and a is the

learning rate (usually

=0.1).

The procedure described in Fig. 3 uses

repetitively equations (2), (3), (4) and (5) to provide

with an FCM, which totally corresponds and

cooperates with the real system. The control nodes

of the system (nodes C3, C4 and C5 of Fig. 2) are

now taking values which take into account the

steady node values (C1 and C2) and the weight

interconnections updated values. In the next section

we extend the weight updating equations to include

two collateral matrices, the one been called

placement matrix and the other calibration matrix.

We will see that by including these two matrices in

the weight updating equations the FCM results in

more balanced and smooth variations of its node

values.

3.1 The Extended Weight Updating

Law

The motivation for developing this new extended

updating law was to find a flexible and credible way

to drive one or more elements (nodes) of a system in

a desired position (value). The proposed extended

method includes two auxiliary collateral matrices Q

and R. Matrix Q incorporates experts’ opinion about

the nodes that should be positively or negatively

affected so that the driven node reaches the desired

value, provided that the node interdependences are

determined by weight matrix W. Matrix R contains

elements that help FCM to converge to the desired

node values by altering the connected to them nodes

in a balanced way, avoiding saturation in the nodes

having already large values. The two matrices Q and

R can be included in the weight updating law with

system feedback, described in the previous section,

leading thus to a new FCM representing the system

in amore desirable and realistic way.

The first matrix, called placement matrix, Q, has

the same dimensions with matrix W. Each element

of the placement matrix Q can take one of the

values {-1, 0, 1}, which reflect the way by which

node C

affects node C

and determines the weights

that should be updated in order to influence the

change of node value C

. A possible formation of

matrix Q is the following: If one wants to drive node

from value

−

to a bigger value

, that is

−

> then:

1010,00,

ji ij ji ij ji ij

Q ifW Q ifW Q ifW

>=− <= =

In the opposite situations, when one wants to drive

node C

from value

−

to a smaller value

, that

−

< then:

1010,00,

ji ij ji ij ji ij

Q ifW Q ifW Q ifW

<=− >= =

The use of this matrix will be clearer in section 4.

Incorporation of matrix Q in the weight updating

equations is performed as follows:

sFCM sFCM

iij

AWA

system

=≠

⎛⎞

⎜⎟

−+

⎜⎟

⎝⎠

=−

∑

*( (1 )

kk sFCM

ij ij ij

WW Qap pA

−

=+ − (6)

The calibration matrix R has the same dimension

with matrix W. Each point R

of the calibration

matrix R is computed by the following formula:

FCM SYSTEM

Feedbac

(

syste

)

Control actions

Figure 3: Control structure

S,FCM

desired

nodes values

erts

A NEW METHOD FOR WEIGHT UPDATING IN FUZZY COGNITIVE MAPS USING SYSTEM FEEDBACK

205

∑

if W

≠ 0 and 0

R = if W

(7)

where n is the learning rate and is defined in the

interval [0.01, 0.1].

It can be seen that for the computation of each

element of R only the elements of each column of

matrix W contribute. This is related to the fact that

each column j of matrix W contains weight

interconnection values from the nodes which affect

node j. When matrix R is incorporated in the weight

updating law, the new weights lead the FCM to a

more balanced equilibrium point and prevent nodes,

which already have large values, to saturate. At the

same time matrix R also causes an enhancement to

the values of nodes which have small values and

which, of course affect the nodes to be changed.

Incorporation of matrix R in the weight updating

equations is performed as follows:

sFCM sFCM

iij

AWA

system

=≠

⎛⎞

⎜⎟

−+

⎜⎟

⎝⎠

=−

∑

*( (1 )

kk sFCM

ij ij

WW ap pAG

−

=+ −

(8)

where :

ij ij

GQ R=

(9)

If C

node must be in a desired value then

system

= A

desired

, so that equation 4 for the nodes in

a desired value becomes:

The complete algorithm which uses system

feedback, the desired node values and the collateral

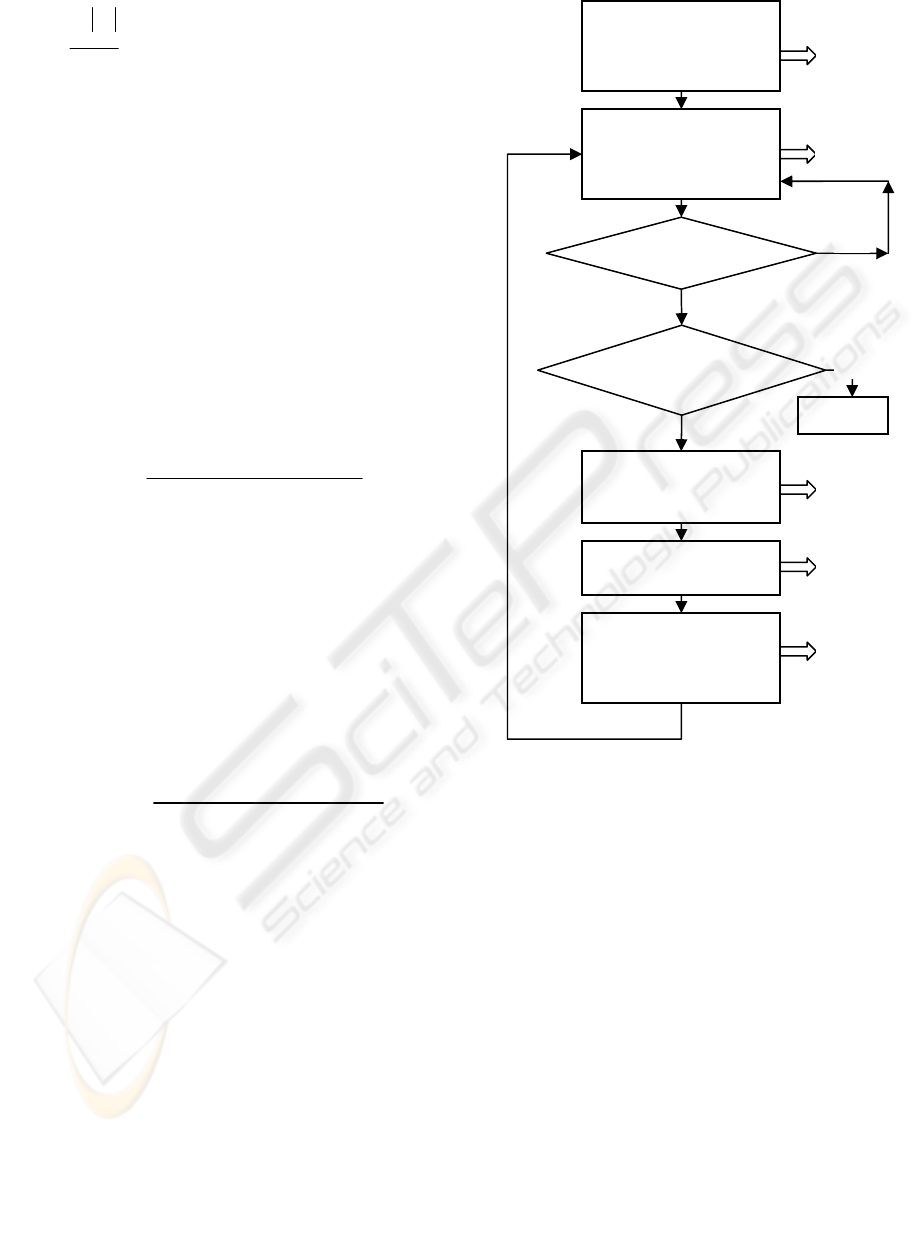
matrices Q, R is shown in Fig. 4.

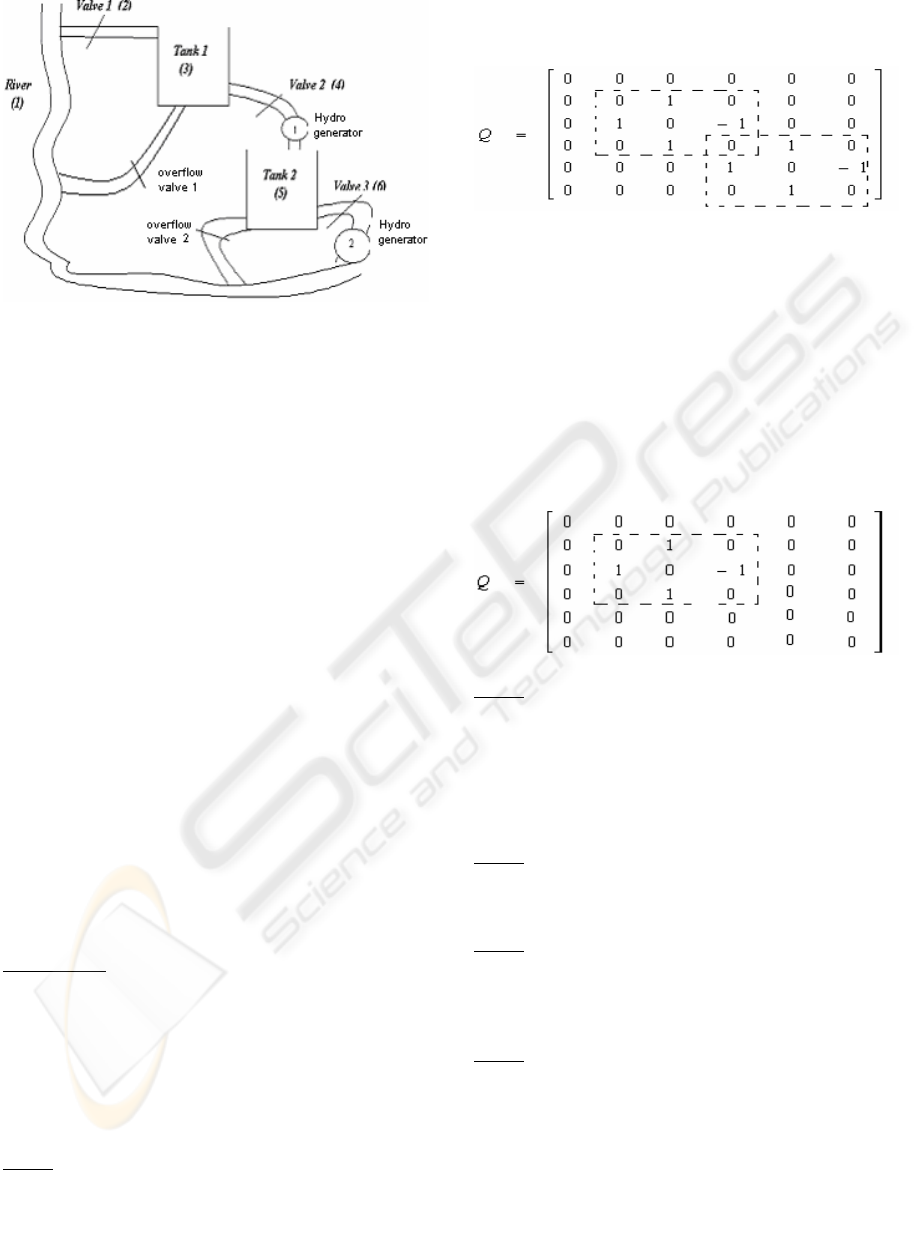
4 SYSTEM SIMULATION STUDY

To demonstrate the method we choose a simple

mechanical problem of a hydroelectric power station

shown in Fig. 5. The FCM representation of the

system is shown in Fig. 6. We want to regulate the

flow in the two Hydro-generators (1 and 2). In order

to achieve this we will use the proposed method, to

control the system and to regulate the values of the

report and control nodes.

The system has one steady value node [River -

reference node1], three control nodes [Valve 2 -

node 4, Valve 3 - node 6 and Valve 1 – node 2] and

two simple operation nodes [Tank 1 - node 3, Tank 2

- node 5]. One or more of nodes 2, 3, 4, 5 and 6

values have to be regulated so that hydro-generators

1 and 2 can receive the desired water flow values.

Based on experts knowledge regarding the

mechanics of the system a possible weight matrix W

is the following:

00.6 0 0 0 0

0 0 0.76 0 0 0

00.81 0 0.38 0 0

0 0 0.6 0 0.8 0

0 0 0 0 .7 0 0 .6

0 0 0 0 0.42 0

⎡

⎤

−

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

−

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

−

⎣

⎦

which, after repetitively applying equations (2) and

(3) will give the following equilibrium values for

sFCM sFCM

iij

desired

AWA

=≠

⎛⎞

⎜⎟

−+

⎜⎟

⎝⎠

=−

∑

(10)

Figure 4: Schematic description of the

roposed

algorithm

Define the desired

nodes values acquire

the initial W matrix

and compute Q matrix

Execute eq. (2) and (3)

to find equilibrium

points for the FCM

nodes.

Send the control nodes

values from the FCM

to the real system.

Calculate the R matrix

and update weights

according to eq. (4),

(8) and (10)

Take the nodes values

from the real s

stem.

Step 5

Step 4

Step 3

S,FCM

= desired

node value

YES

Step 1

Step 2

S,FCM

S-1,FCM

STOP

YES

ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

206

the nodes of the FCM. It should be mentioned that in

this case equation (3) applies only for the steady

node 1 value, which in our example is 0.6.

0.6 0.658 0.65 0.8 0.75 0.7A

⎡⎤

⎣⎦

Since we are not absolutely confident about the

experts’ opinion on matrix W, or we want to

anticipate any physical changes occurred in the

system during its operation we proceed in weight

updating according to the procedure described in

Fig. 3 using equations (2), (3), (4) and (5). It should

be noted that, so far, the only desired node value in

Fig. 3 is the steady node 1 (river). The improved

weight matrix becomes:

00.95390000

0 0 0.7592 0 0 0

0 0.6457 0 0.0729 0 0

0 0 0.598 0 0.7999 0

0 0 0 0.3519 0 0.2959

0 0 0 0 0.4201 0

imp

⎡⎤

−

⎢⎥

−

⎢⎥

−

⎣⎦

which, after applying equations (2) and (3), gives the

following FCM equilibrium node values.

0.6 0.5592 0.6498 0.7402 0.7362 0.7183A

⎡⎤

⎣⎦

Case study 1

We now want to drive node 3 (tank 1) and node

5 (tank 2) to a specific value. We want to do that

because the water height in these tanks will affect

the water flow in Hydrogenerators 1 and 2, which in

turn influences the produced power. In this approach

we will use matrices Q and R and we will proceed

following all the steps of Fig. 4.

Step 1

We assume that we desire the following values:

node (3) = 0.652, node (5) = 0.7398, keeping always

in mind that node 1 (river) has always a steady value

(0.6). Let also the initial weight matrix W equals

matrix W

imp

computed earlier.

We calculate matrix Q according to section 3.1.

The two sub-matrices of Q, enclosed by dotted lines,

refer to nodes 3 and 5. The right sub-matrix refers to

node 5 and declares that in order to drive node 5 in a

specific value we have to update the elements of the

W matrix which correspond to the points of the right

dotted sub-matrix. The same rationale applies for the

left sub-matrix, which now refers to node 3. The

centre of each sub-matrix referring to the C

node

must be the element Q

. If we don’t want to change

node then the corresponding sub-matrix is set to

zero. For example if we want to drive only node 3

the Q matrix is:

Step 2

Now we execute step 2 of Fig. 4 to calculate

equilibrium point for the FCM, which is:

0.6 0.5592 0.6498 0.7402 0.7362 0.7183A

⎡

⎤

⎣

⎦

We must now correct node (3) and node (5) and

drive them to 0.652 and 0.7398 respectively.

Step 3

We apply the FCM control nodes values to the

real system

Step 4

We get the new node values from the real

system. We assume that the real system instantly

responds to the values imposed by step 3.

Step 5

Calculate calibration matrix R according to

equation (7):

00.16760000

0 0 0.179 0 0 0

0 0.247 0 0.58 0 0

0 0 0.226 0 0.152 0

0 0 00.1201

00 0 00.290

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

Figure 5: Hydroelectric station

A NEW METHOD FOR WEIGHT UPDATING IN FUZZY COGNITIVE MAPS USING SYSTEM FEEDBACK

207

Find the new W matrix that arises by using

equations (4), (8) and (10). Go to step 2.

After 12 iterations we will find that the FCM

accurately describes the operation of the real system.

The final W matrix is:

0 0.9539 0 0 0 0

0 0 0.7696 0 0 0

0 0.4148 0 0.0914 0 0

0 0 0.6138 0 0.8081 0

0 0 0 0.3818 0 0.3431

0 0 0 0 0.4121 0

final

⎡⎤

−

⎢⎥

−

⎢⎥

−

⎣⎦

and A vector is:

0.6 0.5655 0.652 0.7485 0.7398 0.7273A

⎡⎤

⎣⎦

if we don’t use matrices Q and R by executing the

case study 1 from step 2 to step 5 we will conclude

to the desired values for nodes 3 and 5 after 45

iterations. The other node values are however

different since W matrix is in this case different than

the one calculated above.

Case study 2

To make the use of the two matrices clearer we

give the following example. Suppose we want to

drive only node 3 (tank 1) in a specific value:

node 3 = 0.76. We keep in mind that node 1 is a

steady value node (0.6). Let also the initial weight

matrix W equals matrix W

final

computed above.

Step 1

Calculate placement matrix Q according to

Section 3.1:

Step 2

Now we execute step 2 of Fig. 4 to calculate

equilibrium points for the FCM, which is:

0.6 0.5655 0.652 0.7485 0.7398 0.7273A

⎡

⎤

⎣

⎦

We must now correct node (3) and drive it to 0.76.

Step 3

We apply the FCM control nodes values ro the

real system

Step 4

We get the new node values from the real

system. We assume that the real system instantly

responds to the values imposed by step 3.

Step 5

Calculate calibration matrix R according to

equation (7):

00.143 0 0 0 0

000.1790 00

00.31 0 0.517 0 0

0 0 0.225 0 0.15 0

00 00.12401

00 0 00.2960

⎡

⎤

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

⎣

⎦

Find the new W matrix that arises by using

equations (4), (8) and (10). Go to step 2.

After 16 iterations we find that matrix W and

vector A are:

0 0.9539 0 0 0 0

0 0 0.7652 0 0 0

0 0.6 0 0.2642 0 0

0 0 0.5472 0 0.8081 0

0 0 0 0.3818 0 0.3431

0 0 0 0 0.4121 0

⎡

⎤

−

⎢

⎥

⎢

⎥

⎢

⎥

−

⎢

⎥

−

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

−

⎣

⎦

0.60.62430.760.68080.72660.7273A

⎡

⎤

⎣

⎦

if we don’t use matrices Q and R by executing the

case study 2 from step 2 to step 5 we will conclude

after 34 iterations to:

00.5674 0 0 0 0

0 0 0.9236 0 0 0

0 0.8834 0 0.0423 0 0

0 0 0.4220 0 0.8962 0

0 0 0 0.2455 0 0.3431

0 0 0 0 0.3242 0

⎡

⎤

−

⎢

⎥

⎢

⎥

⎢

⎥

−

⎢

⎥

−

⎢

⎥

⎢

⎥

⎢

⎥

⎢

⎥

−

⎣

⎦

Tank2 (5)

Valve 1 (2)

Valve 2 (4)

Tank 1 (3)

Valve 3 (6)

W12

W32

W34

W43

W23

W45

W54

W56

W65

Figure 6: A Fuzzy cognitive map representing the

hydroelectric factory of Fig. 5

ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

208

and

0.6 0.7459 0.76 0.7019 0.76 0.7290A

⎡⎤

⎣⎦

It can be observed that, without matrices Q and

R, the FCM drives the system to a different

equilibrium point than the equilibrium reached using

Q and R matrices. It is apparent that when the

matrices are not used, in the new equilibrium points

more node values are different than their initial

values. On the contrary, when Q and R matrices are

used only control nodes 2 and 4 are different than

their initial equilibrium values. This fact is mainly

due to matrix Q. In large systems which are difficult

to change their operation we don’t want main

characteristics to be changed with no reason. Less

changes we manage, in main characteristics (see

valves), more flexible system we make. The effect

of matrix R is made more apparent from the weight

changes and the node value changes in the

equilibrium points. It can be observed that by using

matrix R the changes in the control node values are

made in a more balanced way because in this case

nodes 2 and 4, which affect node 3, change

proportionally. In respect to the internal operation of

the algorithm, this is connected to the fact that the

weights are not allowed to reach their saturation

values because their change is not allowed to be

proportional to their previous value (see for example

and W

5 CONCLUSIONS

In this paper a new method for weight updating in

FCMs using system feedback is proposed. So far,

the existing approaches were using the simple

method of weight updating without taking into

account the feedback from the real system. The

diversity of the proposed method lies in the fact that

FCM reaches its equilibrium point using direct

feedback from the node values of the real system

and the limitations imposed by the reference nodes,

which nodes represents either variables with

constant values or variables with desired (goal)

values. The weights are on-line adjusted during this

operation by using an extended Hebbian updating

law, which uses the system feedback and employs

two specially defined collateral matrices, which help

the FCM to adjust its weights and reach an

equilibrium point in a more realistic and balanced

way. Another benefit of using these matrices, which

is drawn from experimental results, is the faster

convergence of the weight updating algorithm.

REFERENCES

Georgopoulou V.C., Malandraki G.A., Stylios C.D., 2001.

“A fuzzy cognitive map approach to differential

diagnosis of specific language impairment”. Artificial

Intelligence in Medicine 679, pp. 1-18.

Jang J., Sun C., 1995. “Neuro-Fuzzy Modelling and

Control”, Proceedings of the IEEE, vol 83, no 3, pp.

378-40.

Kosko B., 1986, “Fuzzy Cognitive Maps”, International

Journal of Man-Machine Studies, pp. 65-75, January

Kosko B., 1986, “Differential Hebbian Learning”,

Proceedings American Institute of Physics; Neural

Networks for Computing, pp. 277-282, April

Kosko B., 1992. “Neural Networks and Fuzzy Systems”,

Prentice-Hall, Englewood Cliffs, NJ.

Kosko B., 1997.“Fuzzy Engineering “,Prentice-Hall, NU.,

Kottas T. L., Boutalis Y. S., Devedzic G., Mertzios

B.G.,2003. “A new method for reaching equilibrium

points in Fuzzy Cognitive Maps”, Proceedings of 2

International IEEE Conference of Intelligent Systems,

pp. 53-60.

Miao Y., Liu Z., Siew C., Miao C., 2001. “Dynamical

Cogntive Network-an Extension of Fuzzy Cognitive

Map”, IEEE transactions on fuzzy systems , vol 9 , no

5, pp. 760-770.

Papageorgiou E.I., Stylios C.D., Groumpos P.P., 2004.

“Active Hebbian learning algorithm to train fuzzy

cognitive maps” International Journal of Approximate

Reasoning 37, pp.219-249.

Satur R., Liu Z., 1999. “A Contextual Cognitive Map

Framework for Geographic Information Systems”,

IEEE transactions on fuzzy systems, vol 7, no 5, pp.

481-494.

Schneider M., Shnaider E., Kandel A., Chew G., 1998.

“Automatic Construction of FCMs”, Fuzzy Sets and

Systems, 93, pp. 161-172.

Tsadiras A., Margaritis K., 1997 . “Cognitive Mapping

and Certainty Neuron Cognitive Maps”, Information

Sciences, 101, pp. 109-13.

Tsadiras A., Margaritis K., 1999. “An experimental study

of the dynamics of the certainty neuron fuzzy cognitive

maps”, Neurocomputing , 24 , pp. 95-116.

Zhang W.,Chen S. Bezdek J. , 1989. “ Pool2: A Generic

System for Cognitive Map Development and Decision

Analysis “, IEEE Transactions on Systems, Man, and

Cybernetics, vol 19,no 1, pp. 31-39.

Zhang W., Chen S., Wang W., King R., 1992. “A

Cognitive Map Based Approach to the Coordination of

Distributed Cooperative Agents”, IEEE Transactions

on Systems, Man, and Cybernetics, vol. 22, no 1,

pp. 103-114.

A NEW METHOD FOR WEIGHT UPDATING IN FUZZY COGNITIVE MAPS USING SYSTEM FEEDBACK

209