MODEL PREDICTIVE CONTROL FOR DISTRIBUTED

PARAMETER SYSTEMS USING RBF NEURAL NETWORKS

Eleni Aggelogiannaki, Haralambos Sarimveis

School of Chemical Engineering,NTUA, 9 Heroon Polytechniou str. Zografou Campus, 15780 Athens, Greece

Keywords: Distributed parameter systems, Model Predictive Control, Radial Basis Function Neural Networks.

Abstract: A new approach for the identification and control of distributed parameter systems is presented in this

paper. A radial basis neural network is used to model the distribution of the system output variables over

space and time. The neural network model is then used for synthesizing a non linear model predictive

control configuration. The resulting framework is particular useful for control problems that pose

constraints on the controlled variables over space. The proposed scheme is demonstrated through a tubular

reactor, where the concentration and the temperature distributions are controlled using the wall temperature

as the manipulated variable. The results illustrate the efficiency of the proposed methodology.

1 INTRODUCTION

In distributed parameter systems (DPS) inputs,

outputs as well as parameters may change

temporally and spatially due to diffusion, convection

and/or dispersion phenomena. Such systems are

quite common in chemical industries (tubular

reactors, fluidized beds and crystallizers) and are

mathematical described by systems of partial

differential equations (PDE), where time and spatial

coordinates are the independent variables.

The conventional approach for the synthesis of

implementable control schemes for DPSs is based on

methodologies that reduce the infinite order model

to a finite (low) order model, which can capture the

dominant behavior of the system. A comprehensive

analysis of the recent developments in this direction

can be found in Christofides (2001a). The most

common approach found in the literature for an

accurate model reduction implements a linear or a

non linear Galerkin method to derive ODE systems

that capture the slow (dominant) modes of the

original DPS. In Christofides (2001b) one can find

the analytical description of the linear Galerkin

procedure as well as the nonlinear model reduction

method which implements the concept of

approximate inertial manifold. The resulting models

are then used for synthesizing low dimensional

robust output feedback controllers for quasi linear

and nonlinear parabolic systems (Christofides and

Daoutidis, 1996; 1997; Christofides, 1998;

Shvartsman and Kevrekidis, 1998; Christofides and

Baker 1999; Chiu and Christofides, 1999; El-Farra

et al., 2003; El-Farra and Christofides, 2004).

However, the analytical solution of the

eigenvalue problem of the spatial differential

operator is not always possible and consequently the

selection of the appropriate basis to expand the

PDEs is not an easy task. A systematic data driven

methodology to address this problem is the

Karhunen-Loève expansion (KL), also called proper

orthogonal decomposition (POD) or empirical

eigenfunctions (EEF) or principal component

analysis. The KL expansion uses data snapshots and

constructs the empirical eigenfunctions as a linear

combination of those snapshots (Newman, 1996a;

1996b; Chatterjee, 2000). The resulting EEFs have

been used as basis functions in the Galerkin

procedure in a number of publications for accurate

modelling and control in one-dimensional or two-

dimensional systems. (Park and Cho, 1996a; 1996b;

Park and Kim, 2000; Baker and Christofides, 1999;

Shvartsman and Kevrekidis, 1998; Armaou and

Christofides, 2002;)

The Galerkin procedure, mentioned so far uses

analytical or empirical eigenfunctions and requires

the mathematical description of the process, namely

the exact system of PDEs. In case the PDEs are

unknown, Gay and Ray (1995) proposed an

identification procedure based on input-output data.

The methodology employs integral equation models

Aggelogiannaki E. and Sarimveis H. (2005).

MODEL PREDICTIVE CONTROL FOR DISTRIBUTED PARAMETER SYSTEMS USING RBF NEURAL NETWORKS.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics, pages 19-24

DOI: 10.5220/0001156700190024

 SciTePress

to describe the DPS and the singular value

decomposition (SVD) of the integral kernel to

produce an input/output model, suitable for model

predictive control (MPC) methodologies. A

comparison of the efficiency of this data driven

model with the methods mentioned earlier can be

found in Hoo and Zheng (2001). More recently, an

identification method that combines KL and SVD

for low order modeling and control have been

presented (Zheng and Hoo, 2002; Zheng et al.,

2002a; 2002b; Zheng and Hoo, 2004). The discrete

form of the SVD-KL method has also been used in

MPC configurations with improved performance,

comparatively to linear feedback controllers.

A neural network approach for the identification

of DPSs has been attempted by Gonzáles-García et

al. (1998) and more recently a combination of POD

and neural networks has been proposed by

Shvartsman et al. (2000). Padhi et al. (2001) used

two sets of neural networks to map a DPS and a

discrete dynamic programming format for the

synthesis of an optimal controller. The same

concept, also exploiting the POD technique for a

lower order model, is presented by Padhi and

Balakrishnan (2003).

In the present work, a radial basis function

(RBF) neural network is proposed for the

identification of non linear parabolic DPSs. RBF

neural networks are quite popular for lumped system

modeling because of their comparatively simple

structure and their fast learning algorithms

(Sarimveis et al., 2002). In this paper the RBF

neural network is formulated, so that it is able to

predict the distribution of the output variables over

space. This way, an estimation of the system outputs

is available in any position. The RBF model is then

implemented in a nonlinear MPC configuration to

predict the controlled variables in a finite number of

positions.

The rest of the article is formulated as follows:

In section 2 the structure of the RBF neural network

for DPSs is presented. In section 3 the non linear

MPC configuration is described in more details. The

proposed methodology is tested through the

application described in subsection 4.1 The efficien-

u(t-1)

u(t-2)

u(t-N)

()

,ytz

()

,ytz

()

ytz

Figure 1: A radial basis function neural network of C

hidden nodes for a distributed parameter system.

cy of the RBF neural network is examined in

subsection 4.2 and the controller performance in 4.3.

In section 5, the final conclusions are summarized.

2 RBF NEURAL NETWORKS

FOR MODELING

DISTRIBUTED PARAMETER

SYSTEMS

2.1 Quasi-linear parabolic DPS

In general, a quasi linear parabolic distributed

parameter system is described by a set of partial

differential equations and boundary conditions of the

form of Eq. (1):

(

)

() ()

() ()()

()

() () () ()

,,,,0

0, , 0

,0 , , , 0

tz tz

tzz

tz z tz

zzL

tttLtt

∂

∂∂

−+ + >

∂∂∂

=⋅

=≤≤

∂∂

==>

∂∂

υυ

avuG av

yCυ

υυ

(1)

where

(

)

,tzυ are the state variables,

(

)

,tzu the

manipulated variables and

(

)

,tzy the controlled

variables. G(t,z) is an additional non linear term of

the model and C(z) is a function determined by the

location of the sensors. Vectors υ

(z) and g

(t), g

(t)

describe the initial and the Neumann boundary

conditions of the system, respectively.

2.2 RBF neural network for DPS

Radial basis function networks are simple in

structure neural networks that consist of three layers,

namely the input layer, the hidden layer and the

output layer. Development of an RBF network based

on input-output data includes the computation of the

number of nodes in the hidden layer and the

respective centers and the calculation of the output

weights, so that the deviation between the predicted

and the real values of the output variables, over a set

of training data, is minimized

An RBF neural network for modeling a DPS is

constructed so that it can predict the values of the

output variables at a specific spatial point (Figure 1).

The input vector of such network at time point t=kT

(where T

is the sample time) contains past values of

the input variables and the coordinates in space,

ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

where we wish to obtain a prediction:

() ( ) ( ) ( )

, 1 2 ...

TT T

tz t t t N z

⎡⎤

=− − −

⎣⎦

xuu u (2)

For simplification we limit our analysis in only

one dimension in space. Generalization to three

dimensions is straightforward.

The neural network output is a vector containing

the values of the process output variables at the

location that is specified in the input vector:

() () () ()

RBF 1 2

, , , ... ,

tz y tz y tz y tz

∧∧∧∧

⎡⎤

⎢⎥

⎣⎦

(3)

() ()

(

)

,,,1,...,

jc c

ytz w f tz j no

∧

=⋅ − =

∑

xx (4)

In the previous equations N is the number of past

values for the input vector, no is the number of the

process output variables, C is the number of hidden

nodes, w

is the weight vector corresponding to the

output of the cth node, f is the radial basis function

and x

is the center of the c

node. The method

utilized to train neural networks in this work is based

on a fuzzy partition of the input space and is

described in details in Sarimveis et al. (2002).

3 NONLINEAR MPC FOR DPS

The nonlinear MPC configuration that is proposed in

this work for controlling DPSs, uses the RBF model

to predict the values of the controlled variables over

a future finite horizon ph at a number of locations

ns, where measurements are available. Then, an

optimization problem is solved, so that both the

deviations of the controlled variables from their set

points over the prediction horizon and the control

moves over a control horizon ch, are minimized. The

objective function is of the following form:

()

(|)

11 0

0,..., 1

min , | |

ns ch

kj j j k

tkt

jk k

kch

tkzt tkk

−

∧

== =

=−

⎛⎞

⎜⎟

+−+∆+

⎜⎟

⎝⎠

∑∑ ∑

Wy y Ru

(6)

()()()

RBF

,| , ,|,

1,..., , 1,...,

jjj

tkzt tkz tzt

jnsk ph

∧∧

+=++

yy d

(7)

min max

(|) , 0,...,1tkt k ch≤+ ≤ = −uu u

(8)

where

()

tkzt

∧

+y is the prediction made at time

point t for the output vector at time t+k and at

location z

, ns is the number of sensors,

(

)

tz td is

the estimated disturbance at time point t, considered

constant over the prediction horizon and

y is the

set point at the location of the j sensor. For

k=ch,…,ph the manipulated variables are considered

to remain constant. W

and R

are weight matrices

of appropriate dimensions.

4 APPLICATION

4.1 Description of the process

One typical distributed parameter system in

chemical engineering is a tubular reactor, where

variables depend on both time t and reactor length z.

The mass and energy balances, concerning a first

order reaction, diffusion and convention phenomena,

are described by two quasi-linear PDEs with

Neumann boundary conditions (Eqs. (9-(12)).

()

11 1

exp 1 ,

eh e

TTT

cTtzT

tPz Lz T

ηγ µ

⎡⎤

∂∂∂

⎛⎞

=−+ −+ −

⎢⎥

⎜⎟

∂∂ ∂

⎝⎠

⎣⎦

(9)

exp 1

cTc

tPz z T

⎡

⎤

∂∂∂

⎛⎞

=−− −

⎢

⎥

⎜⎟

∂∂∂

⎝⎠

⎣

⎦

(10)

z=0,

() ( )

,0 ( ) ( ,0)

eh i

tPTtTt

∂

−=⋅−

∂

, z=1,

()

,1 0

∂

(11)

z=0,

() ( )

,0 ( ) ( ,0)

em i

tPctct

∂

−=⋅−

∂

, z=1,

()

,1 0

∂

(12)

where

(

)

,Ttz ,

(

)

,ctz are dimensionless temperature

and concentration respectively inside the reactor,

(

)

(

)

are dimensionless temperature and

concentration at the entrance of the reactor and

(

)

Ttz is the wall temperature. The values of the

parameters of Eqs. (9)-(12) can be found in previous

publications (Hoo and Zheng, 2001; 2002).

4.2 RBF model efficiency

An input-output training set was created using the

wall temperature T

, at z= [0 0.33 0.66] as the

manipulated variable, while the output variables

(temperature and concentration) were recorded at 21

spatial locations. The PDEs were solved using the

PDE Matlab toolbox. More specifically, we

simulated the system by changing randomly the

input variables and recording the output responses

using a sample period of T

=0.5 time units. The

training set consisting of 2000 data points was

generated considering N=3 past values of each

manipulated variable. Deviation variables were used

by subtracting from all the input and output values

MODEL PREDICTIVE CONTROL FOR DISTRIBUTED PARAMETER SYSTEMS USING RBF NEURAL

NETWORKS

the corresponding steady states. Several neural

network structures were developed by changing the

initial fuzzy partition in the fuzzy means training

algorithm. The produced neural networks were

tested using a new validation data set of 500 data

that was developed in the same way with the training

set, but was not involved in the training phase. The

sum of squares errors (SSEs) for the different RBF

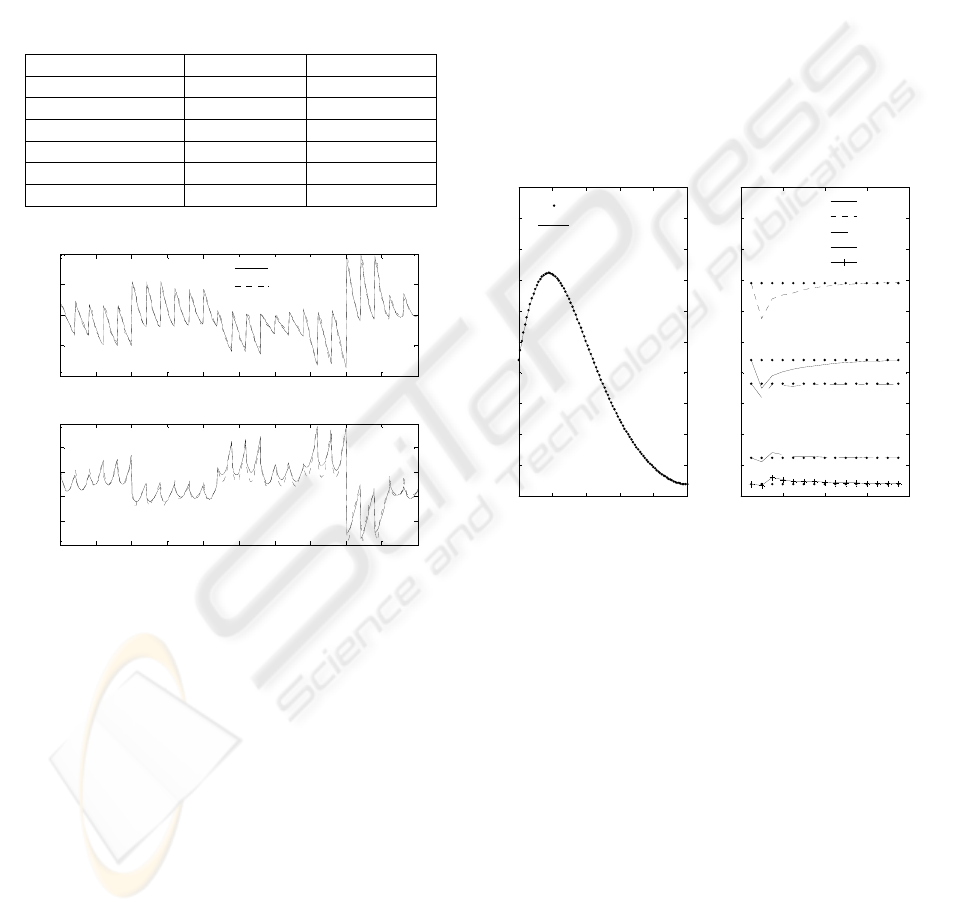
structures are presented in Table 1. In Figure 2, the

actual values and the predictions of the neural

network consisting of 152 nodes are compared.

Table 1: Performance of RBF neural networks

Hidden nodes C SSE T SSE c

13 0.2012 0.8873

27 0.1251 0.7523

68 0.0535 0.3628

86 0.0404 0.2232

152 0.0332 0.1420

207 0.0295 0.1104

0 50 100 150 200 250 300 350 400 450 500

-0.2

-0.1

0.1

0.2

Temperature T(t,z)

0 50 100 150 200 250 300 350 400 450 500

-0.4

-0.3

-0.2

-0.1

0.1

validation data

Concentration c(t,z)

prediction

real values

Figure 2: Actual values and predictions of the deviation

variables for a neural network consisting of 152 hidden

nodes

4.3 MPC performance

To test the proposed MPC configuration, we first

simulated the example presented in Zheng and Hoo

(2002). In that case, the temperature is the only

controlled variable at z=[0:0.25:1] where we assume

that sensors are available, while concentration is

measured at z=1 but is not controlled. A disturbance

is introduced to the system by decreasing the feed

concentration C

by 5%. We tested the proposed

MPC scheme using for prediction the RBF network

that consists of 27 nodes and the following

parameter values: ch=6, ph=10, W=1, R=5·I

. The

optimization problem that was formulated at each

time instance was solved using the fmincon Matlab

function. The performance of the controller is

depicted in Figure 3, where the temperature

distributions at the initial steady state and after 7

time units are compared. The responses at locations

where sensors are available are also presented in the

same figure. The proposed controller managed to

reject the disturbance and produce zero steady state

error. The obtained responses outperform the

performances of a PI controller and an MPC

configuration that utilizes the SVD-KL model. The

responses of the two controllers are presented in

Hoo and Zheng, (2002) and are not shown here due

to space limitations. The temperature at the exit of

the reactor returns to its initial value after 1.5 time

units, while 6 time units are required by the system

to produce zero steady state error along the length of

the reactor.

0 0.2 0.4 0.6 0. 8 1

1.02

1.03

1.04

1.05

1.06

1.07

1.08

1.09

1.1

1.11

1.12

lenght z

Temperature at steady state T(z)

0 2 4 6 8

1.02

1.03

1.04

1.05

1.06

1.07

1.08

1.09

1.1

1.11

1.12

time t

T(t,z)

T(t,0 )

T(t,0.25)

T(t,0.50)

T(t,0.75)

T(t,1 )

initial steady state

final steady state

Figure 3: The final temperature distribution and the

dynamic response to a 5% decrease in

using the RBF

model

A second performance test forces the system to

reach a new steady state distribution. The actual

steady state, where the temperature finally settles, is

compared with the desired set point in Figure 4. The

dynamic responses at locations where sensors are

available are also presented in the same figure. The

responses show that the system approaches the

desired values quickly, avoiding overshoots. The

behavior of the manipulated variables is depicted in

Figure 5.

The last simulation presented in this work uses

concentration at the reactor exit as an additional

controlled variable. As far as the temperature profile

is concerned, the target is to reach the same set point

change as previously. Figures 6 and 7 present the

responses of the temperature (at locations where

sensors are available) and the concentration (at the

ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION

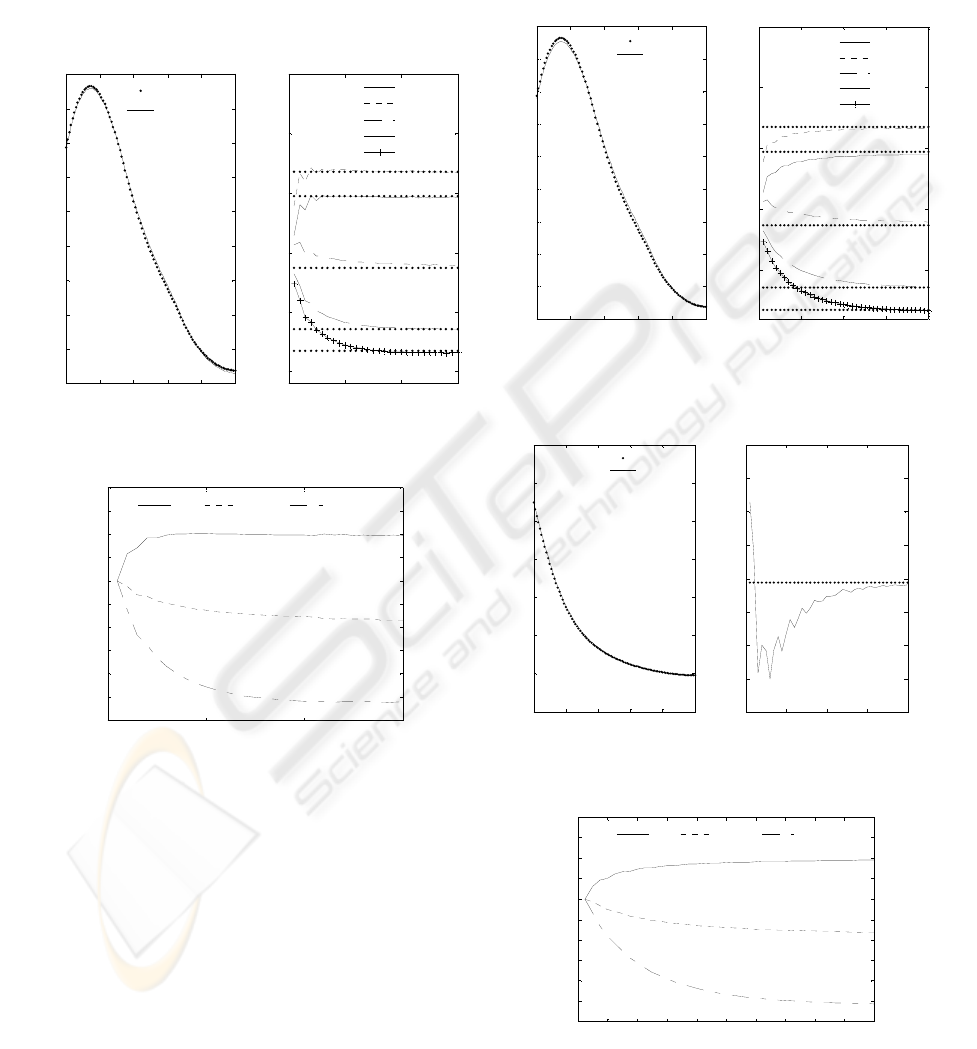
reactor exit) respectively. They also present the final

distribution of both variables, after 20 time units.

Figure 8 depicts the control actions over time. It is

obvious that due to the additional controlled variable

the performance of the controller is slightly

deteriorated as far as the dynamic behavior is

concerned. However, the desired steady state is still

approached satisfactorily.

0 0.2 0.4 0. 6 0.8 1

0.96

0.98

1.02

1.04

1.06

1.08

1.1

1.12

1.14

lenght z

Temperature at stedy state T(z)

0 5 10 15

0.95

1.05

1.1

1.15

1.2

time t

T(t,z)

setpoint

steady state

T(t,0 )

T(t,0.25)

T(t,0.50)

T(t,0.75)

T(t,1 )

Figure 4: The temperature distribution after 15 time units

and the dynamic response to a set point change

0 5 10 15

0.94

0.95

0.96

0.97

0.98

0.99

1.01

1.02

1.03

1.04

Tw(t)

time

z=0 z=0.33 z=0.66

Figure 5: The manipulated variable T

(t) at z=0, 0.33 and

0.66

5 CONCLUSIONS

A nonlinear input/output identification method for

distributed parameter systems is proposed is this

paper. An RBF neural network capable to predict the

output variables over space is developed. The

accuracy of the neural network was established

through a tubular reactor simulation. The model is

then used for the synthesis of a MPC configuration

that minimizes the deviation of the prediction of the

controlled variables at a finite number of positions,

where a sensor is assumed to exist. The proposed

method produced satisfactory results in both

disturbance rejection and set point change problems.

The performance of the controller was found to be

superior to PI controllers or linear MPC

configurations presented in former publications.

0 0. 2 0.4 0. 6 0.8 1

0.96

0.98

1.02

1.04

1.06

1.08

1.1

1.12

1.14

lenght z

Temperature at stedy state T(z)

0 5 10 15 20

1.05

1.1

1.15

1.2

time t

T(t,z)

T(t ,0 )

T(t ,0 .2 5)

T(t ,0 .5 0)

T(t ,0 .7 5)

T(t ,1 )

setpoint

steady state

Figure 6: The temperature distribution after 20 time units

and responses to a set point change when considering

c(t,1) as an additional controlled variable

0 0.2 0.4 0.6 0.8 1

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

lenght z

Concentration at steady state c(z)

0 5 10 15 20

0.188

0.19

0.192

0.194

0.196

0.198

0.2

0.202

0.204

time t

c(t,1)

setpoint

steady state

Figure 7: The concentration distribution after 20 time units

and the response of

c(t,1)

0 2 4 6 8 10 12 14 16 18 20

0.94

0.95

0.96

0.97

0.98

0.99

1.01

1.02

1.03

1.04

Tw(t )

time t

z=0 z=0.33 z=0.66

Figure 8: The manipulated variable T

(t) at z=0, 0.33 and

0.66 when considering

c(t,1) as an additional controlled

variable

MODEL PREDICTIVE CONTROL FOR DISTRIBUTED PARAMETER SYSTEMS USING RBF NEURAL

NETWORKS

REFERENCES

Armaou, A., Christofides, P. (2002). Dynamic

optimization of dissipative PDE systems using

nonlinear order reduction.

Chem. Eng. Sc., 57, 5083-

5114.

Baker, J., Christofides, P. (1999). Output feedback control

of parabolic PDE systems with nonlinear spatial

differential operators.

Ind. Eng. Chem. Res., 38, 4372-

4380.

Chatterjee, A. (2000). An introduction to the proper

orthogonal decomposition.

Current Science, 78, 808-

817.

Chiu, T., Christofides, P. (1999). Nonlinear control of

particulate processes.

AIChE Journal, 45, 1279-1297.

Christofides, P. (1998). Robust control of parabolic PDE

systems.

Chem. Eng. Sc., 53, 2949-2965.

Christofides, P. (2001a). Control of nonlinear distributed

process systems: recent developments and challenges.

AIChE Journal, 47, 514-518.

Christofides, P. (2001b).

Nonlinear and Robust Control of

PDE Systems: Methods and Applications to transport

reaction processes.

Birkhäuser, Boston.

Christofides, P. J. Baker, (1999). Robust output feedback

control of quasi-linear parabolic PDE systems. In

Systems & Control Letters, 36, 307-316.

Christofides, P., Daoutidis, P. (1996). Nonlinear control of

Diffusion-Convection-Reaction processes.

Comp.

Chem. Eng.,

20, 1071-1076.

Christofides, P., Daoutidis, P. (1997). Finite-Dimensional

Control of Parabolic PDE Systems Using

Approximate Inertial Manifolds.

Journal of

mathematical analysis and applications,

216, 398-420.

El-Farra, N., Armaou, A., Christofides, P. (2003).

Analysis and control of parabolic PDE systems with

input constraints.

Automatica, 19, 715-725.

El-Farra, N., Christofides, P. (2004). Coordinating

feedback and switching for control of spatially

distributed process. Comp. Chem. Eng.,28, 111-128.

Gay, D., Ray, W. (1995). Identification and control of

distributed parameter systems by means of the singular

value decomposition.

Chem. Eng. Sc., 50, 1519-1539.

Gonzáles-García, R., Rico-Martínez, R., Kevrekidis, I.

(1998). Identification of distributed parameter

systems: A neural net based approach.

Comp. Chem.

Eng.,

22, 965-968.

Hoo, K., Zheng, D. (2001). Low order control-relevant

models for a class of distributed parameter systems.

Chem. Eng. Sc., 56, 6683-6710.

Newman, A. (1996a). Model reduction via the Karhunen-

Loève Expansion Part I: An exposition.

Technical

Report 96-32,

University of Maryland, College Park,

MD.

Newman, A. (1996b). Model reduction via the Karhunen-

Loève Expansion Part II: Some elementary examples.

Technical Report 96-33, University of Maryland,

College Park, MD.

Padhi, R., Balakrishnan, S. (2003). Proper orthogonal

decomposition based optimal neurocontrol synthesis

of a chemical reactor process using approximate

dynamic programming.

Neural Networks, 16, 719-728.

Padhi, R., Balakrishnan, S., Randolph, T. (2001).

Adaptive-critic based optimal neuro control synthesis

for distributed parameter systems.

Automatica, 37,

1223-1234.

Park, H., Cho, D. (1996a). The use of Karhunen-Loeve

decomposition for the modelling of distributed

parameter systems.

Chem. Eng. Sc., 51, 81-89.

Park, H., Cho, D. (1996b). Low dimensional modelling of

flow reactors.

Int. J. Heat Mass Transfer, 39, 3311-

3323.

Park, H., Kim, O. (2000). A reduction method for the

boundary control of the heat conduction equation.

Journal of Dynamic Systems Measurement and

Control

, 122, 435-444.

Sarimveis, H., Alexandridis, A., Tsekouras, G., Bafas, G.

(2002). A fast and efficient algorithm for training

radial basis function neural networks based on a fuzzy

partition of the input space.

Ind. Eng. Chem. Res., 41,

751-759.

Shvartsman, S., Kevrekidis, I. (1998). Nonlinear model

reduction for control of distributed systems: a

computer –assisted study.

AIChE Journal, 44, 1579-

1595

Shvartsman, S., Theodoropoulos, C., Rico-Martínez, R.

Kevrekidis, I., Titi, E., Mountziaris, T. (2000). Order

reduction for nonlinear dynamic models of distributed

reacting systems.

Journal of Process Control, 10, 177-

184.

Zheng D., Hoo, K. (2002). Low-order model identification

for implementable control solutions of distributed

parameter systems.

Comp. Chem. Eng., 26, 1049-

1076.

Zheng, D., Hoo, K. (2004). System identification and

model-based control for distributed parameter

systems.

Comp. Chem. Eng., 28, 1361-1375.

Zheng, D., Hoo, K., Piovoso, M. (2002a). Low-order

model identification of distributed parameter systems

by a combination of singular value decomposition and

the Karhunen-Loève expansion.

Ind. Eng. Chem. Res.,

41, 1545-1556.

Zheng, D., Hoo, K., Piovoso, M. (2002b). Finite

dimensional modeling and control of distributed

parameter systems. In

2002 American Automatic

Control Conference,

A.A.C.C.

ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION