LQG CONTROL UNDER AMPLITUDE
AND VARIANCE CONSTRAINTS
A. Kr
´
olikowski†, D. Horla, T. Kubiak
Pozna
´
n University of Technology,
Institute of Control and Information Engineering,
ul. Piotrowo 3A, 60-965 Pozna
´
n, POLAND.
Keywords:
LQG, Amplitude constraint, Variance constraint.
Abstract:
In this paper, the amplitude and variance-constrained LQG control is considered for a plant given by discrete-
time ARMAX model. The minimization of constrained quadratic cost is approached by Kalman filter, ap-
proximation of the probability density function (pdf) of the state by the Gaussian one and by by tuning of the
Lagrange multiplier. The obtained optimization algorithm is simulated for second-order stable plant model
and different constraints.
1 INTRODUCTION
Control input constraints are ubiquitous in many con-
trol applications, therefore including them in a con-
trol system design is of practical importance. Hard-
limit input constraint and variance or mean-square in-
put constraint are of the most frequent occurrence in
industrial control processes. Neglecting these con-
straints in the controller design may lead to perfor-
mance deterioration or even instability of the control
system. Specifically, the unstable open-loop systems
in the presence of constrained control signal can not
be globally stabilizable.
The problem addressed in this paper is the LQG con-
trol of ARMAX plant in the presence of simultane-
ous amplitude and variance constrained input. The
constrained control problem is approached using the
Kalman filter and approximation of the pdf of the
Kalman filter output by the Gaussian pdf. Analy-
sis and computer simulations of second-order systems
are given.
It should be noted that in the literature the considered
LQG control problem is treated mostly for separate
control constraints, see for example in (Kr
´
olikowski,
1997, M
¨
akil
¨
a, 1982, M
¨
akil
¨
a et at, 1984, Toivonen,
1983).
2 PROBLEM FORMULATION
The plant is given by a discrete-time ARMAX model
A(q
−1
)y
t
= B(q
−1
)u
t
+ C(q
−1
)e
t
, (1)
where A, B, C are polynomials in the backward shift
operator q
−1
, i.e.,A = 1 + a
1
q
−1
+ · · · + a
na
q
−na
,
B = b
1
q
−1
+ · · · + b
nb
q
−nb
, C = 1 + c
1
q
−1
+
· · · +c
nc
q
−nc
, y
t
is the output, u
t
is the control input,
and {e
t
} is assumed to be a sequence of independent
random variables with zero mean and variance σ
2
e
.
Consider the stationary cost function
J
1
= E[y
2
t
+ q
u
u
2
t
] = σ
2
y
+ q
u
σ
2
u
, (2)
where the output and input variances E[y
2
t
], E[u
2
t
] are
denoted as σ
2
y
and σ
2
u
, respectively, and q
u
≥ 0.
The amplitude and variance constraints imposed on
the control input are given as follows
|u
t
| ≤ α, (3)
σ
2
u
≤ c
2
. (4)
It is known that ARMAX model (1) has an equivalent
innovation state space representation
x
t+1
= F x
t
+ gu
t
+ k
e
e
t
, (5)
y
t
= h
T
x
t
+ e
t
, (6)
for na = nb = nc = n, where the corresponding vec-
tors are g
= (b
1
, . . . , b
n
)
T
, k
e
= (c
1
− a
1
, . . . , c
n
−
292
Królikowski A., Horla D. and Kubiak T. (2005).
LQG CONTROL UNDER AMPLITUDE AND VARIANCE CONSTRAINTS.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics, pages 292-296
Copyright
c
 SciTePress

a
n
)
T
, h = (1, 0, . . . , 0)
T
, and
F =



−a
1
1 . . . 0
. . . . . 0
−a
n−1
. . . . 1
−a
n
. . . . 0



.
The associated Kalman filter is
ˆx
t+1
= F ˆx
t
+ g
u(t) + k˜y
t
, (7)
where k
is the stationary gain vector, and ˜y
t
= y
t
−
h
T
ˆx
t
with variance σ
2
˜y
= h
T
P
k
h
+ σ
2
e
. The matrix
P
k
is the solution to the following Riccati equation
P
k
= F P
k
F
T
−
−(F P
k
h
+ σ
2
ξ
k
ξ
)(F P
k
h
+ σ
2
e
k
e
)
T
× (8)
×(h
T
P
k
h
+ σ
2
e
)
−1
+ k
e
k
T
e
σ
2
e
.
The goal of the control is to minimize the loss func-
tion J
1
under the given structure of the controller
specified by the feedback gain vector f
in the case of
the Kalman filter-based controller subject to the am-
plitude and variance constrints (3), (4). Thus, the con-
strained control law has a form
u
t
= sat(f
T
ˆx
t
; α), (9)
where sat denotes a saturation function and ˆx
t
is the
output of the Kalman filter (7).
3 CONTROL UNDER
AMPLITUDE CONSTRAINT
Consider now the cost function
J = E[x
T
t
Q
x
x
t
+ q
u
u
2
t
] = trQ
x
R
x
+ q
u
σ
2
u
, (10)
where R
x
= Ex
t
x
T
t
, R
x
= R
ˆx
+ P
k
and R
ˆx
=
E ˆx
t
ˆx
T
t
. If the weight matrix Q
x
is such that Q
x
=
h
h
T
then it is easy to see that the cost function J (10)
can be considered as an alternative formulation for J
1
(2) w.r.t. minimization.
Using any stabilizing feedback control law, the fol-
lowing stationary equation for R
ˆx
resulting from (7)
can be derived
R
ˆx
= F R
ˆx
F
T
+ F R
ˆxu
g
T
+ g
R
T
ˆxu
F
T
+
+σ
2
u
g
g
T
+ σ
2
˜y
k
k
T
, (11)
where R
ˆxu
= E ˆx
t
u
t
. The approximate expressions
for σ
2
u
and R
ˆxu
under the constrained control law (9)
are (Toivonen, 1983):
σ
2
u
= σ
2
g
1
(σ), R
ˆxu
= R
ˆx
f
g
2
(σ), (12)
where
σ
2
= f
T
R
ˆx
f
(13)
and g
1
(σ) = erf(ασ
−1
2
−
1
2
) − ασ
−1
2
1
2
ierfc(α×
×σ
−1
2
−
1
2
), g
2
(σ) = erf (ασ
−1
2
−
1
2
). Introducing
(12), (13) into (11) one obtains an equation that en-
ables iterative calculation of R
ˆx
. The corresponding
cost function (10) takes then the form
J(f
) = tr(Q
x
+ q
u
g
1
(σ)ff
T
)R
ˆx
+
+trQ
x
P
k
= (14)
= J
f
(f
) + trQ
x
P
k
.
Using the gradient of J
f
(f) the following iterative
algorithm for calculating the feedback gain f
in the
control law (9) can be proposed (Tovoinen, 1983)
f
(k+1)
= f
(k)
+ α
k
s
(k)
, (15)
where α
k
is the step length and
s
(k)T
= d
(k)

∂J
f
∂f

(k)T

R
(k)
ˆx

−1
(16)
for the gradient given as

∂J
f
∂f

(k)T
= e
(k)T
R
(k)
ˆx
. (17)
Calculations for k-th iteration are performed for
f
(k)
. Expressions for d
(k)
, e
(k)
are given as follows
(Tovoinen, 1983):
d
(k)
= −
1
2
h
g
1
(σ
(k)
) + h
1
(σ
(k)
)σ
2(k)

×
×

g
T
S
(k)
g
+ q
u
i
−1
,
e
(k)T
= 2
h
g
1
(σ
(k)
) + h
1
(σ
(k)
)σ
2(k)

×
×

g
T
S
(k)
g
+ q
u

f
(k)T
+
+ g
2
(σ
(k)
)g
T
S
(k)
F +
+ 2h
2
(σ
(k)
)g
T
S
(k)
F R
(k)
ˆx
f
(k)
f
(k)T
i
,
where S
(k)
is a positive definite solution of the equa-
tion
S
(k)
= F
T
S
(k)
F + Q
x
+
+f
(k)
h
g
1
(σ
(k)
) + h
1
(σ
(k)
)σ
2(k)

×
×

g
T
S
(k)
g
+ q
u

+
+ 2h
2
(σ
(k)
)g
T
S
(k)
F R
(k)
ˆx
f
(k)
i
f
(k)T
+
+g
2
(σ
(k)
)(F
T
S
(k)
g
f
(k)T
+ f
(k)
g
T
S
(k)
F ).
As an initial iteration for calculation of R
(k)
ˆx
one can
take for example R
(0)
ˆx
= Σ
e
= k
k
T
σ
2
e
, and f
(0)
where f
(0)
results from the standard unconstrained

solution of LQG problem. It is convenient to take
the same value of f
(0)
as an initial iteration in (15).
It can be shown (Tovoinen, 1983) that there is a con-
stant a > 0 such that for every α
k
∈ (0, a) it holds
J
f
(f
(k+1)
) < J
f
(f
(k)
),
if (
∂J
f
∂f
)
(k)
) 6= 0. Thus, the proper choice of step α
k
assures the convergence of the algorithm.
4 CONTROL UNDER VARIANCE
CONSTRAINT
In the case of variance constraint given by the inequal-
ity (4) the associated Lagrangian is
L = J + λ(σ
2
u
− c
2
) (18)
or alternatively, the Lagrangian L can be rewritten
L = trQ
x
R
x
+ (q
u
+ λ)σ
2
u
, (19)
where λ ≥ 0 is the Lagrange multiplier. The Kuhn-
Tucker necessary conditions for the constrained min-
imum of L are
∂L
∂λ
≤ 0,
∂L
∂f
= 0. (20)
The optimal variance constrained control strategy can
be computed by solving the conditions (20). In prac-
tice, this is done iteratively, as it will be shown in Sec-
tion 5.
The controller to be designed is of the form
u
t
= f
T
ˆx
t
, (21)
where f
follows from appropriate Riccati equation
and ˆx
t
is the Kalman filter output. The minimiza-
tion of the Lagrangian (19) w.r.t. all admissible u
t
is
closely related to the minimization of the loss func-
tion J subject to the constraint (4). If u
∗
t
= f
∗T
ˆx
t
minimizes the Lagrangian (19), and the inequality
constraint (4) and complementary condition
λ(σ
2
u
− c
2
) = 0 (22)
are fulfilled at u
∗
t
, then u
∗
t
is also an optimal control
signal for variance-constrained control problem.
A major problem is the determination of appropriate
estimates for the Lagrange multiplier λ such that the
conditions (4) and (22) are satisfied for u
∗
t
. In prac-
tice this is done iteratively where each iteration step
k consists of solving a standard LQG problem, i.e.
of minimizing the Lagrangian (19) with λ = λ
(k)
and of updating the Lagrange multiplier according to
a suitable algorithm. A realization of this algorithm
needs the appropriate equations for R
ˆx
and σ
2
u
, (see
eqns.(25), (26)).
An iterative algorithm for updating the Lagrange mul-
tiplier λ
(k)
proposed in (M
¨
akil
¨
a, 1982, M
¨
akil
¨
a et at,
1984) can be combined with an algorithm described
in Section 3 to yield the algorithm given below.
5 SIMULTANEOUS AMPLITUDE
AND VARIANCE
CONSTRAINTS
First, it can be observed that the amplitude constraint
α (3) restricts itself the input variance because σ
2
u
≤
α
2
. Taking into account (4) and assuming c
2
= γσ
2
e
one obtains
γ ≤
α
2
σ
2
e
. (23)
This means that if for a given amplitude constraint α,
a given variance constraint has a form γ ≥
α
2
σ
2
e
then it
is automatically fulfilled and optimization of the feed-
back gain can only be performed wrt amplitude con-
straint as shown in Section 3. On the other hand, if
for a given α, a given variance constraint is such that
γ <
α
2
σ
2
e
then a problem may have an optimization
sense according to the problem formulated in Section
2. The proposed algorithm consists of the following
steps:
step 1: Take λ
(0)
> 0, h
0
= 1, 0 < α
0
< 1.
step 2: Calculate f
(k)
according to the method given
in Section 3 for
q
(k)
u
= q
u
+ λ
(k)
. (24)
step 3: Calculate R
(k)
ˆx
according to eqn. (11) taking
into account (12), (13), i.e.
R
(k)
ˆx
= F R
(k)
ˆx
F
T
+
+(F R
(k)
ˆx
f
(k)
g
T
+ g
f
T (k)
R
T (k)
ˆx
F
T
) ×
×g
2
(σ
(k)
) + g
g
T
f
T (k)
R
(k)
ˆx
f
(k)
g
1
(σ
(k)
) +
+k
k
T
σ
2
˜y
(25)
and
σ
2(k)
u
= f
T (k)
R
(k)
ˆx
f
(k)
g
1
(σ
(k)
), (26)
σ
2(k)
= f
T (k)
R
(k)
ˆx
f
(k)
. (27)
step 4: Check out the value (22), i.e.
ψ
(k)
= λ
(k)
(σ
2(k)
u
− c
2
). (28)
If ψ
(k)
is sufficiently close to zero, according to
some prescribed criterion then STOP, otherwise go
to step 5.
step 5: If k = 0, then go to step 6, otherwise update
h
k
(if positive) according to
h
k
= h
k−1
+
∆λ
(k)
+ h
k−1
∆ψ
(k)
∆ψ
(k)
, (29)
where ∆λ
(k)
= λ
(k)
− λ
(k−1)
, ∆ψ
(k)
= ψ
(k)
−
ψ
(k−1)
and ψ
(k)
is given by (27).

step 6: Update the multiplier λ
(k)
according to
λ
(k+1)
= λ
(k)
+ sat(β
k
h
k
ψ
(k)
; aλ
(k)
), (30)
where 0 < a < 1.
step 7: Calculate β
k+1
according to
β
k+1
= β
k
(γ
0
− β
k
)(γ
0
− 1)
−1
, (31)
where γ
0
> 1. Take k → k + 1 and go to step 2.
It should be noted that in the case of tight constraints
the problem may not have a solution, i.e. the set of
feedback gains for which the cost function has finite
values can be empty.
6 SIMULATION RESULTS
Consider the ARMAX plant described by the fol-
lowing stable model A = 1 + 1.8q
−1
− 0.9q
−2
,
B(q
−1
) = q
−1
, C(q
−1
) = 1 where the noise vari-
ance is set at σ
2
e
= 1.0.
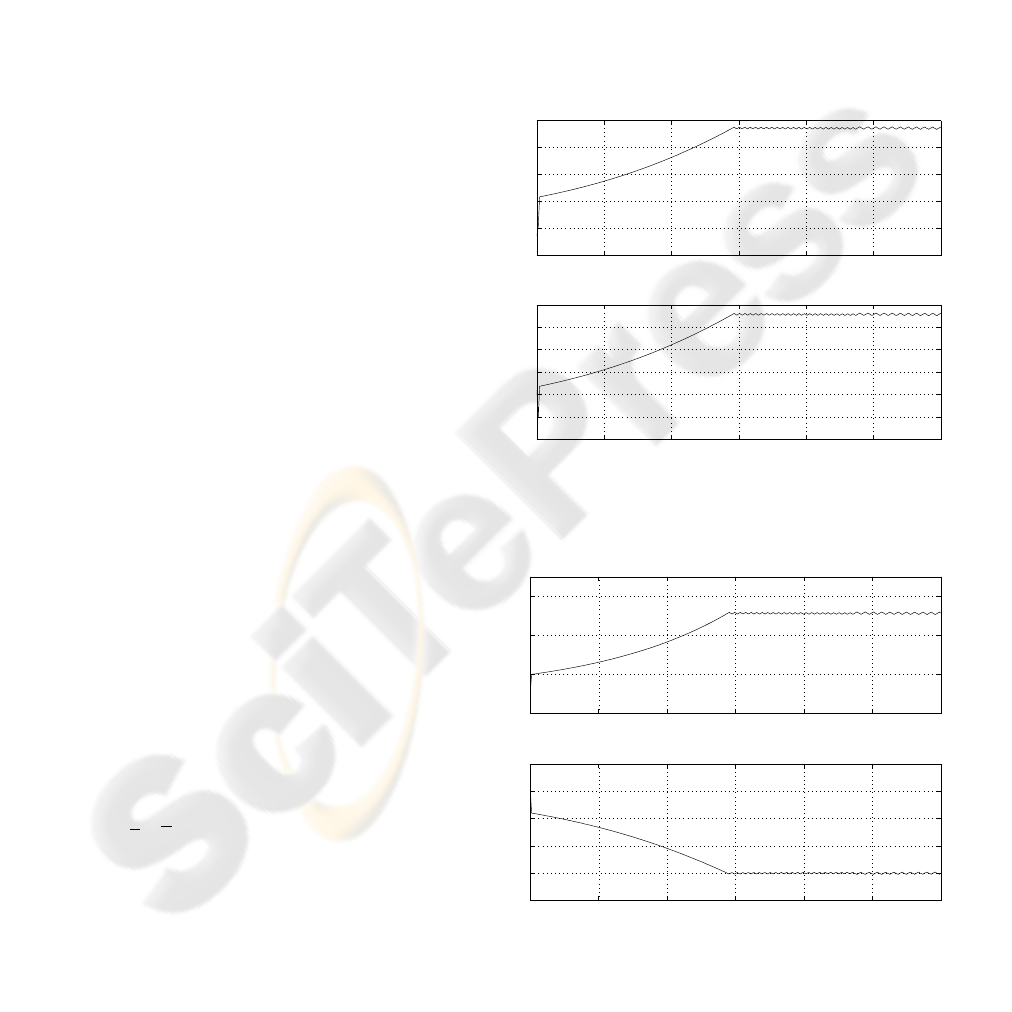
The performance of the iterative algorithm given in
Section 5 is illustrated in Figs.1,2 for constraints
α = 3.0 and c
2
= 2.0, initial value q
u
= 0.01 and
Q
x
= (1, 0)
T
(1, 0), λ
(0)
= 1.0, α
0
= 0.5, γ
0
= 5.0,
a = 0.06. The corresponding plots for α = 3.0 and
c
2
= 3.0 are shown in Figs.3,4. It can be seen that
the input variances attain their constraint values. It is
worthy to notice that the condition (23) is fulfilled for
both values of constraint c
2
. The plots of signals for
α = 3.0 and c
2
= 3.0 are shown in Fig.5, where one
can see that the control signal attains sometimes its
constraint.
7 CONCLUSIONS
The algorithm solving the amplitude and variance-
constrained LQG control problem is given for plant
described by ARMAX model. For unstable open-
loop systems there is a lower bound of variance con-
straint which can be imposed on the control signal to
preserve closed-loop stability, however imposing hard
amplitude constraint is not allowable.
For the self-tuning control implementation the esti-
mates
ˆ
F
t
, ˆg
t
,
ˆ
k
e,t
can be easily obtained from on-
line estimation of the ARMAX model parameters
a
1
, . . . , a
na
, b
1
, . . . , b
nb
, c
1
, . . . , c
nc
.
REFERENCES
Kr
´
olikowski, A. (1997). Self-tuning control under
variance and amplitude constraints, Prepr. 11th
IFAC Symp.on Syst.Ident., SYSID’97, Kitakyushu,
8 - 11 July 1997, Vol.1, pp.345-350.
M
¨
akil
¨
a, P.M. (1982). Constrained liner quadratic
gaussian control for process application,
Academic dissertation, Report 82-6, Process
Control Laboratory, Abo, Finland.
M
¨
akil
¨
a, P.M., T. Westerlund and H.T. Toivonen
(1984). Constrained linear quadratic gaussian con-
trol with process applications. Automatica, 20(1),
pp.15-29.
Toivonen H.T. (1983). Suboptimal control of
discrete stochastic amplitude constrained systems,
Int.J.Control, Vol.37, No.3, pp.493-502.
Toivonen, H.T. (1983). Variance constrained self tun-
ing control, Automatica, 19(4), pp.415-418.
0 50 100 150 200 250 300
−1.4
−1.35
−1.3
−1.25
−1.2
−1.15
f
1
0 50 100 150 200 250 300
−0.9
−0.88
−0.86
−0.84
−0.82
−0.8
−0.78
f
2
Figure 1: Plots of feedback gains f
1
, f
2
; c
2
= 2.0
0 50 100 150 200 250 300
0.2
0.4
0.6
0.8
q
u
0 50 100 150 200 250 300
1.8
2
2.2
2.4
2.6
2.8
σ
2 u
Figure 2: Plots of the weight q
(k)
u
and variance σ
2
u
; c
2
= 2.0

0 50 100 150 200 250 300
−1.8
−1.7
−1.6
−1.5
−1.4
f
1
0 50 100 150 200 250 300
−1
−0.98
−0.96
−0.94
−0.92
f
2
Figure 3: Plots of feedback gains f
1
, f
2
; c
2
= 3.0
0 50 100 150 200 250 300
0
0.05
0.1
0.15
0.2
q
u
0 50 100 150 200 250 300
2.9
3
3.1
3.2
3.3
3.4
σ
2 u
Figure 4: Plots of the weight q
(k)
u
and variance σ
2
u
; c
2
= 3.0
0 20 40 60 80 100 120 140 160 180 200
−4
−2
0
2
4
u
0 20 40 60 80 100 120 140 160 180 200
−10
−5
0
5
x
1
0 20 40 60 80 100 120 140 160 180 200
−5
0
5
10
x
2
Figure 5: Plots of signals for c
2
= 3.0 and α = 3.0