DATA MINING: PATTERN MINING AS A CLIQUE

EXTRACTING TASK

Rein Kuusik, Grete Lind, Leo Võhandu

Institute of Informatics, Tallinn Technical University, Raja 15, Tallinn 12618, Estonia

Keywords: Frequent Patterns, Clique Extracting, Monotone Systems Theory

Abstract: One of the important tasks in solving data mining problems is finding frequent patterns in a given dataset. It

allows to handle several tasks such as pattern mining, discovering association rules, clustering etc. There are

several algorithms to solve this problem. In this paper we describe our task and results: a method for

reordering a data matrix to give it a more informative form, problems of large datasets, (frequent) pattern

finding task. Finally we show how to treat a data matrix as a graph, a pattern as a clique and pattern mining

process as a clique extracting task. We present also a fast diclique extracting algorithm for pattern mining.

1 INTRODUCTION

One of the goals of data mining is knowledge

discovering. There are several methods for that

(Dunham, 2002; Fayyad et al., 1996; Hastie et al.,

2001). One well-known class of methods for solving

this task is to reorder the data matrix to give it a

more informative form, i.e. to see its inner structure

as more typical and fuzzy parts of the data matrix

(Bertin, 1981; Võhandu, 1989a). Below we describe

an algorithm of this class named “Minus technique”

(Võhandu, 1989a) and give a small example of its

using. Problems in the interpretation of results of the

method for large data matrices allowed us to

describe a new task to solve: develop a new method

for frequent pattern extraction. As we had already

developed a quite effective clique extracting

algorithm based on the Monotone System Theory,

we defined pattern mining as a clique extracting task

and developed an effective method for that purpose.

1.1 Method for data matrix ordering

“Minus technique” is a simple method for N*M data

matrix ordering (Võhandu, 1989a). Below we will

shortly describe the algorithm. First we order the

rows and then the columns. To reorder the columns

we can transpose the matrix and use the algorithm

again. As a result we can easily see typical and fuzzy

parts of the data

Assume that we have a data matrix X(N, M),

i=1,…,N, j=1,…,M. Every element Xij has a

discrete value from an interval [1,K].

Algorithm

S1. Calculate frequencies FT(t,j) for every variable’s

values t=1,2,…,Kj in columns j, where

j=1,…,M

S2. For every row i=1,2,…,N find the sums

(weights) P(i) = Σ FT(t, j), j=1,…,M

S3. Find R = min P(i); remember i

S4. Eliminate row i from the matrix

S5. If there are yet rows in the matrix then goto S1

else to S6

S6. Reorder matrix rows in the order of elimination

S7. End

1.2 Example

Initial data matrix

V1 V2 V3 V4 V5

O1 1 2 2 2 2

O2 2 1 2 1 1

O3 2 1 2 1 1

O4 1 1 2 1 2

O5 2 2 1 2 1

O6 2 1 1 1 1

519

Kuusik R., Lind G. and Võhandu L. (2004).

DATA MINING: PATTERN MINING AS A CLIQUE EXTRACTING TASK.

In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 519-522

DOI: 10.5220/0002622905190522

 SciTePress

Frequency table FT

V1 V2 V3 V4 V5

1 2 4 2 4 4

2 4 2 4 2 2

variable \ value 1 2

V1 gender female male

V2 has a flat yes no

V3 education higher secondary

V4 activeness yes no

V5 has a car yes no

Order of elimination of rows (6 iterations): O1, O5,

O4, O6, O2, O3. Order of elimination of variables (5

iterations): V1, V3, V5, V2, V4

Reordered data matrix

V1 V3 V5 V2 V4

O1 1 2 2 2 2

O5 2 1 1 2 2

O4 1 2 2 1 1

O6 2 1 1 1 1

O2 2 2 1 1 1

O3 2 2 1 1 1

As we can see, the reordered data matrix is more

informative and is easier to interpret. To use this

method there are no serious problems if the number

of rows and columns is small (tens or hundreds of

variables and observations). If the data matrix is

large then it is harder to see the patterns and it means

that we need some other methods for pattern mining.

2 FREQUENT PATTERN MINING

There are several algorithms to solve frequent

pattern mining problem (Hand et al., 2001; Agrawal

et al., 1994; Lin et al., 1998; Park et al., 1996;

Võhandu, 1989b). They mainly combine variables

(candidates) by counting their frequencies. As we

had already developed an effective method for

extracting all cliques from undirected graphs based

on other techniques (Kuusik, 1995), we have chosen

a different way. Below we show that we can use

graph theory algorithms for frequent pattern mining

as well.

3 PATTERN MINING AS A

CLIQUE EXTRACTING TASK

Here we describe how to transform data matrix into

a graph and describe a pattern as a clique.

3.1 Data matrix as a graph

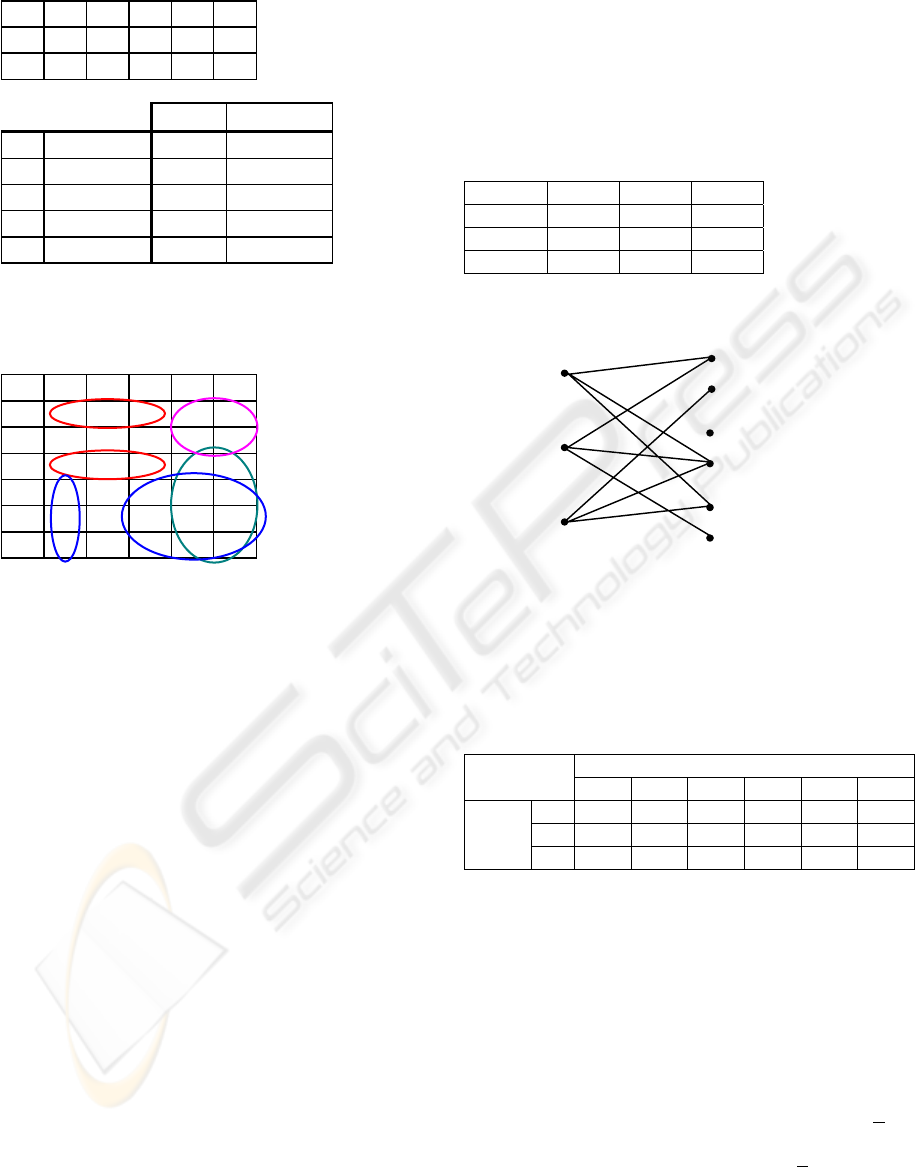
Let a data matrix X(N, M) be given, i=1,...,N;

j=1,...,M, Xij= 1, 2,..., Kj. For transforming we can

create a bipartite graph, where nodes on the left side

A of the graph are observations, nodes on the right

side B are variable values. For example, let X(3,3) is

given, Kj=2, j=1,…, 3

V1 V2 V3

O1 1 2 1

O2 1 2 2

O3 2 2 1

We can present this data matrix as a graph

Figure 1: Data matrix as a graph

Naturally we can present such a graph as a data

table, with rows as nodes of the bipartite graph’s

part A and columns as nodes of the bipartite graph’s

part B. There is „1“ in the table, if these nodes of the

parts A and B are connected and „0“ when not. For

our graph we get:

Nodes of part B

V1=1 V1=2 V2=1 V2=2 V3=1 V3=2

O1 1 0 0 1 1 0

O2 1 0 0 1 0 1

Nodes

of part

O3 0 1 0 1 1 0

3.2 Pattern as a diclique

In general a pattern for the given variables V1,

V2,..., Vm identifies a subset of all possible objects

over these variables (Hand et al., 2001).

We can ask how to describe a pattern on a

graph? It is a diclique. Diclique is a subgraph of the

bipartite graph where all nodes of the parts A and B

are connected together (Haralick, 1974). For our

example there are two dicliques with a frequency>

1) {(O1, O2); (V1=1, V2=2)}, 2) {(O2, O3), (V2=2,

V3=1) (see Figure 2). If the frequency >

1, then we

have 5 dicliques: 1) {(O1), (V1=1, V2=2, V3=1)},

2) {(O2), (V1=1, V2=2, V3=2)}, 3) {(O3), (V1=2,

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

520

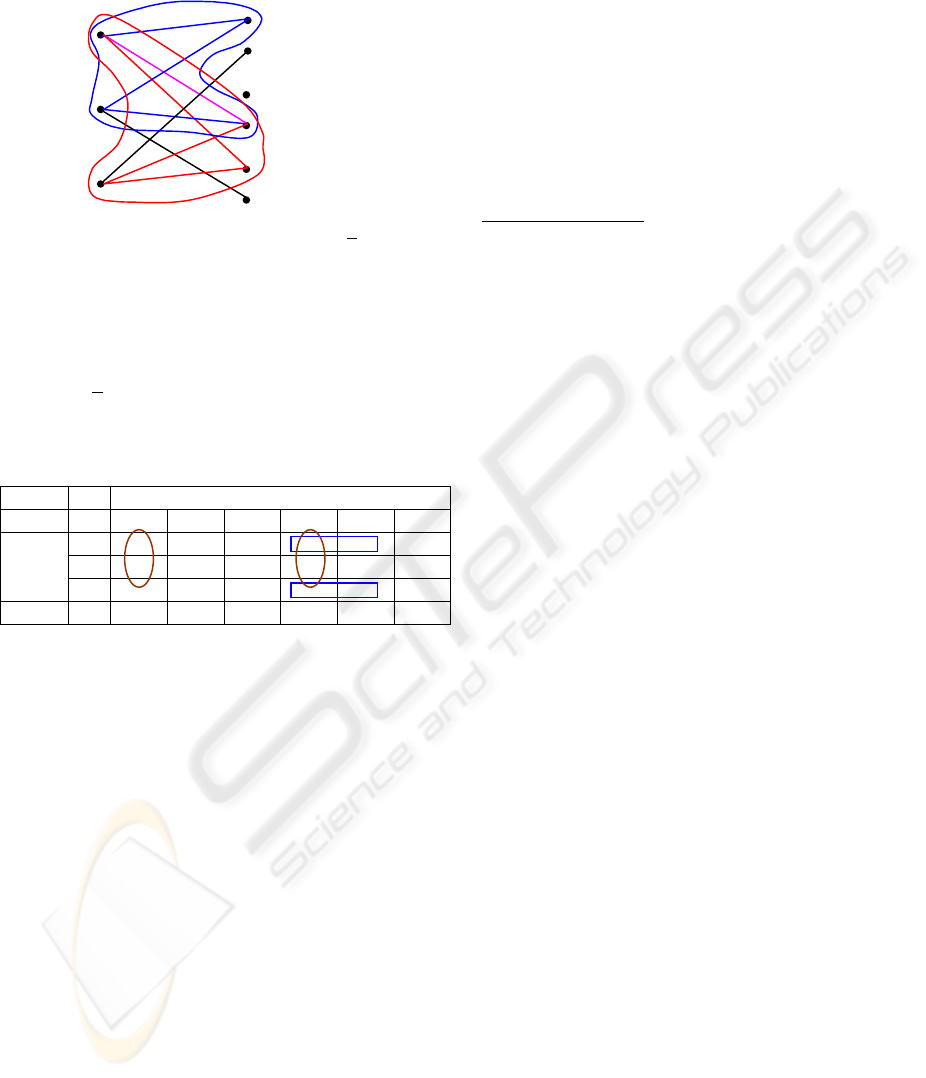
V2=2, V3=1)}, 4) {(O1, O2); (V1=1, V2=2)}, 5)

{(O2, O3), (V2=2, V3=1)}.

Figure 2: Dicliques with a frequency > 2

Now we can formulate pattern mining as a clique

finding task: extract all dicliques from the bipartite

graph G. If we find patterns with frequency

(support) T (for example 75%), then the task on the

graph is following: to find all dicliques with a degree

on part A >

N*T/100 ( in our case N*75/100).

For our example, if T=60%, i.e. frequencies are

at least ⎡0,6*3⎤ =2 then we can extract 2 dicliques:

Nodes of part B

V1=1 V1=2 V2=1 V2=2 V3=1 V3=2

O1 1 0 0 1 1 0

O2 1 0 0 1 0 1

Nodes

of part

O3 0 1 0 1 1 0

Degree 2 1 0 3 2 1

Are there effective algorithms to solve diclique

extraction described by us? Yes, there are.

4 PATTERN MINING (DICLIQUE

EXTRACTION) ALGORITHM

Before we describe the algorithm, we must say, that

it an effective implementation does not need explicit

data matrix transformation to the graph form. It can

extract dicliques directly from initial data matrix.

Algorithm is based on the Theory of Monotone

Systems (Mullat, 1976; Võhandu, 1981).

4.1 Description of the algorithm

In this algorithm the following notation is used:

t the number of the step (or level) of the

recursion

t+1

frequency table for a set X

t+1

⊂ X

Pattern

vector of elements ‘variable.value’ (for

example, V1.1 (V1 value equals 1))

Init activity for initial evaluation

As the algorithm does not combine variables

then the main problem is to avoid repetitive

extraction of extracted patterns. We use following

techniques: zero in FT means that this value is not in

analyze. Bringing zeroes down (from FT

to FT

t+1

)

prohibits arbitrary output repetition of already

separated pattern on level (t+1). Bringing zeroes up

(from FT

t+1

to FT

) does not allow the output of the

separated pattern on the same (current) level t+1 and

on steps t, t-1, ..., 0.

Algorithm MONSA

Init

t=0, Pattern0={}

To find a table of frequencies FT0 for all variables

in X0

DO WHILE there exists FTs#Ø in {FTs}, s≤t

FOR an element hf∈FTt, 1≤f≤M*K with

frequency V=max FTt(hf)#0 DO

To separate submatrix Xt+1⊂Xt such

that Xt+1={Xi∈Xt; i=1,…,Nt⏐X(i,f)=hf}

To find a table of frequencies on Xt+1

Variables j values hj, j=1,…,M with

FTt+1(h)=V form Patternt+1

FOR j=1,…,M, hj=0,…,K-1 DO

IF FTt(hj,j)=0, THEN

FTt+1(hj,j)=0

ENDIF

IF FTt+1(hj,j)=V THEN

FTt(hj,j)=0

FTt+1(hj,j)=0

ENDIF

IF FTt+1(hj,j)=FTt(hj,j) THEN

FTt(hj,j)=0

ENDIF

ENDFOR

IF there exist variables to analyse THEN

t=t+1

Output of Patternt

ENDFOR

t=t-1

ENDDO

All patterns are found

END: end of algorithm

4.2 Complexity of MONSA

It has been proved that if a finite discrete data matrix

X(N,M) is given, where N=K

, then the complexity

of algorithm MONSA to find all (K+1)

patterns as

existing value combinations is O(N

) operations

(Kuusik, 1993). By our estimation in practice the

DATA MINING: PATTERN MINING AS A CLIQUE EXTRACTING TASK

521

upper bound of the number of frequent patterns

(with minimal frequency allowed = 1) is

)K/11(NL +≈ ,

but usually it is less.

4.3 Example of results of MONSA

Extracted patterns (dicliques) from initial data

matrix (see 1.2) with support T>20%:

V1.2&V5.1=4 (V1 equal to 2 and V5 equal to 1; its

frequency equal to 4)

V1.2&V5.1&V2.1&V4.1=3

V1.2&V5.1&V2.1&V4.1&V3.2=2

V1.2&V5.1&V3.1=2

V2.1&V4.1=4

V2.1&V4.1&V3.2=3

V3.2&V1.1&V5.2=2

V2.2&V4.2=2

Sure, the table is small, but the general idea has

been presented.

4.4 Advantages of the algorithm

General properties of the algorithm are as follows:

• The number of results (patterns) can be

controlled via pruning with the T-level

• Several pruning criteria can be used

• Large datasets can be treated easily

• For every pattern its frequency is known at the

moment it is found, also other parameters based

on frequencies can be calculated

• It enables variables having a set of discrete

values (not only binary data!).

5 CONCLUSION

We have developed an effective pattern mining

algorithm on the basis of clique extracting algorithm

using Monotone Systems Theory. It does not use

candidate variables combining for pattern

description, it treats a pattern as a diclique.

Algorithm extracts only really existing in the data

matrix patterns and uses simple techniques to avoid

repetitive extracting of patterns. We implemented

this algorithm to create a method named Hypotheses

Generator for fast generating of association rules

(Kuusik et al., 2003). In the future we hope to find

effective pruning measures to restrict the number of

association rules.

REFERENCES

Agrawal, R., Srikant, R., 1994. Fast algorithms for mining

association rules. In VLDB’94, pp. 487-499

Bertin, J., 1981. Graphics and Graphic Information-

Processing. Walter de Gruyter, Berlin New York

Dunham, M. H., 2002. Data Mining: Introductory and

Advanced Topics. Prentice Hall

Fayyad, U. M., Piatetsky-Shapiro, G., Smyth, P., 1996.

From Data Mining to Knowledge Discovery: An

Overview. In Fayyad, U. M., Piatetsky-Shapiro, G.,

Smyth, P., Uthurusamy, R.; Advances in Knowledge

Discovery and Data Mining. AAAI Press/ The MIT

Press, pp.1-36

Hand, D., Mannila, H., Smyth, P., 2001. Principles of

Data Mining. MIT Press

Haralick, R.M., 1974. The Diclique Representation and

Decomposition of Binary Relations. In JACM, 21,3,

pp. 356-366

Hastie, T., Tibshirani, R., Friedman, J. H., 2001. The

Elements of Statistical Learning: Data Mining,

Inference, and Prediction (Springer Series in

Statistics), Springer Verlag

Kuusik, R., 1993. The Super-Fast Algorithm of

Hierarchical Clustering and the Theory of Monotone

Systems. In Transactions of Tallinn Technical

University, No 734, pp. 37-62

Kuusik, R., 1995. Extracting of all maximal cliques:

monotonic system approach. In Proc. of the Estonian

Academy of Sciences. Engineering, N 1, lk. 113-138

Kuusik, R., Lind, G., 2003. An Approach of Data Mining

Using Monotone Systems. In Proceedings of the Fifth

ICEIS. Vol. 2, pp. 482-485

Lin, D.-I., Kedem, Z. M., 1998. Pincer-Search: A New

Algorithm for Discovering the Maximum Frequent

Set. In Proc. of the Sixth European Conf. on Extending

Database Technology

Mullat, I., 1976. Extremal monotone systems. In

Automation and Remote Control, 5, pp. 130-139; 8,

pp. 169-178 (in Russian)

Park, J. S., Chen, M.-S., Yu, P. S., 1996. An Effective

Hash Based Algorithm for Mining Association Rules.

In Proc. of the 1995 ACM-SIGMOD Conf. on

Management of Data, pp. 175-186

Võhandu, L., 1981. Monotone Systems of Data Analysis.

In Transactions of TTU, No 511, pp. 91-100 (in

Russian)

Võhandu, L., 1989a. Fast Methods in Exploratory Data

Analysis. In Transactions of TTU, No 705, pp. 3-13

Võhandu, L., 1989b. A Method for Automatic Generation

of Statements from Examples. In Proceedings of the

Second Scaninavian Conference on Artificial

Intelligence (SCAI ’89), ed. H. Jaakkola, Tampere,

Finland, pp. 185-191.

ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS

522