FORMALIZATION OF CLASS STRUCTURE EXTRACTION
THROUGH LIFETIME ANALYSIS
Mikio Ohki
Department of Computer and Information Engineering
Nippon Institute of Technology
4-1 Gakuedai Miyashiro-cho, Minamisaitama-gun, Saitama 345-8501 Japan
Keywords: Modeling criteria, Object Oriented Analysis, Lifetime Analysis, Methodology
Abstract: For an analyst who tries to extract class structures from given requirements specifications for an application
area with which he/she is not familiar, it is usually easier first to extract analysis elements, such as attributes,
methods, and relationships, then to compose classes from those elements, than to extract entire classes at the
same time. This paper demonstrates how to define the set of operations that can be used to derive lifetime-
based class structures, provided that methods, including their identification names and lifetimes, can be
extracted from given requirements specifications. The latter part of this paper describes an experiment that
validates the defined operations by deriving typical design patterns, and also describes the differences
between my approach and Pree's meta-pattern approach. Finally, it discusses the important role of lifetime
analysis and an effective style of requirements specifications for object-oriented system development.
1 INTRODUCTION
In the domain of developing enterprise information
systems, since the quality of the systems depends on
the quality of the underlying database, many efforts
have been made to develop effective criteria for
decision-making which can assist in extracting
proper instances of ER (Entity Relationship) model.
For example, DATARUN (D. Pascot,1996),a data-
centered modeling methodology, uses PDG (Primary
Data Generator), which is "a trigger to determine
actual values of data items," as the criterion for
decision-making in order to extract entity types from
the data items gathered from business list forms and
slips. Based on the criterion, primitive data items
with the same PDG, which cannot be produced from
operations on other data items, are classified in the
same entity type of data set. At that time, attribute
names are used to extract actual entity type names.
The author has devised the decision criterion for
ER modeling, which is based on the generalized
PDG concept and incorporates the multiplicity of
produced instances (i.e. the number of
simultaneously determined values) and the number
of situations in which instances are determined. The
author also executed experiments on students in his
conceptual data modeling class, for comparison and
validation of the decision-making criteria. The
result of experiments showed statistically significant
differences between two groups of students. A
larger percentage of students who used the decision-
making criteria reached the proper ER model than
those who did not. However, using these criteria
alone cannot assist well in extracting ER models that
include recursion or method-centered class
structures.
To address these problems, this paper introduces
the concept of software field and lifetime into the
decision-making criteria. It also shows that method-
centered class or recursive class structures can be
extracted through the use of decision-making criteria
formalized as operations, by demonstrating the
results of extraction experiments on "the design
pattern of structures."
This paper consists of five major sections.
Section 2 describes the concept of software filed
which provides the underlying bases of decision-
making criteria developed from the fundamental
features of class analysis. Section 3 discusses the
concept and rules of construction operations to
provide the mathematical base for the decision-
making criteria used in class analysis. Section 4
validates the construction operations by showing
that the operations between the analysis elements
extracted from requirement specifications and the
construction operations can produce the
representative "design patterns for structures" of
GoF (Gamma,Helm,Johnson&Vissides,1995).
635
Ohki M. (2004).
FORMALIZATION OF CLASS STRUCTURE EXTRACTION THROUGH LIFETIME ANALYSIS.
In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 635-642
DOI: 10.5220/0002611206350642
Copyright
c
 SciTePress

Section 5 compares the methodology with Pree's
meta-pattern approach and the final section
describes the conclusion and the future direction of
the methodology.
2 MODELING CLASS ANALYSIS
PROCESS
2.1 Features of Analysis Process
With the bottom-up approach of class analysis, the
analyst usually uses the data items on list forms,
CRC (Class Responsibility Collaborations) card
items, or use-case scenarios to pick up the
candidates for basic data names (attribute names),
function names (method interface names including
parameter parts, hereafter simply referred to as
"method"), then properly groups them and gives
those groups appropriate names. Finding candidates
and grouping them can be characterized as follows.
(1) The only trigger to find analysis elements is the
relationship between meanings of responsibility
names, method names and class names.
(2) The names of attributes, methods and classes are
nothing more than candidates and are not yet
definite. They show ambiguous existence, and
several objects with an identical concept might be
referred to as different names.
(3) Since an object necessarily has its lifetime (a
period from its creation to destruction), the
analyst implicitly uses it to recognize an object.
Among the features mentioned above, (3) plays an
especially important role in extracting class
structures from found attributes and methods. As
mentioned in the first part of this paper, identical
"triggers," which are recognized from the temporal
view in the ER model comparison experiment, can
be good decision-making criteria for extracting
entities, and in the same sense, identical lifetimes
can be effective decision-making criteria for
extracting class structures from found attributes and
methods. However, no analysis method that
positively makes use of lifetime has not been
proposed so far.
2.2 Software Field Meta-model
This paper introduces the concept of "software field"
to naturally describes the above features and to
formally handle the decision-making criteria for
class extraction. The software field represents the
concept introduced to model the process in which
the analyst extracts class structures from the
attributes and methods found in the given
requirements specifications according to the bottom-
up approach. (Since found attributes and methods
are basic elements to construct classes, they are
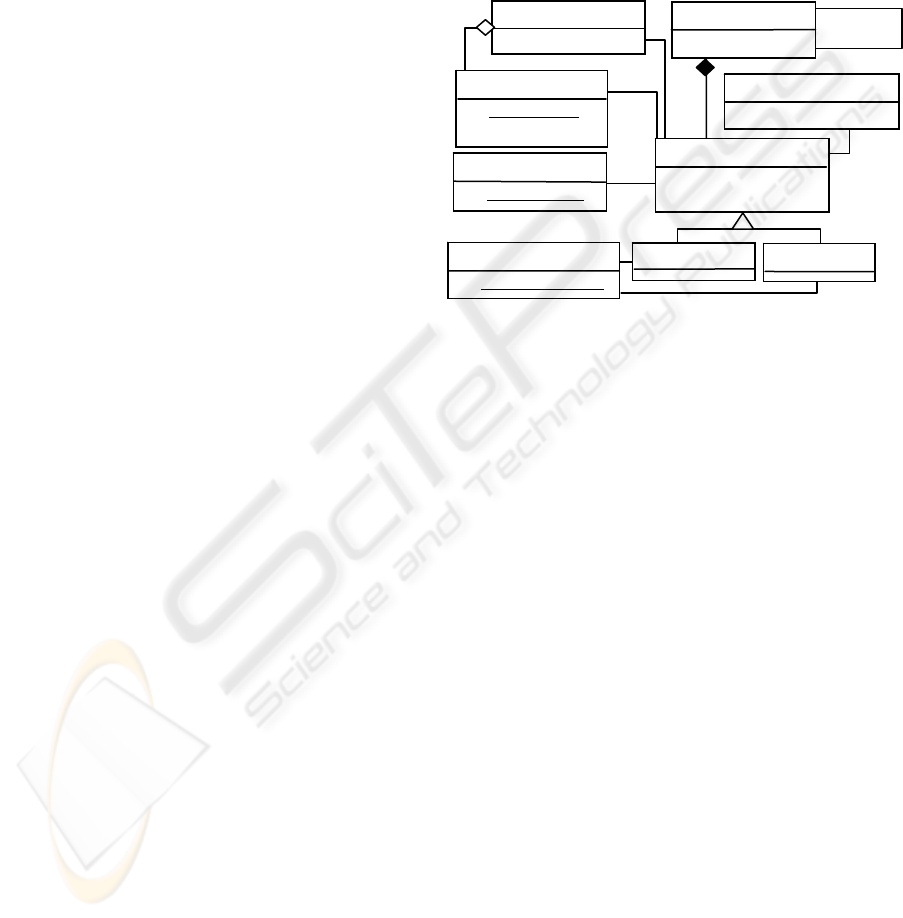
referred to as "constructors" hereafter.) Figure 1
illustrates these software fields as a meta-model
diagram. Underlined items can be used as the
primary key. The meanings of the names of meta-
classes and meta-attributes shown in Figure 1 are
described in detail in the following sections.
2.3 Coordinate System as Meta-
attribute
The software field is a meta-object introduced to
depict the behaviors in which the class structures are
created based on the constructors. Since the
software filed can be more easily understood as an
image of space in which constructors are disposed, I
consider it a space of the following coordinate
system with meta-attributes.
(1) Identifier Axis χ
During analysis, the most basic task is to assign
specific identification names to the constructors
found through domain analysis or defined in the
requirements specifications. The identification axis
χ is used to dispose the terms found in each domain
according to their "names as nominal
measurements" on a one directional axis.
(2) Event Time Axis τ
This axis represents the generalized concept of the
timing along which the attribute values discovered
by the analyst are assigned or the "triggered" time at
which a specific method is requested. An event that
works as a trigger has its own event name such as
"Order Placed," "Lack of Inventory" and so forth.
The event names and the timings at which
constructors are created or destroyed are combined
as couples and disposed along the event time axis τ
according to their topologically sorted time values.
Therefore, what are disposed on the τ axis are event
Upper
Lower
Figure 1: The software field meta-model
Identifier
Identification
1..*
Constraint
Constraint Name
Inheritance
Level
Attribute
Method
1..*
Lifetime
I
de
n
t
ifi
cat
i
o
n
Constructor
Multiplicity
Independent Key
0..1
1..*
Event Time
Event Name
Timin
g
2
Class
Class Name
2
ICEIS 2004 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION
636

names. The time span that begins when a
constructor is created and terminates when the
constructor is destroyed is referred to as a lifetime
hereafter. That is, a lifetime represents the number
of events it contains.
(3) Inheritance Level Axis ν
This coordinate axis corresponds to the
inheritance hierarchy of classes. The constructors
with the same lifetime, discovered through analysis,
are placed on the same inheritance level. The top
level of the inheritance hierarchy has an inheritance
level of 0, and a lower level has a higher value
which is increased by 1 whenever the inheritance
level descend by one step.
2.4 Constructor as Distribution
Function
This paper assumes that the constructors extracted as
ambiguous objects through analysis can be defined
by a probabilistic distribution function in the three
dimensional χ-τ-ρ space. Based on the above
discussion, the following is assumed;
(1) An identification name is unique. That is,
objects with the same meanings are treated by an
identical identification name.
(2) A constructor has one of two states at any time
during its lifetime, one of which indicates that it
exists and the other indicates that it does not exist.
It has no undetermined state.
Based on these assumptions, a constructor has an
identification name χ, and is defined by a
distribution function ϕ(χ, τ; τ
1
, τ
2
), which has a
lifetime of which event interval is [τ
1
, τ
2
]. Here, τ
1
and τ
2
represents the points of time at which the
event is created and destroyed respectively, and the
axis ρ represents the probability of existence (0 or 1)
of the constructor.
The basic concept of my research, in which not
only identification names of constructors but also
their lifetimes are retrieved from the given
requirements specifications, is realized in the
formula that expresses a constructor as a distribution
function of axis τ. The lifetime incorporated in the
distribution function plays an important role in
defining operations that comprise the class structure.
2.5 Meta-characteristics of
Distribution Function
The distribution expression represents the existence
state of a constructor, but it does not represents an
instance of a constructor. That is, it does not
represent an instance of an attribute or the existence
state of the execution process of an implemented
method. An instance generated from a constructor
is placed on a different χ-τ-ρ space and has a
different lifetime from those of the original
constructor, although it shares the axes χ and τ with
the distribution function of the constructor. Based
on the distribution of those instances of a
constructor, the following meta-characteristics are
defined for each constructor.
(a) Multiplicity µ
The multiplicity µ indicates the number of
simultaneous instances existing at the same time,
when instances (ie. implemented values) of a
constructor is generated at an event time. That is, if
the constructor is an attribute, the multiplicity
indicates the "number of attribute values." If the
constructor is a method, the multiplicity indicates
the "number of methods implemented (or required)
with the same interface name." For example, if
multiple instances are implemented with the same
interface name at an event time, the multiplicity is
more than one.
(b) Independent Key κ
If the lifetime of the constructor B is determined
depending on that of the constructor A, the
constructor B is considered to be dependent on the
constructor A. Set of constructors that do not
depend on any other constructors have a meta-
attribute value of "independent key." When a
constructor is an attribute, the independent key
meta-characteristic is nothing more than
paraphrasing the concept of the primary key of data
model. When a constructor is a method, a method
that is modified and defined corresponding to
changes is dependent on the existence of the caller-
side method. When such a relationship takes place
between methods, the caller-side method has a meta-
attribute value of "independent key."
2.6 Constraints of Constructor
A constructor has the following two constraints that
stem from the nature of the object-oriented approach.
(1) Exclusive Constraint π
This constraint defines the number of constructors
that can be placed on the location with the same
identification coordinate value when a set of
constructors is grouped to form a class. The actual
exclusive constraints vary depending on whether the
constructors are attributes or methods. In practice, if
the constructor is an attribute, other constructors
with the same identification name cannot have any
values other than 0 or 1 in the software field. This is
a direct result of the fact that no more than one
attribute with the same identification name cannot
reside in the inheritance hierarchy based on the
constraint of the Private attribute. On the other
FORMALIZATION OF CLASS STRUCTURE EXTRACTION THROUGH LIFETIME ANALYSIS
637

hand, if the constructor is a method, multiple method
interface names with the same identification name
can be placed on the location with the same
identifier coordinate value only if the inheritance
levels are different. This corresponds to redefinition
of methods.
(2) Multiplicity Constraint υ
This constraint indicates that a constructor that
have multiple instances, in other words, an attribute
that has more than one values or an method that has
multiple implementations at the same time, cannot
be used to compose a class with other constructors
that has only one implementation value. This
constraint is the result of the fact that every
implementation value of constraints should be
uniquely defined when generating instanced from
classes.
3 EXTRACTING AND
COMPOSING A CLASS
3.1 Extraction Operation of Class
The following operations are defined based on the
fact that a constructor is a distribution function.
(1) Aggregation Operation of Distribution Function
Formula 1 defines F
ab
as the strength of the force
between two distribution functions ϕ
a
and ϕ
b
that
correspond respectively to two constructors placed
in the software field. Here, as shown in Figure 2, ϕ
a
represents an abbreviated form of the function ϕ
(χ,τ; τ
1
, τ
2
) that has an value 1 during the event
interval (= lifetime τ
a
) that begins at the event
creation time value τ
1
and terminates at the event
destruction time τ
2
. ϕ
b
is also an abbreviation form
of the function ϕ (χ,τ; τ
3
, τ
4
) that has an value 1
during the lifetime τ
b
. Then, as shown in Figure 2,
F
ab
represents the ratio of the area where the
distribution functions ϕ
a
and ϕ
b
overlaps, with the
value between 0 and 1. Here, the absolute values of
the lifetime τ
a
and τ
b
represent the numbers of events
during the lifetimes. Hereafter, subscripts to τ
written in alphabetic character indicate the
identification sign of lifetime.
Formula 1 shows that the operation to aggregate
constructors to compose a class can be defined as an
operation to select constructors of which F
ab
is 1, in
other word their lifetimes are completely identical,
from the set of constructors.
F
ab
::= f
ab
(τ
a
; τ
b
) ≡ 2 * ϕ
a
(τ
a
) * ϕ
b
(τ
b
) / { |τ
a
|+ |τ
b
| }
provided that a ≠ b (Formula 1)
(2) Algebraic Sum Operation of Distribution
Function
Formula 2 uses the aggregation operation shown
in Formula 1 to define the operation to produce an
algebraic sum of two constructor distribution
functions. For example in Figure 2, S
ab
which has
the lifetime of [min(τ
1,
τ
3
),max(τ
2,
τ
4
)] is produced
from ϕ
a
(τ
a
) and ϕ
b
(τ
b
). This operation plays an
essential role in constructing the inheritance
structure of the class later.
S
ab
::= ϕ
a
(τ
a
) + ϕ
b
(τ
b
) – f
ab
(τ
a
; τ
b
) (Formula 2)
3.2 Operation for Class Construction
This section defines operations used to compose the
extracted classes into a structure. Notations used in
expressions are defined as follows.
<For a set of constructors>:
(a) { τ
a
a, τ
b
b } : Is a set of constructors, of which
elements “a” and “b” have the
lifetime of τ
a
and τ
b
respectively.
Here, the identification symbol τ
a
is
the lifetime of the constructor “a”.
(b) τ
a
{ a, b } : Is a set of constructors, of which
elements “a” and “b” have the same
lifetime of τ
a
. It is identical to {τ
a
a,
τ
a
b}.
(c) { a
*
} : Is a constructor “a” of which
multiplicity is more than 1.
(d) τ
b
b ∈ τ
a
a : The constructor “a” contains the
constructor “b” as its element.
(e) { a | b }: Is a set of constructors of which
elements are separated to the sets
“a” and “b” for attributes and
methods respectively.
<For class structures>:
(f) ⇒ : Is the operator that converts a constructors
set to a class structure.
(g) ( τ
a
∨ τ
b
) : Is the algebraic sum of two lifetimes
τ
a
and τ
b
.
(h) τ
a
[a] : Is a class of constructors “a” of which
lifetime identification symbol is τ
a
.
The lifetime of this class is
identical to that of constructors.
(i) [b] ∆ [a] : Indicates that the class [a] of the
constructors “a” is an super-class of
the class [b] of the constructors “b”.
(j) [b] ◊ [a] : Indicates that the class [a] of the
ϕ
a
ϕ
b
Figure 2: Definition of the algebraic product operation
τ
2
τ
3
τ
4
τ
1
τ
b
= [τ
3
, τ
4
]
τ
a
= [τ
1
, τ
2
]
ρ
ICEIS 2004 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION
638

constructors “a” has the composition
relationship with the class [b] of the
constructors “b”. [a] is referred to as
a basis term of composition and [b]
is referred to as a non-basis term.
(k) [b]
*
: Is a class that generates multiple instances.
(l) [a] + [b] : Is a class of which elements are the
constructors “a” and “b”. The
classes [a] and [b] is mutually
independent.
3.2.1 Fundamental Composition Rules
The following sub-sections define the rules to
convert the class structures based on the meta-
characteristics of constructors and the constraints on
the relationships between constructors.
(1) Rules for Composing A Class from A Set of
Constructors
i) Composing A Class from Constructors of
Higher Than Multiplicity 1
When a class is composed from the constructors
of higher than multiplicity 1, based on the
multiplicity constraint (Formula 3), the class is
converted to the one that have only the constructors
of multiplicity 1 and produce multiple instances
simultaneously. Such a class is identified with an
asterisk (*) at the upper right corner of the []
symbol.
{ τ
a
a
*
} ⇒ τ
a
[a]
*
(Formula 3)
ii) Composing A Class Based on The
Characteristics of Elements in A Set
Even if more than one constructors with the same
identification name exists, only one class is
composed as shown in Formula 4.
{ τ
a
a, τ
a
a } = τ
a
a
⇒ ( τ
a
[a] + τ
a
[a] ) = τ
a
[a] (Formula 4)
(2) Generalization Operation Based on Exclusive
Constraint
When more than one constructors with the same
name are found in the constructors set that are to be
aggregated to a class, the exclusive constraint π does
not allow them to be placed on the same hierarchy
level. In this case, a new distribution function is
created by producing the algebraic sum of the two
distribution functions that correspond to the
constructors with the same name, and the newly
produced constructor is placed as an element on the
super-class. Since the resultant class exists as long
as one of the original classes exists, the lifetime of
the super-class generated through the generalization
operation is identical to the logical summation (or
logical summation of the corresponding distribution
functions) of the lifetimes of the lower original
classes. As the result, the lifetime of generalized
class is longer than each of the lifetimes of pre-
generalized classes.
The generalized operation can be defined in two
ways, as shown in Formula 5 and 6, according to the
fundamental features of the object-oriented approach.
Underlined symbols in the formulas indicate the
target constructors for generalization operation.
i) Generalization
{ τ
a
{ a,b }, τ
c
{ a,c } }={ τ
a
a, τ
a
b, τ
c
a, τ
g
c }
⇒ ( t
a
[b] + t
c
[c ] ) ∆ ( t
a
∨ t
c
)[a]
(Formula 5)
ii) Generalization by Abstract Method
{ τ
a
{a,b}, τ
c
{a,c} }={τ
a
a, τ
a
a, τ
a
b, τ
c
a, τ
c
a, τ
c
c }
⇒ ( τ
a
[ a,b ] + τ
c
[ a,c ] ) ∆ ( τ
a
∨ τ
c
)[a]
(Formula 6)
As the nature of generalization operation,
generating a super-class propagates to further higher
classes up to the highest class, and finally extends
the lifetime of the highest class that represents the
whole class structure.
(3) Aggregation Operation Based on Multiplicity
Operation
This operation is used to compose a class
structure that includes aggregation relationship
based on the multiplicity constraint u when there are
several sets of constructors that have the same
lifetime but different multiplicities. The operation is
defined as Formula 7.
υ: τ
a
{ a, b
*
}= { τ
a
{a} , τ
a
{b
*
} }
⇒ τ
a
[b]
*
◊ τ
a
[a] (Formula 7)
From the viewpoint of lifetime, since the
aggregation operation compulsively isolates a
specific class according to the multiplicity constraint
υ, it can be regarded as an operation that extends the
"total value of the lifetimes" of the class structure.
3.2.2 Other Composition Classes
The following sub-sections describe the other
composition classes.
(1) If there is an inclusion relationship between
lifetimes, they can be simplified to the inclusive one.
When τ
c
⊂ τ
a
∆( τ
a
∨ τ
c
)[a] = ∆τ
a
[a] (Formula 8)
(2) The exclusive constraint is applied prior to the
multiplicity constraint.
π:{ τ
b
{ a
*
,b }, τ
c
{ a
*
,c } }
⇒ ( τ
b
[a,b] + τ
c
[a,c] ) ∆( τ
b
∨ τ
c
)[a]
*
(Formula 9)
(3) If each of the elements of a constructors set has
different lifetime, the basis element of the
aggregation relationship is considered as the target
of the operation.
Since a non-basis term depends on basis terms,
only the basis terms are considered to be the target
of generalization operation.
FORMALIZATION OF CLASS STRUCTURE EXTRACTION THROUGH LIFETIME ANALYSIS
639

{ τ
a
[a] , τ
c
[c] ◊ τ
b
[a] } // intermediate state
= τ
a
[a] + τ
c
[c] ◊ τ
b
[a] ) ∆( τ
a
∨ τ
b
) [a] (Formula 10)
(4) If each of the elements of a constructors set has
different lifetime and has the inheritance
relationship, the constructors on the upper level (or,
the level with longer lifetime) are considered to be
the target of generalization operation. Generalization
is introduced to extend the lifetime.
{ τ
a
[a], τ
c
[c] ∆ τ
b
[a] } // intermediate state
= τ
a
[a] + τ
c
[c] ∆ τ
b
[a] ) ∆( τ
a
∨ τ
b
) [a]
(Formula 11)
(5) If the constructors that provide the basis of
aggregation relationship have an identical lifetime,
they are aggregated based on the same reason for
preference of basis term as (3).
{ τ
b
b ∈ τ
a
{ a, m
1
}, τ
c
c ∈ τ
a
{ a, m
2
} }
⇒{ τ
b
b ∈ { τ
a
{ a, m
1
}, τ
a
{ a, m
2
} },
τ
c
c ∈ { τ
a
{ a, m
1
}, τ
a
{ a, m
2
} } }
(Formula 12)
3.2.3 Conversion Rule for Class Structure
Specific types of class structures can be simplified
by the following conversion rules.
(1) Simplification of Self-evident Classes
τ
a
[a] ∆ τ
a
[a] = τ
a
[a] (Formula 13)
(2) Replacement Rule of Lower Classes
If a lower class in the inheritance hierarchy has
the elements that are generated as the result of
aggregation operation of other classes, the
aggregation relationship is transferred to its upper
class, as shown in Formula 14. The aggregation
relationship between classes that have no inheritance
relationship among them can be derived from the
operations that maximize the total value of lifetimes.
( τ
b
[b] ◊ τ
c
[a ] ) + τ
c
[a] ∆ τ
a
[a]
=( τ
b
[b] ◊ τ
c
[a] ) + τ
c
[a] ∆ τ
a
[a] (Formula 14)
4 EXPERIMENT FOR
VARIDATING COMPOSITION
OPERATORS
To validate the above described composition
operations, I conducted experiments on description
and extraction of design patterns for the structures
that were generated by applying the composition
operations on the identification
names and lifetimes
of various constructors, provided that they were
extracted from requirements specifications.
A design pattern does not provide classes or
constructors' lifetimes that are essential for
composition operations. Therefore, several
assumptions should be set for the lifetimes of
constructors from the viewpoint of the objectives
and motivation of the target design patterns. To
avoid the probability to extract a class structure that
is intentionally designed to match a prepared design
pattern, I clearly specified the identification names
and lifetimes of the initial constructors as well as the
requirements to them to facilitate validation of the
extracted set of initial constructors.
4.1 Composing Composite Patterns
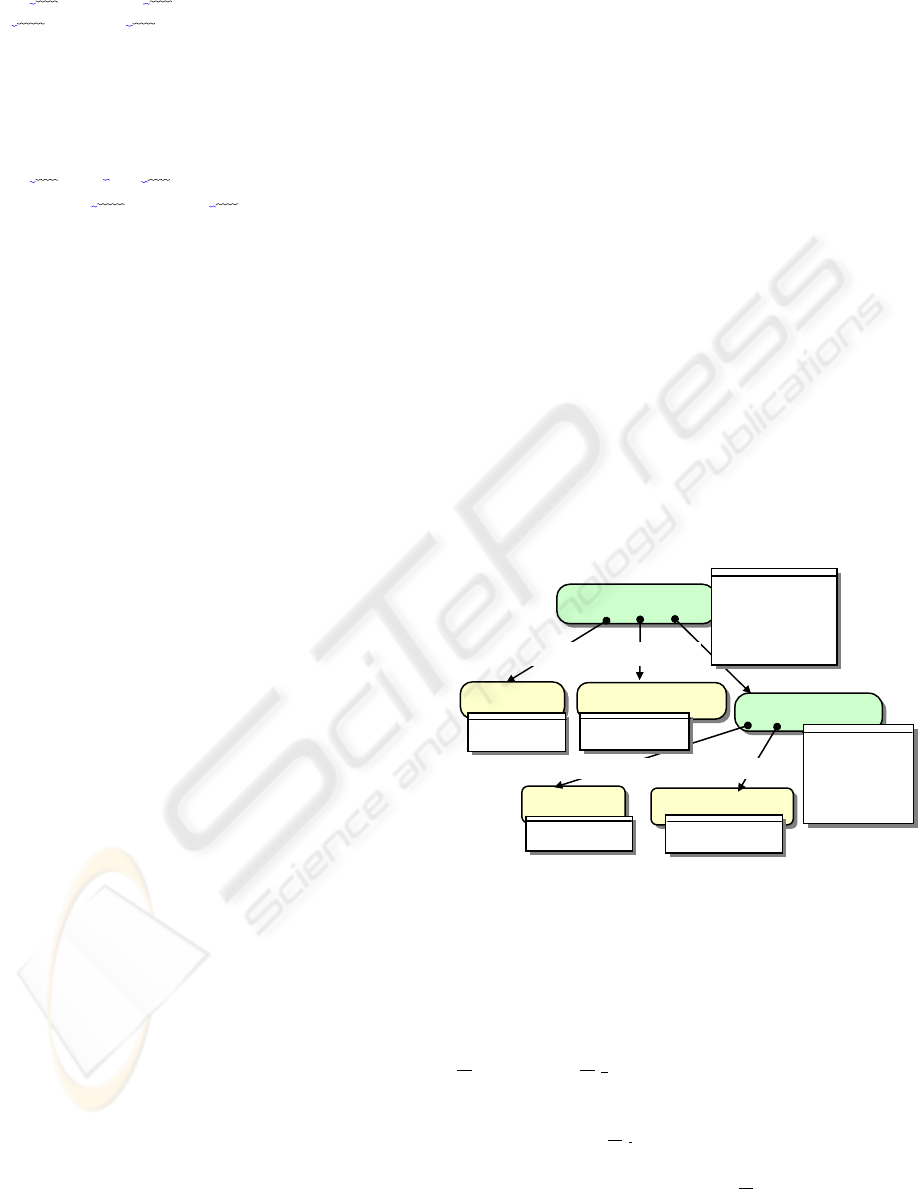
(1) Anticipated Set of Initial Constructors
An instance structure (sample) is used as the
trigger for the set of initial constructors of composite
patterns. As shown in Figure 3, the instance
structure of composite patterns includes other
instances recursively. The identifiers found based on
an instance structure are written in the rectangular
area of the corresponding instance, and the lifetime
is written at the outside of the upper left corner of
the instance. The method Draw() is represented by
“a”, and Add(), Remove() and GetChild() are
represented by “m
1
…m
n
”. The initial constructors
set is represented by Formula 15a, provided that the
lifetimes of the instances aline, aRectangle,aPicture
are τ
a
, τ
b
, τ
c
.
(2) Requirements on Constructors Set
The class structure should be designed to match
the conditions of the instance structure.
(3) Sample of Composition Operations
Applying the class composition operation to
Formula 15a generates Formula 15b.
Ψ
0
= { τ
a
a, τ
b
a, Ψ
0
∈ τ
c
{a, m
1
.. m
n
} } (Formula 15a)
/* Generate an inheritance structure by factoring
out the term of the common identifier “a” */
⇒ ( τ
a
[a], τ
b
[a] ,Ψ
0
◊ τ
c
[a, m
1
.. m
n
] )
∆( τ
a
∨ τ
b
∨ τ
c
) [a]
/* Expand the super-class. Ψ
0
indicates the
structure itself of which highest super-class is ∆(
τ
a
∨ τ
b
∨ τ
c
) [a] */
aRectan
g
le
aLine
aPicture
aPicture
aLine
aRectan
g
le
Draw
()
Draw()
Draw()
aCom
p
onent
2
aComponent
3
aComponent
4
aComponent
5
Draw()
Draw()
Add()
Remove()
GetChild
()
Figure 3: The initial instance structure for the Composite
pattern
aComponent
1
τ
b
τ
a
τ
a
τ
c
τ
a
τ
b
Draw()
Add()
Remove()
GetChild()
ICEIS 2004 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION
640

=τ
a
[a] ∆ ( τ
a
∨τ
b
∨ τ
c
)[a] + τ
b
[a] ∆ ( τ
a
∨ τ
b
∨ τ
c
) [a]
+ [Ψ
0
] ◊ τ
c
[a, m
1
.. m
n
] ∆ (τ
a
∨ τ
b
∨ τ
c
) [a]
(Formula 15b)
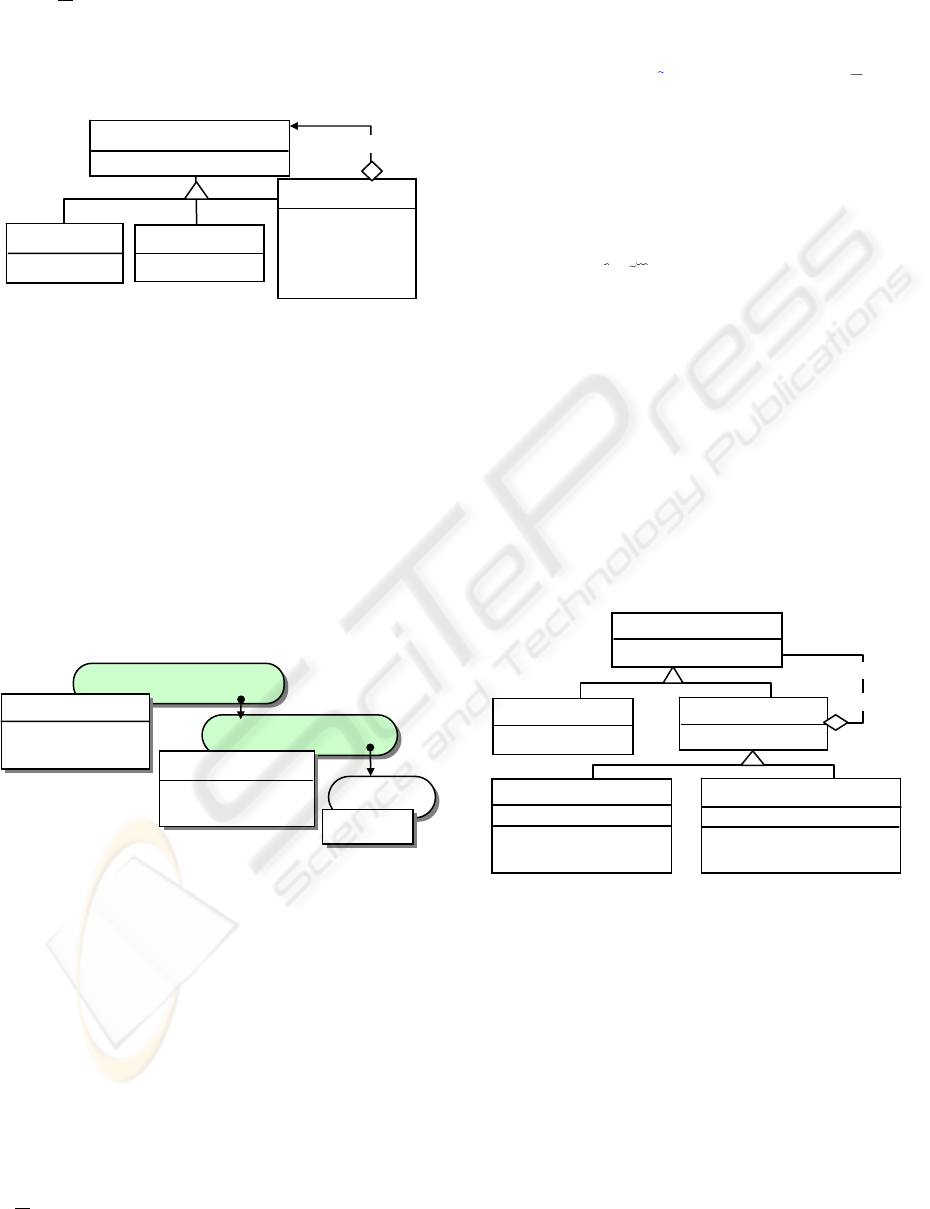
(4) Extracted Class Structure
Formula 15b corresponds to the Composite
pattern shown in Figure 4.
4.2 Composing Decorator Patterns
(1) Assumed Initial Composition Set
The initial constructors set of the Decorator
pattern is also constructed using the instance
structure (= sample) shown in Figure 5 in the same
way as the Composite pattern. The method Draw()
is represented by “a”, and DrawScrollTo() and
DrawBorder() are represented by “m
1
” and “m
2
”
respectively.
The initial constructors set is represented by
Formula 16a, since the lifetime τ
b
of Draw()
possessed by the instance aTextView is clearly
different from the lifetime τ
a
of aScrollDecorator or
aBorderDecorator.
(2) Requirements on Constructors Set
The class structure is required to meet the
conditions of the instance structure.
(3) Sample of Composition Operations
Formula 16b can be finally derived by simplifying
the constructors set of 16a and applying the class
composition operator.
Ψ
0
= {τ
b
a, τ
a
{a, m
1
} ∈ τ
a
{a, m
2
},τ
b
a ∈ τ
a
{a, m
1
} }
(Formula 16a)
/* Factoring out terms that have
τ = τ
a
and χ=a
commonly */
= { τ
b
a, τ
a
{a, m
1
} ∈ { τ
a
{a, m
1
}, τ
a
{a, m
2
} },
τ
b
a ∈{ τ
a
{ a, m
1
}, τ
a
{ a, m
2
}} }
/* Generalize the common term {
τ
a
{a, m
1
}, τ
a
{a, m
2
}
}, and replace the basis terms with the super-class
τ
a
[a] generated in Formula 14. */
⇒{ τ
b
[a], (τ
a
[a,m
1
] + τ
a
[a, m
2
] ) ∆ τ
a
[a],
τ
a
[a, m
1
] ◊ τ
a
[a], τ
b
[a] ◊ τ
a
[a] }
= τ
b
[a] ∆ (τ
a
∨ τ
b
) [a]
+ ( (τ
a
[a, m
1
] + τ
a
[a, m
2
] ) ∆ τ
a
[a] ) ∆ ( τ
a
∨ τ
b
) [a]
+ ( τ
a
[a, m
1
] + τ
b
[a] ) ◊ τ
a
[a]
/* The upper-class
τ
a
[a] that is generated by
generalizing the non-aggregate term
τ
a
[a,m
1
] is
replaced. */
= τ
b
[a] ∆ (τ
a
∨ τ
b
) [a]
+ ( (τ
a
[a, m
1
] + τ
a
[a, m
2
] ) ∆τ
a
[a] )∆( τ
a
∨ τ
b
) [a]
+ ( τ
a
[a]+ τ
b
[a] ) ◊ τ
a
[a]
= τ
b
[a] ∆( τ
a
∨ τ
b
) [a] +
( ( τ
a
[a, m
1
] + τ
a
[a, m
2
] ) ∆ τ
a
[a] )∆ ( τ
a
∨ τ
b
) [a]
+ ( τ
a
[a] + τ
b
[a] ) ∆ ( τ
a
∨ τ
b
) [a] ◊ τ
a
[a]
(Formula 16b)
(4) Extracted Class Structure
Formula 16b corresponds with the class structure
of the Decorator pattern shown in Figure 6.
5 SIMILAR WORKS
One of the similar works is the research on meta-
patterns proposed by Pree( W.Pree,1994,1996). The
concept of meta-pattern based on the composing
relationship has the following similar points and
differences from my approach.
<Differences>:
i) The concept of meta-pattern is essentially based
on the design pattern and its extension. It's focus is
( τ
a
∨ τ
b
)
Decorator
Dr
aw()
VisualComponent
Draw
()
TextVi ews
Draw
()
ScrollDecorator
ScrollPosition
Draw
2
()
ScrollTo()
BorderDecorator
BorderWidth
Draw
3
()
Dr
aw
B
o
r
de
r
()
Decorato
r
Figure 6: The class structure extracted by applying the
configuration operation that corresponds to the Decorator
pattern
Com
p
onent
τ
b
τ
a
τ
a
τ
a
τ
a
Rectangle
Draw
()
Picture
Draw()
Add()
Remove()
GetChild()
GraphicCompenent
Draw
()
Line
Draw()
Co
m
p
onent
Figure 4: The class structure extracted by applying the
configuration operation that corresponds to the Composite
pattern
Com
p
osite
τ
b
τ
c
( τ
a
∨ τ
b
∨ τ
c
)
aComponent
1
aBorde
r
BorderWidth
Draw
3
()
DrawBorder
()
aDecorator
1
aScroll
aCom
p
onent
2
ScrollPosition
Draw
2
()
ScrollTo
()
aDecorator
2
aText
Draw
1
()
Figure 5: The initial instance structure for the Decorator
pattern
τ
b
τ
a
τ
a
FORMALIZATION OF CLASS STRUCTURE EXTRACTION THROUGH LIFETIME ANALYSIS
641

mainly on developing patterns for phenomena, but is
not on investigating the composition process of class
structures in depth to the basic characteristics of the
object-oriented approach such as lifetime. In
contrast, my approach focuses on deriving the
composition process of class structures from the
basic characteristics of the object-oriented approach.
ii) The meta-pattern approach sets the
prerequisites that the Template class and the Hook
class are derived in advance. It does not mention
anything about the difficult method to derive classes.
iii) The meta-pattern approach tries to compose
class structures only from the relationship of
meanings of classes. The validity of inheritance
relationship, such as ascendant or descendant, is
judged based on ambiguous criteria, for example,
"The Template method uses the Hook method, it is
more practical than the Hook method."
iv) The meta-pattern approach does not provide
the idea to use instance structures of practical issues
as the trigger for analysis.
<Similarity>:
Both the meta-pattern approach and my approach
specify the structural attributes as the met-attributes
to provide the class composition process with
theoretical bases. However, whereas the former
provides the class with the meta-attributes, the latter
provides the attributes and methods with the meta-
attributes.
6 CONCLUSION AND FUTURE
DIRECTION
This paper discussed the extraction method of class
structures that requires deep experience in the
object-oriented analysis. Since the constructors to
be analyzed can be easily extracted from list forms,
slips, and use-case scenarios, I tried to translate the
"inspiration" dependent extraction of class structures
into the application of composition sequence on the
software field. Furthermore, to verify the validity
and possibility of composition operations, I
conducted a desk experiment that applied a sequence
of composition operations to the constructors set of
design patterns of GoF structure, and observed the
number of class structures that were extracted for the
design patterns. I showed, as the result, that
extracting proper class structures can be translated
into extracting proper identification names and
lifetimes.
Although the constructors set used in the design
patterns extraction experiment is different from
those actually encountered in practical system
analysis both in size and complexity, they have
common features in their structures. (Not only
design patterns but also analysis patterns are
valuable in this sense.) Since the logical base of the
composition operations is found on the essential
features of the object-oriented concept, I plan to
conduct several larger object-oriented analysis
experiments and to gather evidences for the
usefulness of composition operations.
REFERENCES
R.Wirfs-Brock, B.Wilkerson,,1989. Object-Oriented
Design: A Responsibility-Driven Approach, Proc of
OOPSLA’89, ACM, pp. 71-75.
Jacobson,G.Booch,J.Rumbaugh, 1999. The Unified
Software Development Process, Addison-Wesley.
Craig Larman,,1999. Applying UML and Patterns: an
introduction to object-oriented analysis and design.
B. Adelson , E. Soloway,1985. The Role of Domain
Experience in Software Design, IEEE Trans. on
Software Engineering, Vol.11 No. 11, pp. 1351-1360.
D. Pascot,1996. DATARUN CONCEPT CSA Research
Pte.,.
M. Ohki and K. Akiyama, 2001. A Propose of the
Conceptual Modeling Criteria and Its validity
Evaluation, Trans. of IEICE, Vol. J84-D-I, No. 6,
pp.723-735 In Japanese.
Gamma,Helm,Johnson&Vissides,1995. Design Patterns:
Elements of Reusable Object-Oriented Software ,
Addison-Wesley.
W.Pree,1994. MetaPatterns -A Means For Captureing the
Essentials of Reusable Object-Oriented Desin, Proc. Of
ECOP pp.150-162.
W.Pree,1996. Design Patterns for Object-Oriented
Software Development, Addison-Wesley.
Kambayashi Yasushi ,Ohki Mikio ,2003. Extracting the
software elements and design patterns from the
software field, Proc. of 5th International Conference
on Enterprise Information Systems, pp.603-608.
Ohki Mikio,2003. An Experiment of Design Pattern
Derivation through Class Composite Operations, IPSJ
SIGSE,Proc.of Object-Oriented Symposium 2003
,pp145-148.
L.Lamport,1994. The temporal logic of actions, ACM
Trans. PL ans Systems Vol.16 No.3 pp.872-923.
ICEIS 2004 - INFORMATION SYSTEMS ANALYSIS AND SPECIFICATION
642