Transport Performance for Rough Terrain Sustainable Development

Liudmila P. Bobrik

and Petr P. Bobrik

Department "Engineering graphics" Moscow Aviation Institute (National Research University), Volokolamskoe highway,

4, Moscow, Russian Federation

Laboratory of the organization of transport systems Solomenko Institute of Transport Problems of the Russian Academy of

Sciences 12-th Line VO, 13, St. Petersburg, Russian Federation

Keywords: Rough Terrain, Sustainable Development, Accessibility, Movement Efficiency.

Abstract: The article analyzes the issues of a quantitative assessment of the transport movement efficiency across the

rough terrain. As a quality criterion, the vehicle energy costs are taken, conditioned by doing against rolling

friction forces and load weight of the load. Simplifying assumptions for formula expressions of forces are

formulated. Qualitative conclusions about the action of these forces depending on the road inclination angle

were presented. The attainability domain concept is introduced for a specified consumption value of the

resource. A transport indicator has been defined to compare accessibility areas with similar areas on the plain.

A numerical method for determining accessibility areas was proposed, based on representing the relief using

a weighted graph and determining the shortest distance tree within it. An integral over the territory indicator

of the transport potential of a rugged terrain is considered.

1 INTRODUCTION

Modern socio-economic realities in the world are

such that rough terrain territories (RTT), other things

being equal, are usually considered less favorable for

living, people, and business activity than their plain

counterparts, like the difference between coastal and

inland territories (Bezrukov, 2008). As a result, they

are less populated and less attractive for doing

business, with the exception of traditional types of

activity, mainly, agriculture.

Meanwhile, to explain what is happening from a

purely theoretical point of view, analyze why such a

situation has developed, understand what factors

result in a decrease in the potential for the social and

economic development of RTT, sometimes turns out

to be a non-trivial problem. However, without its

solution, it is impossible to answer the question of

how to increase the investment attractiveness of RTT,

to attract people or living and win the world

competition in the attractiveness of certain places.

Finally, it is necessary to provide the socio-economic

basis for RTT sustainable development for extended



https://orcid.org/0000-0003-2440-3309



https://orcid.org/0000-0001-9038-1852

period of time, as the classics understood it (Meadows

et al., 1972; Meadows, 1992; Forrester, 1974).

RTT occupy a significant part of the land. At the

same time, they are often able to offer a whole range

of unique characteristics for living and economy

(Ivashkina and Kochurov, 2018; Wolfe, 2019).

Therefore, it seems reasonable to use their potential

for all mankind, integrate it into the world labor

division (Podberezkin and Podberezkina, 2014)

The RTT development issues are very

multifaceted and require an integrated approach to

develop practical recommendations for each specific

territory, depending on the profile of its properties

and target objectives. This article will consider one of

the most important factors for territory functioning -

its potential in terms of the transport movement

efficiency.

362

Bobrik, L. and Bobrik, P.

Transport Performance for Rough Terrain Sustainable Development.

DOI: 10.5220/0010590703620367

In Proceedings of the International Scientiﬁc and Practical Conference on Sustainable Development of Regional Infrastructure (ISSDRI 2021), pages 362-367

ISBN: 978-989-758-519-7

2 RESEARCH METHODOLOGY

2.1 Impact of Rough Terrain on

Transport Efficiency

The role of transport in the socio-economic

development of the territory is so important that it can

be named as one of the main reasons slowing down

the economic growth of many RTT (Golts, 1981). In

this case, this or that type of transport is not so

important as its indicators when used for moving a

unit of cargo or a passenger per unit of distance.

These are issues of pure efficiency of movements. In

this sense, the article continues research of work

(Bobrik L.P. and Bobrik P.P., 2016).

As different types of vehicles have their own

characteristics, a significant scatter of results can be

obtained for different studies. To get qualitative

conclusions, the article will consider road transport in

its most general form as an example. The findings can

be generalized with minor accuracy corrections for

other types of movements. In the simplest case, we

assume that the vehicle (V) is counteracted by two

main forces: the rolling friction force of the wheel and

the vehicle weight with its load. Since, as a rule,

during movement RTT, the speed of movement is

low, this allows, in a first approximation, to exclude

from consideration the force of air resistance,

parasitic vibrations of mechanisms, friction forces in

bearings and restrict ourselves to only these two

forces.

2.2 Rolling Friction

The rolling friction force is generally very complex

and requires many different factors. Among these,

surface types appear to be significant. But for our

purposes, as will be shown below, to assess the

influence of the rolling friction force on the efficiency

of movements, it will be possible to use a simple

formula.

кач



(1)

Here

is the total vehicle mass and its load,

is gravity acceleration,

is the vehicle wheel radius.

We will focus on the dependence on the vehicle mass

and its load. As each vehicle has a constant wheel

radius, this formula implies a linear form of this

dependence for each specific vehicle.

The proportionality factor

varies significantly

(by several times and even by orders of magnitude)

depending on surface types, evident from Table 1.

Table 1: Approximate values of rolling frictional resistance

for pneumatic car tires and various types of road surface

(source: Wikipedia).

Road surface and its Rolling resistance

Asphalt concrete in excellent 0.015-0.018

The same in satisfactory 0.018-0.020

Gravel surface 0.02-0.025

Cobblestone 0.035-0.045

Unformed road, dry 0.03-0.035

The same after rain 0.05-0.10

Sand, dry 0.15-0.30

Sand, wet 0.08-0.10

Snow road 0.025-0.03

Ice 0.018-0.02

From this table, an important conclusion can be

made that if we do not take abnormal cases like dry

sand, then the rolling friction force for cars usually

amounts to several percent of the total vehicle weight

with the load. As the car wheel radius rarely exceeds

a third of a meter, then further in the article the total

rolling friction coefficient of 6% of the body weight

will be taken by default.

2.3 Lifting a Load Uphill

The main transport difference between a plain and

RTT in terms of movement efficiency is the presence

of slopes or hills. On the plain, such areas are also

present, but the angles are much less marked, they are

present less frequently so that they can be neglected

in the first approximation.

In the case of a horizontal surface, the vehicle

weight with a load does not generate any additional

forces to the rolling friction force that impede

movement, which is a natural advantage of such

areas. But in rough terrain, extra effort is required

when lifting. At the same time, for the downward

movement, there is practically no compensation for

the energy consumption, since the speed shall be

limited for reasons of road safety, and the engine

operates at approximately the same mode as when

ascending to the same angle.

Transport Performance for Rough Terrain Sustainable Development

363

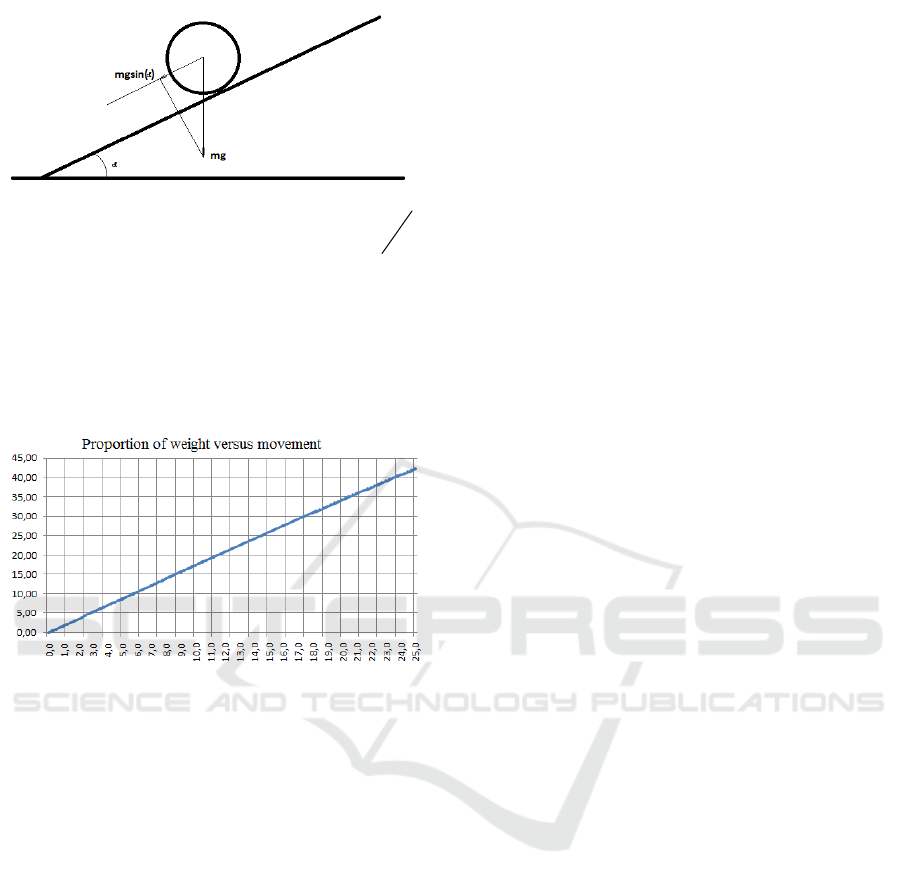
Figure 1: The forces acting on the vehicle during lifting.

If we consider the model problem (see Figure 1) when

lifting a load on an inclined plane, then it is easy to

conclude that an additional force is required for

lifting, proportional to the sine of the lifting angle

))sin(()sin(





качтяжкачтяги

Kmgmg

kFFF

(2)

It is known from the school mathematics course

that at small angles (expressed in radians), the sine

behaves almost like a linear function. But, as we must

quantitatively assess the lifted load effect on the force

required to move, we will propose a graph of the

fraction of the gravity force that needs to be overcome

depending on the ascending angle.

Figure 2: Weight proportion when moving uphill.

Although at first glance, the dependence is very

similar to a linear one, it is not. From a practical point

of view, the most important conclusion is that the

force, required for movement, can be tens of percent

of the body weight. For example, with an ascending

angle of just over 10%, about 17% of the weight

should be lifted. And thus the additional force can be

higher than the rolling friction force, which, as can be

seen from the section above, is a percentage of the

body weight, even by an order of magnitude. The

gravity effect becomes commensurate with rolling

forces already at a few degrees.

This result is qualitative. It shows how

unfavorable the rough terrain is in terms of transport

as compared to a plain. For a similar movement in the

mountains, it is required to apply the force, which is

higher by an order of magnitude.

It is for this reason that road engineers are forced

to build bridges and tunnels, so that there are no

sections with a steep rise, although these are very

expensive facilities to build and maintain

(Biondini

and Frangopol, 2012).

3 RESEARCH RESULTS

3.1 Accessibility Areas

One of the main quantitative approaches to assessing

the efficiency of a particular mode of transport or

their combinations is the approach based on the

concept of accessibility areas (Bobrik, 2018).

In the most general case, the accessibility area is

taken as the territory that can be reached from a

specific point, after spending a certain amount of a

particular resource. These resources may include

time, travel costs, fuel costs, comfort levels, and

many others. That is, this is precisely a general

approach that can generate different definitions,

depending on the problem.

For example, for megalopolises, transport

accessibility is often calculated within an hour, which

is largely explained by the physiological reasons of

the human psyche, since after an hour the trip for

passengers begins to seem tiresome. For international

and intercity trips, as well as in geopolitics, the

accessibility area per day is becoming more

significant. For railway freight transport, it is not time

that is of great importance, but the cost of

transportation. Therefore, it is relevant to consider the

accessibility area, for example, for a $ 1,000 tariff.

As it is obvious from the examples above, the

accessibility area is a point characteristic. There are

various methods of how to match this area with a

certain numerical characteristic so that quantitative

comparisons can be made in the future. The most

common way is to estimate an accessibility area using

its square area. But it is not the only one.

At the same time, quite significant fluctuations of

this numerical indicator for different points can be

observed for the territory. In this case, the average

value of the accessibility area, averaged over the

territory of districts or other small territories, gives a

general idea of the transport of the territory. The

ISSDRI 2021 - International Scientiﬁc and Practical Conference on Sustainable Development of Regional Infrastructure

364

averaging can be performed, among other things, over

calculated ones (for example, a square cell), and not

necessarily by administrative entities. It makes it

possible to plot maps with any degree of detail or

generalization.

Within the framework of this approach, it is

possible to formulate an inverse problem. How many

resources will be required to reach the accessibility

area with the required numerical characteristic. For

example, if for one city a million inhabitants can be

reached on average in 50 minutes, and for another in

70 minutes, then we get a very visual characteristic

for determining where it is better to start a new

business from in terms of the transport component.

For rough terrain, the accessibility area can

change very dramatically, at times, when laying roads

with bridges and tunnels. It forms conditions for

accelerated socio-economic development (Dettwiler

and Schnelli, 1999). On the contrary, territories that

received recharge based on their transit position to a

large extent, with the appearance of bypass tunnels,

can reduce their socio-economic potential

(Knoflacher, 2001).

3.2 Quality Functional

A general approach based on accessibility areas can

be applied to assess the transport potential of RTT. It

will also allow for a quantitative comparison with a

similar flat area. For this, first of all, it is necessary to

strictly define the functional of the quality of

movement. For RTT, it is proposed to take the energy

consumption during the trip as a basis (Drozdov,

2014).

On a road with a slope, there is a sharp asymmetry

in energy consumption when driving in opposite

directions. Some drivers believe, that when driving

along a mountain serpentine, you should stick to

heuristic rule to go downhill in the same gear as when

going uphill with the same inclination angle. If, when

climbing to overcome the rolling force, it is necessary

to additionally add overcoming the gravity of the load

and the vehicle, which, as shown above, can require

many times more energy, then when moving

downhill, there is practically no relief, or it is much

less than the additional energy consumption when

lifting.

Therefore, in the simplest case, at an infinitely

small displacement with a horizontal shift, the

length and liting

, we will calculate the energy

consumption

by the formula

dhFdlFdE

тяжестикачения



(3)

On the same site, but with a slope, the energy

consumption will be assumed to be

dlFdE

качения



. (4)

The proposed formulas are rough and even

incorrect for many types of vehicles. For example, for

rail transport, recuperation devices are quite common,

when, when driving downhill, electrical energy is

generated back into the mains. Although in less

amount than was spent on the lifting to the same

height. Among vehicles of various types, there is a

very high spread in the values of energy consumption

when driving downhill and when climbing. Usually,

on steep slopes, the vehicle speed decreases, i.e.

energy costs become higher than when driving on a

plain. When moving on foot, there is practically no

acceleration of movement.

Summarizing, the proposed formulas describe the

average situation for a wide range of vehicles. They

can only be used as a first approximation to obtain

some general conclusions. However, even these

formulas are already sufficient to get some

conclusions when moving across rough terrain in the

general case.

If some path



is divided into infinitely small

linear sections, then in this case the total energy

consumption on the path will be calculated according

to the classical integral formula of mathematical

analysis

dEE







(5)

This formula allows us to calculate the total cost

of energy when moving between two points,

depending on the chosen path. If we determine a path

where the minimum energy consumption will be

achieved, then by doing so we can calculate the

energy distance between any two points on the

territory.

4 DISCUSSION

4.1 Representation of a Rough Terrain

by a Graph

In the general case, a territory with a variable

landscape is digitally set using a two-dimensional

array, where each pair of geographic coordinates is

assigned a numerical value of the height above sea

level.

Let us take an arbitrary point

of the territory

with coordinates

),( yx

and height above the horizon

),( yxh

. The problem is to calculate the shortest

Transport Performance for Rough Terrain Sustainable Development

365

distances from point

to all the nearest points. To

do this, let us assign an oriented symmetric graph to

a specified territory

Divide the territory into squares with

sides

and

, and calculate the height of the square as the

height of its center. We assume that from the center

of the square you can move to the adjacent squares to

the left - right and up - down, as well as along the

diagonals. If we designate a square as a vertex of a

graph

, then each vertex in it will be adjacent to

eight adjacent vertices, except for the boundary

squares. The topology of connectivity in the graph

looks like a cross on the British flag.

Let us determine the length of each edge of the

graph according to formulas (3-4). If the height of

point

is less than the height of adjacent point

then the length of the edge

),( QP

is calculated by

formula (1), and the length of the edge

),( PQ

calculated by formula (2). And vice versa in the

opposite case.

To determine the minimum distance between

vertices

and

, one can use Dijkstra's algorithm,

widely used in practice (Kristofides, 1978; Ore,

2009). It determines the entire shortest-distance tree

(SDT) (Emelichev, 1990) for the entire set of points

in the area. Among the branches of this tree, there is

also a path on which the minimum energy

consumption between points

and

is achieved.

Moreover, there can be several such paths.

4.2 Indicators of Transport Quality of

the Territory

The SDT obtained as a result of computer

calculations makes it possible to answer a number of

questions about the quality of the territory in terms of

transport.

The SDT for each point allows you to determine

the accessibility area for a given energy consumption

by formula (5).

It is also possible to calculate

its area

)(

. As for a flat territory the

accessibility areas represent a circle, comparing the

area

)(

with the area of a circle, we get the first

indicator of the transport potential of the territory.

circle

)(



(6)

The physical meaning of the indicator

is in

how many times a smaller area we can achieve at a

given level of energy consumption in comparison

with a flat territory.

For the transport characteristics not of single point

, but of a certain territory

, you can consider the

average value of the indicator

on it.





dPPK

K )(

)(

(7)

If a mountain village is selected as a territory, and

the administrative region in which it is located is

selected as the accessibility area, then using the

indicator

it is possible to assess the transport

discrimination of the inhabitants of this village in

comparison with the plain.

5 CONCLUSIONS

The article presents a new approach for assessing the

transport potential of an area with rough relief, based

on the concept of accessibility areas.

Two quantitative indicators are proposed that

characterize the degree of transport discrimination in

the territory.

An algorithm for the computer calculation of

indicators was developed.

REFERENCES

Bezrukov, L.A. (2008). Continental an Oceanic Dichotomy

in International and Regional Development.

Novosibirsk: Academic Publishing House "Geo".

Biondini, F. and Frangopol, D.M.(Eds.) (2012). Bridge

Maintenance, Safety, Management, Resilience and

Sustainability. Proceedings of the Sixth International

IABMAS Conference, pages 8-12.

Bobrik, L.P. and Bobrik, P.P. (2016). Local Factors in

Determining the Optimal Structure of the Backbone

Transport Network. Transport: Science, Technology,

Management, 11: 28-31.

Bobrik, P.P. (2018). On the Competitiveness of the Land

Economy. Materials of the XXXII Annual Session of the

Economic-Geographical Section of MARS.

"Polarization of the Russian Space: Economic, Social

and Cultural_Geographic Aspects", pages 78-86.

Dettwiler, M., and Schnelli, O. (1999). Design &

construction of Zurich's bypass tunnels. Tunnels &

Tunnelling International, 31(5).

Drozdov, B.V. (2014). Development Areas of the Physical

Economy (relative to the transport complex). Electronic

ISSDRI 2021 - International Scientiﬁc and Practical Conference on Sustainable Development of Regional Infrastructure

366

Scientific Publication "Sustainable Innovative

Development: Design and Management", 2(23): 8-94.

Emelichev, V.A. et al. (1990). Lectures on Theory of

Graphs. М.: Nauka.

Forrester, J.W. (1974). World dynamics. Waltham.

MA: Pegasus Communications.

Golts, G.A. (1981). Transport and Accommodation. M.:

Nauka.

Ivashkina, I. and Kochurov, B. (2018). Cities of baikal

region: environmental challenges of spatial

development. Environmental risks for socioeconomic

development. Proceedings of the 3

(2nd STEPS)

Russian-Japanese Collaboration Seminar for

Sustainable Environment, 119–129. MSU Publishers

Moscow.

Knoflacher, H. (2001). Problems caused by the

motorway/railway freight traffic share in the Tyrol.

Proceedings of the Institution of Mechanical Engineers,

Part F: Journal of Rail and Rapid Transit, 215(1): 45-

51.

Kristofides, N. (1978). Theory of Graphs. Algorithmic

Approach.

Meadows, D.H., Meadows, D.L., Randers, J. and Behrens,

W.W. (1972). The limits to growth. New York:

Universe Books.

Meadows, D.H., Meadows, D.L. and Randers, J. (1992).

Beyond the limits. White River Junction. VT: Chelsea

Green.

Ore, O. (2009). Theory of Graphs: Transl. from English.

M.: Book House "LIBROKOM".

Podberezkin, A. and Podberezkina, O. (2014). Eurasianism

as an Idea, Civilizational Concept and Integration

Challenge. Eurasian Integration - The View from

Within. Taylor & Francis. Series: Routledge

Contemporary Russia and Eastern Europe, 46-60.

Wolfe, S. D. (2019). A new road and rail link from the

mountains to the coast. Mega-events: Placemaking,

regeneration and city-regional development.

Transport Performance for Rough Terrain Sustainable Development

367