
The Tonnetz Environment: A Web Platform for Computer-aided
“Mathemusical” Learning and Research
Corentin Guichaoua
1,2
, José L. Besada
3
, Erica Bisesi
4
and Moreno Andreatta
2,1
1
Music Representations Team, IRCAM, 1 Igor Stravinsky Square, Paris, France
2
Institute for Advanced Mathematical Research, CNRS, University of Strasbourg, Strasbourg, France
3
Department of Musicology, Complutense University of Madrid, Madrid, Spain
4
Music Faculty, University of Montreal, Montreal, Canada
Keywords: Tonnetz, Computational Musicology, Computer-Supported Education, Geometry, Topology, Cognition.
Abstract: We describe the Tonnetz web environment and some of the possible applications we have developed within
a pedagogical workshop on mathematics and music that has been conceived for high-school students. This
web environment makes use of two geometrical representations that constitute intuitive ways of accessing
some theoretical concepts underlying the equal tempered system and their possible mathematical
formalizations. The environment is aimed at enhancing “mathemusical” learning processes by enabling the
user to interactively manipulate these representations. Finally, we show how Tonnetz is currently being
adapted in order to lead computer-based experiences in music perception and cognition that will be mainly
carried at universities. These experiences will explore the way in which geometrical models could be
implicitly encoded during the listening process. Their outcome may reinforce educational strategies for
learning mathematics through music.
1 INTRODUCTION
Within the panoply of computer-based approaches on
music education, there is a common agreement that
web environments constitute an excellent device to
support music learning processes (Meredith, 2016;
Conway, 2020). The Tonnetz environment
1
is a
web application based on previous research on
computer-aided topological music analysis (Bigo et
al., 2013; Bigo et al., 2014; Bigo and Andreatta,
2016) and fostering mathematical and computational
thinking through music.
In this paper, we first provide a very short
overview of the most active research axes of the
Structural Music Information Research Project
(SMIR project in short) within which the web
environment has been developed. After discussing the
“mathemusical” dynamics underlying the SMIR
project, we focus in particular on some computational
models of harmonic spaces that have been
implemented in Tonnetz. This environment enables
an interactive exploration of a great variety of
1
We henceforth use Tonnetz for our open-source web
environment and Tonnetz for the neo-Riemannian
representation. The web environment is available at:
geometric spaces for music-theoretical, analytical and
compositional purposes. We will also present a
current research project, supported by the CNRS,
which constitutes the cognitive component of the
SMIR project. This project, entitled Processes and
Learning Techniques of Mathemusical Knowledge
(ProAppMaMu project in short), aims to explore the
link between geometric representations and cognitive
sciences by following some previous work carried out
by researchers in neurosciences and experimental
psychology and by focusing on the interplay between
structural mathematics and computational models.
After some considerations on music cognition, we
show how Tonnetz is currently being adapted to
lead computer-based educational experiences for
music perception and cognition. These experiences
are planned to be systematically conducted at
universities and might shed some new light on the
way in which geometrical models are implicitly
encoded in the listening process, and eventually
suggest how to reinforce the learning techniques in
mathematics through music.
https://guichaoua.gitlab.io/web-hexachord/. We recom-
mend to open it with Chrome.
680
Guichaoua, C., Besada, J., Bisesi, E. and Andreatta, M.
The Tonnetz Environment: A Web Platform for Computer-aided “Mathemusical” Learning and Research.
DOI: 10.5220/0010532606800689
In Proceedings of the 13th International Conference on Computer Supported Education (CSEDU 2021) - Volume 1, pages 680-689
ISBN: 978-989-758-502-9
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
2 THE SMIR PROJECT AND ITS
“MATHEMUSICAL”
DYNAMICS
The SMIR project, hosted by the Institut de
Recherche Mathématique Avancée (IRMA) of the
University of Strasbourg, is currently carried out in
collaboration with musicologists from the Groupe de
Recherche Expérimentale sur l'Acte Musical
(GREAM) and computer science researchers from the
Music Representations Team at IRCAM in Paris.
Ongoing research includes axes such as mathematical
morphology, generalized Tonnetze, formal concept
analysis and computational music analysis (Agon et
al., 2018), persistent homology and automatic
classification of musical styles (Bigo and Andreatta,
2019), category theory and transformational music
analysis (Popoff, Andreatta and Ehresmann, 2018),
homometry and phase retrieval in music analysis
(Mandereau et al., 2011), or tiling musical problems
and Fuglede spectral conjecture (Andreatta, 2015).
All these topics share a common trait, which
positions music at the core of mathematical
formalization and computational modelling. Their
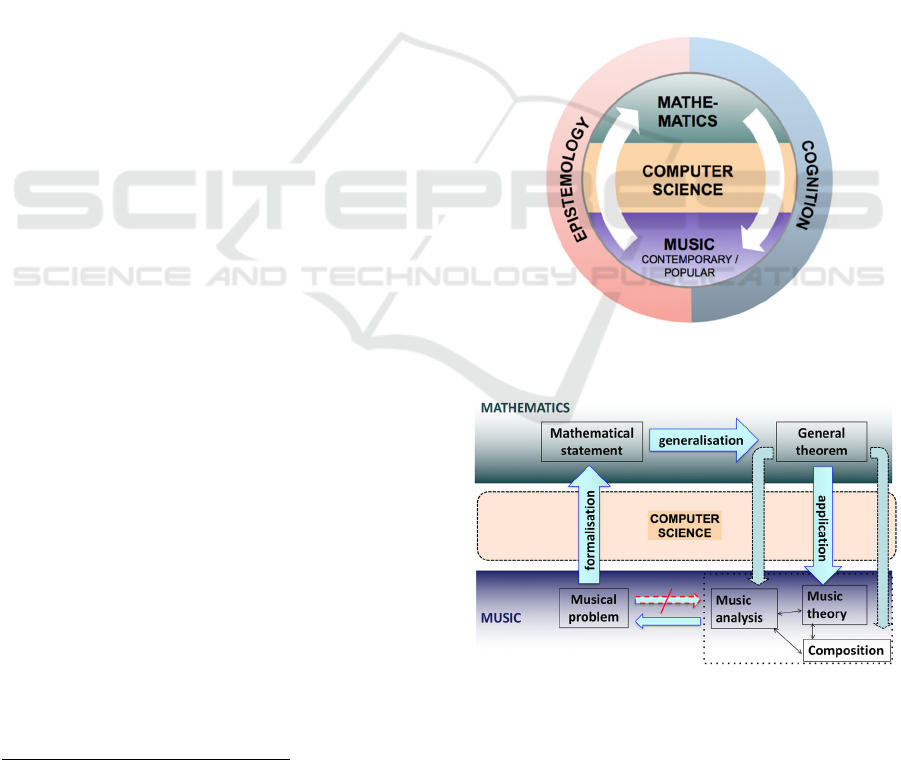
dynamics is captured by the diagram in Figure 1,
which shows how to navigate between music and
mathematics by using computer science as an
interface in the formalization ascending process
(from music to mathematics) and the application
descending process (from mathematics back to
music). This dynamical “mathemusical” process is
detailed deeper in Figure 2. Notice that some musical
problems make use of computational models in an
ascending formalization process, before necessarily
reaching the state of general theorems in the
mathematical realm. This is typically the case of NP-
complete music-theoretical problems for which,
unfortunately, it is not possible to exhibit a
constructive algorithm. Some well-known
compositional problems belong to this class. It is the
case, for instance, of the enumeration of all-interval
twelve-tone series, the estimation of Z-related chords,
or the enumeration of Hamiltonian paths and cycles
in music-theoretical graphs, such as the Tonnetz or its
possible extensions (Cannas and Andreatta, 2018).
The most interesting case for “mathemusical”
research occurs however when a musical problem
reaches the state of a mathematical theorem after the
formalization or generalization process and becomes
2
Available at: https://guichaoua.gitlab.io/web-
hexachord/hexachordTheorem. We recommend to
visualize it with Chrome.
integrated within a computer-aided environment to be
used by composers or music theorists in different
situations within the field of music. One of the most
celebrated theorems that one may find in the literature
is Milton Babbitt’s “hexachordal theorem”, stating
that a hexachord and its complement always have the
same intervallic content (Blau, 1999). Tonnetz, and
in particular its circular representation associated to
the equal-tempered system, can be easily adapted to
this special musical problem. It becomes an
interactive platform for visualising the intervallic
content of two generic collections of pitches related
by complementation. Figure 3 shows the environment
as it has been integrated in an online article retracing
the history of this famous combinatorial problem
(Bayette, 2019). The reader may try to discover the
possible relations between the intervallic content of a
given collection of pitches and its complement by
exploring this special adaptation
2
.
Figure 1: The “mathemusical” dynamics at the core of the
SMIR project.
Figure 2: A more detailed perspective of Figure 1 showing
the different steps of the “mathemusical” dynamics.
The Tonnetz Environment: A Web Platform for Computer-aided “Mathemusical” Learning and Research
681
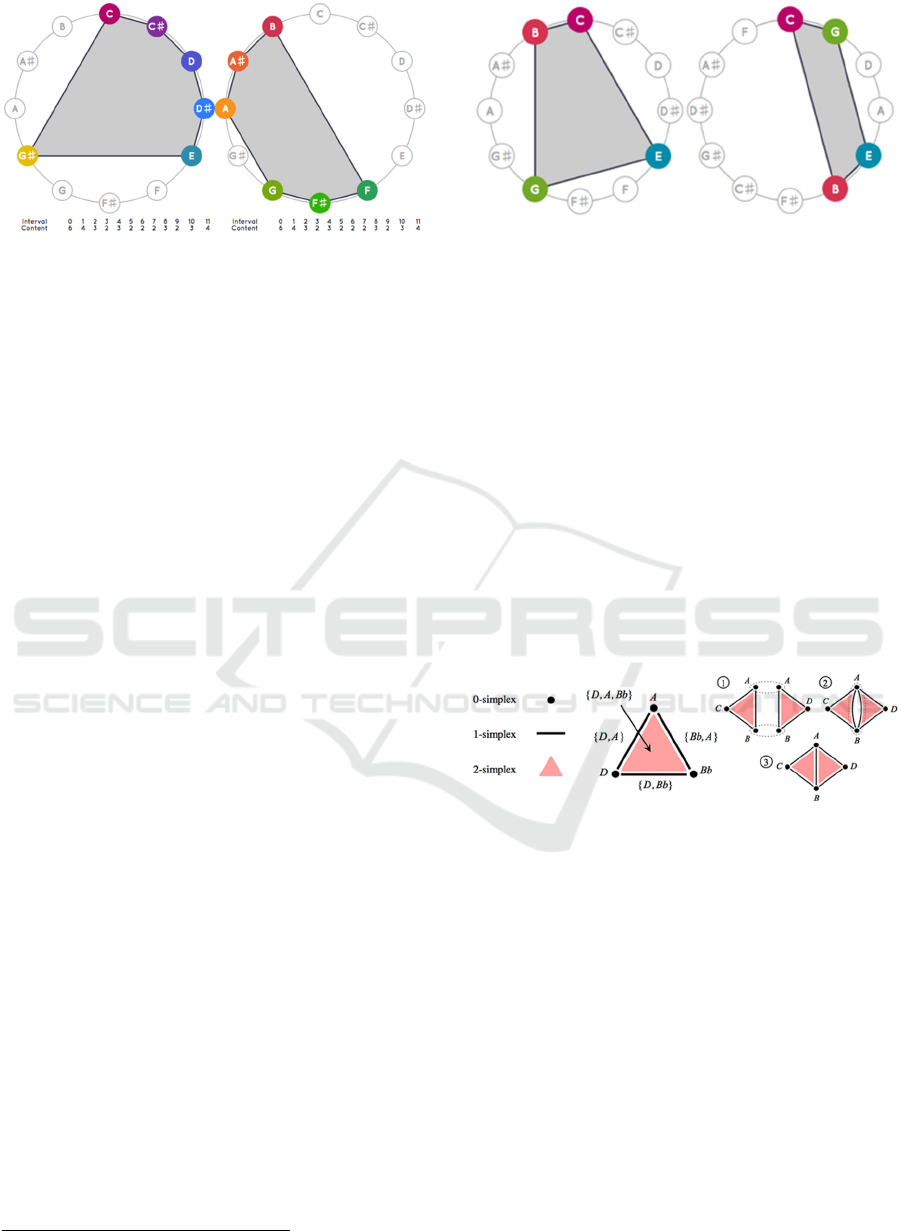
Figure 3: Adaptation of Tonnetz for interactively
visualizing Babbitt’s hexachordal theorem.
3 THE TONNETZ GEOMETRY-
BASED WEB ENVIRONMENT
Tonnetz makes use of two kinds of geometric
representations: a circular representation and a tiling
of the plane by triangles (alternatively by hexagons).
We go now into some details of these geometric
representations by emphasizing their relevance in
supporting music learning and teaching via computer
models.
3.1 The Circular Representation
As in the case of the HexaChord computer
environment
3
, which was the inspirational source for
this web application, two circular representations are
available to the user: the chromatic circle and the
cycle of fifths representation. These representations
are extensively used in both American and European
research around the pitch-class set theory (Andreatta,
Bardez, and Rahn, 2008). Although both circles are
algebraically equivalent (since they are related by an
affine transformation), they highlight different
properties of chord collections and their associated
intervallic content with respect of symmetry, as
shown in Figure 4.
An interesting case, that can be taken as an
exercise for advanced maths students, occurs when
the two representations are exactly the same for a
specific pitch collection. The reason of this
equivalence goes deep into algebraic properties of the
cyclic groups underlying the previous geometric
representations. Apparently simple musical problems
may give rise to deep algebraic investigations that can
be easily modelled within an interactive environment
such as Tonnetz.
3
Available at: https://louisbigo.com/hexachord
Figure 4: Two possible representations of the C7 chord in
Tonnetz. On the left, within the chromatic circle; on the
right, within the cycle of fifths.
3.2 Two Ways of Tiling the Space
Beyond the circles, Tonnetz incorporates further
geometric representations: the tiling of the plane by
triangles and by hexagons. These representations are
widely spread within the neo-Riemannian music
analysis (Gollin and Rehding, 2010). The
triangulation of the 2-dimensional Euclidean space
offers a first geometrical perspective on musical
transformations between two given chords.
According to the simplicial approach previously
introduced by Louis Bigo and Moreno Andreatta
(2015), triangles are 2-simplexes and they are glued
together, as shown in Figure 5, by a self-assembly
process when they share a common edge.
Figure 5: On the left, the first three n-simplexes; on the
right, the self-assembly process. Adapted from Bigo and
Andreatta (2015).
In the standard Tonnetz space, triangles represent
major and minor chords, as Figure 6 puts in evidence,
but one may use any 3-note chord as a 2-simplex
generating the triangular tessellation of the plane via
the self-assembly process. The structural properties of
the resulting non-standard Tonnetz space will be
different depending on the properties of the
generating 2-simplexes (Catanzaro 2011). This fact
leads to a panoply of topological cases, from the torus
(as in the case of the standard Tonnetz) to non-
connected spaces (for instance, when the space is
generated by only augmented triads).
CSME 2021 - 2nd International Special Session on Computer Supported Music Education
682
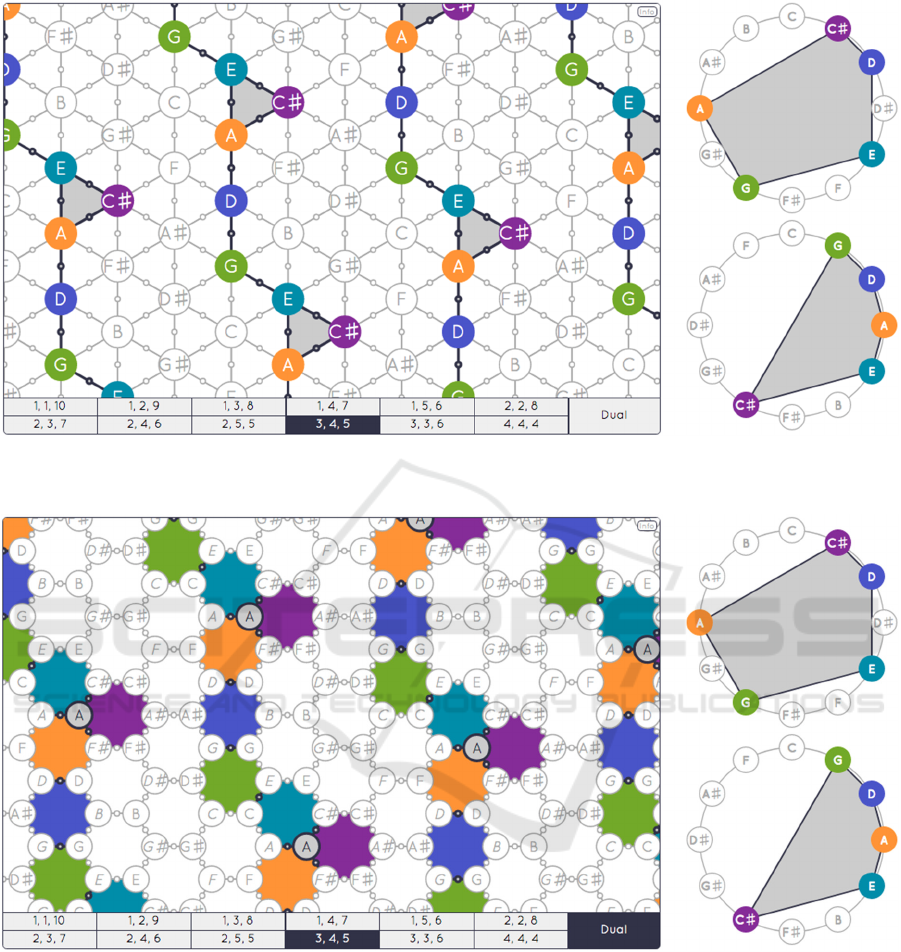
Figure 6: Multiple visualizations of pentachord {C#, D, E, G, A} within the Tonnetz. On the left, its representation within
the standard Tonnetz. On the right, the circular representations associated to this chord.
Figure 7: Multiple visualizations of pentachord {C#, D, E, G, A,} within the Tonnetz, but represented this time in the dual
space of the standard Tonnetz.
Any triangulation of the plane is associated to its
dual one: the graph obtained by replacing every 2-
simplex with a 0-simplex (i.e., a point) and by
connecting two points when they corresponding 2-
simplexes share a common 1-simplex (i.e., an edge).
Figure 7 shows how the pentachord of Figure 6 is
now represented in the dual space, also called
“chicken-wire” torus in the neo-Riemannian music
theory (Douthett and Steinbach, 1998).
In this new visual representation, the vertices are
now major triads (normal font with the name of the
chord root) or minor ones (italic font with the name
of the chord root). Now, for any given collection of
pitches, if the node corresponding to A major is
illuminated, it means that the collection contains the
A major triad as a subset. One may notice that each
hexagon of the dual space represents a single note,
more precisely the note which is common to all the
triads which are associated to the nodes of the
The Tonnetz Environment: A Web Platform for Computer-aided “Mathemusical” Learning and Research
683

hexagonal surface. For instance, pitch class F#
belongs to the F# major, F# minor, D major, D#
minor, B major, and B minor triads.
4 USING TONNETZ IN
OUTREACH AND
EDUCATIONAL CONTEXTS
Tonnetz has taken part of several large public
events, such as the LaLaLab exhibition “Mathematics
and Music” created by IMAGINARY and premiered
at Heidelberg in May 2019. This exhibition was
curated with the advice of several “mathemusical”
researchers around the world and with the
contribution of more than twenty artists and scientists
working in the field. As shown in Figure 8, Tonnetz
was presented by means of tactile screens and
keyboards enabling the public to interactively explore
the different geometric spaces available through the
environment.
Of course, Tonnetz can be used in quite more
controlled scenarios with educational purposes. It has
been recently integrated into a pedagogical workshop
which was conceived by following the new high-
school programs of the French National Education.
These programs introduce the topic of mathematics
and music at the high-school level (typically for 15
years-old students). They put a special emphasis on
the way in which several harmonic structures have
been formalized, from the Pythagorean scales to the
equal-tempered system, and on the use of computer
science to provide computational models of musical
knowledge. In this workshop, designed within the
ProAppMaMu project, we have tried to reinforce the
interplay between standard pedagogical tools (flyers,
slide
presentations, audio and video extracts) and an
interactive manipulation of Tonnetz. Figure 9
shows the typical set-up of such a workshop in a high-
school class, where the students can individually
explore further contents of the presentation through
our web environment, which is available in their
computer screen.
The conception of a traditional paper support
accompanying the “mathemusical” workshop has
been done in synergy with Marie Marty, who is a
designer from the Ecole Estienne of Design in Paris,
specialist in scientific drawings. She has also created
a series of animations for enriching the brochure
support. Some topics within the official programs of
the French National Education were selected for their
potential to be also depicted in a traditional flyer, as
shown in Figure 10. The aim was to describe, in an
visually appealing way, the main features which are
available in Tonnetz. Figure 11 highlights a portion
of the paper flyer that can be “augmented” during a
workshop.
Figure 8: A visitor interacting with Tonnetz and a
keyboard at the LaLaLab exhibition in Heidelberg
(reproduced with the kind permission of IMAGINARY).
Figure 9: A typical set-up of a “mathemusical” workshop
of the ProAppMaMu project.
Figure 10: The flyer for enriching the workshop.
CSME 2021 - 2nd International Special Session on Computer Supported Music Education
684

Figure 11: On the left, the topic “the Tonnetz system” as contained in the brochure (third inner panel); on the right, a still of
its matching gif animation for slide presentations.
Both the animations and the computer-aided
visualisations have been integrated into a pedagogical
film (entitled “Musique et mathématiques: histoire
d’une rencontre”) that aims to artistically summarize
the theoretical content of the high-school workshop.
The two main characters of this film, which appear in
Figure 12, are playing on a stage (which is a
keyboard) surrounded by several animations
generated with Tonnetz. The dialogue between
these characters provides at the same time a journey
through the history of the relations between maths
and music and a condensed presentation of the main
concepts introduced in the workshop via the web
environment
4
.
Figure 12: Screenshot of the pedagogical film “Musique et
mathématiques: histoire d’une rencontre”.
4
The film is hosted at the CNRS AudiDiMath outreach
platform: http://video.math.cnrs.fr/musique-et-
mathematiques/
5 PERCEPTUAL AND
COGNITIVE IMPLICATIONS
So far, the main outcomes of the SMIR project have
been the online uploading of the Tonnetz
environment, its adaptation within the contexts of art
and popular music, and a detailed dissemination plan
trough “mathemusical” workshops and exhibitions,
suitable for pedagogical applications. Besides all
these achievements, the SMIR project disclosed new
interesting research questions belonging to the area of
psychology and cognition. These questions concern
the way in which individuals process the information
carried by the geometrical representations discussed
in the previous sections:
Do the structures implicitly encoded by
Tonnetz have some perceptual foundation,
somehow innate in human cognition?
How could we grasp plausible connections
between its geometrical representations and a
multimodal (in our particular context, auditory
and visual) musical perception?
Which strategies would be the most suitable and
efficient for helping the listeners become more
The Tonnetz Environment: A Web Platform for Computer-aided “Mathemusical” Learning and Research
685

aware and familiar with such structures under
the effect of such stimuli?
ProAppMaMu aims at answering these questions
by means of perceptual tests. Moreover, by focusing
on the interplay between structural mathematics and
computational models, the project will explore the
way in which geometrical models of music theory
might be used to reinforce the learning techniques
within the context of mathematical education.
5.1 Transformational Music Theory
and Cognition
One of the main goals of systematic musicology
during the last decades has been to explore the links
between human cognitive capabilities to process
musical signals and the theoretical foundations of
music (Leman, 1995). As music develops quite
differently within each human culture, the theoretical
representations conceived by Western music theorists
are far from standing as universals. This fact does not
mean, however, that Western representations are
completely arbitrary. Consequently, a search for
some objectification in this sense is highly desirable.
Moreover, a better comprehension of the cognitive
foundations and implications of such representations
would help to improve the pedagogical strategies in
musical and “mathemusical” educational contexts.
Many music representations can be traced back to
two main schemes, which are embedded in Western
music notation: the horizontal flow of time and the
vertical ordering of pitches, as outlined by the image
schema theory (Johnson, 1987). Although such
schemas may seem to be almost trivial within our
culture, the way individuals interact with them is,
cognitively speaking, quite complex. For instance,
there is no one-to-one relationship between the
vertical distribution of pitches and the plethora of
cognitive strategies individuals adopt for pitch
recognition (Letailleur, Bisesi, and Legrain, 2020).
Concerning time, some composers have twisted the
straight left-to-right musical timeline while drafting
their oeuvre (Besada and Pagán Cánovas, 2020;
Besada, Barthel-Calvet, and Pagán Cánovas, 2021).
All these examples rely on relatively simple music
features (pitch and time), which are unfolded
throughout a unidimensional image schema. The
standard Tonnetz is conversely much more complex,
as pitches are placed in the crossroads of three
different linear directions, giving rise to geometrical
shapes matching with particular chords. Previous
research in the field of musical psychology has
encompassed these kinds of problems from diverse
approaches. A key related topic is the study of
perceived distance when hearing pitch collections in
tonal and post-tonal music (Rogers and Callender,
2006; Bisesi, 2017). Concerning our particular
research, Carol L. Krumhansl (1998) compared three
neo-Riemannian models of triadic distance with
psychological data. She surmised that the perceived
distance between chord roots is akin to the dual
standard Tonnetz. Andrew J. Milne and Simon
Holland (2016) have shown through experimental
data that spectral pitch-class distances and the
Tonnetz have high correlations. This evidence led
them to provide a psychoacoustical explanation for
perceived triadic distance. By contrast, very few is
known about how individuals actually apprehend
such abstract structures.
The standard Tonnetz probably stands as the most
exploited model of transformational music theory.
This branch of music theory was formally stablished
by David Lewin (1987; 1993) and privileges the
analysis of the way musical objects transform over
time instead of focusing on their intrinsic features. As
previously defined, the aforementioned gluing self-
assembly process of the Tonnetz unfolds along three
different directions which are respectively orthogonal
to the three linear directions of individual pitches.
Three different transformations (those that generate
the space) relate each triangle (i.e., each triad) with
each contiguous neighbour. As the standard Tonnetz
is a cyclic and connected space (the aforementioned
torus), any pair of triangles can be related by means
of a finite series of combinations of these only three
transformations generating the space.
As highlighted above, how music evolves over
time is a key issue in transformational music theory.
Consequently, these kinds of transformations have
been sometimes described as metaphors of motion by
music theorists (Attas, 2009). Musical software like
Tonnetz allows to perceptually reify this metaphor,
and therefore to observe and potentially describe the
way a user conceives them.
5.2 Adapting Tonnetz for Empirical
Psychology Experiences
We are currently developing a variant of the standard
Tonnetz, in order to collect quantitative and
qualitative data for discussing the cognitive features
of human interaction with its environment. Several
chord sequences will be submitted to listeners of
different expertise, in the double format of sounds and
coloured patterns. All these sequences are
parsimonious (i.e. any pair of contiguous triads share
two of their three respective pitches), but the last triad
does not necessarily follow a parsimonious
CSME 2021 - 2nd International Special Session on Computer Supported Music Education
686

movement, as it happens for instance in the sequence
of Figure 13. There, pitch names on the vertices will
be erased to avoid potential bias, and the first six
chords are associated with red (for major chords) and
blue triangles (for minor chords). When the last chord
sounds, six new triangles are illuminated in a third
colour (yellow). Participants are asked to choose,
according to their subjective intuition, the yellow
triangle that fits best with the sound stimulus. The
task will be presented twice: for the first time, the
participant is unaware of what the Tonnetz is, whereas
the second attempt is performed after a short video
tutorial. The device stores, for each sequence, the
user’s response time and the selected triangle
matching with its triad for a quantitative comparison
with the correct one. In addition, a follow-on
questionnaire will be aimed at qualitatively grasping
the mental strategies brought into play when
elucidating the answer.
Figure 13: Top: A musical sequence among those planned
for the cognitive experiences with our adaptation of
Tonnetz. Bottom: Partial screenshot when executing the
sequence. We provide the pitch names for a better
understanding of this figure, although they will not be
shown during the tests.
We currently test the viability of the protocol with
a few individuals. Our goal is to run it with different
populations. First, we are going to compare subjects
whose cognitive styles are supposed to be very
contrasting from each other. Following the E-S theory
(Baron-Cohen, Knickmeyer, and Belmonte, 2005),
we may distinguish between “the capacity to respond
to feeling states of other individuals” (empathizing
cognitive style) and the “capacity to respond to
regularities of objects and events” (systemizing
cognitive style). The E-S theory has been applied to
the musical domain, (Kreutz, Schubert, and Mitchel,
2008) leading to the development of music
empathizing (ME) and music systemizing (MS)
scales as emerging from principal component
analysis procedures. Questions aimed at distinguish
between the two groups concerned thoughts about the
emotional state of the composer or the performers
when listening to the music, the importance ascribed
to physics and acoustics of musical instruments,
music structure, or the different layers of instruments
and voices.
In our study, we are going adapt the ME-MS
scales to the participants’ mother languages (Schubert
et al., 2014) for a population of trained musicians and
scientific professionals to explore some potential
specificities in achieving a “mathemusical” goal.
While no significant difference between these groups
is awaited at a first stage without training, we expect
to disclose a number of correlations between the
preferred cognitive style and the amount and
specificity of the improvements, after some training
at a second stage. In a follow-on experiment, a group
of university students will be involved, adhering to a
very similar protocol. In the future, we plan to
consider the dual representation of the Tonnetz, as
well as musical sequences related to non-standard
Tonnetze or even more general related structures
(Tymoczko, 2012).
6 CONCLUSIONS
In this paper we have shown how geometry-based and
interactive web environments such as Tonnetz can
be useful for supporting “mathemusical” learning and
research activities. Within the larger SMIR project,
the main goal was to develop a dissemination plan
through several “mathemusical” workshops and
exhibitions, suitable for pedagogical applications.
Our activities primarily targeted high-school and
university students, but were also conceived for larger
audiences.
Besides this outreach achievement, the SMIR
project disclosed new interesting research questions
belonging to the areas of psychology and cognition.
These questions are currently addressed by the
ProAppMaMu project, focusing on how the more
complex geometrical representations implemented in
Tonnetz are processed during an active listening. In
order to tackle this cognitive component of the SMIR
project, we are adapting this web environment by
integrating a series of perceptual tests which are
aimed at better understanding how these geometrical
The Tonnetz Environment: A Web Platform for Computer-aided “Mathemusical” Learning and Research
687

representations are processed by the listeners. These
tests will start by observing small populations with
different musical and scientific skills, but will soon be
generalized to larger groups. Our experimental
approach may hopefully shed some light on the way
in which some geometrical models of music theory
could be used to reinforce educational strategies, even
those beyond music education. They will surely
enhance existing learning techniques within the
exciting context of a musically driven mathematical
education.
ACKNOWLEDGEMENTS
This research has been partially carried on within the
ProAppMaMu project that receives financial support
from the CNRS through the MITI interdisciplinary
programs. In addition José L. Besada is currently
supported by the Atracción del talento investigador
grant (ref. 2019-T2/HUM-14477) from the Madrid
region, and Corentin Guichaoua by the European
Union’s Horizon 2020 research and innovation
program (ref. 788960) under the ERC ADG project
COSMOS.
REFERENCES
Agon C., Andreatta M., Atif J., Bloch I., Mascarade P.,
2018. Musical Descriptions Based on Formal Concept
Analysis and Mathematical Morphology. In Graph-
Based Representation and Reasoning: Proceedings of
the 23
rd
ICCS 2018. P. Chapman, D. Endres, N.
Pernelle, eds. (Cham: Springer), 105-119.
Andreatta, M., 2015. Tiling Canons as a Key to
Approaching Open Mathematical Conjectures? In
Mathemusical Conversations: Mathematics and
Computation in Music Performance and Composition.
J. B. L. Smith, E. Chew, G. Assayag, eds. (Singapore:
World Scientific), 86-104.
Andreatta M., Bardez, J.-M., Rahn, J., (eds.), 2008. Around
Set Theory: A French/American Musicological
Meeting. Sampzon: Delatour France - IRCAM Centre
Pompidou.
Attas, R., 2009. Metaphors in Motion: Agents and
Representation in Transformational Analysis. Music
Theory Online 15(1). https://mtosmt.org/issues/mto.09.
15.1/mto.09.15.1.attas.html.
Baron-Cohen, S., Knickmeyer, R. C., Belmonte, M. K.,
2005. Sex Differences in the Brain: Implications for
Explaining Autism. Science 310, 819-823.
Bayette, C., 2019. Mathémusique: Introduction au
théorème de l’hexacorde. Images des Mathématiques
[outreach website of the CNRS]. https://images.math.
cnrs.fr/Mathemusique-Introduction-au-theoreme-de-l-
hexacorde.html?lang=fr.
Besada, J. L., Barthel-Calvet, A.-S., Pagán Cánovas, C.,
2021. Gearing Time Toward Musical Creativity:
Conceptual Integration and Material Anchoring in
Xenakis’s Psappha. Frontiers in Psychology 11:
611316. doi: 10.3389/fpsyg.2020.611316.
Besada, J. L., Pagán Cánovas, C., 2020. Timelines in
Spectral Composition: A Cognitive Approach to
Musical Creativity. Organised Sound 25(2), 142-155.
Bigo, L., Andreatta, M., 2016. Topological Structures in
Computer-Aided Music Analysis. In Computational
Music Analysis. D. Meredith, ed. (Cham: Springer), 57-
80.
Bigo L., Andreatta, M., 2019. Filtration of Pitch-Class Sets
Complexes. In Mathematics and Computation in
Music: 7
th
International Conference MCM 2019. M.
Montiel, F. Gómez-Martín, O. A. Agustín-Aquino, eds.
(Cham: Springer), 213-226.
Bigo, L., Andreatta, M., Giavitto, J.-L., Michel, O., Spicher,
A., 2013. Computation and Visualization of Musical
Structures in Chord-based Simplicial Complexes. In
Mathematics and Computation in Music: 4
th
International Conference MCM 2013. J. Yust, J. Wild,
J. A. Burgoyne, eds. (Cham: Springer), 38-51.
Bigo, L., Ghisi, D., Spicher, A., Andreatta, M., 2014.
Spatial Transformations in Simplicial Chord Spaces. In
Proceedings of ICMC|SMC 2014. A. Georgaki, G.
Kouroupetroglou, eds. (National and Kapodistrian
University of Athens), 1112-1119.
Bisesi, E., 2017. Measuring and Modelling Perceived
Distance Among Collections in Post-Tonal Music:
Music Theory Meets Music Psychology. Proceedings
of EuroMAC9. https://euromac2017.unistra.fr/wp-
content/uploads/2017/04/Ext-Bisesi-Erica.pdf
Blau, S. K., 1999. The Hexacordal Theorem: A
Mathematical Look at Interval Relations in Twelve-
Tone Compositions. Mathematics Magazine 72(4),
310-313.
Cannas, S., Andreatta, M., 2018. A Generalized Dual of the
Tonnetz for Seventh Chords: Mathematical,
Computational and Compositional Aspects. In
Proceedings of Bridges 2018: Mathematics, Art, Music,
Architecture, Education, Culture. E. Torres et al., eds.
(Phoenix: Tesellations), 301-308.
Catanzaro, M. J., 2011. Generalized Tonnetze. Journal of
Mathematics and Music 5(2), 117-139.
Conway, C. M. (ed.), 2020. Models of Qualitative
Research: An Oxford Handbook of Qualitative
Research in American Music Education (vol. 3). New
York: Oxford University Press.
Douthett, J., Steinbach, P., 1998. Parsimonious Graphs: A
Study in Parsimony, Contextual Transformations, and
Modes of Limited Transposition. Journal of Music
Theory 42(2), 241-263.
Gollin, E., Rehding, A. (eds.), 2010. The Oxford Handbook
of Neo-Riemannian Music Theories. New York: Oxford
University Press.
Johnson, M., 1987. The Body in the Mind: The Bodily Basis
CSME 2021 - 2nd International Special Session on Computer Supported Music Education
688

of Meaning, Imagination, and Reason. Chicago: The
University of Chicago Press.
Kreutz, G., Schubert, E., Mitchell, L. A., 2008. Cognitive
Styles of Music Listening. Music Perception 26(1), 57-
73.
Krumhansl, C. L., 1998. Perceived Triad Distance:
Evidence Supporting the Psychological Reality of Neo-
Riemannian Transformations. Journal of Music Theory
42(2), 265-281.
Leman, M., 1995. Music and Schema Theory: Cognitive
Foundations of Systematic Musicology. Berlin:
Springer.
Letailleur, A., Bisesi, E., Legrain, P., 2020. Strategies Used
by Musicians to Identify Note’s Pitch: Cognitive Bricks
and Mental Representations. Frontiers in Psychology
11: 14480. doi: 10.3389/fpsyg.2020.01480.
Lewin, D., 1987. Generalized Musical Intervals and
Transformations. New Haven: Yale University Press.
Lewin, D., 1993. Musical Form and Transformation: Four
Analytic Essays. New Haven: Yale University Press.
Mandereau J., Ghisi, D., Amiot, E., Andreatta, M., Agon,
C., 2011. Discrete Phase Retrieval in Musical
Structures. Journal of Mathematics and Music 5(2), 99-
116.
Meredith, D. (ed.), 2016. Computational Music Analysis.
Cham: Springer.
Milne, A., Holland, S., 2016. Empirically Testing Tonnetz,
Voice-Leading, and Spectral Models of Perceived
Triadic Distance. Journal of Mathematics and Music
10(1), 59-85.
Popoff A., Andreatta, M., Ehresmann, A., 2018. Relational
Poly-Klumpenhouwer Networks for Transformational
and Voice-Leading Analysis. Journal of Mathematics
and Music 12(1), 35-55.
Rogers, N., Callender, C., 2006. Judgments of Distance
Between Trichords. Proceedings of the 9
th
ICMPC. M.
Baroni et al., eds. (University of Bologna), 1686-1691.
Schubert. E., De Poli, G. Rodà, A., Canazza, S., 2014.
Music Systemisers and Music Empathisers – Do They
Rate Expressiveness of Computer Generated
Performances the Same? In Proceedings of ICMC|SMC
2014. A. Georgaki, G. Kouroupetroglou, eds. (National
and Kapodistrian University of Athens), 223-227.
Tymoczko, D., 2012. The Generalized Tonnetz. Journal of
Music Theory 56(1), 1-52.
The Tonnetz Environment: A Web Platform for Computer-aided “Mathemusical” Learning and Research
689
