Entity Resolution in Large Patent Databases: An Optimization Approach

Emiel Caron and Ekaterini Ioannou

Department of Management, Tilburg University, Tilburg, The Netherlands

Keywords:

Entity Resolution, Data Disambiguation, Data Cleaning, Data Integration, Bibliographic Databases.

Abstract:

Entity resolution in databases focuses on detecting and merging entities that refer to the same real-world

object. Collective resolution is among the most prominent mechanisms suggested to address this challenge

since the resolution decisions are not made independently, but are based on the available relationships within

the data. In this paper, we introduce a novel resolution approach that combines the essence of collective

resolution with rules and transformations among entity attributes and values. We illustrate how the approach’s

parameters are optimized based on a global optimization algorithm, i.e., simulated annealing, and explain how

this optimization is performed using a small training set. The quality of the approach is veriﬁed through an

extensive experimental evaluation with 40M real-world scientiﬁc entities from the Patstat database.

1 INTRODUCTION

Entity Resolution (ER) is a fundamental task for data

integration, cleaning, and search. It aims at detecting

entities, also referred to as instances, proﬁles, descrip-

tions, or references, that provide information related

to the same real-world objects. Such entities are then

merged together. For example, we can merge entities

together that provide information about a particular

real-world event, a location, an organization, or a per-

son.

This paper focuses on the resolution of large col-

lections of structured data. The processing combines

the essence of collective resolution with rules among

entities attributes and values. Thus, instead of just fol-

lowing relations among entities as done by traditional

collective resolution methods, use the rules related to

the particular entities. To the best of our knowledge,

this is the ﬁrst technique that investigates such a com-

bination. The method also illustrates that it is possible

to optimize the overall resolution performance by in-

corporating a global optimization algorithm by using

simulated annealing.

The introduced method starts by pre-cleaning the

entities and extracting values. Next, it constructs rules

based on these values and make use of the tf-idf algo-

rithm to compute string similarities. It then creates

clusters of entities by means of a rule-based scoring

system. Finally, it perform precision-recall analysis

using a golden set of clusters and optimizes the pa-

rameters of the algorithm.

The contributions of this paper are outlined as fol-

lows:

• We advocate a novel generic approach that in-

vestigates collectivity for resolution using rules

among attributes and values. The approach is ca-

pable to operate over collections of very large vol-

umes.

• The approach’s parameters are optimized based

on a global optimization algorithm and using a

tiny percentage of the collection instances for the

training part.

• We evaluate quality using real-world scientiﬁc

references, i.e., Patstat database with 40M in-

stances and a high number of entities describing

the same entity.

The remainder of this paper is structured as follows.

In Section 2, we brieﬂy discuss related work. Section

3 deﬁnes the problem and introduces our method for

entity resolution as well as the parameter optimiza-

tion approach. Section 4 presents and analyzes the

results of the experimental evaluation. Section 5 pro-

vides conclusions and discusses future directions.

2 RELATED WORK

During the last decades a plethora of ER techniques

have been proposed. Each of these techniques intro-

duce mechanisms to handle particular data challenges

and/or environment characteristics. As discussed in

148

Caron, E. and Ioannou, E.

Entity Resolution in Large Patent Databases: An Optimization Approach.

DOI: 10.5220/0010527501480156

In Proceedings of the 23rd International Conference on Enterprise Information Systems (ICEIS 2021) - Volume 1, pages 148-156

ISBN: 978-989-758-509-8

recent surveys Papadakis et al. (2021); Dong and Sri-

vastava (2015), the primary focus of the introduced

techniques was on collections with an increasing data

volume using pay-as-you-go mechanisms, e.g., Pa-

penbrock et al. (2015); Wang et al. (2016), or on col-

lections with unstructured data with high levels of het-

erogeneity, e.g., Papadakis et al. (2011, 2013).

Although the need for handling huge collections

of data with high levels of heterogeneity is clear, a

large portion of current applications are still using

structured data with relatively small amounts of up-

dates. Scientiﬁc collections are the most common ex-

ample used in a plethora of research publications, i.e.,

data describing publications and authors. The primary

ER challenges in such collections are related to dupli-

cates and noise present in the values of the instances.

The typical setting is having a single collection, usu-

ally of a very large size, in which a number of enti-

ties corresponds to the same real-world object. For

example, the Worldwide Patent Statistical Database

(European Patent Ofﬁce, 2019) contains 40M entities

and has a large number of entities describing the same

real-world object (i.e., around 80).

One mechanism found successful for ER focused

on rules among the entities attributes and/or values,

also known as mappings, transformations, and corre-

spondences Yan et al. (2001); Tejada et al. (2002). For

example, Active Atlas Tejada et al. (2002) starts with

a collection of generic transformations (e.g., abbrevi-

ation for transforming ”3rd” to ”third”, acronym for

transforming ”United Kingdom” to ”UK”) and learns

the weight of each transformation given a particular

application domain.

Another mechanism that was proven to be very

successful is collective resolution Rastogi et al.

(2011); Ioannou et al. (2008); Dong et al. (2005);

Kalashnikov et al. (2005). The idea here is to lever-

age the global information (i.e., collective) in order

to detect pairs with low matching similarity (likeli-

hood) and infer indirect matching relations through

relationships detected during the processing. For col-

lections with scientiﬁc data this typically means prop-

agating information between detected pairs of authors

and publications to accumulate additional evidences,

i.e., positive and negative.

In supervised ER approaches, a data set with

labelled records is used to train the learning scheme.

However, large data sets with manually labelled

records would be expensive to collect and are often

not available. For this reason, research has focused

on developing unsupervised approaches for ER.

Unsupervised approaches use similarity metrics and

clustering algorithms to ﬁnd clusters of name vari-

ants. While unsupervised approaches do not require

training data sets, they often perform less well than

supervised approaches (Levin et al., 2012). In this

paper, we therefore adopt a hybrid approach, where

we use an unsupervised approach for clustering and

improve the model result’s on limited training set,

reﬂecting a form of weak supervision.

3 OPTIMIZATION METHOD FOR

ENTITY RESOLUTION

We now introduce our approach. We ﬁrst provide

the formal description of the problem (Section 3.1),

then discuss the optimization of the parameters (Sec-

tion 3.2), and ﬁnally describe the resolution algorithm

(Section 3.3).

3.1 Problem Deﬁnition & Notation

Our optimization problem for ER is expressed in the

following notation. Consider N entities, or represen-

tations of entities, r

, ..., r

, where each entity r

has

features. For i = 1, ..., N, the entity r

has feature vec-

tor f

consisting of M features f

= ( f

(1), ..., f

(M)).

Every feature f

( j) has a domain F

, i.e. f

(1) ∈

, ..., f

(M) ∈ F

which is independent of i.

We label two entities similar if their correspond-

ing feature vectors are similar. Stated more precisely,

we deﬁne

: F

× F

−→ R

∪ {0}, (1)

such that σ

( f

(l), f

(l)) measures the similarity of

any pair ( f

(l), f

(l)) ∈ F

× F

, where i 6= j, and we

deﬁne a distance function

d( f

(l), f

(l)) =

( f

(l), f

(l))

The degree to which r

and r

are different is presented

in the vector S:

S(r

, r

) = (d( f

, f

), d( f

, f

), ..., d( f

, f

)).

To obtain a similarity score as a single number, a

NxN matrix S is deﬁned with elements s

i j

and weight

vector w = (w

, ..., w

i j

∑

k=1

· d( f

(k), f

(k)),

where w

≥ 0, i 6= j, and

∑

k=1

= 1.

(2)

Entities that are similar, are grouped into sets, or clus-

ters, in the following way. Suppose we have Q sets

Entity Resolution in Large Patent Databases: An Optimization Approach

149

, Σ

, . . . , Σ

, and have deﬁned an initial threshold δ,

then

∪

p=1

= {r

, . . . , r

} (3)

and

∈ Σ

, r

∈ Σ

implies d

i j

≤ δ, i 6= j (4)

unless

= 1. The sets Σ

, . . . , Σ

are not necessar-

ily disjoint but are chosen to be maximal, i.e., we only

consider solution of (3) and (4) that have the follow-

ing property:

∀

r∈Σ

d(r

, r) ≥ δ =⇒ r

∈ Σ. (5)

If we deﬁne a undirected graph with vertices r

and r

an edge between r

and r

, and if d(r

, r

) ≥ δ then the

sets Σ

, . . . , Σ

, satisfying (3), (4), and (5) are deter-

mined with algorithms that compute the graph’s con-

nected components (Bondy and Murty, 1976) or max-

imal cliques (Bron and Kerbosch, 1973). Note that

the solution depends on w and δ and is not unique but

depends on the order of merging, i.e. selection of r

The weights w and δ are chosen such that there is an

optimal match with a test ‘golden sample’ H of sets

∆

, ∆

, . . . , ∆

. The golden sample H is a test sample

with veriﬁed sets of entities.

The method’s performance is evaluated using pre-

cision and recall analysis. The F1-score is the har-

monic mean of precision and recall (Fawcett, 2006).

Since the objective is to obtain sets with both high

precision and high recall, we maximize the F1-score.

Therefore we select the parameters w = (w

, ..., w

)

and δ in such a way that

∗

, δ

∗

= argmax

w,δ

L(w, δ) (6)

where our objective function L(w, δ) is the total aver-

age F1-score of the optimal match of H with L. Opti-

mizing the method’s parameters is done using a simu-

lated annealing algorithm (Xiang et al., 1997), which

is discussed next.

3.2 Optimization

In Eq. (6) the objective function is nonlinear and

yields many local optima. The number of local op-

tima typically increases exponentially as the number

of variables increases (Erber and Hockney (1995)),

here represented by w, δ. For this reason, the opti-

mization problem cannot be solved straightforwardly

with linear programming, and a global optimization

method is needed such as, the simulated annealing al-

gorithm, in order to ﬁnd a global optimum, instead of

getting trapped in one of the many local optima that

might appear.

Maximizing the F1-score with respect to w, δ in

Eq. (6) is a combinatorial optimization problem. Re-

search in combinatorial optimization focuses on de-

veloping efﬁcient techniques to minimize or maxi-

mize a function of many independent variables. Since

solving such optimization problems exactly would re-

quire a large amount of computational power, heuris-

tic methods are typically used to approximate optimal

solution. Heuristic methods are typically based on a

iterative improvement strategy. That is, the system

starts in a known conﬁguration of the variables. Then

some rearrangement operation is applied until a con-

ﬁguration is found that yields a better value of the ob-

jective function. This conﬁguration then becomes the

new conﬁguration of the system and this process is re-

peated until no further improvements are found. Since

this method only accepts new conﬁgurations that im-

prove the objective function, the system is likely to

be trapped in a local optima. This is where simulated

annealing plays its part in the method.

The simulated annealing algorithm is inspired by

techniques of statistical mechanics which describe the

behavior of physical systems with many degrees of

freedom. The simulated annealing process starts by

optimizing the system at a high temperature such that

rearrangements of parameters causing large changes

in the objective function are made. The “tempera-

ture”, or in general the control parameter, is then low-

ered in slow stages until the system freezes and no

more changes occur. This cooling process ensures

that smaller changes in the objective functions are

made at lower temperatures. The probability of ac-

cepting a conﬁguration that leads to a worse solu-

tion is lowered as the temperature decreases (Kirk-

patrick et al., 1983). To optimize Eq. (6) the

dual annealing() function of the SciPy library in

Python (SciPy.org, 2021) is used. This implemen-

tation is derived from the research of Xiang et al.

(1997).

3.3 Resolution Algorithm

In this section the optimization problem is captured in

a practical general method for ER. This method is in-

spired by (Caron and Eck, 2014; Caron and Daniels,

2016). An overview of the method and its main steps

is presented in Figure 1. The method’s inputs are N

entities with features f

, i.e. the raw data related to an

ER-problem, and a golden sample H. The method’s

output is a set of parameters w

∗

, δ

∗

that produce opti-

mized sets Σ

, ..., Σ

, that represent clusters of name

variants.

ICEIS 2021 - 23rd International Conference on Enterprise Information Systems

150

Figure 1: Graphical overview of the ER method.

The method consists of ﬁve generic steps:

1. Pre-processing;

2. Filtering;

3. Rule-based scoring and Clustering;

4. Post-processing;

5. Optimization.

In the method ﬁrst steps 1 − 4 are executed in succes-

sion on the sample data, after that equation (6) is op-

timized in step 5. Therefore, steps 3 − 5 are executed

in iteration until the total F1-score is maximized. Af-

ter the ﬁnal iteration the parameters w

∗

, δ

∗

are ob-

tained. With these parameters the steps 1 − 4 are ap-

plied again on the whole data set to disambiguate all

records. This ﬁnal part is typically executed ofﬂine.

In the remainder of this section we describe the steps

in a concise way to give overview of general tasks

within each step. Typically, these tasks need to be

conﬁgured for the practical ER-problem at hand, e.g.

company name disambiguation, (author) name reso-

lution, or the cleaning of scientiﬁc references, and so

on.

(1) Pre-processing. The method starts by pre-

processing the data. During this step the entities N

in raw data are pre-cleaned and harmonized to re-

duce basic variability in the data on the record level.

In addition, the set of features M is completed, with

additional descriptive labels by using techniques like

regular expressions combined with match and replace

actions. Finally, the feature set is evaluated for cor-

rectness.

(2) Filtering. The feature set M is the input for

this step. Here rules are based on (combinations of)

the features of the entities, and often combined with

string similarity measures, e.g. the tf-idf algorithm

(Salton and Buckley, 1988),to start ﬁnding similar

pairs of entities. With the rule set, i.e. the input for the

distance function, similarities are computed between

entities using Eq. (1). By constructing rules based on

the features, ‘proof’ is collected for the similarity be-

tween records and based on that candidate entity pairs

are created. The output of this step is a pool of can-

didate pairs for further evaluation, where pairs that do

not match are ﬁltered out.

(3) Rule-based scoring and clustering. In this

step, for the set of candidate pairs, initial weights w

are assigned to the rules based on ’the strength of each

rule’, to determine Eq. (2). Typically, the strength of

rules are ﬁrst based on domain knowledge, after that

the weights are optimized in iteration in step 5. Fur-

thermore, the total score, i.e. the combined weights,

for every pair is stored in a dataframe and compared

with an initial threshold δ

to obtain the sets in Eq.

(3). The clusters of name variants are now deter-

mined with the connected-components or the maxi-

mal cliques algorithm.

(4) Post-processing. In this step, entities for which

no duplicates are identiﬁed in the previous step are

assigned to new single-record clusters.

(5) Optimization. In this step, the sets are eval-

uated on the golden sample H using precision and

recall analysis. The parameters w, δ are adjusted to

achieve higher values in precision and recall. Using

simulated annealing (Xiang et al., 1997) we obtain the

optimal parameters w

∗

, δ

∗

. Here the average F1-score

over all sets is used, i.e. the harmonic mean of the pre-

cision and recall, as the objective function (Fawcett,

2006) deﬁned in Eq. (6).

4 CASE STUDY EVALUATION

We now present the results of our experimental eval-

uation. The focus was on investigating the quality

of return results as well as the effects of the intro-

duced parameter optimization. The following para-

graphs present the evaluation settings (Section 4.1),

also illustrating the challenges of entity resolution of

the particular data collection. After that, the results of

the evaluation are analyzed (Section 4.2), followed by

the details of the implementation (Section 4.3).

4.1 Setting

For the experimental evaluation, we use the World-

wide Patent Statistical Database (Patstat) (European

Patent Ofﬁce, 2019). This is a product of the Euro-

pean Patent Ofﬁce designed to assist in statistical re-

search into patent information. One of the available

tables, namely TLS214, holds information on scien-

tiﬁc references that are cited by patents. These refer-

ences are collected from patent applications, in which

Entity Resolution in Large Patent Databases: An Optimization Approach

151

Figure 2: A sample, i.e., 20 of 80 records, matching the exact title “A relational model of data for large shared data banks”.

patent applicants reference scientiﬁc papers and pro-

ceedings to acknowledge the contribution of other

writers and researchers to their work.

In the 2019 Spring Edition of Patstat, the TLS214

table contained a bit more than 40 million records

with scientiﬁc references. The particular table is an

important point of reference for researchers that wish

to study the connection between science and technol-

ogy. The main issue of this data, in addition to the col-

lection size, is that amongst the scientiﬁc references

there are many name variants of publications caused

by missing data, inconsistent input convention, differ-

ent order of items, typos, etc. These variants make the

usage and analysis of the data very difﬁcult.

To illustrate the problem with the TLS214 table,

we posed a query search for an exact title of an ar-

ticle. The query returned 80 records, however, there

may be more records referring the same real-world

object. Figure 2 illustrates the ﬁrst 20 results (i.e., en-

tities) of this query. Although every record refers to

the same real-world object they are stored in different

ways or simply duplicated. For example, in entity 11,

Codd’s initials are missing, while record 7 holds an

abbreviation of the word “Communications”. Besides

textual differences the database treats every record as

a unique entity due to the primary keys. These prob-

lems make it difﬁcult to properly retrieve information.

In order for table TLS214 to be a reliable point of

reference for research, its records need to be disam-

biguated.

Table 1: Total number of entities (i.e., records) per golden

sample GS1 and GS2.

GS1 GS2

Journal papers 17,348 11,163

Proceedings 0 1,093

Total 17,348 12,256

4.2 Result Analysis

We now discuss the experiments and results. Our op-

timization method is executed over the TLS214 table

with the 40M entities, i.e., entities. Our goal is to in-

vestigate quality and for this we used two golden sam-

ples that contain the expected matches among the en-

tities. The golden sample 1 (GS1) contains 100 clus-

ters (with 17,348 records), which refer to 100 highly

cited scientiﬁc papers, based on a top 100

. In ad-

dition, we used golden sample 2 (GS2) with in to-

tal 12,256 records, contains references to 50 unique

journal publications and 50 unique conference pro-

ceedings. Both samples are evaluated by human do-

main experts in order to incorporate the expected en-

tity matches (else referred to as clusters). Typically,

the patterns for proceedings are more difﬁcult to clean

because they often show more variation. As can be

seen in Table 1, references to journal publications oc-

cur more often than conference proceedings in Patstat.

Figure 3 gives the distribution of the number of

publication name variants per cluster in GS1. Notice

that the largest clusters contain more than 1,500 name

variants.

We ﬁrst focused on the iterative optimization part,

i.e., Step 5 of the method (Section 3.3). The method

is executed on a basic laptop with the intermediate

results stored and compared against the ground sam-

ples. As expected, the method gradually improves the

overall F1-score until this improvement is stabilized.

The latter occurs after approximately 100 hours. At

that point the simulated annealing algorithm stops,

and the ﬁnal set of parameters w

∗

, δ

∗

is obtained, and

clusters of name variants are derived that maximize

Equation 6.

Details for the top 100 highly cited scientiﬁc papers can

be found here:

https://www.nature.com/news/the-top-100-papers-1.16224

ICEIS 2021 - 23rd International Conference on Enterprise Information Systems

152

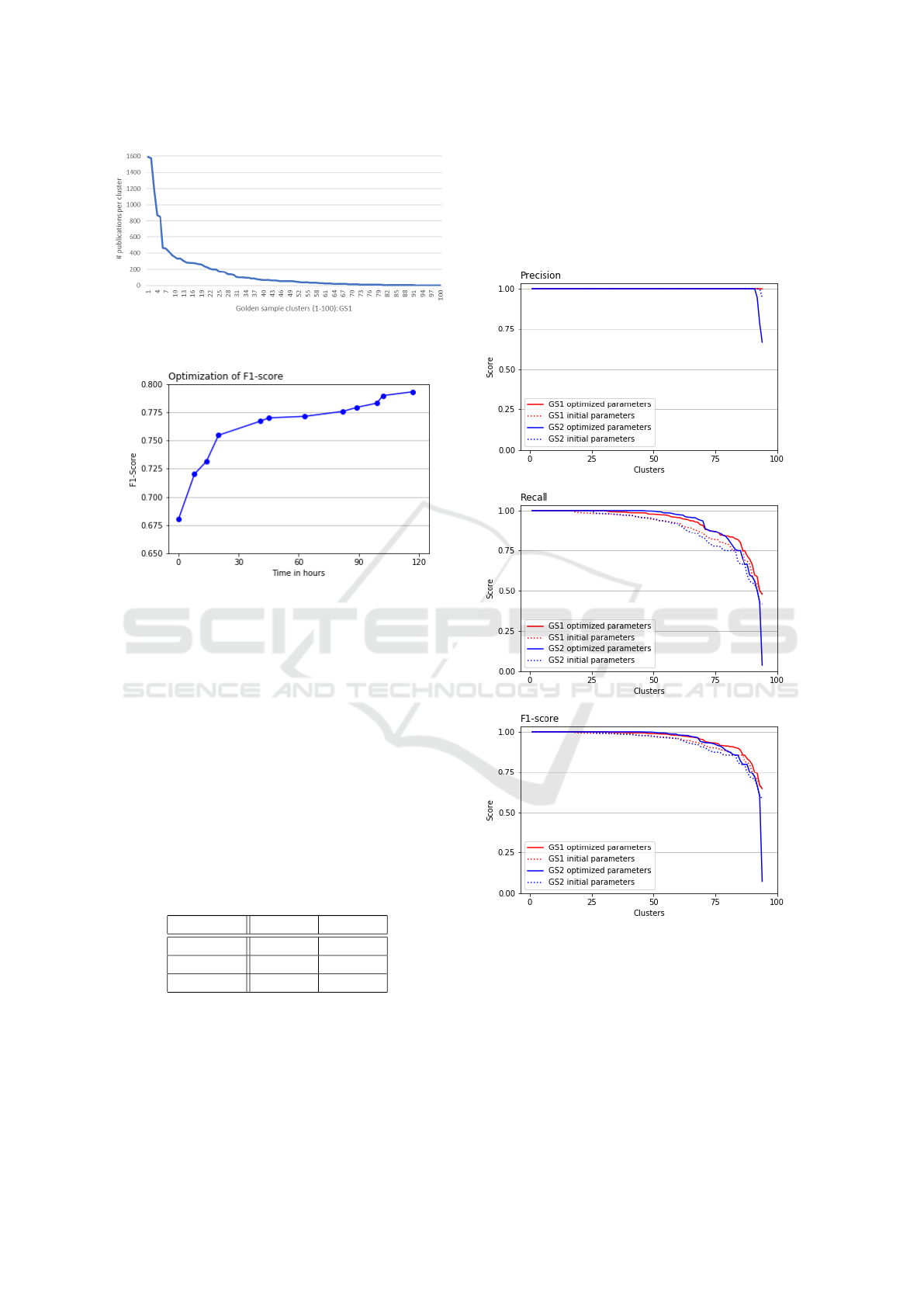
Figure 3: Distribution of the number of publication name

variants per cluster in GS1, ordered descendingly.

Figure 4: Simulated annealing increasing the F1-score over

time.

Figure 4 shows in a plot the increase of the total

average F1-score against the time in hours. The ﬁrst

point of the line is the F1-score of the initial clusters.

This plot shows that the simulated annealing algo-

rithm indeed is able to improve the F1-score and thus

our method produces better clusters compared to the

initial ones. It can be seen that the algorithm makes

large improvements to the F1-score in the beginning

and smaller improvements towards the end. This is

in line with the theory on simulated annealing Xiang

et al. (1997). The F1-score over all clusters increases

from 0.68006 to 0.79304 (≈16.5%).

Table 2 shows precision-recall-F1 analysis of the

ﬁnal clusters for both GS1 and GS2.

Table 2: Statistics of optimized clusters for GS1 and GS2.

GS1 GS2

Precision 0.99997 0.99361

Recall 0.92857 0.92154

F1-score 0.96295 0.95622

The table shows high average values for all per-

formance statistics, all ﬁgures are above 0.90. More-

over, it can be observed that the average precision is

slightly higher than the average recall. Obviously, the

clusters obtained after optimization obtain higher pre-

cision and recall values than the initial clusters before

optimization, as shown in increase of the F1-score in

Figure 4.

The plots in Figure 5 give a further break-down of

the improvement of precision-recall-F1 statistics on

the cluster level with the optimized parameters, com-

pared to initial parameters. The best clusters return

Figure 5: Distribution of the precision-recall-F1 scores of

the clusters before and after optimization for GS1 and GS2.

an average precision and recall close to 100% (Ta-

ble 2). The best cluster is deﬁned as the cluster with

the highest value for the F1 measure. The increase

in recall indicates that the new parameters are better

in creating clusters. In combination with a decrease

in clusters we notice that both golden samples have

larger dominant clusters after optimizing. If the three

best clusters of every entity are grouped in one clus-

Entity Resolution in Large Patent Databases: An Optimization Approach

153

ter the average recall of GS1 increases from 0.92857

to 0.95084 and for GS2 from 0.92154 to 0.96397. In

addition, when analyzing the clusters, we notice that

our method is slightly ‘conservative’, it values pre-

cision over recall. As a result the method is more

likely to create multiple clusters with high precision

than to create one large cluster with potential errors.

Typically, the method splits the name variants of one

golden cluster into one large dominant cluster and

multiple small clusters. The improvement in the re-

call in Figure 5 illustrates the difference in dominant

cluster size. Based on the evaluation we conclude that

with the optimized parameters the rule-based scoring

system ﬁnds more evidence to cluster publications to-

gether.

The slightly lower recall results in Table 2 for

GS2, might origin from the format of conference pro-

ceedings. Table 3 illustrates the problem with the

format of a conference reference, it shows shows an

example cluster of correctly classiﬁed scientiﬁc ref-

erences. Although every reference contains the pri-

mary article information (author, title, and year) each

record follows a different format. In some cases, the

institute name is left out, the conference abbreviated,

or contains additional information (e.g. conference

date or subtitle). Due to the additional information

within references to conference proceedings the dis-

ambiguation method is likely to produce some erro-

neous results. As a result, the rule based scoring sys-

tem does not always ﬁnd sufﬁcient evidence to cluster

all the name variants into one cluster.

Table 3: Different formats for conference proceedings

within one cluster.

Cl. Reference

51 D. Cohen et al., IP Addressing and Routing in a Local Wireless Network,

IEEE Infocom 92: Conference on Computer Communications, vol. 2,

New York (US), pp. 626 632

51 Daniel Cohen, Jonathan B. Postel, and Raphael Rom, Addressing and

Routing in a Local Wireless Network, IEEE INFOCOM 1992, p. 5A.3.1-7

51 Cohen et al., ’IP addressing and routing in a local wireless network’

One World Through Comminications. Florence, May 4-8, 1992, Proceedings

of the conference on Computer Communications (INFOCOM), New York,

IEEE, US, vol. 2, Conf. 11, May 4, 1992, pp. 626632m XP010062192,

ISBN: 0/7803-0602-3

51 Danny Cohen et al.; ’IP Addressing and Routing in a Local Wireless

Network’; One World Through Communications. Florence, May 4-8, 1992,

Proceedings of the Conference in Computer Communications (Infocom),

New York IEEE, US, vol. 2 Cof. 11, May 4, 1992

51 IP Addressing & Routing in a Local Wireless Network, Cohen et al,

IEEE 92, pp. 626 632

. . . . . .

4.3 Implementation

The resolution algorithm is implemented in the

Python programming language. The code

is struc-

tured in the following parts:

https://emielcaron.nl/wp-content/uploads/2020/05/

entity resolution optimization code.7z

• Pre-processing and ﬁltering:

connection.py and rules.py;

• Rule-based scoring-clustering:

rule construction.py,

string matching using tfidf.py,

clustering.py, and evaluation.py;

• Optimization:

find clusters.py and optimize.py.

In the example case of the Patstat table with am-

biguous scientiﬁc references, the entities r

, . . . , r

are found in the records of the table. The features of

the entities are extracted bibliographic meta informa-

tion, such as: publication title and year, author names,

various journal information, and so on. Eq. 1 of the

method refers to the rules that are developed. These

rules provide evidence that two records are similar. In

order to compute the string similarities for the rules

we use an efﬁcient implementation of tf-idf in Python.

The scores that are assigned to the rules correspond to

weight vector w in Eq. 2. The clustering of records

is done using the connected components algorithm

and results in the sets Σ

, . . . , Σ

as described in the

method. Speciﬁcally, the method find clusters()

from the script find clusters.py, implements the

ER method and computes the total F1-score. Its input

parameters are a conﬁguration of variables (w, δ) and

a table containing feature vectors. We use this method

as our objective function for the dual annealing()

method described in the script optimize.py. In this

way we obtain the optimal conﬁguration of the pa-

rameters in Eq. 6.

5 CONCLUSIONS

This paper explores a novel approach for performing

ER over large collections of data using a combination

of collective resolution with rules between entity at-

tributes and values. The approach uses simulated an-

nealing algorithm to optimize the related parameters.

As illustrated by the evaluation on the cleaning of sci-

entiﬁc references in the Patstat database, the intro-

duced optimization ER approach achieves high effec-

tiveness without requiring a large training set, resem-

bling approaches in weak supervised learning. To op-

timize the method’s parameters, the overall F1-score,

that is captured in the non-linear objective function, is

maximized over a limited golden set of clusters. After

the optimization, the obtained parameters are used to

disambiguate the whole data set.

In the case study, the method is applied to the

cleaning of scientiﬁc references, e.g. journal publica-

tions and proceedings, and create sets of records that

ICEIS 2021 - 23rd International Conference on Enterprise Information Systems

154

point to the same bibliographic entity. The method

begins by pre-cleaning the records and extracting bib-

liographic labels. Subsequently, rules are developed

based on the labels combined with string similarity

measures, and clusters are created by a rule-based

scoring system. Lastly, precision-recall analysis is

performed using a golden set of clusters, to optimize

the rule weights and thresholds. The results demon-

strate that it is feasible to optimize the overall F1-

score of disambiguation method using a global opti-

mization algorithm, and obtain the best parameters to

disambiguate the whole database of scientiﬁc refer-

ence. By changing the rules, the method can directly

be applied on on similar ER-problems. Therefore, the

method has a generic perspective.

In future research, several directions might be ex-

plored to obtain the optimal conﬁguration for the

method. Firstly, our method can be analyzed on other

datasets for ER, to study whether the results are sta-

ble and to compare the evaluations. Secondly, this

work revealed additional challenges worth investigat-

ing with respect to the incorporated rules. A possi-

ble future direction is to check the algorithm’s be-

haviour when increasing the number of used rules,

and another direction is moving towards rules that can

evolve over time. Thirdly, more information is nec-

essary about the best clustering algorithm applied to

merge similar name variants, e.g. an in-depth com-

parison between the connected components and max-

clique algorithm. Fourthly, alternative optimization

techniques might be used that produce similar or even

better results in terms of efﬁciency and/or effective-

ness. A comparison between simulated annealing,

Tabu search, and a genetic algorithm is therefore en-

visaged.

ACKNOWLEDGEMENTS

We kindly acknowledge Wen Xin Lin, Colin de

Ruiter, Mark Nijland, and Prof. Dr. H.A.M. Daniels

for their contributions to this work.

REFERENCES

Bondy, J. A. and Murty, U. S. R. (1976). Graph theory with

applications, volume 290. Macmillan London.

Bron, C. and Kerbosch, J. (1973). Algorithm 457: Finding

all cliques of an undirected graph. Communications of

the ACM, 16:48 – 50.

Caron, E. and Daniels, H. (2016). Identiﬁcation of organiza-

tion name variants in large databases using rule-based

scoring and clustering - with a case study on the web

of science database. In ICEIS, pages 182–187.

Caron, E. and Eck, N.-J. V. (2014). Large scale author name

disambiguation using rule-based scoring and cluster-

ing. In Proceedings of the Science and Technology

Indicators Conference, pages 79–86. Universiteit Lei-

den.

Dong, X., Halevy, A., and Madhavan, J. (2005). Refer-

ence reconciliation in complex information spaces. In

Ozcan, F., editor, SIGMOD, pages 85–96. ACM.

Dong, X. L. and Srivastava, D. (2015). Big Data Integra-

tion. Synthesis Lectures on Data Management. Mor-

gan & Claypool Publishers.

Erber, T. and Hockney, G. (1995). Comment on “method

of constrained global optimization”. Physical review

letters, 74(8):1482.

European Patent Ofﬁce (2019). Data Catalog - PATSTAT

Global, 2019 autumn edition edition.

Fawcett, T. (2006). An introduction to roc analysis. Pattern

recognition letters, 27(8):861–874.

Ioannou, E., Nieder

ee, C., and Nejdl, W. (2008). Prob-

abilistic entity linkage for heterogeneous informa-

tion spaces. In Bellahsene, Z. and L

eonard, M.,

editors, Advanced Information Systems Engineering,

20th International Conference, CAiSE 2008, Montpel-

lier, France, June 16-20, 2008, Proceedings, volume

5074 of Lecture Notes in Computer Science, pages

556–570. Springer.

Kalashnikov, D., Mehrotra, S., and Chen, Z. (2005). Ex-

ploiting relationships for domain-independent data

cleaning. In Kargupta, H., Srivastava, J., Kamath,

C., and Goodman, A., editors, SDM, pages 262–273.

SIAM.

Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (1983).

Optimization by simulated annealing. science,

220(4598):671–680.

Levin, M., Krawczyk, S., Bethard, S., and Jurafsky,

D. (2012). Citation-based bootstrapping for large-

scale author disambiguation. Journal of the Ameri-

can Society for Information Science and Technology,

63(5):1030–1047.

Papadakis, G., Ioannou, E., Nieder

ee, C., Palpanas, T.,

and Nejdl, W. (2011). Eliminating the redundancy in

blocking-based entity resolution methods. In Newton,

G., Wright, M., and Cassel, L., editors, JCDL, pages

85–94. ACM.

Papadakis, G., Ioannou, E., Palpanas, T., Nieder

ee, C.,

and Nejdl, W. (2013). A blocking framework for

entity resolution in highly heterogeneous information

spaces. TKDE, 25(12):2665–2682.

Papadakis, G., Ioannou, E., Thanos, E., and Palpanas, T.

(2021). The Four Generations of Entity Resolution.

Synthesis Lectures on Data Management. Morgan &

Claypool Publishers.

Papenbrock, T., Heise, A., and Naumann, F. (2015). Pro-

gressive duplicate detection. TKDE, 27(5):1316–

1329.

Rastogi, V., Dalvi, N. N., and Garofalakis, M. N. (2011).

Large-scale collective entity matching. Proc. VLDB

Endow., 4(4):208–218.

Salton, G. and Buckley, C. (1988). Term-weighting ap-

Entity Resolution in Large Patent Databases: An Optimization Approach

155

proaches in automatic text retrieval. Information Pro-

cessing & Management, 24(5):513 – 523.

SciPy.org (2021). Scipy.optimize package with

dual annealing() function.

Tejada, S., Knoblock, C., and Minton, S. (2002). Learning

domain-independent string transformation weights for

high accuracy object identiﬁcation. In SIGKDD,

pages 350–359. ACM.

Wang, Q., Cui, M., and Liang, H. (2016). Semantic-aware

blocking for entity resolution. IEEE Trans. Knowl.

Data Eng., 28(1):166–180.

Xiang, Y., Sun, D., Fan, W., and Gong, X. (1997). General-

ized simulated annealing algorithm and its application

to the thomson model. Physics Letters A, 233(3):216–

220.

Yan, L., Miller, R., Haas, L., and Fagin, R. (2001). Data-

driven understanding and reﬁnement of schema map-

pings. In Mehrotra, S. and Sellis, T., editors, SIG-

MOD, pages 485–496. ACM.

ICEIS 2021 - 23rd International Conference on Enterprise Information Systems

156