
A Minimal Snap Extension to Improve the Treatment of Integer
Data: A Constructionist Approach
Maria Cristina Carrisi
a
Dipartimento di Matematica e Informatica, Università degli Studi di Cagliari, Via Ospedale 72, Cagliari, Italy
Keywords: Constructionism, Computational Pedagogy, Visual Programming, Numerical Sets, Arithmetic Operations.
Abstract: Block based programming environments are a fundamental resource in introducing students to coding, an
activity that has been proven to be useful in the development of competences laying in the field of mathematics.
Unfortunately, it has been recently shown that Scratch, the most famous and diffused among those languages,
presents an important lack in the treatment of Integer data: it does not provide easy and intuitive instruments
to face problems dealing with the division with remainder. This conflicts with Scratch’s aim and could also
bring students to create misconceptions about the division operation. For this reason, a minimal Snap
extension will be here proposed, which overcomes this problem by creating a block environment more
pertinent from a mathematical perspective.
1 INTRODUCTION
Constructionism (Harel and Papert, 1991), a learning
theory based on constructivism (Kelly, 1955; Piaget
and Inhelder, 1969), focuses on learners’ experience.
Students learn from everyday experiences or from
activities appropriately built by the teacher and
reflecting on them. Teachers should start from pre-
conceptions or from the naive conceptions that
students spontaneously create by observing the
surrounding world and help them formalize or
generalize correctly.
In this pedagogical framework meaningful
activities are to be preferred like
• hands-on activities in which learners build
something (an object, a video, a computer
application, a tale) that can be experienced by
others (Harel and Papert, 1991),
• problem-solving activities based on reality tasks
(Jonassen, 1994).
Activities take place in a specific learning
environment which can be a physical place
(laboratory, museum, garden), a situation or a digital
environment. Students are free to use all the tools at
their disposal to solve the problem, without limiting
themselves to the simple repetition of a known
procedure. This means that in the design and
a
https://orcid.org/0000-0002-2837-3971
construction of learning activities, it is essential that
teachers create or use learning environments that are
not misleading and do not lead students to create
misconceptions.
If a digital environment is used, it must have a
simple interface and must be usable in an intuitive
way without any specific training.
Block programming environments lay in this
pedagogical context. Their main objective is to allow
a simple approach to computer programming:
overcoming the problem of knowing the syntax of a
given language, it is possible to focus exclusively on
the algorithm and on the resolution process.
Designed in 2007, Scratch (Resnick et al., 2009)
is the youngest and probably the most famous among
them (http://scratch.mit.edu/). It was initially
conceived to introduce children to coding, but in
recent years Scratch has proved to be a powerful
instrument also for adults who have no previous
experience in computer programming (Malan and
Leitner, 2007; Federici, 2011; Homer and Noble,
2017; Weintrop and Wilensky, 2017).
Moreover, Scratch revealed to be an environment
that allows the development of abilities laying in the
context of other subjects (see for example Federici et
al., 2019) and, in this sense, it is a powerful tool also
for teachers of disciplines that are not necessarily
technical or scientific.
Carrisi, M.
A Minimal Snap Extension to Improve the Treatment of Integer Data: A Constructionist Approach.
DOI: 10.5220/0010476103030310
In Proceedings of the 13th International Conference on Computer Supported Education (CSEDU 2021) - Volume 2, pages 303-310
ISBN: 978-989-758-502-9
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
303

What about Mathematics?
An interesting perspective (Mor and Noss, 2008)
is that coding represents the link between
mathematics and narrative. In this sense it allows to
contextualize and give meaning to mathematics and
visual environments like Scratch can empower the
narrative aspect of computer programming.
Moreover, the literature shows that there is a
significant correlation between coding activities and
the acquisition or improvement of mathematical skills
such as problem solving, modeling, reasoning (Calao
et al. 2015), but also the ability to argue to motivate
the choices made in the implementation.
Consequently, it could be thought that the use of
some features of Scratch can also help to improve the
understanding of specific mathematical contents, but,
unfortunately, the literature does not exhibit any
evidence in this regard, at least in the knowledge of
the author.
Instead, some studies show that there is an
incorrect transfer and overlap between some
mathematical concepts and the corresponding ones in
computer programming. For example, Guzdial
(Guzdial, 2018) pointed out that students show
difficulties in interpreting the correct meaning of the
‘=’ sign or the fact that, in some programming
environments, variables can change domain (type)
during the program execution. More recently (Carrisi,
2020) it has been shown that some of the most
diffused digital environments, among which Scratch,
manage Integer numbers and arithmetical operations,
in particular the division, in a different way from their
mathematical definition. This can create or reinforce
a misconception regarding the division between
Integers, especially if such environments are used in
primary school when students have not yet created a
solid understanding on numerical sets.
The present paper aims to fill this gap of Scratch,
proposing a possible extension obtained with Snap!,
with two new operators that allow to manage the
division with remainder in a more pertinent way from
a mathematical point of view. In such way an
environment is obtained in which students can move,
explore, try, as prescribed by constructivism, without
the risk of running into something that can generate
incorrect knowledge, at least as regards the division
with remainder.
The article is organized as follows: Section 2
presents an analysis of the Scratch operators from a
mathematical point of view with the aim of motivate
the necessity to introduce the new operators; In
Section 3 the new operators are described and the
advantages of their employment when solving a
problem dealing with the division with remainder are
discussed; Section 4 shows the outcomes of a first
evaluation survey conducted on first year students at
the faculty of Computer Science of the University of
Cagliari; finally, the results are discussed, outlining
limitations and recommendations for future work.
2 AN ANALYSIS OF SCRATCH
FROM A MATHEMATICAL
POINT OF VIEW
Scratch is a visual programming environment in
which graphic objects called "sprites" act on a
background called "stage". Sprites and Stage are
customizable, enhancing user engagement, and can
be controlled by programs created with predefined
blocks, joining them together to create a script. Block
shapes allow them to connect only in a few ways, thus
avoiding syntax errors. The Scratch interface is user
friendly and has a series of sections listing the blocks
belonging to the same topic. Furthermore, in each
section, the blocks are grouped by scope and each
block is named in a way that make immediately
understandable the instruction that will be performed.
An analysis of the Scratch environment with
mathematical lens highlights the presence of a series
of features that could be used to improve
mathematical knowledge, like:
• The presence of an XY grid on the stage that can
be explored through the motion of the sprites
might be used to empower students’ knowledge
about Cartesian coordinates.
• The Pen and Move blocks allow learners to
explore geometric shapes and their properties.
• The Variables blocks can be used to create and
manage variables, introducing students to algebra.
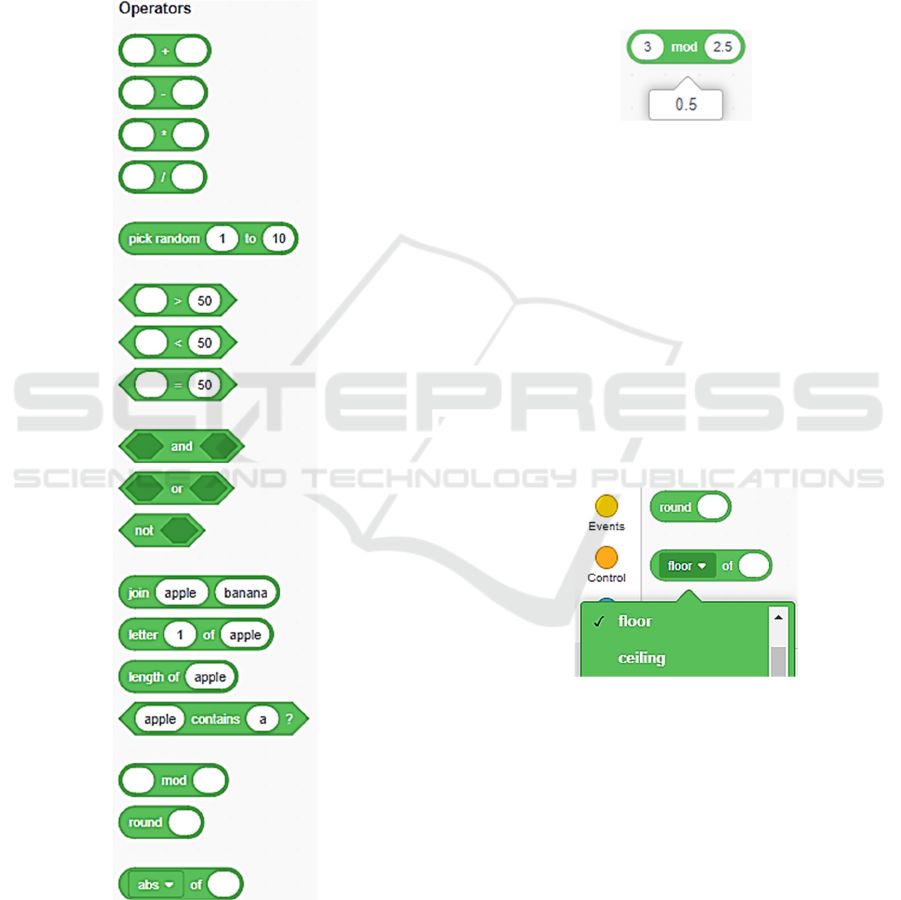
• The Operators section (see Figure 1) contains
arithmetic operators but also logical and relational
operators and mathematical functions.
However, according to Brown (Brown, 2017)
“Programming tools are not pedagogy-neutral”. The
type of instruments the programming environment
provides and the way they work “determines which
programming-related activities are easy and which
are hard, which in turn will affect how” a teacher “use
the tool to teach” and what and how students learn.
Recently, (Carrisi, 2020) Scratch has been
analysed under this perspective, particularly focusing
on variables and on the tools that allow to calculate a
division. It is important to underline that the division
is an operation defined in all numerical sets but,
despite the same name, it has different meaning and
CSEDU 2021 - 13th International Conference on Computer Supported Education
304
properties depending on the numbers it is working on.
When we consider two Integer numbers a and b,
the division, or more properly the division with
remainder, between a and b gives two Integer
numbers q (quotient) and r (remainder) such that
a=b*q+r, r is positive and lower than b.
When we move to Rational numbers the division
takes on a different meaning and it becomes an
operation that gives a unique result.
Figure 1: Scratch Operators section.
Since, for the sake of simplicity, Scratch variables
cannot be typed, numbers and arithmetic operators
are defined in the floating-point set (a subset of
Rational numbers). The division operator ‘/’ always
gives a decimal result.
The calculation of quotient and remainder of a
division between two Integer numbers is a more
difficult task.
The remainder is given by the ‘mod’ operator
which, however, works differently from its
mathematical definition, in fact it acts also on decimal
data giving a decimal result, as we can see in the
following Figure 2.
Figure 2: Scratch ‘mod’ block working on rational data.
There is no specific operator to obtain the
quotient. It could be argued that there is no need for
it because the quotient can be obtained simply by
approximation of the decimal result of the division.
Scratch provides three different operators to
approximate: ‘floor’ truncate the decimal part of the
number, ‘ceiling’ performs an upper approximation,
‘round’ behaves as ‘floor’ when the decimal part of
the number is less than 0.5 and as ‘ceiling’ otherwise.
The last is immediately visible in the Operators
section while the first two are accessible through a
dropdown menu contained in the last operator of the
section (see Figure 1 and Figure 3).
Figure 3: The ‘floor’ and ‘ceiling’ operators.
The blocks ‘mod’ and ‘round’ are grouped like the
relational operators or the logical connectives (see
Figure 1). This induces the user to think that they are
logically related and referred respectively to
remainder and quotient of an Integer division, but it
is not correct as we can see in the example reported
in the following Figure 4.
In order to obtain the correct quotient of a division
between two integer numbers (see Figure 5) it is
necessary to truncate the decimal result of the
division, by using the ‘floor’ block that, as just
stressed, is hidden in the dropdown menu and so its
use is much less intuitive.
A Minimal Snap Extension to Improve the Treatment of Integer Data: A Constructionist Approach
305
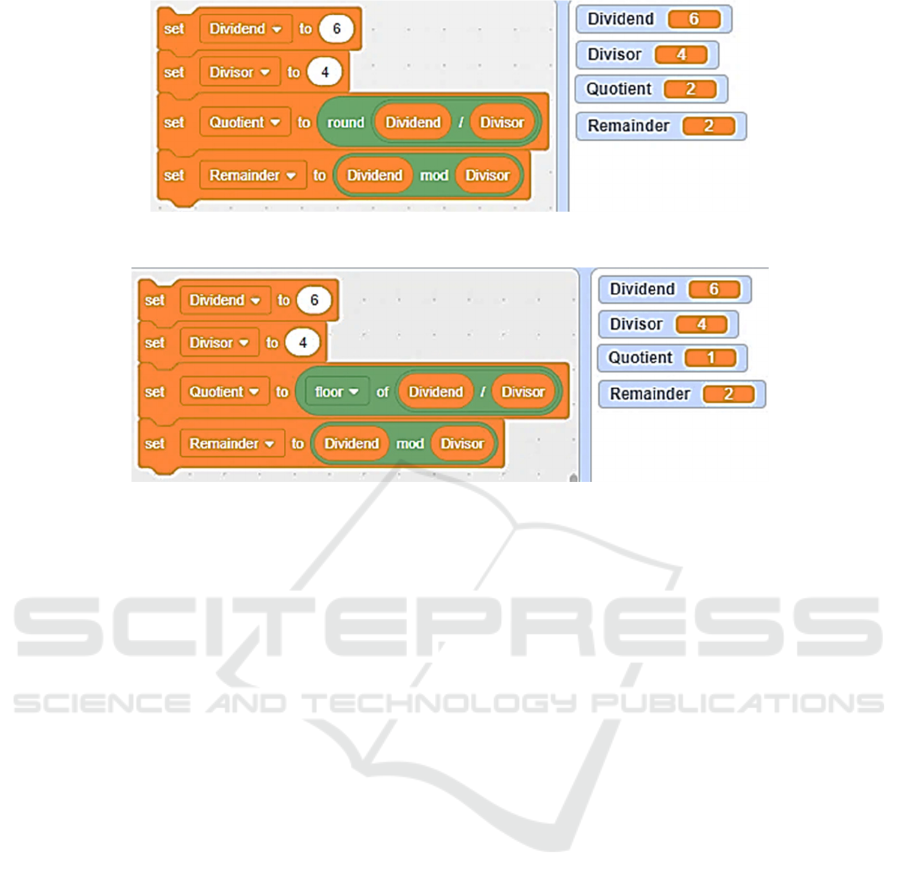
Figure 4: Incorrect use of Scratch blocks ‘mod’ and ‘round’ to calculate a division with remainder.
Figure 5: Correct use of Scratch blocks ‘mod’ and ‘floor’ to calculate a division with remainder.
The interpretation and calculation of the division
with remainder turn out to be a cumbersome, and not
at all intuitive, operation, even for how the interface
is designed.
2.1 Analysis of a Particular Problem
Let’s consider the following problem (Carrisi, 2020):
Problem: In a supermarket, the following sales
promotion is active on a certain product: if you buy
three products of the same type, only two must be paid
for. If the number of products purchased and the price
of the individual product are known, what is the total
purchase price?
The above problem can be proposed at all school
levels (see for example the Italian school curricula
MIUR, 2010; MIUR, 2013; MIUR, 2018) and can be
solved by using different methods and learning
environments.
A possibility is to come to an algebraic
formulation like the following: P = (2 * q + r) * p.
P is the final price, considering the sale
promotion. N is the number of products bought and p
is the price of the single product. q is the quotient of
the division of N by 3 and represents the quantity of
groups of three products. For each group, only two
products must be paid. r is the remainder of the
division of N by 3 and identifies the number of
products that must be paid entirely.
Otherwise, we can calculate P = (N – q) * p where
the variables have the same meaning reported above.
In this case we are subtracting the discount from the
total price. The discount amounts to the price of one
product for each group of 3 products, given by q.
In both cases it is necessary to calculate the
quotient of the division with all the difficulties
evidenced in the previous section if the chosen
learning environment is Scratch.
In Figure 6, reported in the subsequent page, we
see the Scratch implementation of the first solution
proposed.
We see that, it is necessary to do data casting to
avoid incorrect data entry (ensures that the number of
products is an Integer number) and allow the
functions to work properly. This, together with the
considerations exposed in the previous section, makes
evident that the mathematical tools under
consideration are not adequate, from a constructionist
point of view, to properly manage the operation of
division with remainder and this conflicts with
Scratch pedagogical background.
It could be said that this is not very interesting
from the point of view of teaching-learning because
the division with remainder is an operation poorly
used and that the problems in which it is necessary its
use have little application value. The literature shows
that it is not the case.
CSEDU 2021 - 13th International Conference on Computer Supported Education
306
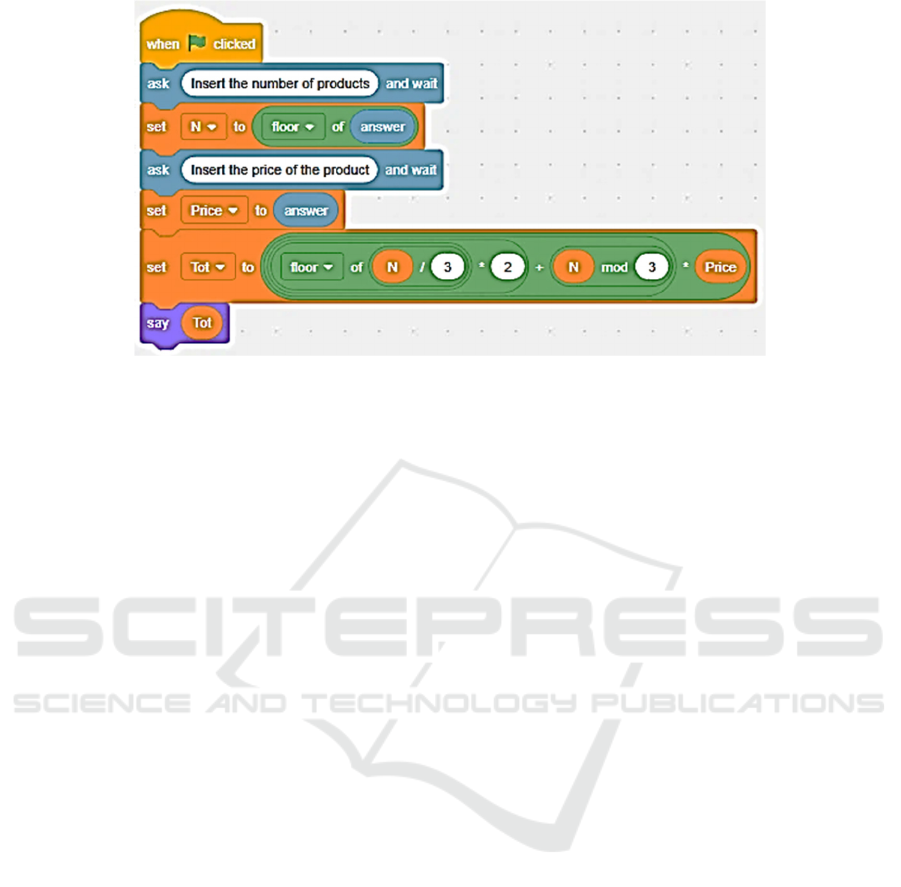
Figure 6: Scratch solution of the Problem.
In a recent paper (Dogan and Ev Cimen, 2019) the
authors pointed out that “the division is the most
difficult for students, compared to the other
operations” especially because of the different
meaning that the operation, the data and the results
may take depending on the context. They also proved
that problems dealing with the division with
remainder are difficult for children, but also for
elementary teachers, precisely because the resolution
is closely related to the interpretation and
contextualization of the problem. This means that
they are particularly appropriate from a
constructionist perspective, as they can be used to
present a wide range of reality tasks. Moreover, they
focus on problem solving procedure more than
computation, enhance the ability of analyse the
domain of data, the presence of eventual constraints,
and of interpret results, all features deemed necessary
for the mathematics of the future because they
complement computers’ “abilities” (Gravemeijer et
al., 2017).
For these reasons, it seems necessary to extend
Scratch adding new operators that make the
calculation of the division with the remainder more
intuitive and mathematically relevant for the students,
especially if they belong to primary school.
3 A SNAP! EXTENSION
Although Scratch is equipped with a large series of
instruments, at a certain time the community has felt
the necessity to extend its capability by adding or
modifying some components. Such modifications
("mods") have been possible thanks to the fact that
Scratch is an open source project and so its source
code is freely available. Mods expand the language,
adding suitable operators to manage more advanced
computational concepts ore including functionalities
like the possibility to communicate with hardware
devices (e.g. Microsoft Kinect), or to build web pages
in a simpler way (e.g. Web Blox). The first Scratch
mod is BYOB, now known as Snap! (Harvey and
Monig, 2010). It has a fundamental add-in: the
possibility to define new customized blocks,
remaining fully compatible with Scratch.
Snap! interface looks like Scratch’s one, except
for the presence of much more blocks. At the bottom
of each section, there is a grey button ‘Make a block’
that gives the opportunity to the user to create a
customized block belonging to a category already
defined or completely new. The new block may be a
command, a reporter (returns a result) or a predicate
(returns a truth value).
The behaviour of the new operators can be
implemented by using Snap! primitives (the existing
blocks) and the usual drag and drop procedure.
See the user’s manual for more details:
https://snap.berkeley.edu/snap/help/SnapManual.
pdf
With the aim to solve the problems evidenced in
the previous section, two new reporter blocks have
been created in the ‘Operators’ category (see Figure
7 in the following page).
A Minimal Snap Extension to Improve the Treatment of Integer Data: A Constructionist Approach
307

Figure 7: Overview of the Operators section with the new
elements.
The first operator, called ‘Quotient’, receives two
Integer numbers n1 and n2 and returns the quotient of
the division between n1 and n2. To prevent incorrect
data entry, the parameters n1 and n2 are cast by
truncation.
Figure 8: Implementation of the Quotient operator.
In Figure 8 we can see the implementation of the
operator while in Figure 9 it is shown how this
operator works on Integer parameter as well as on
Rational numbers.
Figure 9: Quotient operator acting on Integer data and on
Rational data.
The second operator, called ‘Remainder’ receives
two Integer numbers n1 and n2 and returns the
quotient of the division between n1 and n2. In fact, as
it can be seen in Figure 10 and similarly to the
‘Quotient’ operator the parameters n1 and n2 are cast
by truncation.
Figure 10: Implementation of the Remainder Operator.
It is clearly just an adjustment of the ‘mod’
operator but that makes the operator resistant to
incorrect data entry and adherent to its
mathematically meaning.
In building the operators we were inspired by
strongly typed programming languages like C, in
which the assignment of a decimal value to an Integer
variable produces a truncation.
The implementation of the solving algorithm for
the Problem analysed in the previous section, with the
use of the new operators becomes surely more
adherent to its algebraic formulation as we can see in
the Figure 11 in the subsequent page.
4 EVALUATION
A fist evaluation of the new operators that
investigates students’ acceptance has been carried out
in the last months of 2020.
For the reasons behind this research, the author’s
initial intention was to carry out activities with
elementary school students and then conduct a
survey. This was made impossible by the restrictions
imposed by the Covid-19 pandemic that banned the
access of external staff in schools. It was not even
possible to carry out activities remotely as pupils are
already undergoing a large number of hours of
distance teaching.
Consequently, since the purpose was to evaluate a
programming environment, it has been chosen to
involve in the survey the students of the first year at
the faculty of Computer Science of the University of
Cagliari. with whom, given their age, it has been
possible to carry out activities remotely.
Initially, the problem presented in Section 2.1 was
proposed to students and asked them to upload their
complete solution of all steps.
CSEDU 2021 - 13th International Conference on Computer Supported Education
308

Figure 11: The solution of Problem obtained with the Snap! extension.
102 students participated to this first part of the
activity: 58 of them solved the problem correctly and
giving a general solution; 9 were able to produce only
a particular solution valid in the case N multiple of 3;
35 were unable to solve the problem (see Figure 12).
Figure 12: Distribution of students responses.
In the second part of the activity, after correction
of the Problem, students were asked to implement the
algorithm in Snap! and in the modified Snap! with the
two new operators. In the end they were offered a
short questionnaire on the perceived effectiveness of
the new operators.
Figure 13: Outcomes of the evaluation survey.
37 on the 58 students that were able to solve the
problem decided to participate answering to the
following questions:
Q1: Is it natural for you to interpret division between
integers as division with remainder?
Q2: Is it natural for you to interpret the division
between integers as an approximation of a division
between real numbers?
Q3: Do you find that the new operators introduced in
Snap make it more intuitive to use the division with
the rest than in the standard version of Snap?
The results show that the satisfaction with respect
to the new operation is good. As we can see in Figure
13, the 24% declared to be absolutely satisfied by the
new operators and that they make more intuitive the
use of Snap! (at least regarding the problem they
worked on); the 16% was very satisfied; the 46%
sufficiently satisfied; no one was completely
unsatisfied and the remaining 14% express a low
satisfaction. With regard to the latter data, it is
interesting to note that students who have declared a
low satisfaction have also stated that they interpret the
division in the context of Integers with difficulty.
5 DISCUSSION AND FUTURE
WORK
The outcomes reported in the previous section put in
evidence that division with remainder problems are
hostile also for University students making technical
studies. Even if the numbers are low, this is a further
confirmation of what is present in the literature
(Dogan and Ev Cimen, 2019).
According to the introduction of the new
operators we underline that Scratch is a software
designed in a constructivist perspective, and it is built
to allow individual exploration by the student that can
find in an easy way the necessary operators to realize
the resolution algorithm for a certain problem. If the
A Minimal Snap Extension to Improve the Treatment of Integer Data: A Constructionist Approach
309

focus is on the solution process, the student should
not be forced to “bend” the operators to work in a
particular way different from the standard mode. For
this reason, it was deemed necessary to introduce a
new operator in Scratch that makes its use more
suitable for the skills possessed by primary school
students especially in the implementation of
algorithms related to problems in the context of
Integers. Although our first survey shows a high
appreciation, it is considered necessary to strengthen
the evaluation with a study conducted on primary
school students. Moreover, in this study positive
numbers have been treated. As future work, we ain to
extend the analysis also to signed number.
REFERENCES
Brown, N., 2017. Pedagogy of Programming Tools,
[Online] Https://Academiccomputing.Wordpress.Com/
2017/06/23/Pedagogy-of-Programming-Tools/
Accessed 9-3-2021.
Calao L.a., Moreno-Leòn J., Correa H.E., Robles G., 2015.
Developing Mathematical Thinking With Scratch,
Design for Teaching and Learning in a Networked
World. EC-TEL 2015. Lecture Notes in Computer
Science, Vol 9307. Springer.
Carrisi M.C., 2020. Some Considerations on the Use of
Digital Environments in Learning Numerical Sets, in
Proceedings of the 12th International Conference on
Computer Supported Education (CSEDU 2020).
Dogan Coskun, S., Ev Cimen, E., 2019. Pre-Service
Elementary Teachers’ Difficulties in Solving Realistic
Division Problems. Acta Didattica Napocensia, Vol 12
Issue 2, Pp. 183-194. DOI:10.24193/and.12.2.14 .
Federici S., 2011. a Minimal, Extensible, Drag-and-Drop
Implementation of the C Programming Language. in
Proceedings of the 2011 Conference on Information
Technology Education (SIGITE ’11) ACM, West
Point, NY, USA October 20–22 2011, Pp.191–196.
Federici S., Molinas J., Sergi E., Lussu R., Gola E., 2019.
Rapid and Easy Prototyping of Multimedia Tools for
Education. in Proceedings of the 5th World Conference
on Media and Mass Communication, Vol. 5, Issue 1,
Pp. 12-24. DOI:
Https://Doi.Org/10.17501/24246778.2019.5102
Gravemeijer, K., Stephan, M., Julie, C., Lin, F., Ohtani, M.,
2017. What Mathematics Education May Prepare
Students for the Society of the Future?. Int. J. of Sci.
and Math. Educ. Suppl 1, S105-S123.
Guzdial M., 2018. Confusion over the Forms of
Programming Problems: Mathematics/Physics
Versus CS, [Online]
Https://Computinged.Wordpress.Com/2018/02/26/Confusi
on-over-the-Forms-of-Programming-Problems-
Mathematics-Physics-Versus-Cs/. Accessed 9-3-2021.
Harel, I., Papert, S., 1991. Constructionism. Ablex
Publishing. ISBN 978-0893917869.
Harvey, B., Monig, J., 2010. Bringing 'No Ceiling' To
Scratch: Can One Language Serve Kids and Computer
Scientists? in Proceedings of Constructionism 2010.
Homer, M., Noble, J., 2017. Lessons in Combining Block-
based and Textual Programming. Journal of Visual
Languages and Sentient Systems, 3(1), Pp. 22–39.
Https://Doi.Org/10.18293/Vlss2017-007 .
Jonassen D.H., 1994. Thinking Technology, Toward a
Constructivist Design Model. Educational Technology
Vol. 34 N. 4, Pp.34-37.
Kelly G., 1955. the Psychology of Personal Constructs: a
Theory of Personality. London: Routledge.
Malan, D. J., Leitner, H. H., 2007. Scratch for Budding
Computer Scientists. in Proceedings of the 38
th
SIGCSE Technical Symposium on Computer Science
Education (SIGCSE’07), Pp. 223-227.
Ministero Dell’istruzione, Università E Ricerca, 2010. I
Regolamenti - Le Indicazioni Nazionali.
Https://Archivio.Pubblica.Istruzione.It/Riforma_Super
iori/Nuovesuperiori/Index.Html Accessed 9-3-2021.
Ministero Dell’istruzione Università E Ricerca, 2013.
Indicazioni Nazionali per Il Curricolo Della Scuola
Dell’infanzia E Del Primo Ciclo D’istruzione, Gazzetta
Ufficiale Della Repubblica Italiana, Serie Generale
N.30, 5-2-2013.
Ministero Dell’istruzione, Università E Ricerca, 2018.
Indicazioni Nazionali E Nuovi Scenari,
Https://Www.Miur.Gov.It/Documents/20182/0/Indica
zioni+Nazionali+E+Nuovi+Scenari/ Accessed 9-3-
2021
Mor, Y., Noss, R., 2008. Programming as Mathematical
Narrative. International Journal of Continuing
Engineering Education and Life-Long Learning
(IJCEELL), Vol. 18 Issue 2, Pp. 214-
233. Http://Oro.Open.Ac.Uk/30344/ .
Piaget, J., Inhelder, B. 1969. the Psychology of the Child.
New York: Basic Books.
Resnick, M., Maloney, J., Monroy-Hernández, a., Rusk, N.,
Eastmond, E., Brennan, K., Millner, a., Rosenbaum, E.,
Silver, J., Silverman, B., Kafai, Y., 2009. Scratch:
Programming for All. Communications of ACM, 11.
Http://Scratch.Mit.Edu/ .
Weintrop, D., Wilensky, U., 2017. Comparing Block-based
and Text-based Programming in High School
Computer Science Classrooms. in ACM Transactions
in Computing Education, 18, 1, Article 3.
Https://Doi.Org/10.1145/3089799.
CSEDU 2021 - 13th International Conference on Computer Supported Education
310
