Selforganisational High Efficient Stable Chaos Patterns
Bernhard Heiden
1,3 a
, Volodymyr Alieksieiev
2 b
and Bianca Tonino-Heiden
3 c
1
Industrial Engineering and Management Studiengang, University of Applied Sciences, Europastrasse 4, Villach, Austria
2
Faculty of Mechanical Engineering, Leibniz University Hannover, An der Universit
¨
at 1, Garbsen, Germany
3
Philosophy Institute, University of Graz, Heinrichstraße 26/V, Graz, Austria
Keywords:
Logistics, Witness, Mathcad, Multirobots, Selforganisation, Educational Tool, Chaos Theory, IoT
Application, Information Entropy, Stable Chaos.
Abstract:
The aim of this paper is to provide a new solution for the problem of a simple application of swarm robots, and
here the model and its simulation, which shall be later implemented in these Internet of Things (IoT) devices.
For this reason this paper describes how, swarm robots, robot-multirobots, a series of entangled robots or robot-
os, form predictable selforganisational room-time patterns, as a function of a binary sensor and a binary actor
signal interaction, in a triangular cellular automata fashion. The influence of the outer border compared to the
inner border of robot-os is investigated, to answer the question, whether and how they can be distinguished.
So this process can then be regarded as a different level border-order-entity or as a ’solidification process’
of the robot-o. By means of this, the robot-o is itself ’recognising’, as an extended self, that is identified
by the robot-o as the environment. Border as direction change of signal, hence, can be regarded as a basic
selforganisational driving force. Above described sensor actor processes can be regarded as bidirectional
ordering process, according to orgiton theory, a further development of the theory of selforganisation. Based
on the Shannon information entropy, measuring this is methodically demonstrated. Application programs and
respective patterns are given in Mathcad and Witness simulations in detail. These prepare for IoT robot-os
applications, for future research applications, especially for the open source robot-os of Elmenreich et al., that
our work refers to and builds upon.
1 INTRODUCTION
Selforganisational patterns are quite well known, but
it seems, that these become more and more relevant in
technical and cyber-physical applications like Inter-
net of Things (IoT)-devices. There are several reasons
for this. Cybernetic models have become increasingly
complex in the sense of programming on the one side,
on the other side there is the need for efficient designs
of programming in limited resources regions applica-
tions, e.g. in space missions, autonomous vehicles, or
transport-tools, and others. The limited resources are
not only part of some exotic and maybe extreme ap-
plications, but they arise also increasingly in common
applications like production environments. One rea-
son is, that the extreme situation can be understood
as solving an optimality problem of e.g. maximum
production while at the same time a lot of restric-
a
https://orcid.org/0000-0001-8324-6505
b
https://orcid.org/0000-0003-0792-3740
c
https://orcid.org/0000-0001-7648-2833
tions or system-environment conditions have to be
fulfilled. In this field of increasingly complex condi-
tions, not only not all information is available timely,
but also some information is impossible reachable or
in out of distance conditions. We all know now, as in
the current pandemic video-conferencing is becoming
widely common, the acquainted systemic problem is,
that reliant information of the ’end-point’, becomes
increasingly important, which means that the problem
has to be solved to operate safely in industrial produc-
tion, etc. out of a distant operating point.
While this may be clear for military applications,
the civilian applications are now also affected system-
ically.
We can think of this, as increasing growth of inter-
mediate relay stations between information transmit-
ter and receiver used in the path between IoT-devices.
This has been recently named by the term osmotic
manufacturing (Heiden et al., 2020), osmotic comput-
ing (Villari et al., 2016), and also as a generalisation
the osmotic paradigm. (Heiden et al., 2021a; Heiden
et al., 2021b).
Heiden, B., Alieksieiev, V. and Tonino-Heiden, B.
Selforganisational High Efficient Stable Chaos Patterns.
DOI: 10.5220/0010465502450252
In Proceedings of the 6th International Conference on Internet of Things, Big Data and Security (IoTBDS 2021), pages 245-252
ISBN: 978-989-758-504-3
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
245

As such the complexity measure of IoT-systems
becomes increasingly important. One such measure
is the Lyapunov coefficient, another the information
entropy by Shannon (Shannon and Weaver, 1963). In
this work, this measure will be used to order the in-
formation results obtained in the calculation.
The inspiration of this work is that chaotic pat-
terns can be implemented by algorithms looking just
at neighbors, which result in e.g. Sierpinski triangle
patterns (H
¨
utt, 2006).
This has lead to the idea of this work to implement
the pattern generators on IoT devices of swarm type.
That means each IoT device is similar and can imple-
ment cybernetics. One such system can then be re-
garded as a multirobots (Elmenreich et al., 2015) im-
plementation. Synonyms are robots, swarm robots or
robot-os. Robot-o refers to the term robot-orgiton, ac-
cording to the grammar rules of orgiton theory (Hei-
den and Tonino-Heiden, 2021). An orgiton is a cyber-
netic unit with elements of mass, energy and infor-
mation, and hence the robot-o denotes a single robot,
as well as a swarm, which is then a robot-o of poten-
tially higher order. On each ”length” scale a robot-o
denotes a functional unit with a specific composition.
As a consequence, the system can be used to study
chaotic patterns with robot-os or IoT-clusters in gen-
eral.
1.1 Content
This work is, after summarising the goal in section
1.2 with the basic idea of this work of tri-information
patterns, diving in section 2, into the related theoret-
ical background. In section 3 we go to the computa-
tional applications of tri-information-patterns, first in
section 3.1 to a Mathcad application, then in section
3.2 to a Witness application, and we close section 3
with an information entropy investigation in section
3.3. In section 4 we make conclusions of the compu-
tational applications and connect them to IoT appli-
cations. Finally, we give a summary and outlook in
section 5.
1.2 Goal
The goal of this work, is to motivate and give appli-
cation examples of chaotic patterns in computational
and IoT devices, designated for educational purposes,
leading to a deeper understanding of chaotic system
behaviour of cellular automata, implemented in paral-
lelised IoT-swarms, operating in stable chaos regions.
For this basic computational tools for IoT-swarm ap-
plications in general, and educational ones in special
are given.
2 TRI-INFORMATION PATTERNS
In this section we will introduce a concept used in this
paper and based on the following:
Axiom 1. Information flow is a translational infor-
mation chain. - The ”living” function can be inter-
preted as a continuous information flow.
We here regard cybernetic systems, analogously to
Wiener (Wiener, 1963), similar to living ”machines”,
or as Heinz von F
¨
orster noted, biocybernetic ma-
chines.
Axiom 2. Increasingly nested translational patterns
(autoencoders), increase potentially order and allow
for increasingly safety or an integrity informational
check.
When Axiom 2 is true, then this should also be
seen in some informational measure. Such a measure
could be the informational entropy S
i
. The Shannon
information entropy S
i
can be calculated by (1):
H
i
= S
i
= p
i
· ln(p
i
) (1)
p
i
denotes here the probability or frequency. This
measure can be in general used to measure informa-
tion content, as a consequence of its statistical prop-
erties. We will use this when looking at some bit-
information of the core translation process of the cel-
lular automata. The translation process can be re-
garded as an essential process transferring informa-
tion from one moment to the other (event horizon) or
one room to the other (cf. Figure 1). By this means,
information of one observing window in Figure 1 is
divided by ’mirroring’ borders and fulfilling, in each
window, the information balance. By this dynami-
cally information can be kept alive in an open system,
as well as be enriched by open time-rooms or room-
times of possibility.
3 SIMULATION
In the following, we give the two simulation-
programs for the tri-information chaos patterns of
the cellular automata. The translational matrix is U
(see APPENDIX - MATHCAD PROGRAMS). Eight
combinatorial possible states of three elements, or
one element and its two neighbours, are combined
uniquely by one translational configuration, which is
in our case row four in U.
The first simulation is done in Mathcad. A paral-
lelised program for general process simulation is Wit-
ness. This has the advantage to be able to simulate
each virtual IoT device, which is operating in the IoT-
swarm, separately. We show, how this is implemented
in this specific ”parallel” program environment.
IoTBDS 2021 - 6th International Conference on Internet of Things, Big Data and Security
246

information
translation
previous state
information
later state
information
metainformation
information
information
Room Mirror
from inner to outer
actual event location of observer
single to multi
Time Mirror
from earlier to later
actual event horizon of observer
serial to multiparallel
+1
+1+1
+1
+1
information
metainformation
meta-
metainformation
+1
+1
+1
+1
indication of emergence - a new observer reality
-1
indication of disemergence - a past observer reality
-1
-1
-1
-1
-1
-1
-1
mirror axes / planes
x
y
Figure 1: Room-time information multiplication dimension connectivity.
The programs, in Mathcad or Witness itself, can be re-
garded as information-translation in the sense of Fig-
ure 1, and hence the system order is increasing poten-
tially.
3.1 Mathcad Simulation
To simulate the triangular process first two programs
are made in Mathcad (cf. APPENDIX - MATHCAD
PROGRAMS) to implement the cellular automaton.
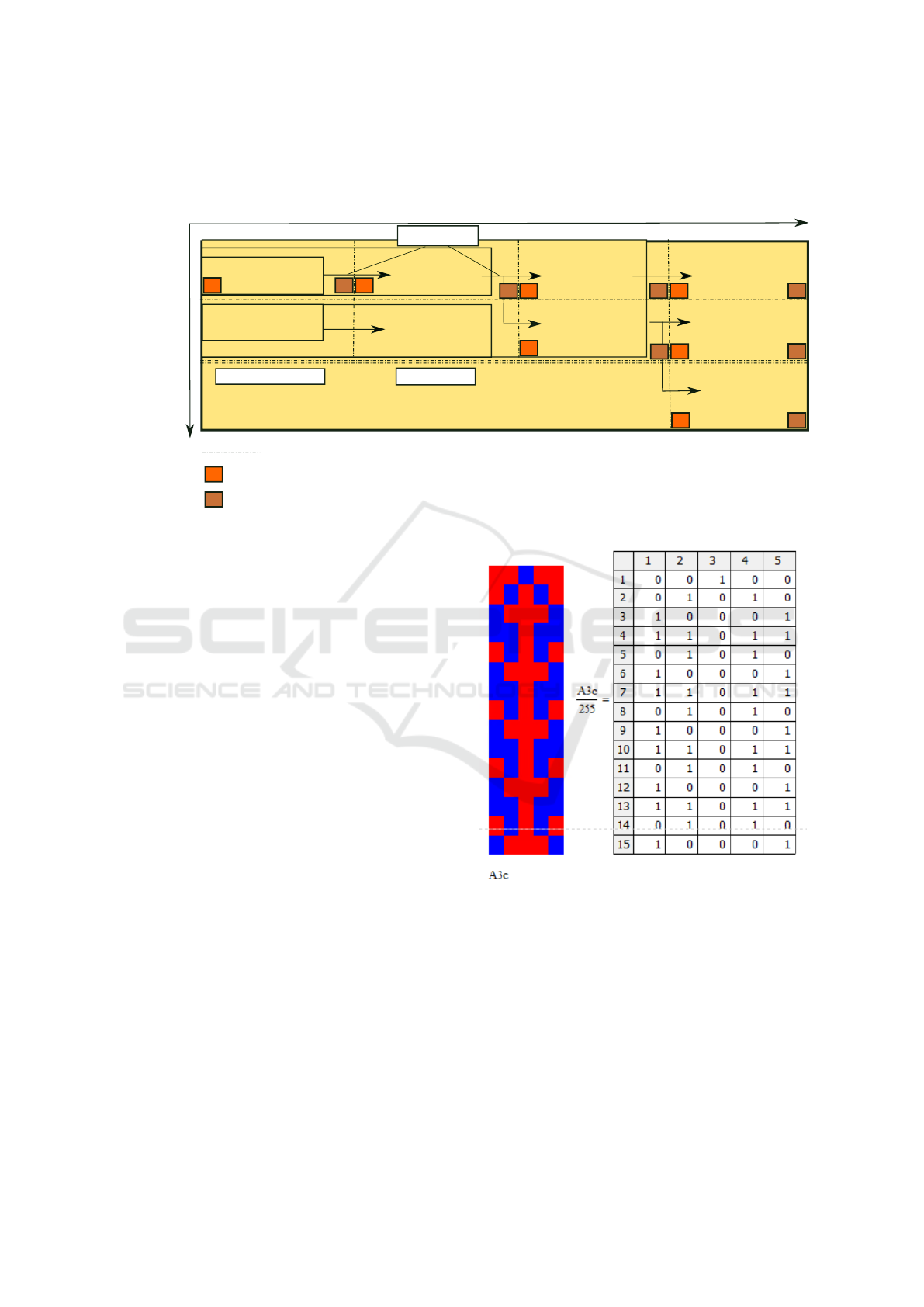
In Figure 2 we see the cyclic implementation. Cir-
cular robot-os, can be imagined in a way having one
neighbour to the left and one to the right and arranged
in a circle.
The other variant is to have robot-os with left and
right neighbours only, which means that there is an
open-end on each side (cf. Figure 3).
In Figure 4 ten (10) variants of open-ended and
cycle robot-os patterns can be seen. They tend to a
stable dynamic pattern, although, each configuration
is more or less chaotic in the pattern structure, or has
different information entropy (cf. Figure 6).
3.2 Witness Simulation
Nowadays the role of Machine-to-Machine (M2M)
communication is becoming increasingly important
in different areas of applications. M2M communi-
cation technology is commonly based on wired or
wireless communication channels, e.g. sensors, In-
ternet, RFID, etc. (Galeti
´
c et al., 2011). The pur-
pose of this chapter is to introduce a simple simula-
Figure 2: With the A3xc(n=5,m=15) function (see AP-
PENDIX - MATHCAD PROGRAMS) calculated cyclic
pattern of five robot-os for 15 time steps (n=5, m=15); left
the pattern-picture and right the corresponding 0/1 repre-
sentational matrix.
tion model as a pattern example of communication be-
tween functional independent and informational open
robots-multirobots as an entangled robotic system.
The model was simulated in the Witness Software
and consists of five functional independent robots,
each of which has binary incoming and outgoing sig-
nals. The functional principle of communication in
this robotic system is based on binary sensor and bi-
Selforganisational High Efficient Stable Chaos Patterns
247

Figure 3: With the A3x(n=5,m=15) function (see AP-
PENDIX - MATHCAD PROGRAMS) calculated cyclic
pattern of five robot-os for 15 time steps (n=5, m=15); left
the pattern-picture and right the corresponding 0/1 repre-
sentational matrix - open-ended variant.
nary actor signals. Each robot recognises and pro-
cesses signals of its neighbouring robots (input sig-
nal) according to the general pattern and generates
the outgoing signals (output). For a demonstration of
outgoing signals, the function of integer variables in
Witness was used. Based on this simulation, the inner
and external border of a robot-o can be distinguished
This methodology of M2M-communication-based on
binary sensors can be also important and applicable
in intralogistics, namely in the context of traffic or-
ganisation of automated guided vehicles and human-
robot-communication in the intelligent warehouse (cf.
(Rey et al., 2019)).
When we look at the Witness simulation, there is
the basic concept of parallelisation of the model. Wit-
ness is an intrinsic simultaneous process simulation
program. By this, each robot can be regarded as a par-
allel and individual separate agent in one room-time
window, according to Figure 1. The parallelisation
process occurs then by going into the y-direction. An
example configuration of the five robot-os is depicted
in Figure 5. In the Witness model, the information
balance of the ’living’ or dynamic cybernetic process
is given by ingoing and outgoing information. In this
context, the ingoing part and outgoing part of every
robot-o simulates the event horizon for each time step.
In this event horizon then the translation to the next
step is calculated inside the robot (cf. Figure 5, 1 and
APPENDIX - WITNESS PROGRAMS). The transla-
tion is done in this case according to the cellular au-
tomaton and is by this restricted to a relatively static
as well as collective behaviour between each state, so
this may be called a swarm.
When we now regard a meta-meta perspective, an
observer who sees the light of the robot-os, this ob-
server gets integrated information of all together as
a pattern. This meta-information then increases the
possibilities of the process, and hence the possible
practical applications.
3.3 Information Entropy
In Figure 6 the information entropy according to
Shannon and equation (1) is calculated for the 2 x 10
variants in Figure 4, as well as the intermediate steps.
The general form in Mathcad can be written:
H(n) := log(n, 2) (2)
So we have calculated the maximum possible entropy
(Hmax = H(n ∗ m) according to (2)), the entropy for
the cycle cases (H cyclic= number of positive values
in A33x (see function summe1(n, m) in APPENDIX -
MATHCAD PROGRAMS)), the entropy of the open-
end cases (H open end), and the difference entropy
for cyclic (DeltaH cyclic) and for the open-end cases
(DeltaH open end) and the maximum time horizon
(regarded time steps). The total bit number is then
time steps x # robot-os (number (n) of robot-os). We
see then peaks in n=3,5,9,17 which correspond to in-
creasing relative entropy in those cases as the signal is
vanishing after a certain time, for the depicted open-
end cases (cf. Figure 4).
We can find also the minimum entropy differ-
ences, and hence the maximum efficiency patterns for
n=3 robots for the cyclic cases and n=7 for the open-
end cases, where the information efficiency is maxi-
mal in the cyclic n=3 cases.
When the difference is minimal with regard to
maximum entropy, information is most effectively
stored in the patterns. This is the case at the local
minima of DeltaH in Figure 6.
Of course, this is only valid for the given time-
horizon and the translational vector in row 4 given in
U. In sum, in this scenario 2
8
= 256 cases are possi-
ble.
4 CONCLUSION
We can conclude from the above given computational
results, that it is possible to implement a stable chaotic
pattern by means of cellular automata and different
forms of translations. Translations are understood
as a program inside of an observer. When progress-
ing with information from inside to outside and or in
IoTBDS 2021 - 6th International Conference on Internet of Things, Big Data and Security
248

Figure 4: Ten (10) variants with the open-ended and the cyclic robot-os implementation.
Figure 5: Triangularity pattern simulation in Witness with
five robot-os.
time, then the possibilities can emerge by the grade of
increasing possibilities triggered by the specific pro-
cess. By this, the difference lies in the expression of
how information is distributed, e.g. with regard to in-
formation entropy.
This then lets order or control the process from
extended mirroring planes by means of observables
that constitute a dynamic memory. In each case, in
these cellular automata, the information balance can
be regarded as fulfilled for each event window, i.e. it
constitutes a living system, only having possibilities
in the ’alive’ state, which means that information is
in- and outgoing with regard to the observer.
More specifically the observer constitutes an
event-horizon decreasing effect of possibilities by ob-
servation. The same is true for acting.
Figure 6: Information entropy.
Hence in the robot-o case, the basic constitution
of a cellular automaton - which can therefore also be
regarded as the most efficient with regard to cause-
effect, as it maximises the possibilities room - is a dy-
namic cybernetic interaction, including sensing and
acting. This in sum is the form of the translation pro-
cess, of an observer/actor reality autoencoder, which
means that ingoing and outgoing information with re-
gard to a process or event relative observer is in dy-
namic equilibrium.
The emergence process is here different. It arises
in each room-time window as a consequence of the
possibilities rooms and is hence related to entropy
resp. negentropy.
Hence stable chaos is bound to this basic infor-
mation and more complex patterns are triggered for
the same translation procedure, if there are employed
more observers or e.g. robot-os.
Selforganisational High Efficient Stable Chaos Patterns
249

An interesting fact is that the same overall pro-
gram, which explicitly excludes different patterns in
individual robot-os, restricts information order, which
can be derived from Figure 6. This is as a sum a
unidirectional process, which can be regarded as ’so-
lidified’ in a state, the translation vector. As a con-
clusion, the bidirectionality would possibly increase
order (cf. (Heiden and Tonino-Heiden, 2021)). The
gaining possibilities are then restricted to the differ-
ence to the unidirectional case, as a consequence. A
future research could then be to investigate, how the
bidirectional process is achieved and what the infor-
mational efficiency gain will be.
As a conclusion with regard to information en-
tropy it can be said, that this is dependent on the room-
time horizon, and there exists a minimum leading to a
stable efficient chaotic pattern. Similar results are to
be expected with other translational patterns and can
be measured with the given method.
In general, the ”efficiency” case, will be also a
question of the specific application, and hence it will
change, according to different patterns. It may then be
optimal with regard to a specific informational goal,
e.g. detection of an error intrusion, detection of sta-
ble operation, signal encryption, signal superposition,
dynamic signal storage, etc.
5 SUMMARY AND OUTLOOK
In this work, we have given the computational tools
to implement stable chaotic patterns by means of cel-
lular automata. The basic principles have been pro-
vided, that can be applied in future research to IoT-
swarm applications like in robot-os.
Future applications in IoT-swarms will have to im-
plement further ”translations” into physical devices
according to the theory section 2.
There can be used similar programs as in the Wit-
ness program section, with the difference, that the
program, e.g. on the Arduino-Board has to be con-
nected to the input (light-sensing) and output (light-
indicating) information resp. signal.
Concerning the translation matrix only one of 256
possibilities, according to permutations has been in-
vestigated. So using other translational codes, a lot of
more configurations are possible. It will be interest-
ing, maybe for future research, to investigate the re-
lation of those different kinds of translational patterns
on the overall informational process, as well as more
dynamic or even more nested translations relation-
matrices, maybe to implement bi-directional cyber-
netic processes to further increase the informational
efficiency of the regarded or implemented processes.
REFERENCES
Elmenreich, W., Heiden, B., Reiner, G., and Zhevzhyk, S.
(2015). A low-cost robot for multi-robot experiments.
In 12th International Workshop on Intelligent Solu-
tions in Embedded Systems (WISES), pages 127–132.
IEEE.
Galeti
´
c, V., Boji
´
c, I., Ku
ˇ
sek, M., Je
ˇ
zi
´
c, G., De
ˇ
si
´
c, S., and
Huljeni
´
c, D. (2011). Basic principles of machine-to-
machine communication and its impact on telecom-
munications industry. In 2011 Proceedings of the 34th
International Convention MIPRO, pages 380–385.
Heiden, B., Alieksieiev, V., and Tonino-Heiden, B. (2021a).
Communication in Human - Machine - Product Trian-
gle - Universal Properties of the Automation Chain -
Witness Simulation Example, unpublished.
Heiden, B. and Tonino-Heiden, B. (2021). Philosophical
Studies - Special Orgiton Theory / Philosophische Un-
tersuchungen - Spezielle Orgitontheorie (English and
German Edition). unpublished.
Heiden, B., Tonino-Heiden, B., and Alieksieiev, V. (2021b).
Artificial Life - Investigations about a Universal Os-
motic Paradigm (UOP), unpublished.
Heiden, B., Volk, M., Alieksieiev, V., and Tonino-Heiden,
B. (2020). Framing Artificial Intelligence (AI) Ad-
ditive Manufacturing (AM). In 14th International
Symposium “Intelligent systems” (INTELS’20), 14-
16. Dec., Moscow.
H
¨
utt, M.-T. (2006). Was ist Selbstorganisation und
was n
¨
utzt sie zum Naturverst
¨
andnis?, pages 91–105.
B
¨
ohlau Verlag, K
¨
oln.
Rey, R., Corzetto, M., Cobano, J. A., Merino, L., and Ca-
ballero, F. (2019). Human-robot co-working system
for warehouse automation. In 2019 24th IEEE Inter-
national Conference on Emerging Technologies and
Factory Automation (ETFA). IEEE.
Shannon, C. E. and Weaver, W. (1963). Mathematical The-
ory of Communication. Combined Academic Publ.
Villari, M., Fazio, M., Dustdar, S., Rana, O., and Ran-
jan, R. (2016). Osmotic computing: A new paradigm
for edge/cloud integration. IEEE Cloud Computing,
3:76–83.
Wiener, N. (1963). Kybernetik : Regelung und
Nachrichten
¨
ubertragung im Lebewesen und in der
Maschine. Econ Verlag. Cybernetics or control
and communication in the animal and the machine
(deutscher Originaltext).
IoTBDS 2021 - 6th International Conference on Internet of Things, Big Data and Security
250

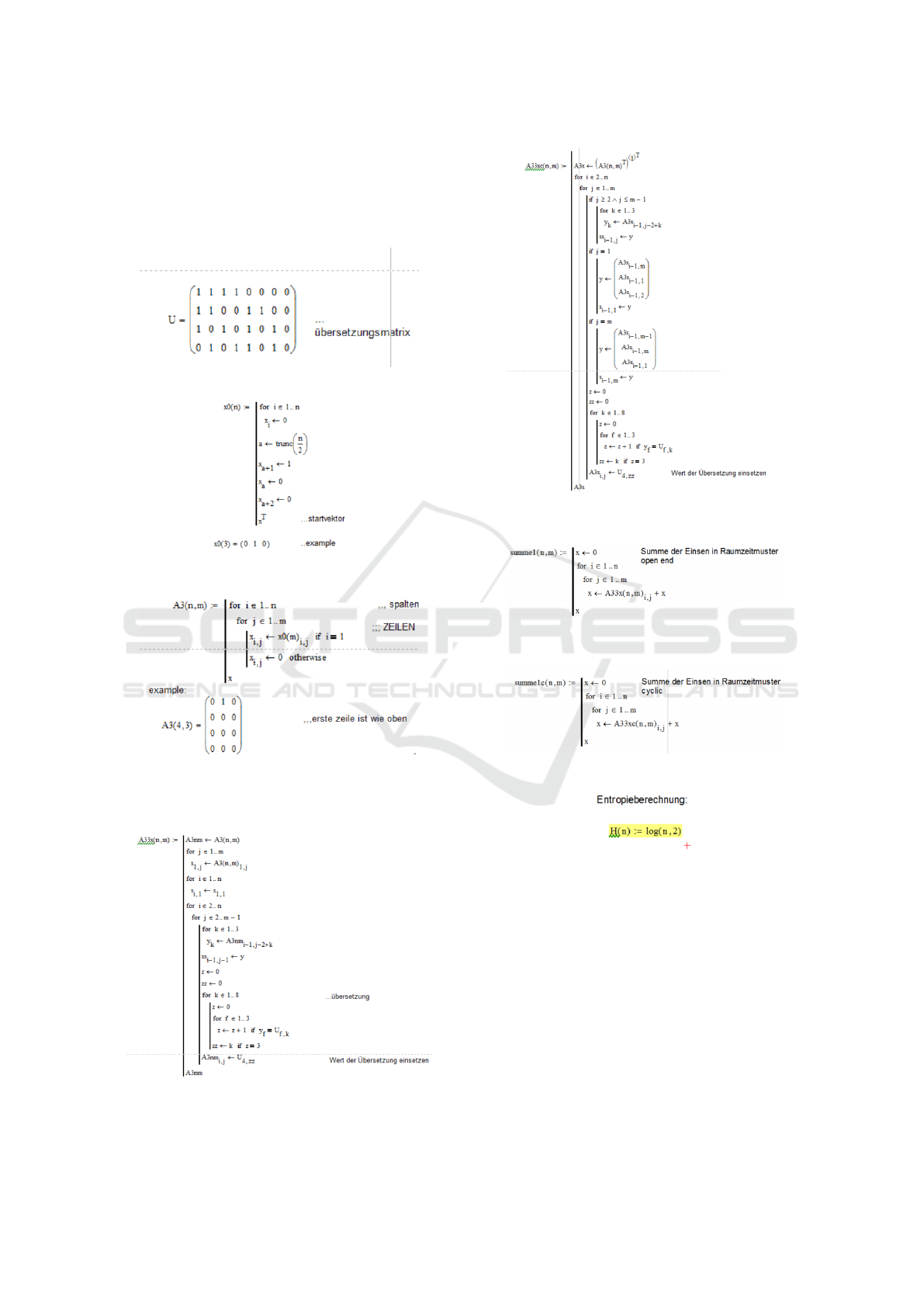
APPENDIX
Mathcad Programs
Translational Matrix U:
Starting Vector:
Initial Matrix:
Mathcad Program A33x(n, m) - non-cyclic (open-
ended) triangular cellular automaton (nxm, n...robots,
m...time steps):
Mathcad Program A33xc(n, m) - cyclic triangular cel-
lular automaton (nxm, n...robots, m...time steps):
summe1(n, m) - for the calculation of entropy in the
open-end case:
summe1c(n, m) - for the calculation of entropy in the
cyclic case:
Calculation of entropy:
Witness Programs
Actions Initialise
R1L = 0
R2L = 0
R3L = 0
R4L = 0
R5L = 0
R1La = 0
R2La = 0
R3La = 1
R4La = 0
R5La = 0
X1 = 0
X2 = 0
X3 = 0
X4 = 0
X5 = 0
r1t = 0
r2t = 0
r3t = 0
r4t = 0
Selforganisational High Efficient Stable Chaos Patterns
251

r5t = 0
timeo = 0
timen = 0
tt = 1
Robot1-Program-Actions: Input Part
IF R5La = 1 AND R1La = 1 AND R2La = 1
X1 = 0
r1t = 1
ELSEIF R5La = 1 AND R1La = 1 AND R2La = 0
X1 = 1
r1t = 2
ELSEIF R5La = 1 AND R1La = 0 AND R2La = 1
X1 = 0
r1t = 3
ELSEIF R5La = 1 AND R1La = 0 AND R2La = 0
X1 = 1
r1t = 4
ELSEIF R5La = 0 AND R1La = 1 AND R2La = 1
X1 = 1
r1t = 5
ELSEIF R5La = 0 AND R1La = 1 AND R2La = 0
X1 = 0
r1t = 6
ELSEIF R5La = 0 AND R1La = 0 AND R2La = 1
X1 = 1
r1t = 7
ELSEIF R5La = 0 AND R1La = 0 AND R2La = 0
X1 = 0
r1t = 8
ENDIF
R1L = X1
timex = TIME
IF TIME > timeo
timen = TIME
timeo = timen - 1
ENDIF
Robot1-Program-Actions: Output Part
IF TIME = 1
XLWriteArray ("Robot-o.xls","x","$A$2",TIME)
XLWriteArray ("Robot-o.xls","x","$B$2",R1La)
XLWriteArray ("Robot-o.xls","x","$C$2",R2La)
XLWriteArray ("Robot-o.xls","x","$D$2",R3La)
XLWriteArray ("Robot-o.xls","x","$E$2",R4La)
XLWriteArray ("Robot-o.xls","x","$F$2",R5La)
ENDIF
IF TIME > 1
R1La = R1L
R2La = R2L
R3La = R3L
R4La = R4L
R5La = R5L
tt = TIME + 1
XLWriteArray ("Robot-o.xls","x","$A$" + @tt,TIME)
XLWriteArray ("Robot-o.xls","x","$B$" + @tt,R1L)
XLWriteArray ("Robot-o.xls","x","$C$" + @tt,R2L)
XLWriteArray ("Robot-o.xls","x","$D$" + @tt,R3L)
XLWriteArray ("Robot-o.xls","x","$E$" + @tt,R4L)
XLWriteArray ("Robot-o.xls","x","$F$" + @tt,R5L)
ENDIF
Robot2-Program-Actions: Input Part
IF R1La = 1 AND R2La = 1 AND R3La = 1
X2 = 0
r2t = 1
ELSEIF R1La = 1 AND R2La = 1 AND R3La = 0
X2 = 1
r2t = 2
ELSEIF R1La = 1 AND R2La = 0 AND R3La = 1
X2 = 0
r2t = 3
ELSEIF R1La = 1 AND R2La = 0 AND R3La = 0
X2 = 1
r2t = 4
ELSEIF R1La = 0 AND R2La = 1 AND R3La = 1
X2 = 1
r2t = 5
ELSEIF R1La = 0 AND R2La = 1 AND R3La = 0
X2 = 0
r2t = 6
ELSEIF R1La = 0 AND R2La = 0 AND R3La = 1
X2 = 1
r2t = 7
ELSEIF R1La = 0 AND R2La = 0 AND R3La = 0
X2 = 0
r2t = 8
ENDIF
R2L = X2
timex = TIME
Robot3-Program-Actions: Input Part
IF R2La = 1 AND R3La = 1 AND R4La = 1
X3 = 0
r3t = 1
ELSEIF R2La = 1 AND R3La = 1 AND R4La = 0
X3 = 1
r3t = 2
ELSEIF R2La = 1 AND R3La = 0 AND R4La = 1
X3 = 0
r3t = 3
ELSEIF R2La = 1 AND R3La = 0 AND R4La = 0
X3 = 1
r3t = 4
ELSEIF R2La = 0 AND R3La = 1 AND R4La = 1
X3 = 1
r3t = 5
ELSEIF R2La = 0 AND R3La = 1 AND R4La = 0
X3 = 0
r3t = 6
ELSEIF R2La = 0 AND R3La = 0 AND R4La = 1
X3 = 1
r3t = 7
ELSEIF R2La = 0 AND R3La = 0 AND R4La = 0
X3 = 0
r3t = 8
ENDIF
R3L = X3
Robot4-Program-Actions: Input Part
IF R3La = 1 AND R4La = 1 AND R5La = 1
X4 = 0
r4t = 1
ELSEIF R3La = 1 AND R4La = 1 AND R5La = 0
X4 = 1
r4t = 2
ELSEIF R3La = 1 AND R4La = 0 AND R5La = 1
X4 = 0
r4t = 3
ELSEIF R3La = 1 AND R4La = 0 AND R5La = 0
X4 = 1
r4t = 4
ELSEIF R3La = 0 AND R4La = 1 AND R5La = 1
X4 = 1
r4t = 5
ELSEIF R3La = 0 AND R4La = 1 AND R5La = 0
X4 = 0
r4t = 6
ELSEIF R3La = 0 AND R4La = 0 AND R5La = 1
X4 = 1
r4t = 7
ELSEIF R3La = 0 AND R4La = 0 AND R5La = 0
X4 = 0
r4t = 8
ENDIF
R4L = X4
Robot5-Program-Actions: Input Part
IF R4La = 1 AND R5La = 1 AND R1La = 1
X5 = 0
r5t = 1
ELSEIF R4La = 1 AND R5La = 1 AND R1La = 0
X5 = 1
r5t = 2
ELSEIF R4La = 1 AND R5La = 0 AND R1La = 1
X5 = 0
r5t = 3
ELSEIF R4La = 1 AND R5La = 0 AND R1La = 0
X5 = 1
r5t = 4
ELSEIF R4La = 0 AND R5La = 1 AND R1La = 1
X5 = 1
r5t = 5
ELSEIF R4La = 0 AND R5La = 1 AND R1La = 0
X5 = 0
r5t = 6
ELSEIF R4La = 0 AND R5La = 0 AND R1La = 1
X5 = 1
r5t = 7
ELSEIF R4La = 0 AND R5La = 0 AND R1La = 0
X5 = 0
r5t = 8
ENDIF
R5L = X5
IoTBDS 2021 - 6th International Conference on Internet of Things, Big Data and Security
252