Trading Agent Competition with Autonomous Economic Agents
David Minarsch
1
, Seyed Ali Hosseini
1
, Marco Favorito
1,2
and Jonathan Ward
1
1
Fetch.ai, U.K.
2
Sapienza University of Rome, Italy
Keywords:
Multi-Agent System, TAC, Trading Agent Competition, Blockchain, Smart Contract.
Abstract:
We provide a case study for the Autonomous Economic Agent (AEA) framework; a toolkit for the develop-
ment and deployment of autonomous agents with a focus on economic activities. The use case is the trading
agent competition (TAC). It is a competition between autonomous agents with customisable strategies and
market parameters. The competition is facilitated by the AEA framework’s native support for decentralised
ledger technologies, i.e. permissionless blockchains and smart contract functionality, for immutable transac-
tion recording and trade settlement. We provide an open-source implementation, study the result of the com-
petitions we ran, and compare it to theoretical results in the economics literature. We conclude by discussing
its real-world applications in crypto-currency, digital assets and token trading.
1 INTRODUCTION
Motivation. Agent frameworks (Kravari and Bassil-
iades, 2015) and multi-agent systems (MAS) have
only found limited real-world applications despite be-
ing developed in the research community (Sonenberg
et al., 2012; Wooldridge, 2009) for multiple decades
(Lesser, 1995). One reason might be the absence of
a native digital financial layer that enables economic
activities.
In general, economic models and activities are an
integral part of MAS (Shoham and Leyton-Brown,
2008). In particular, deployable MAS applica-
tions often incorporate an element of trade between
agents. Examples include those utilising any of the
following notions: incentives (Novikov, 2016), re-
wards/punishments (Hao and Leung, 2016), negotia-
tion (McBurney et al., 2003), and so forth. It is likely
that the realisation of such applications hinges upon
access to a native financial and settlement system de-
signed specifically to address the needs of MAS ap-
plications.
The advent of distributed ledger technology (DLT)
(Maull et al., 2017) makes it possible to finally pro-
vide a native digital financial system that is both de-
centralised and trustless (Chohan, 2019; Klems et al.,
2017), two properties fundamental to MAS itself.
This study, together with its associated implemen-
tation, serves as a practical demonstration of the syn-
ergies between MAS and DLT. It forms an early step
in our efforts to bring multi-agent system applications
to large-scale deployment.
Competition. We introduce a Trading Agent Com-
petition (TAC) as a reusable software package
1
and
use case of the AEA framework (Minarsch et al.,
2020); a framework that enables the development and
deployment of autonomous agents with a focus on
economic activities.
The competition focuses on a scenario that in-
volves one of the most fundamental forms of eco-
nomic interactions; bilateral trades. A society of
agents, each starting with a number of goods, engages
in one-to-one trades using a numeraire money token as
their medium of exchange.
Each agent, in the real world, would represent an
individual or a group of people, tasked with looking
after their interest by maximising their utility. To this
end, the agents must be made aware of their owners’
preferences (von Neumann and Morgenstern, 1944)
and values (Atkinson and Bench-Capon, 2016). In
the competition, this is simulated by explicitly giv-
ing each agent a representation of their owners’ pref-
erences over goods at the beginning of each round.
During the competition, the goal of each agent is to
maximise its owners’ interests by engaging in prof-
itable trades, taking into account their preferences.
1
The TAC framework is accessible here: https://github.
com/fetchai/agents-tac.
574
Minarsch, D., Hosseini, S., Favorito, M. and Ward, J.
Trading Agent Competition with Autonomous Economic Agents.
DOI: 10.5220/0010431805740582
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 1, pages 574-582
ISBN: 978-989-758-484-8
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Application. The trading agent competition is facil-
itated by, and serves as a use case of, the AEA frame-
work. As such, it exploits different features of the
framework that correspond to the various facets of
a multi-agent system, such as search and discovery
services, agent communication, and transaction set-
tlement.
The competition itself has applicability in mul-
tiple areas. It can be used as a multi-agent game,
for instance to trade crypto tokens on the Ethereum
blockchain (Wood et al., 2014). It is a general Wal-
rasian market simulation tool which also allows for
studying the effects of different agent strategies on
trading performance (Kendall and Su, 2003). The
authors use it as an end-to-end test environment for
building scalable multi-agent systems.
2 MODEL
2.1 The Economy
The competition encapsulates a Walrasian economy
(Walras, 2014) with indivisible goods.
(Agents). There is a set A of agents par-
titioned into A
baseline
and A
model−based
such that
A = A
baseline
∪ A
model−based
. Note that A
baseline
or
A
model−based
can be empty as long as the minimum
number min agent of agents register for the compe-
tition (see Section 2.3). Section 3 describes the two
types of agents in more detail. There is also a special
agent c, called the controller, which runs the compe-
tition, and due to its special role, is not included in A.
Section 2.4 describes this agent in more detail.
(Goods). There is a tuple of n sets of goods
X =
h
X
1
, . . . , X
n
i
where each i ∈ {1, . . . , n} represents
one type of good (e.g. a fungible token) and each el-
ement of the set X
i
is an instance of that good type
(e.g. equivalent instances of the same fungible to-
ken). In general, we may have |X
i
| 6= |X
j
| for any
two i, j ∈ {1, . . . , n} where i 6= j; that is, the number
of available good instances (their aggregate supply)
could be different for two different goods.
(Money). There is a special type of good, indexed
by 0, the numeraire good or money. It serves as a unit
of account and medium of exchange to agents.
(Endowments). Agents are provided with en-
dowments in goods and money. That is, each agent
a ∈ A has an endowment e
a
=
h
e
a
1
, . . . , e
a
n
i
, a tuple
of length n, where the set e
a
i
⊆ X
i
is the endowment
of agent a in good i. Each agent is given at least
some base
amount > 0 of each good, thus for any
i ∈ {1, . . . , n}, we have base amount ≤ |e
a
i
| ≤ |X
i
|. We
assume that endowments are allocated such that for
each i ∈ {1, . . . , n} we have
S
a∈A
e
a
i
= X
i
; that is, all
endowments for a good sum to the total instances of
that good. Finally, every agent is endowed with the
same e
a
0
= money amount > 0. Goods and money can
only be traded in integer amounts, that is they are non-
divisible.
(Current Holdings). Each agent a’s current good
holdings are denoted by x
a
=
h
x
a
1
, . . . , x
a
n
i
where for
any i ∈ {1, . . . , n}, x
a
i
⊆ X
i
is the set of instances of
good i that agent a currently possesses. Therefore,
|x
a
i
| ∈ {0, . . . , |X
i
|}; note how agents can have no in-
stance of a good i at some point in time but trivially
never a negative amount. That is, there is no bor-
rowing of goods. We further assume that for each
i ∈ {1, . . . , n} we have
S
a∈A
x
a
i
= X
i
; that is, all agents’
current good holdings of a given good sum to the to-
tal instances of that good available. At the beginning
of a round in the competition, before any trades take
place, the good holding of any agent is equivalent to
its endowment. Furthermore, each agent a’s current
money holding is denoted by x
a
0
and it must always
be the case that
∑
a∈A
x
a
0
= |A| × money
amount and
for each agent a, x
a
0
≥ 0, that means there is also no
borrowing of money.
(Preferences). Agents are assigned preferences
for goods and money by the controller agent c.
Specifically, each agent a ∈ A has a preference
relation 4
a
on goods which totally ranks any possible
combination of good bundles. Preferences are
assumed to be transitive, thus for any three arbitrary
goods x, y and z, x 4
a
y and y 4
a
z means x 4
a
z. For
the purpose of this competition, each agent a has a
utility function u
a
which is quasi-linear in goods and
money:
u
a
(x
a
0
, x
a
) = x
a
0
+ g(x
a
) = x
a
0
+
∑
i∈{1,...,n}
s
a
i
× f (|x
a
i
|) (1)
such that s
a
i
> 0 and
f (|x
a
i
|) =
(
ln(|x
a
i
|) if |x
a
i
| > 0
−L otherwise
(2)
Breaking down the utility function in Equation 1, x
a
0
is agent a’s money holding, s
a
i
is the utility parameter
agent a assigns to good i, and f (|x
a
i
|) parameterizes
the number of instances of good i that agent a has.
The logarithmic nature of f (·) implies decreasing re-
turns; i.e. the agent values acquiring each additional
instance of a good less than acquiring the previous in-
stance. L > 0 is a large constant.
An agent a’s utility parameters for goods are rep-
resented by s
a
=
h
s
a
1
, . . . , s
a
n
i
where s
a
i
is the utility pa-
rameter agent a assigns to good i. Equation 3 ensures
the sum of the utility parameters for all goods are the
Trading Agent Competition with Autonomous Economic Agents
575

same for every agent a:
∑
i∈{1,...,n}
s
a
i
= 1 (3)
With the specific design of the utility function in
Equation 1, we are implementing the well stud-
ied Cobb-Douglas function (Brown, 2017) for g(x
a
)
which has the gross-substitutes property. This prop-
erty means that an increase in the price of one good
causes agents to demand more of the other goods.
The framework can be extended to utilise other
utility representation, the only requirement imposed
is that the utility representation provides a complete
ranking of all goods.
In the context of the competition, the utility func-
tion serves as the metric which the agents have to
maximise. The agent which best achieves this goal
becomes the winner of the competition.
(Trade Cost). We introduce a trade cost k to ex-
plicitly model transaction costs that would incur as a
result of settling trades, with special focus on DLT-
based financial systems. The trade cost has the side
benefit of limiting against some forms of denial-of-
service (DOS) attacks, provided the attacker cares
about winning the competition. Each transaction in-
curs the same cost k.
2.2 Relation to Economic Theory
Under certain assumptions, e.g. if transaction costs
are zero and goods are divisible, the gross-substitutes
property ensures that the game has a unique equilib-
rium.
2
Note however, that since we introduce a trade
cost and goods are indivisible, our game may have
many equilibria.
Furthermore, in the interest of tractability and to
guarantee an equilibrium, the gross-substitute prop-
erty limits preferences in that goods cannot be com-
plements.
Our simulation framework can benefit economic
analysis. It allows studying the properties of a
Walrasian economy populated by agents with non-
standard preferences. And, it enables the analysis of
interactions of heterogeneous trading strategies and
preferences in the same environment.
2.3 Trading Game Phases
The trading game has the following three phases:
Pre-trading: in which agents register with the con-
troller agent. Only if a min agent number of agents
register, then the competition moves to the next phase.
2
This competitive equilibrium is achieved via a so called
Walrasian auctioneer (Walras, 2014).
Trading: consists of k game instances g
1
, . . . , g
k
where at each game instance g
i
:
• The controller sends every participant a new draw
of endowments and preferences.
• Agents trade with each other.
• After some set time period or a sustained period
of no trades, whichever occurs first, the game in-
stance finishes and the controller constructs the
league table for this game instance.
Post-trading: the controller reports the final
league table as the weighted average of all game in-
stance league tables.
2.4 Controller Agent
A distributed ledger technology (DLT) (Maull et al.,
2017) is a secure and decentralised system for stor-
ing information and executing smart contract (Clack
et al., 2016) functionality.
In principle, a DLT provides all the functionalities
to facilitate the running and management of the TAC.
In particular, it allows goods and money to be repre-
sented as fungible (or non-fungible) tokens and stores
the transaction history of participants in a TAC.
As a first step towards a fully DLT-based TAC, we
decided to emulate its functionalities in the TAC via a
special controller agent c. This agent takes on the dual
responsibilities of transaction settlement and compe-
tition management, effectively making it the only en-
tity that holds the global state of the competition.
The controller agent’s responsibilities are detailed
below:
• At the beginning of each game instance, the con-
troller generates and assigns the endowments in
good e
a
and money e
a
0
, and the preferences s
a
of every participating agent a, ensuring they are
somewhat orthogonal.
• During each round, the controller registers and
settles transactions, ensuring the satisfaction of
the feasibility constraints listed in current hold-
ings in Section 2.1. This means that the controller
essentially keeps track of the good and money
holdings of every participating agent during the
competition.
• For every transaction submitted to the controller,
it ensures the transaction is cryptographically
signed by all parties involved. Transactions with
invalid signatures are rejected and deemed invalid.
• At the end of the competition, the controller con-
structs a league table containing the final scores
and ranking of all participating agents.
SDMIS 2021 - Special Session on Super Distributed and Multi-agent Intelligent Systems
576

2.5 Trustless Exchange
The trading environment in this competition is de-
signed to minimise the trust that agents need to place
in each other.
Specifically, the controller agent ensures that ev-
ery transaction sent to it is signed by all parties in-
volved in the transaction. Because the controller is
the only entity with the competition’s global state,
this makes it impossible for agents to submit invalid
transactions according to current holdings, e.g. fake
authenticity or attempt double-spending.
In the current implementation, agents have to rely
on the controller as a trusted third party. There is how-
ever another version where this responsibility of the
controller is pushed to a smart contract on a permis-
sionless DLT system.
3
2.6 Network Environment
The competition is held over a network. The environ-
ment consists of a so-called Open Economic Frame-
work (OEF) node, a controller agent, and a set of par-
ticipating agents. One functionality of the OEF node
is message relaying. This means that through appro-
priate APIs, agents send and receive messages to each
other, and the OEF handles the low level delivery of
the messages over the underlying network. Another
functionality of the OEF node is service registration
and search. Agents can register services (e.g. descrip-
tions of goods to sell/buy in terms of data models) and
search for registered services.
3 AGENTS
There are two types of agents in this competition:
baseline and model-based. In this section, we will
first describe what is common across these two agent
types. We then briefly present the negotiation system
the agents use in the competition in Section 3.1. We
then devote specific sections 3.2 and 3.3 to each agent
type, describing their differences in architecture and
strategy.
Regardless of their type, agents in the competition
focus on discovering how they can arrive at an opti-
mal bundle - as defined by their preferences - through
successive trades. Emphasis for agents is placed on
a) finding the right agents to trade with, and b) doing
the right trade with them. This might involve identi-
fying other agents’ needs to arrive at the optimal trad-
ing sequence. However, a dummy agent which simply
3
A reference to a preliminary newer version is available
on our TAC repository linked to above.
selects random bargaining partners and trades if it is
beneficial to it, without any longer term plan is still
able to improve its score in the competition.
The agents are designed to exhibit goal-oriented
behaviour while having the capability to react to
changes in the environment (Wooldridge, 2009;
Padgham and Winikoff, 2004). From a technical per-
spective, the agents have a so called main loop and an
event loop. The former controls the agent’s proactive
behaviour, where at each ‘tick’ of the loop, the agent
moves towards achieving its goal. The event loop on
the other hand is responsible for processing incom-
ing events. Events in the competition are represented
as messages, much like typical multi-agent systems,
which are placed in a queue by the event loop for pro-
cessing in the main loop.
More specifically, the main loop ticks e.g. every
10
th
of a second, and each time through the loop it:
1. Processes any incoming messages,
2. Updates the agent’s internal state,
3. Allows the agent to make decisions and act,
4. Waits until it is time to ‘tick’ again.
The key is ensuring that any message handling and
internal state update happens fast enough to always
(or mostly) avoid going over the allowed tick dura-
tion. The benefit of this architecture is that the whole
process is kept single threaded and the code straight-
forward to read. If there is a need for some heavy
processing, then one of the following is done:
• Splitting the task up into chunks and processing
them over several ticks (storing any intermediate
internal state).
• Concurrently executing the task in a single thread
(e.g. using co-routines in Python).
• Splitting the process across different threads, hav-
ing the main thread wait for all threads to finish
with their jobs.
3.1 Negotiation
The negotiation protocol agents use in the competi-
tion is inspired by the FIPA ACL (Committee, 2001).
This means, there is a multi-step dialogue during
which agents send messages of the form P(c
1
, . . . , c
n
)
where P, called a performative, conveys the type
of the message and c
1
, . . . , c
n
are the contents (e.g.
Request(resource), Propose(offer, price)). Table 1
lists the allowed messages and for each message spec-
ifies its valid replies.
An agent A initiates a negotiation by sending a
CFP (call-for-proposal) to their counter-party B. If
B processes a CFP, it replies with either a Propose or
Trading Agent Competition with Autonomous Economic Agents
577

Table 1: Negotiation messages.
Message Contents Replies
cfp(q) q : query propose(o, p)
decline()
propose(o, p) o : offer propose(o
0
, p
0
)
p : price accept()
accept() match−accept()
decline()
match-accept()
a Decline. Decline sent at any point in the negotiation
by anyone terminates the negotiation.
A Propose contains a list of offers, which partially
or totally match the query delivered in the CFP. Once
agent A receives the offers, it will either Accept or
Decline. Upon acceptance, A will send a message to
the controller agent c, confirming its transaction with
B. The negotiation is successfully completed if B as
the counter-party follows suit with a matching Accept
and another transaction submission to the controller.
However, B might also Decline at this stage, which
would be the case if its trading position has changed
between when it made the proposal and when it re-
ceives A’s Accept.
The second Accept is referred to as a Match-
Accept. Without it, B would have to send the transac-
tion to the controller after sending its proposal, which
is very limiting. This is because at this point there is a
high probability that the negotiation breaks down, be-
cause other simultaneous trades/negotiations impact-
ing this one might be more beneficial. The reason for
this is that any transaction submitted to the controller
must be considered in the forward looking state of the
agent, i.e. the state the agent finds itself in once all the
trades it committed to have been settled by the con-
troller agent c.
4
3.2 Baseline Agents
Baseline agents are the more basic agents of the two
types participating in a competition.
Recall each agent a has a utility function
u
a
(x
a
, x
a
0
), which given a good holding x
a
and money
holding x
a
0
, gives a number representing “how good
agent a’s current situation is”. The utility number
is used by the agent to compare different states and
4
Depending on their design, DLT systems provide dif-
ferent degrees of transaction finality. A transaction which is
included in the chain and therefore confirmed and executed
might still be reversed until it reaches finality (Rauchs et al.,
2018). Therefore, depending on the underlying DLT system
the forward looking state will have to be defined differently.
helps in decision making. For instance, when decid-
ing how much better off the agent would be if it ac-
quired another copy of a good i. This is equivalent
to comparing the utility values u
a
of the two hold-
ings
h
x
a
1
, . . . , x
a
i
, . . . , x
a
n
i
and
h
x
a
1
, . . . , ˜x
a
i
, . . . , x
a
n
i
where
| ˜x
a
i
| = |x
a
i
| + 1.
In general, an agent a compares two states with
good and money holdings of respectively x
a
, x
a
0
and
˜
x
a
, ˜x
0
a
, by calculating the marginal utility u
a
(
˜
x
a
, ˜x
a
0
)
- u
a
(x
a
, x
a
0
) = g(
˜
x
a
) − g(x
a
) + ˜x
0
a
− x
a
0
. This is the
quantity by which the agent assesses whether an ex-
change resulting in its good and money holdings to
change from x
a
to
˜
x
a
, respectively x
a
0
to ˜x
a
0
, pays off.
In particular, for the exchange to pay off, the change
in the marginal utility has to be positive.
A baseline agent without a world model a ∈
A
baseline
will trade as follows. For each good i in
its current holding
h
x
a
1
, . . . , x
a
n
i
, the agent simultane-
ously offers to buy an instance, and sell an instance
if it has at least two. The price p the agent is will-
ing to sell the instance for is equal or more than the
agent’s marginal utility for i in the goods component
only, i.e. p ≥ g(x
a
) − g(
˜
x
a
), where
˜
x
a
is the current
good holding x
a
minus the instance to be sold. On
the other hand, the price p
0
the agent is willing to pay
to acquire an instance is equal or less than the agent’s
marginal utility for i in the goods component only, i.e.
p ≤ g(
˜
x
a
) − g(x
a
), where
˜
x
a
is the current good hold-
ing x
a
plus the instance of the good to be bought.
With the above trading strategy, the agent will
never make any profit in negotiations where it pro-
poses a price. It can only make a profit in negotiations
where it receives a proposal.
3.3 Model-based Agents
A model-based agent uses information it gains from
acceptances and declines of its proposals to create a
price model for each good. It then uses the price
model to offer the price it assumes has the highest
likelihood to becoming a successful trade.
The algorithm that a model-based agent uses is
presented is pseudo-code in Algorithm 1. It resem-
bles a multi-armed bandit type model. The agents
starts with a beta distribution with parameters α = 1.0
and β = 1.0 (i.e. a uniform distribution), one for
each price bin with resolution 0.2 (see INIT). Dur-
ing the competition, each time an agent gets a success
or failure (Accept/Decline respectively) for a specific
price bin and good, it updates the distributions (see
UPDATE). The prices can then be sampled from the
model by checking for the distribution with the high-
est success probability. The choice must be taken
according to the agent’s role in the negotiation (i.e.
SDMIS 2021 - Special Session on Super Distributed and Multi-agent Intelligent Systems
578

Algorithm 1: Multi-Armed bandit model of price.
Input: goods 1, . . . , n
1: function INIT(a)
2: GoodPriceModels ← []
3: for i ∈ {1, . . . , n} do
4: GoodPriceModels[i] ← []
5: for price ∈ {0.0, 0.2, . . . , 20.0} do
6: GoodPriceModels[i].append(B(1.0, 1.0))
7: end for
8: end for
9: end function
10:
11: function UPDATE(i, price, outcome)
12: modelToUpdate ←
GoodPriceModels[i][price]
13: if outcome then
14: modelToUpdate.α += 1
15: modelToUpdate.β -= 1
16: else
17: modelToUpdate.α -= 1
18: modelToUpdate.β += 1
19: end if
20: end function
buyer/seller) and the last proposed price.
4 SIMULATION RESULTS
We have held an in-person version of the competition
using the provided framework as well as running the
competition in the form of a simulation, on which we
report the results in this section. The simulation runs
contained 10 agents, with half of the agents baseline,
and the other half model-based. We ran the simulation
103 times, each time with a different seed and other-
wise identical configuration. For the details on the
configurations chosen please consult the repository.
We first analyse the scores. The null hypothesis
we test for is that model-based agents have a weakly
smaller mean score than baseline agents. The alter-
nate hypothesis is that the model-based agents have a
strictly larger mean score than the baseline agents. A
one-sided t-test allows us to reject the null hypothesis
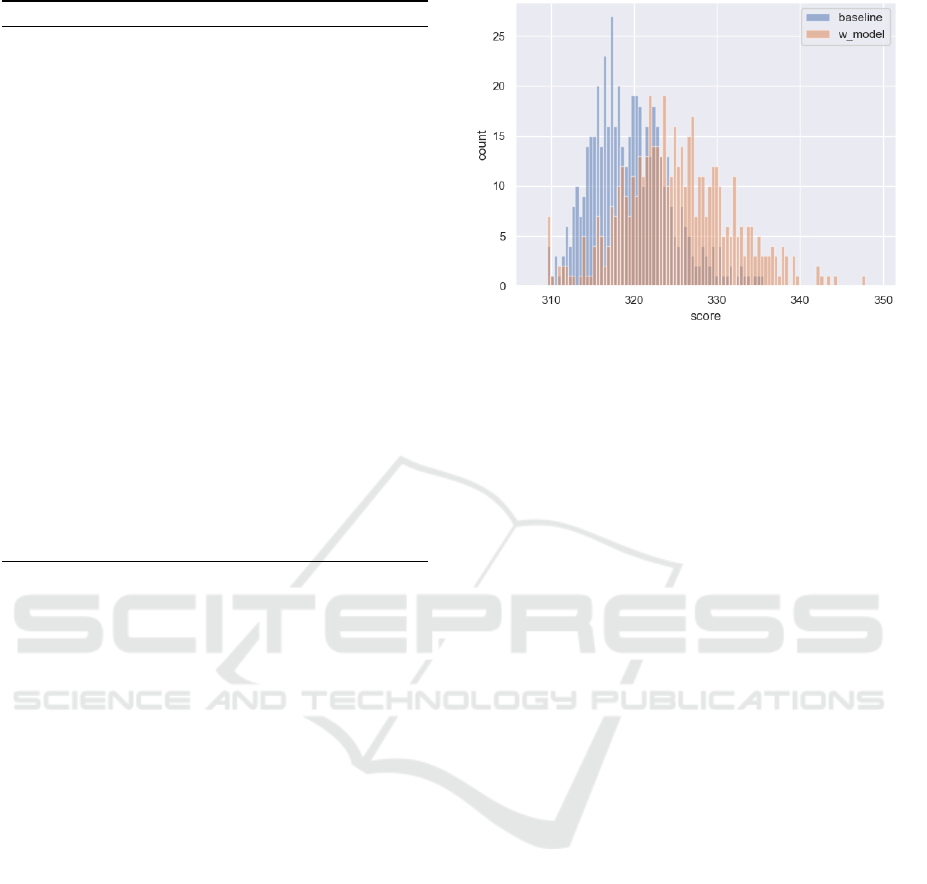
at a significance level α = 0.0001. Figure 1 shows the
distribution of scores for the two groups of agents.
It illustrates that model-based agents have a statisti-
cally significantly higher score than baseline agents.
The mean score of the model-based agents is 325.07
whilst the baseline agents achieve a mean score of
319.53.
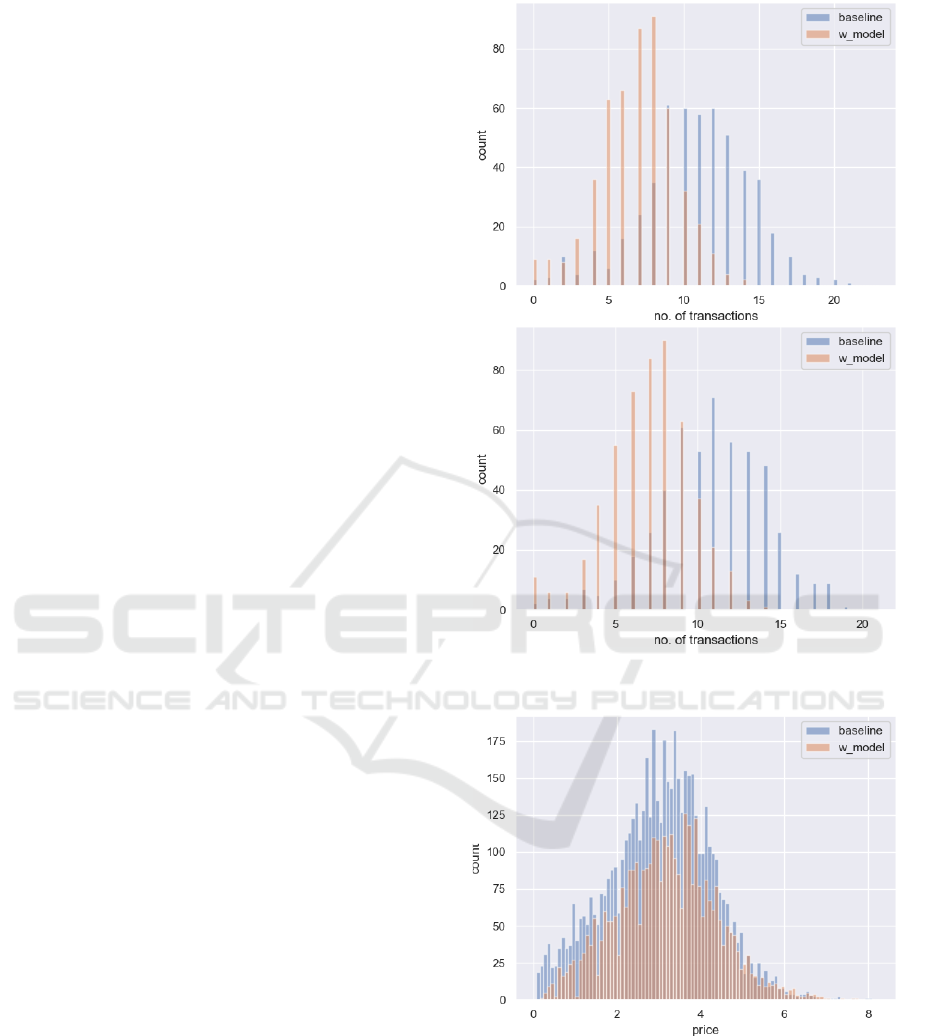
We next look at the number of trades completed
Figure 1: Histogram of scores (in bins) achieved.
by the two groups of agents on average. The null hy-
pothesis we test for is that model-based agents have
a weakly larger average number of transactions than
the baseline agents. The alternate hypothesis is that
the model-based agents have a strictly smaller aver-
age number of transactions than the baseline agents.
We test the hypothesis for the number of transactions
from both the seller and the buyer perspective and the
number of transactions from the buyer perspective.
A one-sided t-test allows us to reject the null hy-
pothesis at a significance level α = 0.0001 in the case
of both the buyer and seller perspective. The mean
number of seller transactions of the baseline agents
is 10.72 whilst model-based agents transact on aver-
age 7.00 times as sellers. The mean number of buyer
transactions of the baseline agents is 10.80 whilst
model-based agents transact on average 6.93 times as
buyers.
Figure 2 visualises the distribution of number of
transactions. The graphs show that the baseline agents
transact significantly more (both statistically and eco-
nomically) than the model-based agents.
Lastly, we look at the prices charged by the two
groups of agents. The null hypothesis we test for is
that model-based agents have a weakly smaller mean
price than baseline agents. The alternate hypothesis
is that the model-based agents have a strictly larger
mean price than the baseline agents.
A one-sided t-test allows us to reject the null hy-
pothesis at a significance level α = 0.0001. The mean
price charged by the baseline agents is 3.02 whilst
model-based agents charge on average 3.18. Fig-
ure 3 shows the distribution of prices charged by the
two groups of agents. It illustrates that on average,
model-based agents charge higher prices than base-
line agents.
The simulation suggests a number of interesting
findings. Firstly, baseline agents trade much more
Trading Agent Competition with Autonomous Economic Agents
579

than their model-based counter-parts. They do so
at lower prices than model-based agents on aver-
age. This leads to outcomes where model-based
agents have a higher score on average than baseline
agents. Since both types of agents operate at the same
frequency, these findings suggest that model-based
agents make offers which do get rejected more often.
However, when they do get accepted they lead to a
relatively larger gain for them.
5 DISCUSSION
The competition setup mirrors a Walrasian Exchange
Economy, the workhorse model in economics for rep-
resenting a market, which demonstrates the concept
of allocative/Pareto efficiency well, i.e. allocating re-
sources to those who will make best use of them
(Mas-Colell et al., 1995).
Since agents negotiate one-on-one, they should
not be able to achieve the efficiency of the Walrasian
Exchange Economy. In particular, it has been shown
that in theory, an auction is more efficient than nego-
tiation under most circumstances (Bulow and Klem-
perer, 1996). However, this does not mean that in-
dividual agents won’t be able to outperform through
negotiations relative to an auction-based market out-
come. Specifically, due to the private information on
preferences and good holdings, there is vast scope
for some agents to perform better than others not by
chance alone.
The reason for the above is that, from a game-
theoretic perspective, the competition is not a zero-
sum game. That is to say, an increase in one partic-
ipant’s score is not necessarily - and in general un-
likely - at the cost of another. As a consequence, op-
position to proposals and potential trade is weak in
this setup since trades can be beneficial to all parties
involved.
In this competition, agents’ preferences and en-
dowments are provided exogenously by the controller
agent. Of course in a real-world use-case, the prefer-
ences and endowments would arise naturally. How-
ever, for the competition it is necessary to explicitly
impose these on the agents to guarantee an interesting
and fair setup.
Moreover, although the competition is designed
so that agents would treat goods independently, for
a hyper-rational agent, price changes in one good
should lead to changes in demand for the other goods
due to the gross-substitutes property embedded in the
utility function of the agents. Hence, the aggregate
supply in one good can affect the demand in another.
Figure 2: Histogram of buyer (top) and seller (bottom)
transactions.
Figure 3: Histogram of prices (in bins) charged.
5.1 Real World Applications
Beyond the competition aspect, this setup has other
applications. The first being a research tool for un-
derstanding markets and trading strategies. Thanks
to the modularity of the AEA framework, the com-
petition package, and the architecture of agents, it is
SDMIS 2021 - Special Session on Super Distributed and Multi-agent Intelligent Systems
580

easy to change the competition’s configuration and
variables, describe other types of markets, and apply
custom rules. Similarly, it is straightforward to write
agents which follow trading strategies other than the
two described in Sections 3.2 and 3.3.
An extension of the above is studying the ef-
fectiveness of implementing reinforcement learning-
based trading strategies on agents’ trading perfor-
mances. The AEA framework’s built-in support for
ML approaches to agent design facilitates this work.
Another use case is a trading platform for crypto-
currencies, tokens, and digital assets in general (Ku-
mar et al., 2020; Radomski et al., 2018). The setup of
this application is fairly close to the competition’s ex-
isting setup because a) users would have well defined
preferences over these assets, and b) computational
representation of their preferences could be provided.
Due to the above, we expect that this application is
straightforward to get at with minimal alterations to
the code base.
6 FUTURE WORK
There are many ways the trading environment could
be made richer, and the domain more complex. A nat-
ural extension is to introduce a market through a cen-
tralised auction process that is operated in a decen-
tralised way by a smart contract. Theoretically, this
should cause the agent-to-agent negotiation to unravel
(Neeman and Vulkan, 2002). However, it would be
interesting to observe what happens in a multi-agent
world where agents are unlikely (programmed to be)
hyper-rational.
Below we list a number of features which can en-
rich the competition:
• Richer Strategies: agents to be required to
deploy strategies based on a variety of tech-
niques (e.g. reinforcement learning (RL), evolu-
tionary/genetic algorithms, logic-based).
• Multiplicity of Issues: so several agent skills are
needed and no single type of agent strategy is su-
perior in all markets.
• Latencies: in real-world blockchain scenarios,
the settlement of trades is not instantaneous and
would need to be accounted for in the agent and
smart contract design. The current implementa-
tion of the forward looking state in the agent can
be improved upon accordingly.
• Temporal Preferences: agents can have different
degrees of urgency for reaching the final state and
different transaction costs. These two factors are
relevant for applications in the real world and so it
would be useful to parameterise them in the com-
petition for further explorations.
ACKNOWLEDGEMENTS
We thank our employer Fetch.ai for supporting this
research and the release of the open-source imple-
mentation.
REFERENCES
Atkinson, K. and Bench-Capon, T. (2016). States, goals
and values: Revisiting practical reasoning. Argument
& Computation, 7(2 - 3):135 – 154.
Brown, M. (2017). The New Palgrave Dictionary of Eco-
nomics. Palgrave Macmillan UK.
Bulow, J. and Klemperer, P. (1996). Auctions versus nego-
tiations. The American Economic Review, 86(1):180–
194.
Chohan, U. W. (2019). Are Cryptocurrencies Truly Trust-
less?, pages 77–89. Springer International Publishing,
Cham.
Clack, C., Bakshi, V., and Braine, L. (2016). Smart contract
templates: foundations, design landscape and research
directions. arxiv:1608.00771. 2016.
Committee, I. F. S. (2001). Communicative act library spec-
ification. Technical report, Foundation for Intelligent
Physical Agents.
Hao, J. and Leung, H.-f. (2016). Interactions in Multiagent
Systems: Fairness, Social Optimality and Individual
Rationality. Springer Publishing Company, Incorpo-
rated, 1st edition.
Kendall, G. and Su, Y. (2003). The co-evolution of trading
strategies in a multi-agent based simulated stock mar-
ket through the integration of individual learning and
social learning. Proceedings of IEEE, pages 2298–
2305.
Klems, M., Eberhardt, J., Tai, S., H
¨
artlein, S., Buchholz,
S., and Tidjani, A. (2017). Trustless intermediation in
blockchain-based decentralized service marketplaces.
In Maximilien, M., Vallecillo, A., Wang, J., and Oriol,
M., editors, Service-Oriented Computing, pages 731–
739, Cham. Springer International Publishing.
Kravari, K. and Bassiliades, N. (2015). A survey of agent
platforms. Journal of Artificial Societies and Social
Simulation, 18.
Kumar, M., Nikhil, N., and Singh, R. (2020). Decentralis-
ing finance using decentralised blockchain oracles. In
2020 International Conference for Emerging Technol-
ogy (INCET), pages 1–4.
Lesser, V., editor (1995). First international Conference on
Multiagent Systems. The AAAI Press.
Mas-Colell, A., Whinston, M. D., and Green, J. R. (1995).
Microeconomic theory, volume 1. Oxford University
Press New York.
Trading Agent Competition with Autonomous Economic Agents
581

Maull, R., Godsiff, P., Mulligan, C., Brown, A., and Kewell,
B. (2017). Distributed ledger technology: Applica-
tions and implications. Strategic Change, 26(5):481–
489.
McBurney, P., Van Eijk, R. M., Parsons, S., and Amgoud,
L. (2003). A dialogue game protocol for agent pur-
chase negotiations. Autonomous Agents and Multi-
Agent Systems, 7(3):235–273.
Minarsch, D., Hosseini, S. A., Favorito, M., and Ward,
J. (2020). Autonomous economic agents as a sec-
ond layer technology for blockchains: Framework
introduction and use-case demonstration. In 2020
Crypto Valley Conference on Blockchain Technology
(CVCBT), pages 27–35.
Neeman, Z. and Vulkan, N. (2002). Markets versus negotia-
tions: the predominance of centralized markets. Tech-
nical report, mimeo.
Novikov, D. (2016). Incentive Mechanisms for Multi-
agent Organizational Systems, volume 98, pages 35–
57. Springer.
Padgham, L. and Winikoff, M. (2004). Developing Intelli-
gent Agent Systems: A Practical Guide. John Wiley
& Sons.
Radomski, W., Cooke, A., Castonguay, P., Therien, J., Bi-
net, E., and Sandford, R. (2018). Eip 1155: Erc-1155
multi token standard. Standard, Ethereum.
Rauchs, M., Glidden, A., Gordon, B., Pieters, G., Reca-
natini, M., Rostand, F., Vagneur, K., and Zhang, B.
(2018). Distributed ledger technology systems a con-
ceptual framework. Technical report, Cambridge Cen-
tre for Alternative Finance.
Shoham, Y. and Leyton-Brown, K. (2008). Multiagent
Systems: Algorithmic, Game-Theoretic, and Logical
Foundations. Cambridge University Press.
Sonenberg, L., Stone, P., Turner, K., and Yolum, P. (2012).
Introduction to the special issue ten years of au-
tonomous agents and multiagent systems. Ai Maga-
zine, 33:11–13.
von Neumann, J. and Morgenstern, O. (1944). Theory of
Games and Economic Behavior. Princeton Classic
Editions. Princeton University Press.
Walras, L. (2014). Principles of economics: unabridged
eighth edition. Cambridge University Press.
Wood, G. et al. (2014). Ethereum: A secure decentralised
generalised transaction ledger. Ethereum project yel-
low paper, 151(2014):1–32.
Wooldridge, M. (2009). An Introduction to MultiAgent Sys-
tems. Wiley, 2 edition.
SDMIS 2021 - Special Session on Super Distributed and Multi-agent Intelligent Systems
582