Advances in Hybrid Evolutionary Algorithms for

Fuzzy Flexible Job-shop Scheduling: State-of-the-Art Survey

Mitsuo Gen

1,3 a

, Lin Lin

1,2 b

and Hayato Ohwada

Fuzzy Logic Systems Institute, Tokyo, Japan

School of Software, Dalian University of Technology, Dalian, China

Tokyo University of Science, Tokyo, Japan

Keywords: Flexible Job-shop Scheduling Problem (FJSP), Fuzzy Scheduling, Evolutionary Algorithm (EA), Genetic

Algorithm (GA), Swarm Intelligence (SI), Particle Swarm Optimization (PSO), Cooperative Co-Evolution

Algorithm (CEA).

Abstract: Flexible job shop scheduling problem (FJSP) is one of important issues in the integration of research area and

real-world applications. The traditional FJSP always assumes that the processing time of each operation is

fixed value and given in advance. However, the stochastic factors in the real-world applications cannot be

ignored, especially for the processing times. In this paper, we consider FJSP model with uncertain processing

time represented by fuzzy numbers, which is named fuzzy flexible job shop scheduling problem (F-FJSP). We

firstly review variant FJSP models such as multi-objective FJSP (MoFJSP), FJSP with a sequence dependent

& set time (FJSP-SDST), distributed FJSP (D-FJSP) and a fuzzy FJSP (F-FJSP) models. We secondly survey

a recent advance in hybrid genetic algorithm with particle swarm optimization and Cauchy distribution

(HGA+PSO) for F-FJSP and hybrid cooperative co-evolution algorithm with PSO & Cauchy distribution

(hCEA) for large-scale F-FJSP. We lastly demonstrate the HGA+PSO and hCEA show that the performances

better than the existing methods from the literature, respectively.

1 INTRODUCTION

The scheduling problem is an important research

topic as it is an interface between typical

combinatorial optimization problems (COP) in the

research area and application models in real-world

production systems (Palacios et al 2015). Shop

problems receive particular attention because they

can model many situations and describe the flexibility

of production systems (Pinedo 2016). Flexible job

shop scheduling (FJSP), which is an extended version

of job shop scheduling (JSP), is a typical shop

problem and is widely studied and applied. FJSP can

be viewed as a combination of two subproblems: the

operation sequence (OS) problem, which means

sequencing all operations of jobs in a reasonable

order, and machine assignment (MA) problem, which

means assigning the suitable and available machine

for each ordered operation. Each operation processed

on different machines has a different machine has a

different processing time.

https://orcid.org/0000-0002-3670-1357

https://orcid.org/0000-0003-1615-6045

https://orcid.org/0000-0001-5621-6984

Most researchers assumed that the processing

time of job was a determined value. In fact, this

assumption is too idealistic as uncertain and

ambiguous factors cannot be ignored in actual

production systems (Behnamian 2016). By modeling

parameters in scheduling problems as fuzzy numbers

such as a triangle fuzzy number (TFN), fuzzy

scheduling can help incorporate flexibility into

scheduling algorithms, and make the scheduling model

meet the needs of users (Guiffrida & Nagi 1998).

Recently, Gao, et al (2019) reported a review on

swarm intelligence and evolutionary algorithms for

solving flexible job shop scheduling problems

including fuzzy and uncertain FJSP Models. Gu, et al

(2019) proposed an improved genetic algorithm with

adaptive variable neighbourhood search method for

solving FJSP. Gao, et al (2020) proposed a

differential evolution (DE) algorithm improved by

selection mechanism for solving fuzzy job-shop

scheduling problem in which the processing time and

due date of operation can be expressed by fuzzy

562

Gen, M., Lin, L. and Ohwada, H.

Advances in Hybrid Evolutionary Algorithms for Fuzzy Flexible Job-shop Scheduling: State-of-the-Art Survey.

DOI: 10.5220/0010429605620573

In Proceedings of the 13th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2021) - Volume 1, pages 562-573

ISBN: 978-989-758-484-8

numbers. Shi, et al (2020) proposed immune genetic

algorithm for solving a MoFJSP with fuzzy

processing time. Lin, et al (2019) proposed a hybrid

multi-verse optimization for solving the fuzzy FJSP

and Zhu and Zhou (2020) proposed a multi-micro-

swarm leadership hierarchy-based optimization

algorithm for solving the FJSP with job precedence

constraints and interval grey processing time. It is

very important to analyse recent papers published on

solution methods of Fuzzy FJSP models for creating

a future research direction and applying them to the

real-world practical problems in the manufacturing or

logistics systems based on the hybrid evolutionary

algorithms (HEA).

In this paper, we firstly review variant FJSP

models such as multi-objective FJSP, FJSP with a

sequence dependent & set time (FJSP-SDST),

distributed FJSP (D-FJSP) and fuzzy FJSP (F-FJSP)

models. We secondly survey a recent advance in

hybrid PSO with GA and Cauchy distribution

(HGA+PSO) for F-FJSP and hybrid cooperative co-

evolution algorithm with PSO & Cauchy distribution

(hCEA) for large-scale F-FJSP. Lastly we demonstrate

the HGA+PSO and hCEA show that the performances

better than the existing methods from the dataset of

FJSP and large-scale F-FJSP, respectively.

2 FLEXIBLE JSP MODELS

The FJSP consists of two sub-problems: machine

assignment and operation sequencing (Garey et al

1976 & Brucker et al 1990). The former is to select a

machine from a candidate set for each operation while

the latter is to schedule all operations on all machines

to obtain satisfactory schedules. The FJSP is very

complex and has been proven to be an NP-hard

problem (Jain et al 1998). Here is a reason to use a

metaheuristic such as a genetic algorithm (GA) for

treating JSP or FJSP models (Gen et al 1994 &

Kacem et al 2002).

Recently hybrid genetic algorithms (HGA) are

proposed to solve the complex re-entrant scheduling

problem with time windows constraint in

manufacturing HDD devices with lot size. This

problem can be formulated as a deterministic

Fm|fmls, rcrc, temp|C

MAX

problem for finding the

scheduling operations of machines in a flow-shop

environment processing fmls job family with the

objective of minimizing the makespan, C

MAX

(Chamnanlor et al 2013). Sangsawang, et al (2015)

proposed metaheuristics optimization approaches for

solving the two-stage reentrant reentrant flexible

flow-shop scheduling (RFFS) problem with blocking

constraint (FFS|2-stage,rcrc,block|Cmax) in which

they applied a hybrid GA and a hybrid particle swarm

optimization (HPSO) with Cauchy distribution.

2.1 Flexible Job-shop Scheduling

Models

Gen, et al. (1994) proposed a genetic algorithm for

solving the job-shop scheduling problem (JSP).

Cheng, et al. (1996 & 1999) reported a tutorial survey

of JSP using genetic algorithms: representation and

hybrid genetic search strategies, respectively.

Flexible job-shop scheduling problem (FJSP) is

an extension of the traditional job-shop scheduling

problem, which provides a closer approximation to

real scheduling problems. The FJSP can be viewed as

a combination of two subproblems: the operation

sequence (OS) problem, which means sequencing all

operations of jobs in a reasonable order, and machine

assignment (MA) assignment problem, which means

assigning the suitable and available machine for each

ordered operation. Each operation processed on

different machines has a different processing time.

The maximum completion time of the jobs is defined

as makespan. The objective is to minimize the

makespan by optimizing the OS and MA. In the job-

shop scheduling problem (JSP), there are n jobs that

must be processed on a group of m machines. Each

job i consists of a sequence of m operations (o

, o

…, o

), where o

(the k-th operation of job i) must be

processed without interruption on a predefined

machine m

for p

time units. The operations o

, o

…, o

must be processed one after another in the

given order and each machine can process at most one

operation at a time. In a flexible job-shop, each job i

consists of a sequence of n

operations (o

, o

,…, o

ini

). The FJSP extends JSP by allowing an operation o

to be executed by one machine out of a set A

of given

machines. The processing time of operation o

machine j is p

ikj

> 0. The FJSP problem is to choose

for each operation o

a machine M(o

) ∈ A

and a

starting time s

at which the operation must be

performed. Wang, et al (2012) reported a hybrid

genetic algorithm combined a population

improvement strategy for solving the multi-objective

FJSP. The flexible job shop scheduling problem is as

follows: n jobs are to be scheduled on m machines and

each job i contains n

ordered operations.

The multiobjective FJSP (Mo-FJSP) model

minimizing 1) the makespan, 2) the maximum

machine workload and 3) the total workload, will be

formulated as a multiobjective mixed integer

programming (MoMIP) model as follows (Gen,

Cheng & Lin 2008).

Advances in Hybrid Evolutionary Algorithms for Fuzzy Flexible Job-shop Scheduling: State-of-the-Art Survey

563

}{maxmin

M ik

ct =

(1)

}{maxmin

(2)



min

(3)

jiKkcxtc

ikiikjikjik

,;,...,2,0.t.s

)1(

∀=≥−−

−

(4)



∀=

ikj

ikx

,,1

(5)

0)[(]0)[( ≥−−∨≥−−

ikjhgjikjhgikikjhgjhgjikhg

xxtccxxtcc

jghki ),,(),,(∀

(6)

ikjx

ikj

,,},1,0{ ∀∈

(7)

ikc

,,0 ∀≥

(8)

The objective functions accounts Eq. (1) is to

minimize the makespan, Eq. (2) is to minimize the

maximal machine workload (i.e., the maximum

working time spent at any machine), Eq. (3) is to

minimize the total workload (i.e., the total working

time over all machines). Inequality (4) states that the

successive operation has to be started after the

completion of its precedent operation of the same job,

which represents the operation precedence

constraints. Eq. (5) states that one machine must be

selected for each operation. Inequality (6) is a

disjunctive constraint, where one or the other

constraint must be observed. Eqs. (7, 8) are variable

restrictions. Gao, Gen and Sun (2006) developed a

new hybrid GA to solve the flexible job-shop

scheduling problem with non-fixed availability

constraints. Gao, Gen, Sun and Zhao (2007) proposed

a hybrid of genetic algorithm combined the bottleneck

shifting for solving multiobjective flexible job-shop

scheduling problems, Gao, Sun and Gen (2008) also

proposed a hybrid genetic algorithm (HGA)

combined with variable neighbourhood descent

(VND) method for solving multiobjective FJSP

model. Gen, Gao and Lin (2009) reported a

multistage-based genetic algorithm (MSGA) with

bottleneck shifting developed for treating the

multiobjective FJSP model. Recently Gong, Deng,

Gong and Liu (2018) proposed a memetic algorithm

(MA) for solving multi-objective flexible job-shop

problem with worker flexibility in which the MA is

one of evolutionary algorithms.

2.2 SDST and Distributed FJSP Models

Most researches of the job-shop scheduling problems

ignored the setup times or considered them as a part

of the processing time. However, in many real-life

situations such as chemical, printing, pharmaceutical

and automobile manufacturing, the setup times are

not only often required between jobs but they are also

strongly dependent on job itself (sequence

independent) and the previous job that ran on the

same machine (sequence dependent). Hence,

reducing setup times is an important task to improve

shop performance (Azzouz, et al 2016). The FJSP has

been widely studied by various methods, however,

few papers have considered this problem with setup

In this Subsection, we introduced the FJSP with a

sequence dependent setup times (SDST). The realistic

application based on the FJSP-SDST model SDST

constraints will be considered manufacturing

scheduling systems for the TFT-LCD (thin-film

transistor-liquid crystal display) in Section: TFT-

LCD Module Assembly Scheduling (Chou et al

2014).

The distributed and flexible jobshop scheduling

problem (DFJSP) is a multi-factory manufacturing

environment and a manufacturing system comprising

several sub-systems (also called manufacturing cells)

in which each cell is a flexible job-shop. DFJS

examples can be a multi-factory network in which

factories are geographically distributed, and can be a

multi-cell plant where several manufacturing cells are

located in the same plant. To reduce overall

completion time, the assignment of jobs to cells is

very important because it shall affect cell loading

profiles. In summary, a DFJS problem involves three

scheduling decisions: 1) job-to-cell assignment, 2)

operation sequencing, and 3) operation-to-machine

assignment (Liu et al 2014).

In the FJSPs, it involves the following problems:

1) the operation sequence for each machine;

2) the precedence constraints for the operations

involved in a job; and

3) machine selection with due consideration of

machine capability constraints.

DFJSPs can be considered as an extension of

FJSPs, but also the selection of suitable factories or

flexible manufacturing units since assigning specific

jobs to different factories results in dissimilar

production schedules, in which influences the supply

chain (Liu et al 2014). Recently, Lu et al (2018)

proposed a new and concise chromosome

representation which models a 3-dimensional

scheduling solution for solving distributed and flexible

job-shop scheduling problem (DFJSP) models.

SDMIS 2021 - Special Session on Super Distributed and Multi-agent Intelligent Systems

564

Table 1: List of Fuzzy FJSP or Uncertain FJSP models and methodology.

Authors (year)

Mathematical or

Problem models

Objectives Methodology

Journal or

Proceedings

Tsujimura, Gen, Kubota

(1995)

Fuzzy-JSP

Triangle Fuzzy Num

Fuzzy makespan Genetic Algorithm

J. Japan Soc. of Fuzzy

The. & Sys.

Kuroda, Wang (1996) Fuzzy-JSP Fuzzy makespan Genetic Algorithm Int. J. Prod. Econ.

Sakawa, Mori (1999)

Fuzzy-JSP

Fuzzy Due Date

Makespan Genetic Algorithm Comput. & Ind. Eng.

Niu, Jiao, Gu (2008) Fuzzy-JSP Makespan

Hybrid Particle Swarm

Opt. & GA

Appl. Math. Comput.

Lei (2010a)

FJSP, Fuzzy processing

time

Fuzzy makespan Genetic Algorithm Int. J. Prod. Res.

Lei (2010b)

FJSP, Fuzzy processing

time

Fuzzy makespan

Swarm Intelligence,

neighborhood search

Comput. & Ind. Eng.

Lei (2010c)

F-JSP, Fuzzy

processing time

Fuzzy makespan

Random key genetic

algorithm

Int. J. Adv. Manuf.

Technol.

Wang, Gao, Zhang, Li

(2012)

Mo-FJSP, Fuzzy

processing time

Tardiness, makespan

Multi-objective Genetic

Algorithm

Int. J. Comp. Appl.

Technol.

Lei (2012)

FJSP, Fuzzy processing

time

Fuzzy makespan

Co-evolutionary genetic

algorithm

Appl. Soft Comput.

Zheng, Li, Lei (2012)

Mo-FJSP, Fuzzy

processing time

Makespan, Tardiness

Multiobjective swarm,

neighborhood search

Int. J. Adv. Manuf.

Technol.

Lei, Guo (2012)

FJSP, Fuzzy processing

time

Makespan

Swarm Intelligence,

neighborhood search

Int. J. Prod. Res.

Wang, Wang, Xu and

Liu (2013)

Mo-FJSP, Fuzzy

processing time

Fuzzy makespan

Estimation of

Distribution Algorithm

Int. J. Product. Res.

Li, Pan (2013)

FJSP, Fuzzy processing

time

Fuzzy makespan Hybrid discrete PSO

Int. J. Adv. Manuf.

Technol.

Hao , Lin, Gen and

Chien (2014)

Bi-criteria stochastic

JSP

Makespan, Tardiness

Markov Network based

EDA

Proc. IEEE Conf. Auto.

Sci. & Eng.

Xu, Wang, Wang, Liu

(2015)

FJSP, Fuzzy processing

time

Fuzzy makespan

Teaching-learning

based Optimization

Neurocomputing

Xu, Wang, Wang and

Liu (2015)

FJSP-Fuzzy processing

time

Fuzzy makespan,

Teaching–Learning

based Optimization

Neurocomputing

Palacios, Gonzlez,

Vela, et al (2015a)

FJSP-Fuzzy processing

time

Fuzzy makespan Coevolutionary EA Fuzzy Sets. Syst.

Palacios, Gonzlez,

Vela, et al (2015b)

FJSP-Fuzzy processing

time

Fuzzy makespan Genetic tabu search Comput. & Oper. Res.

Hao, Gen, Lin and Suer

(2017)

Bi-criteria stochastic

JSP

Makespan, Tardiness Multiobjective EDA J. Intelligent Manuf.

Jamrus, Chien, Gen,

Sethan (2018)

Fuzzy FJSP Fuzzy makespan

Hybrid PSO + GA +

Cauchy distribution

IEEE Trans. Semicon.

Manuf.

Sun, Lin, Li, Gen

(2019)

Stochastic FJSP Expected makespan

Cooperative Co-EA

MRF-based decomp.

Mathematics

Lin, Zhu, Wang (2019) Fuzzy FJSP Fuzzy makespan

Hybrid multi-verse

optimization (HMVO)

Comput. & Ind. Eng.

Sun, Lin, Gen, Li

(2019)

Fuzzy FJSP Fuzzy makespan

Cooperative Co-

Evolution algorithm

IEEE Trans. Fuzzy

Systems

Gao, Wang, Pedrycz,

(2020)

Fuzzy Job-shop

Scheduling Problem

Fuzzy makespan and

due date

DE algorithms with

selection mechanism

IEEE Trans. on Fuzzy

Systems

Shi, Zhang, Li (2020) Mo-FJSP

Fuzzy Makespan and

Energy consumption

immune genetic

algorithm

Int. J. Simulation

Modelling

Zhu, Zhou (2020)

FJSP-Interval grey

processing time

Fuzzy makespan, Inter.

grey makespan

Multi-micro-swarm

leadership hierarchy

Comput. & Ind. Eng.

Advances in Hybrid Evolutionary Algorithms for Fuzzy Flexible Job-shop Scheduling: State-of-the-Art Survey

565

3 FUZZY OR UNCERTAIN FJSP

MODELS

The traditional FJSP always assumes that the

processing time of each operation is fixed value and

given in advance. However, the stochastic factors in

the real-world applications cannot be ignored,

especially for the processing times (Hao et al 2014,

Sun et al 2019). The fuzzy number can be

transformed into an interval number on the basis of a

cut set such as a triangle fuzzy number (TFN). It

translates interval data into real number data through

a specific pre-processing procedure, and then carries

out principle component analysis for a real number

data set. In practice, processing times can be more

accurately represented as intervals with the most

probable completion time somewhere near the middle

of the interval. A fuzzy number which is essentially a

generalized interval can represent this processing

time interval exactly and naturally. The fuzzy number

typically represents more information than an interval

number does.

An overview of the articles on fuzzy or stochastic

FJSP based on the genetic algorithms or related

metaheuristics is given in Table 1. For each article it

separated by Authors, Mathematical or Problem

models, Objectives, Methodology, and Journal or

Proceedings without sequence dependent setup times

(SDST) or distributed FJSP models.

4 FUZZY FJSP MODEL BY

HGA+PSO+CAUCHY

Since the production for semiconductor wafer

fabrication changes rapidly, a scheduling solution

must be able to obtain a near-optimal solution within

a short time that has crucial effects on the overall

efficiency of semiconductor manufacturing (Wang et

al 2015). Indeed, most of wafer fabrication machines

can perform multiple operations, while the processing

time depends on the selected machines. Furthermore,

wafer fabrication scheduling is increasingly

complicated, since multi-chamber machines

equipped with advanced process control and

advanced equipment control. Here is a reason to

combine a fuzzy theory with the manufacturing

(Jamrus et al 2018).

4.1 Mathematical Model of Fuzzy FJSP

In the fuzzy FJSP, each job i consists of a sequence

of ni operations, an operation o

will be executed by

one machine out of a set A

of given machines. The

fuzzy processing time of operation o

on machine j is

˜p

ikj

with a positive integer. The FJSP needs choosing

for each operation oik a machine M(o

) ∈ A

and a

starting time s

that the operation must be performed.

For formulating a F-FJSP model to find the job

sequence which minimizes the makespan with fuzzy

processing time, we assume is the following issues:

1) Each job is processed on one machine at a time.

2) Every machine processes only one job at a time.

3) The setup time for the operations is sequence

independent and are included in the processing

time.

4) The operation sequence of a job is specified in

advance.

5) There are no precedence constraints among

operations of different jobs.

6) The operations are not pre-emptive once an

operation has started. That is, it cannot be

stopped until it has finished.

The typical fuzzy flexible job-shop scheduling

problem (F-FJSP) model minimizing a fuzzy

completion time is formulated as a mixed nonlinear

integer programming (MNIP):

}

max{

min

M in

cc =

(9)

inkjxpcc

iikjikjkiik

∀=∀≥−

−

;,...,2;,

~~~

.t.s

)1(

(10)



∈

∀=

ikj

ikx ,,1

(11)

jghkipxxcc

hgjikjhgjikhg

),,(),,(

∀≥−

(12)

ikjx

ikj

,,},1,0{ ∀∈

(13)

ikc

,,0

∀>

(14)

Eq. (9) is used to minimize the maximum flow time.

Inequality (10) ensures that operations are indexed in

the order they are processed. Eq. (11) states that one

machine could be selected from the set of available

machines of the operation. Inequality (12) ensures

that two operations are not overlapping if both of

them are assigned on the same machine. Eqs. (13) and

(14) are variable restrictions.

To solve a fuzzy FJSP in which the max operation

of two triangular fuzzy numbers (TFNs) are the

plainness and flexibility of the fuzzy arithmetic

operations and the ranking method of fuzzy numbers,

the addition operation is used to calculate the fuzzy

makespan of an operation. The max operation is used

to determine the fuzzy beginning time of an

operation, in which the ranking method is to compare

SDMIS 2021 - Special Session on Super Distributed and Multi-agent Intelligent Systems

566

the maximum fuzzy makespans and we can refer it for

the detailed procedures (Jamrus et al 2018).

4.2 Hybrid GA with PSO & Cauchy

Distribution

Particle Swarm Optimization (PSO) as one of

evolutionary algorithms (EA) is a randomized

population-based optimization method based on the

simulation of social iterations by the flocking

behavior of birds and human social interactions

(Kennedy 1997 and Yu & Gen 2010). It is initialized

with a population of random candidate solutions as

particles (Kennedy & Eberhart 1995). It combines a

local search according to self-experience and a global

search according to neighboring experience, thus

demonstrating high search efficiency. The position of

each particle such as the kth particle x

(t) is a potential

solution of the problem. Each particle remembers the

best position thus far during the search process

bestk

), and knows the global best position of the

swarm (g

best

). The particle’s fitness can be calculated

by entering its position in a designated objective

function as shown in the following equations:

))()(())()(()()1(

2211

txtgrctxthrctvtv

kkkkk

−+−+=+

(15)

)1()()1( ++=+ tvtxtx

kkk

(16)

where h

(t): the historically local best position of the

kth particle, g(t): the global best position of the

swarm, c

and c

positive constants, called the

acceleration constants, r

, r

∈ [0,1]: uniform random

numbers. The PSO is to find optimal regions of

complex search spaces through the interaction of

individuals in a population of particles.

However, PSO cannot yield good solutions for

large scale problems including high-dimensional

variables. For solving this problem, a basic idea

proposes new mutation operation by using the effective

particles moving by the Cauchy distribution. The

Cauchy distribution has a Gaussian-like peak wing that

imply occasional long jumps among local sampling.

)1()1()1(

)1(

+++++

tvtvtv

kNkk



(17)

))1,0[

tan()1()1( randtuts

⋅⋅+=+

(18)

)1()()1( ++=+ tstxtx

kkk

(19)

where u

(t) and s

(t) are variables from updating each

position k in generation t according to the Cauchy

distribution for evaluating each particle and updating

the h

bestk

and g

best

values of the current particle.

Pseudocode of the hybridized PSO with GA and

Cauchy distribution designed as follows (Figure 1):

Algorithm: HGA+PSO for Fuzzy FJSP (minimize

makespan)

Input: problem data and PSO (f(x), v

(0), [hbest

], gbest, b

) and GA parameters (popSize, maxGen, p

, p

)

Output: the best solution: gbest

Process:

1: t <- 0;

2: initialize x

(t) by operation & machine-based encoding;

P(t) ={x

(t)}

3: evaluate x

(t) by decoding and keep the best solution;

4: while (not terminating condition) do end;

5: for each particle x

(t) in swarm do

6: update velocity v

(t+1) using (15);

7: calculate u

(t+1) and s

(t+1) using (17) and (18);

8: update position x

(t+1) using (19) & adjust x

(t+1)

by rounding routine;

9: evaluate x

(t+1) by decoding routine;

10: if f(x

(t+1)) < f(hbest

) then

11: update hbesl

= x

(t+1); update the local best;

12: end

13: if f(x

(t+1)) < f(gbest) then

14: update gbest = x

(t+1); update the global best

15: P(t) = x

(t+1) & create offspring C(t) from P(t) by WMX;

16: create offspring C(t) from P(t) by insertion mutation;

17: check-and-repair C(t) for feasible solution;

18: evaluate C(t) by decoding routine and update best

solution gbest;

19: reproduce P(t+1) from P(t) and C(t) by selection;

19: t <- t+1;

20: end;

Figure 1: Pseudocode of the hybrid PSO with GA and

Cauchy distribution.

4.3 Numerical Experiment by

HGA+PSO

Six problems were generated and all problems

represented different numbers of jobs, operators, and

machines. Each problem was characterized by the

following parameters: number of jobs (n), number of

machines (m), and each operation o

of job i. One

problem instances were a 3×3 problem consisting of

three jobs and three machines as shown in Table 2.

Table 2: 3×3 problem consisting of 3 jobs & 3 machines.

Processing time M

(4,6,7) (1,2,3) (1,2,4)

(3,5,6) (1,2,4) (1,3,4)

(5,8,9) (2,3,4) (1.2.3)

(1,2,3) (2,4,5) (5,6,7)

(2,5,6) (2,3,4) (1,2,3)

(4,6,7) (1,2,4) (1,3,5)

(4,8,9) (2,4,6) (1,2,3)

(5,7,9) (3,4,7) (1,2,3)

(2,3,5) (1,2,3) (1,2,4)

Advances in Hybrid Evolutionary Algorithms for Fuzzy Flexible Job-shop Scheduling: State-of-the-Art Survey

567

In addition, the benchmarks of instances 1 and 2 (Jia

et al 2014) were selected for fuzzy processing time,

for which the author used a decomposition integration

genetic algorithm (DIGA).

To demonstrate the efficiency and effectiveness of

the HGA+PSO in solving a fuzzy FJSP with uncertain

processing time, each numerical experiment was

performed 10 time with maxIter = 500. Moreover, the

PSO parameters for the numerical experiments

included number of particles = 50. For the GA, the

probability of crossover was 0.8 and the probability

of mutation was 0.2. The proposed algorithms were

run using Matlab on a 2.10 GHz PC.

The performance of PSO and HGA+PSO was

evaluated using test problems of different sizes. The

computational results from comparing the best and

average makespans of each solution were derived.

The best scheduling of the 3×3 problem was achieved

by using the HGA+PSO and is shown in Figure 2.

However, the combined approach obtained average

computational time for the best solution.

Table 3 presents ANOVA results, which show a

36.78% improvement from the fuzzy flexible job-

shop scheduling. The percentage improvement

differed significantly from actual practices at the 95%

reliability level and yielded a P value less than 0.05.

The parameter describing this difference was the

fluctuation of demand at 60% of an average of which

yielded the highest average improvement.

Figure 2: The best solution of problem 3x3 by HGA+PSO.

Table 3: Results of ANOVA Analysis.

No.

Factor

Average value of fuzzy

makes

an [unit time]

% of

Pro. % PSO HPSO+GA

1-5 1 20 55.50 32.00 42.34

6-10 1 40 55.84 32.53 41.75

11-15 1 60 58.04 28.75 50.47

16-20 2 20 65.89 45.89 30.36

21-25 2 40 66.64 45.48 31.75

26-30 2 60 66.10 46.06 30.33

31-35 3 20 78.21 51.42 34.25

36-40 3 40 78.23 50.20 35.84

41-45 3 60 80.84 53.45 33.89

Average 67.26 42.86 36.78

The HGA+PSO were a combination of PSO and

GA. The advantages of PSO are intelligent and easy

derivation of the solution and that it can be combined

with the Cauchy distribution for effective particle

movement. The advantage of HGA+PSO is that it

finds the solution quickly and the better solution is

acceptable. Thus, the HGA+PSO outperform the

conventional approaches for solving an FJSP under

uncertain processing time.

5 LARGE-SCALE FUZZY FJSP

Most researchers assumed that the processing time of

job was a determined value. In fact, this assumption

is too idealistic as uncertain and ambiguous factors

cannot be ignored in actual production systems

(Behnamian 2016). Fuzzy sets can provide a bridge

between classical problem models and the needs of

users in real-world applications. Moreover, fuzzy sets

have contributed to enhancing the robustness and

applicability of scheduling (Palacios et al 2015). By

modelling parameters in scheduling problems as

fuzzy numbers, fuzzy scheduling can help incorporate

flexibility into scheduling algorithms, and make the

scheduling model meet the needs of users (Ouelhadj

et al 2009).

The increasing scale of FJSP models results in an

exponential increase in the size of the solution space.

Therefore, the performance of traditional EAs always

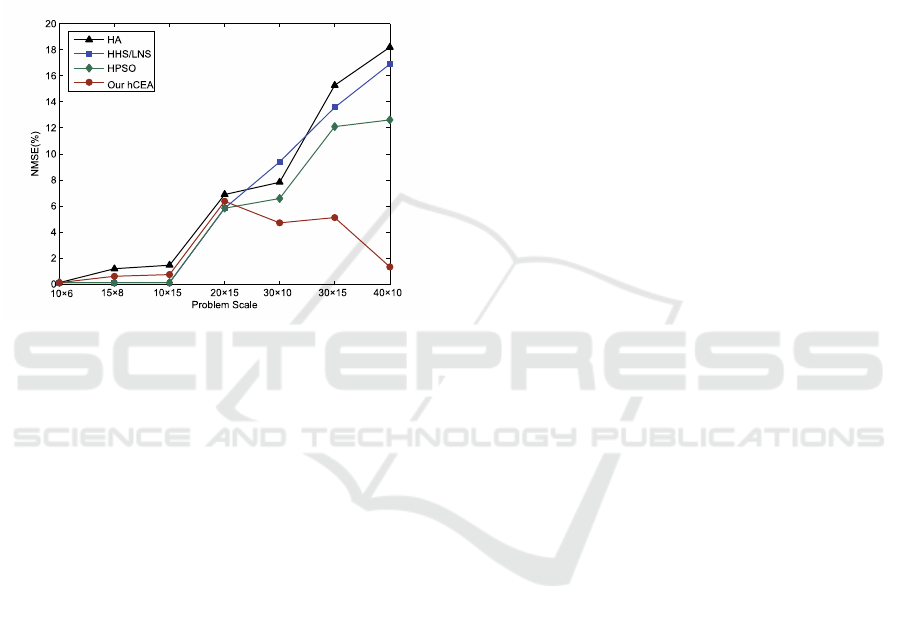
decrease with the increasing problem size, as shown

in Figure 3 (Sun et al 2019). To overcome high

dimensional issues, a divide-and-conquer (D&C)

strategy is a natural approach. Recently, the

cooperative coevolution (CC) framework has become

popular in the research area of high dimensional

optimization, especially for large- scale mathematical

function optimization (Wang et al 2018).

5.1 Mathematical Model of Fuzzy FJSP

In the FJSP, a number of jobs must be scheduled

according to a given sequence of all operations and

assigned the corresponding machines involving the

various constraints. As mentioned early section, the

FJSP consists of two subproblems: OS and MA. The

objective is to find a schedule with minimum

makespan C

max

. The assumptions are as follows:

Each job is only processed once and the

processing time involves the transfer and setup

times.

Each operation can be processed on any available

machine.

SDMIS 2021 - Special Session on Super Distributed and Multi-agent Intelligent Systems

568

3) Each machine can only process one operation at

a time without interruption.

There exist predetermined precedence

constraints among operations within a job.

Machine breakdowns are not considered. The

processing time in Fuzzy FJSP is represented as

a triangular fuzzy number (TFN).

The objective of F-FJSP is to find a schedule with

the minimum fuzzy makespan. For the detailed

operation on the triangular fuzzy number, we can

refer several references such as Gen and Cheng

(2000) and Sun, Lin, Gen and Li (2019).

Figure 3: Trend chart of algorithm performance.

A nonlinear mixed integer programming model is

used to formulate F-FJSP and the detail is shown as

follows:

]}}

[max{max{max]

[min

max

ikj

jki

tECE =

(20)

ikj

ptt

where +=



∀≤

ikj

kix

,1.t.s

(21)

)1(,,

)1(

−∀≥−

−

kkjiptt

ikj

jki

ikj



(22)

jtxtx

txtx

jikjik

ikjikj

jikjik

ikjikj

∀⋅≤⋅

∧⋅≤⋅



====

)

111

（

( 2 3 )

kjix

ikj

,,}1,0{ ∀∈

(24)

jkitt

ikj

,,,0

∀≥

(25)

where the purpose of objective function (20) is to

minimize the fuzzy makespan, (21) ensures that each

machine can only process one operation at a time

without interruption; (22) and (23) denote the

operation precedence constraints, and state that the

successive operation must start after the completion

of its previous operation of the same job; and (24) and

(25) define the domain of variables.

To solve a large scale F-FJSP in which the max

operation of two triangular fuzzy numbers (TFNs) are

the plainness and flexibility of the fuzzy arithmetic

operations and the ranking method of fuzzy numbers,

the addition operation is used to calculate the fuzzy

makespan of an operation. The max operation is used

to determine the fuzzy beginning time of an

operation, in which the ranking method is to compare

the maximum fuzzy makespans and we can refer it for

the detailed procedures (Sun et al 2019).

5.2 Hybridizing Cooperative EA+PSO

5.2.1 Representation and Genetic Operation

The design of evolutionary representation is a

significant issue in EAs as it represents the possible

potential solutions of problems. The fuzzy FJSP can

be viewed as a combination of two subproblems: how

to perform the operations by an OS, and how to

allocate a machine to each operation.

In the hCEA, the job-based and integer-based

encodings are adopted for the OS string and MA

string, respectively (Gen et al 2009). An illustration

of multistage representation for GA is shown in

Figure 4, in which the length of these two strings are

both equal to n

, which denotes the number of total

operations. The OS string consists of the integers

ranging from 1 to the maximum job number n. By

scanning the OS string, the kth appearance of integer

i denotes O

. The MA string consists of the integers

ranging from 1 to the maximum machine number m.

Each integer requires a modular |M

| arithmetic to

ensure feasibility, where |M

| represents the size of

the available machine set for O

As one of the main genetic operators, crossover

plays an important role because suitable genetic

operations can pass the parents’ good features to the

offspring. In this paper, we applied two crossover

operators: precedence operation crossover (POX)

and job-based order crossover (JOX) to the OS

string. The selection operator simulating the rule of

“survival of the fittest” in nature makes efficient

search possible by reserving superior individuals and

eliminating inferior individuals. We adopt both

ranking selection and tournament selection.

5.2.2 Cooperative Coevolution Algorithm

Recently, Sun et al (2019) is designed a CE

framework for scheduling problems with suitable

Advances in Hybrid Evolutionary Algorithms for Fuzzy Flexible Job-shop Scheduling: State-of-the-Art Survey

569

representation and evolutionary operators. The hybrid

EA is embedded into the CE framework and is called

hybrid cooperative coevolution algorithm (hCEA).

The D&C technique decomposes one solution

space to be addressed into several sub solutions,

which is regarded as an effective strategy for solving

large-scale problems. Yao et al proposed a CE

framework that was used to solve large-scale

mathematical function problems with

nonindependent variables (Li & Yao 2012). Yao et al.

first provided the theoretical proof from the

probabilistic view as well. The theoretical proof

provides the reasonableness of importing CE

framework into our algorithm. The pseudocode is

given in algorithm hCEA in Figure 4.

Dynamic Grouping: The individual is

twice the number of total operations, N variables are

grouped into r groups, each subindividual contains

only part of the variables among N variables. The

popSize subindividuals with the same grouping status

form subpopulations (sub p). CEA adopts a similar

but simpler scheme. CEA adjusts group size r

randomly during the process of optimization among a

given set R = {2, 5, 10, 50, 100} when (gbest(h) is not

continuously improved. All variables are regrouped

according to new r’ (line:4–6).

Cooperative Coevolution: In CEA (Sun,

et al 2019), each individual is evaluated according

to the other individuals with the optimal performance

in the same population. This function can be

implemented by b(q, tar, ref), which reflects the

performance between the individual composed by ref

with the q

component replaced by the corresponding

component of tar and the performance of ref.b (q,

sub_ind(h), p_best(h)) returning true means that the

component of sub ind(h) has better performance.

The CEA updates p_best(h) with its q

component

replaced by the q

component of sub ind(h) (line:6–

10). The gbest is updated in the same way (line:11–

12). Then, the local best individual (lbest) is updated

through the calculated fitness. lbest is defined as the

best individual among the (u−1)

, u

, and the (u+1)

individuals (line:18–20).

Self-Adaptive Mechanism: The update

equation of PSO adopted in CEA is expressed as

(h+1) = p

best

(h) + C(1) · |p

best

(h)− g

best

(h)| (26)

where

C(1) represents a Cauchy distribution with 1 as

the parameter. pbest(h) and gbest(h) represent the

personal best individual and the global best individual

in the h

generation, respectively. The new update

strategy is written for searching wider solution space

as follows:

(h+1) = p

best

(h) + N(0,1) · |p

best

(h)− l

best

(h)| (27)

where lbest(h) represents the neighborhood best

individual in the h

generation. N(0,1) represents

standard normal distribution. To strike a balance

between local search and global search, two update

strategies are combined, which can be rewritten as

follows:











≥+

otherwise.),1(

)1,0(randif),1(

)1(

phx

(28)







otherwise,

(0,1)if,N(0.5,0.3)

(29)

where f

is a selection probability. The hCEA adjusts

the selection probability p according to (29). In this

paper, the number of generations for adjusting p is set

to 15.

Algorithm: Hybrid CEA+PSO

Input: Data sets; maxGen; isAdjust

Output: Best solution gbest(h);

Process:

1: get sub p(h) by random grouping, s = N/r;

2: gen(h) ← 0

3: while (gen(h) < maxGen) do

4: if (isAdjust) then

5: adjust the grouping status, s_ = N/r_;

6: for each group q do

7: for each individual sub ind(h) in group q do

8: if b(q, sub ind(h), pbest(h)) then

9: replace (q, pbest, sub ind(h));

10: end

11: if b(q, pbest(h), gbest(h)) then

12: replace (q, gbest, pbest(h));

13: for each individual do

14: updateLBest (lbest(h));

15: end

16: end

17: for each sub p(h) do

18: for each individual do

19: updateLBest (lbest(h));

20: end

21: end

22: Adjust parameters by self-adaptive strategy;

23: gen(h) ← gen(h +1);

24: end

Figure 4: Pseudo code of Hybrid CEA algorithm.

5.3 Numerical Experiments by HCEA

To verify the superiority of the proposed hybrid

cooperational coevolution algorithm (hCEA) in

minimizing the maximum fuzzy makespan, an

existing set of instances and a generated set of

instances are adopted in this paper as numerical

experiments (Sun, et al 2019). The scale varies from

small scale with 40 operations to large scale with 293

SDMIS 2021 - Special Session on Super Distributed and Multi-agent Intelligent Systems

570

Table 4: Performance of our HCEA Comparing with the State-of-the-Arts for the Standard FJSP.

Instance Mk01 Mk02 Mk03 Mk04 Mk05 Mk06 Mk07 Mk08 Mk09 Mk10

JobNum 10 10 15 15 15 10 20 20 20 20

MacNum 6 6 8 8 4 15 5 10 10 10

(LB,UB) (36,42) (24,32) (204,311) (48,81) (168,186) (33,86) (133,157) 523 (209,369) (165,296)

GA 42 32 212 73 185 74 154 523 321 254

GA+LS 40 27 204 66 176 65 144 523 307 208

PSO 42 32 213 74 184 73 155 523 314 245

PSO+LS 40 27 204 64 174 64 143 523 307 207

DE 42 32 210 73 184 76 153 523 316 251

DE+LS 40 27 204 64 175 65 143 523 307 206

HA 40 27 204 60 173 60 140 523 307 203

HHS/LNS 40 27 204 60 172 59 139 523 307 202

HPSO 40 27 204 60 173 59 139 523 307 202

HGA 40 26 204 61 173 59 139 523 307 202

MOGA 40 27 204 60 173 59 139 523 307 201

MAPSO 40 27 207 65 172 61 156 523 307 212

CCGP 40 26 204 61 172 60 140 523 307 202

hCEA 40 26 204 60 173 59 140 523 307 200

operations. All experiments are carried out with 30

independent repetitions. Three typical and classical

EAs, i.e., the GA, DE, and PSO, and seven state-of-

the-art algorithms, i.e., a hybrid GA (HA), hybrid

PSO (HPSO), hybrid harmony search and large-

neighborhood search (HHS/LNS), cooperative

coevolution genetic programming based

hyperheuristics (CCGP), a multiobjective GA

(MOGA), a hybrid GA with various crossovers and

mutations (HGA), and multiagent PSO (MAPSO),

are tested and compared. The instances of FJSP

dataset contain two categories, i.e., benchmarks from

Lei’s study (2010, 2012) and generated large-scale

instances based on Ghrayeb (2003).

Figure 5 is optimal solution of Case 5 found by

hCEA. It is the fuzzy Gantt chart of the optimal

solution obtained by hCEA of Case 5 shown. To show

its superiority clearly and directly, we tested our

proposed algorithm and seven state-of-the-art

algorithms on 5 regular fuzzy FJSP instances (Cases

1–5) and large-scale fuzzy instances (F-Mk10 to F-

Mk15) 30 times, and we use ANOVA with a mean

difference level of 0.05. Figure 6 is a boxplot of all

algorithms with defuzzied processing time for Case 5.

We can see our proposed hCEA has better satiability

from Figure 6. the performance of the proposed

hCEA is remarkably better than that of the other state-

of-the-art algorithms for all large-scale instances.

Figure 7 is a convergence of fuzzy makespan of all

algorithms. Table 4 is a performance of hCEA

comparing with otherer methods for F-FJSP in Case

Figure 5: Optimal solution of Case 5 got by hCEA: Case 2,

which exhibits average fuzzy makespan and the worst fuzzy

makespan.

M10

131

112

(5,7,10)

121

131

(5,7,10)

112

122

(7,10,12)

(8,12,16)

(12,17,22)

113

(12,17,22)

113

132

(13,19,26)

(14,19,23)

(16,24,34)

123

(17,26,34)

123

(18,26,33)

143

(20,30,40)

(22,32,42)

(24,33,41)

155

(26,34,49)

155

134

(26,39,52)

(28,40,53)

(31,42,51)

145

136

(32,47,62)

136

105

(31,42,61)

(36,50,63)

126

(33,50,64)

126

(6,9,11) (12,17,21) (18,25,30) (20,28,35) (29,39,48) (33,44,54) (37,50,63) (43,58,75)

(6,9,11) (12,17,21) (18,25,30) (20,28,35) (29,39,48) (33,44,54) (37,50,63)

(5,6,8) (12,17,22)

(17,26,34)

(22,32,42) (28,40,53) (32,47,62) (39,55,73)

(8,10,13) (14,19,23) (18,26,33) (24,33,41) (31,42,51) (36,50,63) (41,56,71)

(8,10,13)

(5,7,10) (11,16,22) (18,26,33) (20,30,40) (26,39,52) (33,50,64) (38,58,74)

(7,10,12) (8,12,16) (13,19,26) (16,24,34) (22,33,46) (31,42,61) (35,49,70) (39,56,79)

(31,42,61)

(8,11,15)

102

(15,19,26)

103

(21,27,36)

(30,39,53)

(33,43,58)

(38,51,70)O

(8,11,15) (15,19,26) (21,27,36) (30,39,53) (38,51,70) (41,55,75)(33,43,58)

141

(9,13,17)

(14,22,29)

(22,33,46)

104

(30,42,58)

115

(35,48,67)

115

(37,51,72)

(9,13,17) (14,22,29) (20,31,42) (30,42,58) (35,48,67) (31,41,72) (41,57,80)

151

152

(4,5,8)

101

(9,13,17)

153

(12,17,24)

153

154

(20,27,38)

154

125

(26,34,49)

135

(33,44,54)

135

(36,50,53)

(39,55,71)

(4,5,8) (9,13,17)(12,17,24) (20,27,38) (26,34,49)(31,42,60) (35,47,58) (40,57,75)(39,55,71)

(5,7,10)

142

(14,20,28)

142

133

(19,27,38)

133

(26,36,51)

(25,34,47)

(

114

(26,36,51)

(

)

(31,43,61)

)

(33,46,66)

(35,49,70)

(4,7,8) (14,20,28) (19,27,37) (25,34,47)

(31,43,61) (35,49,70) (33,46,66) (40,55,78)

(26,36,51)

111

(5,7,10)

(11,15,21)

(16,21,28)

(20,26,36)

(21,29,40)

(23,34,45)(14,22,29)

144

(27,39,53)

(33,43, 58)

116

(41,53,70)

124

144

116

124

(5,7,10) (11,15,21) (16,21,28) (20,26,36) (21,29,40)

(33,43,58)

(27,39,53)

(23,34,45)(22,31,44) (43,57,76)

(41,53,70)

Advances in Hybrid Evolutionary Algorithms for Fuzzy Flexible Job-shop Scheduling: State-of-the-Art Survey

571

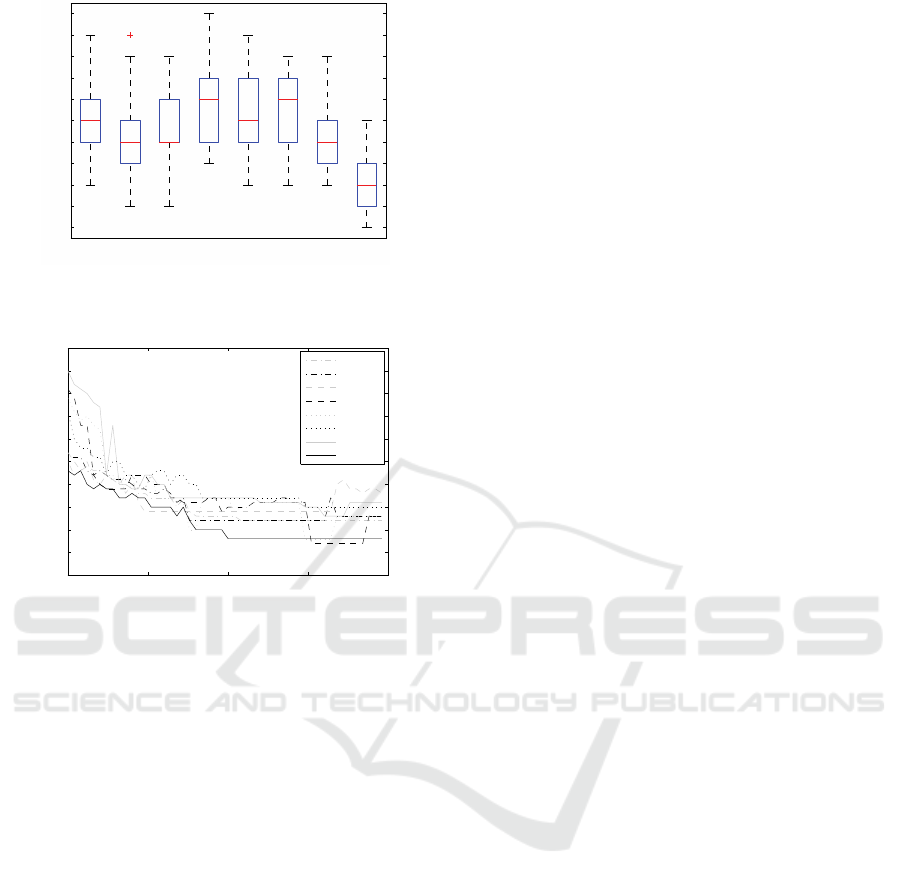
Figure 6: Boxplot of all algorithms with defuzzied

processing time: The boxplot for Case 5.

Figure 7: Convergence of fuzzy makespan of all algorithms.

6 CONCLUSIONS

Flexible job shop scheduling problem (FJSP), is one

of important issues in the integration of real-world

applications. The traditional FJSP always assumes

that the processing time of each operation is fixed

value and given in advance. However, the stochastic

factors in the real-world applications cannot be

ignored, especially for the processing times. In this

paper, we briefly reviewed variant FJSP models such

as multi-objective FJSP, FJSP-SDST, distributed and

FJSP and a fuzzy FJSP models. In particular, we

surveyed a recent advance in hybrid GA with PSO

and Cauchy distribution (HGA+PSO) for F-FJSP and

hybrid cooperative co-evolution algorithm with PSO

& Cauchy distribution (hCEA) for large-scale FJSP.

We lastly demonstrated the performances by the

HGA+PSO and hCEA show that better than the

existing methods from the literature, respectively. As

a future research direction, it should be applied hybrid

cooperative co-evolution algorithms to various real-

world practical problems in manufacturing and

logistics with the stochastic factors or interval data.

ACKNOWLEDGEMENTS

This work is partly supported by Grant-in-Aid for

Scientific Res. (C) of Japan Society of Promotion of

Science. (JSPS: No. 19K12148), the National Natural

Science Foundation of China under Grant 62076053.

The authors would like to thank to the anonymous

reviewers for their valuable comments.

REFERENCES

Palacios, J.J., I. Gonzlez-Rodrłguez, C.R. Vela, J. Puente,

2015. Coevolutionary makespan optimisation through

different ranking methods for the fuzzy flexible job

shop. Fuzzy Sets. Syst., 278, 81–97.

Pinedo, M.L., 2016. Scheduling: Theory, Algorithms, and

Systems. New York, NY, USA: Springer.

Garey, M.R., D.S. Johnson, R. Sethi, 1976. The complexity

of flow shop and job shop scheduling. Math. Oper. Res.,

1(2),117–129.

Brucker, P., R. Schlie, 1990. Job-shop scheduling with

multi-purpose machines. Computing, 45(4), 369–375.

Behnamian, J., 2016. Survey on fuzzy shop scheduling.

Fuzzy Optim. Decis. Making, 15(3), 331–366.

Guiffrida, A.L., R. Nagi, 1998. Fuzzy set theory

applications in production management research: A

literature survey. J. Intell. Manuf., 9(1), 39–56.

Jain, A.S., S. Meeran, 1998. Deterministic job-shop

scheduling: past, present and future. Eur. J. Oper. Res.,

113 (2), 390–434,

Gen, M., Y. Tsujimura, E. Kubota. 1994. Solving job-shop

scheduling problem using genetic algorithms. Proc.

IEEE Int. Conf. on Systems, Man, & Cyber., 1577-1582.

Kacem, I., S. Hammadi, and P. Borne. 2002a. Approach by

localization and multiobjective evolutionary

optimization for flexible job-shop scheduling problems.

IEEE Trans. on Systems, Man and Cyber., Part C, 32,

408-419.

Chamnanlor, C., K. Sethanan, C-F Chien, M. Gen, 2014.

Re-entrant flow shop scheduling problem with time

windows using hybrid genetic algorithm based on

autotuning strategy, Inter. J. Production Res., 52(9),

2612-1629.

Sangsawang, C., K. Sethanan, T. Fujimoto, M. Gen, 2015:

Metaheuristics optimization approaches for two-stage

reentrant flexible flow shop with blocking. Expert Sys.

with Appl., 42, 2395–2410.

Cheng R., M. Gen, Y. Tsujimura, 1996. A tutorial survey

of job-shop scheduling problems using genetic

algorithms: part I. Representation. Computers &

Industrial Eng., 30(4), 983–997.

Cheng R., M. Gen, Y. Tsujimura, 1999. A tutorial survey

of job-shop scheduling problems using genetic

algorithms: part II. Hybrid genetic search strategies.

Computers & Industrial Eng., 36(2), 343–364.

Gen, M., R. Cheng, 2000: Genetic Algorithms and

Engineering Optimization, John Wiley & Sons.

HA HPSO HHS/LNS HGA MOGA MAPSO CCGP hCEA

Algorithms

Makespan

0 500 1000 1500 2000

100

Iteration

Lei’s Ranking Criterion 2

HPSO

HHS/LNS

HGA

MOGA

MAPSO

CCGP

hCEA

SDMIS 2021 - Special Session on Super Distributed and Multi-agent Intelligent Systems

572

Wang, X., L. Gao, C. Zhang, X. Li, 2012. A multi-objective

genetic algorithm for fuzzy flexible job-shop scheduling

problem. Int. J. Comp. Appl. Technol., 45, pp. 115–125.

Gen, M., R. Cheng, L. Lin, 2008. Network Models and

Optimization: Multiple Objective Genetic Algorithm

Approach", Springer, London.

Gao, J., M. Gen, and L. Sun, 2006. Scheduling jobs and

maintenances in flexible job shop with a hybrid genetic

algorithm. J. Intel. Manuf., 17, 493–507.

Gao, J., L. Sun and M. Gen, 2008. A hybrid genetic and

variable neighborhood descent algorithm for flexible

job shop scheduling problems. Computers &

Operations Res., 35, 2892-2907.

Gen, M., J. Gao, L. Lin, 2009. Multistage-based genetic

algorithm for flexible job-shop scheduling problem. in

Intelligent and Evolutionary Systems 187, Springer,

183–196.

Gao, J., M. Gen, L. Sun and X. Zhao, 2007. A hybrid of

genetic algorithm and bottleneck shifting for

multiobjective flexible job shop scheduling problems,

Computers & Industrial Engineering, 53, 149-162.

Yu, X.J. and M. Gen, 2010: Introduction to Evolutionary

Algorithms, Springer, London.

Azzouz, A., M. Ennigrou and L.B. Said, 2016. Flexible job-

shop scheduling problem with sequence-dependent

setup times using genetic algorithm. Proc. The 18th

Inter. Conf. Enterprise Information Sys., 2:47-53.

Gong, X., Q. Deng, G. Gong, W. Liu, 2018: A memetic

algorithm for multi-objective flexible job-shop problem

with worker flexibility, Inter. J. Production Res., 56(7):

2506-2522.

Chou,, C-W, C-F Chien, M. Gen, 2014. A multiobjective

hybrid genetic algorithm for TFT-LCD module

assembly scheduling. IEEE Trans. Autom. Sci. Eng.,

11(3), 692–705.

Lin, L. and M. Gen, 2018. Hybrid evolutionary

optimization with learning for production scheduling:

state-of-the-art survey on algorithms and applications,

Int. J. of Production Research, 56(1-2): 193–223

Liu, T-K, Y-P Chen and J-H Chou, 2014. Solving

distributed flexible job-shop scheduling problem for a

real-world fastener manufacturer, IEEE Access, 2:1598-

1606.

Lu, P-H, M-C Wu, H. Tan, Y-H Peng and C-F Chen, 2018.

A genetic algorithm embedded with a concise

chromosome representation for distributed and flexible

job-shop scheduling problem, J. Intelligent Manuf.,

29:19-34.

Gao, K., Z. Cao, L. Zhang, Z. Chen, 2019. A review on

swarm intelligence and evolutionary algorithms for

solving flexible job shop scheduling problems,

IEEE/CAA J. Automatica Sinica, 6(4):904-916.

Gu, X., M. Huang, X Liang, 2019. An improved genetic

algorithm with adaptive variable neighborhood search

for FJSP. Algorithms, 12, 243, 1-16.

Hao X.C., L. Lin, M. Gen, C-F Chien, 2014. An effective

Markov network based EDA for flexible job-shop

scheduling problem under uncertainty. Proc. IEEE

Conf. on Automation Science & Eng., 131-136.

Sun, L., L. Lin, H. Li, M. Gen, 2019. Cooperative Co-

Evolution algorithm with an MRF-based decomposition

strategy for stochastic flexible job shop scheduling.

Mathematics, 7, 318, 1-20.

Wang, H-K, C-F Chien, M. Gen, 2015. An algorithm of

multi-subpopulation parameters with hybrid estimation

of distribution for semiconductor scheduling with

constrained waiting time. IEEE Trans. Semicond.

Manuf., 28(3), 353–366.

Jamrus, T., C-F Chien, M. Gen, K. Sethanan, 2018. Hybrid

particle swarm optimization combined with genetic

operators for flexible job-shop scheduling under

uncertain processing time for semiconductor

manufacturing. IEEE Trans. on Semicon. Manuf., 31(1),

32-41.

Kennedy, J., 199. The particle swarm: Social adaptation of

knowledge,” in roc. IEEE Int. Conf. Evol. Comput.,

Indianapolis, IN, USA, 303–308.

Kennedy, J., R. Eberhart, 1995. Particle swarm

optimization,” in Proc. IEEE Int. Conf. Neural Network,

Perth, WA, Australia, 39–43.

Jia, S., Z-H Hu, 2014. Path-relinking Tabu search for the

multi-objective flexible job shop scheduling problem.

Comput. Oper. Res., 47, 11–26.

Ouelhadj, D., S. Petrovic, 2009. A survey of dynamic

scheduling in manufacturing systems. J. Scheduling,

12(4), 417–431.

Wang, Y., H. Liu, F. Wei, T. Zong, X. Li, 2018.

Cooperative coevolution with formula-based variable

grouping for large-scale global optimization. Evol.

Comput., 26, 569–596.

Li, X., X. Yao, 2012. Cooperatively coevolving particle

swarms for large scale optimization. IEEE Trans. Evol.

Comput., 16(2), 210–224.

Hao, X.C., M. Gen, L. Lin and G. Suer, 2017. Bi-criteria

stochastic job-shop scheduling problem. J. Intelligent

Manuf., 28:833–845.

Lu, P-H, M-C Wu, H. Tan, Y-H Peng and C-F Chen, 2018.

A genetic algorithm embedded with a concise

chromosome representation for distributed and flexible

job-shop scheduling problem, J. Intel. Manuf., 29:19-34.

Sun, L., L. Lin, M. Gen, H. Li, 2019. A hybrid cooperative

coevolution algorithm for fuzzy flexible job shop

scheduling. IEEE Trans. on Fuzzy Sys., 27(5): 1008-

1022.

Lin, J., L. Zhu, Z.J. Wang, 2019: A hybrid multi-verse

optimization for the fuzzy flexible job-shop scheduling

problem, Computers & Indus. Eng., 127: 1089-1100.

Gao, D., G.G. Wang, W. Pedrycz, 2020: Solving fuzzy job-

shop scheduling problem using DE algorithm improved

by a selection mechanism, IEEE Trans. on Fuzzy

Systems, 28(12)3265-

Shi, D.L., B.B. Zhang, Y. Li, 2020: A multi-objective

flexible job-shop scheduling model based on fuzzy

theory and immune genetic algorithm, Int. J. Simulation

Modelling, 19(1): 123-133.

Zhu, Z.W., X.H. Zhou, 2020: Flexible job-shop scheduling

problem with job precedence constraints and interval

grey processing time, Comp. & Indus. Eng., 149:

106781.

Advances in Hybrid Evolutionary Algorithms for Fuzzy Flexible Job-shop Scheduling: State-of-the-Art Survey

573