
LDBNN: A Local Density-based Nearest Neighbor Classifier
Joel Lu
´
ıs Carbonera
a
Institute of informatics, Federal University of Rio Grande do Sul, Porto Alegre, Brazil
Keywords:
Machine Learning, Classification, Instance-based Learning.
Abstract:
K-Nearest Neighbor (KNN) is a very simple and powerful classification algorithm. In this paper, we propose
a new KNN-based classifier, called local density-based nearest neighbors (LDBNN). It considers that a tar-
get instance should be classified in a class whose the k nearest neighbors constitute a dense region, where
the neighbors are near to each other and also near to the target instance. The performance of the proposed
algorithm was compared with the performance of 5 important KNN-based classifiers. The performance was
evaluated in terms of accuracy in 16 well-known datasets. The experimental results show that the proposed
algorithm achieves the highest accuracy in most of the datasets.
1 INTRODUCTION
The KNN classifier is one of the most attractive
nonparametric techniques in pattern classification be-
cause of its simplicity, intuitiveness and effectiveness
(Wu et al., 2008; Gou et al., 2014). It has been ap-
plied in a wide range of fields, for example, for text
classification (Yong et al., 2009), for estimating for-
est parameters from remote sensing data (Reese et al.,
2005), for predicting economic events (Imandoust
and Bolandraftar, 2013), for different kinds of diagno-
sis in medicine (Sarkar and Leong, 2000; Deekshatulu
et al., 2013), for various tasks in astronomy (Ram
´
ırez
et al., 2001; Li et al., 2008), etc.
Although KNN-based classifiers often achieve
good classification performance in many practical ap-
plications, there are some well-known issues that af-
fect its performance. One of the main issues regard-
ing the approach is its sensitiveness to the choice of
the neighborhood size k. The performance of the al-
gorithm can produce very different results, depending
on the choice of k and the structure of the data (includ-
ing the presence of noise). The second issue is how
to combine the information about the neighbors of a
target instance to support its classification. Originally,
the KNN algorithm considers that the target instance
is classified according to the class of the majority of
its neighbors. Regarding this point, it is important to
notice that a given instance can be more or less repre-
sentative of its class, and this can affect its capability
of supporting the classification of a novel instance.
a
https://orcid.org/0000-0002-4499-3601
In order to deal with the issues previously men-
tioned, a number of variations of the KNN-based ap-
proaches have been developed (Dudani, 1976; Mitani
and Hamamoto, 2006; Gou et al., 2011; Gou et al.,
2014). In this paper, we propose a new KNN-based
classifier called local density-based nearest neighbors
(LDBNN). This approach assumes that the target in-
stance i should be classified in the class c whose near-
est neighbors to i occupy a dense region around i.
That is, the neighbors within class c should be closer
to i and closer to each other. This strategy makes
the LDBNN algorithm more noise-resistant, since,
in general, noisy instances do not constitute dense
regions (they tend to be sparsely distributed) (Ester
et al., 1996).
In order to evaluate the LDBNN algorithm, we
compared its accuracy in a classification task with
other 5 algorithms, in 16 well-known datasets. The
results show that LDBNN algorithm provides the
highest average accuracy in the considered scenarios.
Also, it achieves the highest accuracy in most of the
datasets. This suggests that the local density is a pow-
erful concept that can be further investigated for de-
veloping better classification algorithms.
Section 2 presents some related works. Section 3
presents the notation that will be used throughout the
paper. Section 4 presents our approach. Section 5 dis-
cusses our experimental evaluation. Finally, Section 6
presents our main conclusions and final remarks.
Carbonera, J.
LDBNN: A Local Density-based Nearest Neighbor Classifier.
DOI: 10.5220/0010402003950401
In Proceedings of the 23rd International Conference on Enterprise Information Systems (ICEIS 2021) - Volume 1, pages 395-401
ISBN: 978-989-758-509-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
395

2 RELATED WORKS
In this section, we will discuss some important classi-
fication algorithms that are based on the ideas under-
lying the KNN algorithm.
According to (Murty and Devi, 2011), the NNC
(nearest neighbor classifier) (Cover and Hart, 1967)
constitute one of the simplest classification proce-
dures. It basically classifies the target instance ac-
cording to the class of its nearest neighbor. One of
the main drawbacks of this strategy is its high sen-
sitivity to noise. The presence of noise has negative
impacts on its accuracy (Aggarwal and Reddy, 2014).
The KNN (k-nearest neighbors) (Altman, 1992;
Wu and Ai, 2008) can be viewed as a generaliza-
tion of the NNC. This algorithm classifies a target in-
stance i in the class that includes the majority of the
k nearest neighbors of i. When k = 1, the KNN is
equivalent to NNC. Since it considers more informa-
tion about the neighborhood of the target instance, the
KNN is less sensitive to noise than NNC. However,
noisy instances produce negative impacts also in the
performance of KNN. Besides that, the performance
of KNN is highly sensitive to the choice of the value
of k; the number of neighbors that it should consider.
The LMKNN (local mean-based k-nearest neigh-
bor) (Mitani and Hamamoto, 2006), adopts the notion
of local centroid for avoiding the harmful effects of
noise in the classification. A local centroid is basi-
cally an abstraction (an average) extracted from a set
of neighbors of the target instance i. The first step of
the algorithm is to identify the set NN of the k nearest
neighbors of i. After, the algorithm extracts one local
centroid for each set of neighbors that have the same
class. Finally, LMKNN classifies the target instance
i in the class of its nearest local centroid. The adop-
tion of local centroids makes LMKNN more noise-
resistant than KNN. Due to this, in general, the accu-
racy of LMKNN is higher than the accuracy achieved
by KNN.
The WKNN (distance-weighted k-nearest-
neighbor) (Dudani, 1976) adopts a weighted voting
strategy for classifying the target instance i. In this
strategy, instead of simply counting the class with
more neighbors within the k nearest neighbors of i,
the algorithm determines a weight for each class c,
which is calculated as the sum of the weight of each
neighbor of i in c. At the end, the algorithm classifies
i in the class with the lowest weight. The weight w
j
of a given neighbor n
j
is a function of its distance to
i, such that
w
i
=
d
NN
k
−d
NN
j
d
NN
k
−d
NN
1
, d
NN
k
6= d
NN
1
1, d
NN
k
= d
NN
1
(1)
, where j represents the ascending order of the neigh-
bor n
j
(which is the j-th nearest neighbor of i); and
d
NN
j
represents the distance between the target in-
stance i and the j-th nearest neighbor of i. Thus, no-
tice that the closer a neighbor is from the target in-
stance i, the greater is its weight. The goal of this
strategy is reducing the effects of the parameter k in
the performance of the algorithm.
The DWKNN (dual weighted voting k-nearest
neighbor) (Gou et al., 2011), can be viewed as an im-
provement of WKNN. It also adopts a weighted vot-
ing strategy for classifying the target instance i. The
DWKNN also classifies i in the class with the greatest
weight, which is determined as the sum of the weights
of the individual neighbors of i that belongs to that
class. The weight w
j
of a given neighbor n
j
is a func-
tion of its distance to i, such that
w
i
=
d
NN
k
−d
NN
j
d
NN
k
−d
NN
1
×
1
j
, d
NN
k
6= d
NN
1
1, d
NN
k
= d
NN
1
(2)
Notice that the main difference between WKNN and
DWKNN is regarding the inclusion of an additional
term in the formula that defines the weight of a neigh-
bor. This term increases the weights of the near-
est neighbors of i. The results show that this subtle
change significantly improves the accuracy of the al-
gorithm, compared with the WKNN.
The LMPNN (local mean-based k-nearest neigh-
bor) (Gou et al., 2014) also adopts the notion of local
centroid used by LMKNN (Mitani and Hamamoto,
2006). At a first step, the LMPNN identifies the k
nearest neighbors of i in each of the p classes used
to classify the dataset. Thus, the set of nearest neigh-
bors has k × p neighbors, instead of just the k neigh-
bors considered by other algorithms. After, for each
class, the algorithm generates k subsets of the k near-
est neighbors identified, in a way that each subset in-
cludes the j nearest neighbors of i, where 1 ≤ j ≤ k.
After, the algorithm extracts one local centroid from
each one of the k subsets, in a way that the j-th local
centroid abstracts the information about the j nearest
neighbors of i. Thus, the algorithm produces k local
centroids for each class. After, the LMPNN calculates
the weight w
j
of each local centroid lc
j
( j-th local cen-
troid) of each class, in a way that
w
j
= d(i, lc
j
) ×
1
j
(3)
That is, the weight of a given local centroid is a func-
tion of its distance to the target instance i and its order
j (in an ascending ordering of distance to the target in-
stance). The goal of the second term of the formula is
to reduce the influence of farthest local centroids. Fi-
nally, the algorithm also calculates the weight of each
ICEIS 2021 - 23rd International Conference on Enterprise Information Systems
396

class as the sum of the weights of its local centroids.
With this information, the LMPNN algorithm classi-
fies the target instance i in the class with the lowest
weight. This algorithm is highly noise-resistant and,
in general, it provides a higher accuracy, in compar-
ison with the other algorithms discussed in this sec-
tion.
In this paper, we propose an algorithm that also
decreases the effects of noise by adopting the notion
of local density.
3 NOTATIONS
In this section, we introduce the following notation
that will be used throughout the paper:
• T = {x
1
, x
2
, ..., x
n
} is a non-empty set of n in-
stances (or data objects). It represents the training
dataset.
• U = {x
1
, x
2
, ...} is a non-empty set that includes
every possible instance. Thus, this set is poten-
tially infinite. Notice that T ⊆ U .
• Each x
i
∈ U is a m − tuple, such that x
i
=
(x
i1
, x
i2
, ..., x
im
), where x
ij
represents the value of
the j-th feature of the instance x
i
, for 1 ≤ j ≤ m.
• L = {l
1
, l
2
, ..., l
p
} is the set of p class labels that
are used for classifying the instances in T , where
each l
i
∈ L represents a given class label.
• c: L → 2
T
is a function that maps a given class
label l
j
∈ L to a given set C, such that C ⊆ T , which
represents the set of instances in T whose class is
l
j
. Notice that T =
S
l∈L
c(l). In this notation, 2
T
represents the powerset of T , that is, the set of all
subsets of T , including the empty set and T itself.
• d : U ×U → R is a distance function that maps
two instances in a real number that measures the
distance (or dissimilarity) between them. This
function can be domain-dependent.
4 LDBNN ALGORITHM
As previously mentioned, the LDBNN (local density-
based nearest neighbors) algorithm is based on the
notion of local density. Intuitively, it assumes that a
given target instance i should be classified in the class
whose k nearest neighbors constitute a dense region
around i. In this context, a dense region is a region
where the instances are near to each other. It is lo-
cal in the sense that the density is being evaluated in
the context of the region that includes the k nearest
neighbors of i of each class.
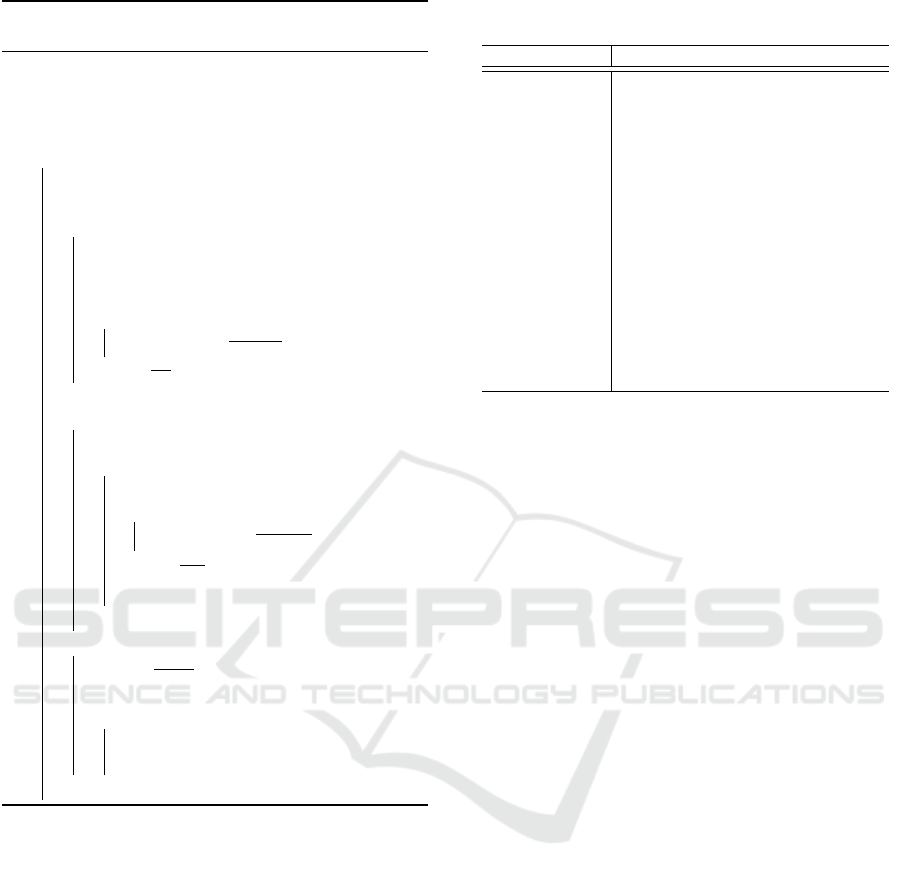
Figure 1 represents the notion of local density
adopted in this work. It represents a target instance
i and the 3 nearest neighbors of the 3 classes of the
training set: A, B and C. Notice that the training set
can have much more instances, but in this context,
our analysis is considering just these 9 instances, and
the density of the instances and classes are consid-
ered only in this context. In this example, the region
occupied by the class A is locally denser than the re-
gions occupied by the classes B and C. Besides that,
this density is distributed around the target instance i,
since all the neighbors of the class A are close to i. In
this situation, our approach assumes that the instance
i should be classified in class A.
i
A
A
A
B
B
B
C
C
C
Figure 1: Illustration of the notion of local density. The
region occupied by the class A is locally denser than the
regions occupied by the classes B and C.
In order to present the LDBNN algorithm, it is nec-
essary first to introduce some formal notions. First
of all, let us consider the function NN : U × R → 2
T
.
This function maps a target instance i ∈ U and a value
k ∈ R to a subset of T that includes the k nearest
neighbors of i in each class of the dataset. That is:
NN(i, k) =
[
l∈L
nn(i, l, k) (4)
Where nn : U × L × R → 2
T
is a function that maps a
given target instance i ∈ U, a given class label l ∈ L
and a given value k ∈ R to a subset of T that includes
the k nearest neighbors of i within c(l). That is:
nn(i, l, k) = {x|x is one of the k
nearest neighbors of i within c(l)} (5)
Another notion that is important in the context of
LDBNN is the similarity-based weight.
Definition 1. The similarity-based weight of a given
class label l ∈ L, regarding a given target instance
i ∈ U, which should be classified, and a given value
k ∈ R, represents the degree to which the k nearest
neighbors of i within the class l are similar to i. Thus,
it can be viewed as a measure of the density of the re-
gion around i within the class l. The similarity-based
LDBNN: A Local Density-based Nearest Neighbor Classifier
397

weight is given by the function sw : L ×U × R → R,
such that:
sw(l, i, k) =
∑
x∈nn(i,l,k)
1
1 + d(x, i)
(6)
Notice that the greater is the similarity-based weight
of a given class l, the closer are the k nearest neigh-
bors of l to the target instance i and the denser is the
region around i within the class l.
The LDBNN also adopts the notion of neighbor
density, which was inspired in the notion of density
adopted in (Bai et al., 2012; Carbonera and Abel,
2015; Carbonera and Abel, 2016; Carbonera, 2017).
Definition 2. The neighbor density of a given neigh-
bor n ∈ NN(i, k), of a given target instance i ∈ T
and considering a value k ∈ R, measures the density
of n within the region occupied by all the neighbors
of i, in NN(i, k). If the density of n is high, this
means that n is very similar to the other neighbors
of i. The neighbor density is given by the function
nd : T ×U ×R → R, such that:
nd(n, i, k) =
∑
x∈NN(i,k)
1
1+d(x,n)
|NN(i, k)|
(7)
With the notion of neighbor density, we can define the
notion of class density.
Definition 3. The class density of a given class l ∈ L,
regarding a target instance i ∈ T and considering a
value k ∈ R, measures the density of the region occu-
pied by the k nearest neighbors of i within the class l.
It is given by the function cd : L × T × R → R, such
that:
cd(l, i, k) =
∑
x∈nn(i,l,k)
nd(x, i, k)
|nn(i, l, k)|
(8)
The class density allows us to define the notion of
density weight.
Definition 4. The density weight of a given class
l ∈ L, regarding a target instance i ∈ T and consid-
ering a value k ∈ R, measures how dense the class l
is in comparison with the other classes, in the region
occupied by the neighbors of i, in NN(i, k). This no-
tion is captured by the function dw: L × T × R → R,
such that:
dw(l, i, k) =
cd(l, i, k)
∑
y∈L
cd(y, i, k)
(9)
Finally, at this point, we can define the notion of clas-
sification weight.
Definition 5. The classification weight of a given
class l ∈ L, regarding a target instance i ∈ T and con-
sidering a value k ∈ R, measures the degree to which
i belongs to the class l. This is given by the function
cw: L × T × R → R, such that:
cw(l, i, k) = dw(l, i, k) × sw(l, i, k) (10)
Thus, the classification weight of a given class is basi-
cally the multiplication of its similarity weight and its
density weight. According to this, the higher are the
similarity weight and the density weight, the higher is
the classification weight.
Considering to the previously presented no-
tions, the LDBNN can be viewed as a function
LDBNN : U × R → L, which maps a target instance
i ∈ U and a value k ∈ R to the class label l ∈ L that
classifies i, such that:
LDBNN(i, k) = l|l ∈ L ∧ ∀y ∈ L :
cw(y, i, k) ≤ cw(l, i, k) (11)
Thus, LDBNN identifies the class l ∈ L that has the
higher classification weight for the target instance i ∈
U and a value k ∈ R. The algorithm 1 provides an
implementation of this strategy.
5 EXPERIMENTS
In our evaluation process, we have compared the
LDBNN algorithm with 5 important instance-based
classification algorithms provided by the literature:
KNN, WKNN, DWKNN, LMKNN and LMPNN.
We considered 16 well-known datasets: Audiology,
Breast cancer, Cars, Diabetes, E. Coli, Glass, Iono-
sphere, Iris, Letter, Mushroom, Promoters, Segment,
Soybean
1
, Splice, Voting, Zoo. All datasets were ob-
tained from the UCI Machine Learning Repository
2
.
In Table 1, we present the details of the datasets that
were used.
For evaluating the accuracy of the algorithms,
we adopted a leave-one-out schema. Thus, for a
given dataset and classification algorithm, each in-
stance was classified using the remaining instances of
the dataset as the training set. At the end, we com-
puted the accuracy of the algorithm in the considered
dataset as the ratio between the number of correctly
classified instances and the number of instances in
the whole dataset. Since that the algorithms KNN,
WKNN, DWKNN, LMKNN and LMPNN need a pa-
rameter k, in our experiments we followed the strat-
egy adopted by (Gou et al., 2014), which considered
the values of k in the interval [1,15]. Thus, we carried
out a complete leave-one-out evaluation process for
1
This dataset combines the large soybean dataset and its
corresponding test dataset.
2
http://archive.ics.uci.edu/ml/
ICEIS 2021 - 23rd International Conference on Enterprise Information Systems
398
Algorithm 1: LDBNN (Local Density-based
Nearest Neighbors) algorithm.
Input: A target instance i, the training set T
and the number k of neighbors.
Output: A class label cl that classify i, such
that cl ∈ L.
begin
MAX ← 0;
class ← null;
all ←
/
0; foreach l ∈ L do
KNN
l
← nn(i, l, k);
all ← all
S
KNN
l
;
sw
l
← 0;
foreach x ∈ KNN
l
do
sw
l
← sw
l
+
1
1+d(x,i)
;
sw
l
←
sw
l
k
;
totalD ← 0;
foreach l ∈ L do
cD
l
← 0;
foreach x ∈ KNN
l
do
nD ← 0;
foreach y ∈ all do
nD ← nD +
1
1+d(x,y)
;
nD ←
nD
|all|
;
cD
l
← classD
l
+ nD;
totalD ← totalD + cD
l
;
foreach l ∈ L do
dw
l
←
cD
l
totalD
;
cW
l
← sw
l
× dw
l
;
if cW
l
> MAX then
MAX ← cW
l
;
class ← l;
return class;
each value of k. This process produces 15 accuracy
values for each combination of algorithm and dataset
(one accuracy value for each value of k). Finally,
from this set of values, we select the greatest accuracy
value obtained by each algorithm in each dataset. The
accuracies obtained during our experiments are pre-
sented in Table 2.
In this evaluation process, we adopted the follow-
ing distance function d : T × T → R:
d(x, y) =
m
∑
j=1
θ
j
(x, y) (12)
where
θ
j
(x, y) =
(
α(x
j
, y
j
), if j is a categorical feature
|x
j
− y
j
|, if j is a numerical feature
(13)
Table 1: Details of the datasets used in the evaluation pro-
cess.
Dataset Instances Attributes Classes
Audiology 226 70 24
Breast cancer 286 10 2
Cars 1728 6 4
Diabetes 768 9 2
E. Coli 336 8 8
Glass 214 10 7
Ionosphere 351 35 2
Iris
150 5 3
Letter 20000 17 26
Mushroom 8124 23 2
Promoters 106 58 2
Segment 2310 20 7
Soybean 683 36 19
Splice 3190 61 3
Voting 435 17 2
Zoo 101 18 7
where
α(x
j
, y
j
) =
(
1, if x
j
6= y
j
0, if x
yj
= y
j
(14)
This distance function was also adopted in (Carbonera
and Abel, 2015) for dealing with data that is described
by both numerical and categorical values.
Table 2 shows that the LDBNN algorithm
achieves the highest accuracy in most of the datasets
and also achieves the highest average accuracy. Also,
although the results achieved by LDBNN are similar
to the ones achieved by LMPNN in some datasets,
it is important to notice that in some datasets (Au-
diology and Breast cancer, for example) the perfor-
mance of LDBNN is significantly better than the per-
formance of LMPNN. Besides that, only in the Seg-
ment dataset the performance of LMPNN was higher
than the performance of LDBNN, and the difference
between the accuracy achieved by both the algorithms
is very small. This shows that LDBNN and LMPNN
have different profiles of performance and suggests
that the notions that underly the LDBNN algorithm
can be used for developing better algorithms in the
future.
6 CONCLUSION
In this paper, we propose a novel knn-based algorithm
called LDBNN (Local Density-based nearest neigh-
bors). This algorithm considers that a target instance
should be classified in a class whose the k nearest
neighbors constitute a dense region, where the neigh-
bors are near to each other and also near to the target
instance. This strategy makes the algorithm more re-
sistant to the effects of noise in the dataset, since noisy
LDBNN: A Local Density-based Nearest Neighbor Classifier
399
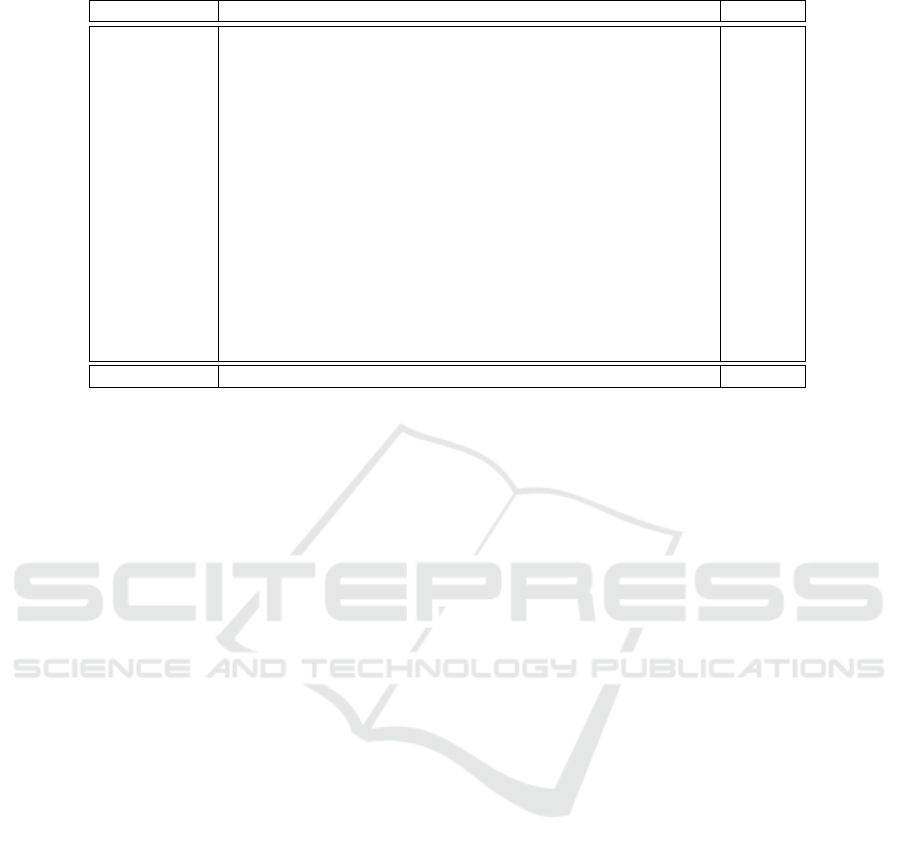
Table 2: The accuracy of each algorithm in each dataset.
Algorithm KNN WKNN DWKNN LMKNN LMPNN LDBNN Average
Audiology 0.73 0.73 0.76 0.73 0.73 0.80 0.75
Breast cancer 0.73 0.73 0.74 0.66 0.71 0.76 0.72
Cars 0.70 0.70 0.95 0.93 0.93 0.95 0.86
Diabetes 0.69 0.69 0.71 0.73 0.72 0.75 0.71
E. Coli 0.82 0.82 0.83 0.87 0.86 0.87 0.84
Glass 0.73 0.73 0.75 0.75 0.76 0.76 0.75
Ionosphere 0.91 0.91 0.91 0.92 0.91 0.91 0.91
Iris 0.95 0.95 0.95 0.97 0.96 0.96 0.96
Letter 0.96 0.96 0.97 0.97 0.97 0.97 0.97
Mushroom 1.00 1.00 1.00 1.00 1.00 1.00 1.00
Promoters 0.78 0.78 0.79 0.80 0.86 0.89 0.82
Segment 0.97 0.97 0.97 0.97 0.98 0.97 0.97
Soybean 0.92 0.92 0.92 0.91 0.93 0.93 0.92
Splice 0.79 0.79 0.80 0.75 0.84 0.87 0.81
Voting 0.92 0.92 0.93 0.93 0.94 0.94 0.93
Zoo 0.96 0.96 0.96 0.98 0.98 0.98 0.97
Average 0.85 0.85 0.87 0.87 0.88 0.89 0.82
instances, are sparsely distributed, in general.
The experiments show that LDBNN achieves the
highest accuracy in most of the considered datasets
and the highest average accuracy. Also, the LDBNN
algorithm is the only algorithm whose accuracy is
higher than the average in all datasets. Although, in
some datasets, the LDBNN achieves accuracy rates
that are similar to those achieved by other algorithms
(such as LMPNN), in some datasets it provides much
higher accuracy rates. This suggests that the concepts
underlying the LDBNN algorithm are powerful no-
tions that should be investigated in the future for de-
veloping better classification algorithms.
In the future, we plan to investigate how to com-
bine the LDBNN algorithm with other algorithms
that achieve a significant performance, such as the
LMPNN algorithm.
REFERENCES
Aggarwal, C. C. and Reddy, C. K., editors (2014). Data
Clustering: Algorithms and Applications. CRC Press.
Altman, N. S. (1992). An introduction to kernel and nearest-
neighbor nonparametric regression. The American
Statistician, 46(3):175–185.
Bai, L., Liang, J., Dang, C., and Cao, F. (2012). A cluster
centers initialization method for clustering categorical
data. Expert Systems with Applications, 39(9):8022–
8029.
Carbonera, J. L. (2017). An efficient approach for instance
selection. In International conference on big data
analytics and knowledge discovery, pages 228–243.
Springer.
Carbonera, J. L. and Abel, M. (2015). A density-based ap-
proach for instance selection. In IEEE 27th Interna-
tional Conference on Tools with Artificial Intelligence
(ICTAI), pages 768–774. IEEE.
Carbonera, J. L. and Abel, M. (2016). A novel density-
based approach for instance selection. In IEEE 28th
International Conference on Tools with Artificial In-
telligence (ICTAI), pages 549–556. IEEE.
Cover, T. M. and Hart, P. E. (1967). Nearest neighbor pat-
tern classification. IEEE TRansactions on Information
Theory, 13(1):21–27.
Deekshatulu, B., Chandra, P., et al. (2013). Classification
of heart disease using k-nearest neighbor and genetic
algorithm. Procedia Technology, 10:85–94.
Dudani, S. A. (1976). The distance-weighted k-nearest-
neighbor rule. IEEE Transactions on Systems, Man,
and Cybernetics, (4):325–327.
Ester, M., Kriegel, H.-P., Sander, J., Xu, X., et al. (1996).
A density-based algorithm for discovering clusters in
large spatial databases with noise. In Kdd, volume 96,
pages 226–231.
Gou, J., Xiong, T., and Kuang, Y. (2011). A novel weighted
voting for k-nearest neighbor rule. Journal of Com-
puters, 6(5):833–840.
Gou, J., Zhan, Y., Rao, Y., Shen, X., Wang, X., and He, W.
(2014). Improved pseudo nearest neighbor classifica-
tion. Knowledge-Based Systems, 70:361–375.
Imandoust, S. B. and Bolandraftar, M. (2013). Application
of k-nearest neighbor (knn) approach for predicting
economic events: Theoretical background. Interna-
tional Journal of Engineering Research and Applica-
tions, 3(5):605–610.
Li, L., Zhang, Y., and Zhao, Y. (2008). k-nearest neigh-
bors for automated classification of celestial objects.
Science in China Series G: Physics, Mechanics and
Astronomy, 51(7):916–922.
Mitani, Y. and Hamamoto, Y. (2006). A local mean-based
nonparametric classifier. Pattern Recognition Letters,
27(10):1151–1159.
Murty, M. N. and Devi, V. S. (2011). Nearest neighbour
ICEIS 2021 - 23rd International Conference on Enterprise Information Systems
400

based classifiers. In Pattern Recognition, pages 48–
85. Springer.
Ram
´
ırez, J. F., Fuentes, O., and Gulati, R. K. (2001).
Prediction of stellar atmospheric parameters using
instance-based machine learning and genetic algo-
rithms. Experimental Astronomy, 12(3):163–178.
Reese, H., Granqvist-Pahl
´
en, T., Egberth, M., Nilsson, M.,
and Olsson, H. (2005). Automated estimation of forest
parameters for sweden using landsat data and the knn
algorithm. In Proceedings, 31st International Sympo-
sium on Remote Sensing of Environment.
Sarkar, M. and Leong, T.-Y. (2000). Application of k-
nearest neighbors algorithm on breast cancer diagno-
sis problem. In Proceedings of the AMIA Symposium,
page 759. American Medical Informatics Association.
Wu, X., Kumar, V., Quinlan, J. R., Ghosh, J., Yang, Q.,
Motoda, H., McLachlan, G. J., Ng, A., Liu, B., Philip,
S. Y., et al. (2008). Top 10 algorithms in data mining.
Knowledge and information systems, 14(1):1–37.
Wu, Y. and Ai, X. (2008). Face detection in color images
using adaboost algorithm based on skin color infor-
mation. International Workshop on Knowledge Dis-
covery and Data Mining, 0:339–342.
Yong, Z., Youwen, L., and Shixiong, X. (2009). An im-
proved knn text classification algorithm based on clus-
tering. Journal of computers, 4(3):230–237.
LDBNN: A Local Density-based Nearest Neighbor Classifier
401
