
AutoGE: A Tool for Estimation of Grammatical Evolution Models
Muhammad Sarmad Ali
a
, Meghana Kshirsagar
b
, Enrique Naredo
c
and Conor Ryan
d
Biocomputing and Developmental Systems Lab, University of Limerick, Ireland
Keywords: Grammatical Evolution, Symbolic Regression, Production Rule Pruning, Effective Genome Length.
Abstract: AutoGE (Automatic Grammatical Evolution), a new tool for the estimation of Grammatical Evolution (GE)
parameters, is designed to aid users of GE. The tool comprises a rich suite of algorithms to assist in fine tuning
BNF grammar to make it adaptable across a wide range of problems. It primarily facilitates the identification
of optimal grammar structures, the choice of function sets to achieve improved or existing fitness at a lower
computational overhead over the existing GE setups. This research work discusses and reports initial results
with one of the key algorithms in AutoGE, Production Rule Pruning, which employs a simple frequency-
based approach for identifying less worthy productions. It captures the relationship between production rules
and function sets involved in the problem domain to identify optimal grammar structures. Preliminary studies
on a set of fourteen standard Genetic Programming benchmark problems in the symbolic regression domain
show that the algorithm removes less useful terminals and production rules resulting in individuals with
shorter genome lengths. The results depict that the proposed algorithm identifies the optimal grammar
structure for the symbolic regression problem domain to be arity-based grammar. It also establishes that the
proposed algorithm results in enhanced fitness for some of the benchmark problems.
1 INTRODUCTION
Grammatical Evolution (GE), since its inception
twenty years back, has found wide acceptance in the
research communities (Ryan et al 2018). It is a
bioinspired population-based methodology from the
domain of evolutionary. Its ability to produce
arbitrary valid data structures and the way executable
programs can be evolved has created wide-scale
appeal. Moreover, due to its simple approach of
evolving programs constrained through the definition
of BNF grammar and the ability to adapt to domain
knowledge through it makes it a valuable tool.
GE uses an innovative mapping scheme in which
variable-length input genomes (also known as
chromosomes or genotype) are represented in binary
form and get mapped to the output program or
phenotype. The values in the genotype control the
choice of production rules and the resulting
phenotype then gets evaluated based on the definition
a
https://orcid.org/0000-0002-7223-5322
b
https://orcid.org/0000-0002-8182-2465
c
https://orcid.org/0000-0001-9818-911X
d
https://orcid.org/0000-0002-7002-5815
of fitness functions that gives a fitness score to the
individuals in the population.
Although the selection and definition of fitness
criteria is dependent on the problem and/or the
problem domain, there exists a good body of
knowledge which serves as guidelines (Koza 1993).
This, however, is not the case when a user is faced
with the problem of choosing a function set and
defining a grammar. There is little guidance in the
literature and no systematic approach exists (Wang
2005, Uy 2013).
Automatic Grammatical Evolution (AutoGE) is
an initiative to create a tool that can aid users to define
and identify proper grammar structures to smoothly
adapt to the application under consideration. Its suite
of algorithms will enable GE users to design
appropriate BNF rules using the right grammar
structures. This will mainly help the users in
identifying appropriate terminals involved in forming
production rules. The algorithm will also facilitate the
selection of correct fitness function definition. Fitness
functions can be composed of single, multiple or
1274
Ali, M., Kshirsagar, M., Naredo, E. and Ryan, C.
AutoGE: A Tool for Estimation of Grammatical Evolution Models.
DOI: 10.5220/0010393012741281
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 1274-1281
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

many objectives. They can be hierarchical in nature.
As such AutoGE will serve to automate the selection
of grammar structure, function sets and fitness
functions depending on the nature of the underlying
problem and its complexity. AutoGE’s suite of
algorithms are designed in a manner to automatically
assist in evolving individuals of shorter lengths
thereby optimizing memory usage (Kshirsagar 2020).
AutoGE’s rich suite of powerful algorithms also
automatically address bloats (Bleuler 2008) through
restricting tree size and tree nodes thereby reducing
computational overhead and complexity (Murphy
2020).
2 BACKGROUND
2.1 Grammatical Evolution (GE)
Grammatical Evolution is a variant of Genetic
Programming (GP) in which the space of possible
solutions is specified through a grammar (Ryan
1998). Although different types of grammars have
been used, the most commonly used is Context Free
Grammar (CFG), generally written in Backus-Naur
Form (BNF). GE facilitates a modular design, which
means that any search engine can be used, although
typically a variable-length Genetic Algorithm (GA) is
employed to evolve a population of binary strings.
In GE, each population individual has a dual
representation, a genotype and a phenotype. When the
underlying search engine is a genetic algorithm, the
genotype is a sequence of codons (a group of 8-bit
substrings), while the phenotype expresses an
individual's representation in the solution space.
Mapping, a key process in GE, maps a given genotype
to the phenotype. While subsequently consuming
each codon, it selects a production from the available
set of alternative productions in a rule and builds the
derivation tree. Although there are other mapping
schemes (Fagan 2018), the conventional scheme
follows left-most derivation.
An important measure in the mapping process is
the effective genome length, which is equal to the
number of codons consumed to generate a fully
mapped individual (the one which does not contain
any non-terminals in this phenotype). The actual
genome length is the total number of codons in the
genome, some of which may remain unused.
2.2 Grammar Design in GE
Since GE exploits the expressive power of grammars,
it can be applied to a multitude of problem domains,
for instance in Symbolic Regression (SR) where the
purpose is to search the space of mathematical
expressions to find a model that best fits a given
dataset (Koza 1993). To construct valid and useful
mathematical expressions in GE, the grammar needs
to be well designed.
A grammar is formally defined as the tuple (T, N,
P, S) where T is a set of terminal symbols, N is a set
of non-terminal symbols, P is a set of production
rules, and S is the start symbol. While the set of
terminals outline the building blocks of a solution, the
choice of non-terminals and deciding how exactly to
organize those into a set of rules and productions is a
design task. By designing an appropriate grammar,
one specifies the syntactic space of possible solutions.
2.2.1 Grammar Structures
Instead of designing grammar from scratch, a
common approach is to utilize and adapt existing
grammar designs for that domain. For example, in
grammatical evolution based symbolic regression
(GESR), typical grammar structures are shown in
Table 1. In a mixed-arity grammar, operations of
multiple arities are combined in a single rule. A
contrasting design is that of arity-based grammars
where productions relevant to arity-1 and arity-2
operations are grouped in separate rules. A balanced
grammar version balances the probabilities of
selecting recursive (non-terminating) productions and
terminating production (Nicolau 2018).
It is important to note how operators and functions
are represented as productions in the grammar.
Besides embodying arithmetic operators, a number of
common mathematical functions are represented as
alternative recursive productions.
Table 1: Grammar structures for symbolic regression.
Mixed-arity
Grammar
<expr> ::= <expr><op><expr>
|sin(<expr>)|cos(<expr>)
|exp(<expr>)|pow(<expr>,2)
|sqrt(<expr>)|<var>
<op> ::= + | - | * | /
<var> ::= X | Y
Arity-based
Grammar
<expr>::= <expr1>|<expr2>|<var>
<expr1>::=sin(<expr>)|cos(<expr>)
|exp(<expr>)|pow(<expr>,2)
|sqrt(<expr>)
<expr2> ::= <expr><op><expr>
<op> ::= + | - | * | /
<var> ::= X | Y
Balanced
Arity-
b
ased
Grammar
<expr> ::= <expr1>|<var>
|<expr2>|<var>
... # The rest is the same as arity-based
AutoGE: A Tool for Estimation of Grammatical Evolution Models
1275
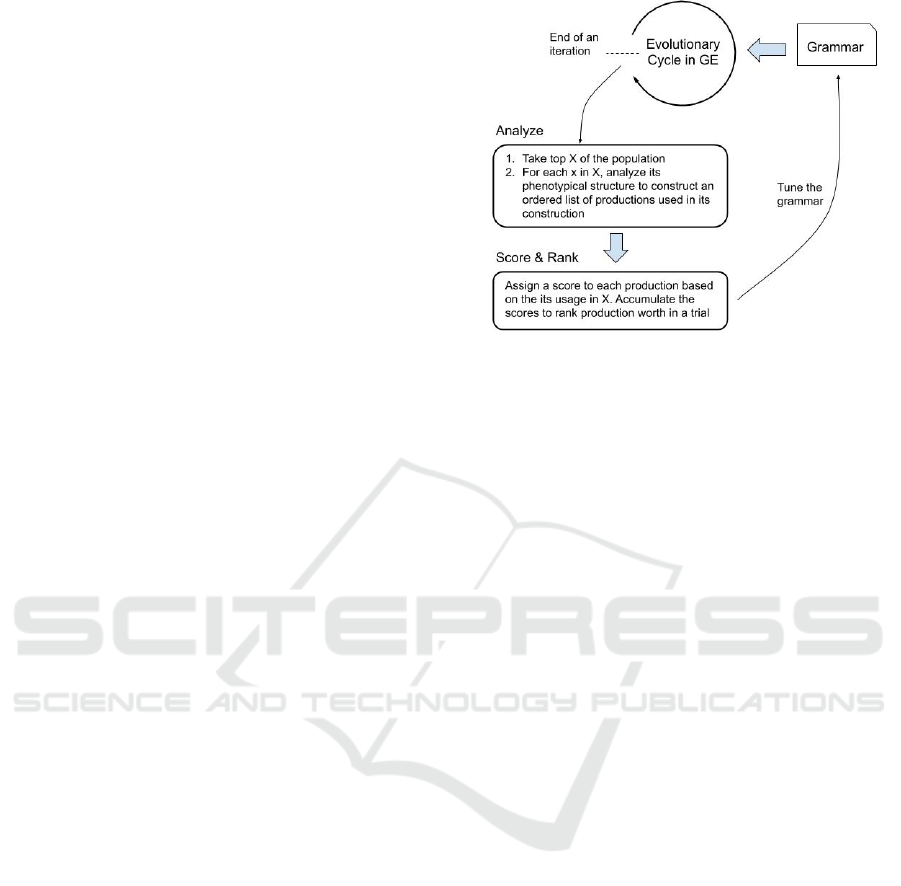
3 METHODOLOGY
We discuss our approach to rank grammar
productions and subsequently pruning of unworthy
productions in this section. Figure 1 depicts the
overall schematic of our approach.
3.1 Production Ranking
With the correct configuration and fitness criteria, an
evolutionary process is geared towards convergence.
Increasingly, the evolved solutions contain more and
more of the right ingredients or building blocks (in
our case, grammar productions). We hypothesize that
the structural composition of evolved solutions
carries information that can be useful in identifying
the right ingredients.
In GE, every individual in the population is
composed of terminals which appear in an order
defined by the derivation tree constructed during
genotype to phenotype mapping. By traversing the
derivation tree, it is possible to obtain a list of
grammar productions used in the mapping process to
generate an individual. Such a list is termed as the
production-list. Once identified, the frequency of
usage of each production in the production-list can be
easily determined.
Productions can be weighed or ranked based on
how frequently they are used in the construction of
individuals in the population. As evolution proceeds,
fitter individuals survive, and the productions which
more frequently shape the structures are the ones that
are considered to be worthy being part of the
grammar. Such productions are assigned a high rank.
On the contrary, productions which harm individual's
fitness such that they become extinct, generally do not
enjoy high usage frequency (although rarely zero, due
to hitch-hiking effects) in the population.
To test our hypothesis, we devised a simple
frequency-based approach to rank productions. Since
frequency counting is a trivial and efficient operation,
it carries minimal overhead. The two basic production
ranking schemes are:
Normalized Frequency-based Ranking (NFR):
This is the simplest ranking scheme where
frequencies of the productions in production-list are
normalized to unity. We compute ranking scores
offline, at the end of each evolutionary cycle (see
Figure 1), which bears minimal overhead. Note that
this does not take the fitness of individuals into
consideration, rather simply the survival of
production rules.
Figure 1: Schematic of production ranking and pruning
cycle. Information about the use of each production rule is
harvested after each iteration and subsequently used to tune
to the grammar.
Fitness Proportionate Ranking (FPR): In this
scheme, the normalized ranks are multiplied with the
individual’s fitness.
An important consideration is to decide how much
of the population to select for ranking. We
experimented with three possible choices: 1) the
whole population, 2) all unique individuals, 3) top
X% of the population (we use X=20, a completely
arbitrary number that seemed reasonable). Potential
issues include, with the 1st option, rankings can be
biased due to repeated individuals, and with the 3rd
option there was a chance of pruning important
productions. The second option turned out to be the
best choice based on our empirical evaluations.
Once individual ranking scores have been
computed, we accumulate the scores to compute run
worth of a production. Figure 2 shows a sample box
and whisker plot of FPR ranking for Pagie-1 problem.
It exposes a nice picture of the utility of each
production in the evolutionary cycle.
3.2 Grammar Pruning
We follow the principle of Occam’s razor which
states “no more things should be presumed to exist
than are absolutely necessary.” Grammar is a key
model of the solution space, so the idea is to remove
unnecessary or less worthy productions (or functions)
from the grammar to tune the grammar design.
The key driver in grammar tuning is the pruning
strategy and the algorithm. There can be a number of
strategies for pruning and we look at two here. The
key concept they have in common is a staged
approach; that is, a small number of runs is
conducted, then one or more rules are pruned, and
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
1276
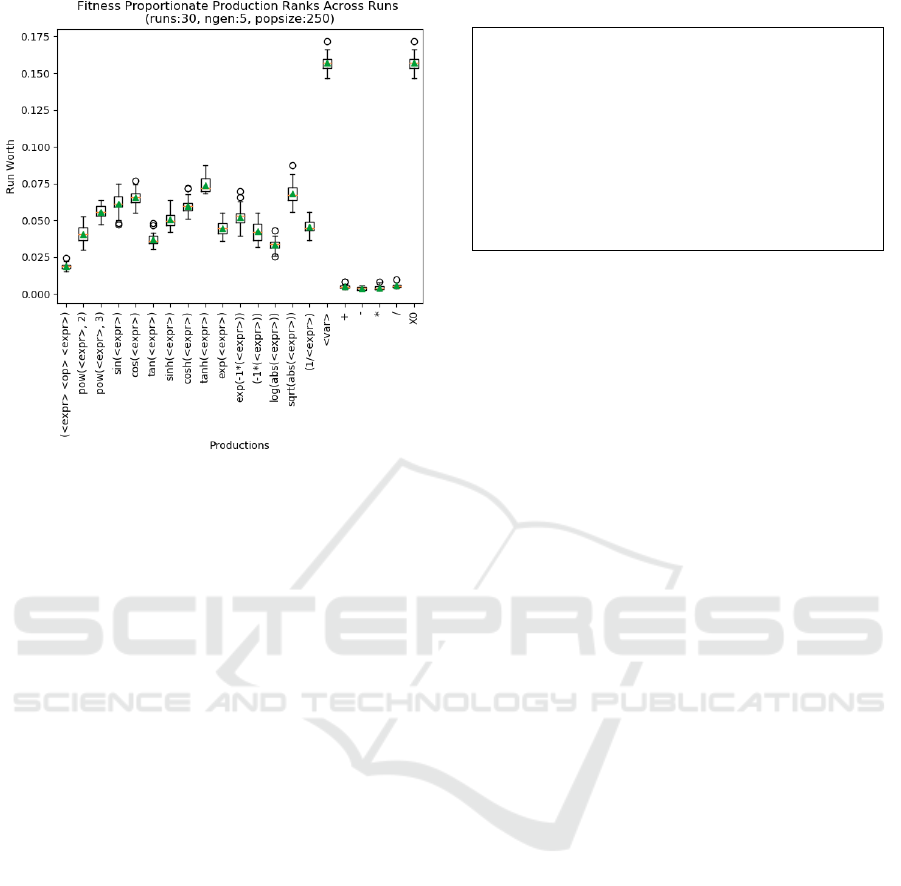
Figure 2: Fitness Proportionate Production ranks across
runs for Pagie-1 problem (runs: 30, ngen: 5, popsize 250).
then more runs are conducted. This second stage (also
true for third and subsequent stages, if they exist) is a
complete restart with the newly modified grammar.
The exact algorithm depends on the strategy being
employed. We experimented with the following two
strategies:
● Strategy 1: Prune for the maximum available
budget. The remaining runs will verify if it was
fruitful.
● Strategy 2: Only proceed with pruning if it results
in improving mean training score at each stage. If
it degrades performance, stop.
Strategy 1 has slightly less overhead but suffers from
blind pruning which in many cases failed to reap any
benefits. For instance, in case of Keijzer-6 problem,
this strategy pruned the production carrying
logarithm function, which is a vital approximating
function for this problem.
Strategy 2 incorporates a feedback loop which
informs on its usefulness. In our preliminary
experiments, we have observed it to be yielding a
much better overall outcome. Coupled with the
pruning policies defined in section 4.3, our
Production Rule Pruning algorithm achieved
excellent results.
3.2.1 Production Rule Pruning Algorithm
The outlines the Production Rule Pruning (PRP)
algorithm is shown in Listing 1:
Listing 1: PRP Algorithm.
procedurePRP():
Prunings=Empty
Stage=0;AvailableBudget=20%;PruningGen=5
DofullrunsforPruningGengenerations
SetthetrainingperformancescoreE
trg
(0)andPRUNE
WhilethereisAvailableBudget:
Proceedtopruningstagei
DofullrunsforPruningGengenerationsandgetE
trg
(i)
IfE
trg
(i)<E
trg
(i‐1):PRUNE
IfE
trg
(i)>E
trg
(i‐1):REVERT
DecrementAvailableBudget
PRUNE is the key procedure in the algorithm. It
performs two important functions:
1) It analyses production ranking scores and
identifies the least worthy productions. Based on
the pruning policy, it identifies how many
productions to prune at a given stage and returns
that many productions as candidates to be pruned.
2) It removes productions from the grammar and
adds them to
Prunings, which is implemented as
a stack. At each stage, pruned productions are
pushed to the stack.
The REVERT function undoes the last pruning action
by popping the last productions from
Prunings and
adding them back to the grammar. When a pruning
stage reverts, the
PruningGen is incremented from 5
to 10.
3.2.2 Consistency of Pruning Suggestions
The output of the PRP algorithm is pruning
suggestions. In order to verify how consistent the
pruning suggestions are, we ran 100 experiments on
certain problems for each grammar structure and
ranking scheme. Each experiment consisted of 50
independent runs evolving for 5 generations with a
population size of 250. Due to space limitations,
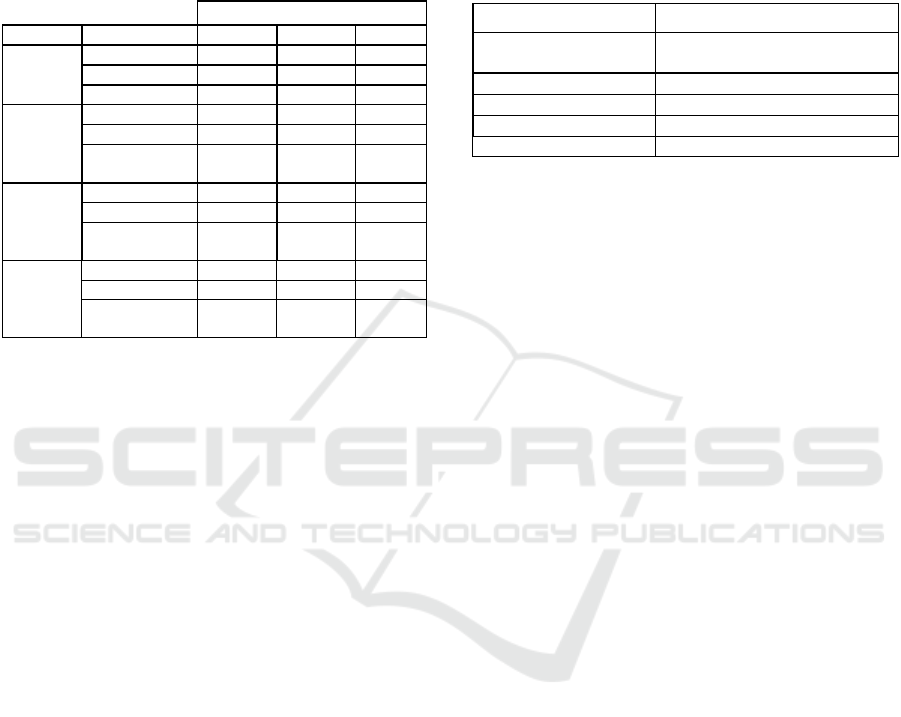
Table 2 only shows the count of experiments for
which the given productions were the first, second,
and third pruning suggestions for mixed-arity
grammar and FPR ranking scheme.
4 EXPERIMENTAL SETUP
4.1 Problems and Function Set
A collection of symbolic regression benchmark
problems was listed in (McDermott 2012). We
utilized a subset of those problems ranging from
simple to more challenging ones. Among the chosen
problems, there is a high variance in terms of problem
difficulty, number of variables, and the sample size
AutoGE: A Tool for Estimation of Grammatical Evolution Models
1277
for training and test data. Table 3 lists the problems
considered in this work and the original function sets.
For details on the mathematical expression, training
and test ranges, please refer to (McDermott 2012).
Table 2: Experimental results to assess the consistency of
pruning suggestions in case of FPR ranking.
Pruning Suggestions
Problem Production 1st 2nd 3rd
Vlad-2
tan(<expr>) 99 1 -
log(abs(<expr>) 1 83 16
pow(<expr>,2) - 16 84
Pagie-1
sinh(<expr>) 99 1 -
log(abs(<expr>) 1 99 -
(-1*(<expr>))
tan(<expr>)
-
-
-
-
93
7
Keijzer-6
(-1*(<expr>)) 98 2 -
tan(<expr>) 2 98 -
log(abs(<expr>)
pow(<expr>,2)
-
-
-
-
78
22
Nguyen-7
log(abs(<expr>) 100 - -
tan(<expr>) - 100 -
pow(<expr>,2)
(-1*(<expr>))
-
-
-
-
66
34
4.1.1 Original Function Set
The function set proposed for each benchmark
problem, as shown in Table 3, is referred to as
Original Function Set. Note that the grammar which
embodies the original function set is termed Original
Grammar in this work, referenced with the letter ‘O’
in Table 4 and 5.
Choosing an appropriate function set is a key
decision in applying GP as it can have a vital impact
on the performance of GP (Wang 2005). However,
there is not enough guidance in selecting a function
set. To date, it is largely considered a decision made
by domain experts. A new user trying to apply
evolutionary search faces a challenge with no clear
guidelines.
4.1.2 Extended Function Set
A few recent studies (e.g. Nicolau 2020) suggested
that using an extended function set (even with
functions that appear to be useless for a particular
problem) can improve performance. Our own
exploratory experiments confirm this, so we create an
Extended Function Set (shown below):
+ - * / sin cos tan sinh cosh tanh
e
x
e
-x
x
2
x
3
-x ln(|x|) √x 1/x
It is the superset of all the original function sets. It
includes arithmetic operators and all common
trigonometric functions, exponentials, and power
functions. Note that we do not use protected division
(Keijzer 2003). The grammar which embodies the
extended function set is termed Extended Grammar
in this work and is referenced with the letter ‘E’ in
Table 4 and 5.
Table 3: Original function sets defined with benchmarks.
Problem Original Function Set
Koza-1, Koza-2, Koza-3,
Pagie-1, Nguyen-7
+ - * / sin cos e
x
ln(|x|)
Keijze
r
-6 + * 1/x -x
√
x
Vla
d
-1, Vla
d
-6 + - * / x
2
e
x
e
-x
Vla
d
-2, Vla
d
-3, Vla
d
-7 + - * / x
2
e
x
e
-x
sin cos
Vla
d
-4, Vla
d
-5, Vla
d
-8 + - * / x
2
4.2 Parameters & Fitness Function
Following evolutionary parameters were used in all
experiments in this work:
Population Size: 250
Number of Generations: 100
Crossover Type: One-point Crossover
Crossover Probability: 0.9
Mutation Probability: 0.01
Selection Type: Tournament
Initialization Method: Sensible Initialization
Maximum Depth: 10
Number of Runs: 30
The objective of the fitness function is to measure
the performance of the algorithm against a predefined
objective goal. The fitness of every individual is
measured using Root Mean Squared Error (RMSE)
against an acceptable threshold. As it is a negatively
aligned metric, it is defined to minimise the fitness
function. The lower the RMSE, the better the value of
objective function
4.3 Pruning Policies
For the problems we examined, the usage frequency
of arithmetic operators, variables, and constant
terminals was low, irrespective of the grammar
structure. We therefore do not consider their
corresponding productions, and the productions
where the right-hand side is only composed of non-
terminals (for example productions in the start rule of
arity-based grammar in Table 1). This resulted in 14
prunable productions which primarily consist of
extended function set excluding arithmetic operators.
It is important to highlight a few other policies
adopted while pruning which server as parameters to
the PRP algorithm:
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
1278
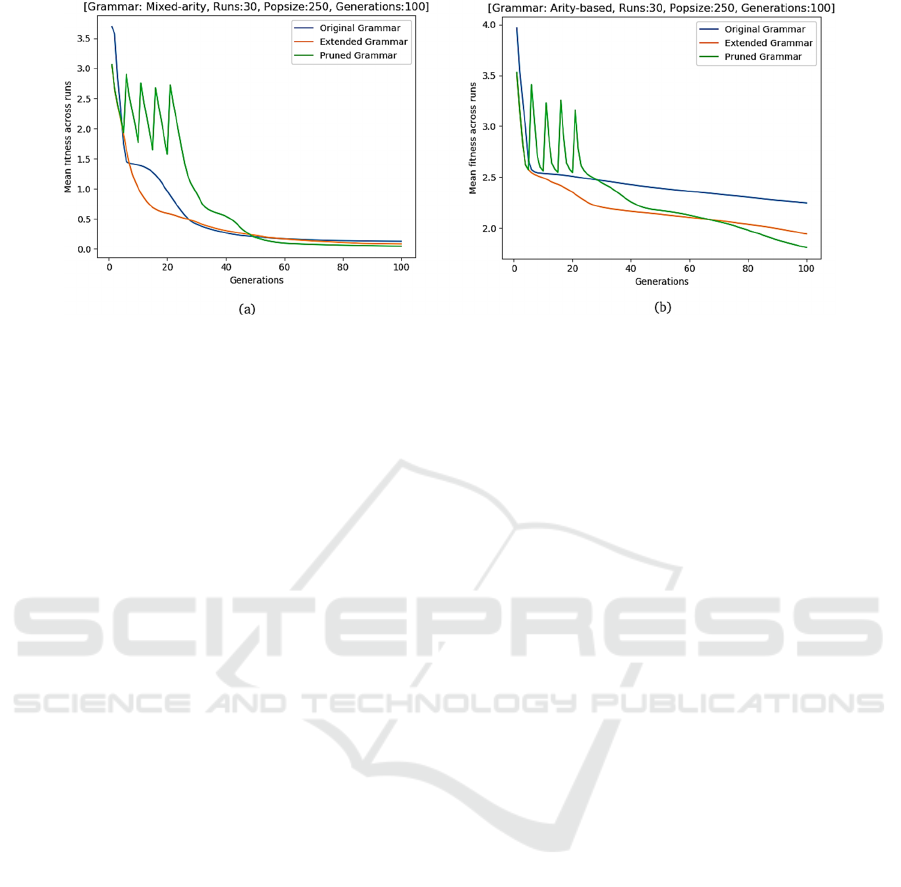
Figure 3: Approximation performance comparisons for (a) Keijzer-6, (b) Vladislavleva-6.
We do not consume more than 20% of the
computational budget on pruning. In our case, it
meant consuming at most 20 generations.
Pruning takes place in stages. At a stage, prune
only 10% of the productions.
In pruning runs, we evolve for 5 generations to
maximize pruning. If 5 generation runs terminate
with a REVERT decision and the pruning budget
is remaining, we proceed with 10 generations.
Note that the grammar which results after pruning is
termed Pruned Grammar in this work and is
referenced with the letter ‘P’ in Table 4 and 5.
5 RESULTS
A summarized view of results from all 42 (14 x 3)
experiments is presented in Table 4 and 5. They show
the impact of using various grammar structures
alongside extended functions set and pruning
approach on performance (both in approximation and
generalization) and mean effective genome length for
the best solution as well as the whole population.
5.1 Statistical Test
We applied statistical test to validate our results and
claims. Student's t-test for statistical significance with
the p-value of 0.05 was used. The outcome of the
significance test is also encoded in Table 4 and 5. The
symbol ‘+’ indicates significant improvement, while
‘-’ is for improvement which is not statistically
significant. Results from the original grammar are
treated as baseline. ‘O -’ indicates that though original
grammar had the best output, it was not significantly
better than the extended grammar. With ‘E -’ or ‘P -’,
the results are only slightly better than original
grammar.
5.2 Impact of Extended Grammar
In general, for most of the problems and for all three
grammar structures, using the extended grammar
(representing the extended function set) significantly
improved performance as well as genome size when
compared with the original grammar. This
observation is consistent with the outcome noted by
(Nicolau 2020). Although the problem set we
experimented with is limited, considering the
diversity in the problem complexity and non-linearity
(Vladislavleva 2009) which makes it a representative
sample, we can suggest utilizing our extended
function set for synthetic symbolic regression
problems.
Koza highlighted that if a function set is not
adequate, GP cannot find (good) solutions, but on the
other hand, if a function set includes many extraneous
functions, the performance is degraded (Koza 1993).
Our results are contrary to this later recommendation.
Besides, extending or adding more productions to the
grammar adds additional dimensions to the search
space, which may result in bigger individuals and
lower performance. However, this is usually not the
case. Finding exactly why warrants an in-depth
analysis. Here we believe that production ranking can
expose some clues.
5.3 Effect of Grammar Structures
It is evident that some grammar structures are more
appropriate for certain types of improvement or for
certain problems. Overall, arity-base grammar
structure results in significant reduction in genome
length, except for vlad-6 where size reductions are not
AutoGE: A Tool for Estimation of Grammatical Evolution Models
1279

Table 4: Summarized results for training and test performance (RMSE). The value in each cell is the best mean fitness/test
score averaged across 30 runs with standard deviation in parenthesis.
Mixed-arity Grammar Arity-based Grammar Balanced Arity-based Grammar
Problem Trainin
g
Test Trainin
g
Test Trainin
g
Test
Koza-1 0.0651 (0.0253) O + 0.254 (0.1187) O + 0.0484
(
0.0376
)
E - 0.2396
(
0.1774
)
O - 0.0161 (0.019) P + 0.1698
(
0.112
)
O -
Koza-2 0.0206
(
0.0172
)
P - 0.0573
(
0.0289
)
P - 0.0081 (0.0048) E + 0.0609
(
0.0377
)
O - 0.0047 (0.0029) P + 0.0458
(
0.0339
)
E -
Koza-3 0.0127
(
0.0046
)
E - 0.0568
(
0.0456
)
E - 0.0010 (0.0029) E + 0.0253 (0.0654) P + 0.0003 (0.0016) E + 0.0017 (0.0064) E +
Kei
j
ze
r
-6 0.0281 (0.0215) P + 0.0351 (0.0297) P + 0.0430 (0.0136) E + 0.0562 (0.0194) P + 0.0286 (0.0126) E + 0.0424 (0.02113) E +
Pa
g
ie-1 0.178 (0.0441) E + 0.1914 (0.0477) E + 0.1771
(
0.0805
)
O - 0.2136
(
0.0304
)
E - 0.1447 (0.0666) O + 0.1914
(
0.0247
)
E -
N
g
u
y
en-7 0.0202 (0.0077) O + 0.0213 (0.0081) O + 0.0186
(
0.0068
)
O - 0.0199
(
0.00737
)
O - 0.0118 (0.0130) E + 0.01277
(
0.0148
)
E -
Vlad-1 0.1092 (0.0082) E + 0.1376
(
0.0177
)
E - 0.1064 (0.0101) P + 0.1239 (0.0134) P + 0.1026 (0.0104) P + 0.1326 (0.0185) P +
Vlad-2 0.2336
(
0.0189
)
O - 0.2279
(
0.0234
)
O - 0.2287
(
0.0396
)
P - 0.243
(
0.05394
)
P - 0.0851 (0.0378) P + 0.0905 (0.0446) P +
Vlad-3 1.0235 (0.0216) E + 0.7116 (0.0627) E + 0.9648 (0.0342) P + 0.9299
(
0.0478
)
P - 0.9874 (0.0336) O + 0.7758 (0.2588) E +
Vlad-4 0.1693 (0.0120) E + 0.1681 (0.0144) E + 0.1795 (0.0055) P + 0.1779 (0.0077) P + 0.1774 (0.0066) E + 0.1771
(
0.009
)
P -
Vlad-5 22.774
(
3.4164
)
E - 2.2087
(
2.0808
)
E - 19.990 (1.4914) E + 1.9437
(
1.5527
)
E - 17.446 (1.5113) E + 2.014
(
1.4189
)
E -
Vlad-6 1.7666 (0.3035) E + 2.6943
(
0.9461
)
P - 1.4347 (0.234) P + 1.887 (0.4259) P + 0.8276 (0.3464) P + 1.0013 (0.4969) P +
Vlad-7 2.2200 (0.1708) E + 2.844 (0.2705) E + 2.376 (0.1574) E + 3.0098 (0.2118) E + 2.2813 (0.2553) E + 2.9105 (0.3917) E +
Vlad-8 0.7159 (0.0544) E + 2.0075 (0.0957) E + 0.7409 (0.0299) P + 2.4189 (0.6991) P + 0.7564 (0.0493) P + 2.444 (0.8646) P +
Table 5: Summarized results for mean effective size. The value in each cell is the best mean effective size with standard
deviation in parenthesis.
Mixed-arit
y
Grammar Arit
y
-based Grammar Balanced Arit
y
-based Grammar
Problem Po
p
Mean Best Ind. Po
p
Mean Best Ind. Po
p
Mean Best Ind.
Koza-1 8.75 (1.715) P + 10.867 (3.73) P + 11.962 (2.16) P + 17.767 (5.245) E + 18.8 (5.188) E + 21.1 (8.125) E +
Koza-2 15.755
(
9.105
)
P - 16.833
(
8.482
)
P - 12.964 (2.758) P + 18.033 (6.385) P + 16.076 (4.96) P + 20.033 (8.376) P +
Koza-3 12.276 (4.991) P + 13.9 (6.199) P + 10.539 (3.047) E + 11.033 (5.456) E + 9.6 (3.094) E + 9.433 (3.03) E +
Kei
j
ze
r
-6 20.88
(
3.592
)
O - 23.3 (9.737) E + 20.342 (4.615) P + 26.967 (9.485) P + 38.442
(
13.769
)
P - 40.467 (18.261) P +
Pa
g
ie-1 14.136 (5.006) P + 17.667 (4.323) P + 13.348 (3.54) P + 21.733 (9.532) P + 22.833 (11.1) P + 30.333 (15.613) P +
N
g
u
y
en-7 5.052 (2.111) P + 5.767 (3.87) P + 19.061 (5.183) P + 23.867 (10.566) P + 20.26 (10.616) P + 28.9 (12.496) P +
Vlad-1 14.157 (4.505) P + 20.433
(
6.657
)
P - 13.105 (4.733) P + 19.362 (5.984) P + 21.098
(
5.995
)
O - 28.3
(
14.055
)
O -
Vlad-2 16.333 (4.767) O + 18.467 (6.796) O - 16.517 (3.425) P + 21.633 (10.206) P + 31.893 (7.419) P + 35.3 (8.017) P +
Vlad-3 17.728
(
4.76
)
P - 20.967 (9.711) P + 19.821 (3.947) P + 28.6
(
12.417
)
P - 30.906
(
14.023
)
P - 38.967
(
20.336
)
O -
Vlad-4 11.325 (3.13) O + 14.1 (4.812) O + 10.566 (0.939) O + 11.867 (2.473) O + 11.343 (2.227) O + 12.6 (3.648) O +
Vlad-5 14.212 (6.447) P - 18.667 (7.44) P + 18.885 (5.04) E - 21.733 (6.547) E + 20.042 (3.586) O + 30.133 (9.629) O +
Vlad-6 13.504 (2.828) P + 16.567 (5.679) P + 19.654
(
3.15
)
E - 26.333
(
10.094
)
E - 25.643
(
5.298
)
E - 31.667 (8.825) E +
Vlad-7 13.765 (4.611) P - 18.633 (7.868) P - 14.416 (3.363) P + 20.467 (9.419) P + 23.815 (6.107) O - 33.0 (11.072) P -
Vlad-8 11.056
(
4.062
)
P - 13.8 (3.525) O + 15.065 (3.328) E + 24.2
(
7.648
)
E - 16.534
(
5.639
)
P - 23.967
(
7.998
)
O -
significant both for best-of-run individuals and the
mean effective size in the population.
To our knowledge, many symbolic regression
studies using GE or Grammar Guided Genetic
Programming (GGGP) use mixed-arity grammar
structure, for instance (Nicolau 2015). Even though,
for many problems, the genome lengths are shortest in
case of mixed-arity grammar and the reductions are
also significant in several cases, the corresponding
performance gains are lower as compared to simple or
balanced arity-based grammars. In general, balanced
arity-based grammar produced best performing
individuals as compared to other structures.
5.4 Effect of Pruning
Pruning was applied in all 42 experiments. The
number of productions pruned varied from 1 to 6, out
of 14 prunable productions. Pruning achieved
significantly shorter effective lengths when looking at
the whole population for 6 different problems with
mixed arity grammar. However, with arity-based
grammar, 9 out of 14 get improvements.
Regarding performance, pruning achieves better
results in only 1 problem (Keijzer-6) with mixed-
arity, and 4 problems with (balanced) arity-based
grammar. However, it is worth noting that in order to
keep the same computational budget, trials with the
pruned grammar lasted for 80 (in some cases 85)
generations. Had the pruned grammar also exercised
for 100 generations, it is likely that it would have
achieved better performance.
Figure 3 shows two sample convergence plots (for
Keijzer-6 and Vladislavleva-6 problems) where
grammar pruning effectively improved
approximation performance when compared with
original and extended grammars. The four spikes in
the plot in case of pruned grammar depict that pruning
runs were carried out in four stages (as explained in
section 3.2) in the first 20 generations.
6 CONCLUSIONS
We propose a new algorithm as part of the AutoGE
tool suite being developed. The proposed Production
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
1280

Rule Pruning algorithm is an approach combining an
extended function set and a frequency counting
mechanism for ranking production rules. Together,
with the choice of extended function set and pruning
algorithm, AutoGE achieved significantly better
genome length in 13 out of 14 problems, with the
(balanced) arity-based grammar structure. Significant
improvement in approximation performance for 13
problems and generalization performance for 8 out of
14 problems is observed with balanced arity-based
grammar. We therefore conclude that arity-based
grammar structure (simple or balanced), as opposed
to commonly used mixed arity grammar, would yield
better results not only in terms of shorter genome
lengths but minimized errors for symbolic regression
problems resulting in enhanced accuracy.
6.1 Future Work
An immediate extension to the current work is to trial
symbolic problems with real-world data, and by
exploring other problem domains for instance
program synthesis, and Boolean logic. The PRP
algorithm performance can be further enhanced by
investigating other search mechanisms, for example
particle swarm optimization or ant colony
optimization. We aim to extend AutoGE’s suite of
algorithms and to make it more robust by exploring
approaches like grammar-based EDAs.
ACKNOWLEDGEMENTS
This work was supported with the financial support
of the Science Foundation Ireland grant 13/RC/2094.
REFERENCES
Bleuler, S., Bader, J., and Zitzler, E. (2008). Reducing Bloat
in GP with Multiple Objectives. In Knowles Corne D.,
Deb K., C. D., editor, Multiobjective Problem Solving
from Nature, pages 177–200. Springer
Fagan D., Murphy E. (2018) Mapping in Grammatical
Evolution. In: Ryan C., O'Neill M., Collins J. (eds)
Handbook of Grammatical Evolution. Springer, Cham.
Keijzer, M. (2003) ‘Improving symbolic regression with
interval arithmetic and linear scaling’, Lecture Notes in
Computer Science, 2610, pp. 70–82. Springer Berlin
Koza, J. R. (1993) Genetic Programming: On the
Programming of Computers by Means of Natural
Selection. MIT Press.
Kshirsagar, M., Jachak, R., Chaudhari, P. and Ryan, C.
(2020), GEMO: Grammatical Evolution Memory
Optimization System, In Proceedings of the 12th
International Joint Conference on Computational
Intelligence (IJCCI), pages 184-191
McDermott J. et. al. (2012). Genetic programming needs
better benchmarks. In Proceedings of the 14th annual
conference on Genetic and evolutionary computation
(GECCO '12). pages 791–798.
Murphy, A., Ali, M., Dias, D., Amaral, J., Naredo, E. and
Ryan C. (2020), Grammar-based Fuzzy Pattern Trees
for Classification Problems., In Proceedings of the 12th
International Joint Conference on Computational
Intelligence (IJCCI), pages 71-80
Nicolau, M. et al. (2015) ‘Guidelines for defining
benchmark problems in Genetic Programming’, In
Proceedings of IEEE Congress on Evolutionary
Computation (CEC’15), pp. 1152–1159
Nicolau M., Agapitos A. (2018) Understanding
Grammatical Evolution: Grammar Design. In: Ryan C.,
O'Neill M., Collins J. (eds) Handbook of Grammatical
Evolution. Springer, Cham.
Nicolau, M. and Agapitos, A. (2020) ‘Choosing function
sets with better generalisation performance for
symbolic regression models’, Genetic Programming
and Evolvable Machines. Springer US
O'Neill, M., Ryan, C., Keijzer, M. et al. (2003) ‘Crossover
in Grammatical Evolution’, Genetic Programming and
Evolvable Machines 4, 67–93.
Ryan C., Collins J., Neill M.O. (1998) Grammatical
evolution: Evolving programs for an arbitrary language.
In: Banzhaf W., Poli R., Schoenauer M., Fogarty T.C.
(eds) Genetic Programming. EuroGP 1998. Lecture
Notes in Computer Science, vol 1391. Springer, Berlin
Ryan C., O’Neill M., Collins J. (2018) Introduction to 20
Years of Grammatical Evolution. In: Ryan C., O'Neill
M., Collins J. (eds) Handbook of Grammatical
Evolution. Springer, Cham.
Uy, N. Q. et. al. (2013) ‘Guiding Function Set Selection in
Genetic Programming based on Fitness Landscape
Analysis’, in Companion Publication of the 2013
Genetic and Evolutionary Computation Conference
(GECCO’13), pp. 149–150.
Vladislavleva, E. J., Smits, G. F. and den Hertog, D. (2009)
‘Order of nonlinearity as a complexity measure for
models generated by symbolic regression via pareto
genetic programming’, IEEE Transactions on
Evolutionary Computation, 13(2), pp. 333–349.
Wang, G. and Soule, T. (2004) ‘How to Choose
Appropriate Function Sets for Genetic Programming’,
Lecture Notes in Computer Science, 3003, pp. 198–207.
AutoGE: A Tool for Estimation of Grammatical Evolution Models
1281
