
FPGA Implementation of Filters in Medical Imaging
Arban Uka
1 a
, Gerald Topalli
2
, Julian Hoxha
1
and Nihal Engin Vrana
3
1
Department of Computer Engineering, Epoka University, Tirane, Albania
2
Department of Electronics and Communication Engineering, Istanbul Technical University, Istanbul, Turkey
3
Spartha Medical, Strasbourg, France
Keywords:
FPGA, Real-time Systems, Medical Image Analysis.
Abstract:
Real time analysis of images is an inherent expectation of the medical imaging research area. Monitoring
of important medical data requires the acquisition of high-quality images at a high rate. Nowadays many
experiments are conducted on multiwell culture plates to determine the influence of different physical and
chemical conditions on a specific biological sample. Often the medical practitioners need to supervise the
complete data acquisition process in order to ensure the collection of reliable data. For this reason, some
pre-processing steps including noise removal, contrast enhancement and preliminary edge detection needs to
be implemented in real time. Here in this work we review important contribution on the implementation of
filters on FPGAs and report runtime of 8 ms for images sized 1000x1000 pixels when two or more filters are
applied subsequently.
1 INTRODUCTION
The implementation of signal processing tasks on
FPGA-s has gained a momentum as the amount of
data to be analysed has increased. One of the ma-
jor fields that requires a real-time implementation and
high throughput at the same time is medical field. Bi-
ological systems can sense or produce low level sig-
nals and these signals can reveal important physiolog-
ical parameters for the cells or tissues (Simon et al.,
2016). The successful signal acquisition, amplifica-
tion and manipulation has closed an important gap
between biology and electronics. The development
of experimental instrumentation has brought forth the
challenge of analysing large data input. The use of
microfluidic chambers facilitates the monitoring of
the cellular material by gathering a series of different
signals that develop in time (Curto et al., 2017). One
important source of input data is the optical imag-
ing. Images acquired at a specific rate reveal the cell
mobility, cell shape and other important parameters
such as circularity, perimeter, area, eccentricity etc.
Cell imaging is one of the most challenging prob-
lems and biologists need real time implementation for
cell detection, counting and classification (Chen et al.,
2006). Even when an experienced medical practi-
tioner uses a medical imaging device, the side help
a
https://orcid.org/0000-0003-0037-0207
of computationally assisted image processing proce-
dures such as auto-focus metrics evaluation, contrast
adjustment and noise removal greatly improve the
data acquisition quality. All these steps constitute a
high throughput of data and it comes with a certain
computational complexity that may compete with the
computing system specification. This challenge can
be overcome with the use of FPGA as they provide
a fast, robust system with a high throughput. Here
in this work we review major contribution of FPGA-s
in medical imaging and then we propose an improve-
ment in the architecture that leads to a shorter run-
time.
2 RELATED WORK
The implementation of complex algorithms on FP-
GAs is reported in the literature all for the same rea-
sons and the major aspects are optimization of the
run-time and physical resources, which in this case
is the number of used LUT and registers. Hauck
and Borrielo developed automatic mapping tools from
high level specification to FPGA programming files
(Hauck and Borriello, 1995). They harness several
FPGA boards at the same time and in the constructed
system they view the pins connecting different FPGA
as the fixed routes whereas the FPGA are viewed as
Uka, A., Topalli, G., Hoxha, J. and Vrana, N.
FPGA Implementation of Filters in Medical Imaging.
DOI: 10.5220/0010392601950200
In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 1: BIODEVICES, pages 195-200
ISBN: 978-989-758-490-9
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
195
dynamic units as they can be routed and rerouted.
They have also worked on how to find partition order-
ings (Hauck and Borriello, 1997). An automatic map-
ping approach goes through five phases, in the follow-
ing order: Synthesis, Partitioning/Global Placement,
Global Routing, FPGA Place, FPGA Route. Anguita
et al., (2003) have provided a detailed description of
the hardware design and implemented support vec-
tor machine learning algorithms on FPGA (Anguita
et al., 2003).This initial fundamental work paved the
way for the implementation of large scale problems
on more complex systems (Cadambi et al., 2009).
Wang and Ni (2004) implemented encryption and de-
cryption algorithms on FPGA as they are more secure
and consume less power (Wang and Ni, 2004). They
optimized all the components and achieved a better
accuracy than all the previous models while using a
minimum number of LUT, registers and slices. Chou
et al., (1993) discussed the implementation of digital
filters on FPGA (Chou et al., 1993). Through many
examples, they illustrated the superior capabilities of
FPGA over other computing units. At the same time,
researchers have developed frameworks to implement
Verilog designs on FPGA devices (Shah et al., 2019).
3 FILTERS AND THE USED
ARCHITECTURE
Important parameters of the filters used in image pro-
cessing are: the type (linear vs nonlinear), size and
sparsity measure. In a common CPU the filter size af-
fects the computational time, whereas in FPGA-s the
clock frequency would not be affected. The only fac-
tor that would be affected would be the latency num-
ber. The same type of filter (for example Laplacian fil-
ter) can be formulated in different ways with different
sparsity levels. In case one constructs the design as a
function of the filter, as in the case of FPGA-s, then a
higher sparsity measure would require a smaller num-
ber of resources.
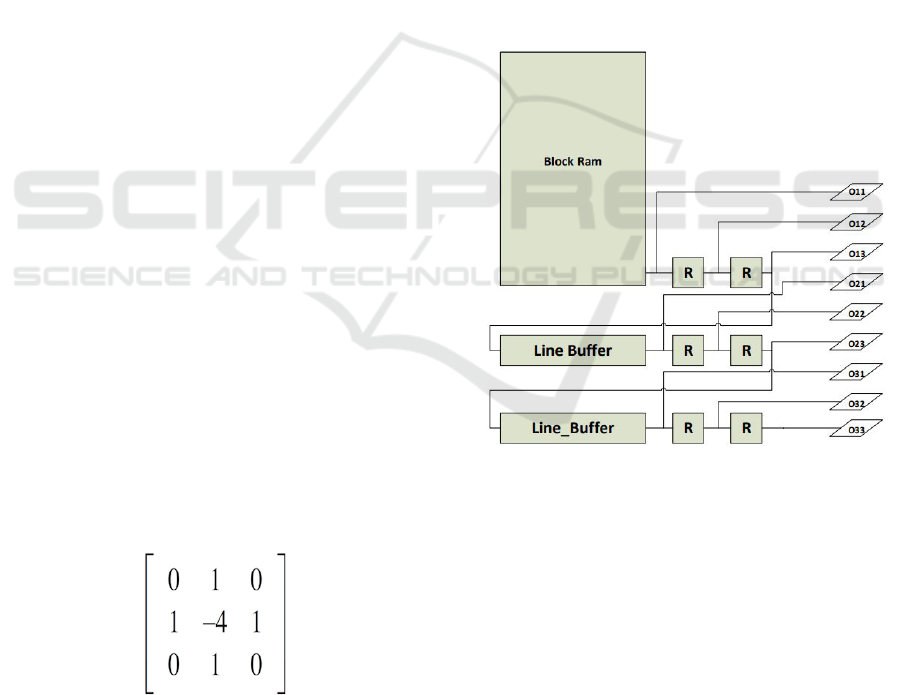
Figure 1: Second derivative Laplacian filter.
3.1 Laplacian Filter
A Laplacian filter is the second derivative of the pixel
intensity in two dimensions and serves as an edge de-
tector. One of the variations of this kernel for this
type of filter with sparsity measure of 44% is shown
in Figure 1. This kernel slides on the pixels of the
image computing the second derivative. The second
derivative of a function shows the behaviour of the
first derivative. At edges, the first derivative of the
image changes, thus the value of the second derivative
will not be zero. The faster the change on the edge in-
formation, the bigger the second derivative will be.
For the implementation of Laplacian filter, two stages
are needed. The first stage should be able to generate
a sliding window which perfectly imitates the sliding
Kernel in convolution systems. The sliding window
will be generated by means of a Block Ram, a set of
8-bit registers and line-buffers connected as shown in
Figure 2.
Figure 2: Sliding window generator.
The second stage should be able to do the mathe-
matical operation that the Laplacian kernel performs.
For the Kernel shown in Figure 1, there are four ad-
ditions and one multiplication which are to be per-
formed in the second stage of the Laplacian filter. The
addition and multiplication operation is performed in
purely combinational circuits that are known in prac-
tice to have a high critical path which contributes neg-
atively to the maximum operating frequency of the
system. In order to reduce the critical path, the sec-
ond stage is pipelined as shown in Figure 3.
BIODEVICES 2021 - 14th International Conference on Biomedical Electronics and Devices
196
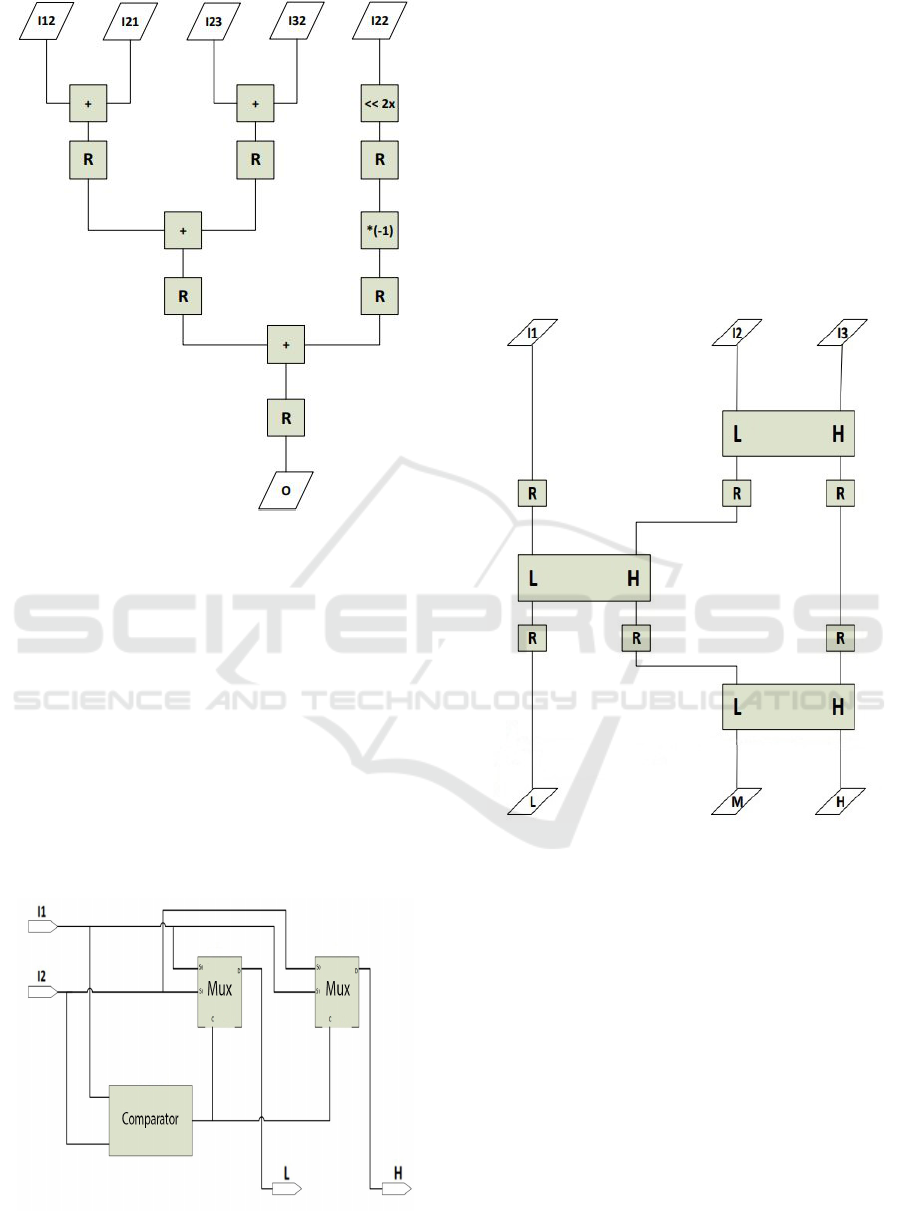
Figure 3: Pipeline adder tree.
3.2 Two Input Sorter
Two Input Sorter is a digital device, which gets two
unsigned 8-bit numbers and produces two unsigned 8-
bit outputs. The two outputs of the device are called
High (the larger of the two 8-bit numbers) and Low
(the smaller of the 8-bit numbers) that are abbreviated
as H and L, respectively. Two Input Sorter utilizes an
unsigned comparator which compares the two inputs
and produces a signal high or low, depending on the
relative size. This signal is then processed by means
of 8-bit 2x1 MUX-s which yield the proper output dis-
tribution. The schematic of the Two input sorter cell
is shown in Figure 4.
Figure 4: Two input sorter.
3.3 Pipeline Shear Sorting
Shear Sorting is a famous algorithm, which can sort
three numbers. In order to reduce the critical path, the
shear sorting can be designed in a pipelined version.
The pipeline registers are clock synchronized and re-
duce the critical path. The pipelined version of the
three-input shear sorter employing the circuit in Fig-
ure 4 (denoted as the LH unit) is shown in Figure 5.
The triple input sorter, shown in Figure 5, is built from
three dual input sorters, along with pipeline buffers
between each dual input sorter. This allows the small-
est possible critical path.
Figure 5: Pipelined three input sorter.
3.4 Median Finder
Median finder shown in Figure 6 will utilize the slid-
ing window generator design (see Figure 2) along
with the pipelined three input sorter. The data from
the window generator output O13, O23, O33 will be
sent to the first ordering comparator for data ordering,
and the results will be sent to the second consecutive
pipeline stage. Before the second comparison is done,
the present data needs to stay in the second stage of
Figure 6 for two clock cycles more. In order to make
this possible, two registers need to be cascaded. The
second comparing results will be sent to the final me-
dian comparator to obtain the final result.
FPGA Implementation of Filters in Medical Imaging
197
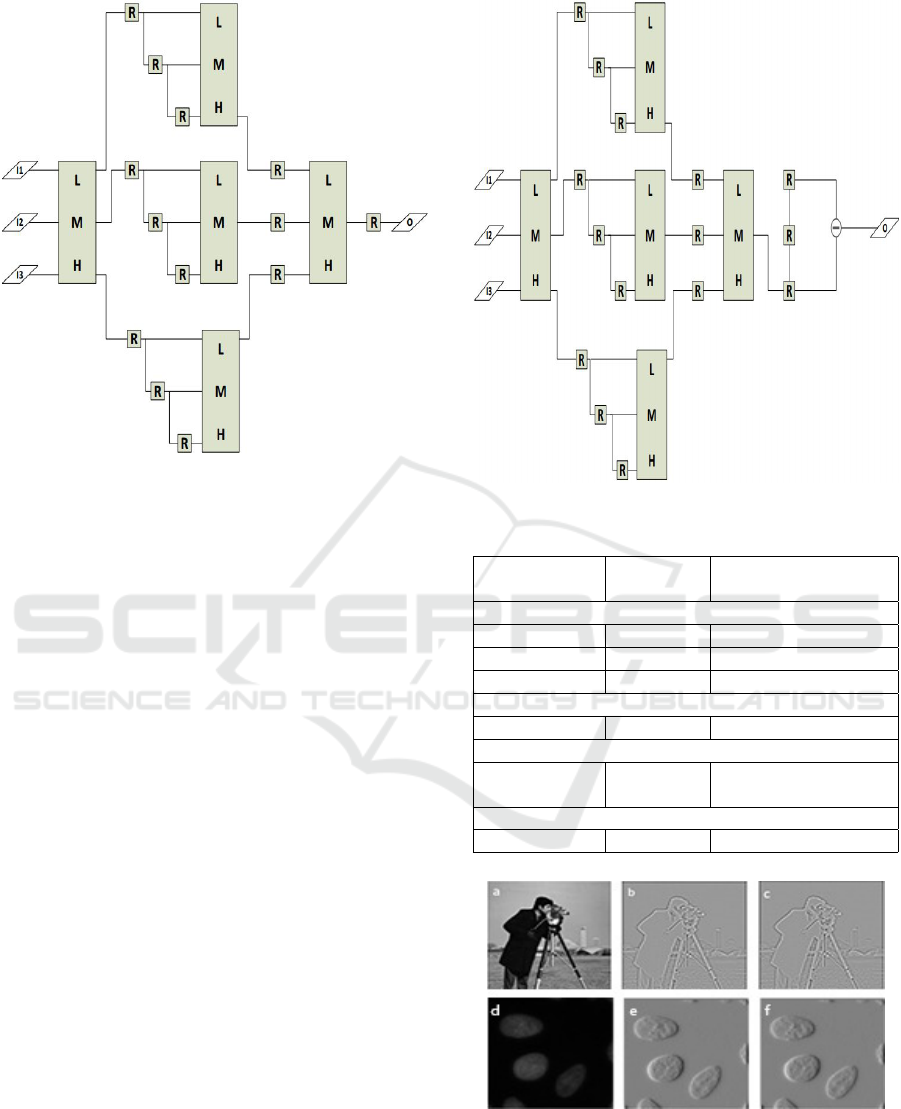
Figure 6: Median Finder.
3.5 Median Finder with First Derivative
We then implemented the first derivative subsequently
to the median filter without changing the frequency
of the system (still operating at one clock-cycle). The
derivative operator commonly used for edge detection
is severely affected by the noise and the implemen-
tation right after the median filter would maintain a
good performance overall.
4 SIMULATIONS
The systems were implemented on a ZCU104 FPGA.
In Table 1, the architecture specifications after the
place and route step are shown. The simulation and
implementation of the filters was carried out on Vi-
vado 2020.2 available in Xilinx packet. The filters
are intended for Zynq Ultrascale+ family of prod-
ucts. The large number of transistors that are avail-
able in the FPGA always brings in the discussion of
the power consumption. In the table below we report
also the power consumption for both combination of
the filters.
The FPGA was operating at 125 MHz and after
each clock-cycle of 8 ns the computed value of a pixel
is recorded after the median filter and the derivative.
Results after applying these two kernels are shown in
Figure 8. For an image of 1000 by 1000 the estimated
run-time on FPGA was 8 ms, whereas on MATLAB
the run-time was 100 ms.
Figure 7: Median finder and derivative for edge detection.
Table 1: Table to test captions and labels.
Laplacian
Filter
Median + Derivative
Filter
CLB Logic
LUT 121 371
Registers 103 585
Carry8 2 2
I/O
IOB 12 9
Frequency
Maximum
Frequency
125M Hz 125M Hz
Power
Power 7.8 W 8.5 W
Figure 8: A: the original image, b: image filtered in MAT-
LAB and c: FPGA generated image with Laplacian filter; d:
original nucleus image, e: MATLAB generated image and
f: the FPGA generated image with median and first deriva-
tive filter.
BIODEVICES 2021 - 14th International Conference on Biomedical Electronics and Devices
198
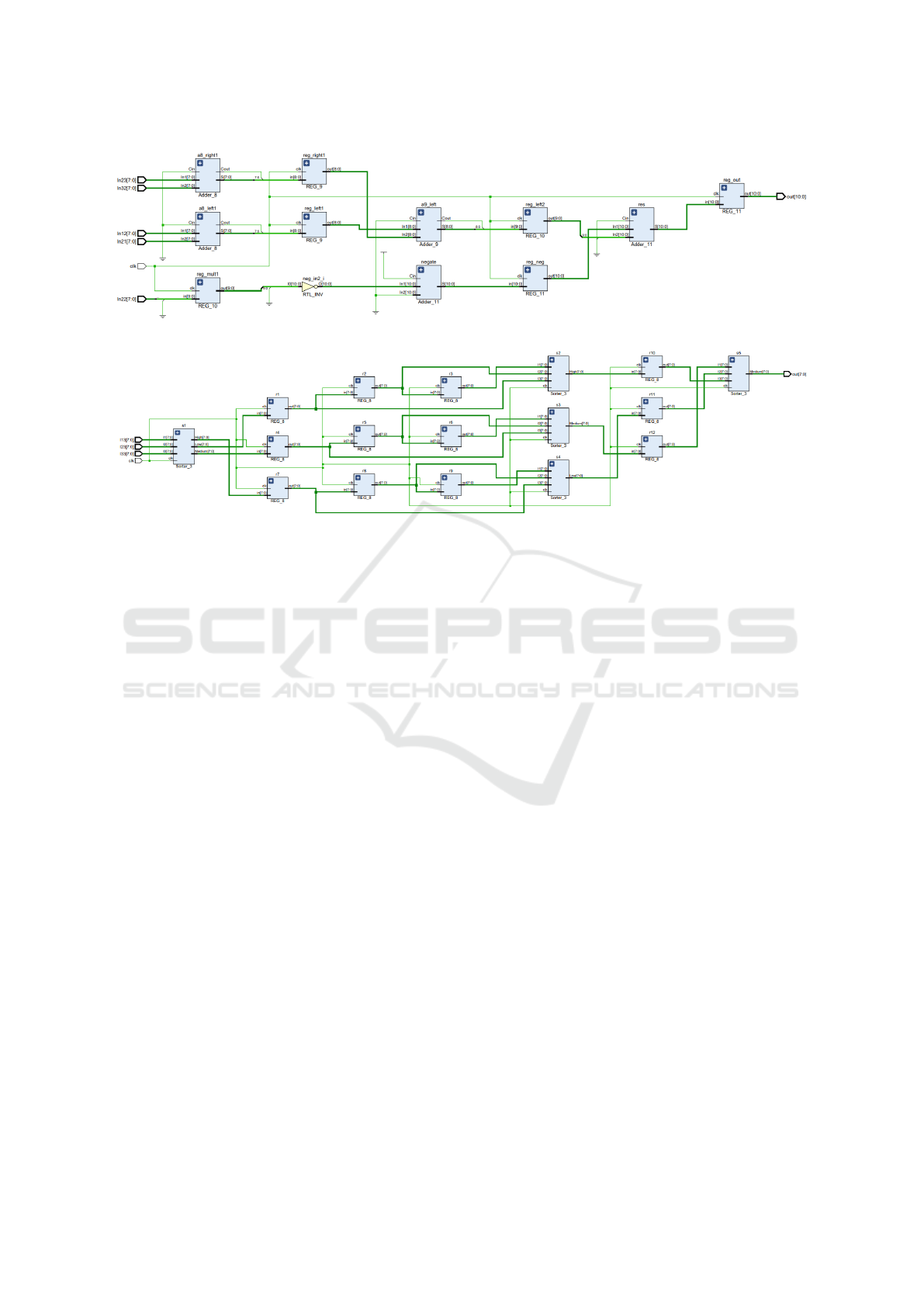
Figure 9: Laplace Filter.
Figure 10: Median Filter.
The RTL schematics of Laplace Filter and Median
Filter are shown in Figure 9 and Figure 10 respec-
tively.
5 CONCLUSION
In this work we reported the designs of the two in-
put sorter, pipelined three-input sorter and median fil-
ter. We implemented Laplacian and Median filters
achieving a shorter run-time than previous reports in
the literature. Then we implemented median filter and
derivative filters for noise removal and edge detection
where the clock period was 8 ns thus maintaining out-
put after each clock cycle. The subsequent application
of derivative filter following the median filters aims at
reducing the common error that is inherent in noisy
data. Also there is a 12.5 fold improvement in run-
time compared to MATLAB run in a i7-8700 3.2 GHz
dual core workstation. Implementation of these pre-
processing steps on portable units would greatly im-
prove the quality and the efficiency of the work of
medical practitioners especially in cases when they
are combined with microscopic image acquisition.
ACKNOWLEDGEMENTS
This project has received funding from the Euro-
pean Union’s Horizon 2020 research and innovation
program under grant agreement No 760921 (PAN-
BioRA).
REFERENCES
Anguita, D., Boni, A., and Ridella, S. (2003). A digital ar-
chitecture for support vector machines: theory, algo-
rithm, and fpga implementation. IEEE Transactions
on neural networks, 14(5):993–1009.
Cadambi, S., Durdanovic, I., Jakkula, V., Sankaradass, M.,
Cosatto, E., Chakradhar, S., and Graf, H. P. (2009). A
massively parallel fpga-based coprocessor for support
vector machines. In 2009 17th IEEE Symposium on
Field Programmable Custom Computing Machines,
pages 115–122. IEEE.
Chen, X., Zhou, X., and Wong, S. T. (2006). Automated
segmentation, classification, and tracking of cancer
cell nuclei in time-lapse microscopy. IEEE Transac-
tions on Biomedical Engineering, 53(4):762–766.
Chou, C.-J., Mohanakrishnan, S., and Evans, J. B. (1993).
Fpga implementation of digital filters. In Proc. Icspat,
volume 93, page 1. Citeseer.
Curto, V. F., Marchiori, B., Hama, A., Pappa, A.-M.,
Ferro, M. P., Braendlein, M., Rivnay, J., Fiocchi, M.,
Malliaras, G. G., Ramuz, M., et al. (2017). Organic
transistor platform with integrated microfluidics for
in-line multi-parametric in vitro cell monitoring. Mi-
crosystems & nanoengineering, 3(1):1–12.
Hauck, S. and Borriello, G. (1995). Logic partition order-
ings for multi-fpga systems. In Proceedings of the
1995 ACM third international symposium on Field-
programmable gate arrays, pages 32–38.
Hauck, S. and Borriello, G. (1997). Pin assignment for
multi-fpga systems. IEEE transactions on computer-
FPGA Implementation of Filters in Medical Imaging
199

aided design of integrated circuits and systems,
16(9):956–964.
Shah, D., Hung, E., Wolf, C., Bazanski, S., Gisselquist,
D., and Milanovic, M. (2019). Yosys+ nextpnr: an
open source framework from verilog to bitstream for
commercial fpgas. In 2019 IEEE 27th Annual Inter-
national Symposium on Field-Programmable Custom
Computing Machines (FCCM), pages 1–4. IEEE.
Simon, D. T., Gabrielsson, E. O., Tybrandt, K., and
Berggren, M. (2016). Organic bioelectronics: bridg-
ing the signaling gap between biology and technology.
Chemical Reviews, 116(21):13009–13041.
Wang, S.-S. and Ni, W.-S. (2004). An efficient fpga imple-
mentation of advanced encryption standard algorithm.
In 2004 IEEE International Symposium on Circuits
and Systems (IEEE Cat. No. 04CH37512), volume 2,
pages II–597. IEEE.
BIODEVICES 2021 - 14th International Conference on Biomedical Electronics and Devices
200
