
Multiple Pursuers TrailMax Algorithm for Dynamic Environments
Azizkhon Afzalov
1a
, Ahmad Lotfi
1b
, Benjamin Inden
2c
and Mehmet Emin Aydin
3d
1
School of Science and Technology, Clifton Campus, Nottingham Trent University, England NG11 8NS, U.K.
2
Max Planck Institute for Mathematics in the Sciences, Inselstraße 22, 04103 Leipzig, Germany
3
University of the West of England, Coldharbour Ln, Bristol BS16 1QY, U.K.
Keywords: Multiple Targets, Multi-agent Path Planning, Path Finding, Search Algorithm.
Abstract: Multi-agent multi-target search problems, where the targets are capable of movement, require sophisticated
algorithms for near-optimal performance. While there are several algorithms for agent control, comparatively
less attention has been paid to near-optimal target behaviours. Here, a state-of-the-art algorithm for targets to
avoid a single agent called TrailMax has been adapted to work within a multiple agents and multiple targets
framework. The aim of the presented algorithm is to make the targets avoid capture as long as possible, if
possible until timeout. Empirical analysis is performed on grid-based gaming benchmarks. The results suggest
that Multiple Pursuers TrailMax reduces the agent success rate by up to 15% as compared to several
previously used target control algorithms and increases the time until capture in successful runs.
1 INTRODUCTION
Search algorithms have been developed and studied
for a long time. The basic scenario is that of a single
agent that is tasked with finding a target or goal
state on a graph within minimal time. Various
assumptions of this scenario can be relaxed, leading
to more difficult problems: there can be several
agents that need to coordinate their search, there can
be multiple targets, all of which need to be caught,
and targets can move on the graph over time rather
than be in a fixed position.
Many suitable algorithms have been proposed for
pursuing agents in the domains of video and computer
games, robotics, warehouses (Li et al., 2020), and
military and surveillance applications (Panait &
Luke, 2005). Some of these algorithms are for single
agent, such as MTS (Ishida, 1992), D* Lite (Koenig
& Likhachev, 2002) or RTTES (Undeger & Polat,
2007) and some are multi-agent, for example, FAR
(Wang & Botea, 2008), WHCA* (Silver, 2005), CBS
(Sharon, Stern, Felner, & Sturtevant, 2015) and
MAMT (Goldenberg, Kovarsky, Wu, & Schaeffer,
2003). These algorithms aim to find the shortest path
a
https://orcid.org/0000-0002-1456-542X
b
https://orcid.org/0000-0002-5139-6565
c
https://orcid.org/0000-0001-6048-6856
d
https://orcid.org/0000-0002-4890-5648
to the target location(s). While the shortest path is
important, the run time is essential, too, as considered
by real-time heuristic algorithms (Loh & Prakash,
2009).
For scenarios with moving targets, the target
algorithms also play an essential role in developing
multi-agent scenarios, but they are less studied. The
goal of such algorithms is to evade capture as long as
possible.
Consider a pursuit and evasion game, where
agents could be humans or computer controlled. To
make the game more interesting, intriguing, and
challenging, the targets need to behave intelligently.
Therefore, good target algorithms are an essential
factor of improving the gaming experience.
Existing target algorithms usually have strategies
such as maximising the escaping distance (Xie,
Botea, & Kishimoto, 2017), random movements to a
selected, unblocked positions in order to evade from
the capturer (Pellier, Fiorino, & Métivier, 2014) or, in
a state of the art approach called TrailMax,
maximising the survival time in the environment
(Moldenhauer & Sturtevant, 2009).
Multi-agent path finding (MAPF) problems have
been analysed in detail in the literature (Sigurdson,
Afzalov, A., Lotfi, A., Inden, B. and Aydin, M.
Multiple Pursuers TrailMax Algorithm for Dynamic Environments.
DOI: 10.5220/0010392404370443
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 437-443
ISBN: 978-989-758-484-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
437

Bulitko, Yeoh, Hernández, & Koenig, 2018), and are
known to be NP-hard (Li et al., 2020). As an example
of such a problem, in a video game, all non-player
agents may need to navigate from a starting location
to the goal location on a conflict free route in a static
or dynamic environment (Chouhan & Niyogi, 2017).
Good algorithms for moving targets can make the
empirical study of MAPF problems more meaningful
and challenging. So how can we improve on existing
ones? This paper introduces an algorithm based on
TrailMax that can be used for multiple moving targets
to escape from multiple agents in a dynamic
environment.
In the remaining parts of this paper, Section 2
presents the related work. Section 3 describes the new
approach to the problem. Empirical comparisons are
described in Section 4, and conclusion is derived in
Section 5.
2 RELATED WORK
This section introduces several existing target
algorithms in the literature. The following is a brief
description of each algorithm.
2.1 Target Algorithms
Although there is plenty of research in the literature
emphasising algorithms for pursuing agents, there are
few studies that are conducted on algorithms for
mobile targets. A classic example is the A* algorithm,
which is implemented for many pursuing agent and
target algorithms (Sigurdson et al., 2018).
2.1.1 TrailMax
TrailMax is a strategy-based algorithm that generates
a path for a target considering the pursuing agent’s
possible moves, i.e. it efficiently computes possible
routes by expanding its position nodes and agent’s
nodes simultaneously (Moldenhauer & Sturtevant,
2009). The aim of the TrailMax algorithm is to make
the targets stay longer by maximising the capture
time. To compute a path, an escape route that
maximises the intersection point, it checks the best
cost of the neighbouring states against the pursuer’s
costs and expands nodes accordingly. The algorithm
expands nodes that are not yet expanded, not in the
target’s list and not in the pursuer’s list. The node
with the best cost is added to the target’s list, which
would generate the path afterwards.
It is a state-of-the-art target strategy algorithm that
performs the best against pursuing agents, aiming to
make the targets less catchable or more difficult to be
caught (Xie et al., 2017).
2.1.2 Minimax
When used as the target algorithm, it runs an
adversarial search that alternates moves between the
agents and the target, where the agent gets closer to
the target state and the target distances itself from the
pursuing agent’s state. To make the algorithm faster,
Minimax is run with alpha-beta pruning search,
where alpha (α) and beta (β) are constantly updated to
avoid the exploration of suboptimal branches
(Bulitko & Sturtevant, 2006). The used depth is 5, i.e.,
the outcomes after at most 5 moves of each party are
considered.
2.1.3 Dynamic Abstract Minimax
Dynamic Abstract Minimax (DAM) is a target
algorithm that finds a relevant state on the map
environment and directs the target using Minimax
with alpha-beta pruning in an abstract space. The
search starts on the highest level of abstraction, an
abstract space created from the original space. If there
is a path, then an escape route is computed using
PRA* (see Section 2.2). If the target cannot escape
and there is no available move to avoid the capture on
the selected abstract space, then the level of
abstraction is decreased and the whole process repeats
until the target can successfully run away from being
caught (Bulitko & Sturtevant, 2006). The used depth
is 5.
2.1.4 Simple Flee
Simple Flee (SF) is another algorithm that can be used
by targets to escape from the pursuing agents (Isaza,
Lu, Bulitko, & Greiner, 2008). The SF algorithm
works as follows. In the beginning of the search, the
target identifies some random locations on the map.
When the target starts moving, it navigates to the
furthest location away from the pursuers. To disorient
the pursuing agents, the direction towards the selected
location changes in every five steps, and if it is the
furthest location, it keeps moving. The number of
locations on the map and the number of steps before
the change are the parameters of the algorithm.
2.2 Pursuing Algorithm
This study sets out to develop a new multiple target
algorithm. Therefore, this part of the section
introduces only one algorithm for pursuing agents,
which will be used in the experiments.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
438

Partial-Refinement A* (PRA*) is an algorithm
that reduces the cost of search by generating a path on
an abstract level of the search space. These abstracted
spaces (graphs) are built from the grid map. The
abstract level is selected dynamically. The A*
algorithm is then used to run a search with sub-goals
on the abstract graph. The abstract path creates a
corridor of states in the actual search space, through
which the optimal path is found .
This is a widely used approach and its variations
have been described with different search techniques
(Sturtevant, Sigurdson, Taylor, & Gibson, 2019).
3 PROPOSED APPROACH
In the following section, a new target algorithm is
described. First, the motivation will be given for the
algorithm. The pseudo code (see Figure 1) provides
more details.
When the problem was described in Section 1, it
was stated that a smart target algorithm is very useful
to have. In the simple scenarios where one agent
pursues a target, the target would know from which
agent it needs to escape, as there is only one. Some of
the strategies to run away from the agent have been
discussed in the previous sections. But if we consider
a situation where multiple targets need to escape from
the current state and move to the safest destination in
the dynamic environment, how would targets know
which agent they need to avoid for a successful run?
Although the TrailMax algorithm, as introduced
in Section 2.1.1, is the state-of-the-art algorithm, it
has been designed to work with only one agent,
meaning a target does not have any strategy to escape
from one pursuer and avoid another approaching
pursuer at the same time.
For this particular reason, a target algorithm that
would be able to identify approaching multiple agents
and escape from all pursuers, a novel algorithm,
called Multiple Pursuers TrailMax (MPTM), is
developed.
The MPTM algorithm uses a similar methodology
as TrailMax but enhanced for MAPF problems. There
are two important reasons for implementing MPTM
algorithm in MAPF problems. First, it can identify the
state location of other targets and collaborate with
them. Second, it can ensure the escape not only from
one pursuing agent, but from any approaching
evading agents. Here the focus is on the second issue.
The pseudo code for the MPTM algorithm is
depicted in Figure 1. First, the current locations of all
pursuers and targets need to be initialised. The next
step is to sort all players according to their role and
insert into the relevant lists, all pursuers to the
pursuer_node_list and a target to the
target_node_list. At this point all players will have a
cumulative cost of zero. To make it easier to follow
the code, each movement cost will be equal to one,
unless it is in wait action, then it is zero. This is with
an assumption that there is no octile distance.
Since this is the target algorithm, it starts first to
check if there are any target nodes in the
target_node_list. Then, it finds the best cumulative
cost c, the highest value, for target and pursuer at line
7 and 8. If the c
t
is lower or equal to the cₐ, then the
target expands its nodes. The expansion of nodes is
computed simultaneously for target and pursuing
agents. During the expansion of nodes, each side
marks nodes as visited and insert into the closed lists,
line 12 and 20.
The main part of this algorithm are the lines in
between 13-22, where each pursuer loops through its
state and expands its nodes independently from other
pursuers. The closed nodes list for the target is
reversed to identify the route. This expansion goes to
the point where one of the pursuing agents occupies
the node of the target.
Figure 1: Pseudo code for the MPTM algorithm.
Multiple Pursuers TrailMax Algorithm for Dynamic Environments
439

For multiple targets, the algorithm is run on each
target, and normally, each will get a different
outcome based on their location. The result will be the
same if they are all in the same state. Even if the
starting position is different, the targets could join
their path if that is the optimal option.
4 EMPIRICAL EVALUATION
In this section the empirical results will be presented
to demonstrate the efficiency of the proposed
algorithm. First, the experimental setup will be
described, then, performance results of the MPTM
algorithm described in Section 3 will be reported.
4.1 Experimental Setup
For better comparability, standardised grid-based
maps from the commercial game industry are used as
a benchmark (Stern et al., 2019). The environments
used are four maps from Baldur’s Gate video game as
shown in Table 1. Within the experiments, these maps
are used with a four-connected grid and impassable
obstacles. Figure 2 displays a sample map used for the
experiments, where black coloured spaces are the
obstacles, and the white space is a traversable area.
The maps were chosen based on the presence of
obstacles and difficulty of navigation. The movement
directions could be up, down, left and right with a cost
of one each. That said, the approach should work with
different moving costs as well.
Figure 2: The experimented sample map (AR0607SR) used
in the Baldur’s Gate video game.
Table 1: The name of testbeds for the experiments with their
height and width sizes.
Map names Height x Width
AR0607SR 54x60
AR0514SR 64x64
AR0313SR 64x60
AR0417SR 54x52
The scenario chosen for the first tests is to have two
targets and twice the number of pursuing agents. The
second set of tests has the number of targets increased
by one. The last configuration increases pursuing
agent number to six versus three targets. All players
are placed at different pre-selected random locations
on each map. Altogether there were five different sets
of starting positions. Only the first set has all pursuers
in the same location and all targets in the same
location, and targets are positioned in far distance
from pursuers. This helps to analyse the behaviour of
the algorithms.
Each configuration runs 30 times. The
implementation of the simulation (Isaza et al., 2008)
is developed using C++. The simulation was
developed for a single target scenario and it was
modified so that the tasks with multiple targets and
assignment strategy for pursuing agents could be
tested. The results were obtained using a Linux
machine on Intel Core i7 with 1.9 GHz CPU and
RAM with 40 GB.
4.2 Experimental Results
The section below reports the results from the
experiments. Performance analysis is conducted with
respect to two key indicators; (i) the number of steps
taken for each target algorithm before being caught
and (ii) its success rate. Both of the measurements are
averaged considering all targets.
During the experiments, some pursuers could
catch one target but miss the second one, and because
the search is not finished yet, the chase continues.
Success is achieved when both targets are caught, and
the number of steps until all targets have been caught
is recorded.
4.2.1 Pathfinding Cost
To evaluate the MPTM algorithm the comparison
with SF and Minimax is displayed in Table 2. This
measures the performance in terms of number of steps
for all targets. The numbers indicate the means of
steps by target algorithms per map.
It is seen from Table 2 that the proposed target
algorithm offers much longer stay on the maps. This
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
440
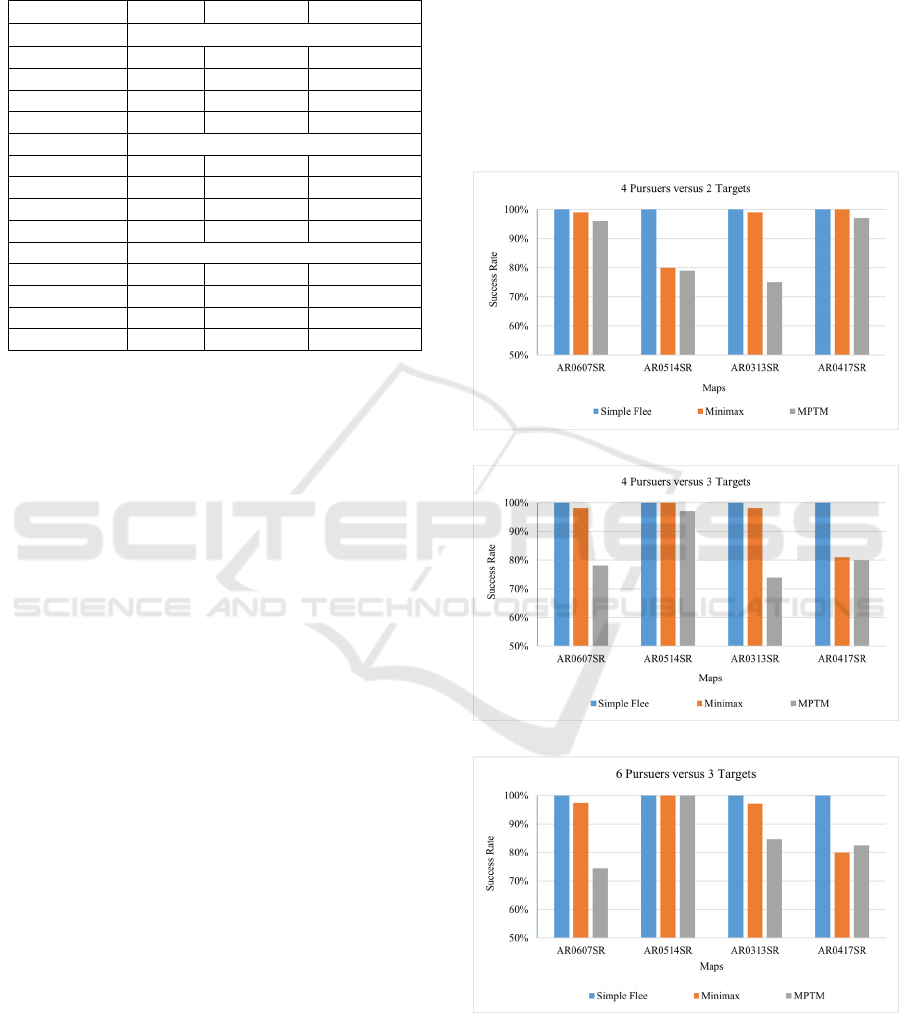
Table 2: The average number of steps for each target
algorithm per map for each set of configurations. Larger
number is better as it avoids the capture from the pursuing
agents.
SF Minimax MPTM
4 pursuers versus 2 targets
AR0607SR 66.59 139.01 206.83
AR0514SR 46.55 62.04 142.82
AR0313SR 57.61 116.07 317.66
AR0417SR 46.32 173.16 260.52
4 pursuers versus 3 targets
AR0607SR 78.21 181.06 331.61
AR0514SR 61.68 87.09 153.13
AR0313SR 65.99 139.84 344.91
AR0417SR 50.81 178.42 228.92
6 pursuers versus 3 targets
AR0607SR 72.76 137.85 325.59
AR0514SR 66.59 85.33 88.55
AR0313SR 62.45 133.57 237.05
AR0417SR 47.82 171.07 197.83
indicates that it avoids capture and demonstrates
smarter decisions. The higher number is better.
In the scenario, when the target number increases
to three versus four pursuing agents, usually the
targets manage to avoid capture longer in comparison
with the first set of tests. In the cases where the
number of pursuing agents are increased to six, 6
pursuers versus 3 targets, this predominance gives
greater advantage to the pursuers and makes it
difficult for targets to escape. Therefore, targets might
get caught quicker.
The evidence shows that the new MPTM
algorithm outperforms SF and Minimax algorithms in
number of steps in all test configurations.
4.2.2 Success Rate
Success for the agents is achieved when a pursuing
agent gets to the position of the target. In the multi-
target scenarios, success is achieved when all targets
have been captured. For the target(s), success is the
absence of agent success. The success of the target
algorithm is shown in Figure 3. There are three
different graphs based on the number of players that
are set for each test configuration.
From these graphs in Figure 3, the SF algorithm
performs the worst, and it always gets caught by
pursuing agents. Minimax shows better results in
comparison with SF, although it has the cases where
it gets caught 100%. Minimax is slightly worse than
the MPTM algorithm on the AR0514SR map (4 vs 2)
and on the AR0417SR map (4 vs 3) but performs
better and escape longer only on one occasion, the
AR0417SR map (6 vs 3). It is possible to say, the
MPTM algorithm performs better than Minimax in
most of the configurations and displays excellent
results in some of these, but on the AR0417SR map
with six pursuers and three targets, it performs
approximately equal to Minimax.
The behaviour of the MPTM algorithm is better
on the maps that have obstacles that could be
navigated around, for example the map illustrated in
Figure 2. These types of maps may be suitable for
adaptive target algorithms as they offer opportunities
for escape but may be difficult for the pursuing agent
(a)
(b)
(c)
Figure 3: The performance rate of success for SF, Minimax
and MPTM target algorithms, lower is better. (a) displays
the results for 4 pursuers versus 2 targets, (b) is for 4
pursuers versus 3 targets and (c) is for 6 pursuers versus 3
targets.
Multiple Pursuers TrailMax Algorithm for Dynamic Environments
441

algorithms if they do not have strategies such as the
trap strategy (John, Prakash, & Chaudhari, 2008). The
maps AR0514SR and AR0417SR have dead-ends or
blind alleys and thus make it more difficult to find an
escape route, leading to lower target performance on
these maps.
The results clearly show that the new target
algorithm, MPTM, performs far better in all of these
simulations on the gaming maps used for
benchmarking.
With the better algorithms, pursuing agents
sometimes fail to catch the targets although these are
outnumbered. They might catch one target but fail to
catch the other, or keep following the target, or end in
a deadlock until timeout.
The result of this study indicates that the MPTM
algorithm exceeds expectations and, on average over
all maps, shows a success rate 9% and 15% better
then Minimax and SF, respectively.
5 CONCLUSION AND FUTURE
WORK
The aim of this paper was to develop and study a
target algorithm in MAPF problems. There have been
many interesting studies done on search algorithms
and among of them are solutions to the MAPF
frameworks. Only several studies have been
conducted on target algorithms, especially in the area
where there are multiple targets.
The investigation shows that TrailMax is a
successful algorithm for control of targets if extended
for dealing with multiple agents. This study proposes
amendments, first time, to TrailMax strategy
algorithm as a state-of-the-art approach modifying
and enhancing its scope to meet the criteria for
multiple targets in the dynamic environment.
This new MPTM algorithm is applicable to
moving targets and the success of having a smart
method makes fast pursuing search algorithms to
timeout. The results of this study demonstrate that the
target algorithms are equally important in comparison
to pursuer algorithms, and that makes the search more
challenging and interesting.
Future studies should also look at computation
time and how it could be improved. A more
systematic approach would also study how the
algorithm behaves on different testbeds and with
different agent configurations, including those with a
larger number of players. The comparison with other
pursuing multi-agent algorithms would be useful.
REFERENCES
Bulitko, V., & Sturtevant, N. (2006). State abstraction for
real-time moving target pursuit: A pilot study.
Proceedings of AAAI Workshop on Learning for
Search, WS-06-11. pp. 72-79.
Chouhan, S. S., & Niyogi, R. (2017). DiMPP: A complete
distributed algorithm for multi-agent path planning.
Journal of Experimental & Theoretical Artificial
Intelligence, 29(6), 1129-1148.
Goldenberg, M., Kovarsky, A., Wu, X., & Schaeffer, J.
(2003). Multiple agents moving target search. IJCAI
International Joint Conference on Artificial
Intelligence, pp. 1536-1538.
Isaza, A., Lu, J., Bulitko, V., & Greiner, R. (2008). A cover-
based approach to multi-agent moving target pursuit.
Proceedings of the 4th Artificial Intelligence and
Interactive Digital Entertainment Conference, AIIDE
2008, pp. 54-59.
Ishida, T. (1992). Moving target search with intelligence.
Proceedings Tenth National Conference on Artificial
Intelligence, pp. 525-532.
John, T. C. H., Prakash, E. C., & Chaudhari, N. S. (2008).
Strategic team AI path plans: Probabilistic pathfinding.
International Journal of Computer Games Technology,
2008, 1-6.
Koenig, S., & Likhachev, M. (2002). D* lite. Proceedings
of the National Conference on Artificial Intelligence,
pp. 476-483.
Li, J., Gange, G., Harabor, D., Stuckey, P. J., Ma, H., &
Koenig, S. (2020). New techniques for pairwise
symmetry breaking in multi-agent path finding.
Proceedings International Conference on Automated
Planning and Scheduling, pp. 193-201.
Loh, P. K. K., & Prakash, E. C. (2009). Novel moving target
search algorithms for computer gaming. Computers in
Entertainment, 7(2), 27:1-27:16.
Moldenhauer, C., & Sturtevant, N. R. (2009). Evaluating
strategies for running from the cops. IJCAI
International Joint Conference on Artificial
Intelligence, pp. 584-589.
Panait, L., & Luke, S. (2005). Cooperative multi-agent
learning: The state of the art. Autonomous Agents and
Multi-Agent Systems, 11(3), 387-434.
Pellier, D., Fiorino, H., & Métivier, M. (2014). Planning
when goals change: A moving target search approach.
12th International Conference on Advances in
Practical Applications of Heterogeneous Multi-Agent
Systems: The PAAMS Collection, 8473. pp. 231-243.
Sharon, G., Stern, R., Felner, A., & Sturtevant, N. R.
(2015). Conflict-based search for optimal multi- agent
pathfinding. Artificial Intelligence, 219, 40-66.
Sigurdson, D., Bulitko, V., Yeoh, W., Hernández, C., &
Koenig, S. (2018). Multi-agent pathfinding with real-
time heuristic search. Paper presented at the 14th IEEE
Conference on Computational Intelligence and Games
(CIG), 2018-August. pp. 1-8.
Silver, D. (2005). Cooperative pathfinding. Proceedings of
the First AAAI Conference on Artificial Intelligence
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
442

and Interactive Digital Entertainment (AIIDE'05),
Marina del Rey, California. pp. 117-122.
Stern, R., Sturtevant, N. R., Felner, A., Koenig, S., Ma, H.,
Walker, T. T., et al. (2019). Multi-agent pathfinding:
Definitions, variants, and benchmarks. Paper presented
at the Proceedings of the 12th International Symposium
on Combinatorial Search, SoCS 2019, pp. 151-158.
Sturtevant, N. R., Sigurdson, D., Taylor, B., & Gibson, T.
(2019). Pathfinding and abstraction with dynamic
terrain costs. Paper presented at the Proceedings of the
15th AAAI Conference on Artificial Intelligence and
Interactive Digital Entertainment, AIIDE 2019, pp. 80-
86.
Undeger, C., & Polat, F. (2007). RTTES: Real-time search
in dynamic environments. Applied Intelligence, 27(2),
113-129.
Wang, K. -. C., & Botea, A. (2008). Fast and memory-
efficient multi-agent pathfinding. ICAPS 2008 -
Proceedings of the 18th International Conference on
Automated Planning and Scheduling, pp. 380-387.
Xie, F., Botea, A., & Kishimoto, A. (2017). A scalable
approach to chasing multiple moving targets with
multiple agents. Proceedings of the 26th International
Joint Conference on Artificial Intelligence, Melbourne,
Australia. 0. pp. 4470-4476.
Multiple Pursuers TrailMax Algorithm for Dynamic Environments
443
