
ECGraph: A Complex Networks Tool to Classify Critical Points
of Ecological Corridors
Gianni Fenu
a
and Enrico Podda
b
Department of Computer Science, University of Cagliari, Via Ospedale 72, 09124 Cagliari, Italy
Keywords:
Complex Networks, Ecological Networks, Ecological Corridors, Connectivity, Graph Analytics.
Abstract:
The analysis of large amounts of information and its representation in a simple model has always been one
of the main purposes of computer science. The field of territorial study is an excellent example to observe
the complexity of the process, from the basic search for information through simple but expensive geometric
calculations to the connection that the information itself has concerning the rest of the territory. The study of
the natural areas identified by the European project Natura 2000 and their interconnection through the use of
ecological corridors is an example of how difficult it can be to define, study and represent a complex problem.
In order to simplify the mentioned tasks, allowing specialists to consult valuable data, the paper exposes how
ECGraph works. This open source software allows extracting important information from any corridor related
to areas of the Natura 2000 project, and can potentially be generalized to any similar case.
1 INTRODUCTION
The delineation of the areas from the Natura 2000
project (Evans, 2012) (Ostermann, 1998) has been
an enormous improvement in the management and
preservation of European flora and fauna (Urban and
Keitt, 2001) (Fenu and Pau, 2015). Natura 2000’s
main purpose is to protect the biodiversity of indige-
nous living beings on European soil, without however
precluding the already developed and massive human
infrastructures. Defining and standardizing protected
areas in which plants and animals can live has allowed
the process of their possible extinction to slow down.
However, it is not enough, as it is trivial to note that
without sufficient biodiversity an ecosystem cannot
thrive nor survive for long.
To help solving this pressing problem, studies
have led to the theorization of a valuable tool, the eco-
logical corridor.
Ecological corridors (Jongman, 1995) (Gill Jr
et al., 2009) have been designed to connect protected
areas through patches of land selected to satisfy spe-
cific walkability standards, allowing to emulate a path
for migration of species. If research progresses in
the standardization and implementation of ecological
corridors, it could allow autonomous sustainability of
a
https://orcid.org/0000-0003-4668-2476
b
https://orcid.org/0000-0001-5635-6610
the species that the Natura 2000 project seeks to pre-
serve. Nonetheless, design and manage such a net-
work would be all but easy.
Considering the territory as a Complex Network
could help to keep track of dangerous patches and pre-
vent possible events that may threaten the territory or
endanger the possibility to walk through the ecologi-
cal corridor (Bodini and Cossu, 2010). Complex Net-
works can in fact help to make useful considerations
on the state of a corridor and allow to read the confor-
mation of the territory in a more efficient and precise
way. The most serious threat that can undermine the
usefulness of an ecological corridor would be its im-
practicability. A cut node (Fenu and Pau, 2018) can
indeed bring to that outcome.
To understand the central role in the research of
cut nodes it is necessary to imagine the ecological
corridor as a graph, where the patches correspond to
the nodes and the edges represent the adjacencies be-
tween neighbor patches. A cut node is a peculiar node
that if removed disconnects part of the nodes from
the graph, actually creating distinct and unconnected
subgraphs. As has already been fully explained in
previous studies (Fenu and Pau, 2018), not all cut
nodes preclude the possibility to walk through the
corridor, but some could represent a threat. Similar
considerations could also be made for the virtual cut
nodes (Fenu and Podda, 2020), which are different
from cut nodes. In fact, virtual cut nodes are formed
Fenu, G. and Podda, E.
ECGraph: A Complex Networks Tool to Classify Critical Points of Ecological Corridors.
DOI: 10.5220/0010388800470054
In Proceedings of the 6th International Conference on Complexity, Future Information Systems and Risk (COMPLEXIS 2021), pages 47-54
ISBN: 978-989-758-505-0
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
47

by a set of nodes which are not capable of breaking
the graph apart if taken individually. Up to this date
there is no open source code that has implemented a
way to detect cut nodes or virtual cut nodes clearly
and efficiently, even though some logic has been the-
orized.
Tools such as QGIS (Team et al., 2015) (Jenson
and Domingue, 1988) and its libraries are extremely
valid for the study and standardization of landscape.
QGIS provides a valid representation of raster and
vector maps and is able to query the attributes of the
layers so that useful information is displayed. The
tool also allows to run scripts developed in Python 3
in a console integrated with the program, but this can
quickly become limiting for our purposes.
ECGraph, the software described in this paper, is
proposed as a tool to identify critical points of the
network, such as cut nodes and virtual cut nodes.
Furthermore, the software also saves in the output
additional information that allows both to have an
overview of the network and to focus on the proper-
ties of the node (patch) in relation to the network it-
self. We decided to develop ECGraph with JavaScript
to be easily integrable by npm (Tilkov and Vinoski,
2010), to simplify future integration in projects with
a graphical interface that can offer features difficult to
implement on QGIS at the moment. The paper will
also present the ECGraph output obtained from the
ecological corridor designed in previous studies (Can-
nas and Zoppi, 2017). The covered area refers to the
metropolitan area of Cagliari, an Italian municipality
located in the south of the island of Sardinia, of which
it is capital.
2 HOW ECGraph WORKS
The software, available on GitHub
1
, shows the algo-
rithm. Given as input an ecological corridor and the
areas it connects, ECGrapgh produces an output co-
incident to the same ecological corridor, but provided
with additional properties.
In the README of the repository, there is also a
link to download the input area. These areas are the
ones distributed by the Natura 2000 project, but ready
to run with the code. Information on how to use the
code and on the allowed commands is also shown in
the README.
It is important to point out that the steps described
below must be performed in the exact order they will
be presented. This will prevent the algorithm from
unnecessary and very time-consuming computations.
1
https://github.com/epilurzu/ecgraph
Furthermore, it assures to return values that would not
be correct otherwise. It should also be specified that
the main role of the software is to act as a valuable
tool for reading the complex relationships shown in
the analyzed network, and its main task is to verify
and give information regarding the conditions of the
network.
2.1 TopoJSON and Connected
Components
First of all, we determined that the best data structure
to use for the algorithm is TopoJSON
2
. The TopoJ-
SON format, being an extension of GeoJSON (But-
ler et al., 2016) that encodes topology, allows saving
data more efficiently than the latter. This is possible
because it simplifies the data by saving the informa-
tion of the arcs that are part of the polygon perimeters
stored in the layer. By saving the geographic data in
this way, redundancy is avoided.
Unless the TopoJSON format is not only com-
posed of polygons with proprietary arcs as in the case
of an archipelago, it offers a reduction of 80% or more
in space without any need for simplification. It is
also significantly smaller than a shapefile, and also
possesses all the readability properties of the JSON
files (Severance, 2012).
For these reasons, we decide to use this format as
an input for corridors and areas, and as an output for
the corridor improved with obtained data.
Among the many other benefits it possesses, we
can take advantage of its neighbors function. The
TopoJSON format makes it especially easy to find
neighbor nodes starting from a node, as neighbors
share an arc with the node. By recursively following
neighbors, we can define which is the connected and
integrated component (Fenu and Pau, 2018) (Fenu
and Nitti, 2011) in linear time. The efficiency in
developing a connected component and its immedi-
ate reading remain key points in the analysis of com-
plex networks in all fields in which it is applied (Orda
et al., 2019).
For the operations we are going to perform, the
connected component is the basis to start from. It
represents a set of nodes that can be reached through
adjacent nodes. From this definition, it is simple to
deduce that only an alteration of these nodes can en-
danger their structure, and nothing else. However, it
is necessary to pay attention to a peculiarity.
In fact, as software development has shown, and
as it can be deduced from the properties of the Topo-
JSON format, neighboring nodes that share a single
2
https://github.com/topojson/topojson-specification/
blob/master/README.md
COMPLEXIS 2021 - 6th International Conference on Complexity, Future Information Systems and Risk
48

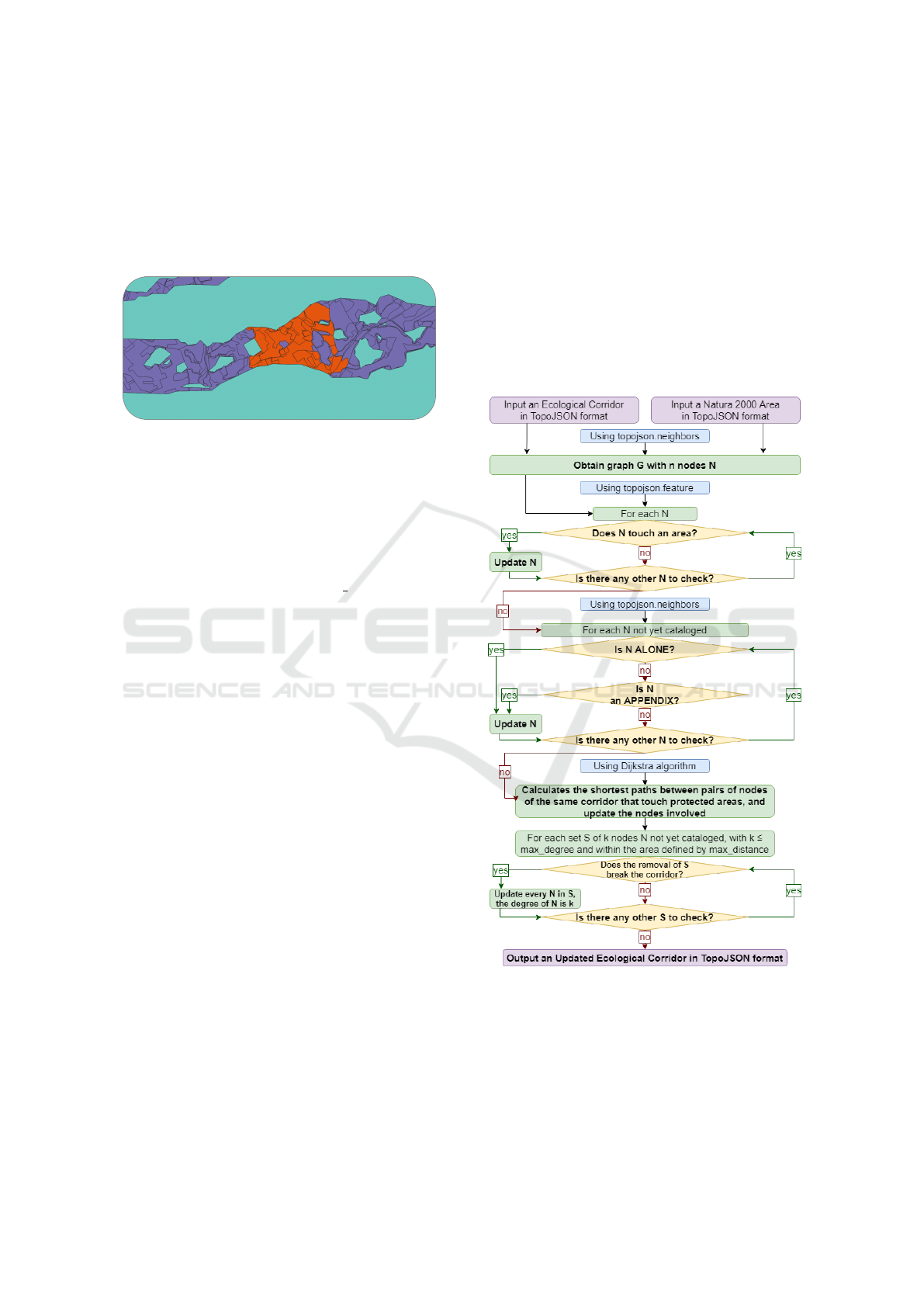
Figure 1: On top an example of a corridor in purple, at the
bottom a zoom of the same corridor. There are some indi-
vidual patches highlighted in orange. These are not consid-
ered to be a part of the main connected component because
they do not share a common arch with their neighbors.
point like the one shown in Figure 1 are not consid-
ered neighbors at all.
Although in a practical case this difference might
seem negligible, it represents a substantial difference
for the algorithm. Furthermore, depending on the an-
imal species whose migration is examined, it may be
unreasonable to consider that they could be channeled
into such a bottleneck.
2.2 Patches with Neighbor Areas
Among the most important patches, we certainly find
those bordering protected areas (Ostermann, 1998).
They represent the source and sink nodes in the pas-
sage between the areas. In case of migration, these
essential nodes are certainly traversed. However, to
identify these patches we cannot use the neighbor
method used in the subsection 2.1, because they are
not part of the same layer. In fact, it is not even cer-
tain that the patches lie on the perimeter of the area,
the two of them could also overlap. A different ap-
proach is needed, which requires more computational
and time resources, but is equally effective.
First of all, it is necessary to momentarily convert
the corridor and area files into GeoJSON via function
topojson.feature. This allows access to the real co-
ordinates representing the individual polygons and to
perform simple intersection operations. We choose to
use the Turfjs
3
library for this task. Identifying bor-
dering areas and patches at this point is a problem of
3
https://turfjs.org/
quadratic complexity, as two nested for are needed to
iterate the various combinations. It is not even pos-
sible to stop the cycle for a specific patch once the
intersection with a protected area has been identified,
as there are areas themselves that intersect other areas,
potentially making a patch bordering both.
To further simplify the calculation is necessary to
filter the protected areas first. Doing so, ECGraph
obtains only those areas that are touched by at least
one patch and avoids unnecessary operations. This is
done by defining a bounding box of the corridor and
filtering the areas that intersect with it. At this point,
the search operation is greatly simplified but is still
expensive enough to demand at least seconds in the
best-case scenario.
As a preliminary operation to the steps described
in the subsection, we decided to simplify the two in-
put layers with the topojson.presimplify function, so
that the number of points that define the polygons
could be decreased. The accuracy of the resulting lay-
ers can be chosen by the user. It must be the object of
particular care because if set poorly it could remove
entire areas, or not find intersections that instead exist.
At the end of this phase, the variable vcn degree
of the identified nodes will be set with a particular
code define as NEIGHBOR OF AREA that will dis-
tinguish them as bordering a protected area.
2.3 Isolated Patches and Appendices
As mentioned in subsection 2.1, some connected
components may be composed of single nodes due to
the conformation of the territory and the specifics of
the TopoJSON format. In subsection 2.2, on the other
hand, it was found that the prior removal of elements
that are not useful for the computation can make a
huge difference, especially in terms of time.
This subsection lays the foundations to avoid un-
necessary operations in following iterations, and with
a linear computational cost. In fact, from this point
on, the algorithm will work only on nodes that do not
have vcn degree initialized, except in some cases for
similar degrees.
For the first skimming, the software removes the
nodes without neighbors, i.e. completely isolated.
These, by definition, could never be cut nodes, but
they still do not have any use in traversing the cor-
ridor. If not cataloged they would only add worth-
less computations later on. Once identified, their
vcn
degree can be set to ALONE.
There are, however, another category of nodes that
are not useful for crossing the corridor, those who
necessarily have to cross the same node twice in or-
der not to get stuck. An example of these nodes is
ECGraph: A Complex Networks Tool to Classify Critical Points of Ecological Corridors
49

the enclaves (Fenu and Pau, 2018), nodes surrounded
by other nodes, and not accessible by any other route.
However, they are not the only ones that fall within
the definition. Generalizing, we could define ap-
pendix nodes all those that have among their neigh-
bors some nodes that are appendix and at most one
neighbor that is not, as shown in the Figure 2.
Figure 2: Some examples of appendices, highlighted in or-
ange, through different corridors, colored in purple.
Once identified, it is possible to set their vcn degree
to APPENDIX. This further simplification can make
a significant difference in terms of time depending
on the conformation of the corridor and does not re-
quire differentiation of the enclaves from the other ap-
pendix nodes, as they all have the same property.
It is however necessary to specify that some nodes
cataloged as appendices could also be cut nodes, but
if removed they could not jeopardize the ability to
walk through the ecological corridor. Once an ap-
pendix node has been eliminated, the excluded sub-
graph would have no access to natural areas, being
therefore negligible.
2.4 Shortest Path
Once the least used nodes have been removed, it is
now necessary to score the nodes based on their fre-
quency of use. We choose to use the Dijkstra algo-
rithm (Dijkstra et al., 1959) to search for the short-
est path in order to identify which nodes are being
traveled and how often. First of all, it is necessary to
identify each pair of nodes that would start and arrive
at different natural areas and who join the same con-
nected component. This step is possible thanks to the
information obtained from the subsection 2.2.
Once the various start and end nodes are found,
the sp score variable of the nodes belonging to the
shortest path has to increase by one. Once finished in-
creasing all the nodes of the various shortest path cal-
culated in the connected component, is now required
to normalize the data by dividing the same variable by
the total number of shortest path calculated.
Doing so, the value can vary from 0, a node never
traveled, to 1, a node traveled by every single short-
est path. In a nutshell, is possible to see the sp score
variable as a betweenness centrality of the network
calculate for nodes source and sink that are adjacent
to protected areas. As a cost variable for the choice of
the least expensive node in Dijkstra’s algorithm, we
choose to use the distance between centroids of the
nodes, so that the algorithm prefers a greater number
of nodes to travel if this means saving time to travel
them in a practical case. The time complexity of this
algorithm is k O(n
2
) with k equal to the number of
source-sink combinations.
2.5 Cut Nodes and Virtual Cut Nodes
Finally, it is possible to give a classification of the
nodes that can affect the possibility to walk through
the connected components if removed. As already
explained in other papers (Fenu and Pau, 2018) a cut
node can be defined as a node that, if removed from
the component, divides it into more subcomponents
not connected. Similarly, virtual cut nodes (Fenu and
Podda, 2020) are groups of nodes that if removed si-
multaneously cause the same consequences as the re-
moval of a cut node.
To identify a cut node among the nodes still with-
out vcn
degree, the algorithm creates a connected
subcomponent starting from a neighbor of the node
under analysis, from which it recursively runs through
the neighbors to create the network as seen in the sub-
section 2.1. However, the subcomponent cannot ex-
pand if one of the neighbors corresponds to the con-
sidered node, in order to simulate its removal. At the
end of the creation of the subcomponent, if it is com-
posed of a number of nodes lower than the original
component -1, we will have the evidence that the cho-
sen node is actually a cut node.
The algorithm can be generalized so that it can
calculate virtual cut nodes of any degree, but there
are some reflections to be made. It is necessary to test
if groups of nodes, currently uncataloged, of size n,
with n corresponding to the degree of the possible vir-
tual cut node, are indeed virtual cut nodes. However,
testing each individual combination would be compu-
tationally expensive. Although it has been shown that
virtual cut nodes can have child nodes even at multi-
COMPLEXIS 2021 - 6th International Conference on Complexity, Future Information Systems and Risk
50
ple nodes apart (Fenu and Podda, 2020), it has been
found that this is not a frequent event. To simplify the
computation, we decide to impose a maximum limit
of steps from the father node in which to search for
candidates neighbors to join the possible virtual cut
node, as shown in Figure 3.
Figure 3: The heart-shaped parent patch in the center is
surrounded by orange highlighted patches. The selected
patches correspond to all the neighbors in the corridor that
are no more than 3 steps from the parent node.
Doing so, in the worst case, the unnecessary iterations
would be limited to that set of neighbors. Always for
time and computation savings reasons, we also decide
not to keep track of founded virtual cut nodes, but in-
stead to mark the corresponding vcn degree or every
single node belonging to the virtual cut node of de-
gree n found. In fact, each of those nodes is sure to
be part of at least one virtual cut node, that is the one
found. Doing so, for every virtual cut node of degree
n, n nodes are set, and numerous cycles are avoided.
As in the cut node search, once created a subcompo-
nent that propagates avoiding the points of the virtual
cut node, if this is less than the size of the component
- n, then a new virtual cut node has been identified.
At the end of the iteration of this part of the algo-
rithm, the search for the various virtual cut node con-
taining a father node can be easily found by repeat-
ing a similar algorithm only on the identified nodes of
the father’s degree. As mentioned above, running the
algorithm in order of increasing degree is necessary.
It not only decreases the number of cycles needed to
calculate higher degrees by removing the lower ones
but also prevents recognizing erroneously some vir-
tual cut node that could break the graph with a subset
of itself. That would result in a virtual cut node with
a lower degree. This information makes a huge dif-
ference as if a virtual cut node is of a lower degree
it is much more threatening for the network structure.
The final user can set at will the maximum distance
in which to search for virtual cut nodes and the maxi-
mum degree wanted.
To calculate the time complexity it is necessary to
consider how many times it is required to build the
check subgraph, with linear time complexity. In the
case of cut nodes, it is simply one. In the case of
virtual cut nodes, it is necessary to take into consider-
ation the set k of possible child nodes that are distant
from the father node the number of steps chosen or
less. In the worst case scenario, the check subgraph
has to be estimated for each n-1 element subset of the
set k, with n being the current virtual cut node degree.
2.6 Time and Score
The Figure 4 shows with a flow chart the main pro-
gresses of the program illustrated in this paper.
Figure 4: A simple flowchart showing the main points of
ECGraph. The inputs and outputs are highlighted in pur-
ple, some functions used by the program in blue, and the
operations it performs in green and yellow.
As seen in previous subsections, ECGraph allows the
user to specify the accuracy wanted to find intersec-
tions between corridors and areas, the maximum de-
gree desired in the research of a virtual cut node and
ECGraph: A Complex Networks Tool to Classify Critical Points of Ecological Corridors
51

the maximum distance where to search for it. This
parameters let the user obtain higher precision of the
output data. This, requiring a greater number of iter-
ations, leads to a consequential increase in execution
time.
The algorithm has been tested giving different ac-
curacy as input to topojson.presimplify. These, by
influencing the precision of the polygons examined
in the calculation of the intersections seen in subsec-
tion 2.2, will directly affect the search times of the
protected areas adjacent to the corridor and neighbor
to specific patches. In a nutshell, greater accuracy
in topojson.presimplify should avoid finding corridor
patches neighbor of protected areas that result in false
positives or false negatives.
As for the maximum degree of virtual cut node to
be searched, we set it to four, while keeping the exe-
cution times of the single degree separate. What can
increase computation times in this case is the exten-
sion of the nodes to be tested as possible children, by
setting a greater maximum distance to choose from as
seen in the subsection 2.5
The results obtained by running the program on
the same input corridor (Cannas and Zoppi, 2017) is
show in Tables 1 and 2 and represented in the Fig-
ure 5. The computer used to run the code is equipped
with an AMD A10 7850k processor and two 4GB
DDR3 1866MHz RAM. The program runs on a single
thread.
The clearest difference lies in the search for nodes
connected with natural areas. As shown in Figure 5,
the algorithm executed with higher accuracy recog-
nized a relatively small protected area, and has conse-
quently found all patches that intersect it. In terms of
search time, the difference is important and as a result,
the inclusion of three more areas occurred. Those
same areas would have been lost in the simplification,
with the consequent reduction in terms of time seen
in Table 1.
This consequently increases the number of short-
est paths requested and leads to an increase in time
in that section of the algorithm as well. As far as
cut nodes and virtual cut nodes are concerned, these
have been partly converted into nodes bordering ar-
eas, but in addition to this, they have not shown dras-
tic increases related to a larger area in their search, as
shown in Table 2.
For a clearer combined representation of the main
values obtained, a new variable containing a normal-
ization of vcn degree and sp score has been imple-
mented. It can be calculated a normalized vcn score
from nodes with vcn degree ≥ 1 by dividing 1 by
vcn degree, so that the variable can only have val-
ues from 0 to 1. Multiplying then the vcn score with
Figure 5: On top, a corridor calculated with an accuracy of
10
−5
and with a max distance of 3. At the Bottom, the same
corridor calculated with an accuracy of 10
−20
and with a
max distance of 10.
sp score will get a combined value that will give a
clearer idea of the most critical and simultaneously
most visited nodes, as visible in Figure 6.
3 CONCLUSION AND FUTURE
WORKS
The study of ecological networks is an increasingly
important topic to be analyzed. ECGraph has demon-
strated with its performances and results that it can be
an useful support tool in the study of the viability of
the ecological network, finding the different paths and
their critical patches.
Like many problems of complex networks, even
the one exposed is highly susceptible to the size and
conformation of the network given as input. As has
been explained, different parts of the algorithm have
a quadratic time complexity, which takes longer to
compute as the required precision increases. Despite
that, there is still room for improvement both in the
data structures used in the execution of the program
COMPLEXIS 2021 - 6th International Conference on Complexity, Future Information Systems and Risk
52

Table 1: The time needed to compute the algorithm with the different Accuracy and Max Distance settings. The vcn degree
ALONE, APPENDIX, and cut node all execute under one second.
Accuracy Max Distance Areas Shortest Path VCN d2 VCN d3 VCN d4
10
−5
3 45s 2m 50s 1m 20s 10m 59s 53m 12s
10
−20
10 1h 16m 46s 6m 24s 2m 48s 15m 49s 1h 7m 55s
Table 2: Type and number of nodes found.
Alone Appendix Neighbor Area Cut node VCN d3 VCN d3 VCN d4
38 873 373 475 1362 454 203
38 823 549 471 1350 445 206
Figure 6: The Figure expresses the score from 0 to 1. On
top, there is a corridor with no shortest path, as it does not
connect areas, and so entirely white. At the bottom, instead,
there is a corridor with several critical areas as they are fre-
quently used and simultaneously cut nodes.
and the implementation of the algorithms exposed.
In its most simplified version, with a relatively low
runtime on a commercial computer, ECGraph allows
establishing the network structure up to the virtual cut
nodes of second degree. The customization of the in-
put values and even more the open source nature of
the project allow having a solid starting point for the
development of even more useful tools.
As a demonstration of this, a software that can be
integrated with ECGraph is already in phase of devel-
opment, which will allow to have a graphic interface
designed for the representation of the data exposed,
and can even give more specific additional informa-
tion, such as the virtual cut nodes generated by the se-
lected parent node, the corridor change when a node
is removed and other useful data in real time.
Ultimately, the creation of a community that can
provide feedbacks and ecological corridors files for
the software improvement would allow refining the
tool more and more, making it more powerful, robust,
and even easier to use.
ACKNOWLEDGEMENTS
This paper is written within the Research Program
”Paesaggi rurali della Sardegna: pianificazione di in-
frastrutture verdi e blu e di reti territoriali complesse
- CUP: J86C17000180002 - Progetto di ricerca di
base dell’Universit
`
a di Sassari e Cagliari finanziato
sul Fondo di Sviluppo e Coesione 2014-2020”. The
research leading to these results has received funding
from the Autonomous Region of Sardinia (Legge Re-
gionale 7/2007).
REFERENCES
Bodini, A. and Cossu, Q. (2010). Vulnerability assess-
ment of central-east sardinia (italy) to extreme rainfall
events. Natural Hazards and Earth System Sciences,
10(1):61–72.
Butler, H., Daly, M., Doyle, A., Gillies, S., Hagen, S.,
Schaub, T., et al. (2016). The geojson format. Internet
Engineering Task Force (IETF).
Cannas, I. and Zoppi, C. (2017). Ecosystem services and
the natura 2000 network: a study concerning a green
infrastructure based on ecological corridors in the
metropolitan city of cagliari. In International Confer-
ence on Computational Science and Its Applications,
pages 379–400. Springer.
Dijkstra, E. W. et al. (1959). A note on two problems
in connexion with graphs. Numerische mathematik,
1(1):269–271.
Evans, D. (2012). Building the european union’s natura
2000 network. Nature conservation, 1:11.
Fenu, G. and Nitti, M. (2011). Strategies to carry and for-
ward packets in vanet. In International Conference on
Digital Information and Communication Technology
and Its Applications, pages 662–674. Springer.
Fenu, G. and Pau, P. L. (2015). Evaluating complex network
indices for vulnerability analysis of a territorial power
ECGraph: A Complex Networks Tool to Classify Critical Points of Ecological Corridors
53

grid. Journal of Ambient Intelligence and Humanized
Computing, 6(3):297–306.
Fenu, G. and Pau, P. L. (2018). Connectivity analysis of
ecological landscape networks by cut node ranking.
Applied network science, 3(1):22.
Fenu, G. and Podda, E. (2020). A model of second-
degree virtual cut nodes applied to complex networks
in ecological landscape. Procedia Computer Science,
170:123–128.
Gill Jr, R. E., Tibbitts, T. L., Douglas, D. C., Handel, C. M.,
Mulcahy, D. M., Gottschalck, J. C., Warnock, N., Mc-
Caffery, B. J., Battley, P. F., and Piersma, T. (2009).
Extreme endurance flights by landbirds crossing the
pacific ocean: ecological corridor rather than barrier?
Proceedings of the Royal Society B: Biological Sci-
ences, 276(1656):447–457.
Jenson, S. K. and Domingue, J. O. (1988). Extracting topo-
graphic structure from digital elevation data for ge-
ographic information system analysis. Photogram-
metric engineering and remote sensing, 54(11):1593–
1600.
Jongman, R. H. (1995). Nature conservation planning in
europe: developing ecological networks. Landscape
and urban planning, 32(3):169–183.
Orda, L. D., Jensen, T. V., Gehrke, O., and Bindner, H. W.
(2019). Efficient routing for overlay networks in a
smart grid context. In SMARTGREENS, pages 131–
136.
Ostermann, O. P. (1998). The need for management of na-
ture conservation sites designated under natura 2000.
Journal of applied ecology, 35(6):968–973.
Severance, C. (2012). Discovering javascript object nota-
tion. Computer, 45(4):6–8.
Team, Q. D. et al. (2015). Qgis geographic information sys-
tem. open source geospatial foundation project. URL:
http://qgis. osgeo. org.
Tilkov, S. and Vinoski, S. (2010). Node. js: Using javascript
to build high-performance network programs. IEEE
Internet Computing, 14(6):80–83.
Urban, D. and Keitt, T. (2001). Landscape connectivity:
a graph-theoretic perspective. Ecology, 82(5):1205–
1218.
COMPLEXIS 2021 - 6th International Conference on Complexity, Future Information Systems and Risk
54
