Logical Duality in Reactions of Amoeba Proteus
Andrew Schumann
a
, Krzysztof Bielas
b
and Jerzy Kr
´
ol
c
Chair of Cognitive Science and Mathematical Modelling, University of Information Technology and
Management in Rzesz
´
ow, Sucharskiego 2, 35-225 Rzesz
´
ow, Poland
Keywords:
Amoeba Proteus, Logical Duality, Logical Square, Emergency.
Abstract:
We consider some emergent properties in the motility of Amoeba Proteus in its reactions on attractants and
repellents. In these reactions, we cannot define a logical composition Ψ(x
1
, . . . , x
n
) as an n-place logical
function Ψ over x
1
, . . . , x
n
, where each x
i
is an atomic proposition or its negation. Each x
i
should occur only
without negation. Nevertheless, we face there a self-organised process with different reaction under stress or
safety conditions.
1 INTRODUCTION
The swarm motion can be quite complicated. In
order to simulate it, there were proposed many al-
gorithms (Cuevas et al., 2013; Dorigo and Stutzle,
2004; Karaboga, 2005; Kennedy and Eberhart, 2001;
Passino, 2002; Rajabioun, 1987). In the Particle
Swarm Optimization (PSO) (Kennedy and Eberhart,
2001; Kennedy and Eberhart, 1995) it is assumed that
the particles (agents) know (i) their best position ‘lo-
cal best’ (lb) and (ii) their neighbourhood’s best po-
sition ‘global best’ (gb). The next position is deter-
mined by velocity. Let x
i
(t) denote the position of
particle i in the search space at time step t, where t is
discrete. Then the position x
i
is changed by adding a
velocity to the current position:
x
i
(t +1) = x
i
(t) + v
i
(t +1),
where v
i
(t + 1) = v
i
(t) + c
1
r
1
(lb(t) − x
i
(t)) +
c
2
r
2
(gb(t) − x
i
(t)) and i is the particle index, c
1
, c
2
are acceleration coefficients, such that 0 ≤ c
1
, c
2
≤ 2,
r
1
, r
2
are random values (such that 0 ≤ r
1
, r
2
≤ 1)
regenerated every velocity update.
One of the possible PSO algorithms can be ex-
emplified by the bird flocking (Reynolds, 1987;
Reynolds, 1994). In flocks ‘local best’ and ‘global
best’ of birds are defined by the following three rules:
(i) collision avoidance (birds fly away before they
crash into one another); (ii) velocity matching (birds
fly about the same speed as their neighbours in the
a
https://orcid.org/0000-0002-9944-8627
b
https://orcid.org/0000-0003-3259-7676
c
https://orcid.org/0000-0002-7296-7355
flock); and (iii) flock centering (birds fly toward the
center of the flock as they perceive it). So, the posi-
tion of a bird i at time t is given by its placement x
i
at
time t − 1 shifted by its current velocity v
i
. This v
i
is
determined by the rules (i) – (iii).
Another type of algorithms was developed for
explicating the motility of multinucleated giant
amoebae Physarum polycephalum (Schumann, 2019;
Tsuda et al., 2004; Tsuda et al., 2012). Here the po-
sition x
i
(t) of particle i at time step t changes due to
biologically active matters: (i) attractants (pheromone
and other good conditions) which attract the particles
and (ii) repellents (strong light and other bad condi-
tions) which repel the amoeboid particles. Some col-
lisions (merging the particles) which are avoided in
PSO are always possible for multiagent reactions of
Physarum polycephalum. From this it follows that the
plasmodium of Physarum polycephalum can respond
to a contradictory situation (consisting of a mixture of
an attractant and a repellent), in which there is no sin-
gle optimal solution, differently. In other words, the
plasmodia showed diverse responses that could not be
explained by a simple model of the stimulus-response
system (Shirakawa et al., 2020). In this paper, we
consider an abstract model of Amoeba Proteus motil-
ity. This model also is based on reactions of amoe-
boid particles on external stimuli: attractants and re-
pellents.
In this approach, we can implement some logical
functions: negation as repelling the particles, con-
junction as attracting both particles simultaneously,
disjunction as attracting one or another particle. We
can assume that in this way we can always define a
logical composition Ψ(x
1
, . . . , x
n
) as an n-place log-
Schumann, A., Bielas, K. and Król, J.
Logical Duality in Reactions of Amoeba Proteus.
DOI: 10.5220/0010386102130217
In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 3: BIOINFORMATICS, pages 213-217
ISBN: 978-989-758-490-9
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
213

ical function Ψ over x
1
, . . . , x
n
, where each x
i
is an
atomic proposition or its negation. But it is impos-
sible. The point is that in any logical composition
Ψ(x
1
, . . . , x
n
) each x
i
should occur only without nega-
tion. Thereby, we are going to show that some emer-
gent properties in the amoeboid motility appear due
to the principal impossibility of composing negations
for atomic propositions into a complex logical func-
tion (see Section 2). It is a more general abstract re-
sult than (Shirakawa et al., 2020). Nevertheless, we
can define the logical duality for this motility, i.e.
reactions on external stimuli under stress or safety
conditions (Section 3). It means that we observe a
proto-psychic structure in reactions with distinguish-
ing stress reactions from safety reactions.
Our model of attraction is based on nutrition in
amoebae. For them, nutrition is holozoic. It means
that experiments can be performed with different or-
ganisms such as algae, rotifers or other protozoans,
which are eaten by amoebae. These organisms can be
captured by pseudopodia of amoebae to form a food
cup and to be completely surrounded by cytoplasm.
In our model, we test reactions of amoebae on several
small organisms (two and more) located near.
2 REACTIONS OF AMOEBA
PROTEUS ON ATTRACTANTS
AND REPELLENTS
Let us consider basic amoeboid reactions of Amoeba
Proteus. These reactions are swarm-like, because the
membrane of this organism is very elastic and can
be readily deformed at different places in reactions
to different external signals. These deformations are
caused by assembling and dissembling actin filament
networks which are represented by different bunches
or trees of F-actin proteins growing either towards
attractants or in the opposite direction of repellents
(Carlier, 1989; Carlier, 1991; Etienne-Manneville,
2004; Hill, 1981; Maly and Borisy, 2001; Mayne and
Adamatzky, 2015; Mogilner and Oster, 1996; Moore
et al., 1970; Mooseker and Tilney, 1975; Pollard and
Cooper, 2009). So, an external signal influences the
grow of actin filaments in one of the following two
directions: either toward the signal (if it is coming
from an attractant), see Fig.1, or counter to the direc-
tion of the signal (if it is coming from a repellent),
see Fig.2. Hence, actin filament wavefronts are pre-
senting some sensitive and reacting agents of Amoeba
Proteus. In other words, active zones of assembling
actin filaments which are responsible for changing
the cell shape are considered agents. They appear
and disappear under different external conditions to
change the membrane of amoeba.
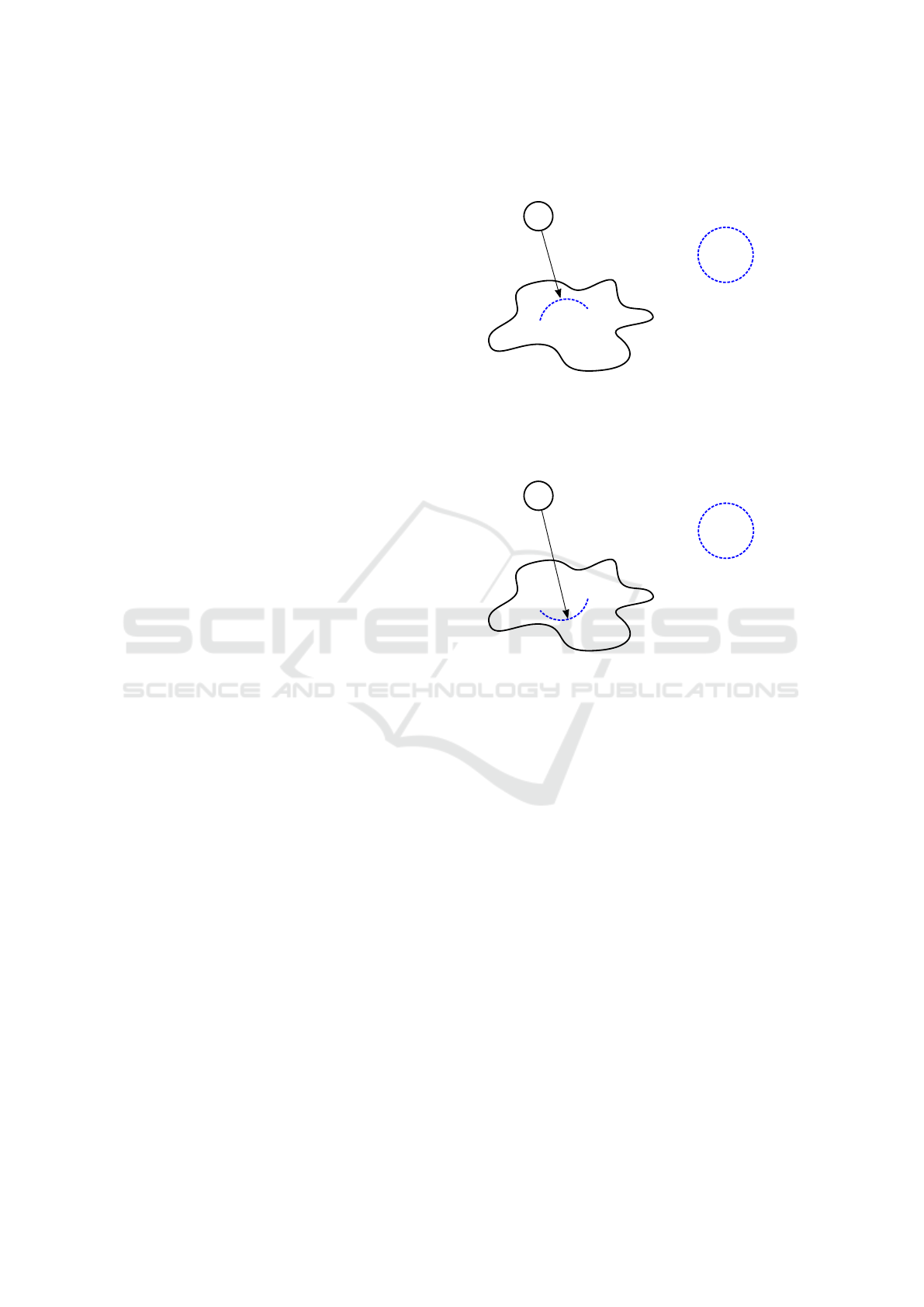
Wavefront of actin �ilaments
Amoeba Proteus
Attractant
Figure 1: If we locate an attractant before the amoeba, then
it causes assembling a wavefront of actin filaments which
begins to make a pseudopodium – a deformation of mem-
brane towards this attractant.
Wavefront of actin �ilaments
Amoeba Proteus
Repellent
Figure 2: If we locate a repellent before the amoeba, then
it causes assembling a wavefront of actin filaments which
begins to make a pseudopodium in the opposite direction –
a deformation of membrane counter to the direction of this
repellent.
Let (A
1
, r
A
1
), . . . , (A
n
, r
A
n
) be different active zones
of an amoeba with their corresponding positions,
where A
i
is an agent (active zone) and r
A
i
is its po-
sition. So, each (A
i
, r
A
i
) can be identified with a zone
of growing actin filaments. They start to grow faster
and to interconnect into bunches and trees through the
adhesion due to external signals. Even if the signal is
the same, it can be detected by (A
i
, r
A
i
) differently be-
cause of their different location.
Similarly, let (X
1
, r
X
1
), . . . , (X
m
, r
X
m
) denote the
family of external signals, where X
i
can be either
an attractant At
i
or a repellent Rp
i
. Suppose that
each signal X
i
carries its own interaction coefficient
χ
i
∈ [−1,1]. While χ
i
> 0 for attractive At
i
and χ
i
< 0
for repulsive Rp
i
, the precise value of an interaction
coefficient depends on the particular signal. Hence,
we propose that zone dynamics due to external sig-
nals can be described by a potential V (χ
j
, r
A
i
, r
X
j
) and,
by an abuse of notation, it holds
V (χ
j
, r
A
i
, r
X
j
) ≡ χ
j
V (


r
A
i
− r
X
j


). (1)
Paradigms-Methods-Approaches 2021 - Workshop on Novel Computational Paradigms, Methods and Approaches in Bioinformatics
214

This gives rise to forces F
A
i j
= −χ
j
∇V (



r
A
i
− r
X
j



),
therefore each zone (A
i
, r
A
i
) is subjected to an exter-
nal, resultant force
F
A
i
=
m
∑
j=1
F
A
i j
= −
m
∑
j=1
χ
j
∇V (


r
A
i
− r
X
j


). (2)
Let us sketch a model for the physical mechanism
of an interaction between the system of amoeba and
some external signals, driving the desired behaviour
eventually. We have already stated that, in princi-
ple, the external signals are classified into those of
attractive and repulsive character. In these reactions
to external forces there is a small memory effect –
a short 4t, when the amoeba continues its motoring
stage even under new conditions. If discretized, the
model would therefore satisfy the so-called Markov
chain property, i.e. the future state depends on both
the present and previous state.
Assume that we have two attractants At
1
and At
2
before the amoeba and these attractants have differ-
ent power of pheromone (intensity) χ
1
and χ
2
, respec-
tively, see Fig.3. As a result, we have two appropri-
ate forces F
A
11
and F
A
22
made on active zones A
1
and
A
2
, respectively. Both attractants are placed close to-
gether and if we add their two force vectors F
A
11
+F
A
22
,
then the sum of these vectors is obtained as a quite
long new vector. We know experimentally that under
this location of two attractants the amoeba will try to
occupy both of them simultaneously. This kind of be-
haviour corresponds to the conjunction of both attrac-
tants. So, we can introduce the following rule: (i) the
longer the sum of two force vectors F
A
11
+ F
A
22
is, the
more appropriate to conjunction the behaviour is; (ii)
the shorter the sum of two force vectors F
A
11
+ F
A
22
is,
the more appropriate to disjunction the behaviour is.
Vector sum
of the power of pheromone A
and the power of pheromone B
Amoeba Proteus
Attractant A
Attractant B
Power of
pheromone B
Power of
pheromone A
Figure 3: The addition of two vectors denoting the power of
intensity of two pheromone pieces A and B.
Suppose, (A
1
, r
A
1
) and (A
2
, r
A
2
) denote two actin
filament wavefronts of amoeba and X
1
and X
2
are
two external signals with two appropriate forces F
A
11
and F
A
22
on A
1
and A
2
, respectively. Define the
fuzzy membership function µ
(A
i
,r
A
i
)
(x) = α ∈ [0, 1]
for i = 1, 2 with the following meaning: an actin
filament x with the location r
x
belongs to the actin
filament wavefront A
i
with a degree of member-
ship (probability) α that corresponds to the force
F
A
i j
of perceived external signal X
j
at the zone A
i
:
µ
(A
i
,r
A
i
)
(x) =
−χ
j
∇V (
|
r
x
−r
X
j
|
)
−χ
j
∇V (



r
A
i
−r
X
j



)
=
F
x
i j
F
A
i j
, see (2), where
−χ
j
∇V (



r
A
i
− r
X
j



) 6= 0, i.e. we suppose that there is a
force F
A
i j
on A
i
indeed.
Let us define a fuzzy set
e
A
i
= {x : µ
(A
i
,r
A
i
)
(x) >
0}. Its complement ¬
e
A
i
is as follows: ¬
e
A
i
=
{x : µ
(A
i
,r
A
i
)
(¬x)) = 1−µ
(A
i
,r
A
i
)
(x))}. Now, we can de-
fine intersection and union for
f
A
1
and
f
A
2
:
intersection:
f
A
1
∩
f
A
2
=
f
A
3
= {z : µ
(A
3
,r
A
3
)
(z) =
µ
(A
3
,r
A
3
)
(x ∧ y) = (
F
x
11
F
A
11
+F
A
22
+
F
y
22
F
A
11
+F
A
22
−
F
x
11
F
A
11
·
F
y
22
F
A
22
) >
0, x ∈
f
A
1
, y ∈
f
A
2
}.
union:
f
A
1
∪
f
A
2
=
f
A
3
= {z: µ
(A
3
,r
A
3
)
(z) = µ
(A
3
,r
A
3
)
(x ∨
y) =
max(F
x
11
,F
y
22
)
max(F
A
11
,F
A
22
)
> 0, x ∈
f
A
1
, y ∈
f
A
2
}.
After that we define the order as follows:
e
A
i
⊆
e
A
j
if and only if for all x ∈
e
A
i
its membership function
µ
(A
i
,r
A
i
)
(x) ≤ µ
(A
j
,r
A
j
)
(x). According to this definition,
(
f
A
1
∩
f
A
2
) ⊆ (
f
A
1
∪
f
A
2
).
3 LOGICAL DUALITY
Suppose that f is an n-place logical composition of
fuzzy sets
f
A
1
,
f
A
2
, . . .
f
A
n
. Another n-place two-valued
logical composition f
0
is said to be dual (or logically
dual) to f if and only if either
f
0
(
f
A
1
, . . . ,
f
A
n
) ⊆ f (
f
A
n
, . . . ,
f
A
n
)
or
f (
f
A
1
, . . . ,
f
A
n
) ⊆ f
0
(
f
A
n
, . . . ,
f
A
n
).
According to this definition, if f
0
is dual to f , then
f is dual to f
0
. So, the duality is always mutual.
Let us notice that intersection and union defined
above are dual to each other:
(
f
A
1
∩
f
A
2
) ⊆ (
f
A
1
∪
f
A
2
).
Now, let us introduce a standard propositional log-
ical language consisting of propositional variables
p, q, r, . . . and logical connectives: ¬ (negation), ∧
(conjunction), ∨ (disjunction). The semantics of this
language is as follows.
Logical Duality in Reactions of Amoeba Proteus
215

atomic proposition: let p be an atomic proposition
and m
A
i
χ
i
,t
be its truth evaluation, then m
A
i
χ
i
,t
(p) = >
if and only if the set
e
A
i
for the active zone A
i
and
interactive coefficient χ
i
at the time step t is not
empty; otherwise m
A
i
χ
i
,t
(p) = ⊥;
negation: let p be a formula and m
A
i
χ
i
,t
be its truth
evaluation, then m
A
i
χ
i
,t
(¬p) = > if and only if the
set
e
A
i
for the active zone A
i
and interactive coeffi-
cient χ
i
at the time step t is not empty and its force
F
A
i
is negative; otherwise m
A
i
χ
i
,t
(¬p) = ⊥;
conjunction: let p, q be two formulas and m
A
i
,A
j
χ
i
,χ
j
,t
be
their truth evaluation, then m
A
i
,A
j
χ
i
,χ
j
,t
(p ∧ q) = > if
and only if the set
e
A
i
∩
e
A
j
for active zones A
i
, A
j
and interactive coefficients χ
i
, χ
j
at the time step t
is not empty; otherwise m
A
i
,A
j
χ
i
,χ
j
,t
(p ∧ q) = ⊥;
disjunction: let p, q be two formulas and m
A
i
,A
j
χ
i
,χ
j
,t
be
their truth evaluation, then m
A
i
,A
j
χ
i
,χ
j
,t
(p ∨ q) = > if
and only if the set
e
A
i
∪
e
A
j
for active zones A
i
, A
j
and interactive coefficients χ
i
, χ
j
at the time step t
is not empty; otherwise m
A
i
,A
j
χ
i
,χ
j
,t
(p ∨ q) = ⊥;
On the basis of logical duality, we can define con-
trary, subcontrary, subaltern, and contradictory logi-
cal functions:
contrary: two functions h and h
0
are contrary if and
only if (h ∧ h
0
) ≡ ⊥, but not always (h ∨ h
0
) ≡ >;
subcontrary: two functions h and h
0
are subcontrary
if and only if (h ∨ h
0
) ≡ >, but not always (h ∧
h
0
) ≡ ⊥;
subaltern: a function h is subaltern to h
0
if and only
if (h
0
⇒ h) ≡ >;
contradictory: two functions h and h
0
are contradic-
tory if and only if (h ∨ h
0
) ≡ > and (h ∧ h
0
) ≡ ⊥.
Now, let us show that (p ∧ q ∧ ·· · ∧ r) can be in-
terpreted as ‘stress from p, q, r’ and (p∨ q∨· ··∨ r) as
‘safety from p, q, r’. Then we can construct a square
of opposition, see Fig.4, 5, where
contrary: (p ∧ q ∧ · ·· ∧ r) and ¬(p ∨ q ∨ ··· ∨ r) are
contrary;
subcontrary: ¬(p ∧ q ∧ ··· ∧ r) and (p ∨ q ∨ · ·· ∨ r)
are subcontrary;
subaltern: (p ∨ q ∨ ··· ∨ r) is subaltern to (p ∧ q ∧
··· ∧ r) as well as ¬(p ∧ q ∧· ·· ∧r) is subaltern to
¬(p ∨ q ∨ ··· ∨ r);
contradictory: (p ∧q ∧ ··· ∧r) and ¬(p ∧q ∧· ··∧ r)
are contradictory as well as (p ∨ q ∨ · ·· ∨ r) and
¬(p ∨ q ∨ ··· ∨ r).
‘stress from p, q, r’
not ‘safety from p, q, r’
‘safety from p, q, r’
not ‘stress from p, q, r’
subaltern
contrary
subaltern
subcontrary
Figure 4: The square of opposition for the expressions
‘safety from p, q, r’ and ‘stress from p, q, r’.
(p ∧ q ∧ ··· ∧ r) ¬(p ∨ q ∨ ··· ∨ r)
(p ∨ q ∨ ··· ∨ r) ¬(p ∨ q ∨ ··· ∨ r)
subaltern
contrary
subaltern
subcontrary
Figure 5: The square of opposition for the expressions (p ∪
q ∪··· ∪ r) and (p ∩ q ∩ ··· ∩ r).
In this square of opposition, the predicates ‘stress
from p, q, r’ and ‘safety from p, q, r’ are considered
dual: if ‘stress from p, q, r’ holds true, then ‘safety
from p, q, r’ holds true. It is shown (Schumann, 2019)
that in each swarm networking, including even net-
works of actin filaments in one cell, there are two
basic reactions to outer stimuli: lateral activation (a
reaction under safety) and lateral inhibition (a reac-
tion under stress). The lateral activation is a reaction
of swarm particles (such as active zones of Amoeba
Proteus) to outer stimuli, according to which differ-
ent particles are not concentrated on the same stimuli.
As a result, we observe a decreasing of the intensity of
the external signals and the contrast of the signals is
made less visible. The lateral inhibition is a reaction
of swarm particles (such as active zones of Amoeba
Proteus) to external stimuli, according to which dif-
ferent particles are concentrated on the same stimuli.
This has led us to an increasing of the intensity of the
outer signals and the contrast of the signals is made
more visible. The amoebae of Amoeba Proteus fol-
low the lateral activation if they detect normal attrac-
tants and they follow the lateral inhibition if they face
standard repellents (Schumann, 2019).
Paradigms-Methods-Approaches 2021 - Workshop on Novel Computational Paradigms, Methods and Approaches in Bioinformatics
216

4 CONCLUSION
To sum up, we see that the amoebae of Amoeba Pro-
teus realize a kind of logical duality in their reac-
tions towards outer stimuli p, q, r, since either they be-
have under lateral activation and realize ‘safety from
p, q, r’ or they can behave under lateral inhibition and
realize ‘stress from p, q, r’, see Fig.4–5. In the mean-
while, the transmission between stress and safety is
smooth and it depends upon force vectors.
REFERENCES
Carlier, M. (1989). Role of nucleotide hydrolysis in the
dynamics of actin filaments and mictrotubules. Int Rev
Cytol, 115:139–170.
Carlier, M. F. (1991). Actin: protein structure and filament
dynamics. J. Biol. Chem, 266:1–4.
Cuevas, E., Cienfuegos, M., Zaldivar, D., and Perez-
Cisneros, M. (2013). A swarm optimization algorithm
inspired in the behavior of the social-spider. Expert
Systems with Applications, 40(16):6374–6384.
Dorigo, M. and Stutzle, T. (2004). Ant Colony Optimiza-
tion. MIT Press.
Etienne-Manneville, S. (2004). Actin and microtubules
in cell motility: which one is in control? Traffic,
5(7):470–477.
Hill, T. L. (1981). Microfilament or microtubule assembly
or disassembly against a force. Proc. Natl. Acad. Sci.
U.S.A, 78(9):5613–5617.
Karaboga, D. (2005). An idea based on honey bee swarm
for numerical optimization. Technical report-tr06,
Engineering Faculty, Computer Engineering Depart-
ment, Erciyes University.
Kennedy, J. and Eberhart, R. (2001). Swarm Intelligence.
Morgan Kaufmann Publishers, Inc.
Kennedy, J. and Eberhart, R. C. (1995). Particle swarm op-
timization. In Proceedings of the 1995 IEEE Inter-
national Conference on Neural Networks, volume 4,
pages 1942–1948, Perth, Australia, IEEE Service
Center, Piscataway, NJ.
Maly, I. V. and Borisy, G. G. (2001). Self-organization of
a propulsive actin network as an evolutionary process.
Proceedings of the National Academy of Sciences of
the United States of America, 98 20:11324–9.
Mayne, R. and Adamatzky, A. (2015). Slime mould forag-
ing behaviour as optically coupled logical operations.
International Journal of General Systems, 44(3):305–
313.
Mogilner, A. and Oster, G. (1996). Cell motility driven by
actin polymerization. Biophys. J, 71(6):3030–3045.
Moore, P. B., Huxley, H. E., and DeRosier, D. J. (1970).
Three-dimensional reconstruction of f-actin, thin fil-
aments and decorated thin filaments. J. Mol. Bioli,
50(2):279–295.
Mooseker, M. S. and Tilney, L. G. (1975). Organization
of an actin filament-membrane complex. filament po-
larity and membrane attachment in the microvilli of
intestinal epithelial cells. J. Cell Biol, 67(3):725–743.
Passino, K. M. (2002). Biomimicry of bacterial foraging for
distributed optimization and control. Control Systems,
22(3):52–67.
Pollard, T. D. and Cooper, J. A. (2009). Actin, a cen-
tral player in cell shape and movement. Science,
326(5957):1208–1212.
Rajabioun, R. (1987). Cuckoo optimization algorithm. Ap-
plied Soft Computing, 11:5508–5518.
Reynolds, C. W. (1987). Flocks, herds, and schools: A
distributed behavioral model. Computer Graphics,
21:25–34.
Reynolds, R. G. (1994). An introduction to cultural algo-
rithms. In Proceedings of the Third Annual Confer-
ence on Evolutionary Programming, pages 131–139.
Schumann, A. (2019). Behaviorism in Studying Swarms:
Logical Models of Sensing and Motoring. Emergence,
Complexity and Computation, vol. 33. Springer,
Cham, Switzerland.
Shirakawa, T., Gunji, Y., Sato, H., and Tsubakino, H.
(2020). Diversity in the chemotactic behavior of
Physarum plasmodium induced by bi-modal stimuli.
Int. J. Unconv. Comput., 15(4):275–285.
Tsuda, S., Aono, M., and Gunji, Y. P. (2004). Robust and
emergent Physarum-computing. BioSystems, 73:45–
55.
Tsuda, S., Jones, J., and Adamatzky, A. (2012). Towards
Physarum engines. Applied Bionics and Biomechan-
ics, 9:221–240.
Logical Duality in Reactions of Amoeba Proteus
217