Separating Local and Propagated Contributors to the Behnke-fried

Microelectrode Recordings

P. Jurczynski

, S. Le Cam

, B. Rossion

1,2

and R. Ranta

Universit

e de Lorraine, CNRS, CRAN, F-54000 Nancy, France

Universit

e de Lorraine, CHRU-Nancy, Service de Neurologie, F-54000, France

Keywords:

Microelectrode, Local Field Potential, Reference Estimation, Zero-reference Montage.

Abstract:

In electrophysiological measurements, a recording electrode is located in an electric ﬁeld and has a certain

electric potential value. Each measured signal is a potential difference between two electrodes, a measuring

electrode and a so-called reference electrode. This reference electrode is not located at inﬁnity and outside of

any electric ﬁeld, thus its electric potential is found in the measured signals. In order to isolate the local activity

of the recorded structure, it is necessary to understand the relationships between the different contributors at

the electrode level and separate these different activities. In this paper, we focus on the particular setup of

Behnke-Fried micro-electrodes. We propose to adapt a previous re-referencing method for separating local and

distant propagated activities taking into account the non-stationarity of the signals and the particular geometry

of these microelectrodes. We demonstrate, on realistically simulated signals, that the new re-referencing

procedure improves the preprocessing of these signals and might help deeper interpretation.

1 INTRODUCTION

Microelectrode recordings make it possible to analyze

the activity of the very close neuronal population in

which the electrode is implanted, within a radius of

a few hundred micrometers depending on the type of

implanted microelectrode. Such measurements have

been widely used to analyze the activity of individual

neurons, the action potentials (AP) of close neurons

being one of the main contributors to the recorded

signal. A second main contributor to the signal are

the inhibitory and excitatory post-synaptic currents,

which mainly originate from the local population, but

can also be picked from more distant structures up

to several millimeters if their activities are synchro-

nized enough (Buzs

aki et al., 2012; Kajikawa and

Schroeder, 2011). The analysis of these dominant

contributors and of their relationships hold precious

information to interpret the activity of the implanted

structure (Einevoll et al., 2013), their separations be-

ing a prerequisite to such analysis.

This separation, which is already a challenging

signal processing task by itself due to overlaps be-

tween their (frequency) contents (Zanos et al., 2011),

is made even more complicated by the presence of

the reference potential. Indeed, the measured elec-

trical activity always corresponds to a potential dif-

ference - one electrode measures the potential rela-

tive to another electrode, considered as the reference.

The relationship between the potentials “seen” by the

reference electrode and by the measuring electrodes

depend on the particular recording setup. For ex-

ample, in the context of macroscopic EEG record-

ings, the reference is often one of the scalp electrodes,

fundamentally similar to the other (measuring) scalp

electrodes. In the intracerebral recordings context

(SEEG), the reference is either considered to be at

zero potential, or at least sufﬁciently far away from

the other electrodes so that the reference potential can

be considered independent (or at least uncorrelated)

with respect to the potential of interest (Libenson,

2012; Yao, 2001; Hu et al., 2007).

By the fact that all signals are potential differences

between measuring and reference electrodes, the po-

tential of the latter is implicitly present in all signals to

be analyzed. This is also the case for microelectrodes

recordings, and in particular for Behnke-Fried elec-

trodes, which are the focus of this work. These elec-

trodes (manufactured by AdTech and one of the few

microelectrode devices certiﬁed for human brain inva-

sive recordings), are mixed macro-micro electrodes,

with nine micro-wires deployed in the brain at the tip

of a SEEG macro electrode, one of them being chosen

as the reference electrode (see ﬁgure 1).

Jurczynski, P., Cam, S., Rossion, B. and Ranta, R.

Separating Local and Propagated Contributors to the Behnke-fried Microelectrode Recordings.

DOI: 10.5220/0010349303430350

In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 4: BIOSIGNALS, pages 343-350

ISBN: 978-989-758-490-9

343

Figure 1: Behnke-Fried electrode. Image from AdTech

website.

In all cases, the reference signal can be seen as

“perturbation” which does not hold information on

the local activity of interest generated around the mea-

suring electrodes, and several methods have been de-

veloped for its cancelling. One of the simplest tech-

niques is the bipolar montage, which subtracts two

signals one from the other, achieving for one hand at

reference cancelling and, for the other hand yielding

an estimate of the local activity originated between

and around the two involved electrodes. While in

theory possible for Behnke-Fried recordings, the in-

terpretation of such a montage is difﬁcult, because

it is impossible to know the microelectrodes respec-

tive positions exactly. Indeed, the microelectrodes are

at the and of ﬂexible microwires, not visible on CT

scan as in the case of SEEG macroelectrodes (Hof-

manis et al., 2011). The same reasoning holds for

Laplacian / CSD estimates of local sources (Mitzdorf,

1985; Hjorth, 1975). Moreover, because the positions

are not known, a forward-inverse model based solu-

tion like REST (Yao, 2001; Salido-Ruiz et al., 2019)

is not possible neither.

Two other solutions are proposed in the literature:

the average reference (i.e estimating the reference po-

tential by averaging all measured signals and sub-

tracting it from them) and a weighted average refer-

ence estimation. The ﬁrst contribution belonging to

this last family of solutions was the PCA-based blind

source separation proposed in (Hu et al., 2008), fur-

ther developed and justiﬁed for the elimination of the

SEEG reference by (Ranta et al., 2010). This solution,

called “zero-reference” (ZR) by the authors, has been

shown to be equivalent to the minimum power distor-

tionless response beamformer (MPDR), well known

in array signal processing, and which also maximises

the signal-to-noise ratio (SNR) (Madhu et al., 2012).

The ﬁrst objective of this paper is to demonstrate

that this zero-reference method can make an impor-

tant contribution to the separation of components in

the context of Behnke Fried electrode recordings. The

solution depends on the quality of the estimation of

some statistical measures from the data (covariance

matrix), which are difﬁcult to estimate in the context

of non-stationary signals. To cope with this problem,

we also propose in this paper an adaptative version of

this zero-reference algorithm.

The paper is organized as follows: ﬁrst we intro-

duce the existing re-referencing methods in the con-

text. We next present the zero-reference method and

its update to make it adaptive over time. Finally, these

common activity estimation methods (average, ZR,

adaptive ZR) will be evaluated on simulated and real

data. In particular, it will be shown that this treat-

ment enhance the robustness of AP detection, which

is very often an important prerequisite to spike sort-

ing algorithms. Also its importance for further spike

to LFP relationship will be illustrated in the context

of Fast Periodic Visual Stimulation (FPVS) simulated

data. Finally, to the extent that propagated distant ac-

tivities can also be seen as external perturbations, re-

referencing becomes an artifact reduction technique.

An example of such artifact reduction and of its ef-

fects on spike analysis is presented on real microelec-

trode signals.

2 COMMON ACTIVITY

ESTIMATION

2.1 Model

In any point inside the brain, the extracellular poten-

tials are a mixture due to close and far current sources

of different natures: synchronized synaptic potentials

seen far from their originating point (like in the EEG

case), local synaptic activities due to the local pop-

ulation, more or less synchronized, and extracellular

action potentials, due to very close neurons. Issued

from different biophysical phenomena, these activi-

ties have different time-frequency characteristics, al-

though partially overlapping (Zanos et al., 2011).

The way we see them depends on the measuring

setup. We will not enter here in the detailed mod-

elling of the electrodes physics (see e.g (Nelson et al.,

2008)), but we will consider an approximate model

of the electrodes that interest us (Behnke-Fried). As

mentioned, they consist of nine microwires deployed

at the tip of an intracerebral macroelectrode. One of

the nine microwires is used as a reference electrode.

But this electrode has the speciﬁcity to be stripped

from its insulation on several millimeters at its ex-

tremity, while the 8 others are not. The former is then

exposed to the brain electrical ﬁeld on a larger sur-

face (≈ 1mm

) compared to the latter, with a much

smaller recording surface (≈ 3000µm

), then a sur-

face ratio of the order of two to three magnitude.

Consequently, the nature of the activity captured on

the reference electrode is different with respect to the

much more local potentials acquired by the 8 remain-

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

344

ing microwires. Indeed, due to averaging effect over

a larger surface (Hagen et al., 2016), the activities due

to very local structure such as individual neurons (AP)

and group of neurons (local LFP) are drastically di-

minished. On the other hand, the reference electrode

itself is not at zero potential, but picks up an average

activity of the surrounding brain structures with suf-

ﬁcient synchronization, such as suggested in (Lind

et al., 2010). Although the other 8 measuring micro-

electrodes are under the inﬂuence of the same prop-

agated electrical ﬁeld originating from distant brain

sources, their impedance is higher thus the amplitude

of the propagated potential is not the same as the one

captured by the reference electrode. To sum up, every

available signal x

(i = 1..8) can be written as:

= x

local

+ αx

distant

− x

distant

(1)

with x

local

a mixture of extracellular action potentials

and local synaptic activity and x

distant

the propagated

synaptic activity of far sources captured by the refer-

ence electrode (x

distant

= r, α standing for the differ-

ent gain that the distant activity has on the measuring

electrodes with respect to the reference electrode). As

the actual amplitude of the propagated x

distant

is un-

known, equation (1) can also be written as:

= x

local

− r (2)

or, in matrix form,

x =







−1











(3)

where x ∈ R

(M×1)

is the vector of measured signals

(M = 8 in our case), A is some mixing matrix ac-

counting for possible correlations between the local

activities, s are a basis for the local signal space (local

neural sources) and r the reference potential equal to

a scaled version of the propagated activities x

distant

In other words, it should be possible to use refer-

ence cancelling techniques for separating between lo-

cal and propagated components of the recorded sig-

nals.

2.2 State of Art

As noted in the Introduction, several techniques al-

ready exist to eliminate common reference activity,

depending on the measuring setup. Biophysically

founded methods such as REST or Laplacian/CSD

(common in EEG but not only), are not adapted for

the Behnke-Fried electrodes because the position are

unknown. One of the simplest remaining solutions is

the average reference estimation, which approximates

r as the average of x

More elaborated methods were developed for the

SEEG setup, for which the basic hypothesis is that

the reference potential is uncorrelated with the po-

tentials of the measuring electrodes. This hypothesis

holds also for the application we study here. Indeed,

the so-called local activities x

local

are a sum of action

potentials and local synaptic potentials. If it is very

unlikely to have correlated spike trains between two

electrodes, it could be in principle possible to have

correlated synaptic activities. But in all cases, we can

rather safely make the hypothesis that these local ac-

tivities are not correlated with the activity of distant

synchronized populations x

distant

and thus to the ref-

erence potential r.

The zero-reference method was introduced in a se-

ries of papers starting with (Ranta et al., 2010), which

propose to improve previous methods developed by

e.g (Hu et al., 2007). It is based on a semi-blind

source separation / beamforming technique. The ba-

sic assumption is that the potential of the common ref-

erence electrode is decorrelated from the potentials of

the measuring electrodes.

Under the decorrelation hypothesis, one can show

that the best estimate (Madhu et al., 2012) (in a min-

imum squares error sense) of the reference potential

(which has to be added to x for re-referencing) is:

ˆr = w

x , with w =

−1

1 (4)

where R

is the covariance matrix of the measured

signals x and 1 is a vector of ones.

2.3 Adaptive RLS Method

The zero-reference method seen above is implicitly

based on the assumption that the signals are station-

ary and thus the correlation matrix does not vary over

time. However, a stationary model is not accurate

when processing brain signals. In order to improve

the method, we propose to make it adaptive by esti-

mating the covariance matrix at every time step, us-

ing the well known exponentially weighted Recur-

sive Least Squares (RLS) signal processing algorithm

(Eleftheriou and Falconer, 1986).

This method makes it possible to calculate itera-

tively the inverse of the covariance matrix R

(see

eq. 4) at time t + 1 thanks to the inverse covariance

matrix at time t:

(t + 1)

−1

= λ

−1

(t)

−1

− G(t + 1)R

(t)

−1

)

(5)

with

G(t + 1) =

−1

(t)

−1

x(t + 1)x

(t + 1)

1 + λ

−1

(t + 1)R

(t)

−1

x(t + 1)

(6)

Separating Local and Propagated Contributors to the Behnke-fried Microelectrode Recordings

345

where x(t) is the M × 1 vector of the measured signals

at instant t, R

(t) is the covariance matrix at instant t,

λ is the forgetting factor and G(t +1) an update factor

including the well-known Kalman gain.

The adaptive estimation of the common potential

r present on the M = 8 electrodes (3) will then be per-

formed at each time step by replacing R

in (4) by its

adaptive estimate given by (5) and (6).

3 RESULTS

3.1 Simulations

We use simulated data to compare the respective

performances of the average montage, the adaptive

and the non-adaptive zero referencing methods. 8

non stationary (two concatenated stationary epochs)

correlated signals are simulated by reproducing re-

alistic frequencies as observed in real electrophysi-

ology (typical theta and gamma physiological brain

rhythms), representing the local potential activities as

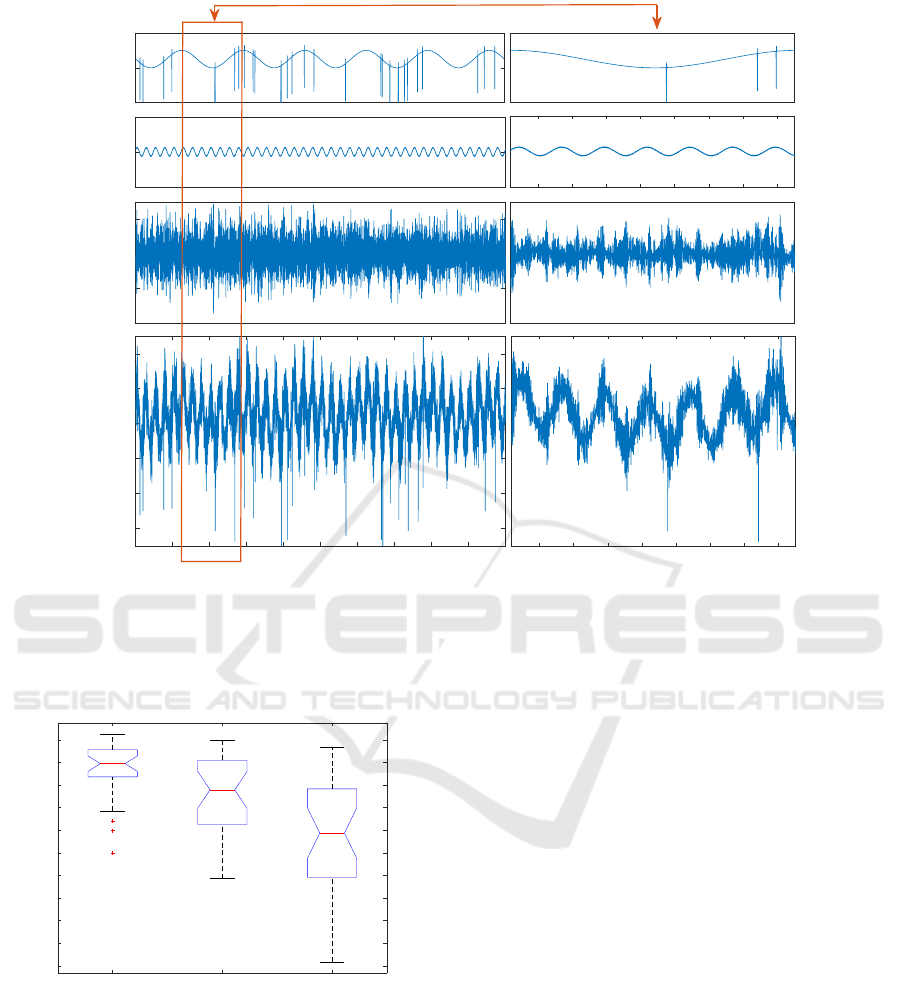
seen by the 8 microelectrodes (Figure 2, second row).

On one signal, a speciﬁc LFP with frequency 1.2Hz is

added, simulating the synaptic response to a speciﬁc

stimuli (e.g. a visual stimuli (Rossion et al., 2020)),

on which a synchronized train of simulated action po-

tentials (Tran et al., 2020) are superimposed following

a Poisson distribution with a 1.2Hz varying ﬁring rate

(Figure 2, ﬁrst row). On 4 of the 7 remaining signals,

action potentials are also randomly added, while the

2 others are left free of spikes. A ninth signal is simu-

lated, having a power spectral density reproducing the

one observed on raw micro recordings, representing

the propagated distant LFP (x

distant

in (1)) as picked

up by the reference electrode. Although mainly ly-

ing in the lower frequency band (below 100Hz), this

signal contains signiﬁcant frequency components up

to 350Hz, thus partly recovering the frequency com-

ponents of the action potentials (Figure 2, third row).

This synthetic reference potential is simulated uncor-

related with the ﬁrst 8 signals representing local mea-

suring microelectrode potentials (x

local

in (1)), to be in

line with the prerequisite of the zero-reference mon-

tage. The former are substracted to the latter to build

the simulated microelectrode recordings x (Figure 2,

last row). Finally, random Gaussian noise is added on

the 8 channels, with a signal to noise ratio SNR=4.

3.2 Reference Signal Estimation

In order to compare the adaptive method with the

non-adaptive one and to the average montage, 50 re-

alizations of simulated sets of signals as described

above have been carried out. The performance crite-

rion is the correlation of the simulated reference with

the estimated reference, calculated for each methods.

From the boxplots of ﬁgure 3, we can see that the

correlation score are signiﬁcantly higher when using

the adaptive method compared to the two other ap-

proaches, the average montage showing the worst per-

formance. The ﬁgure 4 illustrates the ability of the

adaptive method in estimating the reference signal, vi-

sually superior to the ones given by the non-adaptive

as well as the average methods.

3.3 Re-referencing for Spike Detection

The detection of spikes is a pre-requisite to the analy-

sis of the spiking activity of neurons located around

the electrode. This challenging task, if not carried

out with enough care, can lead to misinterpretation

regarding the role of the implanted structure. Remov-

ing the reference that has frequencies straddling the

spikes should improve their detection, as well as their

classiﬁcation. In this paper, we focus on the inﬂuence

of the re-referencing on the accuracy of the detection

task. We consider here the classical method of de-

tection consisting in a bandpass ﬁlter between 300 Hz

and 6000 Hz that removes low frequencies commonly

attributed to the LFP. Then, a threshold calculation

depending on the MAD (Median absolute deviation)

is used to detect the action potential peaks on the sig-

nal (Quian Quiroga et al., 2004).

As described above, trains of simulated spikes

have been added on 5 of the 8 microelectrode chan-

nels. Several simulations were performed, with dif-

ferent spike amplitudes and thus different spike to

LFP ratios (seen as SNR). These amplitudes have

been ﬁxed to reach peaks-to-noise ratio, deﬁned as

the maximum amplitude of the spike divided by the

standard-deviation of the raw microelectrode signal,

in the range 3 to 7.

We compare the result of the detection on the raw

data and on the re-referenced data with the adap-

tive zero-referencing method (for this task, no sig-

niﬁcant difference are reported between the adaptive

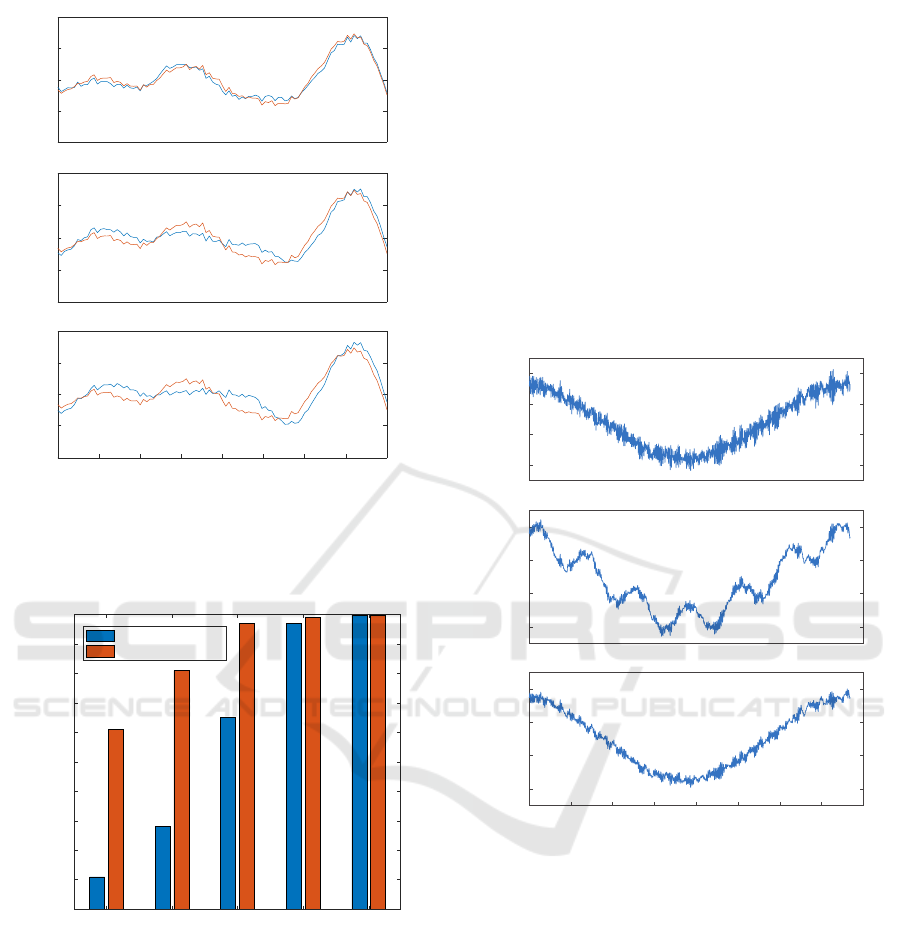
and no-adaptive method). Bar graphs of Figure 5 pro-

vide a summary of the detection results, namely the

percentage of spikes detected with and without re-

referencing, for different amplitudes of the spike to

be detected (different SNRs). It should be noted that

the number of false positives is less than 1% of the

spikes detected in all the simulations, so it will be ne-

glected in this study. The percentage of spikes de-

tected is consistently higher on the zero-referenced

signal than on the raw signal, whatever the amplitude

of the peaks. Clearly, the smaller the amplitude of the

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

346

-100

100

LFP local

+Spikes

-100

100

LFP population

-200

-100

100

propaged LFP

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5

Time (s)

-300

-200

-100

100

200

simulated channel

0.7 0.8 0.9 1 1.1 1.2 1.3 1.4

Time (s)

Figure 2: Example of simulated channel and its components (with a zoom in the right panel). First row : 1.2Hz response to the

stimuli superimposed with a synchronized spike train (one can see bursts of spikes locked to the same phase of the response).

Second row : other local LFP as seen by the microelectrode (correlated with the other channels). The sum of the ﬁrst two

rows yields the local activity x

local

in (1). Third line : propagated LFP as seen by the reference electrode (r = x

distant

). The

last row is the resulting simulated microelectrode recording x obtained as a combination of the ﬁrst three rows.

1 2 3

adaptive method No-adaptive method average method

0.94

0.945

0.95

0.955

0.96

0.965

0.97

0.975

0.98

0.985

0.99

Correlation rate

Figure 3: Correlation coefﬁcients between the simulated

reference and the estimated ones using the adaptive RLS

method (1), the classical ZR method (2) and the average

reference (3), over 50 simulations.

peaks is in relation to the background LFP, the greater

the inﬂuence of the re-referencing for spike detection

will be. When the peak-to-noise ratio fall to 3, only

about 10% of the spikes are detected on the raw sig-

nal, while more than 60% of them are recovered on

the re-referenced signal. This emphasizes the impor-

tance of extracting the local activity from the propa-

gated (reference) signal for accurate spike detection,

in particular for detecting spikes with low amplitudes,

i.e. those originating from neurons that are not in the

very close vicinity of the electrode. The impact of

the re-referencing on the accuracy of spike sorting al-

gorithm might also be signiﬁcant, by eliminating the

overlapping components of the reference signal in the

high frequency band over 300Hz and delivering a bet-

ter estimation of the spike shapes. This will be evalu-

ated in future works.

3.4 Spikes and LFP Synchronisation

The starting point for this section is the study of face

recognition mechanisms in humans with fast periodic

visual stimulation (FPVS). In one of the key FPVS

paradigms, natural variable photographs of faces are

presented at a frequency of 1.2 Hz among images

showing various living and non-living objects at 6

Hz (Rossion et al., 2015). This stimulation leads a

generic neural response in the visual cortex at 6Hz,

and a response at 1.2 Hz from populations of neurons

responding selectivity (i.e. differentially) to faces.

Separating Local and Propagated Contributors to the Behnke-fried Microelectrode Recordings

347

(1)

-20

-10

(2)

-20

-10

Amplitude (µV)

(3)

Times (s)

-20

-10

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8

Figure 4: Simulated reference (orange) and estimated ref-

erence (blue) using the adaptive RLS method (1), the ZR

method (2) and average (3).

3 4 5 6 7

x*SNR

100

Number of spikes detected/ Number of spikes simulated

(%)

raw signals

dereferenced signals

Figure 5: Percent of spike detected on raw signal (blue) and

re-referenced signal (orange).

When recording from a face-selective cortical region

such as the lateral middle fusiform gyrus, it is thus

likely that local neural activity is expressed 1.2 Hz

while distant-neural activity at 6 Hz is mainly cap-

tured by the reference electrode.

Eliminating the reference signal from the micro-

electrode recordings provides a more local vision of

the neural activity (synaptic LFP+spikes) surround-

ing each microelectrode, therefore not corrupted any-

more by remote neural activity unlikely to be related

to the local spiking activity. This procedure will help

in evaluating the synchrony between the local LFP

and the spiking activity, or a consistent response of

the LFP with respect to a given stimuli. The aim of

this section is to illustrate that the activity of the prop-

agated LFP (seen here as the reference) contaminates

the local LFP as seen by a given electrode, and can

mask or make it difﬁcult to identify such relations.

To do this, we consider the microelectrode signal

on which a 1.2Hz face-selectivity response has been

simulated. From stimulus onset, windows of 200 mil-

liseconds succeeding each trigger can be selected and

averaged, and an average LFP pattern (evoked poten-

tial), synchronized with the stimuli, should emerge.

It is immediately noticeable in Figure 6 that a

(1)

(2)

Amplitude(µV)

(3)

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8

Times (s)

Figure 6: Local simulated LFP (1), raw simulated LFP (2)

and re-referenced LFP (3) (same time window as the right

panel in ﬁgure 2).

parasitic frequency appears when such stimuli trig-

gered averaging is applied on the raw signal. This 6Hz

activity originating from the propagated LFP (ref-

erence), is a multiple of the 1.2Hz stimulation fre-

quency, disturbing the identiﬁcation of the local pat-

tern. Once the reference is removed, this frequency no

longer appears and the resulting signal is very close to

the expected one.

3.5 Observations on Real Data

In this section, we evaluate the re-referencing results

on a 2 minutes long window taken from a Behnke-

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

348

Fried micro-electrodes recordings, containing 8 chan-

nels sampled at 32kHz, and recorded in the anterior

human hippocampus of an epileptic patient. The ef-

fect of the re-referencing was evaluated in terms of ar-

tifact reduction, without altering the information con-

tained in the signals (spikes / LFP).

Figure 7: Example of re-referencing. Left: raw (com-

mon reference) signals, Middle: zero-referenced signals,

Right: average-referenced signals. Artifacts are circled in

red, spikes in blue.

Figure 7 presents 130ms of recording on 3 chan-

nels. Artifacts are circled in red (they are considered

artifacts because they are present on all the channels

and have a distinct shape from a spike). Referencing

by zero reference and average reference eliminates

these artifacts, without removing the neural spikes

(circled in blue). However, it can be noted that the

average distorts the low frequency activity of the sig-

nal (right-most panel, ﬁgure 7), which is not the case

with the zero-reference. Moreover, the spike shapes

(obtained here after applying a home-made Bayesian

spike sorting / despiking alogorithm (Le Cam et al.,

2019) inspired from (Zanos et al., 2011)) are pre-

served by the zero-referencing method while they are

distorted by the average referencing (Figure 8, right-

most respectively middle panels).

Figure 8: Superimposed spikes from a single unit (same

order as above).

Re-referencing has very little effect on spike sort-

ing except for the removal of artifacts common to sev-

eral channels. The objective of re-referencing is more

focused on the separation of low frequency compo-

nents in order to optimize the study of relationships.

4 CONCLUSION

The separation of components in the particular case

of Behnke-Fried microelectrodes is important for an-

alyzing the activity of the implanted region, in partic-

ular for understanding the relationships between the

different contributors to these recordings. We de-

velop in this paper an adaptative reference estimation

method which allows a separation of the local activity

close to the electrodes, consisting in spikes and local

LFP, from a propagated LFP activity originating from

distant structures.

The use of such re-referencing as a pre-processing

to microelectrode signals allows a better analysis of

the very local activity around each microelectrode,

consisting of local LFP as well as the spiking activity.

First, the detection of spikes is enhanced in particular

for low amplitude spikes, i.e. produced by mid-distant

neurons. It might then be possible with such methods

to broaden the vision of the micro-electrode by iden-

tifying the action potentials of neurons hidden by the

noise, or for which the shapes are impossible to dis-

tinguish (known as Multi-Units (Quian Quiroga et al.,

2004)).

We also illustrate that eliminating the propagated

LFP clariﬁes the analysis of the local LFP, e.g. it re-

veals possible particular patterns appearing in the ac-

tivity of the local structure with respect to a given

stimuli. We expect that such separation will allow

more accurate evaluation of the relationships between

the detected spikes and the local LFP, but also possi-

ble relations with propagated distant LFP activities.

Separating the reference from the rest of the signal

will also give the opportunity to study the inter-scale

relations between the SEEG and the micro-electrodes.

Indeed, due to its size, the potential as seen by the

reference electrode may be comparable to the one of

a macro SEEG electrode, and then might be consid-

ered as a macro sensor located within the implanted

region. As a perspective, it will then be possible to

separate the activity of the population from more dis-

tant structures by comparing the reference signal with

the SEEG signal of the nearest contact, then splitting

the LFP in three parts as the local LFP, the implanted

population LFP, and the propagated LFP activity of

distant structures.

This new separation method will be further evalu-

ated on real data in acquisition related to FPVS stim-

ulation (Rossion et al., 2015). This methodology is

a promising tool for disentangling the responses of

the targeted brain structure at different scales and will

help in clarifying its involvement in the Human face

recognition process.

Separating Local and Propagated Contributors to the Behnke-fried Microelectrode Recordings

349

ACKNOWLEDGEMENTS

Intracranial data was recorded at the Queen Eliza-

beth University Hospital Birmingham and provided

by Simon Hanslmayr, Bernhard Staresina, Maria

Wimber, George Parish, Marije Ter Wal, Frederic

Roux, Ramesh Chelvarajah, David Rollings and Vi-

jay Sawlani.

REFERENCES

Buzs

aki, G., Anastassiou, C. A., and Koch, C. (2012).

The origin of extracellular ﬁelds and currents - EEG,

ECoG, LFP and spikes. Nature Reviews, Neuro-

science, 13:407–420.

Einevoll, G. T., Kayser, C., Logothetis, N. K., and Panzeri,

S. (2013). Modelling and analysis of local ﬁeld poten-

tials for studying the function of cortical circuits. Nat

Rev Neurosci, 14(11):770–785.

Eleftheriou, E. and Falconer, D. (1986). Tracking proper-

ties and steady-state performance of rls adaptive ﬁlter

algorithms. IEEE Transactions on Acoustics, Speech,

and Signal Processing, 34(5):1097–1110.

Hagen, E., Dahmen, D., Stavrinou, M. L., Lind

en, H., Tet-

zlaff, T., van Albada, S. J., Gr

un, S., Diesmann, M.,

and Einevoll, G. T. (2016). Hybrid scheme for model-

ing local ﬁeld potentials from point-neuron networks.

Cerebral Cortex, 26(12):4461–4496.

Hjorth, B. (1975). An on-line transformation of EEG

scalp potentials into orthogonal source derivations.

Electroencephalography and Clinical Neurophysiol-

ogy, 39(5):526 – 530.

Hofmanis, J., Caspary, O., Louis-Dorr, V., and Maillard, L.

(2011). Automatic depth electrode localization in in-

tracranial space. In 4th International Conference on

Bio-inspired Systems and Signal Processing, Biosig-

nals 2011, Rome, Italie.

Hu, S., Stead, M., and Worrel, G. (2007). Automatic iden-

tiﬁcation and removal of scalp reference signal for

intracranial EEGs based on Independent Component

Analysis. IEEE Transactions on Biomedical Engi-

neering, 54(9):1560–1572.

Hu, S., Stead, M., and Worrell, G. (2008). Removal of

scalp reference signal and line noise for intracranial

EEGs. In Networking, Sensing and Control, 2008. IC-

NSC 2008. IEEE International Conference on, pages

1486–1491.

Kajikawa, Y. and Schroeder, C. E. (2011). How local is the

local ﬁeld potential? Neuron, (72).

Le Cam, S., Tran, H., Ranta, R., and Louis-Dorr, V. (2019).

Simultaneous separation and sorting of extra-cellular

spikes. In 9th International IEEE/EMBS Conference

on Neural Engineering, NER 2019, San Francisco,

USA.

Libenson, M. (2012). Practical approach to electroen-

cephalography. Elsevier Health Sciences.

Lind

en, H., Pettersen, K. H., and Einevoll, G. T. (2010). In-

trinsic dendritic ﬁltering gives low-pass power spec-

tra of local ﬁeld potentials. Journal of computational

neuroscience, 29(3):423–444.

Madhu, N., Ranta, R., Maillard, L., and Koessler, L. (2012).

A uniﬁed treatment of the reference estimation prob-

lem in depth EEG recordings. Med. Biol. Eng. Com-

put., 50(10):1003–1015.

Mitzdorf, U. (1985). Current source-density method and

application in cat cerebral cortex: investigation of

evoked potentials and EEG phenomena. Physiologi-

cal reviews, 65(1):37–100.

Nelson, M. J., Pouget, P., Nilsen, E. A., Patten, C. D.,

and Schall, J. D. (2008). Review of signal distortion

through metal microelectrode recording circuits and

ﬁlters. Journal of Neuroscience Methods, 169:141–

157.

Quian Quiroga, R., Nadasdy, Z., and Ben-Shaul, Y.

(2004). Unsupervised spike detection and sorting with

wavelets and superparamagnetic clustering. Neural

computation, 16(8):1661–1687.

Ranta, R., Salido-Ruiz, R., and Louis-Dorr, V. (2010).

Reference estimation in EEG recordings. In 32nd

Ann. Int. Conf. of the IEEE-EMBS, Buenos Aires, Ar-

gentina.

Rossion, B., Retter, T., and Liu-Shuang, J. (2020). Under-

standing human individuation of unfamiliar faces with

oddball fast periodic visual stimulation and electroen-

cephalography. European Journal of Neuroscience

(review).

Rossion, B., Torfs, K., Jacques, C., and Liu-Shuang, J.

(2015). Fast periodic presentation of natural im-

ages reveals a robust face-selective electrophysiolog-

ical response in the human brain. Journal of Vision,

15(1):18–18.

Salido-Ruiz, R. A., Ranta, R., Korats, G., Le Cam, S.,

Koessler, L., and Louis-Dorr, V. (2019). A uniﬁed

weighted minimum norm solution for the reference

inverse problem in eeg. Computers in Biology and

Medicine, 115:103510.

Tran, H., Ranta, R., Le Cam, S., and Louis-Dorr, V. (2020).

Fast simulation of extracellular action potential signa-

tures based on a morphological ﬁltering approxima-

tion. Journal of Computational Neuroscience, 48.

Yao, D. (2001). A method to standardize a reference of

scalp EEG recordings to a point at inﬁnity. Physiolog-

ical Measurement, 22:693–711.

Zanos, T. P., Mineault, P. J., and Pack, C. C. (2011). Re-

moval of spurious correlations between spikes and lo-

cal ﬁeld potentials. J Neurophysiology, 105:474–486.

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

350