Secrecy-preserving Reasoning in Acyclic DL-Lite
R
Knowledge Bases in
the Presence of BCQs
Gopalakrishnan Krishnasamy-Sivaprakasam
1
and Giora Slutzki
2
1
Math & Computer Science Department, Central State University, Wilberforce, Ohio, U.S.A.
2
Department of Computer Science, Iowa State University, Ames, Iowa, U.S.A.
Keywords:
Description Logic, Theory of Database Privacy and Security, Knowledge Representation and Reasoning.
Abstract:
In this paper we study Secrecy-Preserving Query Answering under Open World Assumption (OWA) for
DL-Lite
R
Knowledge Bases (KBs) with acyclic TBox. Using a tableau algorithm, we construct A
∗
, an in-
ferential closure of the given ABox A, which includes both positive as well as negative assertions. We use a
notational variant of Kleene 3-valued semantics, which we call OW-semantics as it fits nicely with OWA. This
allows us to answer queries, including Boolean Conjunctive Queries (BCQs) with “Yes”, “No” or “Unknown”,
as opposed to the just answering “Yes” or “No” as in Ontology Based Data Access (OBDA) framework, thus
improving the informativeness of the query-answering procedure. Being able to answer “Unknown” plays a
key role in protecting secrecy under OWA. One of the main contributions of this paper is a study of answering
BCQs without compromising secrecy. Using the idea of secrecy envelopes, previously introduced by one of
the authors, we give a precise characterization of when BCQs should be answered “Yes”, “No” or “Unknown”.
We prove the correctness of the secrecy-preserving query-answering algorithm.
1 INTRODUCTION
Preserving secrecy in a database setting is a problem
of paramount importance and it has been studied for
a long time, see (Biskup and Weibert, 2008; Biskup
et al., 2010; Denning and Denning, 1979; Sicher-
man et al., 1983). With the advent of the semantic
web and its increasingly pervasive usage, there is a
lot of interest in studying this problem in knowledge
base (KB) setting, see (Bao et al., 2007; Cuenca Grau
et al., 2013; Tao et al., 2010; Tao et al., 2015; Stouppa
and Studer, 2009; Sivaprakasam, 2016). The concern
here is that in view of the fundamental assumption
that KBs possess incomplete knowledge, despite our
best efforts, a situation could arise in which logical
reasoning (used to produce implicit knowledge from
explicit one stored in the KB) may possibly lead to
disclosure of secret information, see (Cuenca Grau
et al., 2013). Some approaches dealing with “infor-
mation protection” are based on access control mech-
anisms (Bell and LaPadula, 1973), defining appro-
priate policy languages to represent obligation, pro-
vision and delegation policies (Kagal et al., 2003),
and logic based methods applied to protect secrets
of one agent’s knowledge from the other agents in a
multiagent system (Halpern and O’Neill, 2008). One
approach to secrecy in incomplete database was pre-
sented by Biskup et al. in (Biskup and Weibert, 2008;
Biskup et al., 2010; Biskup and Tadros, 2012) in the
form of controlled query evaluation (CQE). The idea
behind CQE is that rather than providing strict access
control to data, the CQE approach enforces secrecy
by checking (at run time) whether from a truthful an-
swer to a query a user can deduce secret information.
In this case the answer is distorted by either simply
refusing to answer or by outright lying. For a study
of confidentiality in a setting that is an adaptation of
CQE framework to ontologies over OWL 2 RL profile
of OWL 2, see (Cuenca Grau et al., 2013).
In response to concerns raised in (Weitzner et al.,
2008), we have developed a secrecy framework that
attempts to satisfy the following, competing, proper-
ties: (a) it protects secret information, and (b) queries
are answered as informatively as possible (subject to
satisfying property (a)), see (Bao et al., 2007; Tao
et al., 2010). This approach is based on Open World
Assumption (OWA) and (so far) it has been restricted
to instance-checking queries. More specifically, in
(Bao et al., 2007) the main idea (which was restricted
to hierarchical KBs) was to utilize the secret informa-
tion within the reasoning process, but then answering
“Unknown” whenever the answer is truly unknown or
360
Krishnasamy-Sivaprakasam, G. and Slutzki, G.
Secrecy-preserving Reasoning in Acyclic DL-LiteR Knowledge Bases in the Presence of BCQs.
DOI: 10.5220/0010335403600372
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 360-372
ISBN: 978-989-758-484-8
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

in case the true answer could compromise confiden-
tiality. The authors defined and used the notion of
an envelope to hide secret information against logi-
cal inference. Further, in (Tao et al., 2015), the au-
thors introduced a more elaborate conceptual frame-
work for secrecy-preserving query answering (SPQA)
problem under OWA with multiple querying agents.
This framework was restricted to instance-checking
queries and illustrated on very simple description
logic languages.
The World Wide Web Consortium (W3C) has pro-
posed OWL 2 profiles which have limited model-
ing features, but provide substantial improvements in
scalability as well as a significant reduction in the
complexity of various reasoning tasks. Based on this
proposal, there has been a lot of work done on devel-
oping languages tailored to specific applications, in
particular those that involve massive amount of data,
i.e., large ABoxes. In addition, a lot of work has dealt
with answering conjunctive queries over these data
sets, see (Ortiz and Simkus, 2012). The goal is to pro-
vide just enough expressive power to deal with those
applications, while keeping low complexity of rea-
soning, see (Calvanese et al., 2007; Krotzsch, 2012).
DL-Lite family is one such family of languages de-
signed with an eye towards precisely these kinds of
applications, see (Artale et al., 2009; Calvanese et al.,
2007; Ortiz and Simkus, 2012).
One of the contributions in this paper is answer-
ing Boolean Conjunctive Assertions/Queries (BCQs)
without revealing secrets, where the secrecy set con-
tains both assertions and BCQs. As explained be-
low, having BCQs in the secrecy set can be avoided
at the expense of considerable “manual labor” of au-
gumenting the secrecy set with all the instances of the
given BCQs. For instance, when we want to protect
the existence of individuals satisfying certain proper-
ties e.g. A(x) and P(x, y), is suffices to add the BCQ
∃x, y [A(x) ∧ P(x, y)] into the secrecy set. Otherwise
we would have to “manually” add all the assertions
of the form A(a) and P(a, b), for all individuals a, b
occurring in the KB; see section 5.1. We note that the
situation is different with respect to query answering.
Here, allowing BCQs indeed adds extra power and
cannot be replaced with any number of membership
queries. Observe that in this work we pursue (secrecy-
preserving) query answering with the answers being
“Yes”, “No” or “Unknown”. For this reason we are
interested in BCQs rather than more general CQs.
Moreover, to the best of our knowledge, this work
presents the first study of secrecy-preserving reason-
ing which allows BCQ queries.
In this paper we continue the work begun in (Tao
et al., 2010; Krishnasamy Sivaprakasam and Slutzki,
2016). The framework introduced in (Tao et al.,
2015), which we use here as well, was illustrated on
very simple examples: the Propositional Horn Logic
and the Description Logic AL. As DL languages be-
come more involved (expressive), the corresponding
SPQA problems become more challenging. Here we
consider SPQA problem under OWA for DL-Lite
R
acyclic KBs
1
. Given a DL-Lite
R
KB (consisting of
an ABox A and an acyclic TBox T ) and a secrecy
set S, the querying agent is allowed to ask queries of
both kinds. Moreover, we allow the ABox of the KB
to contain both positive and negative assertions, see
(Artale et al., 2009) for a survey of DL-Lite family of
logics. By OWA, the answer to a query against a KB
can be “Yes”, “No” or “Unknown”. As the first step in
constructing our SPQA system, we use a tableau algo-
rithm to compute a finite set A
∗
which consists of the
consequences of the KB (with respect to the TBox),
both positive and negative. To prove the completeness
of this algorithm, we use the 3-valued OW-semantics
as introduced in (Tao et al., 2015), see also Section
2.2. Next, starting from the secrecy set S we compute
a finite set of assertions, viz., the envelope E ⊆ A
∗
of
the secrecy set S, whose goal is to provide a “logical
shield” against reasoning launched from A
∗
\ E (out-
side the envelope) and whose aim is to “infiltrate” the
secrecy set S (i.e., to compromise some assertions in
S). Computation of the envelope is based on the ideas
given in (Tao et al., 2010; Tao et al., 2015), viz., inver-
sion of the tableau expansion rules used in computing
A
∗
. Moreover, we add two special expansion rules to
deal with BCQs. The details are presented in Section
5.1.
The answer to the instance-checking queries
posed to the KB is based on membership of those
queries in the set A
∗
\ E. To answer BCQs, we use
graph terminology: we express both the ABox A
∗
\ E
and the BCQ q as node-edge labeled graphs, see also
(Ortiz and Simkus, 2012). The answer is based on
the existence or non-existence of specific mappings
between these two graphs. In more detail, if there
is a (labeled) homomorphism from the query graph
G[q] (for q) to the ABox graph G[A
∗
\ E] (for A
∗
\ E),
then an answer to the query is “Yes”; if there are
no such homomorphisms and there is a ‘non-clashy’
mapping
2
from G[q] to G[A
∗
\ E] then the answer
to the query is “Unknown”; otherwise the answer is
“No”, see Section 5.2 for details. Based on the OW-
semantics, we are able to provide an exact character-
ization of all answers. The rest of the paper is orga-
1
A DL-Lite
R
KB is said to be acyclic if neither ∃P v
∃P
−
nor ∃P
−
v ∃P follows from the KB.
2
The term non-clashy mapping refers to a mapping
which is not clashy, see Definition 4.6.
Secrecy-preserving Reasoning in Acyclic DL-LiteR Knowledge Bases in the Presence of BCQs
361

nized as follows: Section 2 explains the syntax of the
language DL-Lite
R
and its OW-semantics. In Sec-
tion 3, we prove the soundness and completeness of
the tableau algorithm that computes A
∗
. Section 4
deals with syntax and semantics of BCQs. Section
5.1 introduces the secrecy preserving framework and
explains the details of envelope construction. In Sec-
tion 5.2, we explain the procedure to answer queries,
and in Section 6, briefly we provide a summary and
some directions for future research.
2 PRELIMINARIES: SYNTAX
AND SEMANTICS OF DL-LIT E
R
2.1 Syntax
A vocabulary of DL-Lite
R
is a triple < N
O
, N
C
, N
R
>
of countably infinite, pairwise disjoint sets. The ele-
ments of N
O
are called objects or individual names,
the elements of N
C
are called concept names (unary
relation symbols) and the elements N
R
are called role
names (binary relation symbols). The set of basic
concepts and the set of basic roles, respectively de-
noted by BC (generated by
ˆ
B) and BR (generated
by
ˆ
R), are defined below by the grammar (a) where
A ∈ N
C
, P ∈ N
R
and P
−
stands for the inverse of the
role name P. The set of concept expressions and role
expressions in DL-Lite
R
, denoted by C (generated by
ˆ
C) and R (generated by
ˆ
E), is defined by the grammar
(b).
(a)
ˆ
B ::= A | ∃
ˆ
R (b)
ˆ
C ::=
ˆ
B | ¬
ˆ
B
ˆ
R ::= P | P
−
ˆ
E ::=
ˆ
R | ¬
ˆ
R
Note that BC ⊆ C, and BR ⊆ R. For C ∈ C and D ∈ BC,
we write ¬C to stand for D if C = ¬D and for ¬D if
C = D. Similarly, for E ∈ R and R ∈ BR, ¬E denotes
R if E = ¬R and ¬R if E = R. Assertions in DL-Lite
R
are expressions of the form C(a) and E(a, b) where
a, b ∈ N
O
, C ∈ C and E ∈ R; these are called basic
assertions if C ∈ BC and E ∈ BR.
There are two types of subsumptions in DL-Lite
R
,
a) concept subsumptions of the form B v C with B ∈
BC and C ∈ C, and
b) role subsumptions of the form R v E with R ∈ BR
and E ∈ R.
Note the asymmetry between the left-hand side and
the right-hand side of subsumptions in DL-Lite
R
.
2.2 Semantics
In this section we reformulate Kleene’s 3-valued logic
so as to provide semantics for DL-Lite
R
which we
feel is particularly well-suited in the context of OWA,
see also (Tao et al., 2015). It allows us to give an
“epistemic separation” between “known that Yes”,
“known that No” and “Unknown”. We use the idea
of weak 3-partition
3
, defined as follows. Let X be a
non-empty set, and A
1
, A
2
, A
3
(possibly empty) sub-
sets of X. The ordered triple (A
1
, A
2
, A
3
) is a weak
3-partition of X if
1. A
1
∪ A
2
∪ A
3
= X and
2. ∀i, j with i , j, A
i
∩ A
j
= ∅.
An OW-interpretation of the language DL-Lite
R
is a
tuple I =
D
∆, ·
I
E
where ∆ is a non-empty domain and
·
I
is an interpretation function such that
• ∀a ∈ N
O
, a
I
∈ ∆,
• ∀A ∈ N
C
, A
I
= (A
I
N
, A
I
U
, A
I
Y
) is a weak 3-partition
of ∆, and
• ∀P ∈ N
R
, P
I
= (P
I
N
, P
I
U
, P
I
Y
) is a weak 3-partition
of ∆ × ∆.
We extend the interpretation function ·
I
induc-
tively to all concept and role expressions as fol-
lows. Let C ∈ BC, P ∈ N
R
, R ∈ BR and suppose
that C
I
= (C
I
N
, C
I
U
, C
I
Y
), P
I
= (P
I
N
, P
I
U
, P
I
Y
) and
R
I
= (R
I
N
, R
I
U
, R
I
Y
). Then,
• (¬C)
I
= (C
I
Y
, C
I
U
, C
I
N
) and (¬R)
I
=
(R
I
Y
, P
I
U
, R
I
N
),
• (P
−
)
I
= ((P
−
)
I
N
, (P
−
)
I
U
, (P
−
)
I
Y
), where (P
−
)
I
X
=
{(a, b)| (b, a) ∈ P
I
X
}, X ∈ {N, U,Y},
• (∃R)
I
= ((∃R)
I
N
, (∃R)
I
U
, (∃R)
I
Y
), where (∃R)
I
Y
=
{a| ∃b ∈ ∆[(a, b) ∈ R
I
Y
]}, (∃R)
I
N
= {a| ∀b ∈ ∆[(a, b) ∈
R
I
N
]} and (∃R)
I
U
= ∆ \ ((∃R)
I
Y
∪ (∃R)
I
N
).
Remark. The subscripts “N”, “U” and “Y” stand
for “No”, “Unknown” and “Yes”, which represent the
possible dispositions of a domain element with re-
spect to a given OW-interpretation of a concept. Sim-
ilarly, for roles. In addition, all the weak 3-partitions
in this paper are ordered: First the N-component, sec-
ond the U-component and third the Y-component.
Let I =
D
∆, ·
I
E
be an OW-interpretation, B ∈ BC,
C ∈ C, R ∈ BR, E ∈ R and a, b ∈ N
O
. We say that
• I satisfies C(a), notation I |= C(a), if a
I
∈ C
I
Y
;
• I satisfies E(a, b), notation I |= E(a, b), if
(a
I
, b
I
) ∈ E
I
Y
;
• I satisfies B v C, notation I |= B v C, if B
I
Y
⊆ C
I
Y
and C
I
N
⊆ B
I
N
, and
3
It is weak in that we do not require that the sets A
i
are
non-empty.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
362

• I satisfies R v E, notation I |= R v E, if R
I
Y
⊆ E
I
Y
and E
I
N
⊆ R
I
N
.
DL-Lite
R
KB is a pair Σ =
h
A, T
i
, where A, called
the ABox
4
, is a finite, non-empty set of assertions
of the form A(a), ¬A(a), P(a,b) and ¬P(a, b) with
A ∈ N
C
, P ∈ N
R
and a, b ∈ N
O
, and T is a finite set
of concept and role subsumptions, called TBox. An
OW-interpretation I =
D
∆, ·
I
E
is an OW-model of Σ,
notation I |= Σ, if for all α ∈ A ∪ T , I |= α. Let α be
an assertion or a concept/role subsumption. We say
that Σ entails α, notation Σ |= α, if all OW-models of
Σ satisfy α.
3 COMPUTATION OF A
∗
In (Calvanese et al., 2007), the authors had presented
an algorithm based on query rewriting approach to an-
swer CQs over DL-Lite
R
KBs. The strategy used in
this procedure is to convert the given CQ into a union
of conjunctive queries (UCQ) by embedding the given
TBox into the CQ. Note that the number of unions in
the resulting UCQ could be exponential (depending
on the TBox). Then, an answer to the given CQ is ob-
tained by evaluating the UCQ over the given ABox.
Lutz et.al., in (Lutz et al., 2008; Lutz et al., 2009)
adopted the query rewriting approach to answer CQs
in EL and ELH KBs respectively. Finding the set
of all assertions entailed by an E L
+
KB with acyclic
TBox has been considered by Mei et al., see (Mei
et al., 2009). Also in (Mei et al., 2009), the authors
observed that even though the assumption of acyclic-
ity restricts the expressive power of the language, in
practice the idea is really useful, as it is expressive
enough for the commonly used biomedical ontolo-
gies, e.g., Gene Ontology, SNOMED CT. In that pa-
per, the authors had used a mixed approach which
combines the computation of all assertions entailed
by the given KB and the query rewriting method to
answer the CQs. In our paper, we follow an approach
which is different from the query rewriting approach
to answer CQs. Below, we use a tableau-style proce-
dure to construct a set of consequences of the given
KB Σ =
h
A, T
i
, denoted by A
∗
. Then, BCQs are an-
swered based on the information available in the set
A
∗
, for more details see Section 6. Since our main
interest in this paper is studying secrecy-preserving
query answering, we shall henceforth assume that all
TBoxes are acyclic; this will guarantee that A
∗
is fi-
nite.
4
Note that we do not allow assertions of the form ∃R(a)
in the ABox A.
Given Σ =
h
A, T
i
, before we start computing A
∗
,
we first arrange the individual names occurring in
Σ, assertions in A and subsumptions in T in lex-
icographic order. We also program the algorithm
which computes A
∗
in a way that selects these in-
dividual names, assertions and subsumptions in that
order. This ordering will enable us to get a unique
A
∗
, see (Calvanese et al., 2007). The computation of
A
∗
proceeds in several stages. In the first stage, A
∗
is
initialized as A and expanded by exhaustively apply-
ing expansion rules listed in Figure 1. The resulting
ABox is denoted by A
∗
1
. The sets of all the individ-
ual names appearing in A and A
∗
1
are denoted by O
Σ
and O
∗
, respectively. O
∗
is initialized as O
Σ
and ex-
panded with applications of the v
N∃
- and v
∃∃
-rules.
An individual a is said to be fresh if a ∈ O
∗
\ O
Σ
. It
is important to note that all the fresh individuals are
added in the first stage (Figure 1) and no new indi-
viduals are added in the following stages. This can
be easily seen by inspecting the rules in Figures 1, 2
and 3. The rules are designed based on subsumptions
present in the TBox T . To name the rules in Figure
1, we adopt the following conventions. The first sub-
script of v represents the type of the symbol on the
left hand side of the subsumption, and the second rep-
resents the type of the symbol on the right hand side.
For example, the v
N∃
- rule has a concept name on
the left hand side of the subsumption and existential
restriction on the right hand side.
In order to write the rules more succinctly, we de-
fine two functions inv (standing for inverse) and neg
(standing for negation) as follows:
• for P ∈ N
R
, inv(R,a,b) =







P(a, b) if R = P,
P(b, a) if R = P
−
• R ∈ BR, neg(E,a,b) =







inv(R, a, b) if E = R,
¬inv(R, a, b) if E = ¬R
For instance, neg(¬P
−
, a, b) = ¬inv(P
−
, a, b) =
¬P(b, a). In addition, we use L to denote ei-
ther a concept name or a negation of concept
name. We write ¬L with the intended meaning
that ¬L = ¬A if L = A, and ¬L = A if L = ¬A.
To illustrate, we explain application of the rule
v
RE
-rule. Let P(a,b) ∈ A
∗
, P
−
v ¬Q ∈ T and
¬Q(b, a) < A
∗
. Since, neg(P
−
, b, a) = P(a, b) and
neg(¬Q, b, a) = ¬inv(Q, b,a) = ¬Q(b, a), v
RE
-rule is
applicable. Therefore, we add ¬Q(b, a) to A
∗
.
In the second stage, A
∗
1
is expanded by applying
expansion rules listed in Figure 2. These rules deal
with subsumptions in which the right hand side is a
negation of existential restriction. For example, let
A(a) ∈ A
∗
, A v ∃P
−
∈ T and for some e ∈ O
∗
such that
P(e, a) < A
∗
. Then, v
N@
-rule is applicable and there-
Secrecy-preserving Reasoning in Acyclic DL-LiteR Knowledge Bases in the Presence of BCQs
363

fore we should add P(e,a) to A
∗
. The resulting ABox
is denoted as A
∗
12
. Observe that every application of
a rule in Figure 2 adds at most |O
∗
| new assertions
to A
∗
1
. To name the rules in Figure 2, we adopt the
same naming conventions as for the rules in Figure 1
except that the second symbol in the subscript repre-
sents the right hand side of v: @ stands for a negated
unqualified existential restriction.
v
NL
− rule : if A(a) ∈ A
∗
, A v L ∈ T and
L(a) < A
∗
, then A
∗
:= A
∗
∪ {L(a)};
v
N∃
− rule : if A(a) ∈ A
∗
, A v ∃R ∈ T , and
∀d ∈ O
∗
, inv(R, a,d) < A
∗
,
then A
∗
:= A
∗
∪ {inv(R, a,b)}
where b is fresh, and O
∗
:= O
∗
∪ {b};
v
∃L
− rule : if inv(R,a, b) ∈ A
∗
, ∃R v L ∈ T , and
L(a) < A
∗
, then A
∗
:= A
∗
∪ {L(a)};
v
∃∃
− rule : if inv(R,a, b) ∈ A
∗
, ∃R v ∃S ∈ T , and
∀d ∈ O
∗
, inv(S , a, d) < A
∗
,
then A
∗
:= A
∗
∪ {inv(S, a, c)}
where c is fresh, and O
∗
:= O
∗
∪ {c};
v
RE
− rule : if inv(R,a, b) ∈ A
∗
, R v E ∈ T and
neg(E, a,b) < A
∗
,
then A
∗
:= A
∗
∪ {neg(E, a, b)}.
Figure 1: We use the following conventions not stated ex-
plicitly within the individual rules: A ∈ N
C
, L ∈ {A, ¬A | A ∈
N
C
}, R,S ∈ BR and E ∈ R.
v
N@
− rule : Let A(a) ∈ A
∗
and A v ¬∃R ∈ T .
∀c ∈ O
∗
: if ¬inv(R,a, c) < A
∗
,
then A
∗
:= A
∗
∪ {¬inv(R, a,c)};
v
∃@
− rule : Let inv(R,a, b) ∈ A
∗
and
∃R v ¬∃S ∈ T .
∀c ∈ O
∗
: if ¬inv(S,a, c) < A
∗
,
then A
∗
:= A
∗
∪ {¬inv(S, a, c)}.
Figure 2: Computing A
∗
12
: An application of each rule adds
negation of role assertions for all c ∈ O
∗
.
In the third stage, A
∗
12
is expanded by applying rules
listed in Figure 3. The resulting final ABox is de-
noted as A
∗
. To name the rules in Figure 3, we fol-
low the previously adopted conventions. Addition-
ally, negation in the subscript (see Figure 3) should
be thought of as follows: For each rule in Figures 1
and 2, e.g. v
NL
-rule with A v L, we have a corre-
sponding v
NL¬
-rule, which captures the effect of the
subsumption ¬L v ¬A (which is not allowed in our
syntax). It is easy to see that during the execution of
rules in Figure 3 none of the rules in Figures 1 and 2
becomes applicable.
v
NL¬
− rule : if ¬L(a) ∈ A
∗
, A v L ∈ T and
¬A(a) < A
∗
,
then A
∗
:= A
∗
∪ {¬A(a)};
v
N∃¬
− rule : if ∀b ∈ O
∗
, ¬inv(R, a,b) ∈ A
∗
,
A v ∃R ∈ T , and ¬A(a) < A
∗
,
then A
∗
:= A
∗
∪ {¬A(a)};
v
∃L¬
− rule : Let ¬L(a) ∈ A
∗
and ∃R v L ∈ T .
∀c ∈ O
∗
: if ¬inv(R,a, c) < A
∗
,
then A
∗
:= A
∗
∪ {¬inv(R, a,c)};
v
∃∃¬
− rule : Let ∀b ∈ O
∗
, ¬inv(S , a, b) ∈ A
∗
and
∃R v ∃S ∈ T .
∀c ∈ O
∗
: if ¬inv(R,a, c) < A
∗
,
then A
∗
:= A
∗
∪ {¬inv(R, a,c)};
v
RE¬
− rule : if ¬neg(E,a, b) ∈ A
∗
, R v E ∈ T
and ¬inv(R, a, b) < A
∗
,
then A
∗
:= A
∗
∪ {¬inv(R, a,b)};
v
N@¬
− rule : if inv(R,a, b) ∈ A
∗
, A v ¬∃R ∈ T
and ¬A(a) < A
∗
,
then A
∗
:= A
∗
∪ {¬A(a)}.
v
∃@¬
− rule : Let inv(S,a, b) ∈ A
∗
and
∃R v ¬∃S ∈ T .
∀c ∈ O
∗
: if ¬inv(R,a, c) < A
∗
,
then A
∗
:= A
∗
∪ {¬inv(R, a,c)}.
Figure 3: Computing A
∗
: We use the same conventions as
in Figure 1.
We say that A
∗
is completed, or that it is an asser-
tional closure of Σ =
h
A, T
i
, if no assertion expan-
sion rule is applicable. We denote by Λ the tableau
algorithm which (lexicographically) applies assertion
expansion rules, first those in Figure 1 then those in
Figure 2 and finally those in Figure 3, until no further
applications are possible. Since, as explained previ-
ously, Λ works in a lexicographic fashion, for a given
KB Σ =
h
A, T
i
, it outputs a unique A
∗
.
Since some of the expansion rules can in some
cases be applied exponentially many times in the size
of the KB, the size of A
∗
can be exponential in the size
of the KB. As an example consider a DL − Lite
R
KB
Σ =
h
A, T
i
, where A = {A(a)} and T = {A v ∃P
1
, A v
∃Q
1
, ∃P
−
i
v ∃P
i+1
, ∃P
−
i
v ∃Q
i+1
, Q
i
v P
i+1
, 1 ≤ i ≤ n}.
Clearly, in this example the TBox T is acyclic and
the size of the KB is linear in n. To compute A
∗
for
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
364

this KB, the v
∃∃
-rule has to be applied exponentially
many times. It follows that A
∗
can be exponential in
the size of Σ, implying that the computation of A
∗
could require exponential time as well.
Example 1. Let Σ =
h
A, T
i
be a DL-Lite
R
KB,
where A is defined by 1 and 2, and T is defined by 3,
4, 5 and 6,
1 A(a) 3 A v B 5 ∃P
−
v ¬∃R
2 D(b) 4 A v ∃P 6 C v ¬D
Applying the assertion expansion rules in Figure 1,
we can derive the following conclusions.
7 B(a) v
NL
on 1,3
8 P(a, c), c is fresh v
N∃
on 1,4
Therefore A
∗
1
= A ∪ {B(a), P(a, c)}. Now applying the
assertion expansion rules in Figure 2 on A
∗
1
, we cal-
culate A
∗
12
.
9 ¬R(c, a), ¬R(c, b), ¬R(c,c) v
∃@
on 8,5
Thus A
∗
12
= A
∗
1
∪{¬R(c, a), ¬R(c,b), ¬R(c,c)}. Finally,
using the assertion expansion rules in Figure 3 on
A
∗
12
, we get A
∗
.
10 ¬C(b) v
NL¬
on 2,6
Hence, A
∗
= A
∗
12
∪ {¬C(b)}.
Observe that if we restrict the application of ex-
pansions rules in Figure 1, 2 and 3 to those ABox
assertions involving only non-fresh individual names
then we get {A(a), B(a), D(b),¬C(b)}.
In general, if the computation is restricted
to ABox assertions involving non-fresh individual
names, then it is easy to see that the size of A
∗
is poly-
nomial in the size of Σ and that it can be computed in
polynomial time.
3.1 Soundness
The proof of the soundness of the tableau procedure Λ
is split into two parts, dealing separately with rules in
Figures 1 and 2 and Figure 3. The proofs of the next
two Lemmas 1 and 2 are standard and are omitted.
Lemma 1 (Soundness of Λ, Part A). Let A
∗
12
be a
completed ABox obtained from Σ by first applying the
rules listed in Figure 1 and then the rules of Figure 2.
Then for every OW-model I of Σ, there is a OW-model
I
∗
12
of Σ such that I
∗
12
|= A
∗
12
, where the domain of I
∗
12
is same as the domain of I and I
∗
12
remains same as
I except for the interpretation of fresh individuals.
Let O
∗
be the set of individual names that occur
in the completed ABox A
∗
12
. We define a new OW-
interpretation I
∗
=
D
∆
∗
, ·
I
∗
E
, where ∆
∗
= I
∗
12
(O
∗
), i.e.,
∆
∗
is precisely the set of those elements of ∆ that are
interpretations of individuals in O
∗
. The interpreta-
tion function ·
I
∗
is defined as a restriction of I
∗
12
to
∆
∗
:
(i) ∀a ∈ O
∗
[a
I
∗
= a
I
∗
12
];
(ii) ∀A ∈ N
C
[(A
I
∗
N
= A
I
∗
12
N
∩ ∆
∗
, A
I
∗
U
= A
I
∗
12
U
∩ ∆
∗
, A
I
∗
Y
=
A
I
∗
12
Y
∩ ∆
∗
)];
(iii) ∀P ∈ N
R
[P
I
∗
N
= P
I
∗
12
N
∩(∆
∗
×∆
∗
), P
I
∗
U
= P
I
∗
12
U
∩(∆
∗
×
∆
∗
), P
I
∗
Y
= P
I
∗
12
Y
∩ (∆
∗
× ∆
∗
)] and
(iv) I
∗
is extended to compound concepts and roles as
in Section 2.2.
Since every weak 3-partition of ∆ induces a weak 3-
partition of ∆
∗
, we have the following consequence of
Lemma 1,
Corollary 1. I
∗
is an OW-model of
D
A
∗
12
, T
E
.
Lemma 2 (Soundness of Λ, Part B). Let A
∗
be the
completed ABox obtained from A
∗
12
by applying the
rules listed in Figure 3. For any OW-model I of Σ,
let I
∗
=
D
∆
∗
, ·
I
∗
E
be an OW-interpretation as defined
above. Then, I
∗
is an OW-model of Σ and I
∗
|= A
∗
.
In summary, given an OW-model I of Σ, using the
proof of Lemma 1, we transform I to another OW-
model I
∗
12
of Σ such that I
∗
12
|= A
∗
12
, where the do-
main of I
∗
12
is same as the domain of I. In fact, I
∗
12
remains the same as I except for the interpretation of
fresh individuals. Moreover, I
∗
12
is constructed in a
canonical fashion, i.e., it is uniquely determined from
I. Having obtained I
∗
12
, using Lemma 2, we mod-
ify I
∗
12
to obtain yet another OW-model I
∗
of Σ such
that I
∗
|= A
∗
, where the domain of I
∗
was defined
to be I
∗
12
(O
∗
). We use the notation Σ |=
∗
α, where α
is a concept (or role) name assertion or negation of a
concept (or role) name assertion, to represent the fol-
lowing statement: For every OW-model I of Σ, I
∗
is an OW-model of Σ and I
∗
|= α. We can combine
Lemma 1 and Lemma 2 into a single theorem.
Theorem 1. (Soundness of Λ): Let A
∗
be a com-
pleted ABox obtained from Σ by first applying the
rules listed in Figure 1, then rules listed in Figure 2,
and finally the rules listed in Figure 3. Then Σ |=
∗
A
∗
,
i.e., for every α ∈ A
∗
, Σ |=
∗
α.
3.2 Completeness
To prove the completeness of Λ, we first define a
canonical OW-interpretation J =
D
∆, ·
J
E
for a com-
pleted ABox A
∗
as follows:
- ∆ = O
∗
= {a ∈ N
O
| a occurs in A
∗
};
- a
J
= a, for each individual name a ∈ O
∗
;
- for A ∈ N
C
, A
J
= (A
J
N
, A
J
U
, A
J
Y
), where
A
J
Y
= {a| A(a) ∈ A
∗
},
A
J
N
= {a| ¬A(a) ∈ A
∗
} and
A
J
U
= (∆ \ A
J
Y
) \ A
J
N
;
Secrecy-preserving Reasoning in Acyclic DL-LiteR Knowledge Bases in the Presence of BCQs
365

- for P ∈ N
R
, P
J
= (P
J
N
, P
J
U
, P
J
Y
), where
P
J
Y
= {(a,b)| P(a,b) ∈ A
∗
},
P
J
N
= {(a,b)| ¬P(a, b) ∈ A
∗
} and
P
J
U
= ((∆ × ∆) \ P
J
Y
) \ P
J
N
;
- J is extended to compound concepts and roles as
in Section 2.2.
The proof that J is a OW-model of Σ is standard and
is omitted.
Lemma 3. Let Σ =
h
A, T
i
be a DL-Lite
R
KB. Then
∀α ∈ A ∪ T , J |= α.
Theorem 2 (Completeness of Λ). Let A
∗
be a com-
pleted ABox obtained from Σ by applying Λ. Let
α be a concept (or role) name assertion or nega-
tion of a concept (or role) name assertion
5
. Then
Σ |=
∗
α ⇒ α ∈ A
∗
.
Proof. Let J be the canonical model of Σ as defined
above, and let α be an assertion as in the statement of
the theorem. Suppose Σ |=
∗
α. By Lemma 3, J |= Σ
and hence J
∗
|= α. Since A
∗
is completed, J
∗
= J ,
and so J |= α. In the following, we argue by cases for
different α.
- α = A(a), A ∈ N
C
. Then, J |= A(a) ⇒ a ∈ A
J
Y
⇒
A(a) ∈ A
∗
.
- α = ¬A(a), A ∈ N
C
. Then, J |= ¬A(a) ⇒ a ∈
A
J
N
⇒ ¬A(a) ∈ A
∗
.
- α = P(a,b), P ∈ N
R
. Then, J |= P(a, b) ⇒ (a, b) ∈
P
J
Y
⇒ P(a, b) ∈ A
∗
.
- α = ¬P(a, b), P ∈ N
R
. Then, J |= ¬P(a, b) ⇒
(a, b) ∈ P
J
N
⇒ ¬P(a, b) ∈ A
∗
.

4 GRAPH REPRESENTATION OF
ABoxes AND BCQs OVER
DL-Lite
R
KBs
In this section, we will use node-edge labeled directed
graph to represent the completed ABox A
∗
as well as
Boolean conjunctive queries (BCQs), see (Ortiz and
Simkus, 2012) for similar representations. This helps
“visualize” reasoning about such queries as well as
being useful in formulating precise conditions for an-
swering BCQs with ‘Yes’, ‘No’ and ‘Unknown’.
The ABox graph for A
∗
is node-edge labeled
digraph G[A
∗
] = (V[A
∗
], E[A
∗
], L[A
∗
]) with nodes
V[A
∗
] = O
∗
and edges E[A
∗
] = {(a, b) | R(a, b) ∈
5
Recall that assertions of the form ∃R(a) do not belong
to A
∗
.
A
∗
, for some R ∈ R}, where each node a ∈ V[A
∗
] is
labeled with the set of literals L[A
∗
](a) = { L | L(a) ∈
A
∗
} and each directed edge (a,b) ∈ E[A
∗
] is labeled
with a set of roles L[A
∗
](a, b) = { R | R(a, b) ∈ A
∗
}.
Example 2. Let A
∗
= {A(a), ¬D(a), B(b), F(b), H(d),
P(a, b), Q(a, b), P(b, c), Q(b,c), R(a,d), ¬S (a, d),
¬Q(c, c)}. Then ABox graph for A
∗
is:
a
b
c
d
A, ¬D
B, F
H
R, ¬S
P, Q
P, Q
¬Q
Figure 4: The ABox graph G[A
∗
] for the given ABox, A
∗
.
We next define the syntax and semantics of Boolean
conjunctive queries. Let N
V
denote a countably infi-
nite set of variables.
Definition 1. A Boolean conjunctive query over
DL-Lite
R
is a finite expression of the form
∃y
1
, y
2
, ..., y
n
[
V
k
i=1
A
i
(ζ
i
) ∧
V
m
j=1
P
j
(η
j
, µ
j
)], where
- A
i
∈ N
C
for 1 ≤ i ≤ k, P
j
∈ N
R
for 1 ≤ j ≤ m and
y
l
∈ N
V
, 1 ≤ l ≤ n,
- ζ
i
, η
j
, µ
j
∈ {y
1
, y
2
, ..., y
n
} ∪ N
O
for 1 ≤ i ≤ k and 1 ≤
j ≤ m .
Query atoms of a BCQ q are of two sorts: con-
cept atoms A(v), and role atoms P(u, v), where u, v ∈
N
V
∪ N
O
, A ∈ N
C
and P ∈ N
R
. By Atoms(q) we de-
note the set of concept and role atoms occurring in
q. For instance the concept atoms in the BCQ q =
∃y, z[A(a)∧ B(y)∧ B(z)∧ P(a, y)∧ Q(a, z)∧ P(z, y)] are:
A(a), B(y) and B(z) and the role atoms are: P(a, y),
Q(a, z) and P(z,y).
As was the case with the ABox, we can repre-
sent the BCQ as a node-edge labeled directed graph
capturing the syntactic structure of the query. The
query graph of a BCQ q is the node-edge labeled
directed graph G[q] = (V[q], E[q], L[q]) with nodes
V[q] = {v ∈ N
V
∪ N
O
| v occurs in q} and edges E[q] =
{(u, v) | for some role name P, P(u, v) ∈ Atoms(q)};
each node v ∈ V[q] is labeled with the set of con-
cept names L[q](v) = {A| A(v) ∈ Atoms(q)} and each
edge (u,v) ∈ E[q] is labeled with the set of role names
L[q](u, v) = {P | P(u,v) ∈ Atoms(q)}.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
366

Example 3. The query graph of the BCQ q mentioned
above is:
a
y
z
A
B B
P
P
Q
Figure 5: The query graph of q = ∃y, z[A(a) ∧ B(y) ∧ B(z) ∧
P(a, y) ∧ Q(a, z) ∧ P(z, y)].
An interpretation of a BCQ q is provided by an OW-
interpretation I =
D
∆, ·
I
E
together with a valuation
which is a function π : V[q] → ∆ such that π(a) = a
I
for each individual a ∈ V[q] ∩ N
O
. We say that (I, π)
satisfies A(v), notation (I,π) |= A(v), if π(v) ∈ A
I
Y
.
(I, π) falsifies A(v), notation (I, π) |= ¬A(v), if π(v) ∈
A
I
N
. Similarly, (I, π) satisfies P(u,v), notation (I,π) |=
P(u, v), if (π(u), π(v)) ∈ P
I
Y
and (I, π) falsifies P(u, v),
notation (I, π) |= ¬P(u, v), if (π(u),π(v)) ∈ P
I
N
. We say
that (I,π) satisfies q, notation (I, π) |= q, if (I, π) |= α
for every α ∈ Atoms(q). (I, π) falsifies q, notation
(I, π) ||= q, if (I, π) falsifies some atom α ∈ Atoms(q).
I satisfies q, notation I |= q, if there exists a valuation
π : V[q] → ∆ such that (I, π) |= q. In this case, we say
that I is an OW-model of q. I falsifies q, notation
I ||= q, if for all valuations π : V[q] → ∆, (I, π) ||= q.
Recall (subsection 3.1) that given any OW-model
I of Σ we have defined a unique more compact OW-
model I
∗
and we introduced the notation Σ |=
∗
α to
mean that for any OW-model I of Σ, I
∗
is an OW-
model of Σ and I
∗
|= α. Finally, a BCQ q is entailed
from Σ, notation Σ |=
∗
q, if for every OW-model I of
Σ, I
∗
|= q. A BCQ q is disentailed from Σ, notation
Σ ||=
∗
q, if for every OW-model I of Σ, I
∗
||= q, i.e.,
I
∗
falsifies q. Thus the property Σ ||=
∗
q precisely
captures the requirement for answering the query q
with “No”.
Notation. We write h : V[q] −→
c
V[A
∗
] to denote the
fact that h is a mapping h : V[q] → V[A
∗
] which “re-
spects constants”, i.e. h(a) = a, for every individual
a ∈ V[q] ∩ N
O
.
Definition 2. Mapping h : V[q] −→
c
V[A
∗
] is a labeled
graph homomorphism, if
- for every node v in V[q], L[q](v) ⊆ L[A
∗
](h(v)),
and
- for every edge (u, v) in E[q], L[q](u, v) ⊆
L[A
∗
](h(u), h(v)).
In the next two theorems we provide a complete char-
acterization of entailment and disentailment of BCQs
in terms of properties of mappings h : V[q] −→
c
V[A
∗
].
Theorem 3. Let q be a BCQ and Σ a DL-Lite
R
KB.
Then, Σ |=
∗
q iff there exists a labeled graph homo-
morphism h : V[q] −→
c
V[A
∗
].
Proof. (⇒) Suppose Σ |=
∗
q and let J =
D
∆, ·
J
E
be
the canonical OW-model of Σ, see Section 3.2. Then,
J
∗
= J , and by hypothesis, J |= q. Hence, for some
valuation π : V[q] → O
∗
= V[A
∗
], (J , π) |= α, for ev-
ery α ∈ Atoms(q). Note that π : V[q] −→
c
V[A
∗
]. Now,
let v ∈ V[q] and A(v) ∈ Atoms(q). Then, (J , π) |=
A(v) ⇒ π(v) ∈ A
J
Y
⇒ A(π(v)) ∈ A
∗
⇒ A ∈ L[A
∗
](π(v)).
Similarly, for u, v ∈ V[q] with P(u,v) ∈ Atoms(q):
(J , π) |= P(u, v) ⇒ (π(u), π(v)) ∈ P
J
Y
⇒ P(π(u), π(v)) ∈
A
∗
⇒ P ∈ L[A
∗
](π(u), π(v)). It follows that π is a la-
beled graph homomorphism.
(⇐) Assume that h : V[q] −→
c
V[A
∗
] is a labeled
graph homomorphism and let I =
D
∆, ·
I
E
be an arbi-
trary OW-model of Σ. By Lemma 2, I
∗
=
D
∆
∗
, ·
I
∗
E
,
with ∆
∗
= I
∗
(O
∗
), is an OW-model of Σ and I
∗
|= A
∗
.
Since (I
∗
◦ h) : V[q] → ∆
∗
, we have (I
∗
◦ h)(a) =
I
∗
(h(a)) = a
I
∗
for all a ∈ V[q] ∩ N
O
. I.e., I
∗
◦ h is
a valuation. It remains to show that I
∗
is an OW-
model of q. Let v ∈ V[q] and A ∈ L[q](v). Then,
by the definition of labeled homomorphism, A ∈
L[A
∗
](h(v)) ⇒ A(h(v)) ∈ A
∗
⇒ h(v)
I
∗
∈ A
I
∗
Y
⇒ (I
∗
◦
h)(v) ∈ A
I
∗
Y
⇒ (I
∗
, (I
∗
◦h)) |= A(v). Similarly, for u, v ∈
V[q] with P ∈ L[q](u, v): P ∈ L[A
∗
](h(u), h(v)) ⇒
P(h(u), h(v)) ∈ A
∗
⇒ (h(u)
I
∗
, h(v)
I
∗
) ∈ P
I
∗
Y
⇒ ((I
∗
◦
h)(u), (I
∗
◦ h)(v)) ∈ P
I
∗
Y
⇒ (I
∗
, (I
∗
◦ h)) |= P(u, v).
Thus, Σ |=
∗
q. 
Next we define mappings that cannot be extended to
labeled homomorphisms and prove a tight connection
between such mappings and disentailment.
Definition 3. A mapping f : V[q] −→
c
V[A
∗
] is said to
be clashy, if
- there exist v ∈ V[q] and A ∈ L[q](v) such that ¬A ∈
L[A
∗
]( f (v)), or
- there exist u, v ∈ V[q] and P ∈ L[q]((u, v)) such that
¬P ∈ L[A
∗
](( f (u), f (v))).
Theorem 4. Let q be a BCQ and Σ a DL-Lite
R
KB.
Then, Σ ||=
∗
q iff every mapping f : V[q] −→
c
V[A
∗
] is
clashy.
Proof. (⇒) Assume Σ ||=
∗
q and let J =
D
∆, ·
J
E
be
the canonical OW-model of Σ. Then, J
∗
= J and
so for every valuation τ : V[q] → ∆
∗
, there is an α ∈
Atoms(q) such that (J , τ) |= ¬α. Since ∆
∗
= J (O
∗
) =
O
∗
= V(A
∗
) and τ(a) = a
J
= a for all a ∈ V[q] ∩ N
O
,
Secrecy-preserving Reasoning in Acyclic DL-LiteR Knowledge Bases in the Presence of BCQs
367

τ : V[q] −→
c
V[A
∗
] and it follows that τ is clashy. More-
over, since τ is arbitary the conclusion follows.
(⇐) Suppose now that every mapping f : V[q] −→
c
V[A
∗
] is clashy. Let I =
D
∆, ·
I
E
be an arbitrary OW-
model of Σ. By Lemma 2, I
∗
=
D
∆
∗
, ·
I
∗
E
with ∆
∗
=
I
∗
(O
∗
) is an OW-model of Σ such that I
∗
|= A
∗
. Let
π : V[q] → ∆
∗
be an arbitrary valuation and define the
mapping g
π
: V[q] → V[A
∗
] by
g
π
(v)=







a if v = a ∈ N
O
∩ V[q]
c if v ∈ N
V
∩ V[q],
where π(v) = c
I
∗
and c be the first constant
that satisfies in some arbitrary (but fixed) to-
tal ordering of O
∗
, see the end of Section 3.
It is easy to check that π = I
∗
◦ g
π
(in other
words, π factors via V[A
∗
]). Since, by assump-
tion, g
π
is clashy, for some A(v) ∈ Atoms(q),
¬A ∈ L[A
∗
](g
π
(v)) or for some P(u,v) ∈ Atoms(q),
¬P ∈ L[A
∗
]((g
π
(u), g
π
(v))). In the first case,
¬A(g
π
(v)) ∈ A
∗
⇒ g
π
(v)
I
∗
∈ A
I
∗
N
⇒ π(v) ∈ A
I
∗
N
implying, (I
∗
, π) |= ¬A(v). In the second case,
¬P((g
π
(u), g
π
(v))) ∈ A
∗
⇒ (g
π
(u)
I
∗
,
g
π
(v)
I
∗
) ∈ P
I
∗
N
⇒ (π(u),π(v)) ∈ P
I
∗
N
implying,
(I
∗
, π) |= ¬P(u, v). It follows that, Σ ||=
∗
q. 
5 SECRECY-PRESERVING
REASONING: ENVELOPES
AND QUERY ANSWERING
5.1 Computing Envelopes
As mentioned before the main goal of the paper is
to study secrecy-preserving reasoning. The tool we
use are the construction of envelopes (Tao et al.,
2010; Tao et al., 2015; Krishnasamy Sivaprakasam
and Slutzki, 2016). This is discussed in detail in Sec-
tion 5.1. Once envelope is available, query answering
becomes easy. Given a knowledge base Σ and a finite
secrecy set S consisting of assertions in A
∗
and BCQs,
the goal is to answer queries while preserving secrecy.
Here we assume that A
∗
has been computed previ-
ously. Our approach is to compute a subset E ⊆ A
∗
,
called the secrecy envelope for S, so that by protect-
ing E, the querying agent cannot logically infer any
assertions in S, see (Tao et al., 2010; Tao et al., 2015).
It is interesting to note that, though the BCQs in S
are not in E, we can store the information pertinent
to answering BCQs in E. The OWA plays a vital role
in protecting secret information when query answer-
ing is the main objective. When answering a query
with “Unknown”, the querying agent cannot differen-
tiate between the following cases: (1) the case that
the answer to the query is actually unknown to the
KB reasoner and (2) the case that the answer is being
protected in order to maintain secrecy.
Formally, the secrecy set is made of two parts, S =
S
Σ
∪ S
CQ
, where S
Σ
⊆ A
∗
0
⊆ A
∗
with A
∗
0
the subset of
assertions which do not involve fresh individuals, and
S
CQ
is a finite set of BCQs. Clearly, the size of A
∗
0
is
polynomial to the size of the input KB.
Definition 4. Given a knowledge base Σ =
h
A, T
i
and
a finite secrecy set S = S
Σ
∪ S
CQ
, where S
Σ
⊆ A
∗
and
S
CQ
is a finite set of BCQs, a secrecy envelope for S,
denoted by E, is a set of assertions having the follow-
ing properties:
1 S
Σ
⊆ E ⊆ A
∗
,
2 for every α ∈ E, A
∗
\ E 6|=
∗
α, and
3 for every q ∈ S
CQ
, A
∗
\ E 6|=
∗
q and A
∗
\ E |6|=
∗
q.
Property 2 says that no information in E can be en-
tailed from A
∗
\ E. Property 3 makes sure that BCQs
in S
CQ
can neither be entailed nor disentailed from
A
∗
\ E. To compute an envelope, we use the idea of
inverting assertion expansion rules (see (Tao et al.,
2010), where this approach was first utilized). In-
duced by the tableau expansion rules in Figure 1 (ex-
cept for the rules v
N∃
and v
∃∃
) and in Figure 2,
we have the corresponding “inverted” secrecy clo-
sure rules in Figure 6. The reason for the omission
of secrecy closure rules corresponding to the rules
v
N∃
and v
∃∃
is that an application of these rules re-
sults in adding assertions with fresh individual names.
By the hidden name assumptions (HNA), the query-
ing agent is barred from asking any queries that in-
volve fresh individual names, see also (Tao et al.,
2010).
As an illustration of a secrecy closure rules in
Figure 6, consider the v
←
N@
-rule. Let ¬P(a, b) ∈ E,
A v ¬∃P ∈ T and A(a) ∈ A
∗
\ E. If the querying agent
asks the query q = ¬P(a, b), then the reasoner R could
answer “Yes”. This is because of the v
N@
-rule and
the fact that A(a) < E. So, to protect ¬P(a, b), we have
to put A(a) in E. Similarly, in Figure 7 the secrecy
closure rules are given corresponding to the rules in
Figure 3. For instance, consider the v
←
∃L¬
-rule. Let
¬P(a, b) ∈ E, ∃P v B ∈ T and ¬B(a) ∈ A
∗
\ E. If the
querying agent asks the query q = ¬P(a, b), then the
reasoner R could answer “Yes”. This is because of the
v
∃L¬
-rule and the fact that ¬B(a) < E. So, to protect
¬P(a, b), we have to put ¬B(a) in E. In both cases,
these secrecy closure rules are named by adding the
superscript ← in the name of the corresponding as-
sertion expansion rules.
Rules that specifically deal with BCQs are given
in Figure 8 and have been designed to protect BCQ’s
in S
CQ
. Few words of explanation may be helpful in
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
368

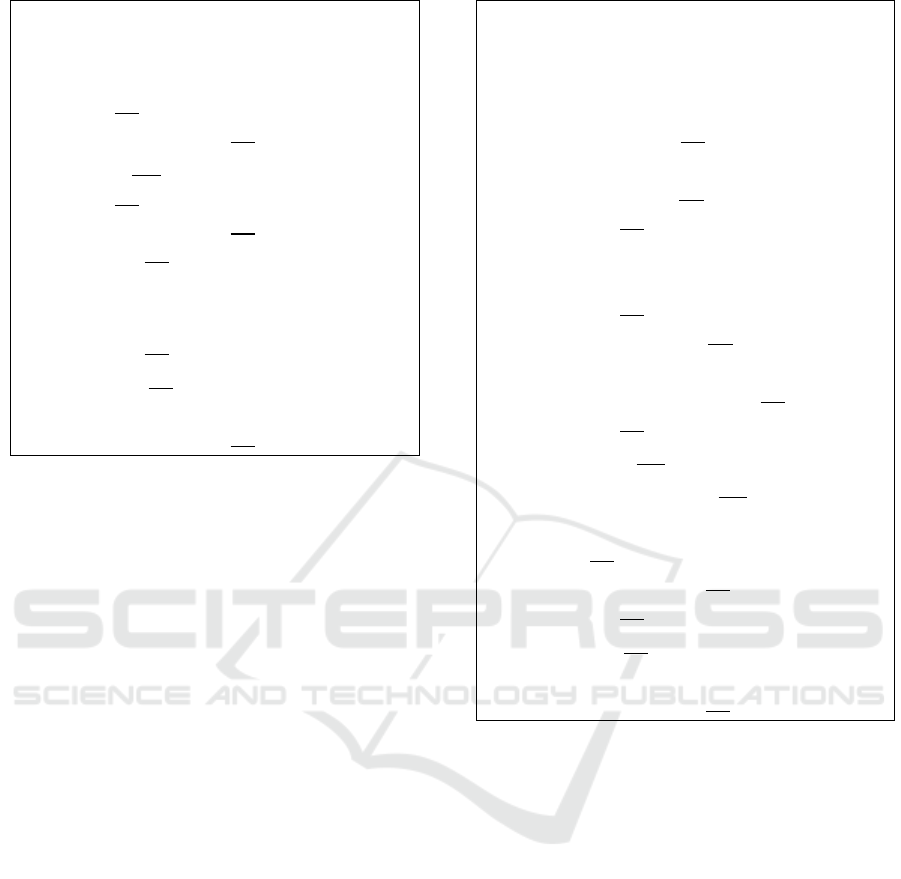
v
←
NL
− rule : if L(a) ∈ E, A v L ∈ T and
A(a) ∈ A
∗
\ E, then E := E ∪ {A(a)};
v
←
∃L
− rule : if L(a) ∈ E, ∃R v L ∈ T and
inv(R, a, c) ∈ A
∗
\ E, for some c ∈ O
∗
then E := E ∪ {inv(R, a,c)};
v
←
RE
− rule : if neg(E,a, b) ∈ E, R v E ∈ T and
inv(R, a, b) ∈ A
∗
\ E,
then E := E ∪ {inv(R, a,b)};
v
←
N@
− rule : if ¬inv(R,a, b) ∈ E, A v ¬∃R ∈ T
and A(a) ∈ A
∗
\ E,
then E := E ∪ {A(a)};
v
←
∃@
− rule : if ¬inv(S,a, b) ∈ E, ∃R v ¬∃S ∈ T
and inv(R, a, c) ∈ A
∗
\ E,
for some c ∈ O
∗
,
then E := E ∪ {inv(R, a,c)}.
Figure 6: Secrecy closure rules obtained by inverting rules
in Figures 1 and 2.
understanding BCQ-rules. Let q ∈ S
CQ
be a BCQ. To
protect q, we use BCQ
h
-rule which “disrupts” each
homomorphism h : G[q] → G[A
∗
\ E] and adds to E
one of the atoms of q (whose variables are evaluated
under h). Similarly, in the BCQ
c
-rule, we pick an
arbitrary clashy mapping g : G[q] → G[A
∗
\ E] and
make it into a non-clashy mapping: This can be done
by considering all the clashing atoms of q under g (A ∈
L[q](v) and ¬A ∈ L[A
∗
\ E](g(v)), or P ∈ L[q]((u, v))
and ¬P ∈ L[A
∗
\ E](g(u), g(v))) and adding them to E.
The computation of E proceeds in two stages. In
the first stage, E is initialized as S
Σ
and expanded by
using secrecy closure rules listed in Figures 6 and 7.
In the second stage, E is expanded by using BCQ
h
and
BCQ
c
-rules. We denote by Λ
S
the tableau algorithm
which computes the envelope E by using secrecy clo-
sure rules listed in Figures 6, 7 and 8 until no more
rules are applicable. Due to non-determinism in ap-
plying the BCQ-rules, different executions of Λ
S
may
result different envelopes. Since A
∗
is finite, the com-
putation of Λ
S
terminates. Let E be the output of Λ
S
.
By the assumption that S
Σ
⊆ A
∗
, and by the BCQ
h
-
and BCQ
c
-rules, it is easy to see that E ⊆ A
∗
.
Example 4. Let Σ =
h
A, T
i
be a DL-Lite
R
KB,
where A = {A(a), B(a), E(a), ¬F(a)} and T =
{A v D, A v ¬C, A v ∃P, B v ∃P, ∃P
−
v ¬C, ∃P
−
v
¬F, P v Q}. Also let S = {D(a), ∃y
1
, y
2
[A(y
1
) ∧
P(y
1
, y
2
)], ∃y
1
, y
2
[P(y
1
, y
2
) ∧ C(y
2
)]} be the se-
crecy set. Using the assertion expansion
rules in Figures 1, 2 and 3, we get A
∗
=
{A(a), B(a),¬C(a), ¬C(b), ¬C(c), D(a), E(a), ¬F(a),
v
←
NL¬
− rule : if ¬A(a) ∈ E, A v L ∈ T and
¬L(a) ∈ A
∗
\ E,
then E := E ∪ {¬L(a)};
v
←
N∃¬
− rule : if ¬A(a) ∈ E, A v ∃R ∈ T and
∀b ∈ O
∗
, ¬inv
(R, a, b) ∈ A
∗
\ E,
then pick a c ∈ O
∗
such that
E := E ∪ {¬inv(R, a,c)};
v
←
∃L¬
− rule : if ¬inv(R,a, b) ∈ E, ∃R v L ∈ T
and ¬L(a) ∈ A
∗
\ E,
then E := E ∪ {¬L(a)};
v
←
∃∃¬
− rule : if ¬inv(R,a, b) ∈ E, ∃R v ∃S ∈ T
and ∀c ∈ O
∗
, ¬inv(S ,a, c)
∈ A
∗
\ E, then pick a d ∈ O
∗
such that E := E ∪ {¬inv(S , a, d)};
v
←
RE¬
− rule : if ¬inv(R,a, b) ∈ E, R v E ∈ T
and ¬neg(E, a,b) ∈ A
∗
\ E,
then E := E ∪ {¬neg(E, a, b)};
v
←
N@¬
− rule : if ¬A(a) ∈ E, A v ¬∃R ∈ T and
inv(R, a, c) ∈ A
∗
\ E, for some c ∈ O
∗
,
then E := E ∪ {inv(R, a,b)};
v
←
∃@¬
− rule : if ¬inv(R,a, b) ∈ E, ∃R v ¬∃S ∈ T
and inv(S, a,c) ∈ A
∗
\ E,
for some c ∈ O
∗
,
then E := E ∪ {inv(S , a, c)}
Figure 7: Secrecy closure rules obtained by inverting rules
in Figure 3.
¬F(b),¬F(c), P(a, b), P(a, c), Q(a, b), Q(a, c)}. Using
the secrecy closure rules in Figures 6, 7 and 8, we
get E = {A(a), D(a), ¬C(b)}. Then graphs for A
∗
and
A
∗
\ E are listed in Figure 9.
The following results show that no assertion in the
envelope E is “logically reachable” from outside the
envelope. The proof of the next Lemma is standard
and is omitted.
Lemma 4. Let A
∗
be a completed ABox obtained
from Σ by first applying the rules in Figure 1, then
in Figure 2 and then rules in Figure 3 as specified in
Section 3. Also, let E be a set of assertions which,
starting from S
Σ
, is completed by first using rules in
Figures 6 and 7, and then rules in Figure 8. Then, the
ABox A
∗
\ E is completed.
The following corollary states, roughly, that the
secret BCQs are not logically reachable from A
∗
\ E.
Corollary 2. Let E
0
be any subset of A
∗
which is com-
pleted with respect to secrecy closure rules listed in
Secrecy-preserving Reasoning in Acyclic DL-LiteR Knowledge Bases in the Presence of BCQs
369

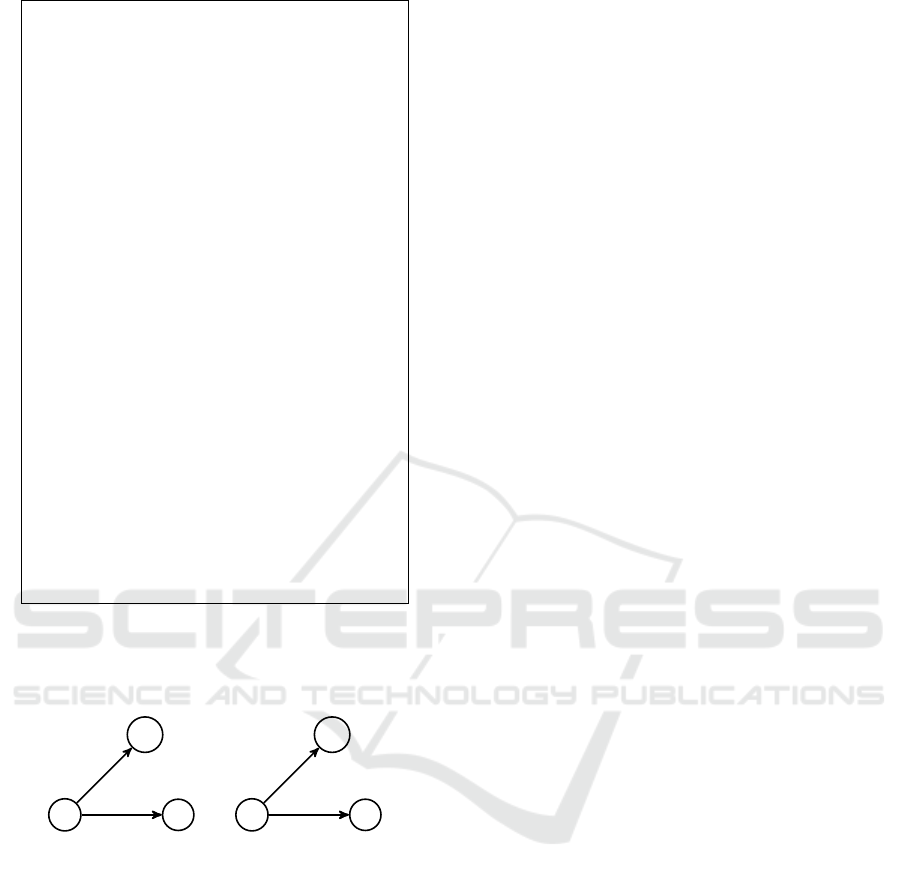
BCQ
h
− rule : if q ∈ S
CQ
, and there is a
labeled homomorphism
h : V[q] −→
c
V[A
∗
\ E] such that
{A
1
(h(ζ
1
)), .., A
k
(h(ζ
k
)),
P
1
(h(η
1
), h(µ
1
)), ..,
P
m
(h(η
m
), h(µ
m
))} ∩ E = ∅
then E := E ∪ {A
p
(h(ζ
p
))}
for some 1 ≤ p ≤ k or
E := E ∪ {P
r
(h(η
r
), h(µ
r
))}
for some 1 ≤ r ≤ m;
BCQ
c
− rule : if q ∈ S
CQ
, and every
f : V[q] −→
c
V[A
∗
\ E] is clashy,
then pick one such
clashy mapping g. Then,
• ∀p,1 ≤ p ≤ k,
if ¬A
p
(g(ζ
p
)) ∈ A
∗
\ E then
E := E ∪ {¬A
p
(g(ζ
p
))}, and
• ∀r,1 ≤ r ≤ m,
if ¬P
r
(g(η
r
), g(µ
r
)) ∈ A
∗
\ E then
E := E ∪ {¬P
r
(g(η
r
), g(µ
r
))}.
Figure 8: Secrecy closure rules for q ∈ S
CQ
:
q = ∃y
1
, ., y
n
[A
1
(ζ
1
) ∧ ... ∧ A
k
(ζ
k
) ∧ P
1
(η
1
, µ
1
) ∧ .... ∧
P
m
(η
m
, µ
m
)].
a
b
c
A, B, ¬C
D, E,¬F
¬C,¬F
¬C,¬F
P, Q
P, Q
A
∗
a
b
c
B,¬C
E, ¬F
¬F
¬C,¬F
P, Q
P, Q
A
∗
\ E
Figure 9: The graphs of A
∗
and A
∗
\ E.
Figure 8. Then, for every q ∈ S
CQ
,
- there is no labeled graph homomorphism h :
V[q] −→
c
V[A
∗
\ E
0
], and
- there exists at least one mapping f : V[q] −→
c
V[A
∗
\
E
0
] which is not clashy.
Proof. Let E
0
be completed with respect to secrecy
closure rules listed in Figure 8. This implies that
for every q ∈ S
CQ
, no BCQ
h
-rule is applicable to q.
Hence, by the conditions of BCQ
h
-rule, there is no
labeled graph homomorphism h : V[q] −→
c
V[A
∗
\ E
0
],
for any q ∈ S
CQ
. Similarly, no BCQ
c
-rule is applica-
ble to q. It follows that for each q ∈ S
CQ
, there exist at
least one mapping f : V[q] −→
c
V[A
∗
\ E
0
] which is not
clashy. 
Finally, we show that the completed set E (an output
of Λ
S
), is in fact an envelope.
Theorem 5. E is an envelope for S.
Proof. We must show that the set E satisfies the prop-
erties of Definition 4. Clearly, S
Σ
⊆ E. First we
show that, for every α ∈ E, A
∗
\ E 6|=
∗
α. Suppose
A
∗
\ E |=
∗
α, for some α ∈ E. By Theorem 2, we have
α ∈ (A
∗
\ E)
∗
and by Lemma 4, α ∈ A
∗
\ E, a contra-
diction.
Next we show that for each q ∈ S
CQ
, A
∗
\ E 6|=
∗
q
and A
∗
\ E |6|=
∗
q.
- Assume A
∗
\ E |=
∗
q. Then, for every OW-model
I = (∆, ·
I
) of (A
∗
\ E, T ), I
∗
|= q where I
∗
=
(∆
∗
= I
∗
(O
∗
), ·
I
∗
), see Section 3.1. Let J be the
canonical model of A
∗
\ E. Then, J
∗
= J , and
π
J
: V[q] −→
c
∆
∗
= J (O
∗
) = O
∗
and (J , π
J
) |= β,
for every β ∈ Atoms(q).
Now, let v ∈ V[q] and A(v) ∈ Atoms(q). Then,
(J , π
J
) |= A(v) ⇒ π
J
(v) ∈ A
J
Y
⇒ A(π
J
(v)) ∈
A
∗
\ E ⇒ A ∈ L[A
∗
\ E](π
J
(v)). Simi-
larly, let u, v ∈ V[q] and P(u, v) ∈ Atoms(q).
Then, (J , π
J
) |= P(u, v) ⇒ (π
J
(u), π
J
(v)) ∈
P
J
Y
⇒ P((π
J
(u), π
J
(v))) ∈ A
∗
\ E ⇒ P ∈
L[A
∗
\ E]((π
J
(u), π
J
(v))). It follows that,
π
J
: V[q] −→
c
V[A
∗
\ E] is a labeled graph homo-
morphism contradicting Corollary 2.
- Assume A
∗
\ E ||=
∗
q. Then, for every OW-model
I = (∆, ·
I
) of (A
∗
\ E, T ), I
∗
||= q where I
∗
= (∆
∗
=
I
∗
(O
∗
), ·
I
∗
). Let J be the canonical model of
A
∗
\ E. Then, J
∗
= J and for each valuation
π : V[q] −→
c
∆
∗
= J (O
∗
) = O
∗
, (J , π) |= ¬β, for
some β ∈ Atoms(q). Let k be any such valuation.
Then, (J , k) |= ¬A(v) for some A(v) ∈ Atoms(q)
or (J , k) |= ¬P(u, v) for some P(u,v) ∈ Atoms(q).
In the first case, k(v) ∈ A
J
N
⇒ ¬A(k(v)) ∈ A
∗
\
E ⇒ ¬A ∈ L[A
∗
\ E](k(v)) and in the second case,
(k(u), k(v)) ∈ P
J
N
⇒ ¬P((k(u), k(v))) ∈ A
∗
\ E ⇒
¬P ∈ L[A
∗
\ E]((k(u), k(v))). Hence, k : V[q] −→
c
V[A
∗
\ E] is clashy. Since k was arbitrary, it fol-
lows that all valuations are clashy. However, E is
completed, so by Corollary 2 there exist at least
one mapping k : V[q] −→
c
V[A
∗
\ E] which is not
clashy. This is a contradiction. Hence, A
∗
\ E |6|=
∗
q.

ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
370

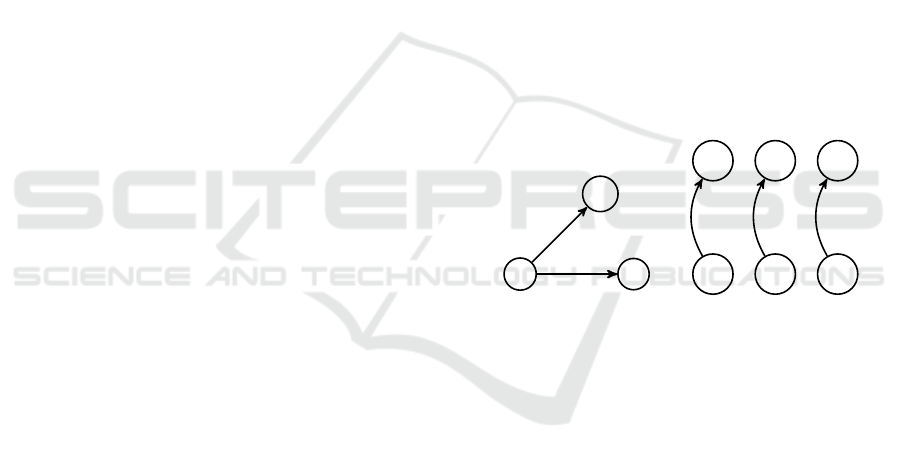
Ideally, we would like to compute a minimum en-
velope E which makes query answering as informa-
tive as possible without compromising secrecy. How-
ever, computing minimum envelope appears to be
hard, see (Tao et al., 2015) where the authors proved
that computing minimum size envelopes is NP-hard
even for propositional Horn KBs. So, our focus now
is to compute a minimal envelope with the property
that removing any one of the assertions in E would
reveal some of the secrets. We call such an envelope
a tight envelope. Formally,
Definition 5. An envelope E is said to be tight if for
every α ∈ E, E \ {α} is not an envelope.
Next, we observe that an envelope computed using the
rules in Figures 6, 7 and 8 need not be tight.
Example 5. Consider a DL-Lite
R
KB, where A
= {W(a,b), W(a, c)} and T = {∃W v A, ∃W
−
v B}.
Let S = {∃y,z[A(y) ∧ W(y, z) ∧ B(z)]} be the secrecy
set. Using the rules in Figure 1, we compute A
∗
=
{A(a), B(b), B(c), W(a, b), W(a, c)}. Since Λ
S
is a non-
deterministic algorithm, Λ
S
may output different en-
velopes. For illustration purposes, we considered two
envelopes namely E
1
= {A(a), W(a, b), W(a, c)} and
E
2
= {W(a, b),
W(a, c)}. It is easy to see that E
2
is tight, whereas E
1
is not.
A simple naive approach to compute a tight enve-
lope could work as follows. Given a precomputed A
∗
and a secrecy set S = S
Σ
∪S
CQ
, we can compute an en-
velope E of S as explained in the beginning of this sec-
tion. An assertion α ∈ E \ S is said to be redundant if
E\{α} is an envelope, i.e., ((A
∗
\E)∪ {α})
∗
∩(E\ {α}) =
∅. To compute a tight envelope, for each β ∈ E \ S
we check whether β is redundant in which case it is
moved from E to A
∗
\ E. Otherwise, β remains in E.
5.2 Query Answering
At this point all the necessary computations have
been done just once, and we are ready to answer
queries while maintaining secrecy. Thus, we assume
that A
∗
and E have been precomputed. From an al-
gorithmic point of view, answering queries may be
based on checking membership in the set A
∗
\ E or
searching for specific graph substructures in the graph
G[A
∗
\ E]. Suppose that the agent poses query q of
the form C(a) or E(a, b). Then, the reasoner checks
for the membership of q and ¬q in the set A
∗
\ E. If
q ∈ A
∗
\ E, then the reasoner should answer “Yes”. If
¬q ∈ A
∗
\ E, then the reasoner should answer “No”. If
neither q nor ¬q is in A
∗
\ E, then the reasoner should
answer “Unknown”. Since assertional queries do not
involve fresh individuals, in this case, the answer can
be computed in polynomial time ( in the size of the
original KB Σ) .
Now suppose that the agent poses a BCQ q. Then,
the reasoner considers the mappings V[q] −→
c
V[A
∗
\E].
If there exists a labeled homomorphism h : V[q] −→
c
V[A
∗
\ E], then the reasoner should answer “Yes” by
Theorem 3. It follows that the problem of deciding
whether answer to a BCQ is “Yes”, is NP-Complete.
If every such mapping is clashy, then the reasoner
should answer “No”, see Theorem 4. Therefore,
the problem of deciding whether answer to a BCQ
is “No”, is coNP. Finally, we should answer “Un-
known” precisely when (a) there is no homomor-
phism V[q] −→
c
V[A
∗
\ E] and (b) not every such map-
ping is clashy. It follows that the problem of decid-
ing whether answer to a BCQ is “Unknown” lies in
DP = {L | L = L
1
∩ L
2
with L
1
∈ NP and L
2
∈ coNP},
see (Papadimitriou, 2003).
Example 6. We use the KB, the secrecy set S and
the envelope E considered in Example 4. Answers for
the BCQs q
1
, q
2
and q
3
whose query graphs are given
below, are computed in the following based on A
∗
\ E.
a
b
c
B,¬C
E, ¬F
¬F
¬C,¬F
P, Q
P, Q
A
∗
\ E
y
1
y
2
E
Q
q
1
y
1
y
2
A
Q
q
2
y
1
y
2
F
Q
q
3
Figure 10: The graphs of A
∗
\ E and queries.
First let us consider the BCQ q
1
= ∃y
1
, y
2
[E(y
1
) ∧
Q(y
1
, y
2
)]. Since there exists a homomorphism from
G[q
1
] to G[A
∗
\ E], namely, y
1
7→ a, y
2
7→ b and
since L[q
1
](y
1
) ⊆ L[A
∗
\ E](a), L[q
1
](y
1
, y
2
) ⊆ L[A
∗
\
E](a, b), L[q
1
](y
2
) ⊆ L[A
∗
\ E](b), the answer to q
1
is “Yes”. Actually, there are two labeled homomor-
phisms from G[q
1
] to G[A
∗
\ E], the other one being,
y
1
7→ a, y
2
7→ c.
Next, q
2
= ∃y
1
, y
2
[A(y
1
)∧ Q(y
1
, y
2
)]. Since there is
no labeled homomorphism and there exist non-clashy
mappings from G[q
2
] to G[A
∗
\ E], e.g., y
1
7→ a, y
2
7→
b, answer to q
2
is “Unknown”.
Finally, consider the BCQ q
3
= ∃y
1
, y
2
[Q(y
1
, y
2
) ∧
F(y
2
)]. It is easy to see that all the mappings from
G[q
3
] to G[A
∗
\ E] are clashy. Hence, answer for the
BCQ q
3
is “No”.
Secrecy-preserving Reasoning in Acyclic DL-LiteR Knowledge Bases in the Presence of BCQs
371

6 CONCLUSIONS
In this paper we have studied the problem of secrecy-
preserving query answering over acyclic DL-Lite
R
KBs. We have extended the conceptual logic-based
framework for secrecy-preserving reasoning which
was introduced by Tao et al., see (Tao et al., 2015),
so as to allow BCQs. As the OWA underlies the foun-
dational aspects of KBs, to show that the reasoner is
sound and complete we used the semantics based on
Kleene’s 3-valued logic, see (Avron, 1991; Tao et al.,
2015). We provide syntactic characterizations for en-
tailment and disentailment of BCQs in terms of prop-
erties of mappings (Section 4).
ACKNOWLEDGMENTS
This research work was done by the first author while
he was a graduate student of Department of Computer
Science, Iowa State University. This work was sup-
ported by the NSF grant CNS1116050. Any opin-
ion, finding, and conclusions contained in this article
are those of authors and do not necessarily reflect the
views of the National Science Foundation.
REFERENCES
Artale, A., Calvanese, D., Kontchakov, R., and Za-
kharyaschev, M. (2009). The dl-lite family and re-
lations. J. of Artificial Intelligence Research, 36:1–69.
Avron, A. (1991). Natural 3-valued logics–characterization
and proof theory. The Journal of Symbolic Logic,
56(01):276–294.
Bao, J., Slutzki, G., and Honavar, V. (2007). Privacy-
preserving reasoning on the semantic web. In
IEEE/ACM/WIC International Conference on Web In-
telligence, pages 791–797. IEEE CS Press.
Bell, D. and LaPadula, L. (1973). Secure computer sys-
tems: Mathematical foundations. Technical report,
DTIC Document.
Biskup, J. and Tadros, C. (2012). Revising belief witwith
revealing secrets. In Lukasiewiez, T, and Sali, A. (eds)
FoLKS 2012, volume 7153 of LNCS, pages 51–70.
Springer.
Biskup, J., Tadros, C., and Wiese, L. (2010). Towards
controlled query evaluation for incomplete first-order
databases. In Link, S. (ed) FoLKS 2010, volume 5956
of LNCS, pages 230–247. Springer.
Biskup, J. and Weibert, T. (2008). Keeping secrets in in-
complete databases. International Journal of Infor-
mation Security, 7,3:199–217.
Calvanese, D., De Giacomo, G., Lembo, D., Lenzerini, M.,
and Rosati, R. (2007). Tractable reasoning and effi-
cient query answering in description logics: The dl-
lite family. J. of Automated Reasoning, 39(3):385–
429.
Cuenca Grau, B., Kharlamov, E., Kostylev, E., and
Zheleznyakov, D. (2013). Controlled query evaluation
over owl 2 rl ontologies. In The Semantic Web–ISWC
2013, pages 49–65. Springer.
Denning, D. and Denning, P. (1979). Data security. ACM
Computing Surveys (CSUR), 11(3):227–249.
Halpern, J. and O’Neill, K. (2008). Secrecy in multiagent
systems. ACM Transactions on Information and Sys-
tem Security (TISSEC), 12(1):5.
Kagal, L., Finin, T., and Joshi, A. (2003). A policy based
approach to security for the semantic web. In The Se-
mantic Web-ISWC 2003, pages 402–418. Springer.
Krishnasamy Sivaprakasam, G. and Slutzki, G. (2016).
Secrecy-preserving query answering in ELH knowl-
edge bases. In Proceedings of 8th International Con-
ference on Agents and Artificial Intelligence, Rome,
Italy.
Krotzsch, M. (2012). Owl 2 profiles: An introduction to
lightweight ontology languages. In Eiter, T; and Kren-
nwallner, T. (eds) Reasoning Web Summer School Pro-
ceedings of Proc. of 8th Int. Summer school, volume
7487 of LNCS, pages 112–183. Springer.
Lutz, C., Toman, D., and Wolter, F. (2008). Conjunc-
tive query answering in EL using a database system.
In Proceedings of the 5th International Workshop on
OWL: Experiences and Directions (OWLED 2008).
Lutz, C., Toman, D., and Wolter, F. (2009). Conjunctive
query answering in the description logic EL using a
relational database system. In IJCAI, volume 9, pages
2070–2075.
Mei, J., Liu, S., Xie, G., Kalyanpur, A., Fokoue, A., Ni, Y.,
Li, H., and Pan, Y. (2009). A practical approach for
scalable conjunctive query answering on acyclicEL
+
knowledge base. In The Semantic Web-ISWC 2009,
pages 408–423. Springer.
Ortiz, M. and Simkus, M. (2012). Reasoning and query
answering in description logics. In Eiter, T; and Kren-
nwallner, T. (eds) Reasoning Web Summer School Pro-
ceedings of Proc. of 8th Int. Summer school, volume
7487 of LNCS, pages 1–53. Springer.
Papadimitriou, C. H. (2003). Computational complexity.
John Wiley and Sons Ltd.
Sicherman, G., De Jonge, W., and Van de Riet, R. (1983).
Answering queries without revealing secrets. ACM
Transactions on Database Systems (TODS), 8(1):41–
59.
Sivaprakasam, G. K. (2016). Secrecy-preserving reasoning
in simple description logic knowledge bases. PhD the-
sis, Iowa State University.
Stouppa, P. and Studer, T. (2009). Data privacy for ALC
knowledge bases. In Logical Foundations of Com-
puter Science, pages 409–421. Springer.
Tao, J., Slutzki, G., and Honavar, V. (2010). Secrecy-
preserving query answering for instance-checking in
EL. In Hitzler, P. and Lukasiwiez, T. (eds) RR 2010,
volume 6333 of LNCS, pages 195–203. Springer.
Tao, J., Slutzki, G., and Honavar, V. (2015). A concep-
tual framework for secrecy-preserving reasoning in
knowledge bases. ACM Transactions on Computa-
tional Logic (TOCL), 16(1):3.
Weitzner, D., Abelson, H., Berners-Lee, T., Feigenbaum,
J., Hendler, J., and Sussman, G. (2008). Information
accountability. Commun. ACM, 51, 6.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
372