
Multi-product, Multi-supplier Order Assignment and Routing for an
e-Commerce Application in the Retail Sector
Louis Rivi
`
ere
1
, Christian Artigues
1
, Azeddine Cheref
1
, Nicolas Jozefowiez
2
, Marie-Jos
´
e Huguet
1
,
Sandra U. Ngueveu
1
and Vincent Charvillat
3,4
1
CNRS, LAAS-CNRS, Universit
´
e de Toulouse, INSA, INP, France
2
LCOMS EA 7306, Universit
´
e de Lorraine, Metz 57000, France
3
Universit
´
e de Toulouse, IRIT, INP, France
4
U Devatics, Toulouse, France
Keywords:
e-Commerce, Retail Market, Order Assignment, Vehicle Routing, Genetic Algorithms.
Abstract:
With the rise of virtualization, the share of e-commerce in the retail market continues to grow in an omnichan-
nel context. We consider an existing software tool, developed by the Devatics company, for pooling inventories
in stores to meet online orders. The problem which arises therefore consists in seeking the optimal allocation
of a set of customers to stores. In this paper we consider a variant of the offline problem corresponding to an
evolution of the existing software, consisting of assigning a set of predefined orders when the transportation
cost depends on a delivery tour to the customer locations. We show that the problem corresponds to a vehicle
routing problem with additional but standard attributes. A mixed-integer linear programming formulation is
given and several heuristics are proposed : a giant tour-based genetic algorithm, a simple cluster-first, route
second heuristic and an assignment-based genetic algorithm. Preliminary computational results on a set of
realistic problem instances suggest that the assignment-based genetic algorithm better scales as the problem
size increases.
1 INTRODUCTION
With the rise of virtualization, the share of e-
commerce in the retail market continues to grow in an
omnichannel context. One of the services offered by
the Devatics company is Onestock
1
, a tool for pool-
ing inventories to meet online orders. The problem
which arises therefore consists in seeking the opti-
mal allocation of a set of customers to stores. Two
modes of assignment are possible. Indeed, we can
consider the ”Online” assignment mode, consisting
of the allocation of each order as they are declared,
and the ”Offline” assignment which consists of as-
signing all the orders in a single large block. In this
paper we consider the offline problem. The Onestock
software solves a variant where the transport cost are
fixed. In this paper we consider an evolution of the
problem towards a variant where the transport costs
depend on delivery tours to the customer locations.
We propose an mixed-integer linear programming for-
mulation (MILP) of the problem. On realistic data
1
https://www.onestock-retail.com/
instances, we compare several heuristics and meta-
heuristics. We show that a cluster-first, route-second
based genetic algorithm obtains the best results. The
problem formulation is given in Section 2. The real-
istic data extraction approach that we use to generate
the data instances is then presented in Section 3. Sec-
tion 4 first gives a quick state of the art review of effi-
cient metaheuristics for vehicle routing problems and
propose adaptations for the considered E-commerce
problem. Section 5 provides a computational compar-
ison of the proposed exact and heuristic approaches.
Concluding remarks are drawn in Section 6.
2 MODELING THE PROBLEM
The problem considers a fixed set of online orders D
for a set of products P. Each order d ∈ D asks for
an amount q
d p
of product p ∈ P. We have a set M of
stores, and each store m ∈ M has a stock s
mp
of prod-
uct p ∈ P. The problem is then to meet the demand
in products of each order by using the store stocks
438
Rivière, L., Artigues, C., Cheref, A., Jozefowiez, N., Huguet, M., Ngueveu, S. and Charvillat, V.
Multi-product, Multi-supplier Order Assignment and Routing for an e-Commerce Application in the Retail Sector.
DOI: 10.5220/0010318304380445
In Proceedings of the 10th International Conference on Operations Research and Enterprise Systems (ICORES 2021), pages 438-445
ISBN: 978-989-758-485-5
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

with the possibility to split the demand across differ-
ent stores. Then, each store must deliver the ordered
packages to the customers in a single tour.
Although in the OneStock software the orders are
served online upon receipt, the offline problem has
concrete applications. Indeed, most real orders take
place in the evening, and therefore cannot be pro-
cessed before the stores open on next morning. In this
case, we have a given number of orders to process at
a time. Another application of interest is the estima-
tion of a ”regret”, i.e. the difference in performance
between the immediate allocation of successive or-
ders and the optimal allocation of these orders. In
this paper, we wish to minimize the distance traveled
on tours. The trucks have no capacity, so each store
only has to deliver the products in at most one tour.
However, a customer can be served by several stores
and therefore by several routes. This model therefore
explicitly incorporates the “assignment + routing” as-
pect.
2.1 Input Data
D : set of orders.
M : set of stores.
P : set of products.
N = M ∪ D : set of nodes.
V = {(i, j) | i, j ∈ N
2
} set of arcs.
R : set of r
i j
∈ R : cost of arc from i to j
Q : set of q
d p
∈ N : amount of product p ∈ P in order
d ∈ D.
S : set of s
mp
∈ N : stock of product p ∈ P in store
m ∈ M.
2.2 Variables
X : set of x
dmp
∈ N : number of products p sent from
store m for order d.
Y : set of y
dm
∈ {0, 1} : indicates whether a package
is sent from store m for order d.
Z : set of z
m
i j
∈ {0, 1} : indicates whether the tour of
store m takes arc (i, j).
U : set of u
m
i
∈ N : number assigned to node i in the
tour of store m (to avoid subtours).
2.3 Objective
min
∑
m∈M
∑
(i, j)∈V
z
m
i j
r
i j
(1)
2.3.1 Constraints
∑
m∈M
x
dmp
≥ q
d p
, ∀d, p ∈ D, P (2)
∑
d∈D
x
dmp
≤ s
mp
, ∀m, p ∈ M, P (3)
x
dmp
≤ y
dm
min(q
d p
, s
mp
), ∀d, m, p ∈ D, M, P (4)
∑
i∈N
z
m
id
≥ y
dm
, ∀d, m ∈ D, M (5)
∑
i∈N
z
m
mi
≥ y
md
, ∀d, m ∈ D, M (6)
∑
i∈N
z
m
i j
=
∑
k∈N
z
m
jk
, ∀m, j ∈ M, N (7)
u
m
i
− u
m
j
+ |D|z
m
i j
≤ |D| − 1, (8)
∀i, j ∈ V \ {m}, i 6= j, ∀m ∈ M
Objective (1) is this time to minimize the total dis-
tance traveled by the store deliverers.
Constraints (2) guarantees that each order is suffi-
ciently supplied. Constraints (3) guarantee that stocks
are sufficient for shipments and constraints (4) ensure
that the number of products p sent from store m to
customer d is set to 0 if no package is sent from m to
d. Constraints (5) and (6) guarantee that the tour of
store m passes through customer d and by store m if
this allocation has been decided, respectively. Con-
straints (7) ensure flow conservation while (8) guar-
antees that only cycles including store m are allowed.
3 REALISTIC DATA INSTANCE
GENERATION
To best stick to reality, we use statistics extracted
from real instances of a Devatics customer. An of-
fline problem generator uses these statistics to create
datasets with an arbitrary number of orders.
Figures 1 and 2 show that for the firm considered
the distribution of orders is not egalitarian.Wednesday
is the busiest day with around 200 orders on average,
with peaks of orders on sales days that do not exceed
1000 orders for a day.
For each product, its popularity is given by the
sum of its purchases. In addition, a matrix of co-
occurrence indicates for each pair of products the
number of orders that include both. We notice that
the popularity of the products is distributed in a way
approaching a Pareto distribution.
We can therefore generate a semi-realistic n-sized
order from the data, first choosing a product randomly
based on its popularity, then adding products accord-
ing to their co-occurrences with the products already
Multi-product, Multi-supplier Order Assignment and Routing for an e-Commerce Application in the Retail Sector
439
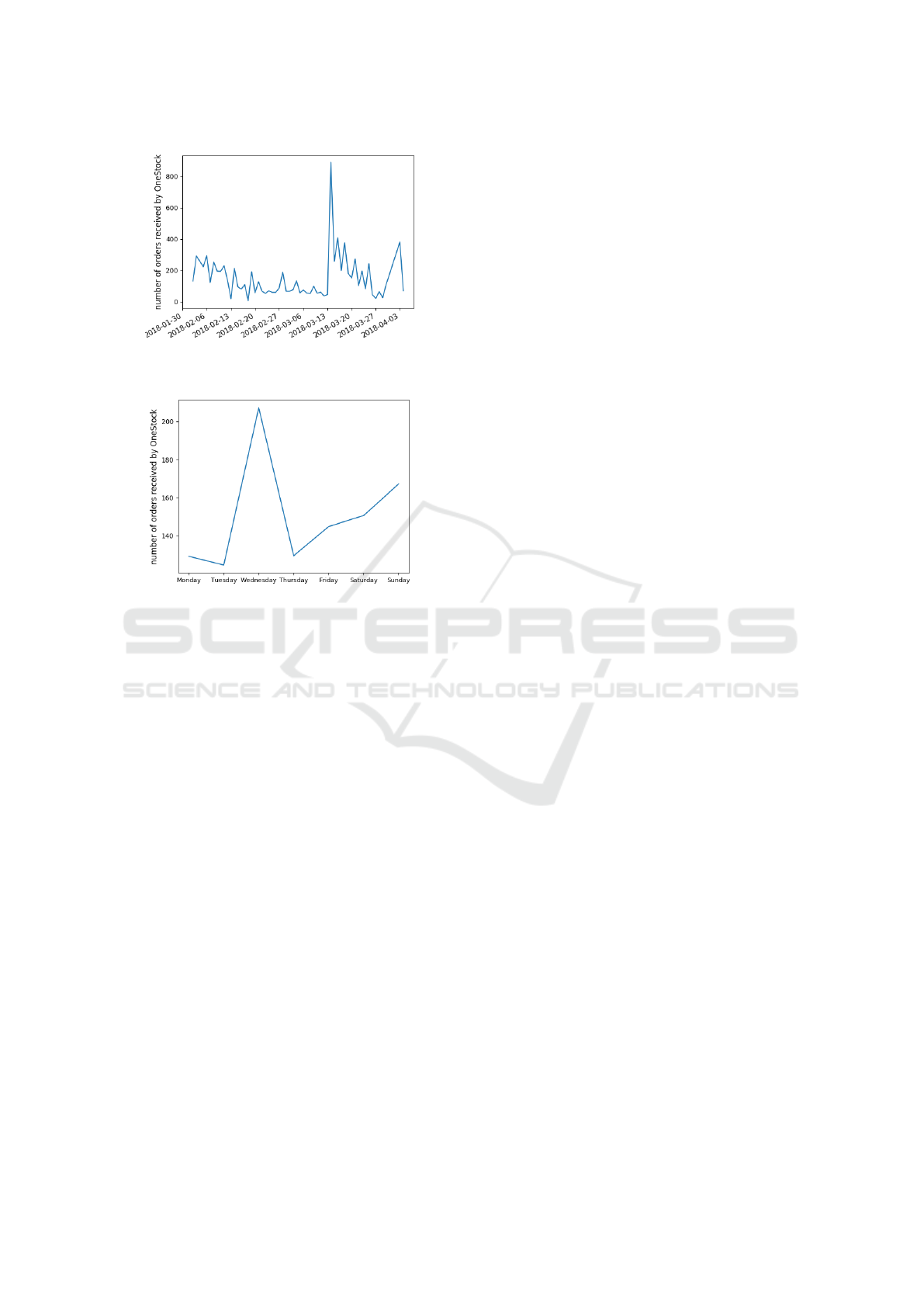
Figure 1: Number of orders per day over a three-month pe-
riod.
Figure 2: Average number of orders per day of the week.
present until we have n products. We also have in-
formation regarding the size distribution of n orders
with an almost binomial distribution of the quantity
of product ordered. We notice that the average order
gathers 2.8 products, or roughly 1% of the available
products (203 in total).
Once the orders are composed, we need to provide
stores to ensure the feasibility of the problem. To do
this, we are inspired by the overall distribution of the
stock of products as well as quantities of stocks of
each product in each store. We noticed that more than
30% of the stock is in the warehouse, while all the
other stores roughly share the rest.
For each unit of product ordered we select a store
to receive a unit of stock of this product. If it is the
first unit of this product in stock, a stock margin of
two units is added. This margin value, given by De-
vatics, corresponds to the risk aversion of stores that
report a quantity of stock below reality to avoid short-
age. We generate a set of problems constituting a test
bench on which we vary the values of the number of
orders and of the stock margin.
4 PROPOSED METHODS
The modeling of the routing problem, in particular
the constraints that eliminate subtours, do not allow
a MILP solver to solve the problem effectively, which
justifies the use of heuristics. This problem is very
close to several well studied problems such as the
traveling salesman problem (TSP) the location and
routing problem (LRP) and in particular the vehicle
routing problem (VRP). Classically, the latter consists
of minimizing the cost of visiting all customers with-
out exceeding a given capacity of the truck. One can
consider that our problem corresponds to the VRP
with additional classical attributes (no capacity on
trucks, multi-products, capacity on stocks, several
warehouses, multiple deliveries, one truck per ware-
house). The VRP as well as many variations involving
some of these attributes are very studied problems for
their many practical applications in the field of logis-
tics. In (Abdulkader et al., 2018; Martins et al., 2020),
heuristics are proposed for a related omnichannel re-
tail problem with the difference that vehicles are not
attached to stores but located in a central depot and
perform pick up and delivery tours. We first review
the efficient metaheuristics designed for the VRP be-
fore describing our solution approaches.
4.1 The Properties of Efficient
Metaheuristics for Vehicle Routing
Problems
Vidal et al. (Vidal et al., 2014b) proposed a unified
heuristic framework to solve ta family of VRP with
many attributes. The approach consists in categoriz-
ing the attributes (additional constraints) of the VRP
to be able to offer solutions adapted to each of these
categories. In addition, others works (Vidal et al.,
2013) try to extract from the profusion of the meth-
ods the main characteristics which make the success
of an approach. Although empirical, this analysis can
guide us in creating our method. Two tracks inspired
by the methods of LRP solution approach emerge. On
the one hand, the giant tour method, which focuses on
the ”routing” aspect of the problem, and on the other,
an approach highlighting the ”assignment” aspect of
the problem.
4.2 Giant Tours: Route-first,
Cluster-second Approach
The giant tour method is proposed for the first time
for the VRP by Beasley (Beasley, 1983). Prins (Prins,
2004) integrates this technique with a memetic algo-
rithm (genetic algorithm with a local search phase).
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
440
Vidal et al. (Vidal et al., 2014b) among others pro-
posed an efficient variant able to solve a large set of
routing problems with various constraints. In this sec-
tion we first recall the principle of the giant tour and
the SPLIT operator for the VRP. Then, we describe the
adaptation of the SPLIT operator to our problem and
we finally describe the proposed giant tour based hy-
brid genetic algorithm that uses a MILP-based repair
operator.
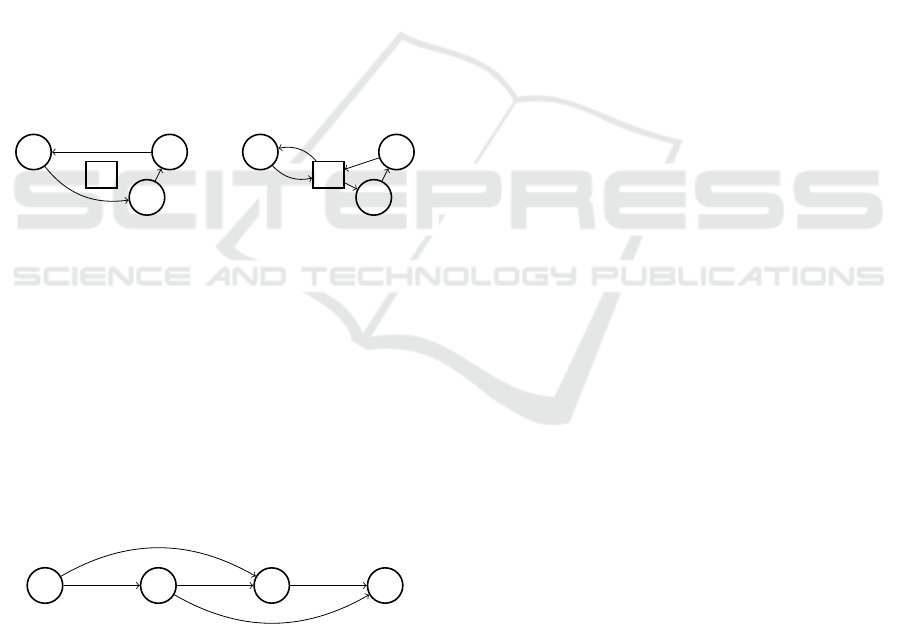
The Principle of the Giant Tour. The representa-
tion by giant tour consists for the classic VRP to con-
sider, instead of explicit solutions, ”giant tours”, a
kind of concatenation of real tours, representing all
the ways to cut this tour in order to respect the ca-
pacity constraint of the trucks. The idea is that if we
know how to quickly find the best solution for this
subset, it is faster to consider ”macro solutions”. An
illustration of the giant tour is given in Fig. 3. In this
figure, a giant tour of size 3: [3,1,2] must be cut for
a truck capacity of 2. The different possible cuts are
therefore [3 — 1 — 2], [3,1 — 2] and [3 — 1,2]where
”—” represents a return to the depot.
M
3
12
M
3
12
⇒
Figure 3: Giant tour [3,1,2] and associated solution.
Finding an optimal division of the giant tour into
subtours is polynomial, as a shortest path algorithm.
Figure 4 shows how this cutting operator (commonly
called SPLIT) determines the optimal solution. It con-
sists in finding the shortest path in a graph whose
nodes are the ordered points visited by the giant tour
and whose arcs each represent a grouping. Each arc
cannot group more points than the capacity of the
trucks and the cost associated with an arc is the cost
of the grouping it represents.
0 3
1 2
c
[3]
c
[3,1]
c
[1]
c
[1,2]
c
[2]
Figure 4: Subgraph for cutting by SPLIT the giant tour
[3,1,2] with capacity 2.
Adapting the Split Operator to Our Problem. To
adapt the method to our problem and its attributes,
we first observe the adaptations considered for these
attributes taken individually. In the literature, to adapt
the method to problems with split-delivery, (Boudia
et al., 2007) brings two changes:
• A node can appear several times in a giant tour.
• Each occurrence of a node is associated with the
quantity of delivered products. The sum of the
delivered quantity must match the request.
The SPLIT operator is also slightly modified since
when a sub-tour is considered, visiting several times
the same node is meaningless. The sum of the de-
livered quantities is therefore carried over to a sin-
gle occurrence of the node. Experience shows that
the choice of this node, if it can be difficult to deter-
mine optimally, can be done deterministically (the lo-
cal search carried out thereafter rectifying a possible
bad choice). In addition to the loss of optimality, the
first of these changes complicates the cutting, in fact,
in a giant tour, a node can appear up to M times if it is
served by all stores. We switch from a fixed size |D|
to a variable size up to |D|.|M|. Especially since in a
multi-product context and with capacities on stocks,
the information associated with the quantity delivered
for each product can be voluminous and, as we will
see later, does not by itself guarantee the existence of
a solution by the SPLIT operator. Indeed, even if the
sum of the delivered products corresponds to the de-
mand for each product, it is still necessary that stores
have stocks to deliver these products. This feasibil-
ity of a sub tour is itself difficult to determine since it
depends on the other sub-routes selected.
Vidal et al. (Vidal et al., 2014a) show how the
giant tour can be adapted to multiple depots. The
change is restricted to the SPLIT method, in which the
costs associated with a sub-tour becomes the cost of
allocating the tour to the best depot. In our case with
capacities, it is not possible to determine the ”best”
assignment independently of other assignments. We
must therefore create for each assignment of a sub-
tour to a store m, an arc with a corresponding cost.
The number of route assignments to be considered be-
comes O(|M|
n
) in the worst case where n is the size
of the giant tour since we do not limit the capacity of
the trucks.
A SPLIT operator adapted to the case of deliv-
eries with capacities is presented by Duhamel et al.
(Duhamel et al., 2010). The authors use a Bellman
algorithm with several labels per node to keep the
stocks available when searching for the shortest path.
A dominance rule between labels makes it possible
to discard some of them, but the method remains too
slow for large instances. Several improvements are
proposed to speed it up, in particular, limiting the
number of labels considered during the evaluation (a
parameter to be set). Despite these complications, one
of the properties of our problem, which can simplify
Multi-product, Multi-supplier Order Assignment and Routing for an e-Commerce Application in the Retail Sector
441

the SPLIT procedure, is that each store performs only
one tour. In this case, the resource whose labels must
report the usage is no longer the stock, but the prior
use or not of a store. However, the giant tour cut
this way represents a less important set of solutions.
So we have a trade-off between speed of cutting and
search efficiency.
From this analysis, a giant tour for our problem
is thus a sequence S of at most |D|.|M| nodes, each
node k corresponding to an order δ(k) associated to
a delivered amount λ
p
(k) such that the sum of deliv-
ered amount for the nodes corresponding to the same
order equals the total required quantity for each prod-
uct, which correspond to the following invariant:
|S|
∑
k=1
δ(k)=d
λ
p
(k) = q
d p
∀d ∈ D, p ∈ P (9)
The SPLIT operator we propose is synthesized in
Algorithmm 1. A solution is represented by a chain
of labels. a label L labels is composed of a node
L.nodein the giant tour S, a score L.score, a store
L.store and a set of available stores L.available m,
and a parent label L.parent. A Label represent
the subsequence from the successor of L. parent to
L.node assigned to store m of cost L .score and such
that the set of stores available for delivering the suc-
cessors of L.node in S is stored in L.available
m
. The
notation µ
i j
denotes the sub-tour comprising nodes
i + 1 up to j in S. To save the propagation of un-
necessary labels, the procedure ADDLABELTONODE
uses a standard dominance rule. A label L
1
dominates
a label L
2
(noted L
1
L
2
) if it uses fewer resources
for a better score. Formally:
L
1
.score < L
2
.score and
L
2
.available m ⊆ L
1
.available m
or
L
1
.score ≤ L
2
.score and
L
2
.available m ⊂ L
1
.available m
One must notice that the SPLIT operator may fail
in obtaining a feasible set of tours. Indeed, it is
possible that all active label at some points fail to
satisfy the condition at Line 8. This condition ex-
press the fact that the stock in store m must be suf-
ficient to deliver all amounts λ
p
(k) of each order k
in the µ
i j
subsequence for all products p. But if the
λ
p
(k) atttached to the giant tour satisfy invariant (9),
which ensure that the customer demand is satisfied,
they are not necessarily compatible with the stock. In
this case, the best set of tours computed by the SPLIT
operator is incomplete.
Algorithm 1: The SPLIT procedure.
1 //Insert start label;
2 L ← (node = 0; cost = 0; available store =
M; parent = nil);
3 ADDLABELTONODE(0, L);
4 for i ∈ {0, .., |S|} do
5 for L
l
i
∈ {Labels on node i} do
6 for j ∈ {i, .., |N|} do
7 for m ∈ L
l
i
.available m do
8 if s
mp
≥
∑
j
k=i+1
λ
p
(k), ∀p ∈ P
then
9 L.score ← L
j
i
.score +
route cost(µ
i j
, m);
10 L.available ←
L
j
i
.available m \ {m};
11 L.node = j;
12 L.store = m;
13 L.parent = L
l
i
;
14 ADDLABELTONODE( j, L);
15 end
16 end
17 end
18 end
19 end
The Giant Tour-based Hybrid Genetic Algorithm.
Given the SPLIT operator, Algorithm 2 describes the
genetic algorithm. Individuals are giant tours. In Line
1, a population of giant tours is initialized randomly
via function INITPOPGT. The a standard tournament
selection is performed to select two parent individuals
I1 and I2 (Line 3, function CHOOSEPARENTSGT).
An adaptation of the classic one point crossover op-
erator is used on the selected giant tours I1 and I2 at
Line 4 with function CROSSOVERGT, which yields
offspring I3. Recall that a giant tour is defined by a
sequence of nodes k and associated λ
p
(k) delivered
values for each product p ∈ P. For the nodes up to the
crossover point, λ
p
(k) values in I3 are the same as in
I1. After the crossover point, the λ
p
(k) values for the
nodes k duplicated from I2 are set so that invariant (9)
is satisfied. If there is not enough nodes for a given
order to satisfy its demand, nodes are duplicated at
the end until the invariant is satisfied. Then, at Line
5, the SPLIT operator is applied to obtain a set T of
tours (one for each store).
If tour T is incomplete (see reasons above), a
MILP-based repairing operator is used (Line 6).
Based on tour T , the repair operator searches to com-
pute a new feasible tour for each store with optimized
cost. Let ¯y the current assignment of orders to stores
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
442

Algorithm 2: Giant tour-based genetic algorithm.
1 Pop = InitPopGT (n);
2 while True do
3 I1, I2 =CHOOSEPARENTSGT(Pop);
4 I3 =CROSSOVERGT(I1, I2);
5 T =SPLIT(I3);
6 T =MILPREPAIR(T );
7 T =LOCALSEARCH(T );
8 I3 =GETGT(T );
9 Pop = Pop + I3;
10 if |Pop| > α then
11 Pop =SELECTSURVIVORSGT(Pop);
12 end
13 if it stale > β then
14 Pop =DIVERSIFYGT(Pop);
15 end
16 end
as stated by tour T such that ¯y
dm
= 1 if store m de-
livers at least a part of order d and ¯y
dm
= 0 if no part
of order d is delivered by store m. A new feasible
assignment of orders to stores is first computed by
solving a variant of multi order, multi product facility
location problem issued from MILP (1–8) while re-
placing the routing constraints by estimated removal
profits and insertion costs. Let T
m
denote the tour on
machine m and T
mk
for k = 1, . . . |T
m
| the kth order
visited by tour T
m
. The repair MILP has variables y
dm
and x
dmp
∈ {0, 1} for all d ∈ D, m ∈ M, d ∈ D and the
following objective and constraints.
min
∑
m∈M
∑
d∈D
¯y
dm
=0
c
+
md
y
dm
−
∑
m∈M
∑
d∈D
¯y
dm
=1
c
−
md
y
dm
(10)
subject to constraints (2–4), where
c
+
md
= min
k=1,...,|T
m
|−1
R
T
mk
d
+ R
dT
m,k+1
− R
T
mk
T
m,k+1
is the insertion cost of d (in the case where it is the
only order inserted in the tour on machine m) and
c
−
md
represents symmetrically the profit of removing
d from T
m
.
Then function MILPREPAIR, use the standard best
insertion algorithm to build the route of each store
given the orders assigned to the stores. A two-opt
local search algorithm (function LOCALSEARCH at
Line 7) further improves tours T . Finally, the gi-
ant tour offpring I3 is rebuilt by deriving the gi-
ant tour from the sequence of tours on T (function
GETGT). The SELECTSURVIVORSGT keeps the best
giant tours in the population up to a maximal number
α. The DIVERSIFYGT diversification function sim-
ply reinitializes part of the population randomly.
4.3 Cluster-first, Route Second
Approaches
Another common approach, in opposition to the giant
tour method, first selects the store assignments to cus-
tomers, then chooses the best routes for visits. The
idea is that once the allocation fixed, the problem is
reduced to an instance of the TSP for each store hav-
ing to visit customers to whom it was assigned. In
the worst case, each customer should be visited, but it
can be expected that in general a store will only visit
a small number of customers; and, due to the combi-
natorial nature of the problem, solving a set of small
problems is much faster than solving a single bigger
problem.
Cluster-first, Route-second Heuristic. In an arti-
cle by Fisher (Fisher and R.Jaikumar, 1981), a heuris-
tic of this type is proposed for the first time for a vari-
ant of the VRP and we adapt this method to our prob-
lem. It solves a general assignment problem to de-
termine the assignments and then solves the resulting
TSP. Intuitively, the problem of allocation resembles
the problem of clustering; indeed, if the sets of cus-
tomers to be visited are located around the stores, we
can hope that the associated routing is of good quality.
Among all the existing clustering criteria, we choose
to minimize the sum of the distances between cus-
tomers and their associated stores (potentially several)
such that the allocation is valid. This criterion has
the merit of being simple and of adapting well to the
strong constraints on stocks. Other criteria such as
minimizing the greatest distance between a customer
and a linked store are not adapted since if an assign-
ment happens to be necessary (for example in the case
where only one store has a given product) yielding
a high cost A, the assignment of other customers to
stores becomes indifferent to the cost as long as it is
less than A. Once the assignment of orders to stores
is made, we use the the MILP (1–8) with fixed vari-
ables y
dm
and x
pdm
, which amounts to solve |M| small
TSPs.
Hybrid Genetic Assignment Algorithm. In addi-
tion to the previously mentioned heuristic, another ge-
netic algorithm based on solving the underlying as-
signment problem is proposed (Algorithm 3). The so-
lutions (or individuals) are represented by a set of |M|
chromosomes, each corresponding to a store tour. The
population is initialized randomly (INITPOP), then,
at each iteration, two individuals are selected to be
crossed (function CHOOSEPARENTS). The classic
one point crossover operator is used on each of the
store tour pairs since it has the advantage of keeping
Multi-product, Multi-supplier Order Assignment and Routing for an e-Commerce Application in the Retail Sector
443

part of the parents’ route ( CROSSOVER). Each indi-
vidual offspring is not not always viable because of
the product stock in the stores and the MILPREPAIR
function is then used to repair the offspring.
The offspring is then inserted into the population.
If the population size exceeds a given threshold, a se-
lection procedure (SELECTSURVIVORS) determines
which individuals are deleted. To choose the sur-
vivors, we compare of course the solution scores, but
we also take into account their diversity, using a mea-
sure based on the average Hamming distance between
an individual and his closest neighbors. When the
search stagnates during a given number of iterations,
the population is diversified (DIVERSIFY). The op-
eration consists in destroying the current solutions by
removing certain visits before applying a random re-
pair of individuals. To do this, we use a random vari-
ant of MILPREPAIR.
Algorithm 3: Assignment based genetic algorithm.
1 Pop = INITPOP(n);
2 while True do
3 T 1, T 2 = CHOOSEPARENTS(Pop);
4 T 3 = CROSSOVER(T 1, T 2);
5 T 3 =MILPREPAIR(T 3);
6 T 3 =LOCALSEARCH(T 3);
7 Pop = Pop + T 3;
8 if |Pop| > α then
9 Pop =SELECTSURVIVORS(Pop);
10 end
11 if it stale > β then
12 Pop =DIVERSIFY(Pop);
13 end
14 end
5 PRELIMINARY
COMPUTATIONAL RESULTS
We compare the four solution methods (MILP us-
ing the IBM Cplex solver, Cluster-first heuristic,
Assignement-based Genetic algorithm, Giant tour-
based Genetic algorithm) on randomly generated
problem instances for given dimensions. Figure 5
presents the performances of the methods compared
to the best solution among the four. A single 15 min
run was performed for each algorithm. Each point
correspond to the average score on 3 instances of the
given size. So a score of 1 corresponds to the best
solution found and a score of 0.5 corresponds to a so-
lution twice as expensive.
As you would expect, The MILP formulation,
even if it finds the optimal solution for small in-
stances, is quickly outperformed when it comes to
solving larger instances. The assignment-based ge-
netic (named AG affectation in Fig. 5) algorithm is
more efficient than the one based on giant tours, es-
pecially for the larger instances with a realistic size
of 100 orders, 10 stores and 10 products. In third po-
sition, the assignment heuristic obtains surprisingly
honorable scores (about 1.25 times higher than the
best score). As parameter tuning was handcrafted and
only single runs were performed, these preliminary
computational experiments should be extended in the
future but they suggest good scaling properties of the
assignment-based genetic algorithm.
6 CONCLUSION
We have considered an industrial problem problem
consisting in finding the optimal allocation and rout-
ing of a set of customer orders to stores, a vari-
ant of the location routing problem / vehicle routing
problem with complicating constraints. We proposed
mixed-integer linear programming formulations and
several heuristics for the problem. Our hybrid genetic
algorithm based on assigning customers to store first
and routing the order second with MILP-based repair
operators showed good scaling properties on prelimi-
nary computational experiments. Regarding the rout-
ing problem, further improvements can be made in
the configuration of genetic algorithms. In particular,
the Split operator could be improved as in (Duhamel
et al., 2011). An idea to experiment would be not
to fix the quantities of products, but that each label
contains a MILP model, enriched with each alloca-
tion of a sub-tour, which determines the feasibility of
an assignment. A simple local search integrating the
cluster-first, route-second phases using combined tour
improvement neighborhoods and assignment neigh-
borhoods deserves also to be tested.
ACKNOWLEDGEMENTS
This research was carried out in the context of the
”One Stock Performance” project, funded by the
EASYNOV program (FEDER / Midi-Pyr
´
en
´
ees re-
gion), in partnership with DEVATiCS.
We also thank the anonymous referees for their
enlightening suggestions.
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
444
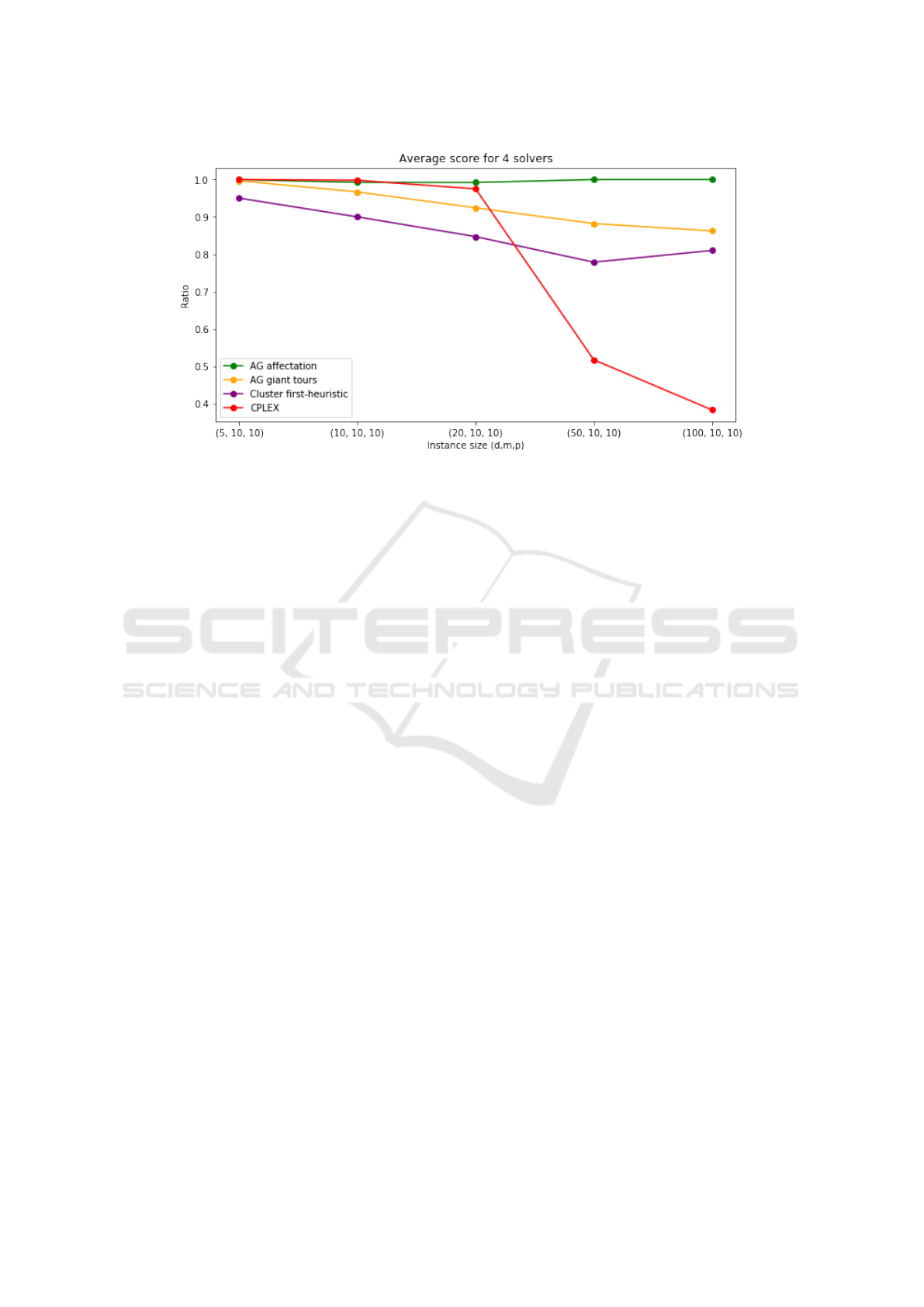
Figure 5: Performance of the different methods compared to the best solution.
REFERENCES
Abdulkader, M. M. S., Gajpal, Y., and ElMekkawy, T. Y.
(2018). Vehicle routing problem in omni-channel re-
tailing distribution systems. International Journal of
Production Economics, 196:43–55.
Beasley, J. (1983). Route first - cluster second methods for
vehicle routing. Omega, 11(4):403–408.
Boudia, M., Prins, C., and Reghioui, M. (2007). An effec-
tive memetic algorithm with population management
for the split delivery vehicle routing problem. In Inter-
national Workshop on Hybrid Metaheuristics, pages
16–30. Springer.
Duhamel, C., Lacomme, P., C.Prins, and C.Prodhon (2010).
A GRASPxELS approach for the capacitated location-
routing problem. Computers & Operations Research,
37(11):1912–1923.
Duhamel, C., Lacomme, P., and Prodhon, C. (2011). Com-
puters & Operations Research, 38(4):723–739.
Fisher, M. and R.Jaikumar (1981). A generalized as-
signment heuristic for vehicle routing. Networks,
11(2):109–124.
Martins, L. d. C., Bayliss, C., Juan, A. A., Panadero, J.,
and Marmol, M. (2020). A savings-based heuristic
for solving the omnichannel vehicle routing problem
with pick-up and delivery. Transportation Research
Procedia, 47:83–90.
Prins, C. (2004). A simple and effective evolutionary algo-
rithm for the vehicle routing problem. Computers and
Operations Research.
Vidal, T., Crainic, T., Gendreau, M., and Prins, C. (2013).
Heuristics for multi-attribute vehicle routing prob-
lems: A survey and synthesis. European Journal of
Operational Research, 231(1):1–21.
Vidal, T., Crainic, T., Gendreau, M., and Prins, C. (2014a).
Implicit depot assignments and rotations in vehicle
routing heuristics. European Journal of Operational
Research, 237(1):15–28.
Vidal, T., Crainic, T., Gendreau, M., and Prins, C. (2014b).
A unified solution framework for multi-attribute ve-
hicle routing problems. European Journal of Opera-
tional Research, 234(3):658–673.
Multi-product, Multi-supplier Order Assignment and Routing for an e-Commerce Application in the Retail Sector
445
