
Single-image Background Removal with Entropy Filtering
Chang-Chieh Cheng
a
Information Technology Service Center, National Chiao Tung University, 1001 University Road, Hsinchu, Taiwan
Keywords:
Background Removal, Segmentation, Entropy, Texture Analysis.
Abstract:
Background removal is often used for segmentation of the main subject from a photograph. This paper pro-
poses a new method of background removal for a single image. The proposed method uses Shannon entropy
to quantify the texture complexity of background and foreground areas. A normalized entropy filter is applied
to compute the entropy of each pixel. The pixels can be classified effectively if the entropy distributions of
the background and foreground can be distinguished. To optimize performance, the proposed method con-
structs an image pyramid such that most background pixels can be labeled in a low-resolution image; thus, the
computational cost of entropy calculation can be reduced in the image with the original resolution. Connected
component labeling is also adopted for denoising to retain the main subject area completely.
1 INTRODUCTION
Background removal is a digital image processing
procedure that can be used to classify parts of an im-
age in terms of unwanted and interest regions. Many
applications of image processing and computer vi-
sion require background removal before further anal-
ysis and processing. For example, object segmenta-
tion within a single photograph requires background
removal (Chen et al., 2016). Background removal
also can be applied to a series of images including
videos and images taken from different views. For
example, background removal can be applied for fore-
ground object extraction from videos (Kumar and Ya-
dav, 2016) and 3D object reconstruction from multi-
view images (Gordon et al., 1999)(Tsai et al., 2007).
Since multiple images can provide more information
regarding backgrounds than a single image can, re-
moving backgrounds from multiple images may be
more accurate than removing a single background
from a single image.
This paper proposes a method of background re-
moval for a single image (BRSI). The fundamental
method of BRSI is the intensity-based region method
(IBR), which classifies pixels according to their back-
ground and foreground intensities. One commonly
used IBR method is the thresholding-based (TB)
method, which uses a specified intensity value as a
threshold and classifies pixels as background if their
intensities are less than the threshold (Gonzalez and
a
https://orcid.org/0000-0002-9103-3400
Woods, 2006). The TB method can be improved by
histogram-based (HB) background removal (Gonza-
lez and Woods, 2006), which constructs an intensity
histogram from an image to find the intensity range
of the background with the maximum bin count of
the histogram. Therefore, the pixels belong to the
background if their intensity values are in the spec-
ified intensity range. Although the implementation of
IBR is easy, misclassification occurs if the intensity
distribution of the background is so wide that decid-
ing the threshold and intensity range of background
is difficult. Nevertheless, the HB method can be im-
proved by intensity clustering. K-means clustering
(Zhang and Luo, 2012) and Gaussian mixture mod-
els (GMMs) (Huang and Liu, 2007) are commonly
used methods for finding K clusters from a set of data.
Therefore, the intensities in an image can be divided
into several groups by using K-means or GMMs. The
background intensity value is decided by the mean of
the most common group. However, clustering may
fail if the intensities of background are distributed
over a wide range.
In recent years, many machine learning tech-
niques, such as the support vector machine (Wang
et al., 2011) and random forest (Schroff et al., 2008),
have been used for BRSI. A convolutional neural net-
work (CNN), which is an artificial neural network
with multiple convolution layers, can be used for seg-
mentation of interesting regions from an image (Ron-
neberger et al., 2015). However, for high-accuracy
classification, most methods of machine learning re-
Cheng, C.
Single-image Background Removal with Entropy Filtering.
DOI: 10.5220/0010301204310438
In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 4: VISAPP, pages
431-438
ISBN: 978-989-758-488-6
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
431

quire large training sets and incur expensive compu-
tational costs in the training phase.
Texture-based segmentation (TEX), a popular
method of images segmentation, segments an image
into several areas with different degrees of texture.
However, TEX requires an appropriate texture anal-
ysis. A commonly used method of texture analysis is
histogram-based texture analysis (HTA), which cre-
ates a histogram to describe the texture around each
pixel. One simple HTA method evaluates the proba-
bility of occurrence of each intensity (Junqing Chen
et al., 2005). Texon is an efficient method of HTA
that creates a histogram of oriented gradients (HOG)
to describe the orientation and complexity of the re-
gion around a pixel (Malik et al., 2001). In informa-
tion theory, Shannon entropy (Shannon, 2001) is often
used to evaluate the complexity of a data set. Several
studies have reported that the Shannon entropy can be
used for image segmentation (Zhang et al., 2003)(Qi,
2014).
This paper proposes an efficient approach to BRSI
based on TEX with Shannon entropy to classify fore-
ground and background areas that have different com-
plexities of texture. The proposed approach uses the
pyramid method (Adelson et al., 1983) to evaluate
the texture complexity in a multiscale representation
of the input image. Connected component labeling
(CCL) (He et al., 2017) is then applied to eliminate
the noisy areas that consist of small fragments and
holes. The following statements briefly describe the
proposed approach: First, an image pyramid structure
is created to represent the input image with different
levels of detail. A filter of normalized Shannon en-
tropy is then used to analyze the complexity of pixels
from the lowest level, that is, the top of pyramid. Dur-
ing texture analysis, each pixel is classified as back-
ground if its entropy is less than a given threshold.
Therefore, the pixels in the higher level can be classi-
fied as background without the texture analysis only
if they can be covered by the background pixels in the
lower level. In the other words, pixels only require
texture analysis if they are covered by nonbackground
pixels of the lower level. After the pixel classification
of each layer, CCL then is applied to eliminate the
noisy areas.
The remainder of this paper is organized as fol-
lows. The Methods section presents the details of the
proposed method, including filtering using normal-
ized Shannon entropy, texture analysis in the image
pyramid, and background classification. The Results
section presents the experimental results from testing
on three colorful photographs. Finally, the Discussion
section presents a summary and discussion.
2 METHOD
The proposed BRSI method consists of four proce-
dures: entropy filtering, background mapping, image
pyramid construction, and denoising. They are re-
spectively detailed in the following four subsections.
2.1 Entropy Filtering
Given an image I(x, y) comprising M × N pixels,
where x ∈ {1, 2,. . . , M} and y ∈ {1, 2, . .. , N}, if the
values of all pixels of I are categorized into B inten-
sities (i.e. I(x, y) ∈ {t
1
,t
2
, . . . ,t
B
} for all x and y), the
Shannon entropy, H, is defined as follows:
H(I) = −
B
∑
i=1
P(t
i
)log
β
P(t
i
), (1)
where P(t
i
) is the probability of t
i
occurring in I.
H is zero if all pixels of I are of a single intensity;
otherwise, H > 0. Notice that H is maximized if
P(t
i
) =
1
B
, ∀i; that is,
maxH(I) = −
B
∑
i=1
1
B
log
β
1
B
= −B(B
−1
log
β
B
−1
)
= log
β
B.
If β = B, H then can be normalized to [0, 1]. Let
ˆ
H be
the normalized Shannon entropy defined as follows:
ˆ
H(I) = −
B
∑
i=1
P(t
i
)log
B
P(t
i
), (2)
where 0 ≤
ˆ
H ≤ 1;
ˆ
H can then be used as a normalized
kernel for image filtering. Given a window with
ˆ
M
columns and
ˆ
N rows, the equation of filtering with I
can be written as follows:
ˆ
I(x, y) =
ˆ
H(C(I, x, y)), (3)
where
ˆ
I is the filtered image of I and C crops a subim-
age of
ˆ
M ×
ˆ
N pixels around I(x, y). Notice that if B is
specified as a large number, the filtering may be sen-
sitive to noise (Knuth, 2006)(Purwani et al., 2017).
However, a small value of B may cause the loss of
certain significant details. This paper suggests that B
can be set as an integer between 16 and 64.
2.2 Background Mapping
The values of
ˆ
I can be separated by a threshold τ,
where 0 ≤ τ ≤ 1. Therefore, the pixel at (x, y) is clas-
sified as background if
ˆ
I(x, y) < τ; otherwise, the pixel
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
432
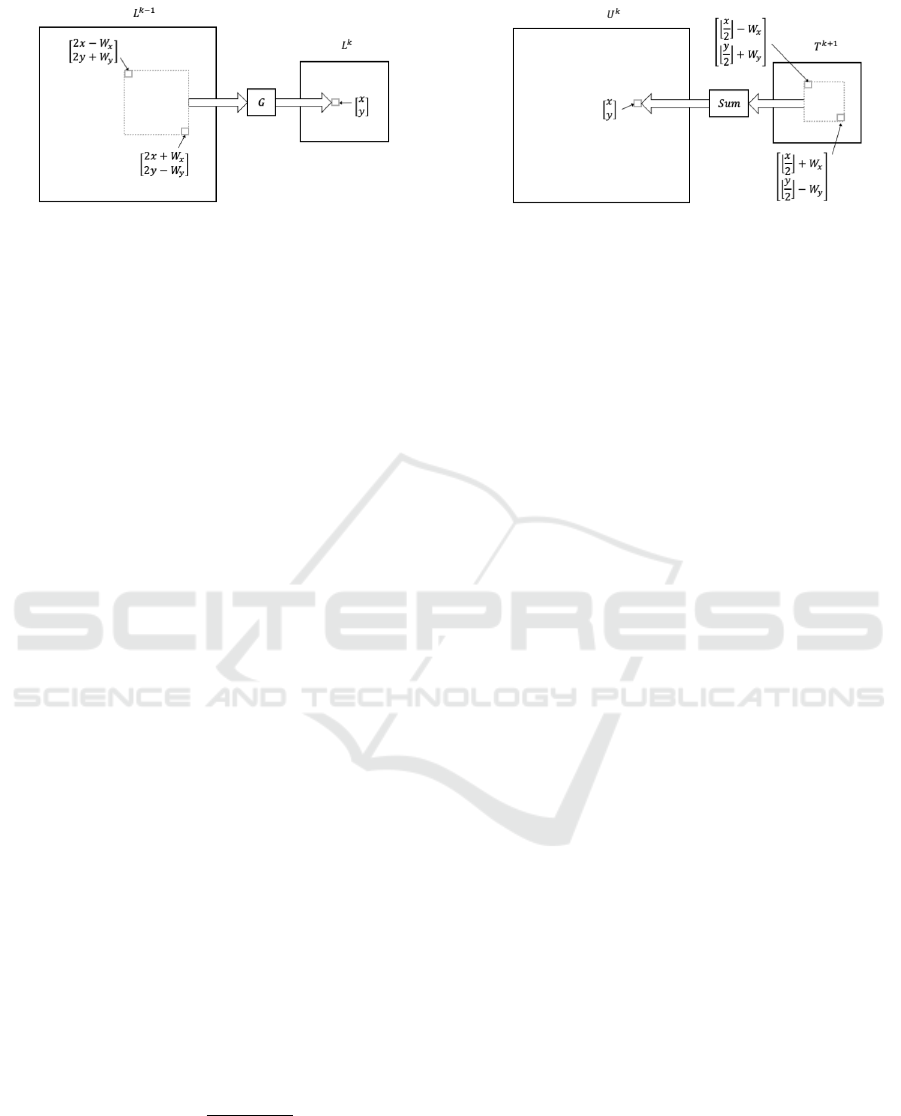
Figure 1: Constructing L
k
.
is classified as foreground. Then, we can create a bi-
nary mapping table, T , to categorize each pixel.
T (x, y) =
0 if
ˆ
I(x, y) < τ;
1 otherwise.
(4)
However, creating T requires the calculation of
ˆ
I, as
in Eq. (3), which may require excessive computa-
tion time if the size of I is large. Let I
0
be the half-
size image of I. Assuming that I
0
has similar textures
to I, the calculation of texture complexity around a
pixel I(x, y) can be approximately ignored if I(x, y) is
covered by the pixels of I
0
with texture complexities
lower than τ. We then can construct an image pyra-
mid comprising several image layers to express I at
different resolutions. Therefore, T can be efficiently
determined from the top layer (lowest resolution) to
the bottom layer (highest resolution). The following
subsection describes the acceleration of T estimation
by constructing an image pyramid.
2.3 Image Pyramid Construction
An image pyramid L of K layers constructed
from I can be expressed as Fig. 1, where
k = {1, 2, . . . , K}, x ∈ {1, 2, . . . , b2
−(k−1)
Mc}, y ∈
{1, 2, . . . , b2
−(k−1)
Nc}, L
1
= I, and G is a low-pass
filter of size (2W
x
+ 1) × (2W
y
+ 1) pixels, for exam-
ple, a 5 ×5 Gaussian filter. Feature enhancement pro-
cessing can be applied to I before the construction of
the pyramid, for example, such as the Sobel opera-
tor for edge detection. Notably, K can be regarded as
the number of downsampling iterations. However, in-
formation may be lost if excessive downsampling is
performed, that is, if K is large. This paper decides K
according to the following condition:
K ≤ log
2
min(M, N)
N
s
, (5)
where N
s
is a given constant to represent the minimum
size of downsampling. Typically, N
s
is specified as
128 or 64.
Figure 2: Constructing U
k
.
We then can apply the entropy filter to L by the
following equation:
ˆ
L
k
(x, y) =
ˆ
H(C(L
k
, x, y)) if U
k
(x, y) ≥ λ
or k = K;
0 otherwise,
(6)
where constructing U
k
(x, y) is shown in Fig. 2 and
T
k
(x, y) =
0 if
ˆ
L
k
(x, y) < τ;
1 otherwise.
(7)
Notice that U
k
(x, y) represents the number of corre-
sponding foreground pixels of (x, y) in layer k + 1.
According to Eq. 6, only the top layer, that is, k = K,
requires that
ˆ
H be applied to all pixels. In the other
layers, that is, k < K, the calculation of entropy,
ˆ
H(C(L
k
, x, y)), depends on whether U
k
(x, y) is larger
than a given constant λ. In other words, pixel (x, y)
of layer k can be classified as background without
a calculation of entropy if U
k
(x, y) < λ. Therefore,
the background mapping table of the bottom layer,
T
1
(x, y), does not require the calculation of
ˆ
H for all
pixels and the construction of the masking table can
be accelerated, especially when the background area
is larger than the foreground area.
2.4 Denoising
We now have a binary mapping table to classify each
pixel of I as background or foreground. However,
many small fragments and holes may be generated in
the foreground and background. To address this prob-
lem, we use CCL to label each set of adjacent pixels
with the same value in a binary image. Given two
constants, α
f
and α
h
, for the area thresholds of frag-
ments and holes, respectively, let Q(T, α
f
, α
h
) be the
CCL function and
(A
f
, A
h
) = Q(T, α
f
, α
h
), (8)
where A
f
= {a
f
|a
f
is a set of adjacent foreground
pixels and |a
f
| ≤ α
f
; and A
h
= {a
h
|a
h
is a set of ad-
jacent background pixels and |a
h
| ≤ α
h
}. Therefore,
Single-image Background Removal with Entropy Filtering
433
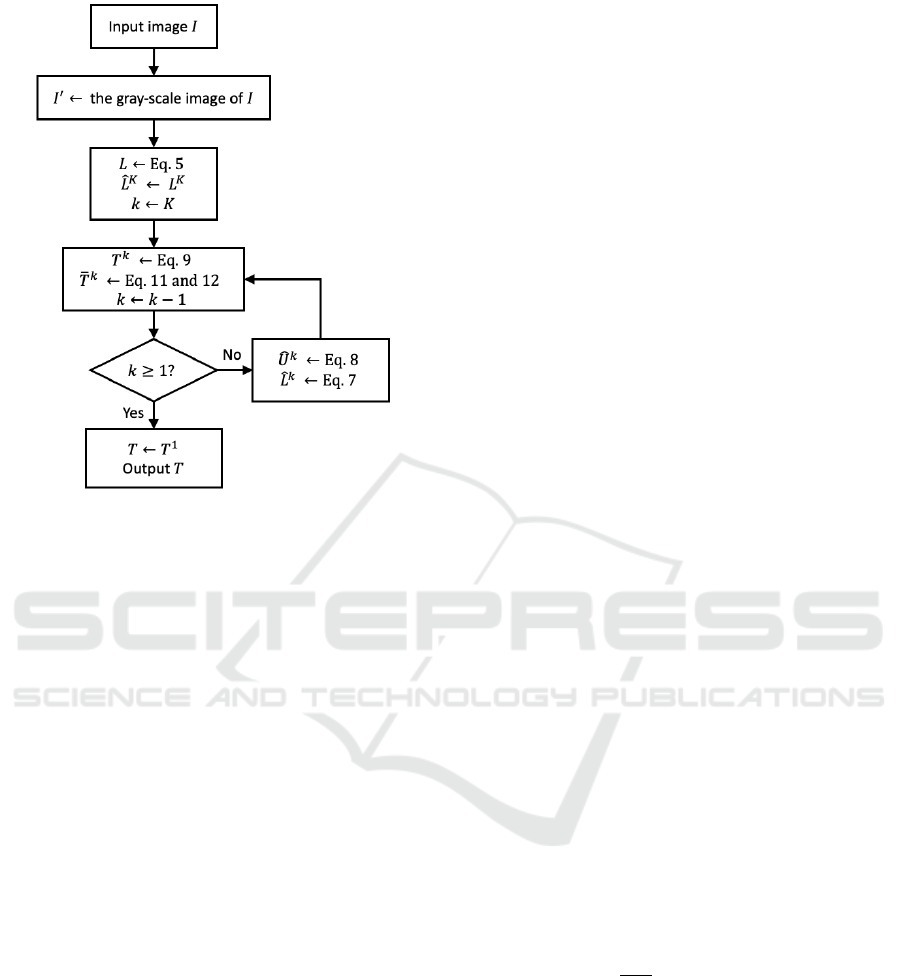
Figure 3: Flowchart of the proposed method.
we can replace T
k
with
¯
T
k
, which is calculated as fol-
lows.
¯
T
k
(x, y) =
0 (x, y) ∈ a
k
f
⊂ A
k
f
;
1 (x, y) ∈ a
k
h
⊂ A
k
h
;
T
k
(x, y) otherwise.,
(9)
where k < K and
(A
k
f
, A
k
h
) = Q(T
k
, α
f
, α
h
). (10)
Notice that the computation cost of Q, which includes
time and memory consumption, may be high if the
image is large. However, many improvement meth-
ods have been proposed to address this problem; for
example, the two-scan approach to label an N ×N im-
age with complexity O(N
2
) (He et al., 2009), and us-
ing parallel computing hardware to accelerate label-
ing (Soman et al., 2010).
The values of α
f
and α
h
can be determined based
on the image size. The experiments described in the
next section indicate that the value of α
f
ranges from
1% to 10% of the image size, and the value α
h
ranges
from 10% to 20% of the image size.
Finally, the proposed method is summarized as a
flowchart as shown in Fig. 3. The parameters are
suggested as follows: B = 64,
ˆ
M = 5,
ˆ
N = 5, 0.2 ≤
τ ≤ 0.3, K = 3,W
x
= 1,W
y
= 1, λ = 5, α
f
= 0.05, and
α
h
= 0.2.
3 RESULTS
The proposed method was implemented in C++ using
the Qt library. The executable file is named EBR and
can be downloaded from https://people.cs.nctu.edu.
tw/
∼
chengchc/ebr/. EBR was validated by numerous
images. This section describes three tests with three
different themes images, which were Girl (USC-SIPI,
), Birds (Kodak, ), and Lighthouse(Kodak, ), as shown
in Fig. 4. Each test image has at least one foreground
subject. The test results demonstrated that these fore-
ground subjects could be segmented with few errors
by EBR. The test machine consisted of an Intel i7-
7700 CPU and 32GB RAM. The test platform was
Windows 10 64-bit.
The first test image was Girl with size 256 × 256
pixels. The foreground is a half-length image of a girl.
The test involved manually creating a binary mapping
image denoted by T
g1
to be the ground truth, as shown
in Fig. 5e. In the mapping image, the intensities
of 1 (white) and 0 (black) represent the foreground
and background respectively. Fig. 5a shows the result
of removing the background from Fig. 5e. This test
also used the HB method to remove the background
of Girl, as shown in Fig. 5b and Fig. 5f; Fig. 5f is the
mapping image denoted by T
h1
. EBR then was used
for Girl. Fig. 5c and 5g show the results of back-
ground removal and the mapping image (T
n1
) gener-
ated by EBR without denoising, respectively, where
B = 64,
ˆ
M = 3,
ˆ
N = 3, τ = 0.25, K = 3, W
x
= 1,
W
y
= 1, and λ = 5. Notice that the 3 × 3 Gaussian fil-
tering with a standard deviation of 1.0 and Sobel edge
detection were used before the proposed method was
applied. However, many obvious fragments and holes
appeared in the results. Therefore, EBR was executed
with α
f
= 0.05 and α
h
= 0.2 for denoising. The ex-
ecution time was 0.167 s. Fig. 5d and 5h show the
result and the mapping image, T
e1
,respectively. For
comparison of EBR with the ground truth and HB
method, mean square error (MSE) was calculated as
follows.
MSE(T
a
, T
b
) =
1
MN
N
∑
y=1
M
∑
x=1
(T
a
(x, y) − T
b
(x, y))
2
.
(11)
Because T is a binary mapping image, meaning that
the value of any pixel in T is either 0 or 1, MSE is
an appropriate measurement of error. MSE(T
h1
, T
g1
),
MSE(T
n1
, T
g1
), and MSE(T
e1
, T
g1
) were 0.124, 0.167,
and 0.015, respectively. For Girl, the error rates of
HB and the proposed method were 12.4% and 1.5%,
respectively.
Fig. 6 shows the process of EBR at each level. The
images in the top row of Fig. 6, which are 6a, 6b,
and 6c, show
ˆ
L
3
,
ˆ
L
2
, and
ˆ
L
1
(Eq. 6), respectively. In
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
434

(a) (b) (c)
Figure 4: Test images: (a) Girl, (b) Birds, , and (c) Lighthouse.
(a) (b) (c) (d)
(e) (f) (g) (h)
Figure 5: Results of Girl. (a) Ground truth. (b) Result of the HB method. (c) Result of EBR without denoising. (d) Result of
EBR with denoising. (e),(f),(g),(h) Mapping images of (a),(b),(c),(d), respectively.
each level, the areas of head, body, and outline contain
the pixels with high entropy. However, the entropies
of the background pixels are near 0. Therefore, the
threshold of entropy, τ, can be a small value (approx-
imately 0.25). Fig. 6d, 6e, and 6f show the mapping
images without denoising, which are T
3
, T
2
, and T
1
(Eq. 7), respectively. The denoised mapping images,
¯
T
3
,
¯
T
2
, and
¯
T
1
(Eq. 9), are shown in Fig. 6g, 6h, and
6i, respectively. As shown in Fig. 6d, the sizes of the
noise areas in T
3
are small, approximately 1 to 30
pixels. These noise of T
2
and T
1
are nearly covered
by the noise of T
3
, and EBR could massively reduce
the noise in T
3
. Therefore, the computational cost of
denoising T
2
and T
1
could also be reduced.
The second test image, Birds, is a colorful photo-
graph measuring 768 × 512 pixels. The foreground
objects of Birds are two parrots. Fig. 7a and 7e
show the results of manual background removal and
its mapping image (T
g2
), respectively. Because the
background of Birds has a wide intensity range, re-
moving the background through the HB method is
difficult, as shown in Fig. 7b. The mapping image
(T
h2
) generated by the HB method is shown in Fig. 7f.
Next, EBR was applied to Birds. Fig. 7c and Fig.
7g show the results of background removal and the
mapping image (T
n2
) generated by EBR without de-
noising, respectively, where B = 64,
ˆ
M = 5,
ˆ
N = 5,
τ = 0.4, K = 3, W
x
= 1, W
y
= 1, and λ = 5. Before
the execution of the proposed method, Birds was pro-
cessed through 5 × 5 Gaussian filtering with a stan-
dard deviation of 1.0 and Sobel edge detection. EBR
was then executed with α
f
= 0.01 and α
h
= 0.2 for
denoising. The execution time was 1.07 s. Fig. 7d
and 7h show the results and mapping image (T
e2
),
respectively. As shown in Fig. 7g and 7h, most
pixels in background could be removed by EBR ex-
cept the pixels in the regions where the brightness
changes drastically. MSE(T
h2
, T
g2
), MSE(T
n2
, T
g2
),
and MSE(T
e2
, T
g2
) were 0.419, 0.254, and 0.013, re-
spectively. Therefore, EBR could remove the back-
ground of Birds, with a small error rate of 1.3%.
Fig. 8 shows the process of applying EBR to
Birds. Fig. 8a, 8b, 8c show
ˆ
L
3
,
ˆ
L
2
, and
ˆ
L
1
, respec-
tively. Fig. 8d, 8e, and 8f show the mapping images
without denoising: T
3
, T
2
, and T
1
, respectively. Be-
cause the texture of the background of Birds is more
complicated than that of Girl, many background pix-
els could not be removed in T
3
. However, the en-
Single-image Background Removal with Entropy Filtering
435

(a) (b) (c) (d) (e) (f)
(g) (h) (i)
Figure 6: Classification results at each level for Girl. (a),(b),(c) Images filtered by the normalized entropy filter. (d),(e),(f)
Mapping images without denoising. (g),(h),(i) Mapping images with denoising. (a),(d),(g) k = 3. (b),(e),(h) k = 2. (c),(f),(i)
k = 1.
(a) (b) (c) (d)
(e) (f) (g) (h)
Figure 7: Results of Birds. (a) Ground truth. (b) Result of HB. (c) Result of EBR without denoising. (d) Result of EBR with
denoising. (e),(f),(g),(h) Mapping images of (a),(b),(c),(d), respectively.
tropies of most background pixels were lower than the
entropies of the pixels in the outlines and textures of
the two parrots. Numerous background pixels could
be removed in T
1
so that only the outlines and tex-
tures of the two parrots were retained. Therefore, ap-
plying EBR with denoising could complete the bodies
of the parrots, as shown in shown in Fig. 8g, 8h, and
8i (
¯
T
3
,
¯
T
2
, and
¯
T
1
), respectively.
The third test image was Lighthouse, which is a
colorful landscape photograph of size 512 × 768 pix-
els. Fig. 9 shows the test results. This test demon-
strated that EBR can remove the background from
a landscape photograph if the texture complexities
of the background and foreground are different. In
Lighthouse, only the pixels in the sky area belong to
the background; the other pixels belong to the fore-
ground. Fig. 9a and 9d are the results of manual
background removal and the mapping image (T
g3
), re-
spectively. The result and mapping image (T
h3
) gen-
erated by the HB method are shown in Fig. 7b and
Fig. 9e, respectively. The HB method classified the
pixels with high intensity as foreground; however,
many background pixels with high intensity were also
classified as foreground. Fig. 9c and 9f present the re-
sult and mapping image (T
e3
), respectively, generated
by EBR with denoising, where B = 32,
ˆ
M = 5,
ˆ
N = 5,
τ = 0.3, K = 3, W
x
= 1, W
y
= 1, λ = 5, α
f
= 0.05, and
α
h
= 0.1. The 5× 5 Gaussian filtering with a standard
deviation of 1.0 and Sobel edge detection were also
applied before the execution of the proposed method.
The execution time was 1.09 s. MSE(T
h3
, T
g3
) and
MSE(T
e3
, T
g3
) were 0.501 and 0.004, respectively.
Therefore, EBR removed the background of Light-
house with an error rate of 0.4%.
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
436

(a) (b) (c) (d) (e)
(f) (g) (h) (i)
Figure 8: Classification results at each level for Birds. (a),(b),(c) Images filtered by the normalized entropy filter. (d),(e),(f)
Mapping images without denoising. (g),(h),(i) Mapping images with denoising. (a),(d),(g) k = 3. (b),(e),(h) k = 2. (c),(f),(i)
k = 1.
(a) (b) (c) (d) (e) (f)
Figure 9: Results of Lighthouse. (a) Ground truth. (b) Result of HB method. (c) Result of EBR with denoising. (d),(e),(f)
Mapping images of (a),(b,)(c), respectively.
4 CONCLUSION
This paper presents a method of background removal
for a single image. The proposed method uses nor-
malized entropy filtering to compute the texture com-
plexities of the foreground and background. The
background can be successfully removed if the en-
tropy distributions of the foreground and background
have little overlap.
The proposed method constructs a pyramid to ac-
celerate the computation because substantial back-
ground area can be detected in the top level of the
pyramid and the entropy computing of this detected
background can be ignored in other levels. Many
noise areas, including fragments and holes, can be re-
duced through CCL in the top level to minimize the
computing of CCL in the other levels.
Graphical processing unit (GPU) implementation
is a topic for future work. The proposed method con-
sists of three main procedures: pyramid construction,
normalized entropy filtering, and CCL. These proce-
dures are appropriate for GPU implementation; the
performance of the proposed method can reach real-
time performance.
The proposed method requires that the textures of
foreground and background be different. An ideal
case is the first test image, Girl, which has no over-
lap between the entropy ranges of the foreground and
background. In other cases, the proposed method may
fail. To address this problem, a clustering method,
such as color- or geometry-based clustering, can be
applied to the original image such that the foreground
can be approximately segmented. The proposed
method then can subtly remove the background. Pa-
rameter selection is another challenger with the pro-
posed method. Although the parameters of the pro-
posed method can be easily decided if the image was
photographed using a shallow depth of field, creating
general guidelines to decide the parameters is diffi-
cult. This problem can be addressed by a machine
learning model or artificial neural network to find an
optimal set of parameters automatically.
In summary, the proposed method of background
removal is efficient for an image if its foreground and
background have different texture complexities. The
experimental results demonstrate that the proposed
method can successfully remove background pixels
with low entropy and retain foreground pixels with
Single-image Background Removal with Entropy Filtering
437

high entropy. The results also demonstrate that the
computation time of the proposed method is reason-
able. An image of 768 × 512 pixels can be processed
in approximately 1 s without any parallel computing
for acceleration.
ACKNOWLEDGMENTS
This work was sponsored by the Ministry of Science
and Technology, Taiwan (109-2221-E-009-142-).
REFERENCES
Adelson, E., Anderson, C., Bergen, J., Burt, P., and Ogden,
J. (1983). Pyramid methods in image processing. RCA
Eng., 29.
Chen, T., Zhu, Z., Hu, S.-M., Cohen-Or, D., and Shamir, A.
(2016). Extracting 3d objects from photographs using
3-sweep. Communications of the ACM, 59:121–129.
Gonzalez, R. and Woods, R. (2006). Digital Image Process-
ing (3rd Edition). Prentice-Hall, Inc.
Gordon, G., Darrell, T., Harville, M., and Woodfill, J.
(1999). Background estimation and removal based on
range and color. In Proceedings. 1999 IEEE Com-
puter Society Conference on Computer Vision and
Pattern Recognition (Cat. No PR00149), volume 2,
pages 459–464 Vol. 2.
He, L., Chao, Y., Suzuki, K., and Wu, K. (2009). Fast
connected-component labeling. Pattern Recognition,
42:1977–1987.
He, L., Ren, X., Gao, Q., Zhao, X., Yao, B., and Chao,
Y. (2017). The connected-component labeling prob-
lem: A review of state-of-the-art algorithms. Pattern
Recognition, 70.
Huang, Z.-K. and Liu, D.-H. (2007). Segmentation of color
image using em algorithm in hsv color space. In 2007
International Conference on Information Acquisition,
pages 316–319.
Junqing Chen, Pappas, T. N., Mojsilovic, A., and Rogowitz,
B. E. (2005). Adaptive perceptual color-texture image
segmentation. IEEE Transactions on Image Process-
ing, 14(10):1524–1536.
Knuth, K. (2006). Optimal data-based binning for his-
tograms. arXiv.
Kodak. The kodak image dataset.
Kumar, S. and Yadav, J. (2016). Video object extraction and
its tracking using background subtraction in complex
environments. Perspectives in Science, 8.
Malik, J., Belongie, S., Leung, T., and Shi, J. (2001). Con-
tour and texture analysis for image segmentation. In-
ternational Journal of Computer Vision, 43:7–27.
Purwani, S., Supian, S., and Twining, C. (2017). Analyzing
the effect of bin-width on the computed entropy. Jour-
nal of Informatics and Mathematical Sciences, 9(4).
Qi, C. (2014). Maximum entropy for image segmentation
based on an adaptive particle swarm optimization. Ap-
plied Mathematics & Information Sciences, 8:3129–
3135.
Ronneberger, O., Fischer, P., and Brox, T. (2015). U-
net: Convolutional networks for biomedical im-
age segmentation. In Medical Image Computing
and Computer-Assisted Intervention – MICCAI 2015,
pages 234–241. Springer International Publishing.
Schroff, F., Criminisi, A., and Zisserman, A. (2008). Object
class segmentation using random forests. In Proceed-
ings of the British Machine Vision Conference, pages
54.1–54.10. BMVA Press.
Shannon, C. E. (2001). A mathematical theory of commu-
nication. SIGMOBILE Mob. Comput. Commun. Rev.,
5(1):3–55.
Soman, J., Kothapalli, K., and Narayanan, P. (2010). Some
gpu algorithms for graph connected components and
spanning tree. Parallel Processing Letters, 20:325–
339.
Tsai, Y.-P., Ko, C.-H., Hung, Y.-P., and Shih, Z.-C. (2007).
Background removal of multiview images by learning
shape priors. IEEE transactions on image processing
: a publication of the IEEE Signal Processing Society,
16:2607–16.
USC-SIPI. The usc-sipi image database.
Wang, x. y., Wang, T., and Bu, J. (2011). Color image
segmentation using pixel wise support vector machine
classification. Pattern Recognition, 44:777–787.
Zhang, H., Fritts, J. E., and Goldman, S. A. (2003). An
entropy-based objective evaluation method for image
segmentation. In Storage and Retrieval Methods and
Applications for Multimedia.
Zhang, Y. and Luo, L. (2012). Background extraction al-
gorithm based on k-means clustering algorithm and
histogram analysis. volume 2, pages 66–69.
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
438
