Statistical Inference of the Inter-sample Dice Distribution for
Discriminative CNN Brain Lesion Segmentation Models
Kevin Raina
a
Department of Mathematics and Statistics, University of Ottawa, Ontario, Canada
Keywords:
Uncertainty, Brain Lesions, MRI, Segmentation Sampling, Convolutional Neural Network, Discriminative.
Abstract:
Discriminative convolutional neural networks (CNNs), for which a voxel-wise conditional Multinoulli distri-
bution is assumed, have performed well in many brain lesion segmentation tasks. For a trained discriminative
CNN to be used in clinical practice, the patient’s radiological features are inputted into the model, in which
case a conditional distribution of segmentations is produced. Capturing the uncertainty of the predictions can
be useful in deciding whether to abandon a model, or choose amongst competing models. In practice, how-
ever, we never know the ground truth segmentation, and therefore can never know the true model variance. In
this work, segmentation sampling on discriminative CNNs is used to assess a trained model’s robustness by
analyzing the inter-sample Dice distribution on a new patient solely based on their magnetic resonance (MR)
images. Furthermore, by demonstrating the inter-sample Dice observations are independent and identically
distributed with a finite mean and variance under certain conditions, a rigorous confidence based decision
rule is proposed to decide whether to reject or accept a CNN model for a particular patient. Applied to the
ISLES 2015 (SISS) dataset, the model identified 7 predictions as non-robust, and the average Dice coefficient
calculated on the remaining brains improved by 12 percent.
1 INTRODUCTION
Discriminative CNNs, such as those constructed by
(Kamnitsas et al., 2017; Havaei et al., 2017; Ron-
neberger et al., 2015), have consistently ranked on the
top of the leaderboard in many brain lesion segmen-
tation challenges (Maier et al., 2017; Winzeck et al.,
2018; Bakas et al., 2018). Commonly, they are formu-
lated by assuming a voxel-wise Multinoulli distribu-
tion, conditional on the MRI intensities of neighbor-
ing voxels where the parameters are obtained and es-
timated with a CNN. For the case of 2 labels, if x
j
de-
notes the 3D MRI intensities used in the prediction of
voxel j over a discrete domain Ω ⊂ R
3
, Y
j
represents
the random label at voxel j, and Θ are the parameters
of a CNN architecture, then the model is formulated
as
Y
j
|x
j
∼ Bernoulli(π
j
= CNN(Θ, x
j
)). (1)
At prediction time, the translational invariance prop-
erty of the CNN allows for a fast way to estimate
all the voxel-wise conditional distributions, without
a
https://orcid.org/0000-0002-6240-9675
having to separately feed their respective covariates.
When a model is fully trained, the parameters in (1)
are replaced with an estimate:
ˆ
Θ. In this way, dis-
criminative CNNs are capable of sampling segmenta-
tions by sampling the associated label at each voxel,
conditionally independent of each other. Despite this
source of variability, a decision rule of selecting the
label with the highest probability is often applied ren-
dering the segmentation deterministic.
Measuring the performance variation of trained
discriminative CNNs in brain lesion segmentation
on a patient by patient basis can help clinical prac-
titioners instill a degree of confidence in the use
of automated segmentation methods. One metric
of model performance is the Dice coefficient (Dice,
1945; Sørensen, 1948), which measures the similar-
ity between two 3D voxel-wise labeled images: S
1
and S
2
. The Dice coefficient is a real number in [0, 1]
given by
Dice(S
1
, S
2
) =
2T P
2T P +FN + FP
, (2)
where a value of 0 indicates no overlap and a value
of 1 indicates perfect similarity. TP, FP and FN re-
fer to the number of true positive, false positive, and
168
Raina, K.
Statistical Inference of the Inter-sample Dice Distribution for Discriminative CNN Brain Lesion Segmentation Models.
DOI: 10.5220/0010286201680173
In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 2: BIOIMAGING, pages 168-173
ISBN: 978-989-758-490-9
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

false negative voxels in the medical image respec-
tively. Formulating this incentive mathematically, if
D denotes the Dice coefficient random variable which
incorporates randomness across patients, and across
model segmentations, and x collects all the covariates
in (1) across all voxels in the image for the patient to
from a high dimensional vector, then the interest lies
in measuring the model variance
Var(D|x,
ˆ
Θ). (3)
Here the Dice random variable is theoretically mea-
sured on the true segmentation, which is never known,
and the random segmentations produced by a trained
discriminative CNN model on the particular patient.
Intuitively, the observations of D can be generated
by: observing a new random patient whose radiolog-
ical features are drawn independently from other pa-
tients, randomly generating a segmentation from the
trained discriminative CNN given their radiological
features, and calculating the Dice coefficient against
the ground truth. In (3), the first source of variation is
eliminated by conditioning on the patient. Estimating
(3) can also help suggest the complete abandonment
of an algorithm in favor of another, as some CNNs
may be better tuned to deal with specific brain lesion
characteristics like small lesion volume.
Despite these advantages, some brain lesion seg-
mentation challenges compute variability in the Dice
metric across patient predictions (Maier et al., 2017).
Moreover, for a particular patient, only a single de-
terministic segmentation is produced by some deci-
sion rule. That is, Var(D|
ˆ
Θ) becomes the measure
to be estimated, but this estimate does not solely ac-
count for model variability. It is important to note this
measure is unconditional on the patient’s radiological
features, and thus inherently incorporates additional
variability. The merit of this metric is in its applica-
bility, as not all segmentation algorithm are capable of
sampling segmentations. However in the case of dis-
criminative CNNs, by its very nature, this metric can
solely be used to quantify variation in the Dice coef-
ficient across patients and could completely discard a
model that may in fact perform well on certain kinds
of patients. Another disadvantage is that this metric
is obtained from the training set, and then must be
generalized to arbitrary cases, which may present sig-
nificant differences. Analysis of model performance
variance on a single patient (3), conditional on their
radiological features, eliminates these extra sources
of variation, and can be more useful in clinical prac-
tice by providing specialized patient care.
One step towards this direction was taken in the
BraTS 2019 challenge, which is an extension of
(Bakas et al., 2018). In particular, voxel-wise mea-
sures of segmentation uncertainty ranging from 0 to
100 were calculated from 3D MRIs for all patients
individually. Then, at specified thresholds, uncer-
tain voxels were filtered out in the calculation of the
Dice coefficient. Depending on the structure of un-
certainties, this method can reward or penalize the
Dice score, but this can never be confirmed in practice
since we never know the ground truth segmentation.
Segmentation sampling and consequent analysis
of the inter-sample Dice distribution has been under-
taken for generative models, for instance, by L
ˆ
e et
al. (L
ˆ
e et al., 2016). In their work, they use a Gaus-
sian process to produce segmentation samples based
on a single expert manual segmentation of grade 4
gliomas. The mean of the inter-sample Dice distribu-
tion and variability of the segmentations can be con-
trolled by a single model parameter. The samples can
then be used in radiotherapy planning by delivering
radiation to certain voxels and avoiding dose to un-
certain voxels, where perhaps there are more sensitive
tissues.
The contribution mentions the applicability of
their method in evaluating uncertainty in the per-
formance of segmentation algorithms, by repeatedly
sampling segmentations off the ground truth and cal-
culating the variability against a deterministic pre-
dicted segmentation. Though this method can be ap-
plied to arbitrary segmentation algorithms, the source
of variation is not produced by the model predictions,
as in the case of discriminative CNNs. As a conse-
quence, the method is effective in assessing the effec-
tiveness of a particular segmentation produced from a
model, but not the model itself. Another related work
by Roy et al. (Roy et al., 2018), shows that the inter-
sample Dice coefficient correlates with Dice perfor-
mance using a discriminative CNN for the segmen-
tation of brain scans from children with psychiatric
disorders (CANDI-13 dataset), and suggests it as a
measure for quantifying uncertainty.
In this proposed work, the inter-sample Dice ob-
servations are shown to be independent and iden-
tically distributed samples from a distribution with
finite variance and mean, under certain conditions.
Segmentations are sampled directly from a discrim-
inative CNN. The mean with a confidence interval of
the inter-sample Dice distribution is then estimated by
the central limit theorem and used in place of (3) to
decide on whether to reject or accept the CNN model
on patients with ischemic stroke. This chapter is or-
ganized as follows: Section 2 describes the methods,
Section 3 presents the results, and a discussion fol-
lows in Section 4.
Statistical Inference of the Inter-sample Dice Distribution for Discriminative CNN Brain Lesion Segmentation Models
169

2 METHODS
2.1 Architecture
The CNN architecture considered is Wider2DSeg,
which was originally constructed by Kamnitsas et al.
(Kamnitsas et al., 2017) and is a two dimensional
variant of their 3D deepMedic architecture. Raina
et al. (Raina. et al., 2020) tuned this architecture
in conjunction with additional symmetry covariates
obtained from a reflective registration step to yield a
0.62 Dice coefficient over a 7-fold cross validation on
the ISLES 2015 SISS dataset. All the implementation
details in this work are exactly as in the Wider2DSeg
implementation of Raina et al. (Raina. et al., 2020)
with nonlinear symmetry covariates.
2.2 Segmentation Sampling
Referencing equation (1), suppose there are V voxels
in an image. The attention is restricted to the case of 2
voxel labels, though this analysis can extend to an ar-
bitrary finite number of labels. Let S ∈ {0, 1}
V
repre-
sent the segmentation random vector of a trained dis-
criminative CNN model, where each element S
k
= Y
j
,
for unique j ∈ Ω. The segmentation vector is un-
conditional and incorporates randomness across pa-
tients. Although in what follows it does not matter
which permutation in the assignment of voxels to ar-
ray elements is used, the assignment must be chosen
and fixed. Then, denote x as the patient’s radiologi-
cal features as formulated in equation (3), and
ˆ
Θ as
the estimated parameters of the CNN. Segmentations
can be sampled conditional on a patient’s radiologi-
cal features if conditional independence is assumed
across voxels. In this case, the distribution is com-
pletely known by
S|x ∼ p(s; x,
ˆ
Θ) =
V
∏
j=1
π
j
(x
j
,
ˆ
Θ)
s
j
(1 − π
j
(x
j
,
ˆ
Θ))
1−s
j
.
(4)
2.3 Inter-sample Dice Distribution
Let S
∗
1
and S
∗
2
represent two iid model segmentation
random vectors for a given patient, each distributed
according to (4). By independence, the joint distribu-
tion of these samples is given by
(S
∗
1
, S
∗
2
) ∼ p(s
∗
1
;x,
ˆ
Θ)p(s
∗
2
;x,
ˆ
Θ). (5)
In this way, the inter-sample Dice random variable is
just a function of the random vectors. In particular,
if S
∗
2
is seen as the ground truth, then the Dice coeffi-
cient of S
∗
1
can be computed against it, and vice-versa.
Define Γ to be the inter-sample Dice random variable.
Then
Γ = Dice(S
∗
1
, S
∗
2
). (6)
In fact, the complete distribution of Γ can be ob-
tained, but can be quite computationally expensive
as the number of voxels are often large. That is,
if D
(·)
represents the support of a random variable,
then |D
S
∗
1
| ≤ 2
V
, where the upper bound is obtained
by having 0 < π
j
< 1 for all voxels in the image.
By independence of S
∗
1
and S
∗
2
, this further implies
that |D
(S
∗
1
,S
∗
2
)
| ≤ 2
2V
. Subsequently, after applying the
Dice transformation (6) which may at most associate
a unique Dice value for each element in D
(S
∗
1
,S
∗
2
)
, the
inequality |D
Γ
| ≤ 2
2V
is obtained. Hence, computing
the exact Dice distribution may require the calcula-
tion of at most 2
2V
probabilities, where V tends to be
in the millions. Though, since D
Γ
is bounded by 2
2V
,
Γ has a discrete distribution with a finite and count-
able support.
In order to conduct statistical inference on E[Γ] it
must also be finite, however, this is not the case. No-
tice that if (S
∗
1
, S
∗
2
) = (0, 0), Γ is undefined, and this
outcome always has a non-zero probability. In fact,
this is the only way for Γ to be undefined. To correct
this, two necessary modifications are introduced: 1)
∃ π
j
6= 0, for some j and 2) The inter-sample Dice
random variable is redefined as
Γ
∗
= Γ|(S
∗
1
, S
∗
2
) 6= (0, 0). (7)
The first condition ensures that (0, 0) can never be the
only sample generated, thereby permitting its removal
and still retaining a distribution through the redefini-
tion in the second condition. The second condition
redefines the inter-sample Dice random variable to
be conditional on all samples drawn from (5) except
(0, 0). Now, ∀γ ∈ D
Γ
∗
, 0 ≤ γ ≤ 1, where D
Γ
∗
6=
/
0.
Then
E[(Γ
∗
)
2
] < ∞. (8)
As a consequence, sampling observations from
this distribution, and estimating its mean from a sam-
ple can be used. Independent and identically dis-
tributed pairs of segmentations can be sampled from
(5), and can generate an iid sample of inter-sample
Dice observations. To adjust for the second modifi-
cation, any (0, 0) sample, or equivalently undefined
Dice score, is removed in the sampling phase. More-
over, since the inter-sample Dice distribution has a fi-
nite mean and variance, the central limit theorem can
be applied, and associated confidence intervals can be
constructed.
BIOIMAGING 2021 - 8th International Conference on Bioimaging
170

Computationally, this method can be undertaken
by first producing the estimated probability tensors.
At each voxel in the probability tensor are the esti-
mated label probabilities obtained from the features
and CNN parameter estimates. Once this tensor is cal-
culated, segmentations are sampled by sampling from
the associated Multinoulli distribution and iterating
over all voxels. Naturally, these will produce segmen-
tation samples that can be appropriately viewed as
such since the format of the probability tensors align
with that of the actual image.
2.4 Decision Rule
Let γ
1
, .., γ
n
be an iid sample of realized inter-sample
Dice coefficients for a given patient, and construct
a (1 − α)% approximate confidence interval, based
on the central limit theorem. For a specified thresh-
old, reject the use of a discriminative CNN model on
a patient if the confidence interval is entirely below
the threshold. In this manner, the clinician can jus-
tify with (1 − α)% confidence that the true mean of
the inter-sample Dice distribution is below the given
threshold, and appropriate actions to reject the model
in favor of another can be undertaken.
3 EXPERIMENTS AND RESULTS
3.1 Dataset
The discriminative CNN model is trained and eval-
uated on the ISLES2015 (SISS) training data, which
consists of 28 patients with sub-acute ischemic stroke.
The radiological features x for a patient are 4 MR se-
quences: FLAIR, DWI, T1 and T1-contrast. Each im-
age has a total of 230 × 230 × 154 voxels. At each
voxel, there are only two possible labels classes: le-
sion or non-lesion.
3.2 Efficacy of Decision Rule
The proposed segmentation sampling based decision
rule is applied to the results of Raina et al. (Raina.
et al., 2020), which yielded an average Dice coef-
ficient (predicted against ground truth) of 0.62 over
a 7-fold cross-validation from single deterministic
segmentations obtained by selecting the label with
the highest probability. For each fold in the cross-
validation and for each brain in the validation fold,
30 inter-sample Dice observations are sampled, and
The central limit theorem confidence interval is com-
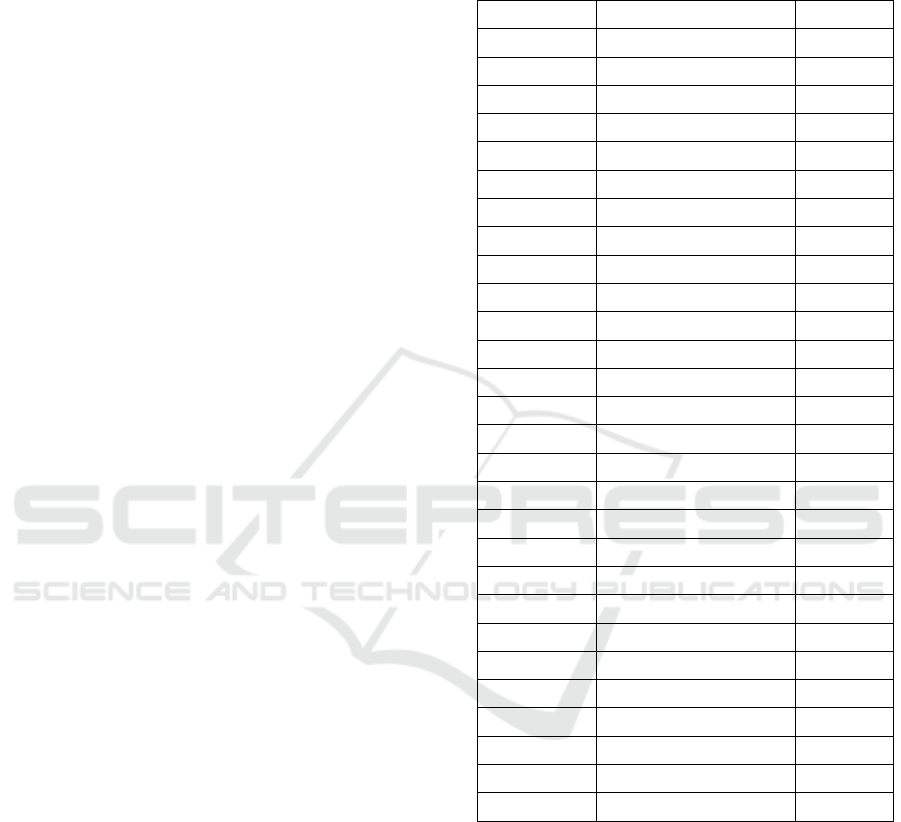
puted. Table 1 displays the patient by patient results.
The Pearson correlation between mean ISD and Dice
Table 1: Case by case hypothesis testing for Wider2dSeg
on ISLES2015 SISS. The inter-sample Dice confidence in-
terval is computed using the central limit theorem with 30
samples. The bolded rows indicate rejecting the use of the
CNN on the patient as per the decision rule.
Patient No. ISD confidence Dice
1 0.940339 ± 0.000116 0.866798
2 0.955828 ± 0.000243 0.815299
3 0.897922 ± 0.001002 0.736231
4 0.946641 ± 0.000122 0.797607
5 0.944956 ± 0.000133 0.857821
6 0.965364 ± 0.000146 0.905630
7 0.943856 ± 0.000178 0.822416
8 0.909659 ± 0.000349 0.702697
9 0.969197 ± 0.000076 0.854602
10 0.875187 ± 0.000340 0.592438
11 0.933384 ± 0.000399 0.775896
12 0.888211 ± 0.000810 0.517170
13 0.850324 ± 0.001449 0.277828
14 0.980536 ± 0.000095 0.815283
15 0.974488 ± 0.000179 0.887611
16 0.580227 ± 0.004708 0.009584
17 0.508344 ± 0.005390 0.164190
18 0.949571 ± 0.000435 0.730066
19 0.730039 ± 0.003967 0.487031
20 0.950651 ± 0.000441 0.795393
21 0.687765 ± 0.003033 0.434674
22 0.863127 ± 0.000823 0.685439
23 0.754482 ± 0.002522 0.634320
24 0.861986 ± 0.001278 0.507946
25 0.916227 ± 0.001130 0.761670
26 0.598502 ± 0.006355 0.191637
27 0.824157 ± 0.000633 0.000156
28 0.887825 ± 0.001183 0.732581
over the 28 patients was computed to be r = 0.81. Fig-
ure 1 plots the mean ISD against Dice score for each
patient, and depicts the fitted regression line. The
threshold was set to 0.85 with reference to the regres-
sion line in Figure 1, and corresponds to a Dice score
of 0.60. In addition, the confidence level is 95%. By
removing the rejected predictions, the average Dice
coefficient increased from 0.62 to 0.74.
Statistical Inference of the Inter-sample Dice Distribution for Discriminative CNN Brain Lesion Segmentation Models
171

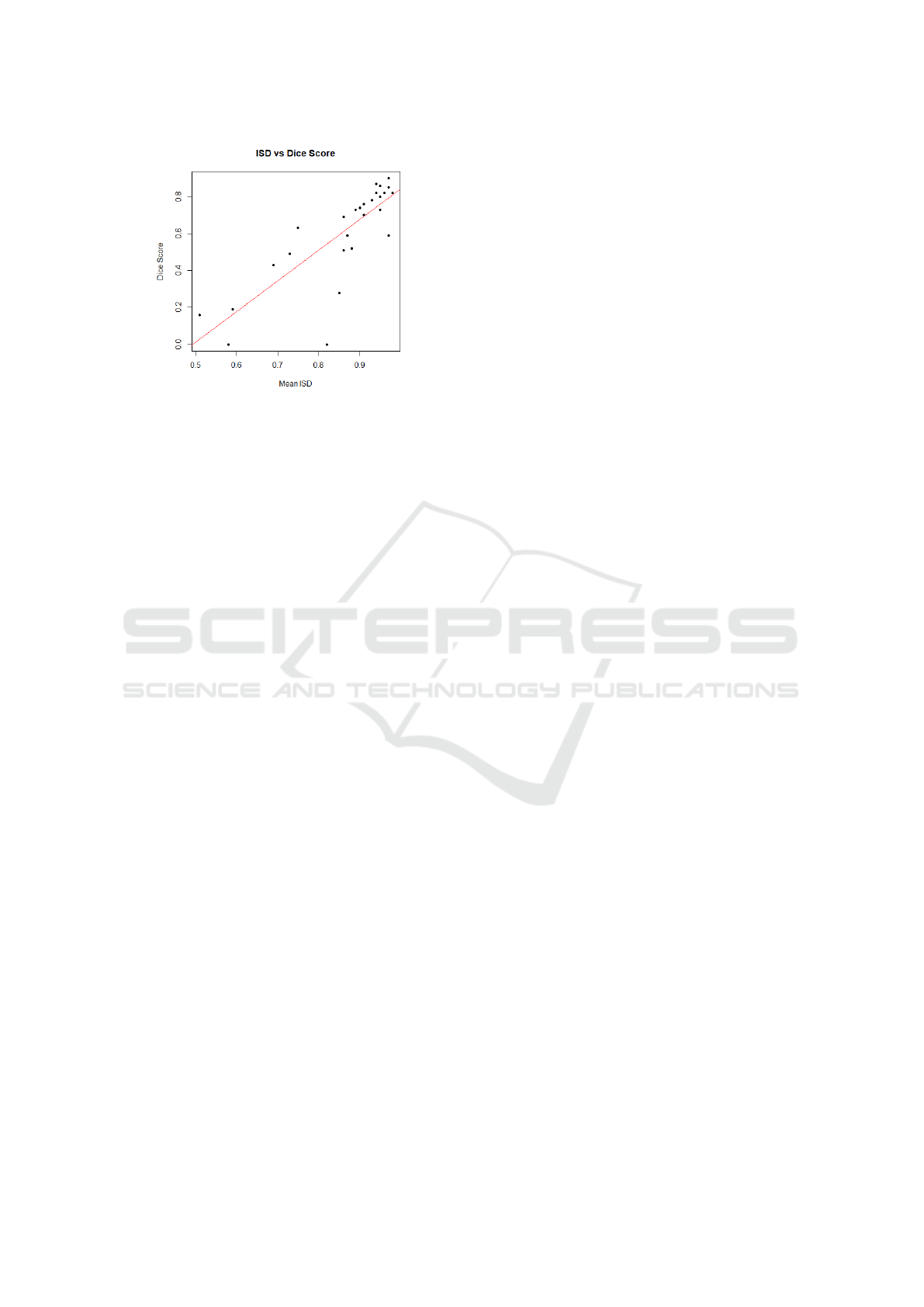
Figure 1: Plot of mean ISD against Dice score with regres-
sion line: y = 1.66x − 0.82, where y is Dice score and x is
mean ISD. The F-test yielded a p-value of 1.4× 10
−7
.
4 DISCUSSION
The reason as to why ISD is highly correlated to
Dice performance for discriminative CNNs, and can
be used to detect weak segmentations is not entirely
clear. As a counter-example, consider a model that
always predicts P(lesion) = 0 for all but one voxel,
which instead has P(lesion) = 1. Then, the ISD
would always be 1, since the model produces exactly
the same segmentation with probability 1, regardless
of the input. However, it would be unexpected to
see a high Dice score for this model. The coupling
of CNN outputs and ISD for detecting uncertain seg-
mentations requires further investigation for a deeper
understanding of its performance.
One important remark is that the Dice metric can
be substituted by other metrics such as the sensitivity,
specificity, mean squared error, or precision and the
preceding analysis would also follow for these distri-
butions, thereby permitting hypothesis testing. More-
over, the computations considered in this work were
over the entire brain, but could also be calculated on
specific regions of interest (ROIs). Deciding on which
metrics to use, and applying them to more detailed
brain sub-regions could improve the decision-making
potential, and is a possible area of development.
Another point to remark is that the proposed
method can be used to rigorously test competing dis-
criminative models based on their respective inter-
sample mean Dice confidence intervals, and select
the most robust one on an individualized patient ba-
sis. Applying this unifying technique for all compet-
ing CNNs in a brain lesion challenge may exhibit the
best possible performance, without any consideration
to the ground truth. Segmentation challenges have re-
cently begun to incorporate uncertainty analysis, but
further work is required to apply these techniques on
various types of brain lesion structures.
REFERENCES
Bakas, S., Reyes, M., Jakab, A., Bauer, S., Rempfler,
M., Crimi, A., Shinohara, R. T., Berger, C., Ha,
S. M., Rozycki, M., et al. (2018). Identifying
the best machine learning algorithms for brain tu-
mor segmentation, progression assessment, and over-
all survival prediction in the brats challenge. arXiv
preprint:1811.02629.
Dice, L. R. (1945). Measures of the amount of ecologic
association between species. Ecology, 26(3):297–302.
Havaei, M., Davy, A., Warde-Farley, D., Biard, A.,
Courville, A., Bengio, Y., Pal, C., Jodoin, P.-M., and
Larochelle, H. (2017). Brain tumor segmentation
with deep neural networks. Medical image analysis,
35:18–31.
Kamnitsas, K., Ledig, C., Newcombe, V. F., Simpson,
J. P., Kane, A. D., Menon, D. K., Rueckert, D., and
Glocker, B. (2017). Efficient multi-scale 3D CNN
with fully connected CRF for accurate brain lesion
segmentation. Medical image analysis, 36:61–78.
L
ˆ
e, M., Unkelbach, J., Ayache, N., and Delingette, H.
(2016). Sampling image segmentations for uncertai-
nty quantification. Medical image analysis, 34:42–51.
Maier, O., , B. H., von der Gablentz, J., H
¨
ani, L., Heinrich,
M. P., Liebrand, M., Winzeck, S., Basit, A., Bentley,
P., Chen, L., et al. (2017). ISLES 2015 - a public eval-
uation benchmark for ischemic stroke lesion segmen-
tation from multispectral MRI. Medical image analy-
sis, 35:250–269.
Raina., K., Yahorau., U., and Schmah., T. (2020). Ex-
ploiting bilateral symmetry in brain lesion segmen-
tation with reflective registration. In Proceedings of
the 13th International Joint Conference on Biomed-
ical Engineering Systems and Technologies - Vol-
ume 2: BIOIMAGING,, pages 116–122. INSTICC,
SciTePress.
Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net:
Convolutional networks for biomedical image seg-
mentation. In International Conference on Medical
image computing and computer-assisted intervention,
pages 234–241. Springer.
Roy, A. G., Conjeti, S., Navab, N., and Wachinger, C.
(2018). Inherent brain segmentation quality con-
trol from fully convnet monte carlo sampling. In
International Conf. on Medical Image Computing
and Computer-Assisted Intervention, pages 664–672.
Springer.
Sørensen, T. J. (1948). A method of establishing groups of
equal amplitude in plant sociology based on similarity
of species content and its application to analyses of
the vegetation on Danish commons. I kommission hos
E. Munksgaard.
Winzeck, S., Hakim, A., McKinley, R., Pinto, J. A., Alves,
V., Silva, C., Pisov, M., Krivov, E., Belyaev, M.,
BIOIMAGING 2021 - 8th International Conference on Bioimaging
172

Monteiro, M., et al. (2018). ISLES 2016 and 2017-
benchmarking ischemic stroke lesion outcome predic-
tion based on multispectral MRI. Frontiers in neurol-
ogy, 9.
Statistical Inference of the Inter-sample Dice Distribution for Discriminative CNN Brain Lesion Segmentation Models
173