On the Prediction of a Nonstationary Bernoulli Distribution
based on Bayes Decision Theory
Daiki Koizumi
a
Otaru University of Commerce, 3–5–21, Midori, Otaru-city, Hokkaido, 045–8501, Japan
Keywords:
Probability Model, Bayes Decision Theory, Nonstationary Bernoulli Distribution, Hierarchical Bayesian
Model.
Abstract:
A class of nonstationary Bernoulli distribution is considered in terms of Bayes decision theory. In this nonsta-
tionary class, the Bernoulli distribution parameter follows a random walking rule. Even if this general class is
assumed, it is proved that the posterior distribution of the parameter can be obtained analytically with a known
hyper parameter. With this theorem, the Bayes optimal prediction algorithm is proposed assuming the 0-1 loss
function. Using real binary data, the predictive performance of the proposed model is evaluated comparing to
that of a stationary Bernoulli model.
1 INTRODUCTION
Binary data is popular subject for data analysis and
is a topic of frequent research (Cox, 1970). From
the perspective of Bayesian statistics, the stationary
Bernoulli distribution and the stationary binomial dis-
tribution are frequently used to deal with binary data
(Press, 2003) (Bernardo and Smith, 2000) (Berger,
1985). For Bayesian posterior parameter estimation
under the stationary Bernoulli and binomial distribu-
tions, one of the most reasonable approaches is to as-
sume the beta distribution as the prior of the param-
eter. This assumption drastically reduces the compu-
tational cost of obtaining the posterior distribution of
the parameter using the Bayes theorem, and this prior
is called the natural conjugate (Bernardo and Smith,
2000) (Berger, 1985).
In contrast, there have been many approaches to
generalize the stationarity of the parameter by consid-
ering certain aspects of the nonstationarity of the pa-
rameter. In general, assuming the nonstationarity of
parameters requires additional parameters compared
to the stationary model. Furthermore, if the Bayesian
approach is used, it is often difficult to save computa-
tional cost when obtaining the posterior of the param-
eter. This point depends on the class of nonstationar-
ity of the parameter, and one important result is the
SPSM, Simple Power Steady Model (Smith, 1979), to
the best of author’s knowledge. Under SPSM, it is
a
https://orcid.org/0000-0002-5302-5346
guaranteed that the posterior of the parameter can be
obtained analytically. Similar aspects were discussed
from the generalized perspective of the Kalman filter
(Harvey, 1989). Some researchers have tried to apply
this result to the discrete probability distributions and
proposed predictive algorithms (Koizumi et al., 2009)
(Koizumi, 2020) (Koizumi et al., 2012) (Yasuda et al.,
2001). Koizumi et al. assumed a nonstationary Pois-
son distribution and proposed the Bayes optimal pre-
diction algorithm under the known nonstationary hy-
per parameter (Koizumi et al., 2009). Koizumi re-
cently generalized this prediction algorithm to the
credible interval prediction (Koizumi, 2020). They
obtained better predictive performance compared to
a stationary Poisson distribution with real web traffic
data. They also assumed a nonstationary Bernoulli
distribution to predict SQL injection attacks in the
field of network security (Koizumi et al., 2012). How-
ever, they defined an incorrect class of nonstationary
parameters. Furthermore, they did not show any proof
that the posterior parameter distribution was analyti-
cally obtained under their nonstationary model. Ya-
suda et al. assumed a similar nonstationary Bernoulli
distribution and proposed the Bayes optimal predic-
tion algorithm under the known nonstationary hyper
parameter (Yasuda et al., 2001). However, they did
not present any proof that the posterior parameter dis-
tribution can be obtained analytically under the non-
stationary model again.
In this paper, a class of nonstationary Bernoulli
distribution is proposed. This class has only one ad-
Koizumi, D.
On the Prediction of a Nonstationary Bernoulli Distribution based on Bayes Decision Theory.
DOI: 10.5220/0010270709570965
In Proceedings of the 13th International Conference on Agents and Artificial Intelligence (ICAART 2021) - Volume 2, pages 957-965
ISBN: 978-989-758-484-8
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
957

ditional hyper parameter to express the nonstationar-
ity of the Bernoulli parameter. Moreover, the pre-
diction problem is considered under the proposed
nonstationary Bernoulli distribution. Bayes decision
theory (Weiss and Blackwell, 1961) (Berger, 1985)
(Bernardo and Smith, 2000) is a powerful theoret-
ical framework to define the prediction error. In
terms of Bayes decision theory, the predictive esti-
mator that minimizes the average predictive error is
called the Bayes optimal prediction. Considering this
point, this paper proposes the Bayes optimal predic-
tion algorithm under a certain class of nonstation-
ary Bernoulli distribution, if the nonstationary hyper
parameter is known. The predictive performance of
the proposed algorithm was evaluated with real bi-
nary data. When considering real data, the above-
mentioned hyper parameter should be estimated. For
this purpose, this study takes the empirical Bayesian
approach, and the objective parameter is estimated by
the approximate maximum likelihood estimation with
numerical calculation.
The remainder of this paper is organized as fol-
lows. Section 2 provides the basic definitions of
the nonstationary Bernoulli distribution, and some
lemmas and corollaries in terms of the hierarchical
Bayesian modeling approach. Section 3 begins with
the basic definitions in terms of Bayes decision the-
ory, then proves the main theorems of the proposed
nonstationary Bernoulli distribution, discusses the hy-
per (nonstationary) parameter estimation, and pro-
poses the Bayes optimal prediction algorithm. Sec-
tion 4 gives some numerical examples with real bi-
nary data. Section 5 discusses the results. Section 6
concludes this paper.
2 HIERARCHICAL BAYESIAN
MODELING WITH
NONSTATIONARY BERNOULLI
DISTRIBUTION
2.1 Preliminaries
Let t = 1, 2, .. . be a discrete time index and X
t
= x
t
be a discrete random variable at t. Assume that
x
t
∈
{
0, 1
}
and X
t
∼ Bernoulli (θ
t
) where 0 ≤ θ
t
≤ 1
is a nonstationary parameter. Then the probability
function of the nonstationary Bernoulli distribution
p

x
t


θ
t

is defined as the following:
Definition 2.1. Nonstationary Bernoulli Distribution
p

x
t


θ
t

= θ
x
t
t
(1 − θ
t
)
1−x
t
, (1)
where 0 ≤ θ
t
≤ 1. 2
Definition 2.2. Function for Θ
t
, A
t
and B
t
Let Θ
t
= θ
t
, A
t
= a
t
, and B
t
= b
t
be random vari-
ables where A
t
and B
t
are mutually independent, then
a function for Θ
t
is defined as,
Θ
t
=
A
t
A
t
+ B
t
, (2)
where 0 < a
t
, 0 < b
t
. 2
Definition 2.3. Nonstationarity of A
t
, B
t
Let C
t
= c
t
, D
t
= d
t
be random variables, then the
nonstationary functions for A
t
and B
t
are defined as,
A
t+1
= C
t
A
t
, (3)
B
t+1
= D
t
B
t
, (4)
where 0 < c
t
< 1, 0 < d
t
< 1 and they are sampled
from the following two types of Beta distributions:
C
t
∼ Beta [kα
t
, (1 − k) α
t
] , (5)
D
t
∼ Beta [kβ
t
, (1 − k) β
t
] , (6)
where k is a real valued constant and 0 < k ≤ 1 . 2
Definition 2.4. Conditional Independence for A
t
,C
t
(or B
t
, D
t
) under α
t
(or β
t
)
p

a
t
, c
t


α
t

= p

a
t


α
t

p

c
t


α
t

, (7)
p

b
t
, d
t


β
t

= p

b
t


β
t

p

d
t


β
t

. (8)
2
Definition 2.5. Initial Distributions for A
1
, B
1
A
1
∼ Gamma(α
1
, 1) , (9)
B
1
∼ Gamma(β
1
, 1) , (10)
where 0 < α
1
and 0 < β
1
. 2
Definition 2.6. Initial Distributions for C
1
, D
1
C
1
∼ Beta [kα
1
, (1 − k)α
1
] , (11)
D
1
∼ Beta [kβ
1
, (1 − k)β
1
] . (12)
2
Definition 2.7. Gamma Distribution for q Gamma
distribution of Gamma(r, s) is defined as,
p

q


r, s

=
s
r
Γ(r)
q
r−1
exp(−sq) , (13)
where 0 < q, 0 < r, 0 < s, and Γ(r) is the gamma func-
tion defined in Definition 2.9. 2
Definition 2.8. Beta Distribution for q
Beta distribution of Beta (r, s) is defined as,
p

q


r, s

=
Γ(r + s)
Γ(r) Γ(s)
q
r−1
(1 − q)
s−1
, (14)
where 0 < q < 1, 0 < r, 0 < s. 2
Definition 2.9. Gamma Function for q
Γ(q) =
Z
+∞
0
y
q−1
exp(−y)dy , (15)
where 0 < q . 2
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
958

2.2 Lemmas
Lemma 2.1. Transformed Distribution for A
t
For any t ≥ 1, the transformed random variable
A
t+1
= C
t
A
t
in Definition 2.3 follows the following
Gamma distribution:
A
t+1
∼ Gamma(kα
t
, 1) . (16)
2
Proof of Lemma 2.1.
See APPENDIX A. 2
Lemma 2.2. Transformed Distribution for B
t
For any t ≥ 1, the transformed random variable
B
t+1
= D
t
B
t
in Definition 2.3 follows the following
Gamma distribution:
B
t+1
∼ Gamma(kβ
t
, 1) . (17)
2
Proof of Lemma 2.2.
The proof is exactly same as Lemma 2.1, replac-
ing A
t+1
by B
t+1
, C
t
by D
t
, and α
t
by β
t
.
This completes the proof of Lemma 2.2. 2
Lemma 2.3. Transformed Distribution for Θ
t
For any t ≥ 2, the transformed random variable
Θ
t
=
A
t
A
t
+B
t
in Definition 2.2 follows the following
Beta distribution:
Θ
t
∼ Beta (kα
t−1
, kβ
t−1
) . (18)
2
Proof of Lemma 2.3.
See APPENDIX B. 2
Corollary 2.1. Transformed Initial Distribution for
Θ
1
The transformed random variable Θ
1
=
A
1
A
1
+B
1
in
Definition 2.2 follows the following Beta distribution:
Θ
1
∼ Beta (α
1
, β
1
) . (19)
2
Proof of Corollary 2.1.
From Definition 2.5,
A
1
∼ Gamma(α
1
, 1) ,
B
1
∼ Gamma(β
1
, 1) .
If Lemma 2.3 is applied to the above A
1
and B
1
, then
the following holds.
Θ
1
∼ Beta (α
1
, β
1
) . (20)
This completes the proof of Corollary 2.1. 2
3 PREDICTION ALGORITHM
BASED ON BAYES DECISION
THEORY
3.1 Preliminaries
Definition 3.1. Loss Function
L (ˆx
t+1
, x
t+1
) =
(
0 if ˆx
t+1
= x
t+1
;
1 if ˆx
t+1
6= x
t+1
.
(21)
2
Definition 3.2. Risk Function
R( ˆx
t+1
, θ
t+1
)
=
1
∑
x
t+1
=0
L (ˆx
t+1
, x
t+1
) p

x
t+1


θ
t+1

, (22)
where p

x
t+1


θ
t+1

is from Definition 2.1. 2
Definition 3.3. Bayes Risk Function
BR( ˆx
t+1
)
=
Z
1
0
R( ˆx
t+1
, θ
t+1
) p

θ
t+1


x
x
x
t

dθ
t+1
. (23)
2
Definition 3.4. Bayes Optimal Prediction
The Bayes optimal prediction ˆx
∗
t+1
is obtained by,
ˆx
∗
t+1
= argmin
ˆx
t+1
BR( ˆx
t+1
) . (24)
2
3.2 Main Theorems
Theorem 3.1. Posterior Distribution for θ
t
Let the prior distribution of parameter θ
1
of
the nonstationary Bernoulli distribution in Defini-
tion 2.1 be Θ
1
∼ Beta (α
1
, β
1
). For any t ≥ 2,
let x
x
x
t−1
= (x
1
, x
2
, . . . , x
t−1
) be the observed data se-
quence. Then, the posterior distribution of Θ
t


x
x
x
t−1
can be obtained as the following closed form:
Θ
t


x
x
x
t−1
∼ Beta (α
t
, β
t
) , (25)
where the parameters α
t
, β
t
are given as,







α
t
= k
t−1
α
1
+
t−1
∑
i=1
k
t−i
x
i
.;
β
t
= k
t−1
β
1
+
t−1
∑
i=1
k
t−i
(1 − x
i
) .
(26)
2
On the Prediction of a Nonstationary Bernoulli Distribution based on Bayes Decision Theory
959

Proof of Theorem 3.1.
For any t ≥ 2, the posterior of parameter distri-
bution p

θ
t


x
x
x
t−1

remains in the closed form Θ
t
∼
Beta (α
t
, β
t
) if X
t
∼ Bernoulli (θ
t
) in Definition 2.1
and Θ
1
∼ Beta(α
1
, β
1
) in Corollary 2.1 according to
the nature of conjugate families (Bernardo and Smith,
2000, 5.2, p.265) (Berger, 1985, 4.2.2, p.130).
Furthermore, assuming that x
t−1
is the observed
data,

α
t
= α
t−1
+ x
t−1
;
β
t
= β
t−1
+ 1 − x
t−1
,
(27)
holds by conjugate analysis (Bernardo and Smith,
2000, Example 5.4, p.271). This is the proof of Eq.
(25).
In this paper, nonstationary parameter model is as-
sumed. Therefore, if both Lemma 2.1, and Lemma
2.2 are recursively applied to Eq. (27), then,

α
t
= k (α
t−1
+ x
t−1
);
β
t
= k (β
t−1
+ 1 − x
t−1
) ,
(28)
holds.
Finally, Eq. (26) is obtained if Eq. (28) is recur-
sively applied until the initial conditions α
1
, β
1
from
both Definition 2.5 and Corollary 2.1 appear.
This completes the proof of Theorem 3.1. 2
Remark 3.1.
For the second terms of the right hand sides of Eq.
(26), each observed data x
i
is exponentially weighted
by k
t−i
where i = 1, 2, . . . ,t − 1. This structure is
called the EWMA, Exponentially Weighted Moving
Average (Harvey, 1989, 6.6, p.350).
Theorem 3.2. Predictive Distribution
p

x
t+1


x
x
x
t

=





β
t+1
α
t+1
+β
t+1
if x
t+1
= 0;
α
t+1
α
t+1
+β
t+1
if x
t+1
= 1,
(29)
where α
t+1
and β
t+1
are in Eq. (26) . 2
Proof of Theorem 3.2.
See APPENDIX C. 2
Theorem 3.3. Bayes Optimal Prediction
ˆx
∗
t+1
=



0 if α
t+1
< β
t+1
;
1 if α
t+1
> β
t+1
,
(30)
2
Proof of Theorem 3.3.
In terms of Bayes decision theory (Weiss
and Blackwell, 1961) (Berger, 1985) (Bernardo
and Smith, 2000), the Bayes optimal prediction
ˆx
t+1
= ˆx
∗
t+1
maximizes the predictive distribution
p

x
t+1


x
x
x
t

if 0 − 1 loss function in Definition 3.1 is
defined. Since ˆx
∗
t+1
∈
{
0, 1
}
and Theorem 3.2 holds,
this maximization can be done by comparing just two
cases. Therefore,
ˆx
∗
t+1
= argmax
x
t+1
p

x
t+1


x
x
x
t

=



0 if α
t+1
< β
t+1
;
1 if α
t+1
> β
t+1
,
This completes the proof of Theorem 3.3. 2
3.3 Hyper Parameter Estimation with
Empirical Bayes Method
Since a hyper parameter 0 < k ≤ 1 in Definition 2.3 is
assumed to be known, it should be estimated in prac-
tice. One of estimation methods can be the maximum
likelihood estimation with numerical approximation
in terms of empirical Bayes approach. This is,
ˆ
k = argmax
k
L (k) , (31)
where 0 < k ≤ 1 and,
L (k)
= p

x
1


θ
1
, k

p(θ
1
)
t
∏
i=2
p

x
i


x
x
x
i−1
, k

=
t
∏
i=1

β
i
α
i
+ β
i

1−x
i

α
i
α
i
+ β
i

x
i
. (32)
Note that Eq. (32) is obtained by applying Theorem
3.2.
Therefore, its log-likelihood function logL (k) is,
logL (k)
=
t
∑
i=1
{
(1 − x
i
)[log β
i
− log(α
i
+ β
i
)]
+x
i
[logα
i
− log (α
i
+ β
i
)]
}
. (33)
Eqs. (31) and (33) can not be solved analytically and
then the approximate numerical method should be ap-
plied.
3.4 Proposed Bayes Optimal Prediction
Algorithm
Based on main Theorems in Subsection 3.2, the fol-
lowing Bayes optimal prediction algorithm is pro-
posed.
Algorithm 3.1. Proposed Bayes Optimal Algorithm
1. Estimate hyper parameter k from training data by
approximate maximum likelihood estimation with
Eqs. (31) and (33).
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
960

2. Set t = 1 and define α
1
> 0, β
1
> 0 in Definition
2.5 in order to set the initial prior of parameter
distribution Θ
1
∼ Beta (α
1
, β
1
) in Corollary 2.1.
3. With test data sequence x
x
x
t
, update the pos-
terior of nonstationary parameter distribution
p

θ
t+1


α
t+1
, β
t+1
, x
x
x
t

with Eq. (26) in Theorem
3.1.
4. Calculate the predictive distribution p

x
t+1


x
x
x
t

in Theorem 3.2.
5. Obtain the Bayes optimal prediction ˆx
∗
t+1
in The-
orem 3.3.
6. If t < t
max
, then update t → t +1 and back to 3.
7. If t = t
max
, then terminate the algorithm.
2
4 NUMERICAL EXAMPLES
This section shows numerical examples to evaluate
the performance of Algorithm 3.1. Subsection 4.1 ex-
plains both the training and test data specifications.
Training data is applied to estimate the hyper param-
eters: k in Definition 2.3 and α
1
, β
1
in Definition 2.5,
where the latter is used for the prior of parameter Θ
1
to predict test data. Test data were applied to evalu-
ate the predictive performances of the proposed algo-
rithm.
4.1 Binary Data Specifications
Table 1 and 2 show the training and test data specifi-
cations, respectively. These binary data were obtained
from the daily rainfall data in Tokyo from January
1, 2018 to December 31, 2019 (Japan Meteorologi-
cal Agency, 2020). Note that the threshold of binary
data is defined by the following rule: ith daily rainfall:
x
i
= 1 if its amount is greater than 0.5 mm, otherwise
x
i
= 0.
Table 1: Training Data Specifications.
Items Values
From: January 1, 2018
To: December 31, 2018
Total Days: 365
Table 2: Test Data Specifications.
Items Values
From: January 1, 2019
To: December 31, 2019
Total Days: 365
4.2 Evaluations for Bayes Optimal
Predictions
This subsection mainly evaluates two aspects of the
Bayes optimal predictions from both the proposed
nonstationary and conventional stationary Bernoulli
distribution models. The first is the predictive per-
formance between two models with non-informative
priors. The second is that with informative priors.
4.2.1 Prediction Results with Non-informative
Priors
Before evaluating the predictive performance, the hy-
per parameter
ˆ
k is estimated using Eq. (31) from train-
ing data. This is the approximate maximum likeli-
hood estimation with numerical calculation. The re-
sults are shown in Table 3.
Table 3: Estimated Hyper Parameter from Training Data.
Item Value
ˆ
k 0.971
In this evaluation, the hyper parameters α
1
and β
1
of
the prior distribution p

θ
1


α
1
, β
1

are assumed to be
non-informative. This initial prior should be a uni-
form distribution. The defined values of the hyper pa-
rameters are shown in Table 4.
Table 4: Defined Hyper Parameters for Non-informative
Priors of Test Data.
α
1
β
1
1.000 1.000
Using
ˆ
k, α
1
, and β
1
from Tables 3 and 4, the predictive
errors for the proposed and stationary Bernoulli mod-
els
∑
365
i=1
L (ˆx
i
, x
i
) are calculated with test data. The
results are shown in Table 5.
Table 5: Predictive Errors with Test Data for Proposed and
Stationary Models with Non-informative Priors.
Items Proposed Stationary
∑
365
i=1
L (ˆx
i
, x
i
) 173 187
4.2.2 Prediction Results with Informative Priors
In this evaluation, the hyper parameters α
1
and β
1
of
the prior distribution p

θ
1


α
1
, β
1

are assumed to be
informative. In this case, the empirical Bayesian ap-
proach is adopted. Both α
1
and β
1
are obtained from
On the Prediction of a Nonstationary Bernoulli Distribution based on Bayes Decision Theory
961

the posterior distribution of p

θ
t


x
x
x
t
, α
t
, β
t

from the
training data, and these are used as the initial prior of
p(θ
1


α
1
, β
1
) to predict the test data. These values
are listed in Table 6.
Table 6: Defined Hyper Parameters for Informative Priors
of Test Data.
α
1
β
1
16.429 34.612
Using
ˆ
k, α
1
, and β
1
from Tables 3 and 6, the predic-
tive errors are calculated for both models with the test
data. The results are shown in Table 7.
Table 7: Predictive Errors with Test Data for Proposed and
Stationary Models with Informative Priors.
Items Proposed Stationary
∑
365
i=1
L (ˆx
i
, x
i
) 178 179
5 DISCUSSIONS
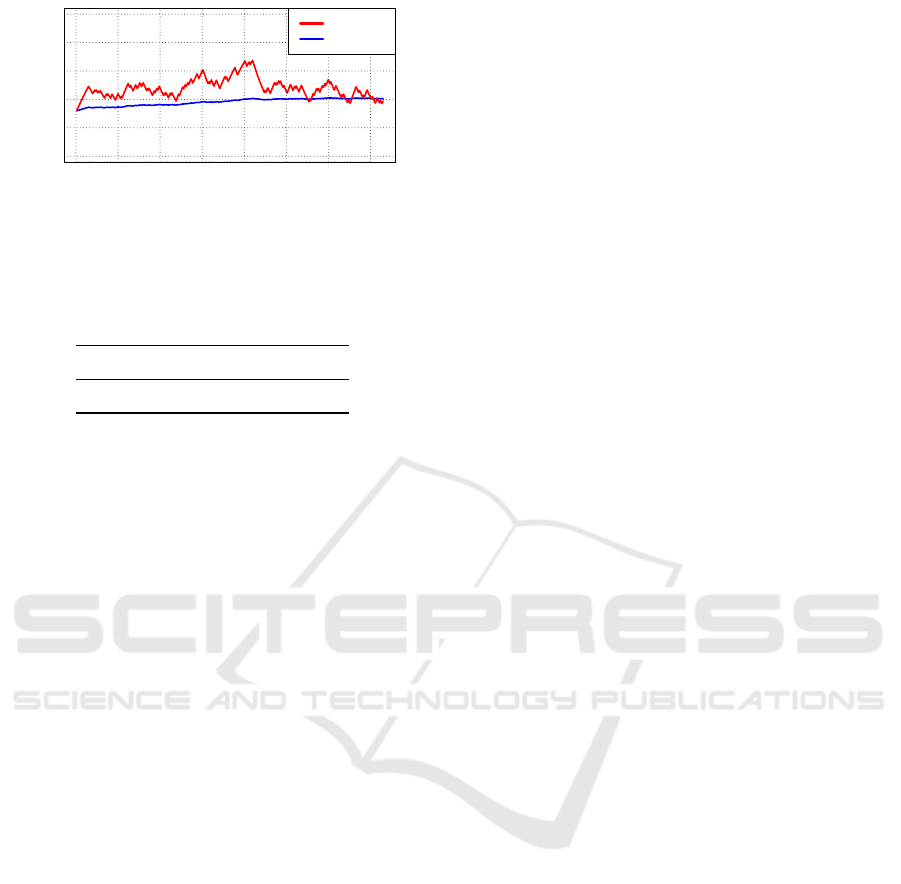
Table 5 shows that the total loss of the proposed
nonstationary Bernoulli model is smaller than that of
the stationary model, with accuracies of 52.6% and
48.8%, respectively. Moreover, the time series of the
posterior probability p(θ
t
= 1


x
x
x
t
)
1
is calculated and
plotted in Figure 1. In Figure 1, the vertical axis is
the posterior probability, the horizontal axis shows the
indices of days, the red line is the time series of the
posterior probabilities from the proposed model, and
the blue line is that from the stationary model. From
Figure 1, it can be observed that the posterior from the
proposed model drifts more drastically than that of the
stationary model. Thus, the extra hyper parameter k
in the proposed model must work relatively well with
a non-informative prior.
However, if the AIC, Akaike Information Crite-
rion (Akaike, 1973) values for both models are cal-
culated with test data, the values in Table 8 are ob-
tained. From the perspective of model selection the-
ory, the smaller the AIC value, the more appropriate
the model is under the observed data. Table 8 indi-
cates that the stationary model is more appropriate
than the proposed model with test data. However,
as mentioned above, the proposed model is superior
to the stationary model in terms of predictive perfor-
mance. Thus, the result of the first evaluation with
a non-informative prior cannot be explained by AIC
1
Each value is the daily probability of rainfall.
with the specific test data in this paper.
days
posterior
0 50 100 150 200 250 300 350
0.0 0.2 0.4 0.6 0.8 1.0
Proposed
Stationary
Figure 1: Posterior Probability Plot of p

θ
t
= 1


x
x
x
t

with
Non-informative Priors.
Table 8: AIC values for Proposed and Stationary Models
with Non-informative Priors.
Items Proposed Stationary
AIC -500.476 -505.316
In contrast, according to Table 7, the difference in
the predictive performance for both models becomes
smaller than that of the first evaluation. In fact, the
result is almost a draw, with accuracies of 51.2% and
51.0%, respectively. Moreover, Figure 2 shows the
time series of the posterior rainfall probability for
both models. Note that an informative prior is as-
sumed in this evaluation. From Figure 2, the first 50
points of the time series of the proposed model (red
line) are more stable than those of the proposed model
in Figure 2. This difference can be interpreted as the
effect of informative priors. However, the predictive
performance becomes worse in the proposed model.
In this case, it can be considered that the setting of the
informative prior weakens the effect of the estimated
nonstationary hyper parameter
ˆ
k. From Figure 2, the
entire blue plot of the stationary model becomes more
stable than that of the stationary model in Figure 1. In
this case, the posterior of the stationary model almost
converges, and its predictive performance is improved
effectively as shown by the comparison of the results
from Tables 5 and 7.
Table 9 shows the AIC values for both mod-
els. From the perspective of AIC, the value of the
proposed model with the informative prior become
slightly smaller than that of the proposed model with
the non-informative prior. For the stationary model,
this difference becomes larger. Thus, the theory of
AIC explains the predictive performance of the sta-
tionary model well. However, the same situation does
not hold true for the proposed model.
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
962

days
posterior
0 50 100 150 200 250 300 350
0.0 0.2 0.4 0.6 0.8 1.0
Proposed
Stationary
Figure 2: Posterior Probability Plot of p

θ
t
= 1


x
x
x
t

with
Informative Priors.
Table 9: AIC values for Proposed and Stationary Models
with Informative Priors.
Items Proposed Stationary
AIC -505.776 -522.896
6 CONCLUSIONS
This paper proposes a class of nonstationary Bernoulli
distribution and the Bayes optimal prediction algo-
rithm under the known nonstationary hyper parame-
ter. The proposed class has only one extra hyper pa-
rameter compared to the stationary Bernoulli distribu-
tion, and it is proved that the posterior distribution of
the Bernoulli parameter is obtained analytically. Fur-
thermore, the predictive performance of the proposed
algorithm is evaluated using real binary data. As a
result, a certain advantage for predictive performance
is discovered by comparing the results to those of the
stationary Bernoulli model; however, this point can-
not be explained in terms of model selection theory.
As important factor in the abovementioned ad-
vantage is the additional nonstationary hyper param-
eter in the proposed model. Because the empirical
Bayesian approach is used in this study and the ad-
ditional hyper parameter is estimated by the approx-
imate maximum likelihood estimation, the objective
likelihood function should be analyzed in detail. This
point will be left for future work.
REFERENCES
Akaike, H. (1973). Information theory and an extension of
the maximum likelihood principle. 2nd International
Symposium on Information Theory, pages 267–281.
Berger, J. (1985). Statistical Decision Theory and Bayesian
Analysis. Springer-Verlag, New York.
Bernardo, J. M. and Smith, A. F. (2000). Bayesian Theory.
John Wiley & Sons, Chichester.
Cox, D. R. (1970). The Analysis of Binary Data. Chapman
and Hall, London.
Harvey, A. C. (1989). Forecasting, Structural Time Series
Models and the Kalman Filter. Cambridge University
Press, Marsa, Malta.
Japan Meteorological Agency (2020). ClimatView
(in Japanese). https://www.data.jma.go.jp/gmd/cpd/
monitor/dailyview/. Browsing Date: Nov. 27, 2020.
Koizumi, D. (2020). Credible interval prediction of a non-
stationary poisson distribution based on bayes deci-
sion theory. In Proceedings of the 12th International
Conference on Agents and Artificial Intelligence - Vol-
ume 2: ICAART,, pages 995–1002, Valletta, Malta.
INSTICC, SciTePress.
Koizumi, D., Matsuda, T., and Sonoda, M. (2012). On the
automatic detection algorithm of cross site scripting
(xss) with the non-stationary bernoulli distribution.
In The 5th International Conference on Communica-
tions, Computers and Applications (MIC-CCA2012),
pages 131–135, Istanbul, Turkey. IEEE.
Koizumi, D., Matsushima, T., and Hirasawa, S. (2009).
Bayesian forecasting of www traffic on the time vary-
ing poisson model. In Proceeding of The 2009 In-
ternational Conference on Parallel and Distributed
Processing Techniques and Applications (PDPTA’09),
volume II, pages 683–689, Las Vegas, NV, USA.
CSREA Press.
Press, S. J. (2003). Subjective and Objective Bayesian
Statistics: Principles, Models, and Applications. John
Wiley & Sons, Hoboken.
Smith, J. Q. (1979). A generalization of the bayesian steady
forecasting model. Journal of the Royal Statistical So-
ciety - Series B, 41:375–387.
Weiss, L. and Blackwell, D. (1961). Statistical Decision
Theory. McGraw-Hill, New York.
Yasuda, G., Nomura, R., and Matsushima, T. (2001). A
study of coding for sources with nonstationary pa-
rameter (in Japanese). Technical Report of IEICE
(IT2001-15), 101(177):25–30.
APPENDIX
A: Proof of Lemma 2.1
Suppose t = 1, A
1
= a
1
and C
1
= c
1
are defined as,
A
1
∼ Gamma(α
1
, 1) , (34)
C
1
∼ Beta [kα
1
, (1 − k) α
1
] , (35)
according to Definition 2.5 and Definition 2.6, respec-
tively.
Since A
2
= C
1
A
1
from Definition 2.3, and A
t
and
C
t
are conditional independent from Definition 2.4,
On the Prediction of a Nonstationary Bernoulli Distribution based on Bayes Decision Theory
963

the joint distribution of p(c
1
, a
1
) becomes,
p(c
1
, a
1
)
= p

c
1


kα
1
, (1 − k) α
1

p

a
1


α
1
, 1

=
Γ(α
1
)
Γ(kα
1
)Γ [(1 − k)α
1
]
c
kα
1
−1
1
(1 − c
1
)
(1−k)α
1
−1
·
a
α
1
−1
1
Γ(α
1
)
exp(−a
1
)
=
c
kα
1
−1
1
(1 − c
1
)
(1−k)α
1
−1
Γ(kα
1
)Γ [(1 − k)α
1
]
a
α
1
−1
1
exp(−a
1
) .
Now, denote the two transformation as,

v = a
1
c
1
;
w = a
1
(1 − c
1
),
(36)
where 0 < v, 0 < w.
Then, the inverse transformation of Eq. (36) be-
comes,

a
1
= v + w;
c
1
=
v
v+w
,
(37)
The Jacobian J
1
of Eq. (37) is,
J
1
=






∂a
1
∂v
∂a
1
∂w
∂c
1
∂v
∂c
1
∂w






=






1 1
w
(v+w)
2
−
v
(v+w)
2






= −
1
v + w
= −
1
a
1
6= 0.
Then, the transformed joint distribution p(v, w) is ob-
tained by the product of p(c
1
, a
1
) and the absolute
value of J
1
.
p(v, w)
= p (c
1
, a
1
)


−
1
a
1


=

v
v+w

kα
1
−1

w
v+w

(1−k)α
1
−1
Γ(kα
1
)Γ [(1 − k)α
1
]
·(v + w)
α
1
−1
exp[−(v + w)] ·
1
v + w
=
v
kα
1
−1
w
(1−k)α
1
−1
Γ(kα
1
)Γ [(1 − k)α
1
]
exp[−(v + w)] .(38)
Then, p(v) is obtained by marginalizing Eq. (38) with
respect to w,
p(v) =
Z
∞
0
p(v, w) dw
=
v
kα
1
−1
exp(−v)
Γ(kα
1
)Γ [(1 − k)α
1
]
·
Z
∞
0
w
(1−k)α
1
−1
exp(−w)dw
=
v
kα
1
−1
exp(−v)
Γ(kα
1
)Γ [(1 − k)α
1
]
· Γ[(1 − k)α
1
]
=
1
Γ(kα
1
)
v
kα
1
−1
exp(−v) . (39)
Eq. (39) exactly corresponds to Gamma(kα
1
, 1) ac-
cording to Definition 2.7. Recalling v = a
1
c
1
from
Eq. (36) and A
2
= C
1
A
1
from Definition 2.3,
A
2
∼ Gamma(kα
1
, 1) .
Thus if t = 1, then A
t+1
∼ Gamma(kα
t
, 1) holds.
For t ≥ 2, by substituting α
t
= kα
t−1
, A
t
= a
t
and
C
t
= c
t
are defined as,
A
t
∼ Gamma(α
t
, 1) , (40)
C
t
∼ Beta [kα
t
, (1 − k) α
t
] . (41)
Eqs. (40) and (41) correspond to Eqs. (34) and (35),
respectively. Therefore the same proof can be applied
for the case of t ≥ 2 and it can be proved that,
∀t, A
t+1
∼ Gamma(kα
t
, 1) .
This completes the proof of Lemma 2.1. 2
B: Proof of Lemma 2.3
From Lemma 2.1 and 2.2,
∀t ≥ 2, A
t
∼ Gamma(kα
t−1
, 1) ,
∀t ≥ 2, B
t
∼ Gamma(kβ
t−1
, 1) .
According to Definition 2.2, two random variables A
t
and B
t
are independent. Therefore, the joint distribu-
tion pf p (a
t
, b
t
) becomes,
p(a
t
, b
t
)
= p

a
t


kα
t−1
, 1

p

b
t


kβ
t−1
, 1

=
"
a
kα
t−1
−1
t
exp(−a
t
)
Γ(kα
t−1
)
#
·
"
b
kβ
t−1
−1
t
exp(−b
t
)
Γ(kβ
t−1
)
#
=
a
kα
t−1
−1
t
b
kβ
t−1
−1
t
Γ(kα
t−1
)Γ (kβ
t−1
)
exp[−(a
t
+ b
t
)] .
Denoting the two transformations,

λ = a
t
+ b
t
;
µ =
a
t
a
t
+b
t
,
(42)
where 0 < λ, 0 < µ.
The inverse transformation of Eq. (42) becomes,

a
t
= λµ;
b
t
= λ(1 − µ) .
(43)
Then, the Jacobian J
2
of Eq. (43) is,
J
2
=







∂a
t
∂λ
∂a
t
∂µ
∂b
t
∂λ
∂b
t
∂µ







=






µ λ
1 − µ −λ






= −λ = −(a
t
+ b
t
).
ICAART 2021 - 13th International Conference on Agents and Artificial Intelligence
964

Then, the transformed joint distribution p(λ, µ) is ob-
tained by the product of p (a
t
, b
t
) and the absolute
value of J
2
as the following,
p(λ, µ)
= p (a
t
, b
t
)·


−(a
t
+ b
t
)


=
(λµ)
kα
t−1
−1
[λ(1 − µ)]
kβ
t−1
−1
Γ(kα
t−1
)Γ (kβ
t−1
)
exp(−λ) · λ
=
µ
kα
t−1
−1
(1 − µ)
kβ
t−1
−1
Γ(kα
t−1
)Γ (kβ
t−1
)
λ
kα
t−1
+kβ
t−1
−1
exp(−λ) .
(44)
Then, p (µ) is obtained by marginalizing Eq. (44) with
respect to λ,
p(µ)
=
Z
∞
0
p(λ, µ)dλ
=
µ
kα
t−1
−1
(1 − µ)
kβ
t−1
−1
Γ(kα
t−1
)Γ (kβ
t−1
)
·
Z
∞
0
λ
kα
t−1
+kβ
t−1
−1
exp(−λ)dλ
=
µ
kα
t−1
−1
(1 − µ)
kβ
t−1
−1
Γ(kα
t−1
)Γ (kβ
t−1
)
· Γ(kα
t−1
+ kβ
t−1
)
=
Γ(kα
t−1
+ kβ
t−1
)
Γ(kα
t−1
)Γ (kβ
t−1
)
µ
kα
t−1
−1
(1 − µ)
kβ
t−1
−1
.
(45)
Eq. (45) exactly corresponds to Beta (kα
t−1
, kβ
t−1
)
according to Definition 2.8.
Recalling µ =
a
t
a
t
+b
t
from Eq. (42) and Θ
t
=
A
t
A
t
+B
t
from Definition 2.2,
∀t ≥ 2, Θ
t
∼ Beta (kα
t−1
, kβ
t−1
) ,
holds.
This completes the proof of Lemma 2.3. 2
C: Proof of Theorem 3.2
Since the predictive distribution is Binomial-Beta
distribution (Bernardo and Smith, 2000, p.117),
p

x
t+1


x
x
x
r

becomes,
p

x
t+1


x
x
x
t

=
Z
1
0
p

x
t+1


θ
t+1

p

θ
t+1


x
x
x
t

dθ
t+1
= c · Γ (α
t+1
+ x
t+1
)Γ (β
t+1
+ 1 − x
t+1
),
where c =
Γ(α
t+1
+β
t+1
)
Γ(α
t+1
)Γ(β
t+1
)Γ(α
t+1
+β
t+1
+1)
.
If x
t+1
= 0, then,
p

x
t+1


x
x
x
t

=
Γ(α
t+1
+ β
t+1
)
Γ(α
t+1
)Γ (β
t+1
)Γ (α
t+1
+ β
t+1
+ 1)
· Γ(α
t+1
)Γ (β
t+1
+ 1)
=
Γ(α
t+1
+ β
t
)
Γ(α
t+1
)Γ (β
t+1
)(α
t+1
+ β
t+1
)Γ (α
t+1
+ β
t+1
)
· Γ(α
t+1
)β
t+1
Γ(β
t+1
) (46)
=
β
t+1
α
t+1
+ β
t+1
.
Note that Eq. (46) in obtained by applying the follow-
ing property of Gamma function: Γ(q + 1) = qΓ(q).
If x
t+1
= 1, then,
p

x
t+1


x
x
x
t

=
Γ(α
t+1
+ β
t+1
)
Γ(α
t+1
)Γ (β
t+1
)Γ (α
t+1
+ β
t+1
+ 1)
· Γ(α
t+1
+ 1)γ(β
t+1
)
=
Γ(α
t+1
+ β
t+1
)
Γ(α
t+1
)Γ (β
t+1
)(α
t+1
+ β
t+1
)Γ (α
t+1
+ β
t+1
)
· α
t+1
Γ(α
t+1
)Γ (β
t+1
)
=
α
t+1
α
t+1
+ β
t+1
.
This completes the proof of Theorem 3.2 . 2
On the Prediction of a Nonstationary Bernoulli Distribution based on Bayes Decision Theory
965