Flower Pollination Algorithm for Detection of Epistasis Associated with a
Phenotype
Jozef Sitar
ˇ
c
´
ık
1
, M
´
aria Luck
´
a
2
and Tibor Kraj
ˇ
covi
ˇ
c
1
1
Faculty of Informatics and Information Technologies, Slovak University of Technology, Ilkovicova 2, Bratislava, Slovakia
2
KInIT - Kempelen Institute of Intelligent Technologies, Mlynske Nivy 5, 811 09 Bratislava, Slovakia
Keywords:
Epistasis Detection, Flower Pollination Algorithm, Single Nucleotide Polymorphisms.
Abstract:
Detecting associations of SNPs with traits like complex diseases can provide valuable insights. However,
due to the epistases - complex interactions between SNPs - SNP combinations need to be evaluated for their
association with a trait. As the number of possible SNP combinations grows rapidly with increase of the
number of SNPs, great computational challenges have to be tackled. In this paper, we propose FPepi, epistasis
detection tool based on flower pollination algorithm with multiple objectives. Two variants of the algorithm are
proposed, one using Gini score and K2 score as objectives, while the second variant uses K2 score and mutual
information score. The flower pollination algorithm selects a small subset of potential SNP combinations, that
are then evaluated by G-test. The proposed tool shown better results in detection power when compared with
other similar tools.
1 INTRODUCTION
Genome-wide association study (GWAS) identified
many single nucleotide polymorphisms (SNPs) as-
sociated with a disease (Easton et al., 2007; Hin-
dorff et al., 2009). However, epistatic interactions
can cause cases where only a specific combination
of SNPs is associated with a disease, therefore SNP
combinations need to be taken into account. This is
a more complex problem as the number of combi-
nations grows rapidly. More precisely, the quantity
of combinations is given by

n
k

, where n is the to-
tal number of SNPs, and k is the number of SNPs
in one SNP combination. Even with high computa-
tional power, it is not viable to test each possible SNP
combination for association with a phenotype. Also,
false positive rate must be as low as possible, which is
problematic, due to the fact, that usually only a very
small subset from all possible SNP combinations is
truly associated with a disease.
In this paper, we introduce FPepi, which uses
flower pollination algorithm (Yang, 2012) to effi-
ciently search solution space - all possible k-way SNP
combinations - to find a candidate set, i.e. a set of po-
tential SNP combinations, that will be then evaluated
for significance of association with a phenotype.
In our paper the following terminology and nota-
tion is used. GWAS datasets are case-control datasets
represented as a m × (n + 1) matrix M, where m is
the number of samples in a dataset, and n is the num-
ber of SNPs. The matrix value M[i, j] then represents
the genotype value of i-th sample at j-th SNP, where
0 ≤ i < m and 0 ≤ j < n. Possible genotype values are
major homozygous allele, heterozygous allele, and
minor homozygous allele, that are usually encoded as
0, 1, and 2, respectively. The last column of M repre-
sents the existence of association of ith sample with a
phenotype, i.e. case or control.
The number of interacting SNPs is denoted as k,
and agents in nature inspired algorithms will represent
such k-way SNP combinations.
1.1 Related Work
The basic approach for solving this problem of de-
tecting SNP combinations associated with a pheno-
type is the exhaustive search approach. When using
this approach, all possible k-way SNP combinations
are evaluated for association with a phenotype using
statistical tests of association, such as χ
2
test, G-test
or Fisher’s Exact test.
The number of possible k-way SNP combinations
for n SNPs is

n
k

, therefore it is not viable to test
all possible SNP combinations. However, BOolean
Operation based Screening and Testing (BOOST) fo-
cuses on improving exhaustive search approach by us-
ing likelihood ratio to filter only a subset of SNP com-
binations, that will be evaluated (Wan et al., 2010).
118
Sitar
ˇ
cík, J., Lucká, M. and Kraj
ˇ
covi
ˇ
c, T.
Flower Pollination Algorithm for Detection of Epistasis Associated with a Phenotype.
DOI: 10.5220/0010254501180126
In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 3: BIOINFORMATICS, pages 118-126
ISBN: 978-989-758-490-9
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

The Bayesian Epistasis Association Mapping tool
(BEAM) uses Bayesian partition model and Markov
chain Monte Carlo sampling strategy to compute the
posterior probability that SNP is associated with a
phenotype (Zhang and Liu, 2007).
Another interesting approach is used in the tool
called Fast method for Detecting High-order Epistasis
based on an Interaction Weight (FDHE-IW), which at
first selects the best SNPs based on symmetrical un-
certainty score. Then, forward selection is used to
produce final SNP combinations based on interaction
weight (Tuo, 2018). Best SNP combinations are eval-
uated by G-test.
1.2 Nature Inspired Algorithms
Other tools use heuristic search based on nature
inspired algorithms optimizing various objectives.
Among such first tools was AntEpiSeeker, based on
ant-colony optimization algorithm (ACO) and χ
2
test
score as the objective function (Wang et al., 2010).
More recent tool based on ACO is MACOED, which
uses two objective functions: Bayesian based K2
score, and Akaike Information Criterion (AIC) score,
used in logistic regression (Jing and Shen, 2014). As
two objective functions are being optimized, MA-
COED uses Pareto optimal optimization technique.
Then, best solutions found are evaluated by χ
2
test.
There are many other tools based on ACO, such as
FAACOSE using AIC score and explain score (Yuan
et al., 2017), or epiACO, that uses newly defined ob-
jective called Svalue, defined as the ratio of mutual
information and K2 score (Sun et al., 2017). An-
other tool based on ACO, which is worth mention-
ing is ACO-Tabu which combines ACO with the Tabu
search (Sapin et al., 2015).
Other nature inspired algorithms are also used in
tools for the epistasis detection, for example, bat algo-
rithm (BA), harmony search algorithm (HS) and parti-
cle swarm optimization algorithm (PSO). BA is used
in epiBAT (Sitar
ˇ
c
´
ık and Luck
´
a, 2019), while HS is
used in FHSA-SED (Tuo et al., 2016) and NHSA-
DHSC (Tuo et al., 2017). As objectives, epiBAT
and FHSA-SED use K2 score and Gini score, while
NHSA-DHSC uses also a third objective - joint en-
tropy. PSO is used in IOBPLSO (Shang et al., 2015),
which uses mutual information score.
Nature inspired algorithms dedicated to epistasis
detection are reviewed in (Tuo et al., 2019). Compar-
ison of epistasis detection tools of all approaches is
presented in (Niel et al., 2015).
2 FLOWER POLLINATION
ALGORITHM
Flower Pollination Algorithm (FPA) is a nature in-
spired algorithm drawing inspiration from the polli-
nation process of flowers, where pollen grains are be-
ing moved from one flower to another (Yang, 2012).
The pollination process can be biotic, i.e. when pol-
linators such as birds move pollen grains; or it can be
abiotic, when pollen grains are moved without requir-
ing pollinators, for example by wind or rain.
Successful applications of FPA are concisely pre-
sented in (Abdel-Basset and Shawky, 2019), while
FPA applications for engineering problems are re-
viewed in (Kayabekir et al., 2018).
In FPA, flowers represent potential solutions in the
searching space. Population of agents is represented
by flowers that are pollinated in iteration t, and such
i-th pollinated flower will be denoted as x
t
i
.
In FPA, biotic pollination represents global
search, and abiotic pollination represents local search.
Flowers can switch their type of pollination, whereas
the the type of pollination which will be used in that
iteration for each flower is controlled by the switch
probability parameter.
In biotic pollination - global search - pollinators
move the pollen of the best flower denoted as g
∗
to
the other flowers. If the flower x
t
i
is determined by
the switch probability parameter to use biotic pollina-
tion, then pollinated flower in the next iteration x
t+1
i
is calculated as follows:
x
t+1
i
= x
t
i
+ L(g
∗
− x
t
i
), (1)
where L is a step based vector drawn from the L
´
evy
flight distribution, as pollinators are usually birds. To
draw a vector L from the L
´
evy flight distribution, we
use Mantegna’s algorithm (Mantegna, 1994):
L =
u
|v|
1
β
, (2)
where β is a user-defined parameter from the interval
[1, 2], and u, v are drawn from the normal distribution
N as follows:
u ∼ N (0, σ
2
u
), v ∼ N (0, σ
2
v
), (3)
where σ
2
u
, σ
2
v
are given by the following relationship:
σ
u
=
(
Γ(1 + β) sin
πβ
2
Γ

(1+β)
2

β2
β−1
2
)
1
β
, σ
v
= 1, (4)
where Γ represents the gamma function, and β is user-
defined parameter, such as 1 < β < 2, usually set to
3
2
.
Flower Pollination Algorithm for Detection of Epistasis Associated with a Phenotype
119

In the local search, pollen is moved from a flower
x
t
i
to a new flower x
t+1
i
as follows:
x
t+1
i
= x
t
i
+ κ(x
t
j
− x
t
k
), (5)
where κ is a random number drawn from the uniform
distribution on the interval [0, 1], and x
t
j
, x
t
o
are j-th
and o-th solutions, such as j 6= o 6= i.
However, newly computed flower x
t+1
i
can be
worse than the previous flower x
t
i
. Therefore, based
on the objective function, new flowers are compared
with the previous ones, and previous flowers are re-
placed by the new ones only if they are better.
2.1 Dynamic Switch Probability
The switch probability parameter controls whether
global or local search will happen. This parameter is
important, as the high probability is good for the ex-
ploration of solution space, while the low probability
is good for the exploitation. However, the probabil-
ity should be dynamic, as global search should occur
more frequently at start, and then its occurrence fre-
quency should decrease as the local search frequency
increases. This is called dynamic switch probabil-
ity (Salgotra and Singh, 2017). Then, the switch prob-
ability at iteration t is given as:
switch prob
t
= init prob − 0.1 ∗ (
T − t
T
), (6)
where T is the total number of iterations, t is the cur-
rent iteration, and init prob is the initial probability,
which is a user-defined parameter.
2.2 Bee Pollinator
Recently, the flower pollination algorithm enhanced
with the bee pollinator (BPFPA) was proposed, show-
ing higher level of stability and faster convergence
speed (Wang et al., 2016). BPFPA uses three addi-
tional optimization strategies to improve FPA perfor-
mance: discard pollen operator, elite based mutation
operator, and crossover operator.
The discard pollen operator is inspired by artificial
bee colony algorithm (Karaboga and Basturk, 2007),
where it is used to discard solutions that are stuck in
local optima. Usually, if a solution is not improved for
a specified number of iterations denoted as limit, that
solution is discarded and replaced by a new solution.
To generate the new solution, BPFPA uses simplex
method, which usually generates better solutions than
just random regeneration of a solution (Wang et al.,
2016).
The elite based mutation operator modifies the lo-
cal search process by incorporating the best solution
g
∗
of population (Wang et al., 2016):
x
t+1
i
= x
t
i
+ κ(g
∗
− x
t
i
) + λ(x
t
j
− x
t
k
), (7)
where κ and λ are random numbers drawn from
the uniform distribution on the interval [0, 1]. This
operator increases convergence speed, however it
can decrease population diversity. To prevent this,
BFFPA uses the crossover operator, which, based on
crossover rate, replaces random part of solution with
random part of another random solution:
x
t+1
i,a
=
(
x
t
i,a
γ < C
r
,
x
t
j,a
γ ≥ C
r
, i 6= j,
(8)
where x
t
i,a
represents a-th variable of i-th solution (i.e.
a-th SNP of i-th SNP combination) at iteration t. C
r
is
the crossover rate, which is a user-defined parameter,
and γ is a random number drawn from the uniform
distribution on the interval [0, 1].
3 DESCRIPTION OF THE FPEPI
ALGORITHM
The FPepi tool similarly as other bio-inspired tools,
such as MACOED or NHSA-DHSC, runs in two
stages. In the first stage, the solution space which con-
sists of all possible SNP combinations is explored to
find a subset of potential SNP combinations, called
the candidate set (CS). In the second stage, called
evaluation stage, SNP combinations from CS are eval-
uated by the significance statistical test.
The first stage of FPepi algorithm is based on
FPA with modifications (discard pollen operator, elite
based mutation operator, crossover operator) pre-
sented in BPFPA (Wang et al., 2016), and with the
dynamic switch probability. In Fpepi, FPA is cou-
pled with taboo table to prevent getting stuck at lo-
cal optima. To evaluate SNP combinations from the
candidate set, FPepi tool uses G-test with Bonferroni-
corrected significance level threshold.
In FPepi, flowers represent possible k-way SNP
combinations, and flowers that are pollinated repre-
sent a population in a iteration. Each pollinated flower
is a vector x of discrete integers y
1
, y
2
, ..., y
k
, where
k represents the epistasis order, i.e. the quantity of
SNPs in one combination. Values y
1
, y
2
, ..., y
k
of vec-
tor x come from discrete range 0, ..., n − 1, where n is
the total number of SNPs, and the condition of unique
values must hold for each flower (i.e. a SNP combi-
nation of two same SNPs is not valid). When this
condition is not fulfilled, a pollen is moved to another
flower randomly in one dimension and random direc-
tion by one. FPepi currently works for k = 2.
BIOINFORMATICS 2021 - 12th International Conference on Bioinformatics Models, Methods and Algorithms
120

As flowers in the general FPA are not in a discrete
solution space but in continuous, in FPepi, they are
thus transformed to discrete values by rounding to the
nearest integer. In the case of a pollinated flower that
is not in the solution space, it is replaced by a new
randomly generated pollinated flower.
The pseudocode of FPepi algorithm is summa-
rized as follows:
Randomly initialize population of m flowers
Let f () be the objective to be minimized
Find the best flower g
∗
t
based on f ()
while termination condition is not reached do
Calculate switch prob
t
via Equation 6
for i = 1 to m do
if rand > switch prob then
x
t+1
i
← do global search via Equation 1
if f (x
t+1
i
) < f (x
t
i
) then
accept x
t+1
i
as new solution
else
if c
i
< limit then
increase the counter c
i
else
update x
i
t
by the simplex method
end if
end if
else
x
t+1
i
← do local search via Equation 7
x
t+1
i
← do crossover via Equation 8
if f (x
t+1
i
) < f (x
t
i
) then
accept x
t+1
i
as new solution
end if
end if
end for
Find the best flower g
∗
t
based on f ()
end while
3.1 Objectives
In FPepi, we experimented with three objective func-
tions: Gini score, K2 score and mutual information.
As some solutions can be very good in one objective,
but be bad in other objectives, we optimize these ob-
jective functions in separate populations. Gini score
and K2 score were already found to be complemen-
tary (Tuo et al., 2017). Mutual information also
shown good results (Shang et al., 2015). As us-
ing three different populations would be too much,
we implemented two variants of FPepi denoted as
FPepi mi and FPepi gini, the former using K2 score
and mutual information as objectives, while the latter
using K2 score and Gini score.
Objectives are computed as follows. At first, the
frequency distribution of two variables I and J is cal-
culated, where I denotes genotype combinations of k
SNPs, and J denotes either case or control (i.e. as-
sociated with a phenotype or not). Each SNP has
three possible genotype values (homozygous reces-
sive, heterozygous dominant, and homozygous domi-
nant). Therefore, for k-way SNP combination, I = 3
k
genotype values exist, and the contingency table has
I ∗J cells, where the cell in i-th row and in j-th column
represents the quantity of samples having i-th geno-
type combination and phenotype j.
Then, from the contingency table, the K2 score is
computed by the following equation:
K2 score =
I
∏
i=1
(
(J − 1)!
(n
i
+ J + 1)!
J
∏
j=1
n
i j
!) (9)
However, due to the very large values that factori-
als can produce, the logarithmic version of K2 score
is used (Jing and Shen, 2014):
K2 score =
I
∑
i=1
(
n
i
+1
∑
b=1
log(b) −
J
∑
j=1
n
i, j
+1
∑
d=1
log(d)) (10)
The Gini score is defined as follows:
Gini score =
I
∑
i=1
p
i
(1 −
J
∑
j=1
p
2
i j
), (11)
where p
i
is the probability of i-th genotype combi-
nation occuring, and p
i j
represents the probability of
i-th genotype combination and phenotype j occuring
together, which can be calculated as p
i j
=
n
i j
n
i
, where
n
i j
is the number of samples with i-th genotype com-
bination and phenotype j as well, and n
i
is just the
number of all samples with i-th genotype combina-
tion.
The third objective we experimented with is mu-
tual information score (MI) based on information en-
tropy. MI score is computed as follows:
MI =
I
∑
i=1
J
∑
j=1
p
i j
log
p
i j
p
i
p
j
, (12)
where p
j
is the probability of j-th phenotype value.
3.2 Taboo Table
In FPepi, FPA is combined with the concept of taboo
table as follows: If the best solution g
∗
representing
SNP combination consisting of SNPs y
g1
, y
g2
, ...y
gk
,
has not improved for the specified number of iter-
ations, the so-called tabu phase is triggered, which
consists of two steps, solution discarding and solution
storing step.
In the solution discarding step, all SNP combina-
tions sharing at least one SNP with g
∗
are discarded.
Flower Pollination Algorithm for Detection of Epistasis Associated with a Phenotype
121

g
∗
is also discarded but also added to the taboo ta-
ble. Taboo table serves as the table of SNPs, that can
not be visited again in future iterations. Finally, dis-
carded solutions are then replaced with new solutions,
that are randomly initialised.
The solution storing step of tabu phase consists
of checking if solutions that were discarded in the
previous step, should be stored in the set of poten-
tial SNP combinations. Storing a solution depends on
its score. A solution x
i
is stored if ζ ∗ f (x
i
) > f (g
∗
)
holds, where ζ is a user-defined parameter such as
ζ > 1, in our experiments we used ζ = 1.001. This al-
lows solutions that are just slightly worse than the best
solution, to stay in the set of potential SNP combina-
tions and thus be later possibly evaluated for associa-
tion with phenotype by statistical significance test.
The flower pollination algorithm of FPepi is also
modified by this concept of taboo table. When itera-
tion ends, all SNP combinations are checked if they
had not moved to a taboo position, i.e. if they do
not share a SNP with SNP combinations that are in
taboo table. In that case, these SNP combinations
are replaced with new solutions that are randomly ini-
tialized. As FPepi uses two separate populations, the
taboo table is also separate for each population.
The usage of taboo table helps to find SNP com-
binations consisting of SNPs that have weak marginal
effects, because SNPs with strong marginal effects
will be added to taboo table, thus forcing the FPA to
explore other SNP combinations.
3.3 Candidate Set
The result of the flower pollination algorithm is the
set of potential SNP combinations, denoted here as
W . Apart from solutions that were added to W during
the solution storing step of taboo phase, W stores also
best solutions of each iteration. Then, the Pareto opti-
mal approach is used to find the set of non-dominated
solutions W
p
, similarly as in MACOED (Jing and
Shen, 2014). The solution is dominated, if there ex-
ists a solution that have better or same score in both
objectives.
Sometimes, the set W
p
of non-dominated solutions
can contain only a few solutions, as some solutions
can have very good scores in both objectives, thus
dominating all other solutions. Therefore, z best solu-
tions of each population are also added into W
p
until
the total size of the set will be exactly Z, where Z is a
user parameter defining the desired size of this set.
Solutions of the set W
p
are then used to be com-
bined mutually to create new SNP combinations.
Thus, the new set W
q
is created. This is realized be-
cause a specific SNP combination of SNPs does not
have to be found directly, however, these SNPs can
be found separately in other SNP combinations. This
handles situations, where there are SNP combinations
containing SNP a but not SNP b, have very good score
in one objective, and SNP combinations containing
SNP b, but not SNP a, have very good score in the
second objective.
Then, the Pareto optimal approach is used again to
find the set of non-dominated solutions in the set W
q
to
obtain the final set CS, which represents the candidate
set.
3.4 Candidate Set Evaluation
Each SNP combination of the set CS is evaluated by
the G-test (McDonald, 2014), which is recent statisti-
cal significance test similar to χ
2
test. Other alterna-
tives are Fisher test used in FAACOSE (Yuan et al.,
2017), or χ
2
test used in MACOED (Jing and Shen,
2014). The G-test statistic is computed using a con-
tingency table as follows:
G = 2
I
∑
i=1
J
∑
j=1
n
i j
ln(
n
i j
E
i j
), (13)
where n
i j
is a cell of contingency table containing
the quantity of samples with j-th phenotype and i-
th genotype combination in used dataset, whereas the
E
i j
represents the expected frequency.
From the G-test statistic, p-value is calculated
based on the number of degrees of freedom, and if
the p-value is lower than the significance level thresh-
old α, that SNP combination is reported as associated
with a phenotype. However, because of the multiple
comparisons problem, α needs to be adjusted to re-
duce the number of false positives. Similarly as in
other tools, we obtain more stricter significance level
threshold α
bon f
by using Bonferroni correction as fol-
lows: α
bon f
=
α
(
n
k
)
.
G-test and other statistical tests are reported to not
be accurate for very low sample sizes, usually lower
than 5 (McDonald, 2014). Therefore, various tools
in this field modify this evaluation stage. In FDHE-
IW, the number of degrees of freedom is decreased
by one from the maximum number for each genotype
combination that have the expected frequency lower
than some user defined parameter, usually set to 5. In
MACOED, the number of degrees of freedom is fixed
to 8 (which is the maximum number of degrees of
freedom for 2-way SNP combinations). In the FPepi
tool, a whole column of the contingency table is not
taken into account when calculating G-test, if cells of
the column contain less samples than a in total, where
a is user defined parameter with default value set to 5.
BIOINFORMATICS 2021 - 12th International Conference on Bioinformatics Models, Methods and Algorithms
122

Some SNPs can have such strong marginal ef-
fects, that even a combination of such SNPs with
other SNPs can pass the G-test. Thus, in the FPepi
tool, we use the filtering technique for the SNP com-
binations that passed the significance threshold α
bon f
similarly as in AntEpiSeeker (Wang et al., 2010). The
filtering technique filters out such SNP combination
S, whose p-value is not smaller than the p-value of all
other SNP combinations, that share at least one SNP
with SNP combination S. This technique reduces the
number of outputted SNP combinations, as only com-
binations of unique SNPs with lowest p-value are pre-
sented as final results.
4 EXPERIMENTS
We compare the FPepi tool with MACOED (Jing
and Shen, 2014), epiBAT (Sitar
ˇ
c
´
ık and Luck
´
a, 2019),
BEAM (Zhang and Liu, 2007), BOOST (Wan et al.,
2010), AntEpiSeeker (Wang et al., 2010). Our tool is
available at https://github.com/xsitarcik/fpepi.
For the evaluation we use simulated disease mod-
els with marginal effects (DME). We experimented
with both variants of the FPepi tool. The first variant
denoted as FPepi gini uses Gini score and K2 score
as objective functions, while the second variant de-
noted as FPepi mi uses mutual information score and
K2 score as objective functions. In both variants the
population is divided into two halves, where each half
optimizes one objective function separately with sep-
arate taboo table.
4.1 Data
The data were taken from MACOED paper (Jing and
Shen, 2014). Three simulated DMEs have been used
in MACOED, here denoted as DME1, DME2 and
DME3, whereas for each model four different pene-
trance tables were simulated with varying minor allele
frequency (MAF) values (0.05,0.1,0.2,0.5), denoted
here as DME1
1
, ..., DME1
4
, DME2
1
, ..., DME2
4
,
DME3
1
, ..., DME3
4
.
For each penetrance table, MACOED simulated
100 datasets, each with 1600 samples, where 800
were cases, and 800 were controls. In each dataset,
there were 100SNPs, and k was fixed to 2. Only one
2-way SNP combination was truly associated with
phenotype (Jing and Shen, 2014).
Each penetrance table was evaluated separately by
averaging results across all datasets of that penetrance
table. As nature inspired algorithms are prone to ran-
domness, FPepi tool was run multiple times per each
dataset. To be precise, we run it 5 times, the same as
in MACOED (Jing and Shen, 2014). Thus, the FPepi
tool was used for each penetrance table 5*100 times.
4.2 Performance Assessment
For performance assessment of epistasis detection
tools, detection power D is commonly used, which
is described as follows:
S =
D
correct
D
all
, (14)
where D
correct
represents the quantity of times when
the outputted SNP combination was correct for that
penetrance table, and D
all
denotes the total number
of times, when the tool was used for that penetrance
table (D
all
= 500 in our case as mentioned above).
We measured S twice, at first, before potential solu-
tions are evaluated by the statistical test, and then sec-
ondly after the evaluation. We denote the results of
the first stage as FPepi mi CS and FPepi gini CS for
FPepi mi and FPepi gini variants, respectively. MA-
COED also outputs the detection power of the first
stage, which here we denote it as MACOED CS.
By approaching this task as classification prob-
lem, we can also use common metrics as precision
(P), recall (R) and F-measure (F), to assess the perfor-
mance of FPepi tool and compare it with other tools.
By using the same terminology as in classifica-
tion problems, we denote true positives (TP) as the
number of cases when the tool outputted the correct
SNP combination, false positives (FP) as quantity of
outputted SNP combinations that were not correct,
and false negatives (FN) as quantity of times, when
the tool did not output the correct SNP combination.
Then, metrics precision (P), recall (R) and F-measure
(F), are defined as follows:
R =
T P
T P + FN
,
P =
T P
T P + FP
,
F =
1
2P + 2R
.
(15)
4.3 Parameters
The FPepi tool uses many parameters that can be set
and optimized. We ran experiments with the follow-
ing settings: the initial switch probability paramater
was set to 0.8, the β parameter of L
´
evy flight was set
to 1.5. The population size was set to 25 in both pop-
ulations, and the number of iterations was set to 50.
The parameter limit denoting the number of itera-
tions when a solution is not being improved and after
which the solution will be discarded, was set to 5. The
Flower Pollination Algorithm for Detection of Epistasis Associated with a Phenotype
123

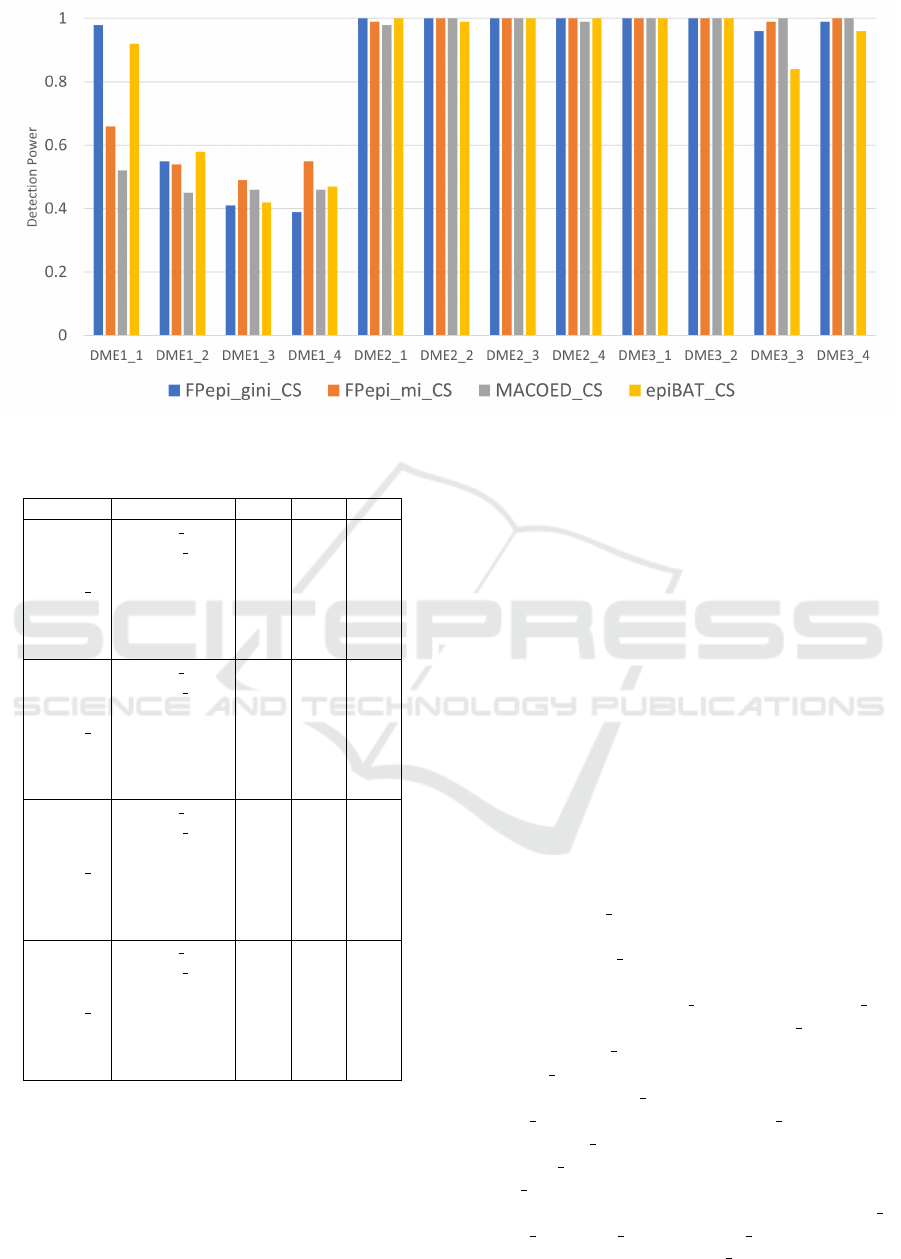
Figure 1: Detection power comparison of potential SNP combinations found before the evaluation stage.
Table 1: Recall, precision and F-measure on the first DME
model.
Model Method R
∗
P
∗
F
∗
DME1 1
FPepi gini 0.05 0.41 0.09
FPepi mi 0.05 0.37 0.09
epiBAT 0.05 0.45 0.09
MACOED 0.03 0.43 0.06
AntEpiSeeker 0.01 0.25 0.02
BEAM 0.03 0.19 0.05
BOOST 0.06 0.1 0.07
DME1 2
FPepi gini 0.06 0.4 0.1
FPepi mi 0.06 0.35 0.1
epiBAT 0.05 0.45 0.09
MACOED 0.06 0.86 0.11
AntEpiSeeker 0 0 0
BEAM 0 0 0
BOOST 0.06 0.11 0.08
DME1 3
FPepi gini 0.19 0.58 0.29
FPepi mi 0.2 0.57 0.3
epiBAT 0.17 0.43 0.25
MACOED 0.26 0.74 0.39
AntEpiSeeker 0.16 0.7 0.26
BEAM 0 0 0
BOOST 0.01 0.01 0.01
DME1 4
FPepi gini 0.21 0.43 0.28
FPepi mi 0.18 0.39 0.25
epiBAT 0.22 0.35 0.27
MACOED 0.34 0.45 0.39
AntEpiSeeker 0.26 0.67 0.37
BEAM 0 0 0
BOOST 0.01 0.02 0.01
∗
The best result is shown in bold.
parameter Q denoting the number of iterations that the
best solution has not been improved, was also set to 5.
Parameters for optimizations of FPA by BPFPA, such
as simplex method parameters and the crossover rate
parameter, were set as recommended in the original
paper (Wang et al., 2016). The significance threshold
α was set to 0.1 as in MACOED and epiBAT experi-
ments.
4.4 Results
Results of BEAM, MACOED, AntEpiSeeker, and
BOOST were taken from MACOED paper (Jing and
Shen, 2014), while the results of epiBAT were taken
from epiBAT paper (Sitar
ˇ
c
´
ık and Luck
´
a, 2019). The
used data were the same, and parameters of FPepi,
such as total population size and the maximum num-
ber of iterations were set the same as in MACOED
and epiBAT, thus allowing fair comparison.
The Figure 1 shows comparison of the detection
power of MACOED, epiBAT, and FPepi variants be-
fore the evaluation stage, in our case, the detection
power is calculated for the candidate set CS as de-
scribed in the paper.
When the genetic heritability was low, for exam-
ple as in DME1 1, Gini score was found to achieve
best results, as it was shown before (Tuo et al., 2016).
Here, both FPepi gini and epiBAT, which use Gini
score, achieved considerably higher detection power
than MACOED and FPepi mi. However, FPepi gini
had better results than epiBAT on DME3 3, but worse
results on DME1 4.
FPepi mi shown better or comparably same
results than FPepi gini on all datasets expect
DME1 1. When comparing FPepi mi with MA-
COED, FPepi mi had lower detection power only
on DME3 3, where the difference was very small.
FPepi mi had considerably higher detection power
than MACOED on the first four models DME1 1,
DME1 2, DME1 3, and DME1 4. Whereas epi-
BAT uses Gini score and FPepi mi does not, epiBAT
BIOINFORMATICS 2021 - 12th International Conference on Bioinformatics Models, Methods and Algorithms
124

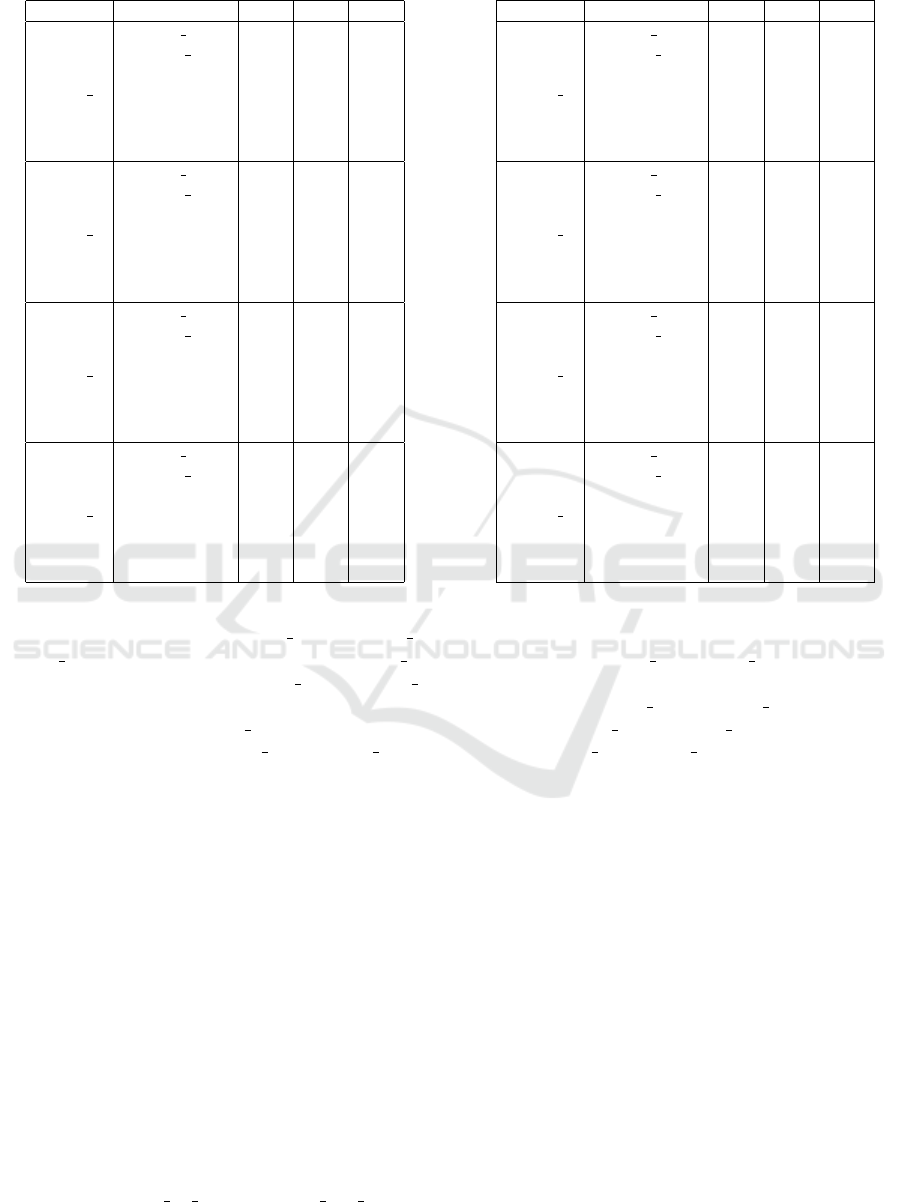
Table 2: Recall, precision and F-measure on the second
DME model.
Model Method R
a
P
a
F
a
DME2 1
FPepi gini 0.88 0.93 0.9
FPepi mi 0.88 0.95 0.91
epiBAT 0.88 0.92 0.9
MACOED 0.43 0.98 0.6
AntEpiSeeker 0.35 0.92 0.51
BEAM 0.58 0.72 0.64
BOOST 0.59 0.51 0.55
DME2 2
FPepi gini 0.97 0.98 0.98
FPepi mi 0.97 0.99 0.98
epiBAT 0.98 0.97 0.98
MACOED 0.94 1 0.97
AntEpiSeeker 0.82 0.91 0.86
BEAM 0.55 0.48 0.51
BOOST 0.71 0.56 0.63
DME2 3
FPepi gini 0.99 0.99 0.99
FPepi mi 0.99 0.99 0.99
epiBAT 1 1 1
MACOED 1 0.96 0.98
AntEpiSeeker 0.92 0.94 0.93
BEAM 0.2 0.12 0.15
BOOST 0.76 0.51 0.61
DME2 4
FPepi gini 0.99 0.99 0.99
FPepi mi 0.99 0.99 0.99
epiBAT 0.99 0.99 0.99
MACOED 0.99 0.94 0.97
AntEpiSeeker 0.99 0.98 0.99
BEAM 0.03 0.01 0.02
BOOST 0.1 0.12 0.11
a
The best result is in bold.
produced better results than FPepi mi on DME1 1,
DME1 2. In comparison with all tools, FPepi mi
achieved the best results on DME1 3 and DME1 4
datasets, while having considerably lower detection
power only in the first DME1 1 dataset, and slightly
lower detection power in DME1 2 and DME3 3.
Recall, precision and F-measure, are presented in
Table 1, Table 2, and Table 3, for the DME1, DME2
and DME3 model, respectively. The interesting com-
parison is between FPepi and MACOED, as G-test is
used in FPepi, instead of χ
2
test, which is used in MA-
COED. MACOED also fixes the number of degrees of
freedom to eight, i.e. as 9 genotype combinations ex-
ist for a 2-way SNP combination. FPepi on the other
hand modifies the degrees of freedom accordingly to
the quantity of samples in cells. FPepi also uses ad-
ditional filtering technique that filter out SNP com-
binations that are worse than other SNP combination
with which they share at least one SNP. This could
potentially lower recall and precision, as the truly as-
sociated SNP combination was not reported because it
was filtered out, as there was SNP combination shar-
ing SNP with the truly associated SNP combination
and having lower p-value.
Although FPepi mi CS and FPepi gini CS had
Table 3: Recall, precision and F-measure on the third DME
model.
Model Method R
a
P
a
F
a
DME3 1
FPepi gini 1 1 1
FPepi mi 1 1 1
epiBAT 1 1 1
MACOED 1 1 1
AntEpiSeeker 0.97 0.96 0.97
BEAM 0.92 0.77 0.84
BOOST 0.1 0.12 0.11
DME3 2
FPepi gini 1 1 1
FPepi mi 1 1 1
epiBAT 1 1 1
MACOED 1 1 1
AntEpiSeeker 0.98 0.99 0.98
BEAM 0.86 0.75 0.8
BOOST 0.86 0.57 0.69
DME3 3
FPepi gini 0.96 0.97 0.96
FPepi mi 1 1 1
epiBAT 0.87 0.99 0.92
MACOED 1 1 1
AntEpiSeeker 0.88 0.99 0.93
BEAM 0.13 0.32 0.18
BOOST 1 0.63 0.77
DME3 4
FPepi gini 0.99 0.96 0.97
FPepi mi 1 0.98 0.99
epiBAT 0.98 0.96 0.97
MACOED 1 0.99 1
AntEpiSeeker 0.98 0.96 0.97
BEAM 0.03 0.02 0.03
BOOST 0.98 0.65 0.78
a
The best result is in bold.
large differences in detection power in some datasets,
for example in DME1 1 or DME1 4, after evaluation
stage, there were no large differences in recall or pre-
cision between FPepi mi and FPepi gini. Compared
to epiBAT, FPepi mi and FPepi gini shown better re-
sults in DME1 3 or DME3 3.
5 CONCLUSION
This paper presents a new tool for detecting SNP
combinations associated with a phenotype called
FPepi, which uses flower pollination algorithm. As
objective functions, FPepi uses either Gini score and
K2 score in the first variant, or mutual information
score and K2 score in the second variant. Objectives
are optimized in separate populations. G-test is em-
ployed to test the final SNP combinations, that were
found by the flower pollination algorithm.
Results confirmed that Gini score performs well
on models with low heritability, where the FPepi vari-
ant using Gini score outperformed other tools. How-
ever, on other models, the FPepi variant using mutual
information score as the second objective achieved
better results than FPepi variant using Gini score, and
Flower Pollination Algorithm for Detection of Epistasis Associated with a Phenotype
125

also shown better or comparable results than other
tools. After evaluation stage, both variants had not
large differences in their performance, and having
better results than the other tools except MACOED,
which although used older χ
2
test, shown better re-
sults for some datasets.
Further research will concern the evaluation stage,
as results after evaluation stage need to improve.
ACKNOWLEDGEMENTS
The authors would like to thank for financial contri-
bution from the STU Grant scheme for Support of
Young Researchers. This work was partially sup-
ported by the Scientific Grant Agency of The Slovak
Republic, Grant No. VG 1/0458/18, and APVV-16-
0484.
REFERENCES
Abdel-Basset, M. and Shawky, L. A. (2019). Flower polli-
nation algorithm: a comprehensive review. Artificial
Intelligence Review, 52(4):2533–2557.
Easton, D. F. et al. (2007). Genome-wide association study
identifies novel breast cancer susceptibility loci. Na-
ture, 447(7148):1087–1093.
Hindorff, L. A. et al. (2009). Potential etiologic and func-
tional implications of genome-wide association loci
for human diseases and traits. Proceedings of the Na-
tional Academy of Sciences, 106(23):9362–9367.
Jing, P.-J. and Shen, H.-B. (2014). MACOED: a multi-
objective ant colony optimization algorithm for SNP
epistasis detection in genome-wide association stud-
ies. Bioinformatics, 31(5):634–641.
Karaboga, D. and Basturk, B. (2007). A powerful and
efficient algorithm for numerical function optimiza-
tion: artificial bee colony (abc) algorithm. Journal
of Global Optimization, 39(3):459–471.
Kayabekir, A. E. et al. (2018). A Comprehensive Review
of the Flower Pollination Algorithm for Solving Engi-
neering Problems, pages 171–188. Springer Interna-
tional Publishing, Cham.
Mantegna, R. N. (1994). Fast, accurate algorithm for nu-
merical simulation of l
´
evy stable stochastic processes.
Phys. Rev. E, 49:4677–4683.
McDonald, J. H. (2014). G–test of goodness-of-fit. Hand-
book of biological statistics, pages 53–58.
Niel, C., Sinoquet, C., Dina, C., and Rocheleau, G. (2015).
A survey about methods dedicated to epistasis detec-
tion. Frontiers in genetics, 6:285–285.
Salgotra, R. and Singh, U. (2017). Application of muta-
tion operators to flower pollination algorithm. Expert
Systems with Applications, 79:112 – 129.
Sapin, E., Keedwell, E., and Frayling, T. (2015). An ant
colony optimization and tabu list approach to the de-
tection of gene-gene interactions in genome-wide as-
sociation studies [research frontier]. IEEE Computa-
tional Intelligence Magazine, 10(4):54–65.
Shang, J. et al. (2015). An improved opposition-based
learning particle swarm optimization for the detection
of snp-snp interactions. BioMed Research Interna-
tional, 2015:524821.
Sitar
ˇ
c
´
ık, J. and Luck
´
a, M. (2019). epibat: Multi-objective
bat algorithm for detection of epistatic interactions. In
2019 IEEE 15th International Scientific Conference
on Informatics, pages 000237–000242. IEEE.
Sun, Y., Shang, J., Liu, J.-X., Li, S., and Zheng, C.-H.
(2017). epiaco - a method for identifying epistasis
based on ant colony optimization algorithm. BioData
Mining, 10(1):23.
Tuo, S. (2018). Fdhe-iw: A fast approach for detect-
ing high-order epistasis in genome-wide case-control
studies. Genes, 9(9):435.
Tuo, S., Chen, H., and Liu, H. (2019). A survey on swarm
intelligence search methods dedicated to detection of
high-order snp interactions. IEEE Access, 7:162229–
162244.
Tuo, S., Zhang, J., Yuan, X., He, Z., Liu, Y., and Liu, Z.
(2017). Niche harmony search algorithm for detect-
ing complex disease associated high-order snp combi-
nations. Scientific Reports, 7(1):11529.
Tuo, S., Zhang, J., Yuan, X., Zhang, Y., and Liu, Z. (2016).
Fhsa-sed: Two-locus model detection for genome-
wide association study with harmony search algo-
rithm. PLOS ONE, 11(3):1–27.
Wan, X. et al. (2010). Boost: A fast approach to detecting
gene-gene interactions in genome-wide case-control
studies. The American Journal of Human Genetics,
87(3):325–340.
Wang, R., Zhou, Y., Qiao, S., and Huang, K. (2016). Flower
pollination algorithm with bee pollinator for cluster
analysis. Information Processing Letters, 116(1):1 –
14.
Wang, Y., Liu, X., Robbins, K., and Rekaya, R. (2010).
Antepiseeker: detecting epistatic interactions for case-
control studies using a two-stage ant colony optimiza-
tion algorithm. BMC Research Notes, 3(1):117.
Yang, X.-S. (2012). Flower pollination algorithm for global
optimization. In Durand-Lose, J. and Jonoska, N., ed-
itors, Unconventional Computation and Natural Com-
putation, pages 240–249, Berlin, Heidelberg. Springer
Berlin Heidelberg.
Yuan, L., Yuan, C.-A., and Huang, D.-S. (2017). Faacose:
A fast adaptive ant colony optimization algorithm for
detecting snp epistasis. Complexity, 2017.
Zhang, Y. and Liu, J. (2007). Bayesian inference of epistatic
interactions in case-control studies. Nature genetics,
39:1167–73.
BIOINFORMATICS 2021 - 12th International Conference on Bioinformatics Models, Methods and Algorithms
126