
Discounted Markov Decision Processes with Fuzzy Rewards Induced by
Non-fuzzy Systems
Karla Carrero-Vera
1
, Hugo Cruz-Su
´
arez
1
and Ra
´
ul Montes-de-Oca
2
1
Benem
´
erita Universidad Aut
´
onoma de Puebla, Av. San Claudio y R
´
ıo Verde,
Col. San Manuel, CU, Puebla, Pue. 72570, Mexico
2
Departamento de Matem
´
aticas, Universidad Aut
´
onoma Metropolitana-Iztapalapa, Av. San Rafael Atlixco 186,
Keywords:
Markov Decision Processes, Dynamic Programming, Optimal Policy, Fuzzy Sets, Triangular Fuzzy Numbers.
Abstract:
This paper concerns discounted Markov decision processes with a fuzzy reward function triangular in shape.
Starting with a usual and non-fuzzy Markov control model (Hern
´
andez-Lerma, 1989) with compact action
sets and reward R, a control model is induced only substituting R in the usual model for a suitable triangular
fuzzy function
˜
R which models, in a fuzzy sense, the fact that the reward R is “approximately” received. This
way, for this induced model a discounted optimal control problem is considered, taking into account both a
finite and an infinite horizons, and fuzzy objective functions. In order to obtain the optimal solution, the partial
order on the α-cuts of fuzzy numbers is used, and the optimal solution for fuzzy Markov decision processes
is found from the optimal solution of the corresponding usual Markov decision processes. In the end of the
paper, several examples are given to illustrate the theory developed: a model of inventory system, and two
others more in an economic and financial context.
1 INTRODUCTION
In various applied areas, such as engineering, opera-
tions research, economics, finance, and artificial in-
telligence, among others, the data required to propose
a mathematical model present ambiguity, vagueness
or approximate characteristics of the problem of in-
terest (see, for instance, (Fakoor et al., 2016), (Efendi
et al., 2018)). Under this context, it is possible to find
in the literature the approach of fuzzy numbers to in-
corporate this kind of characteristics or assertions to
mathematical models. The basic theory on the sub-
ject of fuzzy numbers was proposed by L. Zadeh in
his seminal article written in 1965, which is entitled:
“Fuzzy Sets” (Zadeh, 1965). Subsequently, various
research articles and texts referring to the fuzzy the-
ory can be found in the literature on the subject, more-
over, it is possible to locate extensions of the theory in
other fields of mathematical sciences, such as control
theory, see (Driankov et al., 2013).
In this manuscript, the authors provide a Markov
decision process (MDP, in plural MDPs) with a finite
state space, compact action sets and fuzzy character-
istics in its payoff or reward function. The idea is the
following: a crisp Markov control model (MCM) is
considered, that is, an MCM of the type that has been
analyzed in (Hern
´
andez-Lerma, 1989), with reward R
as a basis, and a new MCM is induced changing only
R for a reward function with fuzzy values. Specifi-
cally, the authors assume that the fuzzy reward func-
tion is triangular. This way, the fuzzy control prob-
lem consists of determining a control policy that max-
imizes the expected total discounted fuzzy reward,
where the maximization is made with respect to the
partial order on the α-cuts of fuzzy numbers.
It is important to mention that triangular fuzzy
numbers have been extensively studied and applied in
fuzzy control (Pedrycz, 1994). Furthermore, the tri-
angular fuzzy numbers could be used to approximate
an arbitrary fuzzy number (see (Ban, 2009) and (Zeng
and Li, 2007)).
The methodology that is followed in this article
to guarantee the existence of optimal policies in the
fuzzy problem consists in applying the existence of
optimal policies and the validity of dynamic program-
ming for the crisp control problem, as well as certain
properties of the fuzzy triangular numbers.
To illustrate the theory developed several exam-
ples are given: a model of inventory system, and two
more in an economic and financial context.
In a short summary, the main contribution of the
Carrero-Vera, K., Cruz-Suárez, H. and Montes-de-Oca, R.
Discounted Markov Decision Processes with Fuzzy Rewards Induced by Non-fuzzy Systems.
DOI: 10.5220/0010231400490059
In Proceedings of the 10th International Conference on Operations Research and Enterprise Systems (ICORES 2021), pages 49-59
ISBN: 978-989-758-485-5
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
49

article is to present an extension of the standard dis-
counted MDPs to discounted MDPs with fuzzy re-
wards. In a general way, a fuzzy reward considered
models the fact that a non-fuzzy reward is “approxi-
mately” received (in a fuzzy sense), and it is obtained
that the optimal control of the fuzzy MDP coincides
with the optimal control of the non-fuzzy one and the
optimal value function for the fuzzy MDP is “approx-
imately” (in a fuzzy sense) the optimal value function
of the non-fuzzy MDP (see Theorem 4.6 and Remark
4.7, below).
Research works related to the topic developed
here are the following: (Kurano et al., 2003) and
(Semmouri et al., 2020). In (Kurano et al., 2003)
a fuzzy control problem with finite state and action
spaces is examined. Under this same context, (Sem-
mouri et al., 2020) presents the problem of maximiz-
ing the total expected discounted reward through the
use of ranking functions.
The paper is organized as follows. Section 2
presents the basic results about fuzzy numbers (arith-
metic, metric, order, among others) as well as the
notation used in subsequent sections. The following
section presents a sketch of definitions and results re-
garding the control problem under the criterion of ex-
pected total discounted reward for both, finite and in-
finite horizons. Section 4 presents the main results
of the paper. In this section the theory on the fuzzy
control problem is studied under the criterion of a to-
tal expected discounted reward. Finally, in Sections
5 and 6 examples to illustrate the theory developed
are given. One of them refers to an inventory con-
trol system considered in a fuzzy environment; this
example is taken into account with a finite planning
horizon. The other two examples refer to finance and
economics issues addressed in (Webb, 2007) for the
crisp versions, and then the respective fuzzy versions
are given in this document. Both examples contem-
plate an infinite horizon.
2 BASIC THEORY OF FUZZY
NUMBERS
In this section definitions and results about the fuzzy
theory are presented. The fuzzy set theory was pro-
posed by Zadeh in 1965 (Zadeh, 1965), an interesting
feature of using a fuzzy approach is that it allows the
use of linguistic variables such as: low, very, high,
advisable, highly risky, etc. The following definition
describes the concept of a fuzzy number.
Definition 2.1. Let Θ be a non-empty set. Then a
fuzzy set A on Θ is defined in terms of the member-
ship function µ, which assigns to each element of Θ
a real value from the interval [0,1]. Consequently a
fuzzy set A can be expressed as a set of ordered pairs:
{(x,µ(x)) : x ∈ Θ}.
The value µ(x) in the previous definition repre-
sents the degree to which the element x verifies the
characteristic property of a set A ⊂ Θ. Then, using
the membership function, a fuzzy number can be de-
fined as follows.
Definition 2.2. A fuzzy number A is a fuzzy set de-
fined on the real numbers R characterized by means
of a membership function µ, µ : R −→ [0,1],
µ(x) =
0, x ≤ a
l(x), a < x ≤ b
1, b < x ≤ c
r(x), c < x ≤ d
0, d < x,
(1)
where a,b,c, and d are real numbers, l is a non-
decreasing function and r is a non-increasing func-
tion. The functions l and r are called the left and right
side of fuzzy number A, respectively.
In the manuscript the following class of fuzzy
numbers are considered.
Definition 2.3. A fuzzy number A is called a triangu-
lar fuzzy number if its membership function has the
following form:
µ(x) =
0, x < a
x − a
β − a
, a ≤ x ≤ β
γ − x
γ − β
, β ≤ x ≤ γ
0, x > γ,
(2)
i.e. making l(x) =
x − a
β − a
and r(x) =
γ − x
γ − β
in (1),
where a, γ and β are real numbers such that a < β < γ.
In the subsequent sections, a triangular fuzzy number
is denoted by µ = (a,β,γ).
The next example shows a triangular fuzzy num-
ber.
Example 2.4. Figure 1 illustrates a graphical rep-
resentation of the triangular fuzzy number A =
(1/2,3,7).
Definition 2.5. Let A be a fuzzy number with a mem-
bership function µ and let α be a real number of the
interval [0,1]. Then the α-cut of A, denoted by µ
α
, is
defined to be the set {x ∈ Θ : µ(x) ≥ α}.
Remark 2.6. a) Equivalently to Definition 2.2, a
fuzzy number is a fuzzy set with a normal mem-
bership function, i.e. there exists x ∈ Θ such that
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
50
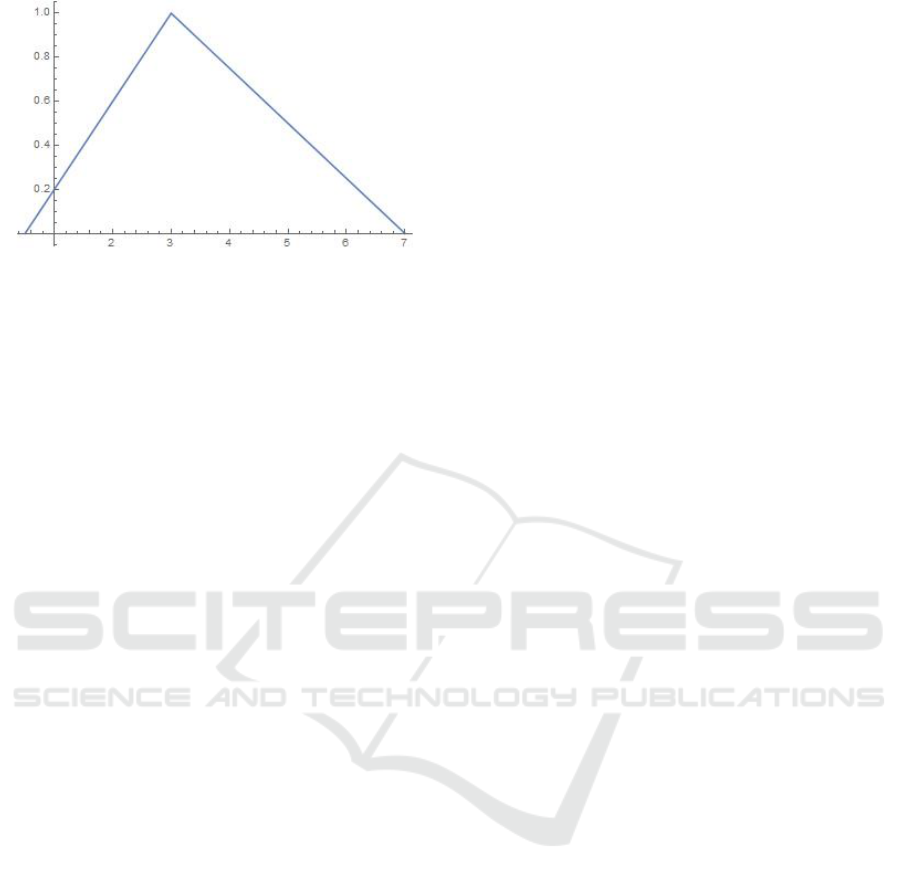
Figure 1: A triangular fuzzy number.
µ(x) = 1 (Klir and Yuan, 1996). Let F(R) denote
the set of all fuzzy numbers.
b) According to Definition 2.2 and Definition 2.5,
for a fuzzy number A, its α-cut set, µ
α
=
[A
−
(α),A
+
(α)] is a closed interval, where
A
−
(α) = inf{x : µ
A
(x) ≥ α} and A
+
(α) = sup{x :
µ
A
(x) ≥ α}. Consequently, for each α ∈ [0,1],
(a,β,γ)
α
= [(β − a)α + a,γ − (γ − β)α] for trian-
gular fuzzy numbers.
Definition 2.7. Let ? denote any of the four basic
arithmetic operations and let A and B be fuzzy num-
bers. Then, a fuzzy set is defined on R, A ? B, by the
expression
µ
A?B
(u) = sup
u=x?y
min{µ
A
(x),µ
B
(y)}, (3)
for all u ∈ R.
A direct consequence of the previous definition is
the following result.
Lemma 2.8. If A = (a
l
,a
m
,a
u
) and B = (b
l
,b
m
,b
u
)
are two triangular fuzzy numbers, then the basic op-
erators for triangular fuzzy numbers are as it follows,
a) A ⊕ B = (a
l
+ b
l
,a
m
+ b
m
,a
u
+ b
u
);
b) A B = (a
l
− b
u
,a
m
− b
m
,a
u
− b
l
);
c) A ⊗ B = (min{a
l
b
l
,a
l
b
u
,a
u
b
l
,a
u
b
u
},a
m
b
m
,
max{a
l
b
l
,a
l
b
u
,a
u
b
l
,a
u
b
u
});
d) A B = (min{a
l
/b
l
,a
l
/b
u
,a
u
/b
l
,a
u
/b
u
}),
a
m
/b
m
,max{a
l
/b
l
,a
l
/b
u
,a
u
/b
l
,a
u
/b
u
}).
e) λA = (λa
l
,λa
m
,λa
u
), for each λ ≥ 0.
Let D denote the set of all closed bounded inter-
vals A = [a
l
,a
u
] on the real line R. For A,B ∈ D,
A = [a
l
,a
u
], B = [b
l
,b
u
] define
d(A,B) = max(
|
a
l
− b
l
|
,
|
a
u
− b
u
|
). (4)
It is possible to check that d defines a metric on D
and (D,d) is a complete metric space.
Furthermore, for A,B ∈ D define: A . B if and
only if a
l
≤ b
l
and a
u
≤ b
u
, where A = [a
l
,a
u
] and
B = [b
l
,b
u
]. Note that “.” is a partial order in D.
Now, define
ˆ
d : F(R) × F(R) −→ R by
ρ(µ,ν) = sup
α∈[0,1]
d(µ
α
,ν
α
), (5)
with µ,ν ∈ F(R). It is straightforward to see that ρ is
a metric in F(R) (Kurano et al., 2003).
Furthermore, for µ,ν ∈ F(R) define
µ 4 ν i f and only i f µ
α
. ν
α
(6)
with α ∈ [0,1].
Remark 2.9. Observe that “4” corresponds to a
partial order of F(R). A partial order is a reflexive,
transitive and antisymmetric binary relation (Alipran-
tis and Border, 2006). In this case, (F(R),4) is a par-
tially ordered set or poset. Moreover, if ˜x satisfies that
x 4 ˜x for each x ∈ F(R), then ˜x is an upper bound for
F(R). If the set of upper bounds of F(R) has a least
element, then this element is called the supremum of
F(R) (Topkis, 1998).
The proof of the following result can be consulted
in (Puri et al., 1993).
Lemma 2.10. The metric space (F(R),ρ) is com-
plete.
Definition 2.11. A sequence {l
n
} of fuzzy numbers is
said to be convergent to the fuzzy number l, written as
lim
n−→∞
l
n
= l, if for every ε > 0 there exists a positive
integer N such that ρ(l
n
,l) < ε for n > N.
The following result is an extension of Lemma 2.8
and its proof is straightforward.
Lemma 2.12. For triangular fuzzy numbers the fol-
lowing statements hold:
a) If {(a
n
l
,a
n
m
,a
n
u
) : 1 ≤ n ≤ N} where N is a positive
integer, then
N
M
n=1
(a
n
l
,a
n
m
,a
n
u
) = (
N
∑
n=1
a
n
l
,
N
∑
n=1
a
n
m
,
N
∑
n=1
a
n
u
).
b) If u
n
= {(a
n
l
,a
n
m
,a
n
u
) : 1 ≤ n} and
∑
∞
n=1
a
n
i
<
∞, i ∈ {l,m,u}, then S
n
:=
L
n
m=1
X
m
,n ≥
1, converges to the triangular fuzzy number
(
∑
∞
n=1
a
n
l
,
∑
∞
n=1
a
n
m
,
∑
∞
n=1
a
n
u
).
The next remark provides the Zadeh’s extension
principle which provides a general method for fuzzi-
fication of non-fuzzy mathematical concepts.
Remark 2.13 (Zadeh’s Extension Principle). Let L be
a function such that L : X −→ Z and let A be a fuzzy
subset of Θ with a membership function µ. Zadeh’s
extension of L is the function
ˆ
L which, applied to A
Discounted Markov Decision Processes with Fuzzy Rewards Induced by Non-fuzzy Systems
51

gives the fuzzy subset
ˆ
L(A) of Z with the membership
function given by
ˆµ(z) =
sup
x∈L
−1
(z)
µ(x), L
−1
({z}) 6= ∅
0, L
−1
({z}) = ∅.
(7)
Observe that, if A is a fuzzy subset of Θ, with the mem-
bership function µ, and if L is bijective, then the mem-
bership function of
ˆ
L(A) is given as follows
ˆµ(z) = sup
{x:L(x)=z}
µ(x)
= sup
{x∈L
−1
(z)}
µ(x)
= µ(L
−1
(z)).
Now, a fuzzy random variable will be defined. In this
case, the definition proposed in (Puri et al., 1993) will
be adopted.
Definition 2.14. Let (Ω, F ) be a measurable space
and (R, B(R)) be the measurable space of the real
numbers. A fuzzy random variable is a function
˜
X :
Ω −→ F(R) such that for all (α,B) ∈ [0,1] × B (R),
{ω ∈ Ω :
˜
X
α
∩ B 6= ∅} ∈ F . Equivalently,
˜
X must be
viewed as a generalized interval with a membership
function µ and α-cut: X(ω)
α
= [X
−
(ω),X
+
(ω)].
Definition 2.15. Let (Ω,F ,P) be a probability space
and let
˜
X be a discrete fuzzy random variable with
the range { ˜s
1
, ˜s
2
,..., ˜s
l
} ⊆ F(R). The mathematical
expectation of
˜
X is a fuzzy number, E(
˜
X), such that
E(
˜
X) =
l
M
i=1
˜s
i
P(
˜
X = ˜s
i
). (8)
A proof of the following result should be consulted in
(Puri et al., 1993).
Lemma 2.16. Let
˜
X and
˜
Y be discrete fuzzy random
variables with finite range. Then
a) E[
˜
X] ∈ F(R).
b) E[
˜
X +
˜
Y ] = E[
˜
X] + E[
˜
Y ].
c) E[λ
˜
X] = λE[
˜
X], λ ≥ 0.
3 DISCOUNTED MARKOV
DECISION PROCESSES WITH
FUZZY REWARD FUNCTIONS
In this section the theory on Markov decision pro-
cesses necessary for this article is introduced. This
kind of processes are used to model dynamic systems
in a discrete time. Firstly the optimal control prob-
lem with a crisp reward is presented, later the reward
function is changed by a fuzzy reward function and
the new optimal control problem is given.
3.1 Markov Decision Models
Detailed literature on the theory of Markov deci-
sion processes can be consulted in the references:
(Hern
´
andez-Lerma, 1989) and (Puterman, 1994).
A Markov decision model is characterized by the
following five-tuple:
M := (X,A,{A(x) : x ∈ X}, Q, R), (9)
where
a) X is a finite set, which is called the state space.
b) A is a Borel space, A is denominated the control
or action space.
c) {A(x) : x ∈ X} is a family of nonempty subsets
A(x) of A, whose elements are the feasible ac-
tions.
c) Q is the transition law, which is a stochastic ker-
nel on X given K := {(x,a) : x ∈ X ,a ∈ A(x)}, K is
denominated the set of feasible state-actions pairs.
d) R : K −→ R is the one-step reward function.
Now, given a Markov control Model M, the concept
of policy will be introduced. A policy is a sequence
π = {π
t
: t = 0,1,...} of stochastic kernels π
t
on the
control set A given the history H
t
of the process up to
time t, where H
t
:= K × H
t−1
,t = 1, 2,... and H
0
=
X. The set of all policies will be denoted by Π. A
deterministic Markov policy is a sequence π = { f
t
}
such that f
t
∈ F, for t = 0,1,..., where F denotes the
set of functions f : X −→ A such that f (x) ∈ A(x),
for all x ∈ X. A Markov policy π = { f
t
} is said to be
stationary if f
t
is independent of t, i.e., f
t
= f ∈ F, for
all t = 0, 1, .... In this case, π is denoted by f and F is
denominated the set of stationary policies.
Let (Ω,F ) be the measurable space consisting
of the canonical sample space Ω = H
∞
:= (X ×
A)
∞
and F be the corresponding product σ-algebra.
The elements of Ω are sequences of the form ω =
(x
0
,a
0
,x
1
,a
1
,...) with x
t
∈ X and a
t
∈ A for all t =
0,1,.... The projections x
t
and a
t
from Ω to the sets
X and A are called state and action variables, respec-
tively.
Let π = {π
t
} be an arbitrary policy and µ be an
arbitrary probability measure on X called the initial
distribution. Then, by the theorem of C. Ionescu-
Tulcea (Hern
´
andez-Lerma, 1989), there is a unique
probability measure P
π
µ
on (Ω,F ) which is supported
on H
∞
, i.e., P
π
µ
(H
∞
) = 1. The stochastic process
(Ω,F , P
π
µ
,x
t
) is called a discrete-time Markov control
process or a Markov decision process.
The expectation operator with respect to P
π
µ
is de-
noted by E
π
µ
. If µ is concentrated at the initial state
x ∈ X, then P
π
µ
and E
π
µ
are written as P
π
x
and E
π
x
, re-
spectively.
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
52

The transition law of a Markov control process
(see 9) is often specified by a difference equation of
the form
x
t+1
= F(x
t
,a
t
,ξ
t
), (10)
t = 0, 1,2,..., with x
0
= x ∈ X known, where {ξ
t
} is
a sequence of independent and identically distributed
(i.i.d.) random variables with values in a finite space
S and a common distribution ∆, independent of the
initial state x
0
. In this case, the transition law Q is
given by
Q(B|x,a) = E[I
B
(F(x,a,ξ))],
B ⊆ X, (x,a) ∈ K, E is the expectation with respect to
distribution ∆, ξ is a generic element of the sequence
{ξ
t
} and I
B
(·) denotes the indicator function of the set
B.
Definition 3.1. Let (X ,A,{A(x) : x ∈ X },Q,R) be a
Markov model, then the expected total discounted re-
ward is defined as follows:
v(π,x) := E
π
x
"
∞
∑
t=0
β
t
R(x
t
,a
t
)
#
, (11)
π ∈ Π and x ∈ X, where β ∈ (0,1) is a given discount
factor. Furthermore, the T -stage expected total dis-
counted reward, for each x ∈ X and π ∈ Π, is defined
as follows:
v
T
(π,x) := E
π
x
"
T −1
∑
t=0
β
t
R(x
t
,a
t
)
#
, (12)
where T is a positive integer.
Definition 3.2. The optimal value function is defined
as
V (x) := sup
π∈Π
V (π,x), (13)
x ∈ X. Then the optimal control problem is to find a
policy π
∗
∈ Π such that
v(π
∗
,x) = V (x),
x ∈ X, in which case, π
∗
is said to be the optimal pol-
icy. Similar definitions can be stated analogously for
v
T
. In this case, V
T
denotes the optimal value func-
tion.
Assumption 3.3. a) For each x ∈ X , A(x) is a com-
pact set on B(A), where B(A) is the Borel σ-
algebra of space A.
b) The reward function R is a non negative and
bounded function.
c) For every x,y ∈ X, the mappings a 7→ R(x,a) and
a 7→ Q(y|x, a) are continuous in a ∈ A(x).
The proof of the following theorem can be con-
sulted in (Hern
´
andez-Lerma, 1989).
Theorem 3.4 (Dynamic Programming). Under As-
sumption 3.3 the following statements hold:
a) Define W
T
(x) = 0 and for each n = T − 1, ..., 1, 0,
consider
W
n
(x) = max
a∈A(x)
{R(x,a) + βE[W
n+1
(F(x,a,ξ))]}.
(14)
x ∈ X. Then for each n = 0, 1, ..., T −1 there exists
f
n
∈ F such that
W
n
(x) = R(x, f
n
(x)) + βE[W
n+1
(F(x, f
n
(x),ξ))],
x ∈ X. In this case, π
∗
= { f
0
,..., f
T −1
} is a Marko-
vian optimal policy and v
T
(π
∗
,x) = W
0
(x), x ∈ X .
b) The optimal value function V , satisfies the follow-
ing dynamic programming equation:
V (x) = max
a∈A(x)
{R(x,a)+βE[V (F(x,a,ξ))]}, (15)
x ∈ X.
c) There exists a policy f
∗
∈ F such that the control
f
∗
(x) ∈ A(x) attains the maximum in (15), i.e. for
all x ∈ X,
V (x) = R(x, f
∗
(x)) + βE[V (F(x, f
∗
(x),ξ))].
(16)
d) Define the value iteration functions as follows:
V
n
(x) = min
a∈A(x)
{
c(x,a) + βE[V
n−1
(F(x, f
∗
(x),ξ))]
}
,
(17)
for all x ∈ X and n = 1,2,. . ., with V
0
(·) = 0. Then
the value iteration functions converge point-wise
to the optimal value function V , i.e.
lim
n→∞
V
n
(x) = V (x),
x ∈ X.
3.2 Objective Functions
Consider a Markov decision model M = (X,A,{A(x) :
x ∈ X },Q,
˜
R), where the first four components are the
same as in the model given in (9). The fifth compo-
nent corresponds to a fuzzy reward function on K.
The evolution of a stochastic fuzzy system is as
follows: if the system is in the state x
t
= x ∈ X at time
t and the control a
t
= a ∈ A(x) is applied, then two
things happen:
a) a fuzzy reward
˜
R(x,a) is obtained.
b) the system jumps to the next state x
t+1
according
to the transition law Q, i.e.
Q(B|x,a) = Prob(x
t+1
∈ B|x
t
= x,a
t
= a),
with B ⊆ X.
Discounted Markov Decision Processes with Fuzzy Rewards Induced by Non-fuzzy Systems
53

For each policy π ∈ Π and state x ∈ X , let
˜v
T
(π,x) :=
T −1
M
t=0
β
t
˜
E
π
x
˜
R(x
t
,a
t
)
, (18)
where T is a positive integer and
˜
E
π
x
is the expectation
with respect to
˜
P
π
x
and its expectation of a fuzzy ran-
dom variable is defined by (8). The expression given
in (18) is called the T -stage fuzzy reward. Further-
more, the following objective function will be consid-
ered:
˜v(π,x) :=
∞
M
t=0
β
t
˜
E
π
x
˜
R(x
t
,a
t
)
. (19)
In this way, the control problem of interest is the max-
imization of the finite/infinite horizon expected total
discounted fuzzy reward (see (18) and (19), respec-
tively). In the next section it will be proved that (18)
converges to the objective function (19) with respect
to the metric ρ (see (5)). The following assumption is
considered for the reward function of fuzzy model M.
Assumption 3.5. Let B,C and D be real numbers,
such that 0 < B < C < D. It will be assumed that the
fuzzy reward is a triangular fuzzy number (see Defini-
tion 2.3), specifically
˜
R(x,a) = (BR(x,a),CR(x,a),DR(x,a)) (20)
for each (x, a) ∈ K, where R : K −→ R is the reward
function of the model introduced in Section 3.1.
Remark 3.6. Observe that, under Assumption 3.5
and Lemma 2.12, the T -stage fuzzy reward (18) is a
triangular fuzzy number.
4 OPTIMAL CONTROL
PROBLEM WITH FUZZY
REWARDS
In this section results will be presented which refer
to the convergence of the T -stage fuzzy reward (18)
to the infinite horizon expected total discounted fuzzy
reward (19). Later, the existence of optimal policies
and validity of dynamic programming will be verified.
Lemma 4.1. For each π ∈ Π and x ∈ X,
lim
T −→∞
ρ( ˜v
T
, ˜v) = 0,
where ρ is the Hausdorff metric (see (5)).
Proof. Let π ∈ Π and x ∈ X fixed. To simplify the
notation in this proof v = v(π, x) and v
T
= v
T
(π,x)
will be denoted. Then, according to (18) and (20) the
α-cut of the fuzzy reward function, is given by
∆
T
: = (Bv
T
,Cv
T
,Dv
T
)
α
= [B(1 − α)v
T
+ αCv
t
,D(1 − α)v
T
+ αCv
T
].
Analogously, the α-cut of (19) is given by
∆ : = (Bv,Cv, Dv)
α
= [B(1 − α)v + αCv, D(1 − α)v + αCv].
Hence, by (5), it is obtained that
ρ(∆
T
,∆) = sup
α∈[0,1]
d(∆
T
α
,∆
α
).
Now, due to the identity max(c,b) = (c + b +
|
b − c
|
)/2 with b,c ∈ R, it yields that
d(∆
T
α
,∆
α
) = (1 − α)D(v − v
T
) + αC(v − v
T
).
Then,
ρ(∆
T
,∆) = sup
α∈[0,1]
(v − v
T
)(D − α(D −C))
= (v − v
T
)D.
(21)
Therefore, when T goes to infinity in (21), it con-
cludes that
lim
T −→∞
ρ( ˜v
T
, ˜v) = lim
T −→∞
(v − v
T
)D
= 0.
The second equality is a consequence of the domi-
nated convergence theorem (see (11) and (12)).
Definition 4.2. The optimal control fuzzy problem
consists in determining a policy π
∗
∈ Π such that
˜v(π,x) 4 ˜v(π
∗
,x),
for all π ∈ Π and x ∈ X . In consequence,
˜v(π
∗
,x) = sup
π∈Π
˜v(π,x),
for all x ∈ X (see Remark 2.9). In this case, the opti-
mal fuzzy value function is defined as follows:
˜
V (x) = ˜v(π
∗
,x),
x ∈ X and π
∗
is called the optimal policy of the fuzzy
optimal control problem. Similar definitions can be
stated for ˜v
T
, the T -stage fuzzy reward, in this case
the optimal fuzzy value is denoted by
˜
V
T
.
A direct consequence of a previous definition and
Theorem 3.4 is the next result.
Theorem 4.3. Under Assumptions 3.3 and 3.5 the fol-
lowing statements hold.
a) The optimal policy π
∗
of the crisp finite optimal
control problem (see (12)) is the optimal policy for
˜v
T
, i.e. ˜v
T
(π
∗
,x) = sup
π∈Π
˜v
T
(π,x) for all π ∈ Π
and x ∈ X.
b) The optimal fuzzy value function is given by
˜
V
T
(x) = (BV
T
(x),CV
T
(x),DV
T
(x)), (22)
x ∈ X, where
˜
V
T
(x) = sup
π∈Π
˜v
T
(π,x), x ∈ X.
Theorem 4.4. Under Assumptions 3.3 and 3.5 the fol-
lowing statements hold:
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
54

a) The optimal policy of the fuzzy control problem
is the same as the optimal policy of the optimal
control problem.
b) The optimal fuzzy value function is given by
˜
V (x) = (BV (x),CV (x),DV (x)), x ∈ X . (23)
Proof. a) Let π ∈ Π and x ∈ X be fixed. First, ob-
serve that (19) is equivalent to
˜v(π,x) := (Bv(π, x),Cv(π, x), Dv(π, x)),
as a consequence of Assumption 3.5. Then, the
α-cut of ˜v(π,x) is given by
˜v(π,x)
α
= [Bv(π,x) + α(C − B)v(π,x),Dv(π,x)+
α(D −C)v(π,x)].
Now, by Theorem 3.4, there exists f
∗
∈ F such
that
Bv(π,x) + α(C − B)v(π,x) ≤ Bv( f
∗
(x),x)+
α(C − B)v( f
∗
(x),x),
Bv(π,x) + α(D −C)v(π,x) ≤ Dv( f
∗
(x),x)+
α(D −C)v( f
∗
(x),x)
and since x ∈ X and π ∈ Π are arbitrary, the result
follows, due to Definition 4.2.
b) By Theorem 4.4 a), it follows that
˜
V (x) = (Bv( f
∗
(x),x),Cv( f
∗
(x),x),Dv( f
∗
(x),x)),
for each x ∈ X, thus applying Theorem 3.4, it is
concluded that
˜
V (x) = (BV (x),CV (x),DV (x)), x ∈ X .
It is important to observe that Assumption 3.5 could
be changed for the following one:
Assumption 4.5. Let B and D be real numbers, such
that 0 < B < R(x,a) < D for all x ∈ X and a ∈ A(x). It
will be assumed that the fuzzy reward is a triangular
fuzzy number of the type:
˜
R(x,a) = (B,R(x,a),D) (24)
for each (x, a) ∈ K, where R : K −→ R is the reward
function of the model introduced in Section 3.1.
Note that it is possible to prove with similar ideas to
the ones given in the proof of Theorem 3.5 the follow-
ing result:
Theorem 4.6. Under Assumptions 3.3 and 4.5 the fol-
lowing statements hold:
a) The optimal policy of the fuzzy control problem
is the same as the optimal policy of the non-fuzzy
optimal control problem.
b) The optimal fuzzy value function is given by
˜
V (x) = (
B
1 − β
,V (x),
D
1 − β
), (25)
x ∈ X.
Remark 4.7. Using Theorem 4.6, the main interpre-
tation of the fuzzy extension presented here is ob-
tained: the original non- fuzzy reward R is substi-
tuted by the fuzzy reward
˜
R(·,·) = (B,R(·,·), D) which
modelled the fact that “approximately” R, measured
in a fuzzy sense is gotten, and it is deduced that the
optimal control of the fuzzy MDP coincides with the
optimal control of the non-fuzzy one and the optimal
value function for the fuzzy MDP is “approximately”
(in a fuzzy sense) the optimal value function of the
non-fuzzy MDP.
5 A FUZZY INVENTORY
CONTROL SYSTEM
In this section, first a classical example of inventory
control system (Puterman, 1994) will be presented,
later a triangular fuzzy inventory control system will
be introduced. The optimal solution of the fuzzy
inventory is obtained by an application of Theorem
4.3 and the solution of the crisp inventory system.
The following example is addressed in (Puterman,
1994), below there is a summary of the points of
interest to introduce its fuzzy version. Consider
the following situation, in a warehouse where every
certain period of time the manager carries out an
inventory to determine the quantity of product stored.
Based on such information, a decision is made
whether or not to order a certain amount of additional
product from a supplier. The manager’s goal is
to maximize the profit obtained. The demand for
the product is assumed to be random with known
probability distribution. The following assumptions
will be treated to propose the mathematical model.
Inventory Assumptions.
a) The decision to additional order is made at the
beginning of the period and is delivered immedi-
ately.
b) Product demands are received throughout the pe-
riod of time but are fulfilled in the last instant of
the time of the period.
c) There are no unfilled orders.
c) Revenues and the distribution of demand do not
vary with the period.
Discounted Markov Decision Processes with Fuzzy Rewards Induced by Non-fuzzy Systems
55

d) The product is only sold in whole units.
e) The warehouse has a capacity for M units, where
M is a positive integer.
Then, under previous assumption, the state space is
given by X := {0,1,2,..., M}, the action space and ad-
missible action set are given by A := {0, 1, 2, ...} and
A(x) := {0, 1,2,...,M − x}), x ∈ X, respectively.
Now, consider the following variables: let x
t
de-
note the inventory at time t = 0,1,..., the evolution
of the system is modeled by the following dynamic
system Lindley kind:
x
t+1
= (x
t
+ a
t
− D
t+1
)
+
, (26)
with x
0
= x ∈ X known, where
a) a
t
denotes the control or decision applied in the
instant t and it represents the quantity ordered by
the inventory manager (or decision maker).
b) The sequence
{
D
t
}
is conformed by indepen-
dent and identically distributed non-negative ran-
dom variables with common distribution p
j
:=
P(D = j), j = 0,1,..., where D
t
denotes the de-
mand within the period of time t.
Observe that the difference equation given in (26) in-
duces a stochastic kernel defined on X given K :=
{
(x,a) : x ∈ X ,a ∈ A(x)
}
, as follows
Q(X
t+1
∈ (−∞, y])|X
t
= x,a
t
= a) = 1 − ∆(x + a − y),
where ∆ is the distribution of D with x ∈ X, y, a ∈
{0,1,...} and Q(X
t+1
∈ (−∞,y])|X
t
= x,a
t
= a) = 0,
if x ∈ X, a ∈ {0, 1, ...} and y < 0. Then it follows that
Q(X
t+1
= y|x,a) =
0 i f M ≥ y > x + a
p
x+a−y
i f M ≥ x + a ≥ y > 0
q
x+a
i f M ≥ x + a, y = 0
The step reward function is given by R(x,a) =
E[H(x + a − (x + a − D)
+
)], (x,a) ∈ K, where H :
{0,1,...} → {0,1,...} is the revenue function, which
is a known function and D is a generic element of
the sequence {D
t
}. Equivalently, R(x,a) = F(x + a),
(x,a) ∈ K, where
F(u) :=
u−1
∑
k=0
H(k)p
k
+ H(u)q
u
, (27)
with q
u
:=
∑
∞
k=u
p
k
. The objective in this section is
to maximize the total discounted reward with a finite
horizon, see (18).
In particular, suppose that the horizon is T = 50,
the state space X = {0,1,...,10}, the revenue function
H(u) = 10u and the transition law is given in Figure
2. Then, in accordance with Theorem 4.3, which was
programmed in the statistical software R using the
next algorithm:
Algorithm: To calculate the optimal value and opti-
mal policy.
Input: MDP
Output: The optimal value vector.
An optimal policy
Initialize W
N
(x,A) = 0, W
∗
N
(x) = 0,
K
N
(x) = W
∗
N
(x).
t = N − 1
repeat
for x ∈ S do
f
x
= 0
a(x) = f
x
W (x,a(x)) = R(x,a(x))+
β
∑
Z
i=0
Q(y|x + a(x))W
t+1
(y, 0)
A(x) = 1,...,M − x
for a ∈ A(x) do
W
t
(x,a) = R(x, a)+
β
∑
Z
y=0
Q(y|x + a)W
t+1
(y, 0)
if W
t
(x,a) ≥ W (x,a(x)) do
W (x,a(x)) = W
t
(x,a)
f
x
= a
end for
W
t
(x) = W
t
(x, f
x
)
W
t
(x,0) = W
t
(x)
if W
t
(x) ≥ K
t+1
(x) do
K
t
(x) = W
t
(x)
W
∗
(x) = K
t
(x)
end for
t = n − 1
until t = 0
In consequence, the output of the program is obtained
as illustrated in Figure 3. In this matrix the last col-
umn represents the optimal policy and the penulti-
mate column the value function, for each state x ∈
{0,1,..., 10}. The other input of the matrix represents
the following:
G(x,a) := R(x, a) + αE[W
1
(F(x,a,D))],
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
56

Figure 2: Transition law.
(x,a) ∈ K.
In conclusion, the optimal value function is
V
T
(x) = 693.39 for each x ∈ X and the optimal pol-
icy is given by f (x) = M − x, x ∈ X with M = 10.
Now, considering that in operations research it is
often difficult for a manager to control inventory sys-
tems, due to the fact that data in each stage of ob-
servation is not always is certain, then a fuzziness
approach should be applied. In this way, take into
account the previous inventory system in a fuzzy en-
vironment, that is, the reward function given in As-
sumption 3.5 will be considered:
˜
R(x,a) = (BR(x,a),CR(x,a),DR(x,a)),
with 0 < B < C < D. Then, by Theorem 4.3, it follows
that the optimal policy of the fuzzy optimal control
problem is given by
˜
π
∗
= { f
0
,..., f
T −1
},
where f
t
(x) = M − x, x ∈ X and the op-
timal value function is given by
˜
V
T
(x) =
(BV
T
(x),CV
T
(x),DV
T
(x)), x ∈ X.
6 ECONOMIC/FINANCIAL
APPLICATIONS
In this section, two examples on applications in Eco-
nomics and Finance are presented. Firstly the crisp
model of both examples and the respective solution is
proposed. Later a fuzzy version of these problems is
introduced.
6.1 Example 1
Let X = {χ
0
,χ
1
}, 0 < χ
0
< χ
1
, A(χ) = [0,1], χ ∈ X.
The transition law is given by
Q({χ
0
}|χ
0
,a) = p, (28a)
Q({χ
1
}|χ
0
,a) = 1 − p, (28b)
Q({χ
1
}|χ
1
,a) = q, (28c)
Q({χ
0
}|χ
1
,a) = 1 − q, (28d)
for all a ∈ [0, 1], where 0 ≤ p ≤ 1 and 0 ≤ q ≤ 1. The
reward is given by a function R(χ,a), (χ, a) ∈ K that
met:
Assumption 6.1. (a) R depends only of a, that is
R(χ,a) = U (a), for all (χ,a) ∈ K, where U is non-
negative and continuous.
(b) There is a
∗
∈ [0,1] such that
max
a∈[0,1]
U(a) = U (a
∗
), (29)
for all χ ∈ X.
An interpretation of this example is given in the fol-
lowing remark.
Remark 6.2. The states χ
0
and χ
1
could represent
the behavior of a certain stock market, which is bad
(≡ χ
0
) and good (≡ χ
1
). It is assumed that , for each
a and t = 0, 1, · ··, the probability of going from χ
0
to
χ
0
is p (resp. the probability of going from χ
0
to χ
1
is
1− p); moreover, for each a and t = 0,1,···, the prob-
ability of going from χ
1
to χ
1
is q (resp. the probabil-
ity of going from χ
1
to χ
0
is 1 − q). Now, specifically,
suppose that in a dynamic portfolio choice problem,
two assets are available to an investor. One is risky-
free, and the risk-rate r > 0 is assumed known and
constant over time. The other asset is risky with
a stochastic return having mean µ and a variance
σ
2
. Following Example 1.24 in (Webb, 2007), the ex-
pected utility of the investor could be given for the
expression:
U(a) = aµ + (1 − a)r −
k
2
a
2
σ
2
, (30)
where a ∈ [0,1] is the fraction of its money that the
investor invests in the risky asset and the remainder
1 − a, he/she invests in the riskless asset. In (30),
k represents the value that the investor places on
the variance relative to the expectation. Observe
that if µ >
kσ
2
2
, then U defined in (30) is positive
in [0, 1] (in fact, in this case U(0) = r > 0 and
U(1) = µ −
kσ
2
2
> 0 ); moreover, it is possible to
prove (see (Webb, 2007)) that if 0 < µ − r < kσ
2
, then
max
a∈[0,1]
U(a) is attained for a
∗
∈ (0,1) given by
Discounted Markov Decision Processes with Fuzzy Rewards Induced by Non-fuzzy Systems
57

Figure 3: V
0
state-action matrix.
a
∗
=
µ − r
kσ
2
. (31)
Hence, taking R(χ,a) = U (a), χ ∈ X , and a ∈ [0,1],
where U is given by (30), and considering the last two
inequalities given in the previous paragraph, Assump-
tion 6.1 holds.
Lemma 6.3. Suppose that Assumption 6.1 holds.
Then, for Example 2, V (χ) =
U(a
∗
)
1 − α
and f
∗
(χ) = a
∗
,
for all χ ∈ X.
Proof. Firstly, the value iteration functions will be
found: V
n
, for n = 1,2,....
By definition,
V
1
(χ
0
) = max
a∈[0,1]
U(a), (32)
this implies that V
1
(χ
0
) = U (a
∗
). In a similar way, it
is possible to obtain that V
1
(χ
1
) = U(a
∗
).
Now, for n = 2,
V
2
(χ
0
) = max
a∈[0,1]
{
U(a) + β[V
1
(χ
1
)(1 − p) +V
1
(χ
0
)p]
}
= U (a
∗
) + β[V
1
(χ
1
)(1 − p) +V
1
(χ
0
)p]
= U (a
∗
) + β[U(a
∗
)(1 − p) +U (a
∗
)p]
= U (a
∗
) + βU(a
∗
).
Analogously, V
2
(χ
1
) = U(a
∗
) + βU(a
∗
). Continuing
this way, it is obtained that
V
n
(χ
0
) =V
n
(χ
0
) =U(a
∗
)+βU(a
∗
)+.. .+β
n−1
U(a
∗
),
(33)
for all n = 1,2,....
By Theorem 3.4 d), V
n
(χ) → V (χ), n → ∞, χ ∈ X,
which implies that V (χ) =
U(a
∗
)
1 − β
, χ ∈ X. And, from
the Dynamic Programming Equation (see (15)), it fol-
lows that f
∗
(χ) = a
∗
, for all χ ∈ X.
Lemma 6.4. For the fuzzy version of Example 2, fol-
lowing Theorem 4.6, it results that
e
V (χ) =
0,
U(a
∗
)
1 − β
,
D
1 − β
,
χ ∈ X, with
˜
R(x,a) = (0,U(a),D), χ ∈ X , a ∈ A(χ),
where D > U(a
∗
) and f
∗
(χ) = a
∗
, for all χ ∈ X.
6.2 Example 2
Let X = {χ
0
,χ
1
}, 0 < χ
0
< χ
1
, A(χ) = [0,χ], χ ∈ X.
The transition law is given by
Q({χ
1
}|χ
0
,a) = 1, (34a)
Q({χ
0
}|χ
1
,a) = 1, (34b)
for all χ ∈ X and a ∈ [0,χ].
For this example, consider a person who will have
some kind of resource available to him/her at each pe-
riod of time; he/she will receive a profit depending on
the amount of resource consumed. Then, χ
0
and χ
1
are the amounts available to the person at each time
t. The reward R will be specified in Assumption 6.5
below.
Assumption 6.5. R is given by
R(χ,a) = U(a) = a
γ
, (35)
a ∈ [0,χ], χ ∈ X and 0 < γ < 1. Observe that U is
non-negative, concave and continuous (taking, as it is
common U(0) = 0), and that
max
a∈[0,χ]
U(a) = U (χ) = χ
γ
, (36)
for all χ ∈ X.
Lemma 6.6. Suppose that Assumption 6.5 holds.
Then, for Example 3,
V (χ
0
) =
χ
γ
0
1 − β
2
+
βχ
γ
1
1 − β
2
, (37a)
V (χ
1
) =
χ
γ
1
1 − β
2
+
βχ
γ
0
1 − β
2
, (37b)
and f
∗
(χ) = χ, for all χ ∈ X.
Proof. Similar to the proof of Lemma 6.3.
Lemma 6.7. For the fuzzy version of Ex-
ample 3, following Theorem 4.6, it results
that
e
V (χ) = (0,V(χ),
D
1−β
), χ ∈ X, with
˜
R(χ,a) = (0,U(a),D), χ ∈ X, a ∈ A(χ), where
D > max{χ
γ
1
,χ
γ
2
} and f
∗
(χ) = χ, for all χ ∈ X.
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
58

7 CONCLUSION
In this article, Markov decision processes were stud-
ied under the total expected discounted reward crite-
rion and considering for each of them a fuzzy reward
function, specifically of the triangular type. These
processes were induced from crisp processes taking
into account some of their properties to cause certain
properties in the fuzzy case, and the main interpreta-
tion of them is given in Theorem 4.6 and Remark 4.7.
The theory was illustrated by three interesting exam-
ples from applied areas, as operations research, eco-
nomics, and finance. Future work in the direction of
this paper consists in applying the methodology used
to other criteria of optimality such as the average case
or the risk-sensitive criterion. Moreover, it is possi-
ble to contemplate the extension to another class of
fuzzy payment function, for example, to trapezoidal
numbers.
REFERENCES
Aliprantis, C. D. and Border, K. (2006). Infinite dimen-
sional analysis. Springer.
Ban, A. I. (2009). Triangular and parametric approxima-
tions of fuzzy numbers inadvertences and corrections.
Fuzzy Sets and Systems, 160(21):3048–3058.
Driankov, D., Hellendoorn, H., and Reinfrank, M. (2013).
An introduction to fuzzy control. Springer Science &
Business Media.
Efendi, R., Arbaiy, N., and Deris, M. M. (2018). A new
procedure in stock market forecasting based on fuzzy
random auto-regression time series model. Informa-
tion Sciences, 441:113–132.
Fakoor, M., Kosari, A., and Jafarzadeh, M. (2016). Hu-
manoid robot path planning with fuzzy Markov deci-
sion processes. Journal of Applied Research and Tech-
nology, 14(5):300–310.
Hern
´
andez-Lerma, O. (1989). Adaptive Markov control
processes, volume 79. Springer Science & Business
Media.
Klir, G. J. and Yuan, B. (1996). Fuzzy sets and fuzzy
logic: theory and applications. Possibility Theory Ver-
sus Probab. Theory, 32(2):207–208.
Kurano, M., Yasuda, M., Nakagami, J.-i., and Yoshida, Y.
(2003). Markov decision processes with fuzzy re-
wards. Journal of Nonlinear and Convex Analysis,
4(1):105–116.
Pedrycz, W. (1994). Why triangular membership functions?
Fuzzy Sets and Systems, 64(1):21–30.
Puri, M. L., Ralescu, D. A., and Zadeh, L. (1993). Fuzzy
random variables. In Readings in Fuzzy Sets for Intel-
ligent Systems, pages 265–271. Elsevier.
Puterman, M. L. (1994). Markov decision processes: dis-
crete stochastic dynamic programming. John Wiley &
Sons.
Semmouri, A., Jourhmane, M., and Belhallaj, Z. (2020).
Discounted Markov decision processes with fuzzy
costs. Annals of Operations Research, pages 1–18.
Topkis, D. M. (1998). Supermodularity and complementar-
ity. Princeton university press.
Webb, J. N. (2007). Game theory: decisions, interaction
and Evolution. Springer Science & Business Media.
Zadeh, L. A. (1965). Fuzzy sets. Information and Control,
8(3):338–353.
Zeng, W. and Li, H. (2007). Weighted triangular approx-
imation of fuzzy numbers. International Journal of
Approximate Reasoning, 46(1):137–150.
Discounted Markov Decision Processes with Fuzzy Rewards Induced by Non-fuzzy Systems
59
