Effect of Phase Mismatch between the Bragg Gratings on the Stability of
Gap Solitons in Semilinear Dual-core System
Shuvashis Saha and Javid Atai
School of Electrical and Information Engineering, The University of Sydney, NSW 2006, Australia
Keywords:
Gap Soliton, Fiber Bragg Grating, Gratings Phase Mismatch.
Abstract:
The existence and stability of quiescent gap solitons are studied in a semilinear dual-core optical system,
in which Bragg gratings (BGs) are written on the both cores with a phase shift and one core has the Kerr
nonlinearity, while other one is linear. When the relative group velocity c in the linear core is zero, three
separate band gaps are observed through the spectrum analysis, including one central band gap surrounded by
upper and lower band gaps. Three band gaps are entirely filled with the stationary soliton solutions. However,
in case of c is non-zero, only central band gap contains the stationary solution. Numerical techniques are used
to find the stability of the quiescent gap solitons in terms of their frequency detuning.
1 INTRODUCTION
It is widely known that a strong effective dispersion
induced from the cross-coupling between counter
propagating waves on the fiber Bragg grating (FBG)
and this dispersion can be up to six orders more than
the standard fiber induce dispersion in magnitude.
The grating originated dispersion can be compensated
by the Kerr nonlinearity at sufficiently high intensity
and that can generate a vast family of quiescent gap
solitons (de Sterke and Sipe, 1994).
Solitons in FBG have been analyzed exten-
sively by the researchers through theoretical analy-
sis (Aceves and Wabnitz, 1989; Christodoulides and
Joseph, 1989) and experimentally (Eggleton et al.,
1996; Eggleton et al., 1999) in the last few decades
due to their promising applications in novel optical
devices, optical signal processing, filtering, switch-
ing, memory devices, sensing and pulse compression
(Kashyap, 1999; Taverner et al., 1998). In the case
of uniform Bragg grating, a two parameters family
of gap solitons have been found from the theoreti-
cal studies. One of these parameters is the intrin-
sic frequency that determines the solitons’ amplitude
and width and the other parameter represents the soli-
ton’s velocity, which can range from zero to the speed
of light in the medium (Aceves and Wabnitz, 1989;
Christodoulidesand Joseph, 1989; Barashenkovet al.,
1998). The observation of quiescent or zero velocity
soliton as well as slow gap soliton has been a sub-
ject of intensive experimental studies. Experimen-
tally, gap solitons with a velocity as low as 23% of
the speed of light in the medium have been reported
(Mok et al., 2006).
Gap solitons have been investigated in different
types of periodic structures and nonlinear systems, in-
cluding grating assisted couplers (Atai and Malomed,
2005; Atai and Malomed, 2001; Mak et al., 1998),
waveguide arrays (Mandelik et al., 2004), photonic
crystals (Biancalana et al., 2008), cubic-quintic non-
linearity (Islam and Atai, 2014), and nonuniform grat-
ings (Baratali and Atai, 2012; Chowdhury and Atai,
2014).
In Ref. (Tsofe and Malomed, 2007), gap soli-
tons in gratings with phase mismatch in the dual-core
system with identical cores were investigated. Since
dual-core systems with non-identical cores (particu-
larly semilinear dual-core fibers) have been shown to
have superior switching characteristics, in this work
we consider the existence and stability of quiescent
gap solitons in a semilinear dual-core fiber where both
cores are equipped with a grating and there is a phase
mismatch between the gratings.
2 THE MODEL
The propagation of light in a linearly coupled Bragg
grating with a phase shift between the gratings where
one core has Kerr nonlinearity and the one is linear is
governed by the following system of equations:
36
Saha, S. and Atai, J.
Effect of Phase Mismatch between the Bragg Gratings on the Stability of Gap Solitons in Semilinear Dual-core System.
DOI: 10.5220/0010229800360039
In Proceedings of the 9th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2021), pages 36-39
ISBN: 978-989-758-492-3
Copyright
c
 2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

iu
t
+ iu
x
+

|v|
2
+
1
2
|u|
2

u+ v+ κφ = 0
iv
t
− iv
x
+

|u|
2
+
1
2
|v|
2

v+ u + κψ = 0
iφ
t
+ icφ
x
+ ψe
i
θ
2
+ κu = 0
iψ
t
−icψ
x
+ φe
−i
θ
2
+ κv = 0
(1)
where, u(x,t) and v(x,t) are the amplitudes of for-
ward and backward traveling waves in the nonlinear
core, φ(x,t) and ψ(x,t) are their counterparts in the
0 1 2 3 4
k
-2
-1
0
1
2
ω
(a)
0 1 2 3
k
-2
-1
0
1
2
ω
(b)
Figure 1: Dispersion relation diagrams obtained from Eq.
(2) for κ = 0.5 and (a) c = 0.0 ; (b) c = 1.0. The solid and
dashed lines correspond to θ = 0 and θ = π, respectively.
linear core, respectively. κ is a real positive param-
eter and accounts for the linear coupling coefficient
between the cores. c defines the relative group ve-
locity in the linear core, while group velocity term in
the nonlinear core is set equal to 1. θ represents the
phase mismatch between the two gratings . The range
of θ is limited to the interval 0 ≤ θ ≤ 2π (Tsofe and
Malomed, 2007).
To determine the bandgap structure, Eqs. (1) are
first linearized and upon substitution of plane wave
solutions {u, v, φ, ψ} ∼ exp(ikx− iωt) into the lin-
earized equations followed by some algebraic manip-
ulations we arrive at the following dispersion relation:
ω
4
−

2+ 2κ
2
+

1+ c
2

k
2

ω
2
+

c
2
− 2cκ
2
+ 1

k
2
+

κ
4
− 2κ
2
cos

θ
2

+ 1

+ c
2
k
4
= 0 (2)
From the straightforward analysis of Eq.
(2), it is
found that in the case of c = 0 and 0 ≤ θ ≤ 2π, the
spectrum contains three disjoint band gaps. It should
be noted that the stationary soliton solutions fill with
the entire three gaps. In the case of c 6= 0, only the
central gap contains soliton solutions.
-40 -20 0 20 40
2000
0
t
(a)
-40 -20 0 20 40
2000
0
t
(b)
Figure 2: Evolution of quiescent gap solitons for (a) ω =
0.10 and θ = 0.0 (Unstable) ; (b) ω = 0.30 and θ = 2π (Sta-
ble). The values of other parameters are κ = 0.2, c = 0.
Only the u−component is shown here.
In the case of θ = 0, maximum value of frequency de-
tuning in the central band gap is limited to |ω
max
| <
(1− κ). However, when θ 6= 0, the central gap’s edge
Effect of Phase Mismatch between the Bragg Gratings on the Stability of Gap Solitons in Semilinear Dual-core System
37

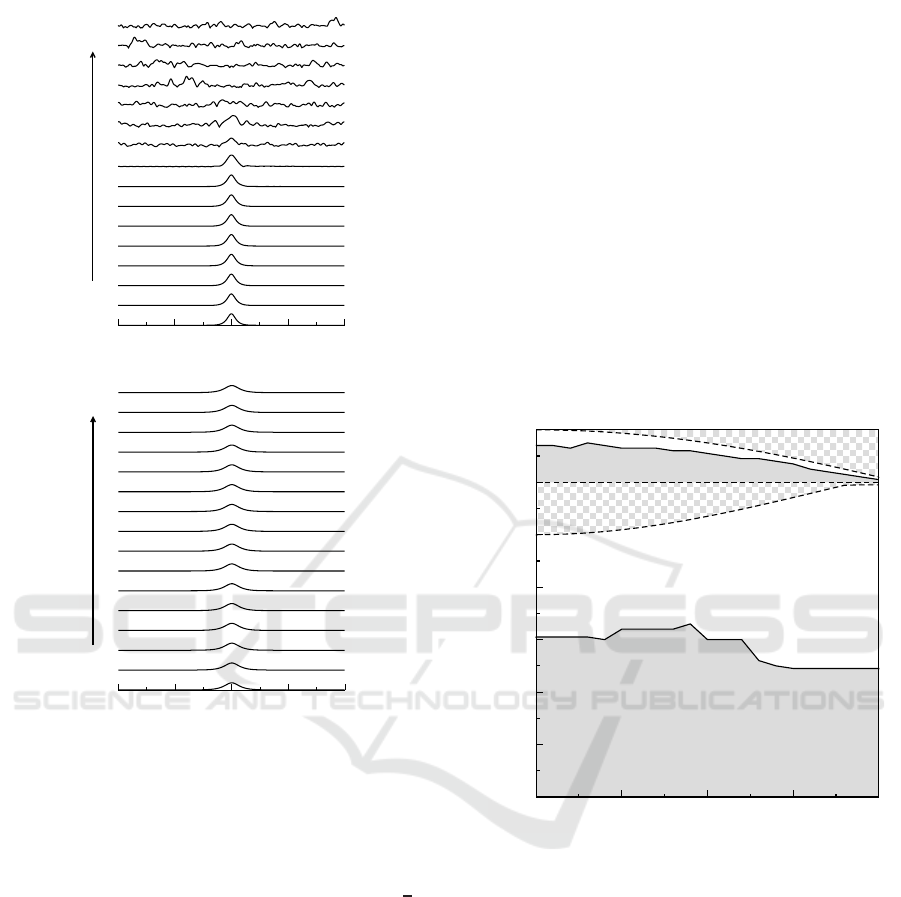
-40 -20 0 20 40
2000
0
t
(a)
-40 -20 0 20 40
2000
0
t
(b)
Figure 3: Evolution of quiescent gap solitons in the upper
band gap for (a) θ = 0.0 (Unstable) ; (b) θ = π (Stable). The
values of other parameters are κ = 0.2, c = 0 and ω = 1.11.
u components only shown here.
change significantly. In a specific case, when the
group velocity term of both cores is similar, i.e., c = 1,
two different situations are possible. If κ ≤ cos

θ
4

,
the maximum value of frequency detuning ω
max
in the
central band gap is obtained at k = 0.
3 STABILITY ANALYSIS
Since there are no exact analytical solutions for
Eqs. (1), the soliton solutions have to be ob-
tained numerically. This is done by substi-
tuting {u(x,t), v(x,t)} = {U (x) ,V (x)} e
−iωt
and
{φ(x,t), ψ(x,t)} = {Φ(x), Ψ(x)} e
−iωt
into Eqs. (1)
which results in a set of ordinary differential equa-
tions that can be solved by means of a relaxation al-
gorithm. In the case of c = 0, quiescent solitons exist
in the upper, lower and the central bandgaps. On the
other hand, for c 6= 0, soliton solutions exist only in
the central bandgap.
We have investigated the stability of the numer-
ically obtained gap soliton solutions using the split-
step Fourier method. It is found that there exist stable
and unstable solitons in the system. Figs. 2 and 3
show the examples of stable and unstable quiescent
gap solitons for different values of c, κ , ω and θ. It is
noteworthy that unstable solitons may either evolve to
another quiescent soliton (see Fig. 2 (a)) or be com-
pletely destroyed.
Fig. 4 summarizes the results of the stability for
c = 0.0 and κ = 0.2 in the (θ, ω) plane. A notable
feature shown in this figure is there exist a vast stable
region in both the central and upper bandgaps. How-
ever, no stable solitons are observed in the lower band
gap.
0
0.5
1
1.5
2
θ/π
-0.2
0
0.2
0.4
0.6
0.8
1
1.2
ω
Unstable
Stable
Stable
Unstable
No Soliton Solutions
No Soliton Solutions
Figure 4: Stability diagram of the quiescent gap solitons in
the (θ, ω) plane for κ = 0.2 and c = 0.0.
4 CONCLUSIONS
We have introduced a model of semilinear dual-core
system, where Bragg gratings with a phase shift θ be-
tween them are written on both cores, and one core
has Kerr nonlinearity, while the other one is linear.
When the group velocity mismatch is zero, three dis-
joint band gaps are found including one central gap
and two lower and upper gaps. In this case, quiescent
solitons exist throughout the three band gaps. How-
ever, in case of c6= 0, only the central gap contains the
quiescent soliton solutions and no solitons are found
in the lower and upper gaps. Stability of gap solitons
is investigated numerically. For c = 0, stable solitons
PHOTOPTICS 2021 - 9th International Conference on Photonics, Optics and Laser Technology
38

are found only in the upper and central bandgaps.
REFERENCES
Aceves, A. B. and Wabnitz, S. (1989). Self-induced trans-
parency solitons in nonlinear refractive periodic me-
dia. Phys. Lett. A, 141:37–42.
Atai, J. and Malomed, B. A. (2001). Solitary waves in sys-
tems with separated bragg grating and nonlinearity.
Phys. Rev. E, 64:066617.
Atai, J. and Malomed, B. A. (2005). Gap solitons in bragg
gratings with dispersive reflectivity. Phys. Lett. A,
342:404–412.
Barashenkov, I. V., Pelinovsky, D. E., and Zemlyanaya,
E. V. (1998). Vibrations and oscillatory instabilities
of gap solitons. Phys. Rev. Lett., 80:5117–5120.
Baratali, B. H. and Atai, J. (2012). Gap solitons in dual-core
Bragg gratings with dispersive reflectivity. J. Opt.,
14(6):065202.
Biancalana, F., Amann, A., and O’Reilly, E. P. (2008). Gap
solitons in spatiotemporal photonic crystals. Phys.
Rev. A, 77:011801.
Chowdhury, S. A. M. S. and Atai, J. (2014). Stability of
bragg grating solitons in a semilinear dual core sys-
tem with dispersive reflectivity. IEEE J. Quant. Elect.,
50:458–465.
Christodoulides, D. N. and Joseph, R. I. (1989). Slow bragg
solitons in nonlinear periodic structures. Phys. Rev.
Lett., 62:1746–1749.
de Sterke, C. M. and Sipe, J. E. (1994). Gap solitons. Prog.
Optics, 33:203–260.
Eggleton, B. J., de Sterke, C. M., and Slusher, R. E. (1999).
Bragg solitons in the nonlinear schr¨odinger limit: ex-
periment and theory. J. Opt. Soc. Am. B, 16:587–599.
Eggleton, B. J., Slusher, R. E., Krug, P. A., and Sipe, J. E.
(1996). Bragg grating solitons. Phys. Rev. Lett.,
76:1627–1630.
Islam, M. J. and Atai, J. (2014). Stability of gap solitons
in dual-core bragg gratings with cubic-quintic nonlin-
earity. Las. Phys. Lett., 12:015401.
Kashyap, R. (1999). Fiber bragg gratings. San Diego; Lon-
don.
Mak, W. C. K., Malomed, B. A., and Chu, P. L. (1998).
Solitary waves in coupled nonlinear waveguides with
Bragg gratings. J. Opt. Soc. Am. B, 15:1685–1692.
Mandelik, D., Morandotti, R., Aitchison, J. S., and Silber-
berg, Y. (2004). Gap solitons in waveguide arrays.
Phys. Rev. Lett., 92:093904.
Mok, J. T., de Sterke, C. M., Littler, I. C. M., and Eggle-
ton, B. J. (2006). Dispersionless slow light using gap
solitons. Nature Phys., 2:775–780.
Taverner, D., Broderick, N. G. R., Richardson, D. J. R.,
Laming, I., and Ibsen, M. (1998). Nonlinear self-
switching and multiple gap-soliton formation in a
fiber bragg grating. Opt. Lett., 23:328–330.
Tsofe, Y. J. and Malomed, B. A. (2007). Quasisymmetric
and asymmetric gap solitons in linearly coupled bragg
gratings with a phase shift. Phys. Rev. E, 75:056603.
Effect of Phase Mismatch between the Bragg Gratings on the Stability of Gap Solitons in Semilinear Dual-core System
39