An Analytic Attack against ARX Addition Exploiting Standard

Side-channel Leakage

Yan Yan

, Elisabeth Oswald

and Srinivas Vivek

University of Klagenfurt, Klagenfurt, Austria

IIIT Bangalore, India

Keywords:

ARX Construction, Side-channel Analysis, Hamming Weight, Chosen Plaintext Attack.

Abstract:

In the last few years a new design paradigm, the so-called ARX (modular addition, rotation, exclusive-or)

ciphers, have gained popularity in part because of their non-linear operation’s seemingly ‘inherent resilience’

against Differential Power Analysis (DPA) Attacks: the non-linear modular addition is not only known to be a

poor target for DPA attacks, but also the computational complexity of DPA-style attacks grows exponentially

with the operand size and thus DPA-style attacks quickly become practically infeasible. We however propose

a novel DPA-style attack strategy that scales linearly with respect to the operand size in the chosen-message

attack setting.

1 INTRODUCTION

Ciphers that base their round function on the sim-

ple combination of modular addition, rotation, and

exclusive-or, (short ARX) have gained recent popu-

larity for their lightweight implementations that are

suitable for resource constrained devices. Some re-

cent examples include Chacha20 (Nir and Langley,

2015) and Salsa20 (Bernstein, 2008) family stream

ciphers, SHA-3 ﬁnalists BLAKE (Aumasson et al.,

2008) and SKEIN (Ferguson et al., 2010), as well as

other block ciphers such as SPECK (Beaulieu et al.,

2015), SPARX (Dinu et al., 2016) and the related

SPARKLE (Beierle et al., 2008) which made into the

second round of the NIST lightweight cipher compe-

tition. Another second round candidate of the NIST

lightweight competition Gimli (Bernstein et al., 2017)

also proposed a variation, namely Gimli-SPARX, that

has adopted the ARX paradigm.

The fact that the round function has an efﬁcient

and simple expression via functions that are typi-

cally available as instructions on small embedded de-

vices enables excellent performance with respect to

code size, execution time and energy consumption.

Any implementation on an embedded device however

also needs to be able to withstand the threat of Side-

Channel (timing, power, EM, cache) Attacks (SCA,

for short). The absence of key dependent loops, or

indeed tables, implies resistance to timing and cache

attacks. Power (and synonymously EM) attacks how-

ever are different: they offer a potentially ‘high reso-

lution’ for the adversary. In principle, under suitably

strong assumptions, adversaries can not only observe

leaks for all instructions that are executed on a proces-

sor, but indeed attribute leakage points (more or less

accurately) to instructions (Mangard et al., 2007).

Achieving security in this scenario has proven to

be extremely challenging, and countermeasures such

as masking (secret sharing) are well understood but

costly (Schneider et al., 2015). In the case of ARX

constructions one has to cope with the fact that there

are Boolean operations (requiring Boolean masking

or secret sharing) and arithmetic operations (requir-

ing arithmetic masking or secret sharing). Thus se-

curing ARX ciphers against power (and EM) attacks

is potentially very costly; unless, it could be argued

that they are inherently ‘secure enough’ against such

attacks that “non-provable” countermeasures (such as

hiding via randomisation of instructions, etc.) could

possibly sufﬁce. The most recent work on securing

ARX implementations is (Jungk et al., 2018).

It is well known that completely linear targets such

as the rotation and the exclusive-or operation are dif-

ﬁcult to attack with differential (power or EM) anal-

ysis (DPA for short): attacks on such targets require

many more traces than attacks on highly non-linear

target functions, and even with a very large number

of leakage traces there remains some keys that cannot

be distinguished from each other (Prouff, 2005).

Yan, Y., Oswald, E. and Vivek, S.

An Analytic Attack against ARX Addition Exploiting Standard Side-channel Leakage.

DOI: 10.5220/0010223600890097

In Proceedings of the 7th International Conference on Information Systems Security and Privacy (ICISSP 2021), pages 89-97

ISBN: 978-989-758-491-6

1.1 Background and Related Work on

SCA on ARX Ciphers

The idea of combining addition modulo 2

, exclusive-

or, and rotation as a round function, has been sug-

gested as early as 1987 in the block cipher FEAL

(Shimizu and Miyaguchi, 1988). Since NIST kick-

started its lightweight cryptography project in 2015,

the interest in ARX constructions has received re-

newed interest. The ciphers SIMON and SPECK

(Beaulieu et al., 2015), which were submitted to the

ﬁrst of the two workshops hosted by NIST, gained

a considerable amount of interest from within the

crypto community. In 2016 the SPARX family of ci-

phers was introduced (Dinu et al., 2016).

The appeal of the ARX construction is primarily

in the fact that when choosing n equal to the word size

of a processor, software implementations gain consid-

erable speedups. Furthermore, because the non-linear

component is given by the addition modulo 2

, it does

not need to be encoded as a table lookup which sig-

niﬁcantly reduces the memory usage. The absence

of lookup tables is also perceived as a distinctive ad-

vantage when the threats of various side channel at-

tacks are considered (Biryukov et al., 2016; Biryukov

and Perrin, 2017; Dinu et al., 2016). The absence

of cache also implies that the instructions are always

performed in a constant time and thus there is unlikely

any key dependent leakage exploitable in the execu-

tion time (Dinu et al., 2016). Being free from the ta-

bles also signiﬁcantly reduces the number of mem-

ory accesses as these instructions have shown to be

the most exploitable targets in power analysis attacks

(Biryukov et al., 2016).

However, it has been shown in (Yan and Os-

wald, 2019) that na

ıve implementations of ARX ci-

phers may still leave vulnerabilities easily exploitable.

In (Yan and Oswald, 2019), the authors simply

attempted straightforward correlation power analy-

sis attacks on the reference implementation of the

SPARX cipher (Dinu et al., 2016) on some real plat-

forms, and found that the key was efﬁciently recov-

ered exploiting the leakage ampliﬁed by consecutive

XOR and shifting instructions.

Nevertheless, for the modular addition in ARX-

Boxes, the authors of (Yan and Oswald, 2019) re-

ported unsuccessful attacks targeting the addition in-

struction which coincide with the previous results re-

ported by (Biryukov et al., 2016) and that align with

(Yan and Oswald, 2019; Zohner et al., 2012; Dinu

et al., 2016): their argument is that the weak non-

linearity of modular addition leaves a relatively lower

margin in distinguishing the keys comparing to a typ-

ical S-Box instruction.

To date, the Butterﬂy attack (Zohner et al., 2012)

remains the most effective result in attacking modular

addition. This attack demonstrated that it is possi-

ble to improve on straightforward DPA-style attacks

when targeting modular additions by testing pairs of

correlations induced by the symmetrical structure of

modular additions. However Butterﬂy attacks are

constrained by the fact that knowledge of one adder is

required which does not hold for some ARX ciphers

such as SPECK (Beaulieu et al., 2015) and SPARX

(Dinu et al., 2016).

1.2 Our Contribution

In this paper we propose a novel attack strategy

against the modular addition in ARX-Boxes. Our

method, in comparison to previous work, requires no

knowledge of the adders and thus is more generally

applicable on targets where a Butterﬂy attack is not

an option, such as SPECK (Beaulieu et al., 2015) and

SPARX (Dinu et al., 2016).

Our method requires to obtain the leakage from

the result of the modular addition only, which we need

to be a bit-linear function (e.g. Hamming Weight, or

weighted Hamming weight with positive weights of

similar magnitude). We only need to be able to ob-

serve if the leakage increases, decreases, or remains

the same upon a single-bit ﬂip in the plaintext. Based

on this information, we show how to reconstruct the

adder output. With the adder output, and based on a

further related plaintext, we then show how to recon-

struct the secret key.

We consider our novel methodology of indepen-

dent theoretical interest as we leverage minimal side

channel leakage to perform a cryptanalytic-style anal-

ysis for ARX constructions.

1.3 Organisation of the Paper

In Section 2 we formalise our attack on ARX-Boxes

as the (Noisy) Hidden Adder Problem, (N)HAP, and

propose its sub-problem the (Noisy) Hidden Sum

Problem, (N)HSP. In Section 3 we explain how HSP

can be solved, then use the solution to solve HAP in

Section 4 thus providing a full key recovery attack

given ideal leakage. Section 5 completes the attack by

adapting the attack to noisy leakage. We present sim-

ulation results in Section 5.1 and also discuss practical

considerations.

1.4 Notation

In this work we frequently use both the integer and the

binary representation of operands. The notation [x]

ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy

indicates the binary representation of a non-negative

integer x:

x = [x]

n−1

[x]

n−2

...[x]

[x]

n−1

∑

i=0

[x]

hence [x]

denotes the i-th bit of [x]. The notation [x][y]

implies the concatenation of two bit strings [x] and

[y]. The notation [x]

denotes k times repetition of [x].

Speciﬁcally, [∗]

denotes an arbitrary k-bit string.

In this paper we assume that all integers are drawn

from Z

, where n ∈ N

. The  denotes modular ad-

dition over Z

. HW (x) denotes the Hamming weight

of [x]. For a n-bit integer x,

x refers to the (one’s)

complement of x, where all the bits are ﬂipped. That

is,

x = x ⊕ (2

− 1).

We often require to be able to change the value of

a single bit to its complement (i.e. we ﬂip a bit, but

leave all other bits unchanged). For this purpose we

deﬁne the ﬂip function F

(x) which returns x with the

i-th bit ﬂipped:

(x) = x ⊕ 2

2 PROBLEM DESCRIPTION

In this work we explore alternative SCA strategies

when targeting the modular addition in a more gen-

eral setting as described by the generalised ARX-Box

in (Yan and Oswald, 2019):

s(x,y) := (x ⊕ α)  (y ⊕ β), (1)

where (x,y) are some known input values and (α, β)

are the unknown sub-keys. All x,y,α,β and s(x,y) are

n-bit variables. We further assume an adversary who

is able to choose input pairs (x,y), and observe the

(noisy) leakage of s(x, y). For simplicity we assume

that the (noisy) leakage is the Hamming weight with

Gaussian noise, which is the most commonly consid-

ered leakage model in side-channel literature:

L(x,y) = HW (s(x, y))+e = HW ((x⊕α)(y⊕β))+e,

where the Gaussian noise e ∼ N (0,σ

). We note that

our statements also hold for a more general bit-linear

model assuming that all coefﬁcients have the same

sign.

The goal of the adversary is to recover the subkeys

(α,β) given a set of chosen inputs (x, y) and their as-

sociated leakage L(x,y). Later in Section 5 we ex-

plain that how the chosen inputs requirement can be

relaxed in different settings.

We model our attack that exploits ideal and noisy

leakage as the Hidden Adder Problem (HAP) and

Noisy Hidden Adder Problem (NHAP), respectively,

as formalised in Deﬁnition 1 and Deﬁnition 2.

2.1 Outline of Our Attack

In a nutshell, there are two steps in our attack strat-

egy. The ﬁrst step is to recover the sum s(x,y) from

the leakage. From there, we then recover the subkeys

(α,β) by solving equations involving x,y and s(x,y).

We begin by explaining how the attack works in an

ideal world where the adversary observes ideal leak-

age without the Gaussian noise e, and then we show

how such solution can be adapted to realistic noisy

leakage by using statistical methods. To this end, we

deﬁne the following problems:

Deﬁnition 1 (Hidden Adder Problem (HAP)). Let

(α,β) be randomly chosen from Z

× Z

. The ad-

versary chooses as many pairs x, y ∈ Z

and obtains

leakage of the form HW (s(x, y)) = HW ((x⊕α) (y⊕

β)) for each pair. The adversary must then recover

(α,β).

Deﬁnition 2 (Noisy Hidden Adder Problem

(NHAP)). Let (α,β) be randomly chosen from

× Z

. The adversary chooses as many pairs

x,y ∈ Z

and obtains leakage of the form L

α,β

(x,y) =

HW (s(x,y)) + e = HW ((x ⊕ α)  (y ⊕ β)) + e where

e ∼ N (0,σ

). The adversary must then recover

(α,β).

Note that HAP (and so is NHAP) reﬂects the ul-

timate goal of the adversary to reveal the subkeys

(α,β). To explain our attack, we further deﬁne

two sub-problems of HAP and NHAP called Hidden

Sum Problem (HSP) and Noisy Hidden Sum Problem

(NHSP):

Deﬁnition 3 (Hidden Sum Problem (HSP)). Let

(α,β) be randomly chosen from Z

× Z

. The ad-

versary chooses as many pairs x, y ∈ Z

and obtains

leakage of the form HW (s(x, y)) = HW ((x⊕α) (y⊕

β)) for each pair. The adversary must then recover

s(x,y).

Deﬁnition 4 (Noisy Hidden Sum Problem (NHSP)).

Let (α,β) be randomly chosen from Z

× Z

The adversary chooses pairs x, y ∈ Z

and obtains

leakage of the form L

α,β

(x,y) = HW (s(x,y)) + e =

HW ((x ⊕ α)  (y ⊕ β)) + e where e ∼ N (0,σ

). The

adversary must then recover s(x,y).

The adversaries in the problems HSP and NHSP

are given exactly the same form of leakage as the

adder problems (HAP and NHAP). Only their goals

are changed to recover the sum s(x, y) in the sum

problems rather than the sub-keys in the adder prob-

lems.

In this paper, we always consider the general case

where n ≥ 2. For the special case where n = 1, we

have

HW (s(x,y)) = s(x, y) = x ⊕ α ⊕ y ⊕ β

An Analytic Attack against ARX Addition Exploiting Standard Side-channel Leakage

which immediately gives α ⊕ β given HW (s(x,y)),x

and y. It should also be noted that as shown in (Yan

and Oswald, 2019), any side-channel attack target-

ing the modular addition of the generalised ARX-Box

will yield at least two pairs of the subkeys. Conse-

quently, as we will see later in Section 4, all the above

problems have at least two pairs of solutions in (α,β).

3 SOLVING THE HIDDEN SUM

PROBLEM

Our solution to the HSP recovers s(x,y) one bit at a

time. Starting from the MSB down to the LSB, we ﬂip

each bit of x and observe the resulting differences in

the Hamming weight leakage. In the end we recover

all bits of the hidden sum s(x, y). We abbreviate s :=

s(x,y) and s

:= s(F

(x),y), which are the sum, and

the sum with [x]

ﬂipped, respectively.

Since ﬂipping [x]

also ﬂips the bit [x ⊕ α]

, this

effectively changes the sum by ±2

due to commuta-

tivity of addition. In the following sections we explain

how to exploit this property of s(x,y) to solve HSP.

Deﬁne ∆s

([x]

) to be the difference in s(x,y) in-

duced by ﬂipping [x]

. We have:

∆s

([x]

) ≡ s(F

(x),y) − s(x, y) ≡ ±2

(mod 2

(2)

Equivalently,

s(F

(x),y) = s(x, y) ± 2

. (3)

3.1 Recovering the MSB

In this section we give a solution that recovers the

MSB of s, which is the base case for our algorithm.

Note that the MSB of s can be reduced to XORing

the carry bit c from the sum of the lower-order bits,

and the MSBs of x ⊕ α and y ⊕ β. Because ﬂipping

[x]

n−1

ﬂips [x ⊕ α]

n−1

and thus [s]

n−1

, the adversary

can determine that [s]

n−1

= 0 if the Hamming weight

increases (from 0 to 1) and vice versa.

Lemma 1. Given x, y, Hamming weights of the sums

s(x,y) and s(F

n−1

(x),y), the MSB of the sum s is:

[s]

n−1

(

0 if HW (s

n−1

) − HW (s) > 0,

1 if HW (s

n−1

) − HW (s) < 0.

Proof. We can write HW (s) as:

HW (s) = HW ([s]

n−1

) + HW ([s]

n−2

[s]

n−3

...[s]

[s]

(4)

Also,

n−1

≡ ∆s

([x]

n−1

) + s

≡ ∆s

([x]

n−1

) + [s]

n−1

n−2

∑

i=0

[s]

· 2

(mod 2

(5)

Note that [s]

n−1

∈ {0,1}, ∆s

([x]

n−1

) ∈

{+2

n−1

,−2

n−1

} according to Equation (2), and

−2

n−1

mod 2

= +2

n−1

. Equation (5) can, there-

fore, be categorised into four cases:

1. If [s]

n−1

= 0, ∆s

([x]

n−1

) = +2

n−1

, then

n−1

= (+2

n−1

+ 0 · 2

n−1

n−2

∑

i=0

[s]

) (mod 2

)

= [1][s]

n−2

...[s]

[s]

2. If [s]

n−1

= 0, ∆s

([x]

n−1

) = −2

n−1

, then

n−1

= (−2

n−1

+ 0 · 2

n−1

n−2

∑

i=0

[s]

) (mod 2

)

= [1][s]

n−2

...[s]

[s]

3. If [s]

n−1

= 1, ∆s

([x]

n−1

) = +2

n−1

, then

n−1

= (+2

n−1

+ 1 · 2

n−1

n−2

∑

i=0

[s]

) (mod 2

)

= [0][s]

n−2

...[s]

[s]

4. If [s]

n−1

= 1, ∆s

([x]

n−1

) = −2

n−1

, then

n−1

= (−2

n−1

+ 1 · 2

n−1

n−2

∑

i=0

[s]

) (mod 2

)

= [0][s]

n−2

...[s]

[s]

Observe that in Cases 1 and 2, where [s]

n−1

= 0,

we have

n−1

= [1][s]

n−2

...[s]

[s]

Similarly, in Cases 3 and 4 where [s]

n−1

= 1, we have

n−1

= [0][s]

n−2

...[s]

[s]

Therefore, we obtain

HW (s

n−1

) =



HW (1) + HW ([s]

n−2

[s]

n−3

...[s]

[s]

)if [s]

n−1

= 0,

HW (0) + HW ([s]

n−2

[s]

n−3

...[s]

[s]

)if [s]

n−1

= 1.

(6)

Denote by ∆HW

n−1

the (signed) difference in

Hamming weight between s to s

n−1

. Subtracting

Equation (6) by Equation (4), we have:

∆HW

n−1

= HW (s

n−1

) − HW (s)



HW (1) − HW (0) = +1 if [s]

n−1

= 0,

HW (0) − HW (1) = −1 if [s]

n−1

= 1.

(7)

ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy

Algorithm 1: Compute MSB of s.

function [s]

n−1

= GetMsb(x, y)

∆HW = HW (s

n−1

) − HW (s);

if ∆HW > 0 then

return 0;

else

return 1;

end if

end function

Observing Equation (7), we can see that the sign

of ∆HW

n−1

solely depends on [s]

n−1

. Since both

HW (s

n−1

) and HW (s) can be obtained as (ideal)

leakage, we can thus recover [s]

n−1

by computing

∆HW

n−1

and then applying Equation (7).

Algorithm 1 provides the pseudo code for recov-

ering the MSB.

3.2 Recovering the m-th Bit

In Section 3.1 we explained how the MSB of s =

s(x,y) can be recovered by the noiseless Hamming

weight leakage. We now show how to recover the

remaining bits.

Lemma 2. Suppose we ﬂip the bit [x]

n−m

. If:

• HW (s

n−m

) > HW (s), then [s]

n−m

= 0,

• HW (s

n−m

) = HW (s), then [s]

n−m

[s]

n−(m−1)

• HW (s

n−m

) < HW (s), then [s]

n−m

= 1,

for 2 ≤ m ≤ n.

Proof. We assume that the higher-order m − 1 bits of

known

= [s]

n−1

[s]

n−2

...[s]

n−(m−1)

has been determined. The goal is then to recover

the next bit [s]

n−m

. According to Equation (3), when

[x]

n−m

is ﬂipped, we have the ﬂipped sum s

n−m

= s + ∆s

([x]

n−m

) (8)

where ∆s

([x]

n−m

) = ±2

n−m

In the RHS of Equation (8), bits “lower” than

[s]

n−m

is unchanged after the addition operation and

thus does not affect the Hamming weight. On the

other hand, the addition to (or subtraction from)

[s]

n−m

may potentially generate a carry bit that propa-

gates through bits “higher” than [s]

n−m

and result into

a change of Hamming weight.

Let ∆HW

n−m

be the (signed) change of Hamming

weight induced by ﬂipping [x]

n−m

∆HW

n−m

= HW (s

n−m

) − HW (s). (9)

We can categorise ∆HW

n−m

by:

• Whether there exists or not a carry bit (either pos-

itive or negative),

• If there exists a carry bit, then

– Whether the carry triggers an overﬂow (and

hence modular reduction).

We next analyse each of the above cases.

No Carry Bit. In the following conditions there is no

carry bit:

1. If [s]

n−m

= 0 and ∆s

([x]

n−m

) = +2

n−m

, then

∆HW

n−m

= +1.

2. If [s]

n−m

= 1 and ∆s

([x]

n−m

) = −2

n−m

, then

∆HW

n−m

= −1.

Otherwise there must exist a carry bit.

Carry Bit. The existence of a carry bit implies either

one of the following conditions:

• Case C

: [s]

n−m

= 1 and ∆s

([x]

n−m

) = +2

n−m

• Case C

: [s]

n−m

= 0 and ∆s

([x]

n−m

) = −2

n−m

is satisﬁed. This can be further categorised into:

Overﬂow. In this case, all the bits of s

known

are

ﬂipped after the addition:

1. In the Case C

, it is required that s

known

[1]

m−1

. The propagation results in s

known

ﬂipped to [0]

m−1

, with ∆HW

n−m

= −m.

2. In the Case C

, it is required that s

known

[0]

m−1

. The propagation results in s

known

ﬂipped to [1]

m−1

, with ∆HW

n−m

= +m.

No Overﬂow. In this case, only a part of s

known

ﬂipped after adding ∆s

([x]

n−m

). Denote by k ∈

[0,m − 2] the number of bits ﬂipped in s

known

before the carry propagation terminates, then

1. In the Case C

, the carry propagation termi-

nates at the least signiﬁcant [0] of s

known

which

is required to have the form

known

= [s]

n−1

...[s]

n−(m−(k+2))

[0][1]

After the addition with ∆s

([x]

n−m

) = +2

n−m

known

changes to

[s]

n−1

...[s]

n−(m−(k+2))

[1][0]

Therefore ∆HW

n−m

= −k.

2. The Case C

is just the opposite of C

with

∆HW

n−m

= +k.

Table 1 summarises the above scenarios. It is

shown that positive ∆HW

n−m

implies [s]

n−m

= [0]

and negative ∆HW

n−m

implies [s]

n−m

= [1] as both

m,k ≥ 0. The case ∆HW

n−m

= 0 is only possible when

k = 0, which indicates a carry bit exists without over-

ﬂow. In such a case s

known

is required to be either:

• s

known

= [∗]

m−2

[1], for [s]

n−m

= 0, or

An Analytic Attack against ARX Addition Exploiting Standard Side-channel Leakage

Table 1: ∆HW under different conditions, where 2 ≤ m ≤ n,

0 ≤ k ≤ m.

Conditions

∆HW

n−m

[s]

n−m

∆s

([x]

n−m

) Overﬂow? s

known

[0]

n−m

No [∗]

m−1

−2

n−m

Yes [0]

m−1

No [∗]

m−(k+2)

[1][0]

[1]

n−m

Yes [1]

m−1

-m

No [∗]

m−(k+2)

[0][1]

-k

−2

n−m

No [∗]

m−1

-1

Algorithm 2: Compute m-th signiﬁcant bit [s]

n−m

(2 ≤ m ≤

n).

function [s]

n−m

GetNextBit(x,y,m,[s]

n−1

[s]

n−2

...[s]

n−(m−1)

)

∆HW = HW (s

n−1

) − HW (s);

if ∆HW > 0 then

return 0;

else if ∆HW < 0 then

return 1;

else  ∆HW == 0

if [s]

n−m+1

== 0 then

return 1;

else

return 0;

end if

end function

• s

known

= [∗]

m−2

[0], for [s]

n−m

= 1.

In either case, [s]

n−m

can be determined by the LSB

of s

known

To summarise, given ∆HW

n−m

, we can uniquely

determine [s]

n−m

Algorithm 2 provides the pseudo code that com-

putes s

n−m

for 2 ≤ m ≤ n.

3.3 Complete Solution to HSP

Combining the methods described in Section 3.1 and

Section 3.2, we now have a full solution to the HSP,

as summarised in Algorithm 3. Notice that the same

HW (s) can indeed be reused in Algorithm 1 and Al-

gorithm 2 ; hence Algorithm 3 only needs n+ 1 traces

to recover s(x,y).

4 SOLVING HAP

In this section we show how HAP (cf. Deﬁnition 1)

can be solved using a solution to HSP (cf. Section 3).

Algorithm 3: Compute s.

function s = GetSum(x, y)

 We initialise the sum to its MSB

s = GetMsb(x, y);

 Recover one bit at a time from 2nd MSB to

LSB

for (m = 2; m ≤ n; m + +) do

s = [s][GetNextBit(x, y,m, s)];

end for

return s;

end function

Lemma 3. Let ∆ := ((s(x,y) − s(

x,y) − 1)

(mod 2

))  1 (here  refers to the right shift

operator).

The solutions to HAP are:



α = ∆ ⊕ x

β = y ⊕ ((s(x, y) − ∆) (mod 2

))

(

α = (∆  2

n−1

) ⊕ x

β = y ⊕ ((s(x, y) − (∆ + 2

n−1

)) (mod 2

)),

for arbitrary x,y ∈ Z

Proof. Observe that for any x ∈ Z

, we have

x ⊕ α =

]

x ⊕ α = 2

− 1 − (x ⊕ α).

Hence

s(x,y) − s(

x,y)

= ((x ⊕ α) + (y ⊕ β)) − ((

x ⊕ α) + (y ⊕ β)) (mod 2

= (x ⊕ α) − (2

− 1 − (x ⊕ α)) (mod 2

= 2(x ⊕ α) + 1 (mod 2

Note that we have already computed the values s(x, y)

and s(

x,y) in Section 3. Since 2 is not co-prime to the

modulo 2

, there are exactly two values of x ⊕ α that

satisfy the above equation: ∆ and ∆ 2

n−1

. Hence the

lemma follows.

Algorithm 4 provides the pseudo code for solving

HAP. The algorithm has trace complexity O(n) - re-

quiring 2n + 2 calls to the (ideal) leakage function.

5 CONVERTING TO NOISY

LEAKAGE

In a real world attack setting an adversary is unlikely

to have noise free leakages. We thus now consider

how to translate the developed attack strategy into a

more realistic setting.

ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy

Algorithm 4: Compute (α,β).

function (α,β) = GetAl phaBeta(void)

Pick arbitrary (x,y);

 Compute s(x,y) and s(

x,y) by Algorithm 3

S0 = GetSum(x,y);

S1 = GetSum(

x,y);

 Recover (α,β) using Lemma 3

a1 = ((S0 − S1 − 1) (mod 2

)) >> 1;

a2 = a1 ⊕ 2

n−1

;

b1 = y ⊕ ((S0 − a1) mod 2

);

b2 = y ⊕ ((S0 − a2) mod 2

);

return {(a1,b1), (a2, b2)};

end function

In principle, the reduction explained in Section 4

also holds for NHAP to NHSP, as long as the adver-

sary is able to recover s(x, y) given the noisy leak-

age in NHSP. Further examining the HSP solution

in Section 3, we see it is indeed sufﬁcient to solve

HSP given only the signs of the difference ∆HW

HW (s

) − HW (s), i ∈ [0,n − 1]. In the case of noisy

leakages we can reveal this difference by sampling the

leakage function (i.e. the device) multiple times on

the same input. We thus get two sets of leakages:

= {HW (s

) + e},

= {HW (s) + e}.

Clearly by subtracting the averages of these sets, we

can recover ∆HW

also in the noisy case. Moreover

because we are only interested in the sign of ∆HW

we can hope that in practice we don’t require ‘large’

sets. To add a bit more rigour, we opted to implement

a standard two-tailed t-test in our experiments. A two-

tailed test can tell us if

• HW (s

) = HW (s),

• HW (s

) > HW (s), or

• HW (s

) < HW (s).

Algorithm 5 summarises the pseudo code that de-

termines the sign of ∆HW . It ﬁrst conducts a two-

tailed test:

: S

= S

: S

6= S

using a set signiﬁcance level, and interprets the result

in terms of the sign of ∆HW

Alternative to Chosen Input Requirement. Due to

the symmetric structure of Equation (1), Lemma 2

also applies when the i-th bit of y is ﬂipped. It should

also be noted that ﬂipping the i-th bit of α is effec-

tively equivalent of ﬂipping the i-th bit of x:

x ⊕ F

(α) = F

(x) ⊕ α = F

(x ⊕ α)

and vice versa for y and β. Therefore our attack can

also be achieved in a fault attack set up where the

Algorithm 5: Determine sign of ∆HW .

function ∆HW = CompareHW (S

)

(t, p) = test(S

)

if p/2 ≥ Signi f icanceLevel then  Accept

∆HW = 0

return 0

else

if t > 0 then  +1 for positive ∆HW .

return +1

else  −1 for negative ∆HW .

return −1

end if

end function

plaintexts are known to the adversary and for each bit

the adversary can induce an i-th bit ﬂip of either x, y,

α or β.

Checking the Recovered Key-pair. In many attacks

utilising side channel information another practically

relevant question is that of which part of the side

channel trace to use (often not just a single value is

available but a vector of leakages). Typical side chan-

nel attacks proceed via applying the analysis to all

leakage points independently (this lends itself to an

efﬁciently parallelisable algorithm). This technique

applies also to our attack: each leakage point eventu-

ally gives one key pair. We can test each key pair via

a pair of known plaintext and ciphertext. In case of a

plaintext only attack, another test would be possible:

if we set x = α and y = β then both adder inputs are

equal to 0 which can be detected by a collision anal-

ysis (Schramm et al., 2004; Bogdanov, 2007; Moradi

et al., 2010).

5.1 Experiments

Attack simulations are a valuable tool because they

enable us to produce results quickly for different sets

of parameter choices. In the absence of detailed char-

acterisations of devices and their actual power mod-

els, one cannot fall back on established statistical

techniques such as a power-based sample size anal-

ysis to derive how many leakage traces are necessary

in practice to conduct successful attacks. Thus simu-

lations are the established ‘workaround’ when exam-

ining new attack techniques. The attack is mainly af-

fected by three parameters in practice. These are the

noise distribution (characterised by σ), the number of

repeat queries to the leakage function N, and the sig-

niﬁcance level of the two-tailed test. It is well under-

stood that these three quantities jointly determine how

well a test performs, and thus in turn, how often our

attack succeeds.

An Analytic Attack against ARX Addition Exploiting Standard Side-channel Leakage

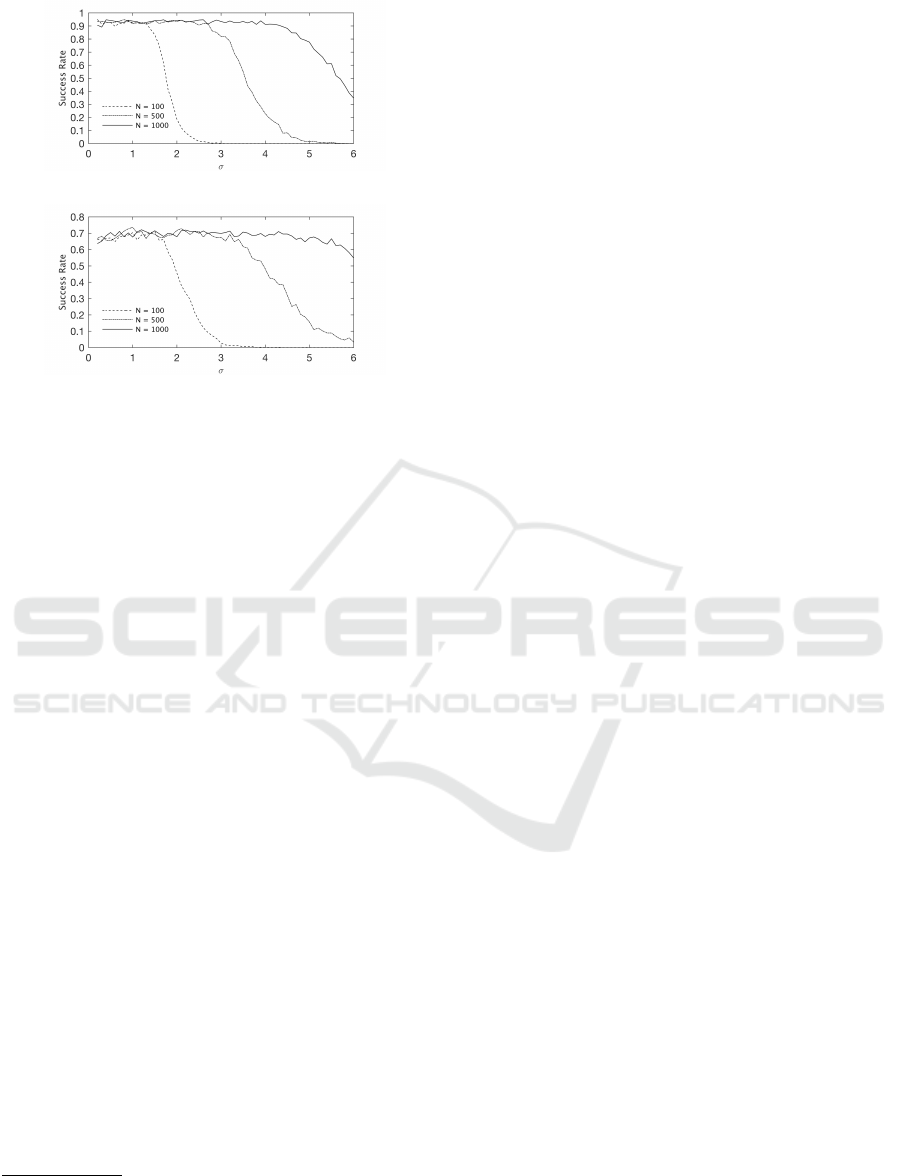
(a) Signiﬁcance level of 0.01

(b) Signiﬁcance level of 0.05

Figure 1: Simulation results for the attack. The left ﬁgure

shows the success rate as a function of the number of leak-

age traces (per query) when choosing a signiﬁcance of 0.01.

The right ﬁgure is identical but for a signiﬁcance of 0.05.

We simulated the attack with 16-bit word size

(n = 16) which has been chosen in certain ARX ci-

phers such as SPARX. Algorithm 5 is implemented

using a t-test

. S

and S

are chosen to have the same

sample size for simplicity. We simulated the attack

using different conﬁgurations where σ ∈ [0.1,6] and

N ∈ [100,1000]. Recall that N is the number of sam-

ples used for each tests. A complete attack hence uses

2N(n + 1) traces.

The result follows our expectations in general. For

the same choice of signiﬁcance level, the number of

traces required to achieve the same success rate in-

creases as the noise variance increases. This directly

derives from the fact that the power of t-test weak-

ens as the noise variance increases. With the same

amount of traces and the same noise level, the signif-

icance level of 0.05 has a lower success rate cap than

0.01, which are around 0.74 and 0.96, respectively.

But in return the former also showed a better noise

tolerance than the latter. Since the signiﬁcance level

of 0.05 implies a higher rate of false positives in re-

turn for less traces required; thus the results follow an

expected and natural trend.

We follow the assumption of Gaussian noise, which

motivates the choice of the t-test. Thus if noise follows a

different distribution, then a different two-tailed test could

be used.

6 CONCLUSIONS

We present a novel theoretical concept to attack the

modular addition in the context of ARX ciphers us-

ing side channel leakage. Our assumptions are mini-

mal w.r.t. the leakage because we only require to ob-

serve a change in the leakage magnitude relating to

the adder output in an implementation. Our paper de-

tails the mathematical idea using idealised Hamming

weight leakage information at ﬁrst, and then discusses

an adaptation to cope with a noisy leakage function.

To ascertain the impact of noise we provide a case

study and via simulations we demonstrate the impact

and trade-off between noise and signiﬁcance level that

would need to be considered in practice.

Purely from a practical perspective, there exists

a more powerful attack for ARX ciphers on a spe-

ciﬁc class of devices as described in (Yan and Os-

wald, 2019). They observe a device speciﬁc effect

called leakage ampliﬁcation that makes the attack on

the rotation very trace efﬁcient on a speciﬁc type of

device. We are not aware of any successful attack

however, beyond the Butterﬂy attack that requires a

known adder input, on the modular addition in the

context of an ARX cipher.

Thus we believe our contribution is of general

cryptanalytic interest because it opens up a new av-

enue for analysing modular additions utilising rather

generic leakage from the adder output.

ACKNOWLEDGEMENTS

This work has been funded in parts by the European

Union (EU) via the ERC project 725042 (acronym

SEAL). The third author’s work was funded by the

INSPIRE Faculty Award (DST, Govt. of India).

REFERENCES

Aumasson, J.-P., Henzen, L., Meier, W., and Phan, R. C.-

W. (2008). SHA-3 proposal BLAKE. Submission to

NIST.

Beaulieu, R., Shors, D., Smith, J., Treatman-Clark, S.,

Weeks, B., and Wingers, L. (2015). The SIMON and

SPECK lightweight block ciphers. In Proceedings of

the 52nd Annual Design Automation Conference, San

Francisco, CA, USA, June 7-11, 2015, pages 175:1–

175:6. ACM.

Beierle, C., Biryukov, A., dos Santos, L. C., Großsch

adl,

J., Perrin, L., Udovenko, A., Velichkov, V., and Wang,

Q. (2008). SchwaemmandEsch: Lightweight Authen-

ticated Encryption andHashing using the Sparkle Per-

mutation Family. Inf. Comput., 206(2-4):378–401.

ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy

Bernstein, D. J. (2008). The Salsa20 Family of Stream Ci-

phers. In Robshaw, M. J. B. and Billet, O., editors,

New Stream Cipher Designs - The eSTREAM Final-

ists, volume 4986 of Lecture Notes in Computer Sci-

ence, pages 84–97. Springer.

Bernstein, D. J., K

olbl, S., Lucks, S., Massolino, P. M. C.,

Mendel, F., Nawaz, K., Schneider, T., Schwabe, P.,

Standaert, F.-X., Todo, Y., and Viguier, B. (2017).

Gimli : A cross-platform permutation. In Fischer,

W. and Homma, N., editors, Cryptographic Hardware

and Embedded Systems – CHES 2017, pages 299–

320, Cham. Springer International Publishing.

Biryukov, A., Dinu, D., and Großsch

adl, J. (2016). Cor-

relation power analysis of lightweight block ciphers:

From theory to practice. In Manulis, M., Sadeghi,

A., and Schneider, S., editors, Applied Cryptogra-

phy and Network Security - 14th International Confer-

ence, ACNS 2016, Guildford, UK, June 19-22, 2016.

Proceedings, volume 9696 of Lecture Notes in Com-

puter Science, pages 537–557. Springer.

Biryukov, A. and Perrin, L. (2017). State of the art in

lightweight symmetric cryptography. IACR Cryptol-

ogy ePrint Archive, 2017:511.

Bogdanov, A. (2007). Improved side-channel collision at-

tacks on AES. In Adams, C. M., Miri, A., and Wiener,

M. J., editors, Selected Areas in Cryptography, 14th

International Workshop, SAC 2007, Ottawa, Canada,

August 16-17, 2007, Revised Selected Papers, volume

4876 of Lecture Notes in Computer Science, pages

84–95. Springer.

Dinu, D., Perrin, L., Udovenko, A., Velichkov, V.,

Großsch

adl, J., and Biryukov, A. (2016). Design

strategies for ARX with provable bounds: SPARX

and LAX. In Cheon, J. H. and Takagi, T., editors,

Advances in Cryptology - ASIACRYPT 2016 - 22nd

International Conference on the Theory and Applica-

tion of Cryptology and Information Security, Hanoi,

Vietnam, December 4-8, 2016, Proceedings, Part I,

volume 10031 of Lecture Notes in Computer Science,

pages 484–513.

Ferguson, N., Lucks, S., Schneier, B., Whiting, D., Bel-

lare, M., Kohno, T., Callas, J., and Walker, J. (2010).

The Skein hash function family. Submission to NIST

(round 3), 7(7.5):3.

Jungk, B., Petri, R., and St

ottinger, M. (2018). Efﬁ-

cient side-channel protections of ARX ciphers. IACR

Transactions on Cryptographic Hardware and Em-

bedded Systems, 2018(3):627–653.

Mangard, S., Oswald, E., and Popp, T. (2007). Power

analysis attacks - revealing the secrets of smart cards.

Springer.

Moradi, A., Mischke, O., and Eisenbarth, T. (2010).

Correlation-enhanced power analysis collision attack.

In Mangard, S. and Standaert, F., editors, Crypto-

graphic Hardware and Embedded Systems, CHES

2010, 12th International Workshop, Santa Barbara,

CA, USA, August 17-20, 2010. Proceedings, volume

6225 of Lecture Notes in Computer Science, pages

125–139. Springer.

Nir, Y. and Langley, A. (2015). ChaCha20 and Poly1305

for IETF Protocols. RFC 7539 (Informational).

Prouff, E. (2005). DPA attacks and s-boxes. In Fast Soft-

ware Encryption: 12th International Workshop, FSE

2005, Paris, France, February 21-23, 2005, Revised

Selected Papers, pages 424–441.

Schneider, T., Moradi, A., and G

uneysu, T. (2015). Arith-

metic addition over boolean masking - towards ﬁrst-

and second-order resistance in hardware. In Applied

Cryptography and Network Security - 13th Interna-

tional Conference, ACNS 2015, New York, NY, USA,

June 2-5, 2015, Revised Selected Papers, pages 559–

578.

Schramm, K., Leander, G., Felke, P., and Paar, C. (2004).

A collision-attack on AES: combining side channel-

and differential-attack. In Joye, M. and Quisquater, J.,

editors, Cryptographic Hardware and Embedded Sys-

tems - CHES 2004: 6th International Workshop Cam-

bridge, MA, USA, August 11-13, 2004. Proceedings,

volume 3156 of Lecture Notes in Computer Science,

pages 163–175. Springer.

Shimizu, A. and Miyaguchi, S. (1988). FEAL - fast data

encipherment algorithm. Systems and Computers in

Japan, 19(7):20–34.

Yan, Y. and Oswald, E. (2019). Examining the practical

side channel resilience of ARX-boxes. In Palumbo,

F., Becchi, M., Schulz, M., and Sato, K., editors, Pro-

ceedings of the 16th ACM International Conference

on Computing Frontiers, CF 2019, Alghero, Italy,

April 30 - May 2, 2019., pages 373–379. ACM.

Zohner, M., Kasper, M., and St

ottinger, M. (2012).

Butterﬂy-attack on Skein’s modular addition. In

Schindler, W. and Huss, S. A., editors, Construc-

tive Side-Channel Analysis and Secure Design - Third

International Workshop, COSADE 2012, Darmstadt,

Germany, May 3-4, 2012. Proceedings, volume 7275

of Lecture Notes in Computer Science, pages 215–

230. Springer.

An Analytic Attack against ARX Addition Exploiting Standard Side-channel Leakage