Genetic Algorithm based L4 Identiﬁcation and Psoas Segmentation

Namitha V. Benjamin

, Robert D. Boutin

, Abhijit J. Chaudhari

and Kwan-Liu Ma

Department of Computer Science, University of California, Davis, CA 95616, U.S.A.

Department of Radiology, Stanford University School of Medicine, Stanford, CA 94305, U.S.A.

Department of Radiology, University of California Davis, Sacramento, CA 95817, U.S.A.

Keywords:

Genetic Algorithm, Psoas Muscle, L4 Identiﬁcation, Region Growing, Edge Linking.

Abstract:

Segmentation of the Psoas muscle is an important ﬁrst step in identifying sarcopenia. Physicians use computed

tomography (CT) images to track changes in muscle mass, which, in turn, act as indicators of how well a

patient is responding to treatment. To measure the muscle, a radiologist segments a CT manually. This is

often time consuming task and can be prone to error. In this paper we propose a novel method to segment

psoas muscles from abdominal CT images. The novel approach uses imaging techniques augmented with

medical anatomic knowledge. The outcome of the algorithm is two fold; ﬁrst, the 4

lumbar vertebra (L4) is

identiﬁed from a series of CT images. Second, the psoas muscle in the identiﬁed slice, is segmented based

on a genetic algorithm based edge linking method. The algorithm was applied to a series of datasets of 61

patients over the age of 65 with hip fractures, and we obtained an average match (true positive percentage) of

91%.

1 INTRODUCTION

“Sarcopenia” is deﬁned as the age-related loss of

skeletal muscle mass and function (Cornet et al.,

2015; Santilli et al., 2014). Such a loss directly im-

pacts muscle strength, which in turn, increases occur-

rence of disability in the elderly. It has become recog-

nized as a major public health threat in our aging pop-

ulation, reaching an epidemic prevalence of up to 50%

by the age of 80 years (Santilli et al., 2014). Recent

studies show that this condition is known to occur not

only with age advancement, but also as a side eﬀect

of diseases, such as cancer and cardiovascular condi-

tions. While there is now extensive data showing sar-

copenia as an important predictor of future negative

outcomes for patients (e.g., physical disability, com-

plications after surgery, death), muscle depletion is

often occult clinically. The medical community now

identiﬁes it as an independent risk factor for predict-

ing future failing human health in adults. More and

more studies (Alfonso J. Cruz-Jentoft, 2019; Van An-

cum, 2020) are proving that sarcopenia can be a pre-

dictive factor of post-operative morbidity as well as

recovery after cancer surgeries. In an eﬀort to stan-

dardize this process, the “European Working Group

on Sarcopenia in Older People” (EWGSOP), deﬁned

mechanisms and assessment techniques to character-

ize sarcopenia (Alfonso J. Cruz-Jentoft, 2019). One

of the techniques identiﬁed was muscle mass. This

has led to several studies aiming to characterize the re-

lationship between lean muscle mass and patient out-

comes.

One of the key muscles identiﬁed for such studies

is the psoas muscle. Muscle mass can be measured via

either computed tomography (CT) or magnetic reso-

nance imaging (MRI), which are diagnostic imaging

techniques considered as a ground truth, by the med-

ical community. They allow for precise determina-

tion of body composition, including non-invasive as-

sessment of muscle mass and quality. Although these

body composition data are routinely collected on 90

million CT scans and 35 million MRI scans annu-

ally in the USA, those data are not analyzed quantita-

tively because of two unsolved problems: 1) the mas-

sive time burden, cost, and tediousness of perform-

ing manual measurements on individual imaging ex-

aminations, and 2) the lack of normative data across

large populations. If segmentation of muscle from

fat and other tissues could be automated, these prob-

lems could be solved and usher in a new era of “per-

sonalized medicine”, with quantitative body compo-

sition analysis performed automatically on all routine

anatomical imaging exams. Diagnosis of the type and

severity of sarcopenia would allow optimal prescrip-

tion of treatments for muscle depletion that include

120

Benjamin, N., Boutin, R., Chaudhari, A. and Ma, K.

Genetic Algorithm based L4 Identiﬁcation and Psoas Segmentation.

DOI: 10.5220/0010207701200127

In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 2: BIOIMAGING, pages 120-127

ISBN: 978-989-758-490-9

speciﬁc diets and exercises, as well as medications.

By manually outlining muscle, the diagnosis of sar-

copenia has been validated in research settings, com-

monly by isolating the psoas muscle at the level of the

lumbar vertebra (L4) on CT scans (Kamiya et al.,

2012; Ulf Tiede, 1996; Meesters et al., 2012). The

lumbar vertebrae has been chosen since the psoas

muscle is seen most prominently in this slice. In ad-

dition, anatomical landmarks can be reliably used to

identify this slice, thereby enabling the complete au-

tomation of this algorithm.

In this pilot study, manual segmentation by a

physician expert is used as a gold standard (“ground

truth”) for validating the accuracy of the proposed

method. Our aim was to develop an algorithm that

could automate the process of 1) reliably ﬁnding the

appropriate anatomic slice on a routine CT scan, and

then 2) accurately segmenting the psoas muscle of in-

terest.

2 RELATED WORKS

In addition to psoas muscles, there has been a growing

interest in abdominal muscle segmentation, as a strat-

iﬁcation tool in cancer treatment, pre-surgery treat-

ment, surgical procedures and radiation. Early work

done in this area used pre-deﬁned Hounsﬁeld Units

(HU) to develop threshold based segmentation tech-

niques. This approach can be reliably used to segment

adipose tissue whose HU uniquely ranges from -190

to -30. However, muscle segmentation poses more

challenges, since its HU values of -29 to 150, overlap

with those of neighbouring organs.

Prior research in psoas muscle segmentation, pri-

marily focuses on shape based models. Kamiya et

al.(Kamiya et al., 2012) derived a mathematical func-

tion based shape model for segmenting the psoas mus-

cle. However, this method still required the interven-

tion of a radiologist in selecting the slice of interest.

Meesters et al.(Meesters et al., 2012) presented an au-

tomatic system to assist the segmentation of abdomi-

nal organs, using the medially positioned psoas mus-

cle’s shape and location along with previously accom-

plished segmentation of the liver and spleen. How-

ever, owing to anatomical diﬀerences in patients, this

method showed varying results. Gilles et al.(Gilles

et al., 2006) introduced a modeling method for mus-

cles in the crural area for analyzing their motor func-

tion in MR images. Ng et al.(Ng et al., 2007) intro-

duced a recognition method, for surgical planning and

analysis of loss of mastication function of the tempo-

ral muscle. These two methods, however, were used

for MR images. The scalability of these methods to

CT images still remains unclear since the boundaries

between muscle and adjacent organs are not funda-

mentally diﬀerent in such datasets.

Genetic Algorithms (GAs) have not been explored

as a solution for psoas muscle segmentation. It proves

to be a strong candidate if image segmentation is for-

mulated as a numerical optimization problem. (Sheta

et al., 2012) demonstrate how GAs complement exist-

ing optimization methods and has proved to be insen-

sitive to noise. This characteristic proves extremely

beneﬁcial in medical imaging, in that GAs require no

gradient information and hence they are less likely

to get trapped in local minima on multimodal sur-

faces. Segmentation methods frequently use thresh-

olds to decide whether two pixels are in the same re-

gion or not. However, the thresholds negatively aﬀect

the image segmentation and often result in inaccura-

cies. Therefore, the tuning values of the thresholding

algorithms must be set up carefully (Levialdi et al.,

2003; Hamdaoui et al., 2015). A multilevel thresh-

olding method which allows the determination of the

appropriate number of thresholds as well as the ade-

quate threshold values has been proposed in (Ham-

daoui et al., 2015). The paper combines both GA

and wavelet transform. In this paper we propose a

new method for image segmentation using GAs, by

posing the segmentation problem as an optimization

problem. The contribution of this work is the for-

mulation of a set of tuning parameters for GAs to

be eﬀectively used on CT images. The authors have

shown that GAs can be used as an intermediate step to

develop an accurate segmentation map, which when

combined with medical anatomical knowledge, pro-

duces accurate segmentation results for psoas muscle

delineation. We will describe our works according to

the following organization. The proposed model and

the segmentation procedure are described in Section

3. The experimental results of the proposed model

and some results compared with region growing mod-

els are shown in Section 4. At last, the conclusions are

provided in Section 5.

3 PROPOSED METHOD

The proposed algorithm consists of two modules. The

ﬁrst module implements an automated identiﬁcation

of the L4 slice from the original CT images of the ab-

domen, which are provided as the module input. The

slice containing the image of the L4 vertebra is deter-

mined. This is done by detecting the top of the iliac

crest that acts as an anatomical landmark. The sec-

ond module implements a GA based edge linking that

identiﬁes the pixels of the psoas muscle in the L4 slice

Genetic Algorithm based L4 Identiﬁcation and Psoas Segmentation

121

obtained from the ﬁrst module.

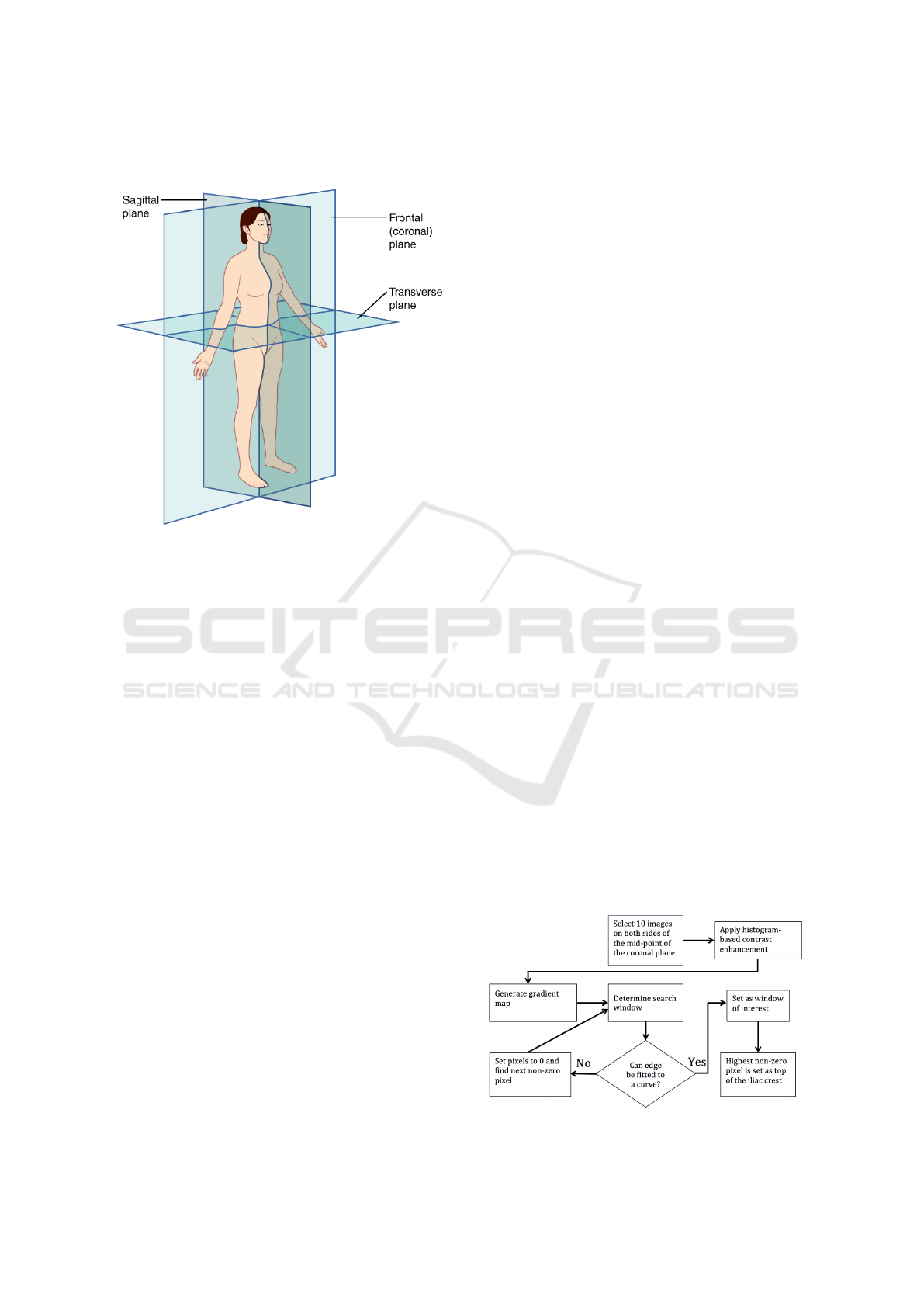
Figure 1: Planes of the Body.

3.1 L4 Identiﬁcation

Before delving into the proposed method, it is im-

portant to understand terms used in the next sections,

for describing anatomical landmarks. Fig. 1 (Jones,

2018) shows how a landmark can be represented in

three dimensions. The terms superior and inferior

are used for describing the position along the main

body axis (representing top and bottom). Horizon-

tally, the terms anterior and posterior are used for the

front and back of the body respectively, while right

and left is used for description of lateral points. Two-

dimensional planes are used for describing cross-

sections of the body. The sagittal plane is parallel

to the body long axis and divides the body into left

and right sections. The coronal plane is also paral-

lel to the body axis and it divides the body to ante-

rior and posterior sections. Finally, the axial plane,

also known as transverse plane, is perpendicular to

the body long axis and divides it to superior and in-

ferior sections. The ﬁrst module of our algorithm de-

termines the L4 slice from the images of a CT scan.

Medical literature highlights that the cross-section of

the psoas muscle’s transverse section is maximal at

the longitudinal center and minimal at its origin and

insertion. Parts of the skeletal muscles are connected

to the skeleton. Hence, at the L4 vertebra, the radius

of these muscles is likely the largest. Fig. 2 displays

the ﬂowchart of the L4 identiﬁcation module. The

identiﬁcation method is mainly based on the anatom-

ical location of the L4 vertebra.

In current clinical practice, radiologists com-

monly determine the L4 level in three steps (Farshad-

Amacker et al., 2015): i) identifying the superior mar-

gin of the iliac crests in the coronal plane, followed

by ii) connecting these points along the mediolateral

axis, and then iii) selecting the vertebra superior to

this axis. In our algorithm, this process is automated

and streamlined by identifying the L4 level consis-

tently at a level 2 cm above the iliac crests. Thus, we

consider ’n’ slices as candidates to implement the al-

gorithm to determine the L4 slice, where ’n’ depends

on the separation of the slices in the series (for ex-

ample, 5 mm or 2 mm or 1.25 mm, depending on the

slice). For example, if the input images have a 5 mm

separation, then we deﬁne the L4 level by selecting

the image four slices above the top of the iliac crest.

To do this manually over a large dataset proves to be

extremely time consuming, and hence uneconomical.

The ﬁrst author of this paper manually extracted

the muscle regions. These regions were then in-

spected, and, if necessary, the results were revised by

the third author, who is a medical expert on anatomy.

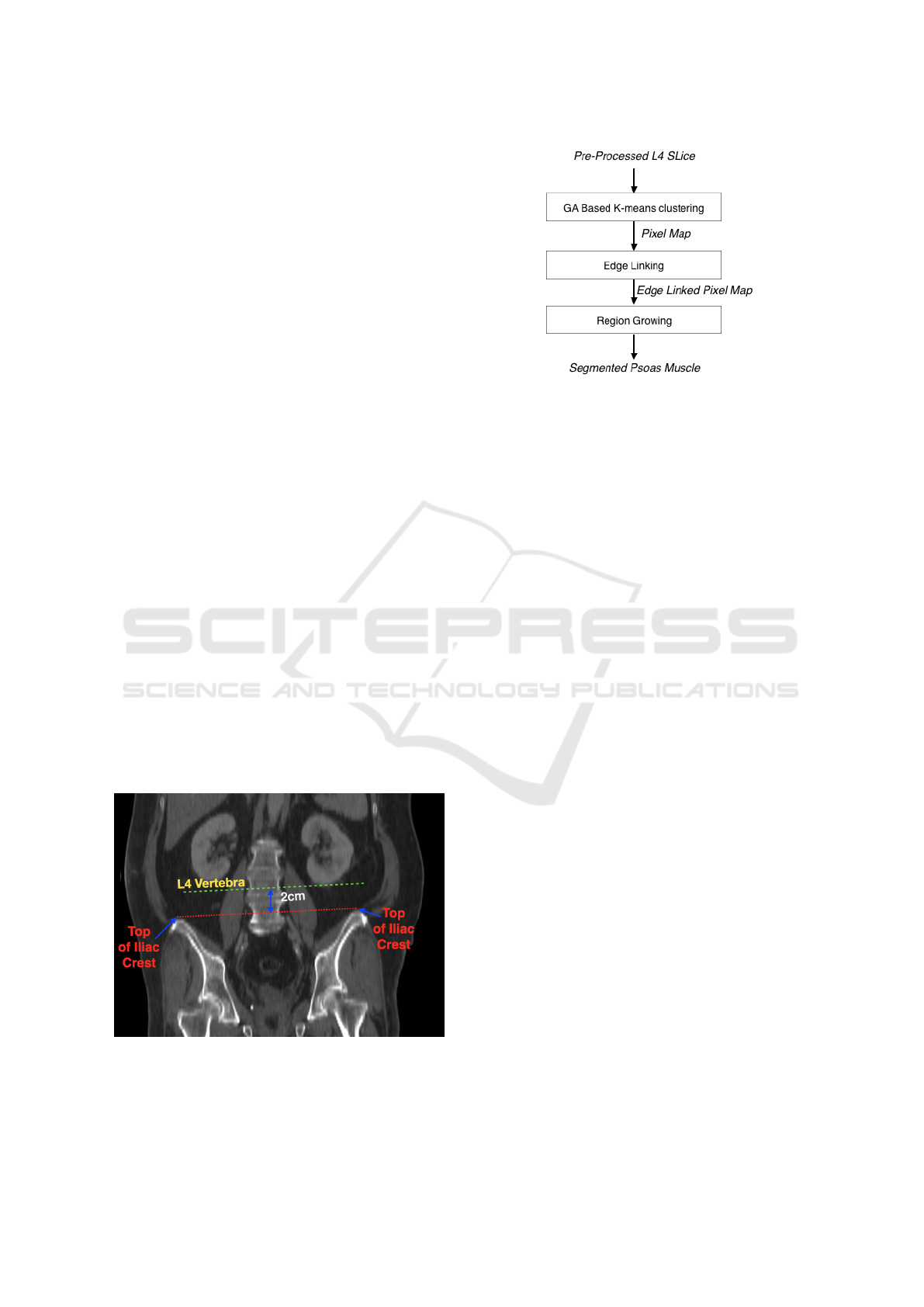
3.1.1 Pre-processing

In order to identify the iliac crests, the three-

dimensional data was processed in the coronal plane.

This required up-sampling followed by rotation while

translating from axial to coronal plane. Fig. 3 shows

the image of a slice from the coronal plane where the

top of both the iliac crests are marked by red dots and

the L4 vertebra is identiﬁed as 2 cm.

In order to optimize the algorithm we ran the

next phase only on twenty slices. To determine these

twenty slices, the contrast of all slices was enhanced

by histogram equalization, after which the number of

bone pixels in each slice were determined, based on

a threshold. In order to determine this threshold, the

image was ﬁrst normalized after which it was ﬁt to a

normal distribution. A cumulative distributive func-

tion was used to determine the threshold, as the in-

tensity value of the upper 90% of the pixels. Twenty

Figure 2: Flowchart of L4 Identiﬁcation.

BIOIMAGING 2021 - 8th International Conference on Bioimaging

122

slices with the most number of bones pixels were cho-

sen for the next step, in which the edge map was com-

puted using a Canny edge detector. This step found

edges by looking for local maxima in the image gra-

dient (Canny, 1986). The gradient was then calculated

using the derivative of a Gaussian ﬁlter. The method

used two thresholds, to detect strong and weak edges,

and included the weak edges in the output only if they

are connected to strong edges. The algorithm was im-

plemented in MATLAB and the default threshold val-

ues were chosen.

3.1.2 Search Window

Owing to the symmetric nature of the iliac crests, the

recursive portion of the algorithm was run on each

half of the image. The search window was initialized

at the ﬁrst pixel encountered on the edge map, towards

the superior end of the image. The search window

was then expanded with a maximum of 8x8 pixels,

until the next pixel on the edge map was hit. This

continued until the search window stopped growing

in all directions. In a search window, if the non-zero

pixel could be ﬁtted to a curve, that was the window

of interest containing the iliac crest. Otherwise, all

pixels in that region were set to zero and the search

window was initialized at the next non-zero pixel. In

the search window of interest, the superior-most pixel

on the edge map was the tip of the iliac crest. This L4

slice was determined at 2 cm above this point (tak-

ing into consideration the sampling performed during

transformation between planes).

3.2 Proposed Genetic Algorithm (GA)

based Edge Linking Method

Figure 3: L4 Slice Detection.

In this paper, we propose a novel segmentation tech-

nique that has its foundation in GAs, to perform a se-

mantic segmentation of the image. Fig. 4 highlights

Figure 4: Overview of GA based Region Growing Method.

the main blocks of the proposed algorithm. At a high

level, the GA is used to obtain a pixel map, where

pixels are grouped by the likelihood that they belong

to one class. The pixel map is then used, to perform

a region growing in an edge linked constraint to ob-

tain the ﬁnal segmented image of the left and right

psoas muscle. In the subsequent sections, we will go

over details of each of these functional blocks. Before

feeding the L4 slice into this part of the algorithm, the

image is ﬁrst pre-processed to highlight the bone and

the areas surrounding it. This is done based on Otsu’s

thresholding.

3.2.1 Genetic Algorithm based K-means

Clustering

Genetic algorithms have been proven to solve numeri-

cal optimization problems by stochastic search meth-

ods of the solution space. The premise of this algo-

rithm is that a ﬁtness function is used to obtain the

best possible candidates for the ﬁnal solution, in an

iterative manner, through mutation, crossover and se-

lection. GA’s used earlier (Krishna and Murty, 1999)

in clustering employ either an expensive crossover

operator to generate valid child chromosomes from

parent chromosomes or a costly ﬁtness function or

both. To circumvent these expensive operations, we

hybridize GA with a classical gradient descent al-

gorithm used in clustering like K-means algorithm.

Hence, the name genetic K-means algorithm.

The GA consists of the following steps (Sheta

et al., 2012):

1. Initialize population.

2. Compute ﬁtness function at every pixel, based on

ﬁtness function.

3. Fittest individuals are selected for next iteration

based on selection function.

4. Generate next population based on reproductive

operators and ﬁt members of current population.

5. Stop if stopping criterion is met, else go to step 3.

Genetic Algorithm based L4 Identiﬁcation and Psoas Segmentation

123

These steps are represented in Fig. 5.

Figure 5: Segmentation using Genetic Algorithms.

Fitness Function:

In GAs, a ﬁtness function is used to evaluate if in-

dividuals are capable of producing oﬀsprings. In the

proposed algorithm, a ﬁtness function has been de-

ﬁned on the basis of the Euclidean distance computed

between a given chromosome (i.e. pixel) and a region

S. The ﬁtness of an individual pixel, i is deﬁned as

follows

= min((G

− i)

) (1)

where:

, denotes the centroid of the kth cluster,

i, represents the pixel value at that location.

Selection Function:

The selection function used in the proposed algorithm

is Roulette wheel, developed by Holland (Holland,

1992). The probability, P

, for each individual is

deﬁned by:

PopulationS ize

j=1

(2)

where F

, equals the ﬁtness of individual i.

The use of roulette wheel selection limits the genetic

algorithm to maximization since the evaluation

function must map the solutions to a fully ordered set

of values on ﬁt. Extensions, such as windowing and

scaling, have been proposed to allow for minimiza-

tion and negativity.

Stopping Criteria:

The GA algorithm iterates through several genera-

tions until a stopping criteria is met. The proposed al-

gorithm uses the speciﬁed number of maximum gen-

erations as its termination criterion.

3.2.2 Edge Linking and Region Growing

The technique of edge-based region growing (Singh

et al., 2011) (Jamil et al., 2011) is chosen, as the

left and right psoas muscles are in a contained region

above the L4. As a ﬁrst step, the edge map of the re-

duced region of interest is obtained by using canny

edge operator. Edge linking is then performed by

merging edges (Sappa and Vintimilla, 2008). Edge

merging is done if the edge map contains discontinu-

ities lesser than a given threshold, between pixels hav-

ing similar gradient values. Fig. 6 shows the linked

edges highlighted in red on the edge map.

(a) Gradient Image (b) Highlighted Linked Edges

Figure 6: Edge Linking.

This makes the region growing much less noisy

and is contained to the closed regions of the edges.

Following the edge linking process, region growing is

applied starting at the seed location determined in the

previous section. The two parameters considered in

the region growing process are: 1) the diﬀerence be-

tween a pixel’s intensity value and the region’s mean

which is a measure of the similarity of the pixel to a

given region and 2) if the pixel lies on the edge map.

This process stops when the intensity diﬀerence be-

tween region mean and new pixel become larger than

a certain threshold or if the pixel lies on the edge

map. Region growing on the edge-linked edge map

contains the region growing process to only the psoas

muscle margin even if the diﬀerence in pixel inten-

sity between the psoas and the surrounding abdominal

muscles is not large.

4 RESULTS

We validated our algorithm on a dataset consisting of

abdominal CT scans of 61 patients all over the age of

65 years with hip fractures (32 female and 29 male).

The CT scans on average have 90 images in every

series. These images are 512x512, with a bit depth of

16 bits captured via helical scan mode. 90% of these

images do not have any contrast agent. The presence

of a contrast agent is seen to boost the accuracy of

BIOIMAGING 2021 - 8th International Conference on Bioimaging

124

the algorithm. In this cohort all the scans have a slice

thickness of 5mm. The algorithm performs well at

this value. However, for some, 1.25mm slice thick-

ness were also available. The algorithm did not show

promising results at this thickness owing to the high

amount of noise in these images.

Table 1: Results of L4 Identiﬁcation.

Range of L4 L4 Slice

Slices (proposed

(ground truth) method)

patient1 27-32 31

patient2 51-56 51

patient3 2-7 4

patient4 41-46 42

patient5 33-37 36

patient6 44-49 49

patient7 42-47 44

patient8 39-44 43

patient9 37-42 50

To evaluate the accuracy of the L4 identiﬁcation,

a radiologist was asked to identify the range of L4

slices in each dataset. The accuracy of this module

is determined by the number of slices by which the

algorithm misses the required L4 range, as manually

determined by a domain expert (radiologist). Table 1

shows a sampling of the results for the L4 identiﬁca-

tion module of the algorithm. The datasets were cho-

sen such that each has a unique position for the L4

slice. This ensures the robustness of the algorithm.

Even when the iliac crests were not exactly symmet-

ric, the algorithm performed accurately across such

datasets. As can be seen in Table 1, our algorithm

failed to correctly identify the position of L4 slice

of patient9 and obtained a diﬀerence of 8 slices rel-

ative to the ground truth. This was the case where

the algorithm performed the worst. On retrospective

analysis, we found out that this dataset did not have

suﬃcient contrast diﬀerence between the psoas and

the surrounding abdominal soft tissues. Out of the 61

CT images, about 12 datasets missed the L4 window

with an error of 1-8 slices. This will be addressed in

future research, by incorporating the shape model of

the psoas muscle to improve the accuracy of the al-

gorithm. The initial population of the Genetic Al-

gorithm was randomly selected. The population size

of 50 was chosen. A stopping factor of 100 genera-

tions was selected for these runs. Fig.7 shows that,

for a CT image at the L4 slice, the ﬁtness function

converges within the selected stopping criteria of 100

generations. At the end of this stage, the GA driving

k-means segmentation generates a segmentation map

as shown in Fig.8 and Fig.9. Note, Fig.8, shows the

Figure 7: Convergence of Genetic Algorithm.

Figure 8: Segmentation map produced by Genetic Algo-

rithm.

various classes highlighted in HSV color space. This

is done for the sake of representation only. The pro-

posed method consumes a gray scale version of this,

as represented in Fig 9. For evaluating the accu-

racy of the psoas muscle segmentation algorithm, we

compared the manual segmentation as performed by

a radiologist and our semi-automatic segmentation al-

gorithm of the abdominal CT scans. The results of

two datasets are shown in ﬁgures 10 and 11.

In order to quantify our results, we have computed

the true positive percentage as the number of pixels la-

belled as psoas in both the ground truth and the output

of our algorithm. False positives are pixels marked as

psoas by our algorithm and not psoas in the ground

truth. Finally, we have false negatives as pixels that

are actual psoas muscle pixels in the ground truth, and

that are not labeled by our algorithm.

Genetic Algorithm based L4 Identiﬁcation and Psoas Segmentation

125

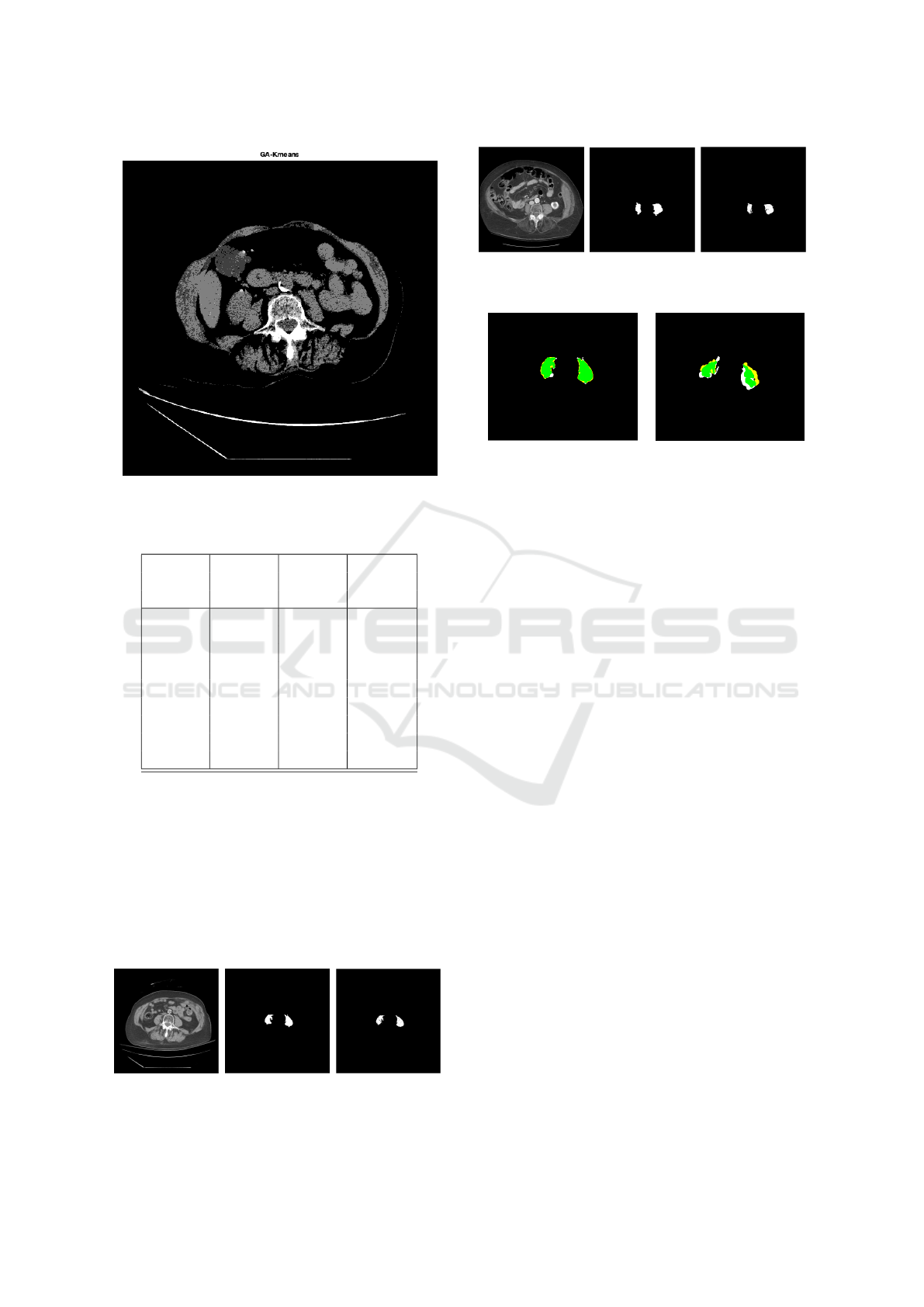
Figure 9: Segmentation map produced by Genetic Algo-

rithm.

Table 2: Results of Psoas Segmentation.

True False False

positive positive negative

rate (%) rate (%) rate (%)

patient1 86.47 7.64 25.87

patient2 87.33 16.70 15.96

patient3 91.59 5.11 3.28

patient4 84.25 7.44 8.30

patient5 89.62 1.88 8.49

patient6 92.76 1.82 14.41

patient7 83.64 13.42 2.92

patient8 83.10 3.11 13.79

patient9 95.10 1.72 19.18

These results that are computed across the dataset are

tabulated in Table 2. Our algorithm showed relatively

low detection rates on three datasets, i.e. patient 1, 2

and 9. Because these three datasets of lower contrast,

result in the details around edges be lost. In particular,

our algorithm failed to identify the correct position of

L4 slice for patient9. The dataset corresponding to

patient9 showed lower true positive percentage, as it

failed to correctly identify the correct L4 slice.

(a) L4 Slice (b) Ground Truth (c) Our Result

Figure 10: Psoas Segmentation Results.

(a) L4 Slice (b) Ground Truth (c) Our Result

Figure 11: Psoas Segmentation Results.

(a) patient2 (b) patient1

Figure 12: Accuracy of Psoas Segmentation Algorithm.

In Fig. 12(a) and (b) we use the detected results

of patients1 and patient2, respectively, to show how

the numbers in Table 2 are calculated. The true pos-

itives (TP) are highlighted in green, false negatives

(FN) are highlighted in white and false positives (FP)

are shown in yellow.

5 CONCLUSION

We present a semi-automatic method to identify im-

ages corresponding to the 4

lumbar vertebra and

then identify the left and right psoas muscles in this

slice. Anatomical landmarks were set up in a com-

pletely automatic manner with the use of spatial posi-

tioning information on the images. The algorithm was

tested on 61 datasets. The L4 identiﬁcation module of

the algorithm shows accurate results in about 80% of

the cases. The failing cases were primarily scans with

poor resolution and contrast, which resulted in irreg-

ularities of muscle boundaries. This proved to be a

breaking point of this algorithm, that relied on edge

linking.

The psoas muscle segmentation module recorded

average true positive rate of 91%. As next steps, the

accuracy of the algorithm will be enhanced by im-

proving the accuracy of the edge linking phase of the

segmentation algorithm. This will in turn preserve de-

tails around edges of the psoas muscle. Our approach

met the criterion laid out by radiologists to replace the

current manual process of psoas muscle identiﬁcation

around the L4.

BIOIMAGING 2021 - 8th International Conference on Bioimaging

126

ACKNOWLEDGEMENTS

The research in this paper was partially supported

by National Institutes of Health under award num-

ber R01 AR076088. The authors would like to thank

Dr. Stephen Henrichon of the University of Califor-

nia, Davis, who provided access to scans as well as

training on image interpretation.

REFERENCES

Alfonso J. Cruz-Jentoft, Jean Pierre Baeyens, e. a. (2019).

Clinical deﬁnition of sarcopenia. Sarcopenia: Euro-

pean consensus on deﬁnition and diagnosis: Report of

the European Working Group on Sarcopenia in Older

People, Age and Ageing, 39(4):412–423.

Canny, J. (1986). A computational approach to edge detec-

tion. Pattern Analysis and Machine Intelligence, IEEE

Transactions on, PAMI-8(6):679–698.

Cornet, M., Lim, C., Salloum, C., Lazzati, A., Compagnon,

P., Pascal, G., and Azoulay, D. (2015). Prognostic

value of sarcopenia in liver surgery. Journal of vis-

ceral surgery, 152(5):297-304.

Farshad-Amacker, N. A., Aichmair, A., Herzog, R. J., and

Farshad, M. (2015). Merits of diﬀerent anatomical

landmarks for correct numbering of the lumbar verte-

brae in lumbosacral transitional anomalies. European

Spine Journal, 24(3):600–608.

Gilles, B., Moccozet, L., and Magnenat-Thalmann, N.

(2006). Anatomical Modelling of the Musculoskele-

tal System from MRI. Medical Image Computing

and Computer-Assisted Intervention – MICCAI 2006,

4190:289–296.

Hamdaoui, F., Sakly, A., and Mtibaa, A. (2015). An eﬃ-

cient multi level thresholding method for image seg-

mentation based on the hybridization of modiﬁed pso

and otsu’s method. Computational Intelligence Appli-

cations in Modeling and Control, 2003:343–367.

Holland, J. H. (1992). Adaptation in Natural and Artiﬁcial

Systems: An Introductory Analysis with Applications

to Biology, Control and Artiﬁcial Intelligence. MIT

Press, Cambridge, MA, USA.

Jamil, N., Soh, H., Tengku Sembok, T., and Bakar, Z.

(2011). A Modiﬁed Edge-Based Region Grow-

ing Segmentation of Geometric Objects. Visual

Informatics: Sustaining Research and Innovations,

7066(4):99–112.

Jones, O. (2018). Anatomical Planes.

Kamiya, N., Zhou, X., Chen, H., Muramatsu, C., Hara, T.,

Yokoyama, R., Kanematsu, M., Hoshi, H., and Fujita,

H. (2012). Automated segmentation of psoas major

muscle in X-ray CT Images by use of a shape model:

preliminary study. Radiological Physics and Technol-

ogy, 5(1):5–14.

Krishna, K. and Murty, M. (1999). Genetic k-means algo-

rithm. IEEE transactions on systems, man, and cyber-

netics. Part B, Cybernetics: A publication of the IEEE

Systems, Man, and Cybernetics Society, 29:433–9.

Levialdi, S., Cinque, L., Cucchiara, R., and Pignalberi, G.

(2003). Tuning range image segmentation by genetic

algorithm. EURASIP Journal on Advances in Signal

Processing, 2003.

Meesters, S., Yokota, F., Okada, T., Takaya, M., Tomiyama,

N., Yao, J. J., Liguraru, M., Summers, R., and Sato,

Y. (2012). Multi atlas-based muscle segmentation in

abdominal CT images with varying ﬁeld of view. Med

Image Anal.

Ng, H., Hu, Q., Ong, S., Foong, K., Goh, P., Liu, J., and

Nowinski, W. (2007). Segmentation of the temporalis

muscle from MR data. International Journal of Com-

puter Assisted Radiology and Surgery, 2(1):19–30.

Santilli, V., Bernetti, A., Mangone, M., and Paoloni, M.

(2014). Clinical deﬁnition of sarcopenia. Clinical

cases in mineral and bone metabolism: the oﬃcial

journal of the Italian Society of Osteoporosis, Mineral

Metabolism, and Skeletal Diseases, 11(3):177-180.

Sappa, Angel, D. and Vintimilla, Boris, X. (2008).

Edge Point Linking by Means of Global and Local

Schemes. Signal Processing for Image Enhancement

and Multimedia Processing, 31(4):115–125.

Sheta, A., Braik, M. S., and Aljahdali, S. (2012). Genetic

algorithms: A tool for image segmentation. In 2012

International Conference on Multimedia Computing

and Systems, pages 84–90.

Singh, R., Singh, J., Sharma, P., and Sharma, S. (2011).

Edge based region growing. International Journal of

Computer Technology and Applications, 2(4).

Ulf Tiede, Thomas Schiemann, K. H. (1996). Visualizing

the Visible Human. IEEE Computer Graphics and

Applications, 16(1):7–9.

Van Ancum, J. M. (2020). Impact of using the updated ewg-

sop2 deﬁnition in diagnosing sarcopenia: A clinical

perspective. Archives of gerontology and geriatrics.

Genetic Algorithm based L4 Identiﬁcation and Psoas Segmentation

127