
Improvement of Secure Multi-Party Multiplication of (𝒌,𝒏)
Threshold Secret Sharing using Only 𝑵=𝒌 Servers
Ahmad Akmal Aminuddin Mohd Kamal
1
and Keiichi Iwamura
2
1
Graduate School of Engineering, Department of Electrical Engineering, Tokyo University of Science, Tokyo, Japan
2
Faculty of Engineering, Department of Electrical Engineering, Tokyo University of Science, Tokyo, Japan
Keywords: Secure Multi-Party Computation, MPC, Secure Multiplication, (𝑘,𝑛) Threshold Secret Sharing, Information
Theoretic Secure.
Abstract: Secure multi-party computation (MPC) allows a set of 𝑛 servers to jointly compute an arbitrary function of
their inputs, without revealing these inputs to each other. A (𝑘,𝑛) threshold secret sharing is a protocol in
which a single secret is divided into 𝑛 shares and the secret can be recovered from a threshold 𝑘 shares.
Typically, multiplication of (𝑘,𝑛) secret sharing will result in increase of polynomial degree from 𝑘−1 to
2𝑘− 2, thus increasing the number of shares required from 𝑘 to 2𝑘− 1. Since each server typically hold only
one share, the number of servers required in MPC will also increase from 𝑘 to 2𝑘− 1. Therefore, a set of 𝑛
servers can compute multiplication securely if the adversary corrupts at most 𝑘−1<𝑛/2 of the servers. In
this paper, we differentiate the number of servers 𝑁 required and parameter 𝑛 of (𝑘,𝑛) secret sharing scheme,
and propose a method of computing (𝑘 −1) sharing of multiplication 𝑎𝑏 by using only 𝑁=𝑘 servers. By
allowing each server to hold two shares, we realize MPC of multiplication with the setting of 𝑁=𝑘,𝑛≥
2𝑘− 1. We also show that our proposed method is information theoretic secure against a semi-honest
adversary.
1 INTRODUCTION
1.1 Background
In recent years, advancement of IoT ecosystem and
big data had attracted considerable anticipation that it
will be possible to utilize big data to obtain valuable
statistical data. Here, big data refer to large quantities
of unstructured and semi structured data. Analyzation
of these data allows researchers and businesses to
extract important and useful information. However,
since big data also includes individuals’ privacy
information, there is a risk that their privacy
information can be leaked if it is not used correctly.
Therefore, a method that allows for the utilization of
big data while protecting sensitive information such
as individuals’ privacy information is required. One
of the methods that can realize this is known as secure
multi-party computation (Yao, 1982). Secure multi-
party computation allows for a set of servers to jointly
compute an arbitrary function of their inputs, without
revealing these inputs to each other. Typically, there
are two main techniques that had been proposed to
realize secure multi-party computation: homomorphic
encryption (Bendlin et al. 2011; Brakerski et al.,
2011; Damgard et al., 2012; Damgard et al., 2013;
Gentry, 2009) and secret sharing schemes (Ben-Or et
al., 1988; Chaum et al., 1988; Cramer et al., 2000;
Gennaro et al., 1998; Shingu et al., 2016; Watanabe
et al., 2015). However, homomorphic encryption is
known to be typically computationally very expensive
in term of computation cost. Therefore, secret sharing
schemes that have a relatively low computational cost
are preferable to homomorphic encryption when
considering utilization in a cloud system.
A secret sharing scheme is a protocol in which a
single secret is divided into shares, which are then
distributed. An example of a secret sharing scheme is
Shamir’s (𝑘,𝑛) threshold secret sharing scheme
(Shamir, 1979). It divides a secret 𝑠 into an 𝑛 number
of shares, distributes the shares, and restores the
original secret 𝑠 from a threshold 𝑘 number of shares.
Any 𝑘−1 or smaller number of shares reveals
nothing about the secret.
The classical result of secure multi-party
computation using secret sharing scheme state that 𝑛
servers can compute any function in such a way that
any subset of up to 𝑘−1<𝑛/2 servers obtains no
information about the other servers’ inputs, except for
Kamal, A. and Iwamura, K.
Improvement of Secure Multi-Party Multiplication of (k, n) Threshold Secret Sharing Using Only N = k Servers.
DOI: 10.5220/0010206400770088
In Proceedings of the 7th International Conference on Information Systems Secur ity and Privacy (ICISSP 2021), pages 77-88
ISBN: 978-989-758-491-6
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
77

what can be derived from the public information
(Ben-Or et al., 1988; Hirt, 2001). Conventional
methods of secure multi-party computation using
Shamir’s (𝑘,𝑛) secret sharing scheme perform
addition by locally adding the shares together.
However, this is not so in the case of multiplication.
For example, let secrets 𝑎 and 𝑏 be encoded by
polynomials 𝑓(𝑥) and 𝑔(𝑥) of (𝑘− 1) degree. Note
that the free coefficient of the polynomial ℎ(𝑥) =
𝑓(𝑥)𝑔(𝑥) is 𝑎𝑏. However, the problems of using
ℎ(𝑥) to encode the product of 𝑎 times 𝑏 is that the
degree of ℎ(𝑥) increase from 𝑘−1 to 2𝑘− 2. In
most conventional methods, this poses no problem of
interpolating ℎ(𝑥) from its 𝑛 shares since it is
assumed that parameter 𝑛≥2𝑘−1. Since each
server holds only one share for each secret, this means
that, for each multiplication performed, the number of
servers required will increase from 𝑘 to 2𝑘− 1.
Shingu et al. proposed a solution for
multiplication method called the TUS method
(Shingu et al, 2016). In this method, the secret is first
encrypted with a random number; when performing
multiplication, the encrypted secret is momentarily
restored as a scalar value and multiplication is
realized using the (𝑠𝑐𝑎𝑙𝑎𝑟 𝑣𝑎𝑙𝑢𝑒 × 𝑝𝑜𝑙𝑦𝑛𝑜𝑚𝑖𝑎𝑙)
approach to prevent an increase in the polynomial
degree. However, in the TUS method, there is a
limitation where input with a value of 0 is not allowed
in the protocol.
On the other hand, Watanabe et al. proposed a
solution by taking an approach of differentiating the
relationship between the number of servers required
𝑁 and parameter 𝑛 of Shamir’s (𝑘,𝑛) secret sharing
(Watanabe et al., 2015). In other word, Watanabe et
al. had proposed a method using 𝑁≤𝑘 servers to
realize 𝑛≥2𝑘−1 multiplication. However, this
method still did not solve the problem of increase in
the polynomial degree. Therefore, although the
multiplication was performed using only 𝑁=𝑘
servers, shares required to restore the multiplication
result are 2𝑘− 1 and not 𝑘.
1.2 Our Results
In this study, we focus on solving the problem of
increase in polynomial degree during multiplication.
We propose a new method of multiplication that
could compute 𝑘−1 sharing of multiplication 𝑎𝑏
using only 𝑁=𝑘 servers. The contributions of this
paper can be summarized as follows:
Our Contributions:
─ We propose a new protocol that allows for
multiplication with the setting of 𝑛≥2𝑘−1 to be
performed using only 𝑁=𝑘 servers, and show
that 𝑘−1 sharing of 𝑎𝑏 can be computed by using
only 𝑁=𝑘 servers. (we also include protocols for
addition and scalar multiplication in Appendices 1
and 2)
─ We present a clear security evaluation and show
that our proposed method is secure against semi-
honest adversaries.
─ Finally, we present a clear evaluation of efficiency
of our method. In addition, we also present a
comparison between the methods in (Watanabe et
al., 2015; Shingu et al., 2016).
System Model:
In this paper, we assume a client/server model, where
the clients (e.g. the owner of the secret information
𝑎,𝑏) send shares of their inputs to 𝑛 number of
servers. The servers then carry out the computation
and return the results to them without learning
anything about secret information 𝑎 and 𝑏 . This
model is widely used nowadays and in fact is the
business model used in Cybernetica (Sharemind). In
addition, we assume a semi-honest adversary, where
the adversary follows the protocol specification but
may try to learn more than is allowed by the protocol,
with at most 𝑘 − 1 corrupted servers. We also
assume that secure communication exists between the
client and the servers.
The organization of this paper is as follows. In
Section 2, we present preliminaries. In Section 3, we
explain the related works. In Section 4, we present our
new protocol for multiplication. In Section 5, we
discuss the security of our proposed method of
multiplication. In addition, in Chapter 6, we evaluate
our proposed method. Finally, in Chapter 7, we show
the comparison between our proposed method and
conventional methods.
2 PRELIMINARIES
In this section, we introduce some notations and
known techniques.
2.1 (𝒌,𝒏) Threshold Secret Sharing
Scheme
A secret sharing scheme that satisfies both conditions
stated below is known as (𝑘,𝑛) threshold secret-
sharing scheme.
─ Any 𝑘−1 or fewer number of shares will reveal
nothing about the original secret information 𝑠.
ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy
78

─ Any 𝑘 or greater number of shares will allow for
the reconstruction of the original secret
information 𝑠.
The classic methods for the (𝑘,𝑛) threshold secret
sharing scheme is Shamir’s (𝑘,𝑛) threshold secret
sharing scheme, proposed by Shamir (Shamir, 1979)
(Shamir’s (𝑘,𝑛) method). In our protocol, all
computations are performed in finite field 𝐺𝐹(𝑝) and
shares of secret information 𝑠 is represented by
𝑠
.
The protocol for the distribution and
reconstruction of Shamir’s
(
𝑘,𝑛
)
method is as
follows.
Distribution Protocol:
1. The dealer selects 𝑛 number of 𝑥
(
𝑖 =
0,1,…,𝑛 − 1
)
and assigns them as the server
𝐼𝐷.
2. The dealer selects 𝑘 − 1 random numbers
𝛼
(
𝑙=1,2,…,𝑘 − 1
)
and generates a random
polynomial 𝑊(𝑥
).
𝑠
=𝑊(𝑥
)=𝑠 + 𝛼
𝑥
+ 𝛼
𝑥
+ …
+ 𝛼
𝑥
3. The dealer then inserts the server 𝐼𝐷 into 𝑥
,
calculates the shares
𝑠
corresponding to
each 𝐼𝐷, and distributes them.
Restoration Protocol:
1. The player who wishes to restore the original
secret collects 𝑘 shares
𝑠
(𝑗 = 0,…,𝑘 − 1).
2. The player restores the original secret 𝑠 by using
Lagrange’s Interpolation.
𝑠=
𝛼
𝛼
−𝛼
,
𝑠
2.2 Multiplication based on Shamir’s
(𝒌,𝒏) Method
Let 𝑎 and 𝑏 be two secrets. Shares of each secret are
produced by Shamir’s (𝑘,𝑛) method as shown below
and are distributed to 𝑛 servers. Note that 𝑖=
0,1,…,𝑛 −1.
𝑎
=𝑎 + 𝛼
𝑥
+ 𝛼
𝑥
+ … + 𝛼
𝑥
𝑏
=𝑏 + 𝛽
𝑥
+ 𝛽
𝑥
+ … + 𝛽
𝑥
Each server then computes the multiplication
between shares of 𝑎 and 𝑏, and produces
𝑎𝑏
as
shown below.
𝑎𝑏
=𝑎𝑏 + … +
(
𝛼
𝛽
)
𝑥
Although secrets 𝑎 and 𝑏 are shared using
polynomials of
(
𝑘−1
)
degree, the result of
multiplication 𝑎𝑏 is a polynomial of
(
2𝑘− 2
)
degree. Therefore, the problem with conventional
method of multiplication of Shamir’s (𝑘,𝑛) method
is that the number of shares required to reconstruct 𝑎𝑏
increase from 𝑘 to 2𝑘− 1. Thus, the following
Theorem 1 was proposed for the passive model (Ben-
Or et al., 1988).
Theorem 1. In the passive mode, a set 𝒫=
𝑃
, …,𝑃
of 𝑛 servers can compute every
specification securely if and only if the adversary
corrupts at most 𝑘−1<𝑛/2 of the servers.
2.3 Multiplication of Shares using
Recombination Vector
As mentioned in Section 2.2, the result of
multiplication of two polynomials of degree (𝑘− 1)
will be a polynomial of degree (2𝑘− 2). Note that
𝑛≥2𝑘−1 implies that the 𝑛 product shares are
sufficient for recovering 𝑎𝑏. However, any further
multiplication will raise the degree, and once the
degree passes 𝑛, there will be not have enough points
for the interpolation. Hence, a (𝑘− 1) sharing of 𝑎𝑏
can be achieved by using recombination vector as
shown in (Cramer et al. 2015).
To better understand this, let us assume that the
parameter 𝑘=2,𝑛=2𝑘−1=3, the resulting
multiplication will be a quadratic polynomials
𝑦(𝑥
) = 𝛼
+𝛼
𝑥
+ 𝛼
𝑥
, where 𝛼
is the result
of the multiplication. Since 𝑛=3, the shares for each
server 𝐼𝐷 are as follows.
𝑦
(
1
)
= 𝛼
+ 𝛼
+ 𝛼
𝑦
(
2
)
= 𝛼
+ 2𝛼
+ 4𝛼
𝑦(3) = 𝛼
+ 3𝛼
+ 9𝛼
By solving the equations above, we can state that
multiplication result 𝛼
can always be computed
from the shares 𝑦(1),𝑦(2) and 𝑦(3) as 𝛼
=
3𝑦(1) − 3𝑦(2) + 𝑦(3) . This formula was found
using simple Gaussian elimination, but is also given
by the Lagrange interpolation formula, where 𝑟 =
(3,−3,1) is known as the recombination vector.
More precisely, each party first shares its value of
multiplication result
𝑎𝑏
using polynomials of (𝑘−
1) degree to all parties. The parties then locally
combine their shares by an inner product with the
recombination vector. By this, each party will hold
(𝑘− 1) sharing of 𝑎𝑏. However, the problem with
Improvement of Secure Multi-Party Multiplication of (k, n) Threshold Secret Sharing Using Only N = k Servers
79

this method is that it still requires 𝑛>2𝑘−1
number of servers, therefore increasing the total
operation cost of the system.
3 RELATED WORKS
3.1 Watanabe Method
Typically, in a (𝑘,𝑛) threshold secret sharing
scheme, a server possesses only one share. When
multiplication of shares is performed, the number of
servers required will also increase from 𝑘 to 2𝑘− 1.
Watanabe et al. solved this problem by allowing
a server to hold two shares (Watanabe et al., 2015).
However, this method does not solve the problem of
increase in degree of polynomial from 𝑘 − 1 to 2𝑘−
2. This means that the number of shares required to
reconstruct the result remain at 2𝑘− 1 instead of 𝑘.
Therefore, the communication cost between the client
and the servers remain the same as all conventional
methods. Our method solves this by proposing
method of computing (𝑘− 1) sharing of 𝑎𝑏 using
only 𝑁=𝑘 servers.
Due to the page limit, we only included the
distribution and multiplication protocols below. Note
that variables 𝑎, 𝑏 and all random numbers generated
are derived from finite field 𝐺𝐹(𝑝) and all
computations are performed under finite field 𝐺𝐹(𝑝).
Distribution Protocol:
1. Players 𝐴 and 𝐵 each generates 2𝑛 shares from
secrets 𝑎 and 𝑏 and distributes
𝑎
,
𝑏
(𝑖=
0,…,𝑛 −1)
to 𝑛 servers 𝑆
.
2. Player 𝐴 generates a random number 𝑟
and
distributes
𝑟
𝑎
,….,
𝑟
𝑎
to 𝑛 servers 𝑆
.
Then, distributes shares
𝑟
of 𝑟
to 𝑛 servers 𝑆
.
3. Player 𝐵 generates a random number 𝑟
and
distributes
𝑟
𝑏
,…,
𝑟
𝑏
to 𝑛 servers 𝑆
.
Then, distributes shares
𝑟
of 𝑟
to 𝑛 servers 𝑆
.
Multiplication Protocol:
1. Each server calculates the following:
𝑎𝑏
=
𝑎
×
𝑏
(
𝑖=0,1,…,𝑛−1
)
𝑟
𝑟
𝑎𝑏
=
𝑟
𝑎
×
𝑟
𝑏
3.2 The TUS Method
Shingu et al. proposed a 2-inputs-1-output multi-
party computation named the TUS method (Shingu et
al., 2016), where the secret (e.g. 𝑎) is first encrypted
with a random number (e.g. 𝛼). When performing
multiplication, the encrypted secret is momentarily
restored as a scalar value (e.g. 𝛼𝑎) and multiplication
is realized using the
(
𝑠𝑐𝑎𝑙𝑎𝑟 𝑣𝑎𝑙𝑢𝑒× 𝑝𝑜𝑙𝑦𝑛𝑜𝑚𝑖𝑎𝑙
)
approach to prevent an increase in the polynomial
degree. However, the TUS method introduced
another problem: when the reconstructed scalar value
𝛼𝑎=0, the adversary will learn that secret 𝑎=0.
Therefore, condition where the secret does not
include the value 0 is required.
Due to the page limit, we only included the
distribution and multiplication protocols below. Note
that variables 𝑎,𝑏 and all random numbers generated
are derived from finite field 𝐺𝐹(𝑝), provided that the
secret inputs 𝑎,𝑏 and all random numbers do not
include 0.
Distribution Protocol:
1. Players 𝐴 and 𝐵 each selects 𝑘 random numbers
𝛼
,𝛽
(𝑗=0,1,…,𝑘− 1) and computes the value
of 𝛼=
∏
𝛼
and 𝛽=
∏
𝛽
, respectively.
2. Player 𝐴 computes 𝛼𝑎=𝛼× 𝑎 and distributes
𝛼𝑎,𝛼
to 𝑛 servers using Shamir’s (𝑘,𝑛) method.
3. Player 𝐵 computes 𝛽𝑏=𝛽× 𝑏 and distributes
𝛽𝑏,𝛽
to 𝑛 servers using Shamir’s (𝑘,𝑛) method.
4. Each server 𝑆
(𝑖=0,1,…,𝑛− 1) holds the
following as set of shares about secrets 𝑎,𝑏:
𝑎
=
𝛼𝑎
,
𝛼
,…,
𝛼
,
𝑏
=
𝛽𝑏
,
𝛽
,…,
𝛽
Multiplication Protocol:
1. One of the servers (here, we assume server 𝑆
)
collects
𝛼𝑎
from 𝑘 servers. Server 𝑆
then
restores 𝛼𝑎 and sends it to all servers 𝑆
.
2. Servers 𝑆
compute
𝛼𝛽𝑎𝑏
=𝛼𝑎×
𝛽𝑏
.
3. 𝑘 number of servers 𝑆
each collect
shares
𝛼
ℓ
,…,
𝛼
ℓ
,
𝛽
ℓ
,…,
𝛽
ℓ
(ℓ=
0,1,…,𝑘− 1) and restore 𝛼
,𝛽
. Servers 𝑆
then
calculate 𝛼
𝛽
=𝛼
×𝛽
.
4. Servers 𝑆
distribute 𝛼
𝛽
to all servers 𝑆
by using
Shamir’s (𝑘,𝑛) method.
5. Each server 𝑆
now holds the following as a set of
shares for the result of 𝑎𝑏.
𝑎𝑏
=
𝛼𝛽𝑎𝑏
,
𝛼
𝛽
,…,
𝛼
𝛽
ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy
80

4 PROPOSED METHOD OF
MULTIPLICATION
Our protocol focus on an approach that differentiate
between parameter 𝑁, which is the number of servers
that is actually needed, and parameter 𝑛 of the (𝑘,𝑛)
threshold secret sharing scheme, and realizes
multiplication under a setting of 𝑁=𝑘,𝑛≥2𝑘−1.
In addition, to solve the problem of Watanabe
method, where the result of multiplication can only be
reconstructed by collecting 2𝑘 shares from 𝑘 servers,
we propose a new method of reducing the polynomial
degree of 𝑎𝑏 from 2𝑘−2 to 𝑘−1 by using
recombination vector with only 𝑁=𝑘 servers.
Below, for ease of understanding, we demonstrate
multiplication under the setting of 𝑁=𝑘,𝑛≥2𝑘−
1. In the protocol below, secrets 𝑎,𝑏, all random
numbers and all computations are performed in finite
field 𝐺𝐹(𝑝).
Notation:
─
𝑎
: Share of 𝑎 for server 𝑆
where the number of
shares required for reconstructing 𝑎 is 𝑘
─
𝛼
𝛽
𝑎𝑏
∗
: Share of 𝛼
𝛽
𝑎𝑏 for server 𝑆
where
the number of shares required for reconstructing
𝛼
𝛽
𝑎𝑏 is 2𝑘−1.
Distribution Protocol:
1. Player 𝐴 generates 2𝑘 random numbers
𝛼
,
,…,𝛼
,
,𝛼
,
,…,𝛼
,
and computes the
following.
𝛼
=𝛼
,
𝛼
=𝛼
,
2. Player 𝐴 generates 2𝑘 shares of secret 𝑎 using
Shamir’s (𝑘,2𝑘) method and computes the
following.
𝛼
𝑎
=𝛼
×
𝑎
,…,
𝛼
𝑎
=𝛼
×
𝑎
𝛼
𝑎
=𝛼
×
𝑎
,…,
𝛼
𝑎
=𝛼
×
𝑎
3. Player 𝐴 sends
𝛼
𝑎
,
𝛼
𝑎
,𝛼
,
,𝛼
,
to server
𝑆
(𝑖=0,1,…,𝑘− 1).
4. Player 𝐵 generates 2𝑘 random numbers
𝛽
,
,…,𝛽
,
,𝛽
,
,…,𝛽
,
and computes the
following.
𝛽
=𝛽
,
𝛽
=𝛽
,
5. Player 𝐵 generates 2𝑘 shares of secret 𝑏 using
Shamir’s (𝑘,2𝑘) method and computes the
following.
𝛽
𝑏
=𝛽
×
𝑏
,…,
𝛽
𝑏
=𝛽
×
𝑏
𝛽
𝑏
=𝛽
×
𝑏
,…,
𝛽
𝑏
=𝛽
×
𝑏
6. Player 𝐵 sends
𝛽
𝑏
,
𝛽
𝑏
,𝛽
,
,𝛽
,
to server
𝑆
(𝑖=0,1,…,𝑘− 1).
Multiplication Protocol:
1. Each server 𝑆
(𝑖=0,1,…,𝑘− 1) computes the
following.
𝛼
𝛽
𝑎𝑏
∗
=
𝛼
𝑎
×
𝛽
𝑏
𝛼
𝛽
𝑎𝑏
∗
=
𝛼
𝑎
×
𝛽
𝑏
𝛼
,
𝛽
,
=𝛼
,
×𝛽
,
𝛼
,
𝛽
,
=𝛼
,
×𝛽
,
2. Each server 𝑆
generates random number 𝛾
,
computes the following and sends to one of the
servers (here, we assume server 𝑆
).
𝛾
𝛼
,
𝛽
,
,
𝛾
𝛼
,
𝛽
,
3. Server 𝑆
computes the following and sends to all
servers.
𝛾
𝛼
𝛽
=
𝛾
𝛼
,
𝛽
,
𝛾
𝛼
𝛽
=
𝛾
𝛼
,
𝛽
,
4. Each server 𝑆
computes
𝛾𝑎𝑏
∗
,
𝛾𝑎𝑏
∗
as
follows, and distribute
𝛾𝑎𝑏
∗
,
𝛾𝑎𝑏
∗
using
Shamir’s (𝑘,𝑘) method to all servers 𝑆
.
𝛾𝑎𝑏
∗
=
𝛾
𝛼
𝛽
×
𝛼
𝛽
𝑎𝑏
∗
𝛾𝑎𝑏
∗
=
𝛾
𝛼
𝛽
×
𝛼
𝛽
𝑎𝑏
∗
Improvement of Secure Multi-Party Multiplication of (k, n) Threshold Secret Sharing Using Only N = k Servers
81

𝛾𝑎𝑏
∗
⟹
𝛾𝑎𝑏
,
⟹𝑠𝑒𝑛𝑑 𝑡𝑜 𝑆
⋮
𝛾𝑎𝑏
,
⟹𝑠𝑒𝑛𝑑 𝑡𝑜 𝑆
𝛾𝑎𝑏
∗
⟹
𝛾𝑎𝑏
,
⟹𝑠𝑒𝑛𝑑 𝑡𝑜 𝑆
⋮
𝛾𝑎𝑏
,
⟹𝑠𝑒𝑛𝑑 𝑡𝑜 𝑆
5. Each server 𝑆
computes the following (𝜆
are the
recombination vector).
𝛾𝑎𝑏
=𝜆
×
𝛾𝑎𝑏
,
+⋯+𝜆
×
𝛾𝑎𝑏
,
Reconstruction Protocol:
1. The player collects
𝛾𝑎𝑏
,𝛾
from 𝑘 servers 𝑆
,
reconstructs 𝛾𝑎𝑏 and computes 𝛾 as follows.
𝛾=𝛾
2. Finally, the player reconstructs multiplication
result 𝑎𝑏 as follows.
𝑎𝑏=
𝛾𝑎𝑏
𝛾
5 SECURITY OF THE PROPOSED
METHOD
In a 2-input-1-output multiplication process, when the
adversary has information of one of the inputs (e.g.
input 𝑎) and output (e.g. output 𝑎𝑏), the second input
(e.g. input 𝑏) will be leaked. Therefore, we only
consider the following adversaries. The attack is
considered a success if the adversary can achieve the
aim of learning the information that he/she wants to
know. Therefore, we can state that our proposed
method is secure if it is secure against the following
adversaries.
Adversary 1: The adversary has information from
𝑘 − 1 servers. According to this information, the
adversary attempts to know inputs 𝑎,𝑏 and output
𝑎𝑏.
Adversary 2: One of the players who inputted a
secret is the adversary. In addition, the adversary also
has information from 𝑘 − 1 servers. According to this
information, the adversary attempts to know the
remaining one input 𝑎 or 𝑏, and output 𝑎𝑏.
Adversary 3: The player who reconstructed the
output is the adversary. In addition, the adversary has
information from 𝑘 − 1 servers. According to this
information, the adversary attempts to know two
inputs 𝑎 and 𝑏.
In the following, we evaluate the security of our
proposed method.
Evaluation of Security against Adversary 1:
Here, Adversary 1 has information from 𝑘−1
number of servers. In the distribution protocol,
Adversary 1 has the following information 𝐷
from
Player 𝐴 and 𝐷
from Player 𝐵.
𝐷
=
𝛼
𝑎
,
𝛼
𝑎
,𝛼
,
,𝛼
,
(𝑙=0,…,𝑘− 2)
𝐷
=
𝛽
𝑏
,
𝛽
𝑏
,𝛽
,
,𝛽
,
(𝑙=0,…,𝑘− 2)
However, encrypted secrets 𝛼
𝑎,𝛼
𝑎,𝛽
𝑏,𝛽
𝑏 are
not leaked from 𝑘−1 shares. Moreover, Adversary 1
is not able to learn about random numbers
𝛼
,𝛼
,𝛽
,𝛽
from 𝑘−1 servers. Therefore, even
with this information, secrets 𝑎 and 𝑏 are not leaked.
Thus, the following are true.
𝐻
(
𝑎
)
=𝐻(𝑎|𝐷
)
𝐻
(
𝑏
)
=𝐻(𝑏|𝐷
)
In Step 1 of the multiplication protocol, Adversary 1
learns about 𝛼
,
𝛽
,
,𝛼
,
𝛽
,
(𝑙=0,…,𝑘− 2), in
Step 2 about 𝛾
,𝛾
𝛼
,
𝛽
,
⁄
,𝛾
𝛼
,
𝛽
,
⁄
, in Step 3
about 𝛾𝛼
𝛽
⁄
,𝛾 𝛼
𝛽
⁄
, in Step 4 about
𝛾𝑎𝑏
∗
,…,
𝛾𝑎𝑏
∗
,
𝛾𝑎𝑏
∗
,…,
𝛾𝑎𝑏
∗
and in
Step 5 about
𝛾𝑎𝑏
,…,
𝛾𝑎𝑏
. As a result, we can
transform the problem into determining whether the
adversary can learn about inputs 𝑎,𝑏 or output 𝑎𝑏
from the following information.
𝛼
,
,𝛼
,
,𝛽
,
,𝛽
,
,𝛾
,
𝛾
𝛼
𝛽
,
𝛾
𝛼
𝛽
,
𝛾𝑎𝑏
∗
,
𝛾𝑎𝑏
∗
,
𝛾𝑎𝑏
(𝑙=0,…,𝑘− 2)
Since
𝛾𝑎𝑏
∗
is represented by polynomial of (2𝑘−
2) degree, 2𝑘− 1 number of shares are required to
reconstruct 𝛾𝑎𝑏. However, Adversary 1 only has
information of 2𝑘− 2 number of shares, therefore,
𝛾𝑎𝑏 is not leaked. The same is true when Adversary
1 only has information of 𝑘−2 number of shares
𝛾𝑎𝑏
, 𝛾𝑎𝑏 is not leaked. Moreover, because
Adversary 1 has no information 𝛼
,𝛼
,𝛽
,𝛽
,
random number 𝛾 used to encrypt the output 𝑎𝑏 is not
leaked. Therefore, our proposed method is secure
against Adversary 1 and the following are true:
𝐻
(
𝛾
)
=𝐻𝛾|𝛼
,
,𝛼
,
,𝛽
,
,𝛽
,
,𝛾
,
𝛾
𝛼
𝛽
,
𝛾
𝛼
𝛽
ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy
82

𝐻
(
𝛾𝑎𝑏
)
=𝐻𝛾𝑎𝑏|
𝛾𝑎𝑏
∗
,
𝛾𝑎𝑏
∗
,
𝛾𝑎𝑏
(
𝑙
=0,…,𝑘−2
)
Evaluation of Security against Adversary 2:
Assume that the player who inputted input 𝑎 is
Adversary 2. Adversary 2 also has information from
𝑘 − 1 servers. Therefore, in the distribution
protocol, Adversary 2 has information about
𝑎,𝛼
,
,𝛼
,
,𝛼
,𝛼
(𝑖=0,…,𝑘−1) in addition to
information from 𝑘−1 servers (Adversary 1).
Therefore, the evaluation of security against
Adversary 2 can be translated to the problem of
determining whether the adversary can learn about
the remaining input 𝑏 and output 𝑎𝑏 from the
following information:
𝑎,𝛼
,
,𝛼
,
,𝛼
,𝛼
,𝛽
,
,𝛽
,
,𝛾
,
𝛾
𝛽
,
𝛾
𝛽
,
𝛽
𝑏
,
𝛽
𝑏
,
𝛾𝑎𝑏
∗
,
𝛾𝑎𝑏
∗
,
𝛾𝑎𝑏
(
𝑙
=0,…,𝑘−2
)
To obtain information about secret 𝑏, the adversary
must first obtain information of 𝛽
𝑏,𝛽
𝑏 and random
numbers 𝛽
,𝛽
. The information that is related to
random numbers 𝛽
,𝛽
are 𝛽
,
,𝛽
,
,𝛾
,𝛾 𝛽
⁄
,𝛾𝛽
⁄
.
However, even from this information, random
numbers 𝛽
,𝛽
are not leaked. Moreover, encrypted
secret 𝛽
𝑏,𝛽
𝑏 will not be leaked from 𝑘−1
number of shares. Therefore,
𝐻
(
𝛽
𝑏
)
=𝐻
(
𝛽
𝑏
|
𝛽
𝑏
,…,
𝛽
𝑏
)
𝐻
(
𝛽
𝑏
)
=𝐻
(
𝛽
𝑏
|
𝛽
𝑏
,…,
𝛽
𝑏
)
𝐻
(
𝛽
)
=𝐻𝛽
𝛽
,
,𝛾
,
𝛾
𝛽
𝐻
(
𝛽
)
=𝐻𝛽
|𝛽
,
,𝛾
,,
𝛾
𝛽
Finally, to obtain multiplication result 𝑎𝑏, the
adversary must first obtain information 𝛾𝑎𝑏 and
random number 𝛾. However, from 𝑘−1 shares
𝛾𝑎𝑏
and 2𝑘− 2 shares of
𝛾𝑎𝑏
∗
,
𝛾𝑎𝑏
∗
, and
random numbers 𝛾
,𝛾𝛽
⁄
,𝛾 𝛽
⁄
, information of 𝛾𝑎𝑏
and random number 𝛾 are not leaked. Therefore,
𝐻
(
𝛾𝑎𝑏
)
=𝐻𝛾𝑎𝑏|
𝛾𝑎𝑏
∗
,
𝛾𝑎𝑏
∗
,
𝛾𝑎𝑏
(
𝑙
=0,…,𝑘−2
)
𝐻
(
𝛾
)
=𝐻𝛾|𝛾
,
𝛾
𝛽
,
𝛾
𝛽
In addition, the evaluation above remains valid even
if the adversary is the player who inputted input 𝑏.
Therefore, our proposed method is secure against
Adversary 2.
Evaluation of Security against Adversary 3:
Assume that the player who reconstructed output 𝑎𝑏
is Adversary 3. Adversary 3 also has information from
𝑘−1 servers. Therefore, in the reconstruction
protocol, Adversary 3 has information about
𝛾𝑎𝑏
,𝛾
,𝛾𝑎𝑏,𝛾 (𝑖=0,…,𝑘−1) in addition to
information from 𝑘−1 servers (Adversary 1).
Therefore, the evaluation of security against
Adversary 3 can be translated to the problem of
determining whether the adversary can learn about
the inputs 𝑎,𝑏 from the following information:
𝐴={𝑎𝑏,𝛾
,𝛾,𝛼
,
,𝛼
,
,𝛽
,
,𝛽
,
,𝛼
𝛽
,𝛼
𝛽
,
𝛼
𝑎
,
𝛼
𝑎
,
𝛽
𝑏
,
𝛽
𝑏
(
𝑙=0,…,𝑘−2
)
}
To obtain information about secret 𝑎,𝑏, the adversary
must first obtain information of 𝛼
𝑎,𝛼
𝑎,𝛽
𝑏,𝛽
𝑏
and random numbers 𝛼
,𝛼
,𝛽
,𝛽
. The information
that is related to random numbers 𝛼
,𝛼
,𝛽
,𝛽
are
𝛼
,
,𝛼
,
,𝛽
,
,𝛽
,
,𝛼
𝛽
,𝛼
𝛽
. However, even from
these information, random numbers 𝛼
,𝛼
,𝛽
,𝛽
are
not leaked. Moreover, encrypted secret
𝛼
𝑎,𝛼
𝑎,𝛽
𝑏,𝛽
𝑏 will not be leaked from 𝑘−1
number of shares. Finally, even with the
multiplication result 𝑎𝑏, Adversary 3 will not be able
to learn about each secret 𝑎,𝑏. Therefore,
𝐻
(
𝑎
)
=𝐻(𝑎|𝐴)
𝐻
(
𝑏
)
=𝐻(𝑏|𝐴)
Therefore, we can state that our proposed method is
also secure against Adversary 3.
6 EVALUATION OF OUR
PROPOSED METHOD
In this section, we perform evaluation of our proposed
method in term of computation and communication
costs. Below is the definition of parameters used
throughout our analysis. Note that in secret sharing
scheme, size of share 𝑑
is usually almost the same
size as the original secret. Moreover, in a secret
sharing scheme, the computational cost of the
distribution and the reconstruction process differs, but
for ease of understanding, we consider that the
computation cost of both the distribution and
reconstruction process of a secret sharing scheme to
be the same. Table 1 shows the communication cost
Improvement of Secure Multi-Party Multiplication of (k, n) Threshold Secret Sharing Using Only N = k Servers
83
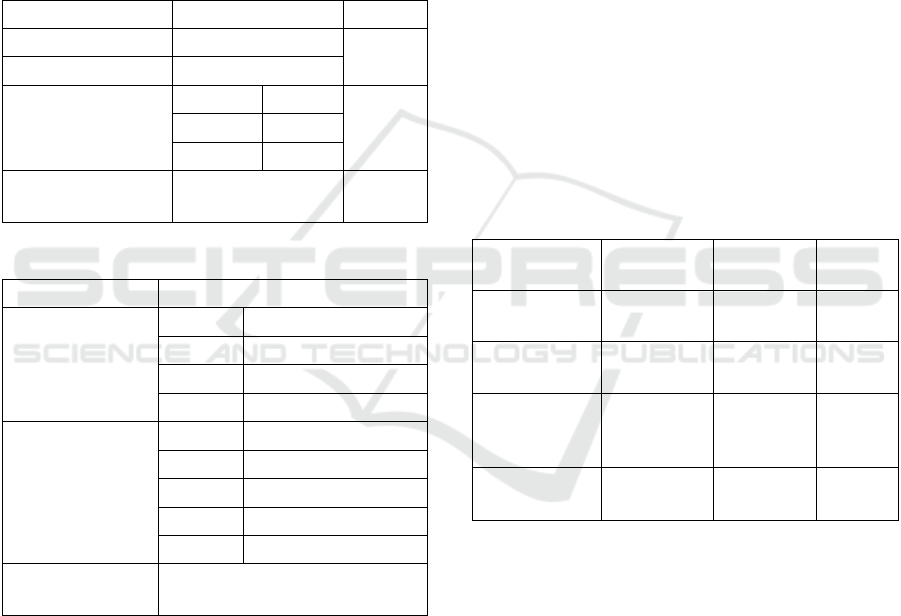
and number of rounds of our proposed method. Table
2 shows the computational cost of our method.
Definition of Parameters:
─ 𝑑
: Size of share from secret sharing scheme
─ 𝐶
: Computational cost of Shamir’s (𝑘,2𝑘) secret
sharing scheme
─ 𝐶
: Computational cost of Shamir’s (𝑘,𝑘) secret
sharing scheme
─ 𝑀: Computational cost of multiplication
─ 𝐷: Computational cost of division
─ 𝐴: Computational cost of addition
Table 1: Communication and number of rounds of the
proposed method.
Process Communication Rounds
Distribution of 𝑎
4𝑘𝑑
1
Distribution of 𝑏
4𝑘𝑑
Multiplication of
𝑎 and 𝑏
Step 2
2𝑘𝑑
3
Step 3
2𝑁𝑑
Step 4
2𝑁𝑘𝑑
Reconstruction of
𝑎𝑏
2𝑘𝑑
1
Table 2: Computational cost of the proposed method.
Process Computation Cost
Distribution of
𝑎,𝑏
Step 1
2
(
𝑘−1
)
𝑀
Step 2
𝐶
+
(
2𝑛− 1
)
𝑀
Step 4
2
(
𝑘−1
)
𝑀
Step 5
𝐶
+
(
2𝑛− 1
)
𝑀
Multiplication
of 𝑎 and 𝑏
Step 1
4𝑘𝑀
Step 2
2𝑘(𝑀+ 𝐷)
Step 3
2(𝑘 − 1)𝑀
Step 4
2𝑘(𝑀+ 𝐶
)
Step 5
2𝑁𝑘(𝑀+
𝐴
)
Reconstruction
of 𝑎𝑏
𝐶
+
(
𝑘−1
)
𝑀+𝐷
7 COMPARISON WITH
CONVENTIONAL METHODS
In this section, we perform comparison with
conventional methods (Watanabe method (Watanabe
et al., 2015) proposed by Watanabe et al. and the TUS
method (Shingu et al., 2016) proposed by Shingu et
al.) that also realize multiplication of secret sharing
schemes using only 𝑁=𝑘 servers.
First, the TUS method allows for multiplication in
the setting of 𝑁=𝑛≥𝑘 since multiplication is
performed by multiplying scalar value with a share,
therefore, allowing the result of multiplication to be
restored by only 𝑘 shares instead of the conventional
2𝑘− 1 shares. However, the TUS method requires
one precondition where the input does not include the
value 0 to securely perform multiplication. In contrast,
our method allows for any values (including 0) to be
used since the encrypted secret is not reconstructed in
the protocol.
Next, Watanabe method also allows for
multiplication in the setting of 𝑁≥𝑘 and 𝑛≥2𝑘−
1; however, the number of shares required to
reconstruct the result remain at 2𝑘− 1 instead of 𝑘.
On the other hand, our method allows for
multiplication in the setting of 𝑛≥2𝑘−1 and
number of servers 𝑁 to remain at 𝑘. Moreover, our
protocol produces 𝑘−1 sharing of 𝑎𝑏, therefore, we
only need to collect 𝑘 instead of 2𝑘− 1 shares for
reconstruction. All the comparisons discussed above
are summarized in Table 3.
Table 3. Comparison with conventional methods (for
multiplication).
Proposed
method
Watanabe
method
TUS
method
Parameter of
𝑛,𝑘
𝑛≥2𝑘−1 𝑛≥2𝑘−1 𝑛≥𝑘
Number of
servers 𝑁
𝑁=𝑘 𝑁≥𝑘 𝑁≥𝑘
Number of
shares for
reconstruction
𝑘 2𝑘− 1 𝑘
Number of
Precondition
0 0 1
Next, in Table 4, we show comparison with
conventional methods. However, since the
computation cost of secret sharing scheme 𝐶
,𝐶
are
typically larger than local computation cost of 𝑀,𝐷
and 𝐴, we omit the cost of 𝑀,𝐷 and 𝐴 when either 𝐶
or 𝐶
is present in the computation cost.
Table 4 shows that the computation cost for
distribution of 𝑎,𝑏 and reconstruction of 𝑎𝑏 of our
method are lower than both Watanabe and TUS
methods. Next, since our proposed method includes the
process of redistributing of local shares to all servers,
we learnt that the computation cost of multiplication of
our proposed method is larger than Watanabe method.
However, we were able to reduce the computation cost
for the reconstruction, and therefore, reducing the
computation cost needed by the client.
ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy
84
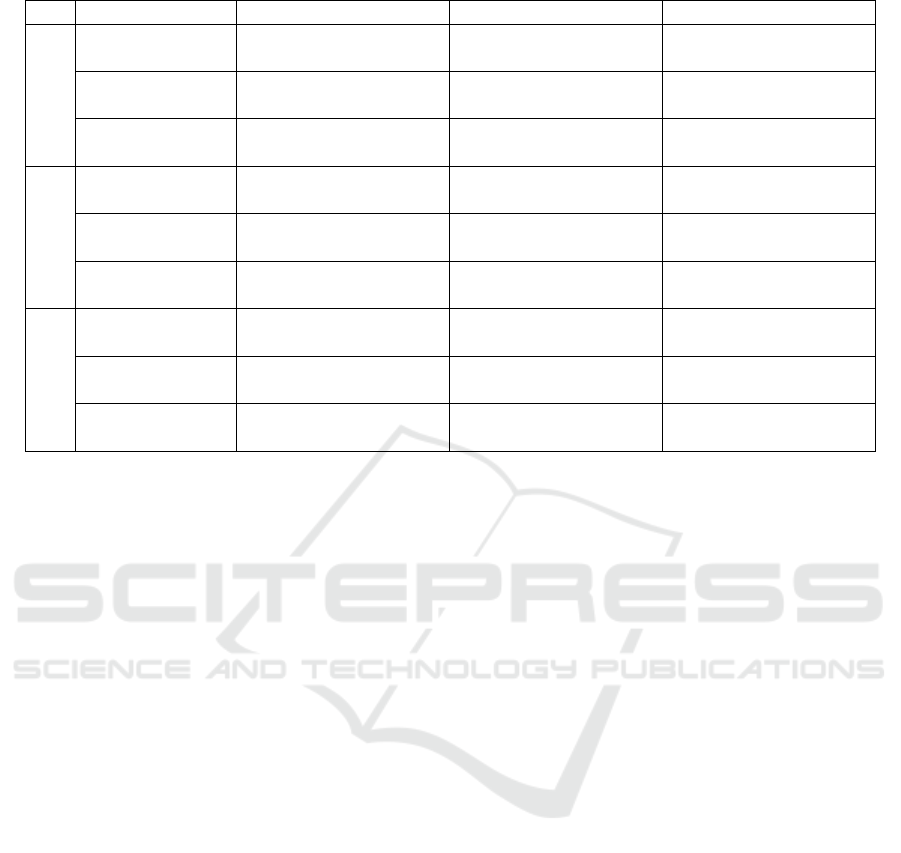
Table 4: Comparison with conventional methods.
Process Proposed method Watanabe method TUS method
Computation
Distribution
of 𝑎,𝑏
2𝐶
2(𝐶
+𝐶
) 2(𝑘+ 1)𝐶
Multiplication
of 𝑎𝑏
2𝑘𝐶
2𝑛𝑀 (3𝑘+ 1)𝐶
Reconstruction
of 𝑎𝑏
𝐶
𝐶
+2𝐶
(𝑘+ 1)𝐶
Communication
Distribution
of 𝑎,𝑏
8𝑘𝑑
8𝑛𝑑
2𝑛𝑑
(𝑘+ 1)
Multiplication
of 𝑎𝑏
(2𝑘+ 2𝑁+2𝑁𝑘)𝑑
0
(𝑘+𝑛+2𝑘
+𝑛𝑘)𝑑
Reconstruction
of 𝑎𝑏
2𝑘𝑑
4𝑘𝑑
(𝑘
+𝑘)𝑑
Rounds
Distribution
of 𝑎,𝑏
1 1 1
Multiplication
of 𝑎𝑏
3 0 4
Reconstruction
of 𝑎𝑏
1 1 1
In terms of communication cost, the merits and
demerits of each method depend on 𝑑
,𝑛,𝑘.
However, when comparing with Watanabe method,
since our proposed method produce a polynomial of
(𝑘− 1) degree instead of polynomial of (2𝑘− 2)
degree, we were able to reduce the communication
cost for reconstruction of 𝑎𝑏 by half. Finally, a
comparison of each method’s number of rounds,
since our proposed method includes the process of
redistributing and computation of random numbers,
Table 4 shows that the number of rounds of our
proposed method is considerably more than
Watanabe method but lower than the TUS method.
8 CONCLUSIONS
In this paper, we proposed an improved method of
multiplication of shares by using only 𝑁=𝑘 number
of servers. Furthermore, by implementing the use of
recombination vector, we proposed a method of
computing 𝑘−1 sharing of multiplication 𝑎𝑏 by
using only 𝑘 servers instead of the previous 2𝑘 −1
servers. Through this proposed method, we realized
secure multi-party computation of multiplication
using Shamir’s (𝑘,𝑛) method in the setting of 𝑛≥
2𝑘− 1,𝑁=𝑘.
In a future study, we will focus on including the
function for verification of shares in addition to
allowing for different combination of computation
(such as product-sum operation) to be performed
simultaneously.
REFERENCES
Ben-Or M., Goldwasser S., Wigderson A., 1988.
Completeness theorems for non-cryptographic fault-
tolerant distributed computation. In Proceedings of the
20th Annual ACM Symposium on Theory of
Computing, pp. 1-10. ACM, New York, NY, USA.
Bendlin R., Damgård I., Orlandi C., Zakarias S., 2011.
Semi-homomorphic encryption and multiparty
computation. In Paterson K. G. (eds) Advances in
Cryptology-EUROCRYPT 2011. LNCS, vol. 6632, pp.
169-188. Springer, Berlin, Heidelberg.
Brakerski Z., Vaikuntanathan V., 2011. Fully
homomorphic encryption from ring-LWE and security
for key dependent messages. In Rogaway P. (eds)
Advances in Cryptology – CRYPTO 2011. LNCS, vol
6841, pp. 505-524. Springer, Berlin, Heidelberg.
Chaum D., Crépeau C., Damgård I., 1988. Multiparty
unconditionally secure protocols. In Proceedings of the
20th Annual ACM Symposium on Theory of
Computing. pp. 11-19. ACM, New York, NY, USA.
Cramer R., Damgård I., Maurer U., 2000. General secure
multiparty computation from any linear secret sharing
scheme. In Preneel B. (eds) Advances in Cryptology-
EUROCRYPT 2000. LNCS, vol. 1807, pp. 316-334.
Springer, Berlin, Heidelberg.
Cramer R., Damgård I., Nielsen J., 2015. Secure multiparty
computation and secret sharing. Cambridge University
Press, 1st edition.
Improvement of Secure Multi-Party Multiplication of (k, n) Threshold Secret Sharing Using Only N = k Servers
85

Damgård I., Pastro V., Smart N., Zakarias S., 2012.
Multiparty computation from somewhat homomorphic
encryption. In Safavi-Naini R., Canetti R., (eds)
Advances in Cryptology-CRYPTO 2012. LNCS, vol
7417, pp. 643-662. Springer, Berlin, Heidelberg.
Damgård I., Keller M., Larraia E., Pastro V., Scholl P.,
Smart N.P., 2013. Practical covertly secure MPC for
dishonest majority or: breaking the SPDZ limits. In
Crampton J., Jajodia S., Mayes K. (eds) Computer
Security – ESORICS 2013. LNCS, vol. 8134, pp. 1-18.
Springer, Berlin, Heidelberg.
Gennaro R., Rabin M. O., Rabin T., 1998. Simplified VSS
and fast-track multiparty computations with
applications to threshold cryptography.” In Proceedings
of the 17th Annual ACM Symposium on Principles of
Distributed Computing. pp. 101-111. ACM, New York,
NY, USA.
Gentry C., 2009. A fully homomorphic encryption scheme,
Ph.D Thesis, Stanford University, Stanford, CA, USA.
Hirt M., 2001. Multiparty computation: efficient protocols,
general adversaries, and voting. PhD Thesis, ETH
Zurich. Reprint as ETH Series in Information Security
and Cryptography vol. 3.
Shamir A., 1979. How to share a secret. Communications
of the ACM, 22, (11), pp. 612-613.
Sharemind, Cybernetica. https://sharemind.cyber.ee
Shingu T., Iwamura K., Kaneda K., 2016. Secrecy
computation without changing polynomial degree in
Shamir’s (𝑘,𝑛) secret sharing scheme. In Proceedings
of the 13th International Joint Conference on e-
Business and Telecommunications, vol.1, pp. 89-94.
SCITEPRESS.
Watanabe T., Iwamura K., Kaneda K., 2015. Secrecy
multiplication based on a (𝑘,𝑛)-threshold secret-
sharing scheme using only 𝑘 servers. In Park J.,
Stojmenovic I., Jeong H., Yi G. (eds) Computer Science
and Its Applications. LNEE, vol. 330, pp. 107-112.
Springer, Berlin, Heidelberg.
Yao A. C., 1982. Protocols for Secure Computations. In
23rd Annual Symposium on Foundations of Computer
Science. pp. 160-164. Chicago, IL, USA.
APPENDIX 1: ADDITION (𝒂 + 𝒃)
Protocol for computing addition of 𝑎+ 𝑏 using our
proposed method of distribution is as follows:
1. Each server 𝑆
(𝑖=0,1,…,𝑛− 1) generates
random number 𝛾
, computes the following and
sends to one of the servers (here, we assume server
𝑆
).
𝛾
𝛼
,
,
𝛾
𝛽
,
2. Server 𝑆
computes the following and sends to all
servers.
𝛾
𝛼
=
𝛾
𝛼
,
,
𝛾
𝛽
=
𝛾
𝛽
,
3. Each server 𝑆
computes
𝛾
(
𝑎+𝑏
)
as follows.
𝛾
(
𝑎+𝑏
)
=
𝛾
𝛼
×
𝛼
𝑎
+
𝛾
𝛽
×
𝛽
𝑏
Security.
Here, due to the page limit, we had omitted the
security proof against Adversaries 2 and 3. Below, we
show the security against Adversary 1, where the
adversary has information from 𝑘−1 servers. In the
distribution protocol, Adversary 1 has the following
information 𝐷
from Player 𝐴 and 𝐷
from Player 𝐵.
𝐷
=
𝛼
𝑎
,
𝛼
𝑎
,𝛼
,
,𝛼
,
(𝑙=0,…,𝑘− 2)
𝐷
=
𝛽
𝑏
,
𝛽
𝑏
,𝛽
,
,𝛽
,
(𝑙=0,…,𝑘− 2)
As shown in Section 5, Adversary 1 will not able
to learns neither 𝑎 nor 𝑏 from the information above.
Moreover, in the protocol for addition, the adversary
learns about the following.
𝛾
𝛼
,
𝛾
𝛽
,𝛾
,𝛼
,
,𝛽
,
,
𝛾
(
𝑎+𝑏
)
(𝑙=0,…,𝑘− 2)
To learn the output 𝑎+𝑏, Adversary 1 has to
obtain information 𝛾
(
𝑎+𝑏
)
and random number 𝛾.
However, from 𝑘−1 shares
𝛾
(
𝑎+𝑏
)
and
random numbers 𝛾
, information of 𝛾(𝑎+𝑏) and 𝛾
are not leaked. Therefore, we can state that the
addition protocol is secure against Adversary 1.
APPENDIX 2: SCALAR
MULTIPLICATION (𝒄𝒂)
Protocol for computing scalar multiplication between
constant 𝑐 and secret 𝑎 is as follows:
1. Let 𝑐∈𝐺𝐹
(
𝑝
)
,𝑐≠0 be some constant. Each
server 𝑆
(𝑖=0,1,…,𝑛− 1) computes the
following locally.
𝛼
(
𝑐𝑎
)
=𝑐×
𝛼
𝑎
Security. In the protocol for scalar multiplication
between constant 𝑐 and secret 𝑎, all computations are
performed locally without any communication
between players. Therefore, the security will depend
on the distribution of secret 𝑎 (which was proven to
be secure in Section 5). Moreover, the adversary will
not be able to learn the result of 𝑐𝑎 if no more than
ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy
86

𝑘−1 shares of
𝛼
(
𝑐𝑎
)
are leaked. Therefore, we
can state that our protocol for scalar multiplication of
𝑐𝑎 is also secure against semi-honest adversary (we
omitted the detailed proof due to the page limit).
APPENDIX 3: EXAMPLE OF
COMPUTATION
Below, for ease of understanding, we demonstrate the
computation of multiplication between secrets 𝑎=3
and 𝑏=2 of Players 𝐴 and 𝐵, respectively, under the
setting of 𝑁=𝑘=2,𝑛≥3. Since 𝑘=2,
multiplication of shares of 𝑎 and 𝑏 will produce a
(
2𝑘− 2
)
=2 degree polynomial. As shown in
Section 2.3, the process of reducing the degree of
polynomial from
(
2𝑘− 2
)
=2 to
(
𝑘−1
)
=1 can
be achieved by using the recombination vector 𝑟 =
(3,−3,1). In the example shown below, secrets 𝑎,𝑏,
all random numbers and all computations are
performed with 𝑝=97.
Distribution Protocol:
1. Player 𝐴 generates 2𝑘=4 random numbers
𝛼
,
,𝛼
,
,𝛼
,
,𝛼
,
and computes the following.
𝛼
,
=2, 𝛼
,
=4
𝛼
,
=3, 𝛼
,
=6
𝛼
=𝛼
,
×𝛼
,
=2×4=8
(
𝑚𝑜𝑑 97
)
𝛼
=𝛼
,
×𝛼
,
=3×6=18 (𝑚𝑜𝑑 97)
2. Player 𝐴 generates 2𝑘=4 shares of secret 𝑎=3
using Shamir’s (2,4) method and computes the
following. Here, let
𝑎
=3+𝑥.
𝛼
𝑎
=8 × 4=32 (𝑚𝑜𝑑 97)
𝛼
𝑎
=8 × 5=40 (𝑚𝑜𝑑 97)
𝛼
𝑎
=18 × 6=11 (𝑚𝑜𝑑 97)
𝛼
𝑎
=18 × 7=29 (𝑚𝑜𝑑 97)
3. Player 𝐴 sends
𝛼
𝑎
,
𝛼
𝑎
,𝛼
,
,𝛼
,
to server
𝑆
and
𝛼
𝑎
,
𝛼
𝑎
,𝛼
,
,𝛼
,
to server 𝑆
.
4. Player 𝐵 generates 2𝑘=4 random numbers
𝛽
,
,𝛽
,
,𝛽
,
,𝛽
,
and computes the following.
𝛽
,
=1, 𝛽
,
=6
𝛽
,
=8, 𝛽
,
=2
𝛽
=𝛽
,
×𝛽
,
=1×6=6
(
𝑚𝑜𝑑 97
)
𝛽
=𝛽
,
×𝛽
,
=8 × 2=16 (𝑚𝑜𝑑 97)
5. Player 𝐵 generates 2𝑘=4 shares of secret 𝑏=2
using Shamir’s (2,4) method and computes the
following. Here, let
𝑏
=2+3𝑥.
𝛽
𝑏
=6 × 5=30 (𝑚𝑜𝑑 97)
𝛽
𝑏
=6×8=48 (𝑚𝑜𝑑 97)
𝛽
𝑏
=16 × 11=79 (𝑚𝑜𝑑 97)
𝛽
𝑏
=16 × 14=30 (𝑚𝑜𝑑 97)
6. Player 𝐵 sends
𝛽
𝑏
,
𝛽
𝑏
,𝛽
,
,𝛽
,
to server
𝑆
and
𝛽
𝑏
,
𝛽
𝑏
,𝛽
,
,𝛽
,
to server 𝑆
.
7. Finally, each server 𝑆
(𝑖=0,1) holds the
following.
─ Server 𝑆
holds the following:
𝛼
𝑎
=32,
𝛼
𝑎
=11,𝛼
,
=2,𝛼
,
=3
𝛽
𝑏
=30,
𝛽
𝑏
=79,𝛽
,
=1,𝛽
,
=8
─ Server 𝑆
holds the following:
𝛼
𝑎
=40,
𝛼
𝑎
=29,𝛼
,
=4,𝛼
,
=6
𝛽
𝑏
=48,
𝛽
𝑏
=30,𝛽
,
=6,𝛽
,
=2
Multiplication Protocol:
1. Each server 𝑆
(𝑖=0,1) computes the following.
─ Server 𝑆
computes the following:
𝛼
𝛽
𝑎𝑏
∗
=
𝛼
𝑎
×
𝛽
𝑏
=32×30
=87 (𝑚𝑜𝑑 97)
𝛼
𝛽
𝑎𝑏
∗
=
𝛼
𝑎
×
𝛽
𝑏
=11×79
=93 (𝑚𝑜𝑑 97)
𝛼
,
𝛽
,
=𝛼
,
×𝛽
,
=2×1=2 (𝑚𝑜𝑑 97)
𝛼
,
𝛽
,
=𝛼
,
×𝛽
,
=3 × 8=24 (𝑚𝑜𝑑 97)
─ Server 𝑆
computes the following:
𝛼
𝛽
𝑎𝑏
∗
=
𝛼
𝑎
×
𝛽
𝑏
=40×48
=77 (𝑚𝑜𝑑 97)
𝛼
𝛽
𝑎𝑏
∗
=
𝛼
𝑎
×
𝛽
𝑏
=29×30
=94 (𝑚𝑜𝑑 97)
𝛼
,
𝛽
,
=𝛼
,
×𝛽
,
=4 × 6=24 (𝑚𝑜𝑑 97)
𝛼
,
𝛽
,
=𝛼
,
×𝛽
,
=6 × 2=12 (𝑚𝑜𝑑 97)
Improvement of Secure Multi-Party Multiplication of (k, n) Threshold Secret Sharing Using Only N = k Servers
87

2. Each server 𝑆
(𝑖=0,1) generates random
number 𝛾
, computes the following and sends to
one of the servers (here, we assume server 𝑆
).
─ Server 𝑆
generates 𝛾
=4, computes the
following and sends to server 𝑆
.
𝛾
𝛼
,
𝛽
,
=
4
2
=2
(
𝑚𝑜𝑑 97
)
𝛾
𝛼
,
𝛽
,
=
4
24
=81 (𝑚𝑜𝑑 97)
─ Server 𝑆
generates 𝛾
=2, computes the
following and sends to server 𝑆
.
𝛾
𝛼
,
𝛽
,
=
2
24
=89
(
𝑚𝑜𝑑 97
)
,
𝛾
𝛼
,
𝛽
,
=
2
12
=81 (𝑚𝑜𝑑 97)
3. Server 𝑆
computes the following and sends to all
servers.
𝛾
𝛼
𝛽
=
𝛾
𝛼
,
𝛽
,
×
𝛾
𝛼
,
𝛽
,
=2×89
=81 (𝑚𝑜𝑑 97)
𝛾
𝛼
𝛽
=
𝛾
𝛼
,
𝛽
,
×
𝛾
𝛼
,
𝛽
,
=81×81
=62 (𝑚𝑜𝑑 97)
4. Each server 𝑆
(𝑖=0,1) computes
𝛾𝑎𝑏
∗
,
𝛾𝑎𝑏
∗
as follows, and distribute
𝛾𝑎𝑏
∗
,
𝛾𝑎𝑏
∗
using Shamir’s (2,2) method to
all servers 𝑆
.
─ Server 𝑆
computes the following:
𝛾𝑎𝑏
∗
=
𝛾
𝛼
𝛽
×
𝛼
𝛽
𝑎𝑏
∗
=81×87
=63 (𝑚𝑜𝑑 97)
𝛾𝑎𝑏
∗
=
𝛾
𝛼
𝛽
×
𝛼
𝛽
𝑎𝑏
∗
=62×93
=43 (𝑚𝑜𝑑 97)
𝑙𝑒𝑡 𝑡ℎ𝑒 𝑝𝑜𝑙𝑦𝑛𝑜𝑚𝑖𝑎𝑙 𝑏𝑒
𝛾𝑎𝑏
∗
=63+𝑥
𝛾𝑎𝑏
,
=64⟹𝑠𝑒𝑛𝑑 𝑡𝑜 𝑆
𝛾𝑎𝑏
,
=65⟹𝑠𝑒𝑛𝑑 𝑡𝑜 𝑆
𝑙𝑒𝑡 𝑡ℎ𝑒 𝑝𝑜𝑙𝑦𝑛𝑜𝑚𝑖𝑎𝑙 𝑏𝑒
𝛾𝑎𝑏
∗
=43+2𝑥
𝛾𝑎𝑏
,
=45⟹𝑠𝑒𝑛𝑑 𝑡𝑜 𝑆
𝛾𝑎𝑏
,
=47⟹𝑠𝑒𝑛𝑑 𝑡𝑜 𝑆
─ Server 𝑆
computes the following:
𝛾𝑎𝑏
∗
=
𝛾
𝛼
𝛽
×
𝛼
𝛽
𝑎𝑏
∗
=81×77
=29 (𝑚𝑜𝑑 97)
𝛾𝑎𝑏
∗
=
𝛾
𝛼
𝛽
×
𝛼
𝛽
𝑎𝑏
∗
=62×94
=8 (𝑚𝑜𝑑 97)
𝑙𝑒𝑡 𝑡ℎ𝑒 𝑝𝑜𝑙𝑦𝑛𝑜𝑚𝑖𝑎𝑙 𝑏𝑒
𝛾𝑎𝑏
∗
=29+𝑥
𝛾𝑎𝑏
,
=30⟹𝑠𝑒𝑛𝑑 𝑡𝑜 𝑆
𝛾𝑎𝑏
,
=31⟹𝑠𝑒𝑛𝑑 𝑡𝑜 𝑆
𝑙𝑒𝑡 𝑡ℎ𝑒 𝑝𝑜𝑙𝑦𝑛𝑜𝑚𝑖𝑎𝑙 𝑏𝑒
𝛾𝑎𝑏
∗
=8+3𝑥
𝛾𝑎𝑏
,
=11⟹𝑠𝑒𝑛𝑑 𝑡𝑜 𝑆
𝛾𝑎𝑏
,
=14⟹𝑠𝑒𝑛𝑑 𝑡𝑜 𝑆
5. Each server 𝑆
(𝑖=0,1) computes the following
using the recombination vector 𝑟 =(3,−3,1,0).
─ Server 𝑆
computes the following:
𝛾𝑎𝑏
=3×
𝛾𝑎𝑏
,
+
(
−3
)
×
𝛾𝑎𝑏
,
+1
×
𝛾𝑎𝑏
,
+0×
𝛾𝑎𝑏
,
=3×64−3×30+1×45+0×11
=50
(
𝑚𝑜𝑑 97
)
─ Server 𝑆
computes the following:
𝛾𝑎𝑏
=3×
𝛾𝑎𝑏
,
+
(
−3
)
×
𝛾𝑎𝑏
,
+1
×
𝛾𝑎𝑏
,
+0×
𝛾𝑎𝑏
,
=3×65−3×31+1×47+0×14
=52 (𝑚𝑜𝑑 97)
Reconstruction Protocol:
1. The player collects
𝛾𝑎𝑏
=50,
𝛾𝑎𝑏
=
52,𝛾
=4,𝛾
=2 from 𝑁=𝑘=2 servers
𝑆
(𝑖=0,1), reconstructs 𝛾𝑎𝑏 using Shamir’s (2,
2) method and computes 𝛾 as follows.
𝛾𝑎𝑏=48
𝛾=𝛾
×𝛾
=4×2=8 (𝑚𝑜𝑑 97)
2. Finally, the player reconstructs multiplication
result 𝑎𝑏 as follows.
𝑎𝑏=
𝛾𝑎𝑏
𝛾
=
48
8
=6 (𝑚𝑜𝑑 97)
ICISSP 2021 - 7th International Conference on Information Systems Security and Privacy
88
