Wavelet Correlation of Non-stationary Bursts of EEG

S. V. Bozhokin

and I. B. Suslova

Peter the Great Saint-Petersburg Polytechnic University, Polytechnicheskaya str. 29, Saint-Petersburg, Russia

Keywords: EEG, Continuous Wavelet Transform, Wavelet Correlation Function.

Abstract: The problem of non-stationary correlation of signals recorded in various EEG channels of the human brain

is considered. Each signal is represented as a sequence of bursts occurring at different times in different

spectral ranges. To solve the problem of detecting the relationship of these signals, the authors introduced a

new wavelet correlation function WCF. The WCF function allows you to detect the correlation of individual

bursts of different EEG channels that have the same frequency, but different times of occurrence. The WCF

function is built on the basis of continuous wavelet transforms of two signals taken at different points in

time. For the considered recording data of two EEG channels, the burst correlations were classified. The

proposed solution to the problem of correlation of EEG signals makes it possible to trace the propagation of

disturbances in the cerebral cortex (traveling waves) and to reveal the synchronization of movement of

evoked potentials.

https://orcid.org/0000-0001-5653-6574

https://orcid.org/0000-0002-4497-1867

1 INTRODUCTION

It is known that human electroencephalogram (EEG)

shows electrical activity of a great number of

neurons in the brain. The signal from each EEG

channel is an alternation of bursts in different

spectral ranges

{}

,, ,μ= δθαβ

. EEG is essentially a

nonstationary process, since its spectral and

statistical properties change over time (Mandel and

Wolf, 1995; Papandreou-Suppappola, 2003; Adeli

and Ghost-Dastidar, 2010; Hramov et al., 2015). The

unsteady character of EEG signal can be observed

both at rest of the subject and during functional tests

(photo-stimulation, hyperventilation).

To analyze changes in the spectral composition

of nonstationary signals (NSs), the windowed

Fourier transform (STFT - Short Time Fourier

Transform) is often used (Subha et al., 2010). In this

case, the entire measurement interval

is divided

into a number of consecutive windows, each having

the duration equal to

/WTN=

, where

is the

total number of windows. The consistent behavior of

two different processes

()

and

()

recorded

from different EEG channels

and

characterized by the value of coherence. The

coherence of the brain shows the degree of intra-

cortical interactions in different parts of the brain

and the presence of functional relations between

them.

The calculation of the coherence function

includes the averaging of Fourier components of two

signals over many realizations (Kulaichev, 2011;

Sheikhani and Behnam, 2008; Seleznov et al., 2019;

Reiser et al., 2012; Kropotov, 2012; Bendat and

Pierrsol, 2011). Phase coherence of the two signals

is characterized by the value

()

LV f

called the

Phase Locking Value (Piqueira, 2011; Trofimov et

al., 2015; Duc et al. 2019). However, we should note

that as shown in (Kulaichev, 2011), the value of the

coherence of two signals depends on the averaging

procedure, choice of the window size, window

function, and the value of the window step shift.

Therefore, the coherence value cannot be

considered as a strict quantitative measure of the

correlation of two signals

()

and

()

, where

and

are the numbers of EEG channels. In

addition, various computer programs use different

types of windows and numbers of averaging. Thus,

142

Bozhokin, S. and Suslova, I.

Wavelet Correlation of Non-stationary Bursts of EEG.

DOI: 10.5220/0010196701420149

In Proceedings of the 14th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2021) - Volume 4: BIOSIGNALS, pages 142-149

ISBN: 978-989-758-490-9

it is difficult to compare the results obtained in the

works of various authors.

The purpose of this work is to find the

correlation of nonstationary signals from different

EEG channels. We introduce the new type of

correlation function, and use it to determine the

matching of various EEG bursts occurring in

different spectral ranges at different points in time.

2 WAVELET CORRELATION

FUNCTION

Currently, the continuous wavelet transform (CWT)

method is often used to quantitatively describe the

nonstationary EEG (Mallat, 2008; Cohen, 2003;

Advances in Wavelet, 2012; Chui and Jiang, 2013;

Addison, 2017; Hramov, 2015; Bozhokin and

Suvorov, 2008; Bozhokin and Suslova, 2014, 2015;

Wavelets in Physics, 2004).

We determine continuous wavelet transform

()

,Vt

for the time-dependent signal

()

by the

formula

() () ( )

()

,ΨV ν t ν Zt ν ttdt

∞

−∞

′′′

=−



. (1)

The function

()

Ψ is a mother wavelet. The * sign

means complex conjugation. The mother wavelet in

(1) has two properties. The average value of

()

over the entire argument

−∞ < < ∞

is zero. The

squared norm

()

is equal to one. The main

types of mother wavelets are given in the book

(Hramov, 2015). In our study we use the Morlet

mother wavelet function

()

Ψ with the control

parameter

() ()

()

exp exp 2 exp

xD ix





Ψ= − π− −Ω











, (2)

where

mΩ=π . The control parameter

allows us to change the spectral and temporal

resolution of the signal under study. The Fourier

component

()

Ψ of the mother wavelet function

and the normalization constant

(2) are given in

(Bozhokin et al. 2017). We derive the formula

() () ()

,exp2

Vt Zf iftdf

∞

−∞



ν= Ψ π







(3)

by performing twice the Fourier transform of (1).

Here

()

f is the Fourier component of the signal

()

Consider the particular case of an infinite

harmonic signal

()

cos 2

tft=π with constant

frequency

. The Fourier component of such a

signal is the superposition of two Dirac delta

functions:

()

()()

/2Zf f f f f=δ + +δ −









. The

maximum value of

()

,Vt

(1) will be observed

exactly at the frequency value

. For

()

exp 2 1

−Ω <<

, this maximum will not depend on

time.

Assume that

()

corresponds to

()

t and

()

, − to

()

t . The cross wavelet spectrum

of two signals is determined by the formula

() ()()

,,,

JK J K

CWS t V t V t

=ν ν

. (4)

By averaging the function

()

CWS t

both

over frequencies

and time

, and by normalizing

this value, one can obtain the square of the wavelet

coherence function

()

,tΓν

. The details of the

averaging procedure for calculating the function

()

,tΓν

, as well as its application to various non-

stationary signals, can be found in (Lachaux et al.,

2002; Klein et al., 2006; Banfi et al., 2012; Grinsted

et al., 2004; Li et al., 2007; Kang et al., 2019;

Chaves and Cazelles, 2019; Yang et al., 2019;

Schuck and Bodmann, 2019).

Unfortunately, the values of

()

,tΓν

depend on

the mother wavelet, as well as on the averaging

procedure over

and

. It is important to

emphasize that the time-averaging procedure of the

wavelet coherence function associated with the idea

of the short time Fourier transform (STFT) negates

the main advantage of CWT for studying NS, whose

spectral and temporal properties can vary

significantly over time. Indeed, the correlations of

NS signals can develop and disappear at small time

scales. However, the function

()

,tΓν

based on the

averaging procedure over many epochs cannot

detect this effect.

Let us introduce the wavelet correlation function

()

WCF t

for two signals

()

t and

()

t as

Wavelet Correlation of Non-stationary Bursts of EEG

143

()( )

(,) , ,

JK J K

WCF ν tVν tV ν ttdt

∞

−∞

′′′



. (5)

In contrast

()

CWS t

(4), the function

()

WCF t

(5), describes the correlation between

two signals at different times. The complex

conjugate wavelet transform of the first signal

()

′

is taken at the time moment

′

. The

wavelet transform of the second signal

()

Vtt

′

is taken at time

′

. Representing (5) in terms of

Fourier components, we get:

( ) () () ()

ˆˆ ˆ

,Ψexp2

JK J K

WCF ν tZfZf πift df

∞

−∞









. (6)

Using the wavelet correlation function

()

WCF t

(5)-(6), we get an opportunity to study the

correlation in time of various channels in the EEG

record. The EEG signal from each channel will be a

sequence of bursts occurring at different points in

time in different spectral ranges

(,, ,,)

=δθα

βγ

3 RESULTS

In this study, we use a spontaneous EEG of a healthy

subject at rest with his eyes closed. The background

of the EEG signal represents desynchronized activity

of the neural ensembles of the cerebral cortex. In

addition to the background activity, the EEG signal

includes various oscillatory patterns. Such patterns

represent continuously appearing and disappearing

bursts of rhythms related to the coherent electrical

activity of neural ensembles. When registering EEG,

standard channels are used according to the 10-20%

scheme, where index

=1,2, ... 21 takes the values

{Fp1, Fpz, Fp2; F7, F3, Fz, F4, F8; T3, C3, Cz, C4,

T4; T5, P3, Pz, P4, T6; O1, Oz, O2}. The shifts of

the electrical activity maxima for different channels

are small, therefore the signal sampling frequency is

F = 500 Hz, which corresponds to the signal

sampling time 2 ms.

By the burst of EEG activity in the frequency

range

{

}

,, ,

=δθα

, we mean appearance and

disappearance of a group of waves different from the

background EEG activity in frequency, shape and

amplitude. The maximum electrical activity of such

a burst is localized at a certain point in time

max

Each burst has its beginning and end, as well as its

own characteristic duration. For each burst, it is

possible to estimate the characteristic spectral range.

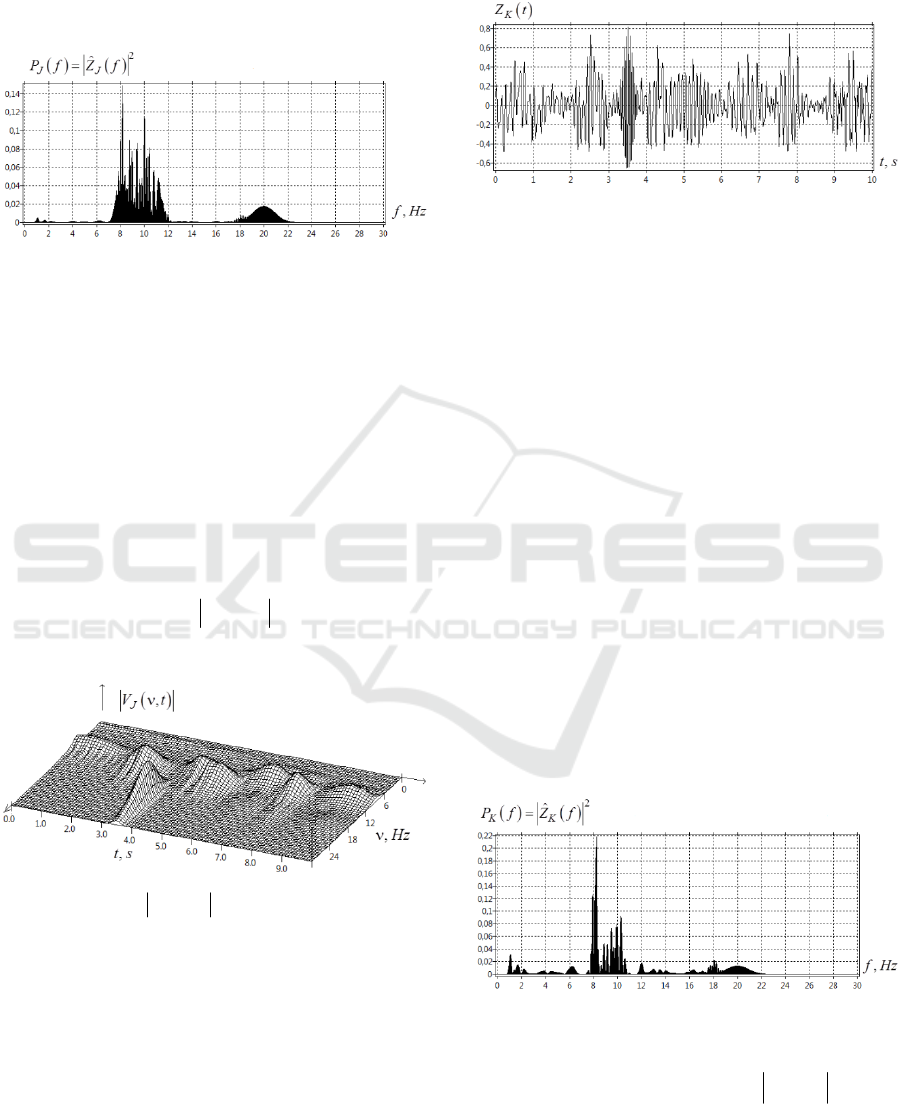
Fig.1 shows the signal

()

t from occipital

channel

Figure 1: EEG signal time dependence (channel

Visual analysis of

()

t shows the presence of

alpha activity bursts (

[7 14 ]

zα= −

) in the rhythm.

The centers of these bursts are localized at the

moments of time approximately equal to

t =

{0.5;

2.5; 4.3; 5.0; 6.5; 7.6; 9.2 s}. Let us analyze the

characteristic frequencies of all flashes in the

[7 14 ]

zα= −

and

[14-30 Hz] ranges using the

STFT method with the window

2W =

s. For each

burst, the STFT estimation gives a characteristic

burst maximum

, measured in s, and one or

several characteristic frequencies

in Hz. For

signal

()

t , we have the burst matrix

{

}

;

atrixZ tαν= {{8.2; 0.51}, {12.0; 0.49},

{10.2; 2.58}, {13.0; 2.59}, {9.2; 4.28}, {14.0; 4.30},

{11.2; 5.10}, {7.8 ; 6.41}, {9.8; 7.62}, {8.8; 9.23},

{6.2; 9.21}}.

In addition to the natural signal

()

t , we insert

into the signal the artificial (model) burst of activity

having a Gaussian shape located at

t =

0.35 s. This

burst has constant frequency

Нz and

characteristic half-width

= 0.09 s. In

-range, the

total matrix of signal bursts

()

t has the form

{

}

;

atrixZ tβν={{20.0; 3.50}, {15.1; 5.18},

{16.3; 6.11}, {16.9; 7.43}, {18.1; 9.21}}. All bursts

and

frequency ranges are sorted by the time

of their occurrence.

The power spectrum

() ()

Pf Z f=

signal

()

t is determined as the squared modulus

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

144

of the signal Fourier component

()

f . This

Fourier spectrum is calculated for the entire

observation interval of the signal

010t≤≤

(Fig.2).

Figure 2: Power spectrum

()

Pf of the signal

()

t .

The analysis of the signal power spectrum

()

Pfshows that throughout the signal duration

010t≤≤

s, its spectrum contains bursts with

frequencies in

-range. The chaotic bursts of

rhythm appear in the range [17-19 Hz]. In addition

to these

- bursts, in the power spectrum, we have

an ideal Gaussian peak located at

= 20 Hz with

the width

1/ 1.1Δν = τ ≈

Hz. This peak is

associated with the model Gaussian burst of activity

with the parameters

{

}

;tν ={20; 3.50}. Fig.3

represents the modulus

()

of CWT image for

signal

()

t .

Figure 3: Modulus

()

Vtν of CWT image for the signal

()

t .

The advantage of applying CWT method over

the STFT is that for the CWT method the window

size is selected automatically depending on the

frequency of the signal. In addition, for the control

parameter of the Morlet mother wavelet

1m =

, the

shape of the envelope and the value of the burst

frequency completely coincide with the parameters

of the test Gaussian signals (Bozhokin et al., 2017).

A similar problem is solved for the second signal

()

t obtained from the central channel

KC=

Figure 4: Time dependence of EEG signal

()

(channel

The matrix of bursts for

()

t in

-range has

the form

{

}

;

atrixZ tαν= {{8.1; 0.52}, {12.0;

0.52}, {10.1; 2.53}, {13.1; 2.53}, {8.9; 4.31}, {14.0;

4.31}, {10.1; 5.25}, {8.1; 6.68}, {9.0; 7.81}, {8.1;

9.55}, {6.2; 9.27}}. In

-range, the total matrix of

bursts in signal

()

t has the form

{

}

;

atrixZ tβν={{20.0; 3.52} {15.0; 5.25},

{16.0; 6.73}, {16.9; 7.85}, {18.1; 9.58}}.

Similarly to signal

()

t , we insert an artificial

model signal into

-range of the signal

()

spectrum. It is an ideal Gaussian peak with the

characteristics

{

}

;tν ={20.0; 3.52}. This specially

introduced

-burst in the signal

()

t has the same

frequency

as that in

()

t . However, the

burst in the signal

()

t lags behind in time from

the burst in the signal

()

t by

tΔ

tt−

= 0.02 s.

Figure 5: Power spectrum

()

Pf of the signal

()

t .

The power spectrum

() ()

Pf Z f=

for the

signal

()

t calculated over the entire observation

interval

010t≤≤

s (Fig.5) differs from that for the

Wavelet Correlation of Non-stationary Bursts of EEG

145

signal

()

t (Fig.2). The power spectrum

()

(Fig.5) has much more bursts in the low-frequency

region

[1 7f =−

Hz]

and

- rhythms in

comparison with the spectrum

()

Pf (Fig.2). The

spectrum

()

Pf in

-range [7-14 Hz] has fewer

harmonics compared to

()

Pf. However, the

spectrum of bursts in

-range in the signal

()

is much wider than in the signal

()

t . Fig.6 shows

the modulus of CWT

()

for the signal

()

Figure 6: Modulus of CWT

()

for the signal

()

t .

Three-dimensional patterns of EEG bursts for the

signal

()

t (Fig.3) plotted on the

Hz and

, s

plane differ from those for

()

t (Fig.6).

To study the dynamics of the rise and fall of the

bursts with different frequencies, we introduce

spectral integrals

()

, which depend on time

(Bozhokin and Suvorov, 2008; Bozhokin and

Suslova, 2014, 2015).

() ()

,Et td

ν−Δν

=ενν

Δν



. (7)

Spectral integral

()

is the average value of

signal energy spectrum local density

() ()

()

,2 ,/tVt C

εν = ν ν

, integrated over the

certain frequency interval

/2; /2

μμ





ν−Δν ν+Δν





where

is the middle of the corresponding

spectral interval,

Δν

is the width of the interval.

Studying the behavior of spectral integrals over time

()

, we perform a kind of filtering of our signal

by summing the contributions from the local

spectrum density

()

, tεν in a certain frequency

range

{

}

,, ,

=δθα

. The constant C

was

calculated in the article (Bozhokin et al, 2017).

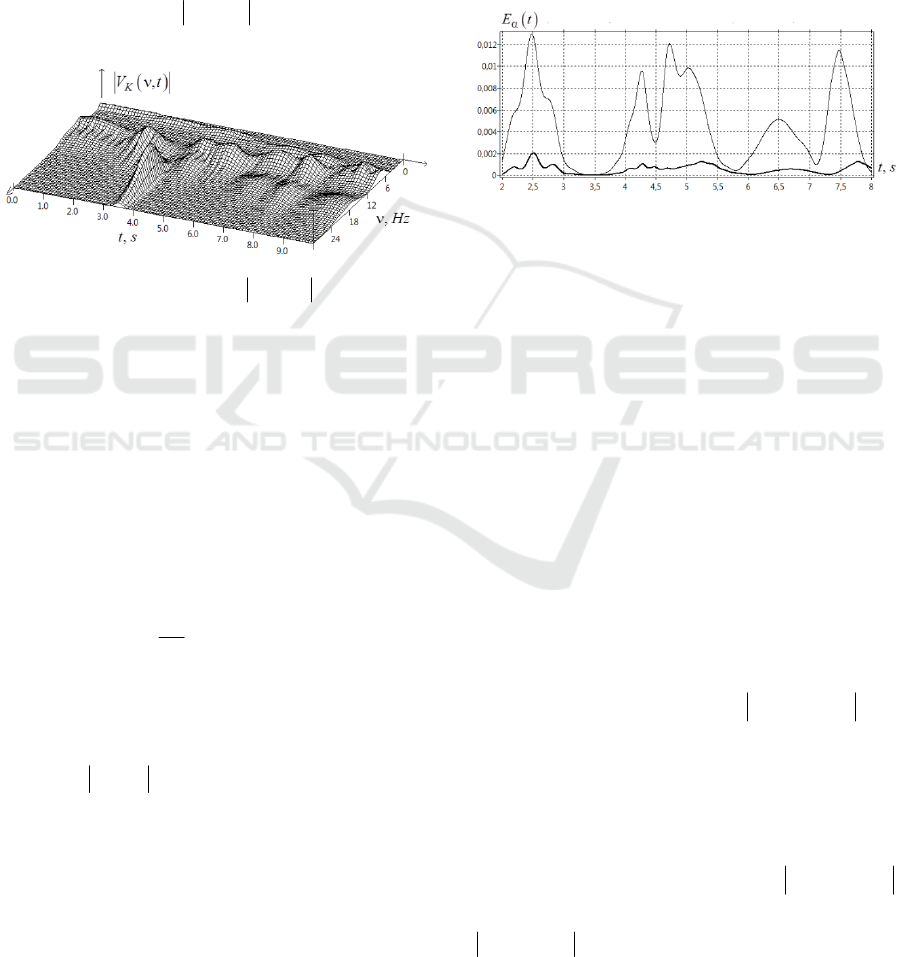
To compare the bursts accurately let us consider

the values of the spectral integral

()

in the

range for the signals

()

and

()

. For this

purpose, we take the time interval

= [2-8 s] (Fig.7),

where the main bursts of these signals are

concentrated.

Figure 7: Spectral integrals

()

versus time

for

range. The thin line corresponds to the signal

()

(channel

). The bold line is for the signal

()

(channel

The analysis of spectral integrals

()

range shows (Fig.7) that the structure of the bursts

changes when the disturbance moves from the

occipital channel

()

to the channel

()

. With this movement, the amplitude of the

bursts decreases. The speed

≈

3-5 m/s of

-burst

maximum movement can be estimated from the shift

of this maximum, which is

tΔ≈

0.02-0.03 s.

Thus, using two EEG channels as an example,

we have shown that the frequency spectrum and

temporal position of bursts change as they propagate

through the cerebral cortex. Then, let us calculate

the wavelet correlation function

()

WCF t

(5)-

(6) for the signals

()

t and

()

t . This function

will allow us to find the correlation of two bursts,

whose maxima of which are located at different time

moments for the fixed frequency

varying in the

interval

[1 30 ]

=−

We consider the time argument of

()

WCF t

varying in the interval

[10;10t =−

s]. The graph of

()

WCF t

is shown in Fig.8.

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

146

Figure 8: Wavelet correlation function

()

WCF t

two signals

and

depending on frequency

, Hz

and

time

,ts

Let us explain the main peaks of

()

WCF t

in Fig.8. Suppose that there is a single burst in

signal

()

t , characterized by frequency

time

of its maximum. In this case, the maximum value

of CWT image

()

′

will be observed at the

moment of time

′

In turn, there is a single burst in signal

()

t ,

characterized by the same frequency

and the time

moment

. The maximum of

()

Vtt

′

+ will be at

tt t

′

. The consequence of these two equalities

is the condition that the maximum of

()

WCF t

(5), (6) will be observed at the frequency

at the

moment of time

tt t=−

Let us explain the origin of the maxima in Fig.8

in the range of the alpha rhythm

[7;14 ]

zα=

the time interval

[10;10]ts=−

. We introduce the

designation

{

}

;

tν

⇔

{

}

;

tν , which means

the correlation of an individual burst

()

t ,

characterized by frequency

and center

localization time

, with a specific burst having the

parameters

and

The leftmost maximum of

()

WCF t

(Fig.8)

is located in the frequency range

[8;9 ]

in the

time interval

[6;5]ts=− −

. This leftmost maximum

is associated with the correlations of the following

bursts:

{

}

7.8;6.41

⇔

{

}

8.1;0.52

;

{

}

8.8;9.23

⇔

{

}

8.9;4.31

. The next leftmost maximum of

()

WCF t

is located in the frequency range

[9;10 ]

in the time interval

[3.5;2]ts=− −

This maximum is associated with the following

correlations:

{

}

9.8;7.62

⇔

{

}

10.1;5.25

A large number of bursts in

-range, which

have approximately the same frequencies and times

of occurrence, form a large correlation peak located

nearby

0t =

. Reasoning similarly, the rightmost

peak of

()

WCF t

located in the interval of

times

[6 10 ]ts=−

near the frequencies

≈

associated with correlations:

{

}

8.2;0.51

⇔

{

}

8.1;9.55

;

{

}

8.2;0.51

⇔

{

}

8.1;6.68

. The most

striking correlation (5), (6) in

-range is a high

peak centered at the point

{

}

20.0;0.02 . The reason

for this peak is the correlation of two bursts:

{

}

20.0;3.50

⇔

{

}

20.0;3.52

Thus, we introduced the function

()

WCF t

which adequately describes the wavelet correlation

of two signals

()

t and

()

t , each consisting of

a large number of EEG bursts. The ensemble of

signal bursts

()

t differs from the ensemble of

signal bursts

()

t both in the time of their

occurrence and in the frequency composition. In

addition, each burst has its own amplitude, phase,

and characteristic time scale.

4 CONCLUSIONS

The aim of the article is to introduce a new wavelet

correlation function

()

WCF t

. The electrical

activity of neural ensembles is analyzed using EEG

signals from many brain channels in different

spectral ranges. We discussed the shortcomings of

the methods based on the windowed Fourier

transform (short-time Fourier transform - STFT) for

the study of the synchronization of various EEG

channels. The disadvantages include the ambiguity

in the choice of the window duration, the problems

of selecting the window function, and the degree of

window overlapping.

The known wavelet methods for studying signal

correlation make it possible to analyze the

interdependence of two EEG signals occurring only

at the same time. The study of real EEG signals, in

which correlated bursts occur at different times,

requires the use of another type of wavelet

correlation function.

Wavelet Correlation of Non-stationary Bursts of EEG

147

In the article, we use the modification

()

,Vt

continuous wavelet transform, which has advantages

over the standard CWT form

()

,Wt

(Mallat, 2008;

Chui and Jiang, 2013; Hramov, 2015). These

involve the accurate reflection of the ratios by both

frequencies and amplitudes of the signals and their

CWT images. Furthermore, by including an

additional control parameter

into the Morlet

mother wavelet, we get the opportunity to further

adjust both the amplitude and frequency resolution

of signals.

An example of two EEG channels is analyzed.

The signals from these channels

()

t and

()

are the alternation of bursts, which occur at different

times in different frequency intervals. The spectral

powers of these signals

()

Pfand

()

Pf are

calculated, as well as their CWT images

()

and

()

. A new correlation function

()

WCF t

is introduced and calculated. It allows

us to determine the correlation of bursts occurring in

signals at different times, but having the same

frequency. For the specific example of two

nonstationary signals from different EEG channels, a

classification of correlations of different bursts is

suggested.

The proposed method assuming the calculation

of the function

()

WCF t

can be used to analyze

the propagation of disturbances over the surface of

the brain, and to study the synchronicity of the

evoked potentials arising as a response of neural

ensembles to the sensory stimulation. The

()

WCF t

can be useful in the study of rapidly

changing burst processes in plasma physics and

astrophysics, as well as for the determination of

coherent space-time structures for media with strong

dispersion.

ACKNOWLEDGMENTS

The work was performed within the framework of

the Russian State tasks for conducting fundamental

research (topic code FSEG-2020-0024).

REFERENCES

Addison, P.S., 2017. The illustrated wavelet transform

handbook. Introductory theory and application in

Science, engineering, medicine and finance, CPC

Press, Second Edition.

Adeli, H., Ghost-Dastidar, S., 2010. Automated EEG-

based diagnosis of neurological disorders: Inventing

the future of neurology, CRC Press.

Advances in Wavelet Theory and Their Applications in

Engineering, Physics and Technology. 2012. Edited by

Dumitru Baleanu

Banfi, F., Ferrini, G., 2012. Wavelet cross-correlation and

phase analysis of a free cantilever subjected to band

excitation,

Beilstein J. Nanotechnol. 3: 294–300.

Bendat, J. S., and Piersol, A. G., 2011. Random Data:

Analysis and Measurement Procedures, (Vol. 729),

NY: John Wiley & Sons, New York.

Bozhokin S.V., Suvorov N.B., 2008. Wavelet analysis of

transients of an electroencephalogram at

photostimulation, Biomed. Radioelektron, N3: 21-25.

Bozhokin, S.V., Suslova, I.B., 2014. Wavelet Analysis of

Non-Stationary Signals in Medical Cyber-Physical

Systems (MCPS), International Conference on Next

Generation Wire/Wireless Networking, Lecture Notes

of Computer Science, LNCS, 8638: 467-480.

Bozhokin, S.V., Suslova, I.B., 2015. Wavelet-based

analysis of spectral rearrangements of EEG patterns

and of non-stationary correlations, Physica A.

421:151–160.

Bozhokin, S.V., Zharko, S.V., Larionov, N.V., Litvinov,

A.N., Sokolov, I.M., 2017. Wavelet Correlation of

Nonstationary Signals, Technical Physics, 62(6):837-

845.

Chavez, M., Cazelles, B., 2019. Detecting dynamic spatial

correlation patterns with generalized wavelet

coherence and non-stationary surrogate data, Scientific

Reports 9(1): 7389-7398.

Chui, C.K., Jiang O., 2013. Applied Mathematics. Data

Compression, Spectral Methods, Fourier Analysis,

Wavelets and Applications. Mathematics Textbooks

for Science and Engineering, v.2, Atlantis Press.

Cohen A., 2003. Numerical Analysis of Wavelet Method,

Elsevier Science, North-Holland.

Duc N.T., Lee B., 2019. Microstate functional

connectivity in EEG cognitive tasks revealed by a

multivariate Gaussian hidden Markov model with

phase locking value, Journal of neural engineering,

16(2):026033

Grinsted, A., Moore, J.C., Jevrejeva S., 2004. Application

of the cross wavеlet transform and wavelet coherence

to geophysical time series, Nonlinear Processes in

Geophysics 11(5/6): 561-566.

Hramov, A.E., Koronovskii, A.A., Makarov, V.A.,

Pavlov, A.N., Sitnikova, E., 2015. Wavelets in

neuroscience, Springer Series in Synergetics,

Springer-Verlag, Berlin, Heidelberg.

Klein, A., Sauer, T., Jedynak,A., Skrandies,W., 2006.

Conventional and wavelet coherence applied to sensory-

evoked electrical brain activity, IEEE transaction on

biomedical engineering. 53(2): 266-272.

Kropotov, J. D., 2010. Quantitative EEG, Event-Related

Potentials and Neurotherapy, San Diego, CA:

Academic Press.

BIOSIGNALS 2021 - 14th International Conference on Bio-inspired Systems and Signal Processing

148

Kulaichev, A.P., 2011. The informativeness of coherence

analysis in EEG studies, Neuroscience and behavioral

physiology. 41(3): 321-328.

Lachaux, J.-P, Lutz, A., Rudrauf, D., Cosmelli, D., Quyen,

L.V., Martinerie, J., Varela, F., 2002. Estimating the

time-course of coherence between single-trial brain

signals: an introduction to wavelet coherence,

Neurophysiologie Clinique. 32: 157-174.

Li, X., Yau, X., Fox,J., Jefferys,J.G., 2007. Interactions

dynamics of neuronal oscillations analysed using

wavelet transform, Journal of Neuroscience Methods.

160:178-185.

Kang, S.H., McIver,R.P., Hernandes,J.A., 2019. Co-

movements between Bitcoin and Gold: A wavelet

coherence analysis, Physica A: Statistical Mechanics

and its Applications, 536: 120888.

Mallat, S., 2008. A Wavelet Tour of Signal Processing,

Academic Press, New York, 3rd ed.

Mandel L, Wolf E., 1995. Optical Coherence and

Quantum Optics, Cambridge University Press.

Papandreou-Suppappola A., 2003. Application in time-

frequency signal processing, CRC Press.

Piqueira J.R.C., 2011. Network of phase-locking

oscillators and a possible model for neural

synchronization, Commun. Nonlinear Sci. Numer.

Simul., 16(9): 3844–3854.

Reiser, E. M., Schulter, G., Weiss, E. M., Fink, A.,

Rominger, C., and Papousek, I., 2012. Decrease of

prefrontal-posterior EEG coherence: loose control

during social-emotional stimulation, Brain Cogn.. 80,

144–154. doi: 10.1016/j.bandc.2012.06.001

Schuck, Jr. A., Bodmann, B.E.J., 2019. On the

Development of an Alternative Proposition of Cross

Wavelet Analysis for Transient Discrimination

Problems, Integral Methods in Science and

Engineering, 409-423.Springer Nature Switzerland.

https://doi.org/10.1007/978-3-030-16077-7

Seleznov I., Zyma I., Kiyono K., Tukaev S., Popov.A.,

Chernykh M., Shpenkov O., 2019. Detrended

fluctuation, coherence, and spectral power analysis of

activation rearrangement in EEG dynamics during

cognitive workload, Frontiers in Human

Neuroscience, https://doi.org/10.3389/fnhum.2019.00

270

Sheikhani A., Behnam H., 2008. Connectivity analysis of

quantitative electroencephalogram background activity

in Autism disorders with short time Fourier transform

and coherence values, Congress on Image and Signal

Processing. IEEE, DOI: 10.1109/CISP.2008.595.

Subha, D.P., Joseph, P.K., Acharya, R.U., Lim C.M.,

2010. EEG Signal Analysis: A Survey, Journal of

medical systems. 34: 195-212.

Trofimov, A.G., Kolodkin, I.V., Ushakov, V.L.,

Velichkovski, B.M., 2015. Agglomerative method for

isolating microstates related to the characteristics of

the traveling wave, Neuroinformatic-2015, Russian

Scientific and Technical Conference, M.:MIFI. Part 1:

66-77.

Wavelets in Physics, 2004. Edited by J.C. Van.den Berg,

Cambridge University Press.

Yang, Xi. X., Shi C., et al., 2019. Surface

Electromyography-Based Daily Activity Recognition

Using Wavelet Coherence Coefficient and Support

Vector Machine, Neural Process Lett. 50:2265–2280.

Wavelet Correlation of Non-stationary Bursts of EEG

149