
Generic User-guided Interaction Paradigm for Precise
Post-slice-wise Processing of Tomographic Deep Learning
Segmentations Utilizing Graph Cut and Graph Segmentation
Gerald A. Zwettler
1,2,3 a
, Werner Backfrieder
3
, Ronald A. Karwoski
2
and David R. Holmes III
2b
1
Research Group Advanced Information Systems and Technology (AIST), Department of Software Engineering,
University of Applied Sciences Upper Austria, Softwarepark 11, 4232 Hagenberg, Austria
2
Biomedical Analytics and Computational Engineering Lab, Department of Physiology and Biomedical Engineering,
Mayo Clinic College of Medicine, 200 First St. SW, 55905 Rochester, MN, U.S.A.
3
Medical Informatics, Department of Software Engineering, University of Applied Sciences Upper Austria,
Softwarepark 11, 4232 Hagenberg, Austria
Keywords: Graph Cut, Graph Segmentation, U-Net, Deep Learning Image Segmentation, Evolution-strategy,
User-guided Medical Image Analysis.
Abstract: State of the art deep learning (DL) manifested in image processing as an accurate segmentation method.
Nevertheless, its black-box nature hardly allows user interference. In this paper, we present a generic Graph
cut (GC) and Graph segmentation (GS) approach for user-guided interactive post-processing of segmentations
resulting from DL. The GC fitness function incorporates both, the original image characteristics and DL
segmentation results, combining them with weights optimized by evolution strategy optimization. To allow
for accurate user-guided processing, the fore- and background seeds of the Graph cut are automatically
selected from the DL segmentations, but implementing effective features for expert input for adaptions of
position and topology. The seamless integration of DL with GC/GS leads to marginal trade-off in quality,
namely Jaccard (JI) 1.3% for automated GC and JI 0.46% for GS only. Yet, in specific areas where a well-
trained DL model may potentially fail, precise adaptions at a low demand for user-interaction become feasible
and thus even outperforming the original DL results. The potential of GC/GS is shown running on ground-
truth seeds thereby outperforming DL by 0.44% JI for the GC and even by 1.16% JI for the GS. Iterative slice-
by-slice progression of the post-processed and improved results keeps the demand for user-interaction low.
1 INTRODUCTION
Precise segmentation with the need of no or only
marginal user interaction is of high importance in
computer-assisted medical diagnostics, both in
research and clinical practice. Thereby automated and
generally applicable image processing methods are
still in focus of research. A fully automated albeit
highly precise segmentation approach shipping as
black box thereby is not necessarily of highest interest
as the diagnostician always holds the ultimate
responsibility for segmentation accuracy and
diagnostic outcome. With the advances in medical
image processing, a broad range of semi-automated
a
https://orcid.org/0000-0002-4966-6853
b
https://orcid.org/0000-0003-2466-5245
approaches is available for processing tomographic
datasets, such as Region Growing, Live-Wire, Level
Sets, Graph Cuts or Graph segmentation that are
provided by various frameworks and tools (Strakos et
al. 2015). While the radiographer or diagnostician
using these tools and algorithms keeps full control of
his actions, the achievable accuracy, the high demand
for user interaction and the subjectivity of the
findings and interpretations are a constant drawback
during the last decades.
In recent years, the application of deep learning
(DL) neural networks led to a sustainable impact in
many segmentation domains in industry as well in
medicine. Trained on a huge amount of reference
datasets, these DL models allow for fully automated
Zwettler, G., Backfrieder, W., Karwoski, R. and Iii, D.
Generic User-guided Interaction Paradigm for Precise Post-slice-wise Processing of Tomographic Deep Learning Segmentations Utilizing Graph Cut and Graph Segmentation.
DOI: 10.5220/0010190702350244
In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 4: VISAPP, pages
235-244
ISBN: 978-989-758-488-6
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
235

and highly precise segmentation, analysis and
classification in specific diagnostic domains. Due to
their black-box nature, the user must accept the
generally impressive results as they are. Nevertheless,
this is only acceptable as long as there is no need for
adaptions. As no machine learning approach ever will
have perfect sensitivity and specificity, the seamless
integration of DL models in clinical routine necessita-
tes for user-centric post-processing paradigms.
1.1 State of the Art and Related Work
In the domain of fully automated segmentation,
classic approaches such as Statistical Shape Models
(Cootes et al. 1992) utilizing PCA or Active
Appearance Models (Cootes et al. 1998) need to be
adapted for specific domains, modeling the shape
variability and finding individual concepts for robust
positioning, registration and reference point
determination.
In recent years, the advance in GPU hardware and
machine learning frameworks enable deep neural
networks to find their way into industrial and medical
image processing and computer vision domains.
While feed forward neural networks are successfully
applied for multi-modal image fusion (Zhang and
Wang 2011), self-organizing neural networks allow
clustering in complex domains such as classification
of renal diseases (Van Biesen et al. 1998). Deep
semantic knowledge as present in natural language
processing is covered by incorporation of recurrent
cycles introduced by Hochreiter (Hochreiter and
Schmidhuber 1997) as long short-term memory
(LSTM) showing huge potential for predicting
diagnostics from several input sources (Lipton et al.
2015). First deep feature networks were introduced
with Haar Cascades (Viola and Jones 2011), thereby
combining and boosting a large number of weak
convolution features at varying scale. A specific CNN
architecture perfectly applicable for medical image
segmentation in 2D and 3D is the U-Net architecture
(Ronneberg et al. 2015) (Cicek et al. 2016).
In the field of user-centric segmentation
approaches, conventional Region Growing, LiveWire
Segmentation (Mortensen and Barrett 1995) and
Graph cut (GC) (Boykov et al. 1998) are of high
relevance utilizing input image intensities or edges.
Graph cut refers to application of min-cut/max-flow
algorithms from the domain of combinatorial
optimization, generally utilizing Gaussian mixture
models (GMM) as fitness function. Graph cut is
perfectly applicable to user-guided video processing
at low demand for interaction and high accuracy.
With the GMM iteratively improved along the border
areas, denoted as Grab cut (Rother et al. 2004), the
results achievable by conventional Graph cuts are
further improved.
Combination of high-quality DL segmentation
with applications for user-guided post-processing is a
topic of ongoing research. In the work of (Sakinis et
al. 2019), the DL model is trained together with
reference user markers roughly indicating the target
shape. Thus, after training, these markers are placed
and adapted to control the contour in incorrect areas
in an iterative optimization process. Thereby, the DL
model has learned to obey the user markers. While
this is a very intuitive and adequate solution, the
application to arbitrary DL models is not possible as
the image data always has to be trained together with
reference user adaptions. A similar approach for real-
world RGB images is presented in the work of Xu et
al. (Xu et al. 2016), where Euclidean distance maps
calculated from user-clicks are provided as channel
for a fully convolutional network (FCN) and graph
cut is used to refine the probability segmentation
resulting from the FCN.
In the domain of GC, Boykov demonstrated the
benefit of arbitrary fitness functions, thus modelling
an energy function similar to snakes or geodesic
contours where edges are incorporated too (Boykov
and Funka-Lea 2006).
1.2 Graph Cut / Segmentation for
User-guided Post-processing of DL
To overcome the limitations of DL segmentation
models with respect to frequently needed post-
processing, the utilization of Graph cut and Graph
segmentation technology is evaluated in this paper.
We present a generic approach that is perfectly
applicable for post-processing all kinds of
segmentations. Instead of a GMM, the graph weights
are derived from the DL segmentation combined with
edge information from the original slice. To allow for
inevitable user intervention only, the foreground (FG)
and background (BG) seeds for the graph are derived
from the DL segmentation, too. Thus, user-interaction
after visual inspection is in the range between simple
confirmation of the initial segmentation result and
mild adaptions by altering the FG and BG graph.
2 MATERIAL
For training, validation and testing 131 abdominal CT
datasets of the liver from the Medical Segmentation
Decathlon database (MedDecathlon 2019) providing
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
236
reference segmentations are used. After scaling to iso
voxel spacing, 27,000 slices are split into a training
set (22,500) and a validation set (4,500) with strict
separation of the volumes. All slices are clipped to
size 308x372 with a 10 pixel outer margin around the
borders for reasons of data augmentation during DL
model training.
The input slice intensities a
i
are rescaled to 8bit in
range 0 to 255 with mean intensity value µ
liver
per
volume shifted to 127.0, transformed according to
scale factor s and truncated to [0;255], see Eqn. 1-2.
𝑠
115
3∙σ
(1)
T
𝑎
127
|
𝑎
µ
|
∙𝑠 𝑎
µ
127
|
𝑎
µ
|
∙𝑠 𝑎
µ
(2)
For DL segmentation, a U-net cascade approach
is utilized, thereby incorporating axial, sagittal and
coronal views for improved robustness (Zwettler et
al. 2020), see Fig.1. The reconstructed axial
segmentations from S
axial
, S
sagittal
and S
coronal
input are
thereby slightly varying and combined with another
U-net expecting these three input channels per slice
leading to robust segmentation S
comb
. These DL
segmentations utilized as testing data for this research
work are of good quality with DSC=97.5 and JI=95.2
for S
comb
. The single slice results are e.g. DSC=96.2
and JI=92.6 for S
axial
. In the work of Zwettler et al.
(Zwettler et al. 2020) another improvement
incorporating spatio-temporal aspects between
neighbouring slices was presented increasing to
DSC=98.9 and JI=97.9 overall. This improvement is
not applied for this paper to allow the evaluation of
the GC and GS potential for correcting DL models in
an unbiased and objective manner.
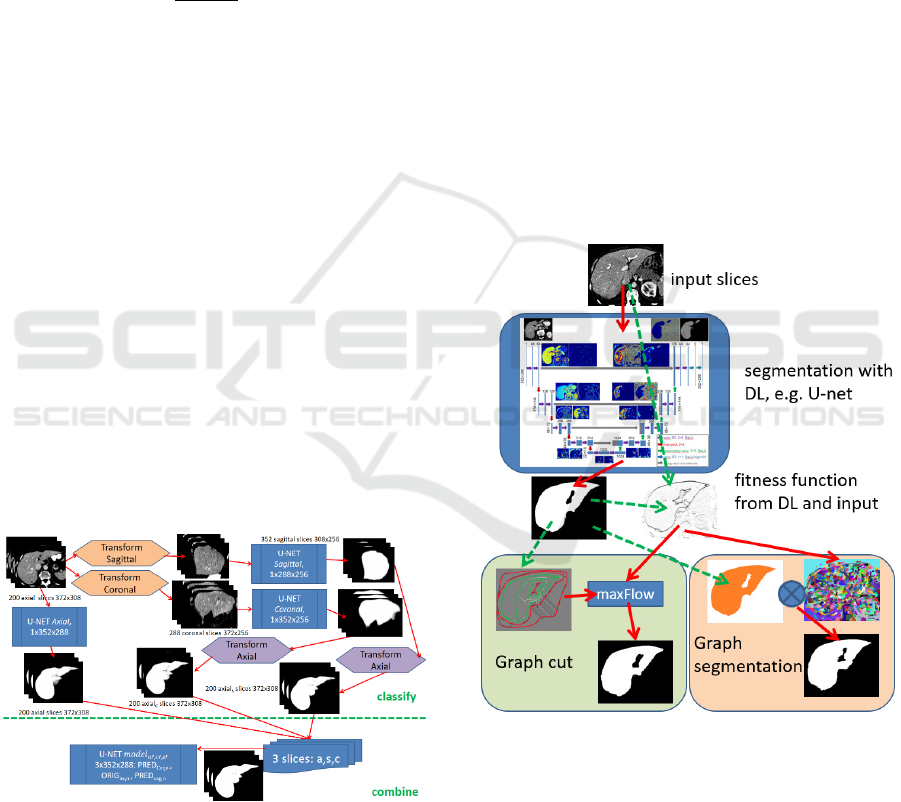
Figure 1: The slice-wise segmentations are performed in
axial, sagittal and coronal view utilizing specific U-nets.
Another U-net then combines the three slices as input for
processing the final segmentation result.
To perform a GC study, two test sets with each
n=30 slices randomly selected from the validation set
are utilized. The test sets refer thereby to intervention
with and without skeleton support. Within the 30
slices, the initial segmentation comes from the axial
view only (10), from combined U-net model (10) and
axial with manually applied errors (10), i.e. left out
parts, closed/opened vessels or attached artefacts. A
group of three test persons, all experts in medical
image segmentation, evaluates these 60 slices.
To test the result propagation in case of user post-
processed DL results with Graph cut/segmentation,
the m=10 volumes from the Medical Segmentation
Decathlon database are manipulated within the 3D
volume in areas of topographic changes of the liver
parenchyma in axial view. This way, the propagation
of corrected results is evaluated on the slice stack.
3 METHODOLOGY
To allow for seamless post-processing of DL
segmentation results utilizing GC or GS, a specific
fitness function is required as input. Thereby, the
Figure 2: Process Overview. Based on DL segmentation
results and original image (gradients), a fitness function is
calculated. Graph cut is then performed with FG and BG
seeds (red and green) from the DL segmentation and the
fitness function utilizing maxFlow. For Graph
segmentation, the fitness function is used for pre-
fragmentation. The pre-fragmented regions are selected
according to at least 0.5 overlap-ratio compared with the
DL segmentation. Both GC and GS allow for expert user
adaption by either altering the FG and BG seeds or
selecting/unselecting the GS regions.
Generic User-guided Interaction Paradigm for Precise Post-slice-wise Processing of Tomographic Deep Learning Segmentations Utilizing
Graph Cut and Graph Segmentation
237

fitness function incorporates the DL results as seeds
to conserve the high accuracy at the provided
flexibility of expert user-centered post-processing.
The process overview is shown in Fig. 2 while the
utilized fitness functions are illustrated in Fig. 3.
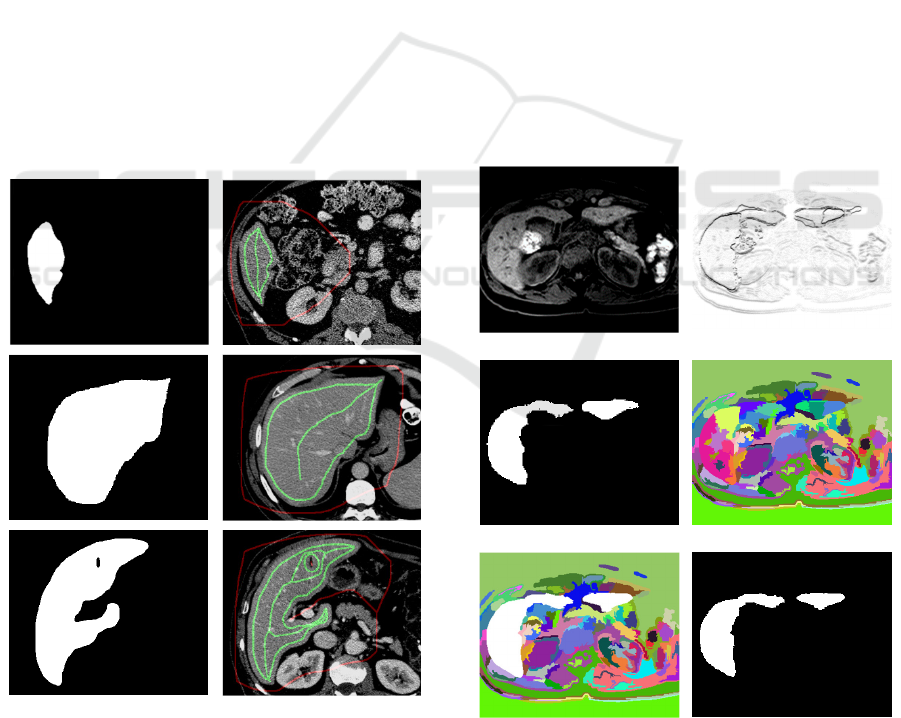
Figure 3: Per column illustration of horizontal results
ORIG, EXP, S1 and S4 for the datasets #506, #13789 and
#11623 as basis for fitness-function.
For each slice i, the original image ORIG
i
, the
expected intensity profile EXP
i
, and the
segmentations Sax
i
, Ssag
i
, Scor
i
and Scomb
i
(axial,
sagittal, coronal and combined) are incorporated in
the fitness function:
ORIG
i
: horizontal (H) and vertical (V) edges of
the original intensity profile after shift to 𝜇
127
window centre as ORIG
Hi
and ORIG
Vi
respectively,
cf. Eqn. 1.
EXP
i
: H and V edges of the original image
damped or amplified by a difference image from the
expected intensity level processed by a median filter
𝑟1 followed by Gaussian smoothing (𝑟5, 𝜎
2.5), referred to as EXP
Hi
and EXP
Vi
respectively.
S1
i
and S4
i
: H and V edges from the binary
segmentation results from axial, sagittal, coronal and
combined with 1 and 4 hits per voxel respectively as
S1
Hi
, S1
Vi
, S4
Hi
and S4
Vi
. The 2 and 3 hit cases are
omitted due to expected high correlation and thus low
entropy. Thus, either a pixel is an element of all
segmentations or only of one to handle the optional
segmentation regions S1
i
.
Conservation of the gradient magnitude is of high
relevance for calculating the cumulated fitness
function. Thus, for the combination of ORIG
i
, EXP
i
,
S1
i
and S4
i
, a max-operation is preferred over
building the mean. To combine the four edge images
utilizing a max function
𝐹
max
𝑠
𝑂𝑅𝐼𝐺
,𝑤
,𝑠
𝐸𝑋𝑃
,𝑤
,
𝑠
𝑆1
,𝑤
,𝑠
𝑆4
,𝑤
(3)
with function s() for scaling to [0; 𝑤
], an adequate
set of weights 𝑤
is required, thereby conserving the
segmentation outcome of the DL model and still
allowing adaption with respect to original image
intensities. These weights need to be calculated for
each segmentation domain, e.g. liver parenchyma
from CT modality, only once. The weights are
thereby optimized utilizing Evolution Strategy (ES)
with recombination (μ/ρ+, λ) with epochs=100,
batchSize=8, populationSize=8, children λ=32,
mutationChance=0.4, mutationRate=0.25 dropping
by around 4% each epoch. The fitness function is
calculated for vertical and horizontal orientation as
F
Hi
and F
Vi
, respectively.
The fitness landscape is considered very flat and
ambiguous as only the proportion of the weights is of
relevance. As max-flow execution takes 400ms per
slice, a higher number of epochs or larger batch sizes
are not practical. Instead, iterative refinement using
the ES is applicable.
3.1 Graph Cut Method
To facilitate little need for user interaction, the FG
and BG markers for Graph cut are derived from the
DL segmentation mask Scomb
i
for slice i as
initialization. The FG and BG markers thereby
comprise a skeleton with minimal distance
minDist=5 from the FG/BG borders together with
inner region boundaries at a distance of
borderDist=10, see Fig. 4. A topological cut of the
skeleton graph when demanding minDist=5 is
omitted which is of high relevance in narrow sections,
i.e. the minimum distance is only enforced for leaf-
sections of the skeleton graph.
In case of inaccuracies, the user alters the FG and
BG markers suggested by the algorithm, i.e. by
removing/adding seeds for both, the BG and the FG.
With the FG and BG seed markers provided, the
Graph cut is performed on fitness image F
i
leading to
graph-cut post-processed image GC
i
.
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
238
3.2 Graph Segmentation Method
Based on the same fitness function F
i
as used for the
Graph cut, a graph segmentation algorithm is
applicable leading to a watershed-like fragmentation
of the input image denoted as GS
i
with fragmented
regions 𝑅
⊆𝐹
. To transfer GS
i
with j region labels
back to a binary segmentation representation, each
region R
j
is either assigned a FG or BG label,
according to the largest intersection set with DL result
Scomb
i
leading to result segmentation GS’
i
, see
Equation 4 with pixel 𝑥,𝑦 ∈ 𝑅
.
𝐺𝐶
𝑥,𝑦
𝐹𝐺 𝑅
∩𝑆
𝐹𝐺 𝑅
∩𝑆
𝐵𝐺
𝐵𝐺 𝑒𝑙𝑠𝑒
(4)
Thus, the binary label assigned to the pixel
coordinates of each region R
j
result from majority
voting of pixel-wise AND operation with the DL
segmentation Scomb
i
, see Fig. 5.
Besides running this process in a fully automated
way, i.e. utilizing the DL outcome for selecting the
FG regions from Graph segmentation, the user can
correct results too by selecting/unselecting the
fragmented regions.
Figure 4: From the deep learning result Scomb
i
(left
column), the FG markers (green) are derived as skeleton
besides the inner contour with distance borderDist=10 to
the binary contour borders. The outside marker (red) is
calculated as skeleton from background in Scomb
i
.
3.3 Slice-wise Propagation of
Post-processed Results
In case of slice-wise processing a tomographic
volume in axial direction, due to the high resolution
of the imaging modalities the pixel-wise differences
of two neighbouring slices slice
i
and slice
i+1
is
expected to be marginal. Furthermore, the
automatically derived FG and BG markers for Graph
cut show a safety margin to the border areas. Thus,
the manually corrected results after user-guided
Graph cut post-processing of slice slice
i
denoted as
GC
i
can be applied as basis for FG and BG markers
of the subsequent slice slice
i+1
. Consequently, FG and
BG markers are derived from GC
i
instead of Scomb
i+1
for slice slice
i+1
.
The same slice-wise propagation of corrected
results is applicable for the Graph segmentation
approach elucidated in section 3.2, too. Thereby, the
corrected / post-processed GS’
i
replaces Scomb
i+1
for
slice slice
i+1
by combining with 𝐺𝑆
𝑖1
𝐺𝑆
𝑖
′
∩
𝐺𝑆
𝑖1
instead. The fragmented regions after Graph
segmentation yield sharp edges in the border sections
and thus expected to be tolerant by applying the
corrected previous slice for logic combination.
(a)
(b)
(c) (d)
(e) (f)
Figure 5: Based on input slice i (a) the fitness function F
i
(b) is used for Graph segmentation GS
i
(d). With DL
segmentation result Scomb
i
(c) the regions are combined as
𝑆𝑐𝑜𝑚𝑏
∩ 𝐺𝑆
(e) leading to binary result GS’
i
(f).
Generic User-guided Interaction Paradigm for Precise Post-slice-wise Processing of Tomographic Deep Learning Segmentations Utilizing
Graph Cut and Graph Segmentation
239
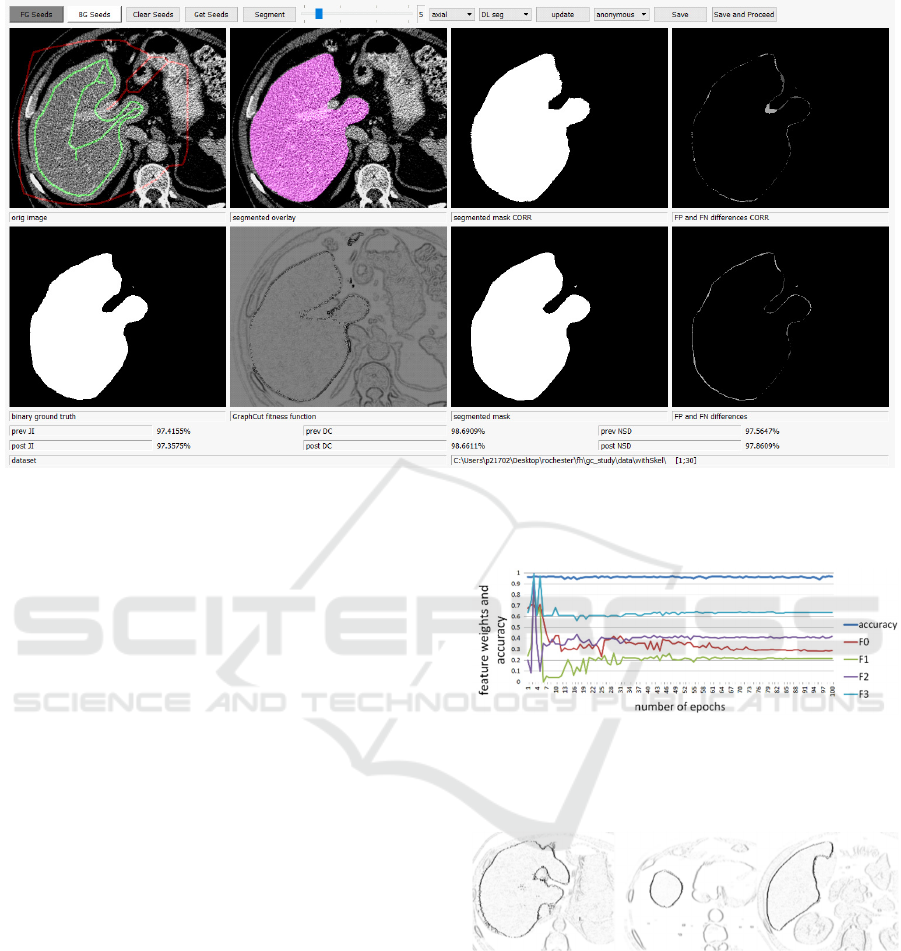
Figure 6: GC GUI in non-study mode showing full information. After adaptions by the user, the JI is increased from 0.974 to
0.977 compared to the axial DL model.
4 IMPLEMENTATION
A prototype for GC post-processing is implemented
with Python using PyQt5 for the GUI and library
maxflow for the GC implementation as proposed in
(Zabriskie 2020) for RGB images.
Besides the input slice, the GC fitness, the GC
result and a FP/FN view of the adapted result, also the
results from the DL model together with a FP/FN
view of the initial results as well as the ground truth
are presented. Furthermore, the quality metrics JI, DC
and NSD are evaluated, see Fig. 6.
For the study, only input slice and GC results are
presented and no quality metrics reported to do not
give the test persons a hint for the correct and
expected outcome regarding the ground truth.
5 RESULTS
Evolution Strategy optimizes the weights for ORIG
(w
0
), EXP (w
1
), S1 (w
2
) and S4 (w
3
) with w
0
=0.287,
w
1
=0.217, w
2
0.419, w
3
0.641, cf. Fig. 7.
The result slices with maximum-function applied
and scaled to the target weights are shown in Fig. 8.
Thereby, the fitness function combines an edge
representation of the binary segmentation as well as
input image information.
Figure 7: Parameter optimization of weights w
0-
w
3
for the
first 100 epochs with achievable accuracy close to 1.0.
Despite the absolute weights, only the relative proportion is
of relevance with stability in rank after around 60 epochs.
Figure 8: Horizontal edges of the combined fitness function
for slices #506, #13789 and #11623 respectively.
5.1 Graph Cut Post-processing
5.1.1 Automated GC Test Runs
With the FG and BG derived from the initial DL
segmentation, cf. Fig. 9, almost the same accuracy is
reached in a fully automated way, see Tab. 1
processing all n=4859 slices. Due to the Graph cut
processing, the JI marginally drops by 1.3% on
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
240
average (+537=55-4267) yet allowing the user to
correct obviously incorrect areas on demand. If the
FG and BG marker skeletons are derived from ground
truth reference segmentations, the DL accuracy is
even outperformed by the GC based post-processing
by 0.44% JI and improving 2846 of the slices
(+2846=1-2012), indicating the GC potential in post-
processing.
Table 1: Achievable Jaccard (JI), Dice Coefficient (DC)
and Normalized Surface Distance (NSD) tested on n=4859
slices for original DL models, GC with skeleton from DL
and GC with skeleton seeds from the ground truth (GT).
Thereby, GC is applied in a fully automated way.
metric DL GC, DL seeds GC, GT seeds
JI .9488 .9358 .9532
DC .9737 .9668 .9760
NSD .9507 .9488 .9602
Figure 9: The FG (green) and BG (red) skeletons and inner
surface borders are well suited for performing GC
segmentation almost at the same accuracy as the input DL
model results.
5.1.2 Manual Post-processing
With support of the skeleton for the three test persons,
processing of the 30 slices took on average 35.3sec
per slice and 51.3sec for the 30 slices of the dataset
without skeleton support. With the preset skeleton to
adapt, the average amount of FG and BG seeds per
slice is 1915.8 achieving an average accuracy of
JI=.9573 and DC=.9782 and NSD=.9589 compared
to the axial DL model with JI=.9548, DC=9769 and
NSD=9577 at 1772.6 seeds per slice on average, see
Fig. 10.a. Thus, due to manual post-processing, the
average accuracy is increased. On average 16 out of
30 slices outperform the DL model, mainly the ones
with small applied errors. For slices with already a
high quality result from the DL model, results rather
get worse as expected due to GC discretization.
Without skeleton support, the test persons place
1099.7 seed pixels on average achieving an accuracy
of JI=.9265, DC=.9618 and NSD=.9206 compared to
JI=.9251, DC=.9611 and NSD=.9192 at 1873.6 seeds
per slice on average, see Fig. 10.b. Generally, results
are quite invariant w.r.t. placed FG and BG markers.
Thus, results are very robust and “drawing” close
to the borders is not necessitated, see Fig. 11.
(a)
(
b
)
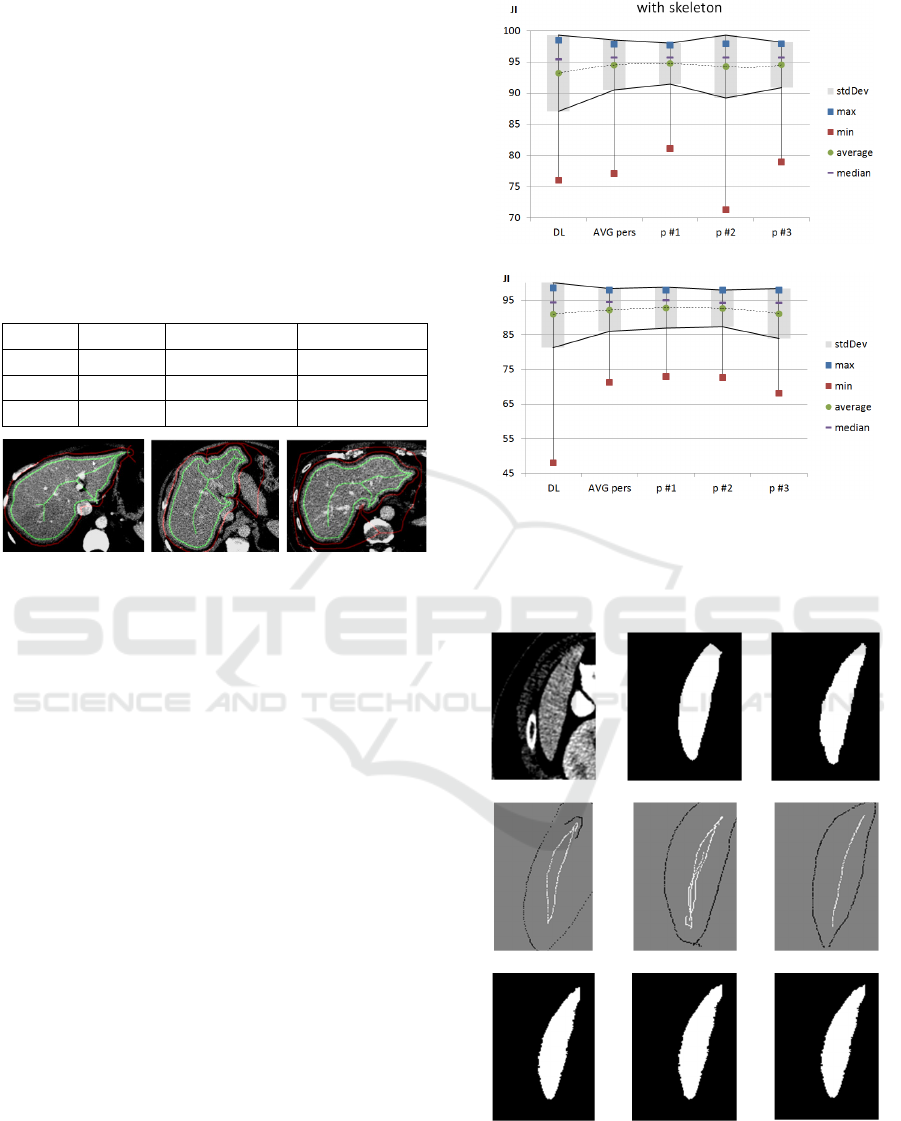
Figure 10: JI for GC results with (a) and without skeleton
support (b). The accuracy of the DL model is conserved,
while the standard deviation and min/max range is
generally reduced.
(a) (b) (c)
(d)
(e) (f)
(g) (h) (i)
Figure 11: Slice 28 (a) without skeleton support and
expected ground truth (c) with suboptimal DL result
JI=.877 (b) can be improved by all test persons (g-i) in
range [.911;.920]. The axial error of missing upper part can
be corrected with different skeleton interpretations (d-f).
Generic User-guided Interaction Paradigm for Precise Post-slice-wise Processing of Tomographic Deep Learning Segmentations Utilizing
Graph Cut and Graph Segmentation
241
With GC post-processing the obvious errors are
corrected as indicated by the smaller JI standard
deviation calculated for the slices with σ
JI,users
=.0400
compared to σ
JI,DL
=.0614 for the DL model all with
skeleton support. Without the skeleton support,
similar results are noted, namely σ
JI,users
=.0613
compared to σ
JI,DL
=.0964.
5.2 Graph Segmentation
Post-processing
Running Graph segmentation on DL results of the
MedDecathlon test datasets in an automated way, the
trade-off between the deep learning results and the
Graph segmentation results is low. While for DL,
accuracy of JI=94.88% is reported, the Graph
segmentation leads to JI=94.42%, which is a marginal
drop by 0.46%, see Table 2.
Table 2: Achievable Jaccard (JI), Dice Coefficient (DC)
and Normalized Surface Distance (NSD) tested on n=4857
slices for original DL models, GS with auto-selection from
DL and GS with selection from the ground truth (GT).
metric DL GS auto-run
GS, using
GT
JI .9488 .9442 .9604
DC .9737 .9713 .9798
NSD .9507 .9478 .9702
If the ground truth (GT) is used for assigning the
fragmented regions the BG and FG label respectively,
then the accuracy can theoretically be gained to
JI=0.9604 showing high potential in post-processing.
The n=4,857 test slices are thereby fragmented
into 2,829,228 regions utilizing a minimum region
size 𝑟𝑒𝑔
40 and a constant border threshold
𝐾50. Most of these regions are perfectly
overlapping with the DL pre-segmentation, namely
27.86% for the FG and 64.84% for the BG. These
perfect matches are thus classified at very high
confidence. Only the remaining regions close to the
border areas that are partly overlapping with both, BG
and FG areas of the DL segmentation, need to be
assigned according to majority voting. From these
regions, 1.96% are probably FG, i.e. FG ratio >= 0.5
and 5.33% probably BG, i.e. BG ratio < 0.5.
Nevertheless, even these regions show a clear trend
for either FG or BG, which becomes obvious from the
average DL classification values per region. For the
probably FG regions, this average 𝜇
230.18
is far above the equilibrium at 127.5. Similarly, for
the probably BG regions, 𝜇
28.52 indicates
high confidence. Thus, even for the small amount of
regions fluctuating between FG and BG, they show a
clear trend for either BG or FG.
5.3 Slice-wise Propagation of
Post-processed Results
To test the propagation of both, GC and GS post-
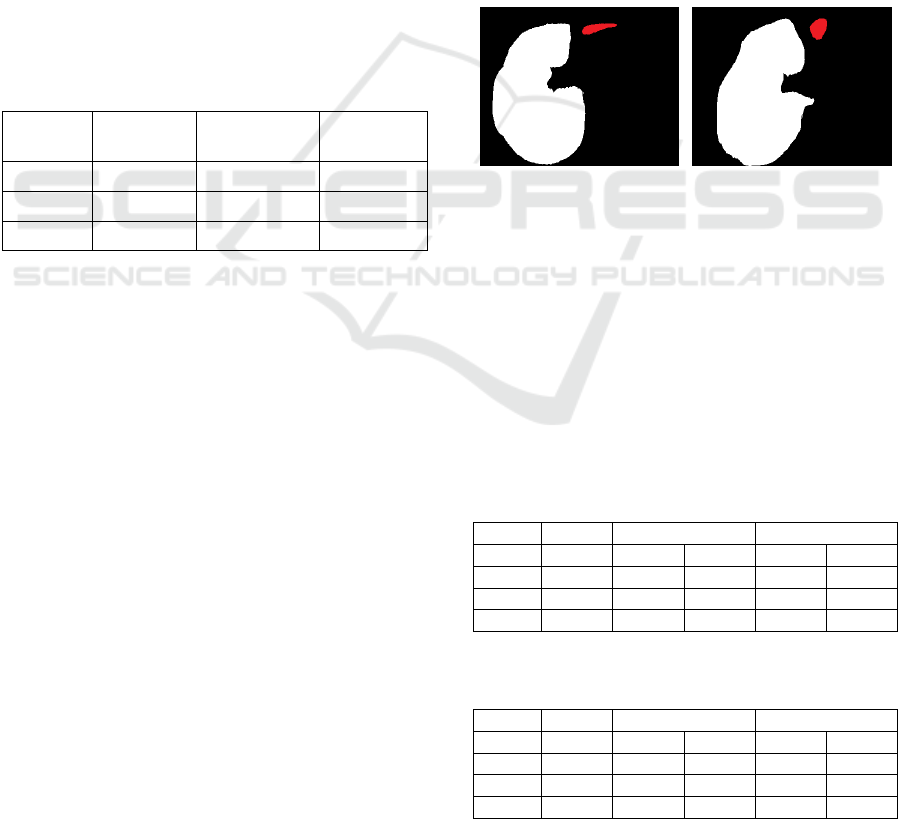
processing, four datasets are prepared, namely:
case 0: slices 22504-22516 with correct axial
case 1: slices 22504-22516, all views invalid
case 2: slices 25004-25012 with correct axial
case 3: slices 25004-25012, all views invalid
For these test cases, the sagittal, coronal and
combined DL results are manipulated in the selected
slice range, cutting a part of the liver parenchyma, see
Fig. 12. By adding test cases with and without invalid
axial input the 1 or 4 hit count of the fitness function
is tested.
Figure 12: For the test cases 0/1 (left, combined slice
#22505) and 2/3 (right, combined slice #25005) the caudal
part of a liver lobe is removed from the DL results, shown
as red areas in the images.
As shown in Table 3 and Table 4, for all test
datasets the automated propagation of the corrected
first slice leads to an improvement of the subsequent
slices too. Thus, the missing part in the DL
segmentation, i.e. parts removed for testing purposes,
are precisely reconstructed, see Fig. 13 for slice
#2512.
Table 3: Slice-wise propagation of the corrected first slice
for test cases 0 and 1 in slice-range 22504-22516.
case 0 case 1
metric DLer
r
GC GS GC GS
JI 0.9176 0.9403 0.9584 0.9385 0.9534
DC 0.9570 0.9692 0.9788 0.9683 0.9762
NSD 0.9019 0.9424 0.9632 0.9405 0.9575
Table 4: Slice-wise propagation of the corrected first slice
for test cases 2 and 3 in slice-range 25004-25012.
case 2 case 3
metric DLer
r
GC GS GC GS
JI 0.9073 0.9246 0.9321 0.9216 0.9262
DC 0.9514 0.9608 0.9648 0.9592 0.9617
NSD 0.8850 0.9306 0.9292 0.9275 0.9190
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
242
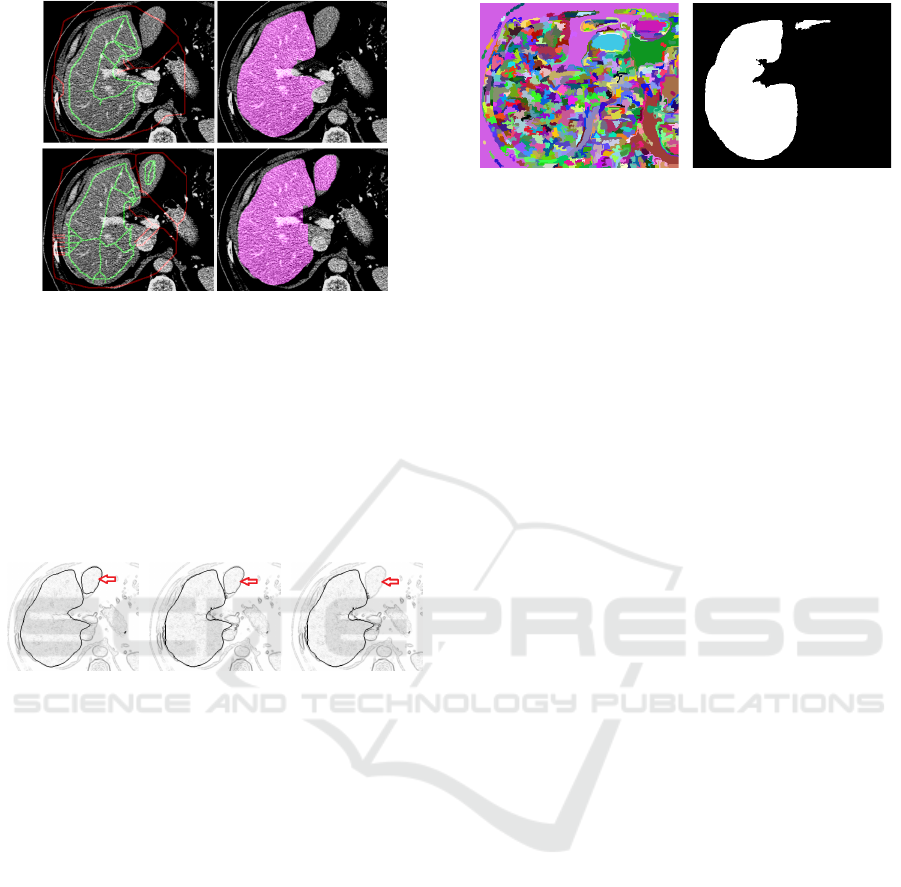
Figure 13: Results prior and post propagating the
corrections from slice to slice. By adding the missing part
thanks to FG/BG marker from previous slice, the JI is
increased from JI
prev
=0.8624 to JI
post
=0.8971.
Comparing test case 0 to 1 and test case 2 to 3 it
becomes obvious, that results drop a bit.
Consequently, the fitness function decreases in
quality, if not even the axial direction is correct and
all segmentation is solely performed on input image
edges, see Fig. 14.
Figure 14: With correct DL results (left), the fitness
function shows sharp edges in the test area, while for one
axial hit (middle) and zero hits (right) the missing liver part
is vanishing, marked with red arrows.
The slice-wise automated propagation of user
corrected slices is applicable for GS strategy too as
compared in Tables 3-4, thereby even outperforming
the Graph cut approach. For case 0 the JI
prev
=0.9176
is increased to JI
postGS
=0.9584 while JI
postGC
=0.9403 is
around 1.8% below.
Analysing the FG/BG ratio it becomes obvious,
that most regions still show 100% congruency with
either FG or BG and for the in-between regions,
𝜇
230.75 and 𝜇
24.24
recpectively indicate, that at high resolution of the
tomographic volume in z-direction, the corrected
results of the previous slice can be applied in a very
robust way. With GS propagation, the one and zero
hit cases (0/2 and 1/3) perform at very comparable
accuracy, see Fig. 15 for slice #25012 in test case 1
with the object borders strong enough for GS
fragmentation even in case the DL models lack
correct results.
Figure 15: For the test case with zero hit count, shows still
borders strong enough to facilitate result-propagation with
GS for significantly improved accuracy.
6 DISCUSSION
Preparing results of binary segmentation together
with edge information of the original slices allows the
utilization of GC or GS as generic tool for user-
guided post-processing. In case of significant
misclassification, results from DL models or other
segmentation strategies can be corrected in a post-
processing step by experienced analysts. Thus, one
can benefit from the high classification accuracy of
well-trained DL models and yet overrule the black
box outcome in case of obvious discrepancies.
The trade-off in quality of the GC method with
seeds derived from the DL results is marginal due to
fitness function weights optimized by ES. Utilizing
the same fitness function, the trade-off for GS is to be
considered even lower.
Propagation of corrected slices as pattern mask to
the subsequent slices for automated post-processing
allows for significant reduction in user interaction,
yet featuring high quality result. Thereby, GS
outperforms GC w.r.t. both, accuracy and robustness.
This is the fundament for innovation in user-guided
image processing, thereby incorporating the accuracy
and precision of well-trained DL models together
with adequate interaction paradigms for user-guided
post-processing in rare cases of error.
Although the trade-off in accuracy of GC post-
processing is marginal compared to particular DL
models, there is still potential for further
improvement. Instead of constructing the pixel graph
with N
4
adjacency based on vertical and horizontal
edges derived from the fitness function, one can
extend to N
8
additionally incorporating diagonal
edges to overcome the GC tendency of straight edges
and discrepancies in narrow region areas. The same
improvement is applicable to GS strategy.
With respect to the user interaction, instead of
mouse-based FG and BG pixel-area masking for GC,
the skeleton graph could be manipulated too, i.e. sub-
Generic User-guided Interaction Paradigm for Precise Post-slice-wise Processing of Tomographic Deep Learning Segmentations Utilizing
Graph Cut and Graph Segmentation
243

tree parts removed by selection, thus further
improving efficiency.
7 CONCLUSION AND OUTLOOK
In diagnostic domains with initial lack of training
data, DL models cannot be trained at highest accuracy
from the very beginning. Yet, both the GC and the GS
post-processing allow to post-process routine datasets
and thus allow for steady improvement and adaption
of the DL models if iteratively trained on the enlarged
reference data. The chicken-egg problem of an
insufficient amount of training data in the DL domain
tackling new diagnostic domains is conquered by
applying the proposed strategy.
Future test runs will focus on different imaging
modalities and anatomies as well as on low-data DL
training tasks with incrementally enriching the
database with GC or GS post-processed reference
segmentations.
To conclude, the proposed method shows a very
high potential for application in medical diagnostics,
meeting the needs of a real hospital environment, i.e.
large number of patients and highly accurate
segmentation. The generic approach does not require
adaptions on the network architecture or training
process and thus is applicable to both, arbitrary deep
learning models and arbitrary diagnostic domains.
ACKNOWLEDGEMENTS
Many thanks to the BIR (biomedical imaging
resource) research team at Mayo Clinic, Rochester,
MN, USA for valuable discussion, great support and
the provided GPU infrastructure.
REFERENCES
Boykov, Y., Veksler, O., Zabih, R., 1998. Fast
Approximate Energy Minimization via Graph Cuts. In
IEEE Transactions on PAMI, vol. 23(11), pp. 1222-
1239.
Boykov, Y., Funka-Lea, G., 2006. Graph Cuts and Efficient
N-D Image Segmentation. In International Journal of
Computer Vision, vol.70(2), pp.109-131.
Cicek, Ö., Abdulkadir, A., Lienkamp, S.S., Brox, T.,
Ronneberg, O., 2016. 3D U-Net: Learning Dense
Volumetric Segmentation from Sparse Annotation. In
Proc. of MICCAI 2016.
Cootes, T.F., Taylor, C.J., Cooper, H.D., Gramah, J., 1992.
Training Models of Shape from Sets of Examples. In
Proceedings of the British Machine Vision Conference,
pp. 9-18, Leeds UK.
Cootes, T. F., Edwards, G.J., Taylor, C.J., 1998. Active
Appearance Models. In Proceedings of the 5th
European Conference on Computer Vision, pp.484-
498.
Hochreiter, S., Schmidhuber, J., 1997. Long Short-Term
Memory. In J. Neural Computation 9(8), pp.1735-1780
Lipton, Z.C., Lale, D.C., Elkan, C., Wetzel, R., 2015.
Learning to Diagnose with LSTM Recurrent Neural
Networks. In CoRR, abs/1511.03677.
MedDecathlon, 2019. MSD-Ranking Scheme,
http://medicaldecathlon.com/files/MSD-Ranking-
scheme.pdf, last accessed 2019-11-26
Mortensen, E.N., Barrett, W.A., 1995. Intelligent scissors
for image composition. In Proceedings of the
SIGGRAPH '95, pp.191-198.
Ronneberg, O., Fischer, P., Brox, T., 2015. U-Net:
Convolutional Networks for Biomedical Image
Segmentation. In Proc. of the International Conf. on
Medical Image Computing and Computer Assisted
Intervention (MICCAI) 2015, pp. 234— 241.
Rother, C., Kolmogorov, V., Blake, A., 2004. “GrabCut":
interactive foreground extraction using iterated graph
cuts. In Proc. of the ACM SIGGRAPH '04, pp. 309-
314.
Sakinis, T., Milletari, F., Roth, H., Korfiatis, P., Kostandy,
P., Philbrick, K., Akkus, Z., Xu, Z., Xu, D., Erickson,
B.J., 2019. Interactive segmentation of medical images
through fully convolutional neural networks. In Proc. of
the International Conf. on Medical Image Computing
and Computer Assisted Intervention (MICCAI) 2019
Strakos, P., Janos, M., Karasek, T., Vavra, P., Jonszta, T.,
2015. Review of the Software Used for 3D Volumetric
Reconstruction of the Liver. In: Int. Journal of
Computer and Information Engineering vol. 9(2).
Van Biesen, W., Sieben, G., Lameire, N., Vanholder, R.,
1998. Application of Kohonen neural networks for the
nonmorphological distinction between glomerular and
tubular renal disease. In Nephrol Dial Transplant vol.
13(1), pp. 59-66.
Viola, P., Jones, M., 2011. Rapid Object Detection using a
Boosted Cascade of Simple Features. In Conf. on
Computer Vision and Pattern Recognition.
Xu, N., Price, B., Cohen, S., Yang, J., Huang, T., 2016.
Deep Interactive Object Selection. In CoRR,
abs/1603.04042
Zabriskie, N., 2020. Graph cut image segmentation with
custom GUI. In https://github.com/NathanZabriskie/,
last visited 2020-1-2
Zhang, J., Wang, X.W., 2011.
The application of feed
forward neural network for the X ray image fusion. In
Journal of Physics: Conference Series 312.
Zwettler, G.A., Backfrieder, W., Holmes, D.R., 2020. Pre-
and Post-processing Strategies for Generic Slice-wise
Segmentation of Tomographic 3D datasets Utilizing U-
Net Deep Learning Models Trained for Specific
Diagnostic Domains. In Proc. of VISAPP 2020, Valetta,
Malta.
VISAPP 2021 - 16th International Conference on Computer Vision Theory and Applications
244
