
Robust Emergency Medical System Design as a Multi-objective Goal
Programming Problem
Marek Kvet
Faculty of Management Science and Informatics, University of Žilina, Univerzitná 8215/1, 010 26 Žilina, Slovakia
Keywords: Location Problems, Emergency Medical Service, Robustness, Multi-objective Problem, Radial Formulation.
Abstract: The main goal of this paper is to introduce and compare three different mathematical modelling approaches
to robust emergency medical service system design. The idea of system robustness follows from the necessity
of making the system resistant to various detrimental events, which may unexpectedly occur in the associated
transportation network and thus negatively affect service. Such viewpoint is important mainly in different
kinds of public service systems including rescue services, in which time necessary for service delivery plays
a very important role. While the standard method of robust system designing takes into account only the worst
possible situation considering the set of detrimental scenarios, suggested modeling approaches compute a
separate objective function value for each scenario and then a special constraint is added to the original
mathematical model. This way, an epsilon-constraint principle to the problem solution is applied. In this paper,
numerical experiments to study the performance characteristics of suggested solving methods accompany the
theoretical explanation of all presented models.
1 INTRODUCTION
This research paper deals with a special class of
discrete network location problems, which are solved
under uncertainty following from randomly and often
unexpectedly occurring failures in the transportation
network (Correia and Saldanha da Gama, 2015, Pan
et al., 2014, Scaparra and Church, 2015). The main
focus is on the application of suggested optimization
approaches to the emergency medical system (EMS)
designing. The rescue system performance efficiency
is directly influenced by locations of service centers,
which send the emergency vehicles to satisfy the
requests raised at system users’ locations. Obviously,
the number of service providing centers is limited due
to economic and technological restrictions. It is not
possible to locate a separate service center to each
served geographical area or to each system users’
community.
The most commonly used objective function in
the mathematical models for EMS designing takes
into account the service accessibility of an average
user. This way, the emergency service system design
problem can be described as the weighted p-median
problem broadly studied by many researchers (Avella
et al., 2007, Current et al., 2002, Ingolfsson et al.,
2008, Jánošíková, 2007, Snyder and Daskin, 2005)
mainly from the points of developing effective exact
and approximate solving techniques. It is worth
mentioning, for example, the radial formulation of the
problem, successfulness of which is based on the fact
that there is only finite set of radii, which need to be
taken into account (Elloumi et al., 2004, García et al.,
2011, Janáček, 2008). Such model reformulation
makes the problem easier, smaller and thus better
solvable.
Simultaneously, several approximate approaches
have been developed to get a good solution of the
problem in acceptably short time (Doerner et al. 2005,
Gendreau and Potvin, 2010).
It is often assumed that service center has enough
capacity to serve all assigned users and thus, each
system user can be serviced from the nearest located
service center. Otherwise, the concept of so-called
generalized disutility can be applied to incorporate
stochastic behavior of real system into the
mathematical model (Kvet and Janáček, 2018). This
model extension enables to consider more service
centers, which can provide the associated service to
the same user. In the research reported in this paper,
only the nearest located service centers for each
system user are considered.
Kvet, M.
Robust Emergency Medical System Design as a Multi-objective Goal Programming Problem.
DOI: 10.5220/0010179600210028
In Proceedings of the 10th International Conference on Operations Research and Enterprise Systems (ICORES 2021), pages 21-28
ISBN: 978-989-758-485-5
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
21

When the emergency service system is designed,
the designer must take into account that the transfer
time from a service center to the affected user might
be negatively impacted by various random events
caused by weather or traffic. Furthermore, possible
failure of a part of critical infrastructure should be
taken into account because of congestion, disruptions
or blockages. In other words, the system resistance to
such critical events should be included into the
decision-making process.
Most of available approaches to increasing the
system robustness (Correia and Saldanha da Gama,
2015, Kvet and Janáček, 2017b, Pan et al., 2014,
Scaparra and Church, 2015) are based on making the
system resistant to possible failure scenarios, which
can appear in the associated transportation network as
a consequence of random failures due to congestion,
disruptions or blockages. Thus, a finite set of failure
scenarios is considered and each individual scenario
is characterized by particular time distances between
the users’ locations and possible center locations.
The most commonly used objective function in
the above-mentioned weighted p-median problem
consists in minimizing the time accessibility of the
service for an average user, i.e. a min-sum objective
function is minimized subject to associated solution
feasibility constraints. On the other hand, the most
frequently used objective function of the robust
design focuses on minimizing the maximal objective
function of the individual instances corresponding
with particular scenarios. It means that the worst
possible impact of individual scenarios is minimized.
It follows that the original min-sum objective
function used in the weighted p-median problem is
replaced by the min-max criterion. The min-max
model uses the link-up constraints to limit the
individual scenario min-sum objectives by their upper
bound corresponding to the objective function of the
resulting min-max model. In addition, incorporating
the scenarios into the model causes the model soize to
increase proportionally to the cardinality of the
scenario set. Both the model structure and the
increase in model size represent a burden to the
computational process of most available IP-solvers.
Thus, complementary approximate approaches to the
robustness constitute a big challenge to operational
researchers and professionals in the field of Applied
Informatics (Janáček and Kvet, 2016, Janáček and
Kvet, 2017, Kvet and Janáček, 2017a, Kvet and
Janáček, 2017b).
This paper focuses on the main disadvantage of
the min-max approach to robust EMS design; only the
worst impact of individual scenarios is minimized.
The set of scenarios may contain a bad scenario with
very low probability of occurring, yet this scenario
may seriously affect the optimal robust system
design. This paper discusses three approaches to the
problem based on multi-objective optimization
(Antunes and Henriques, 2016). These techniques
consider each scenario to form a separate objective
function and they apply epsilon-constraint principle
to the problem solution.
The remainder of this paper is organized as
follows: Section 2 is devoted to the description of the
original min-max robust design of emergency
systems, in which all scenarios are taken into account.
Section 3 explains two coefficients for robustness
evaluation. The core of this contribution is reported in
Section 4, in which all suggested multi-objective
approaches are introduced and explained. The fifth
Section discusses numerical experiments and yields a
brief comparative analysis of the resulting designs.
The results and findings are summarized in Section 6.
2 STANDARD APPROACH TO
ROBUST EMS DESIGN
The standard approach to emergency medical service
system design usually leads to formulation of a min-
sum problem (Current et al., 2002, Ingolfsson et al.,
2008, Jánošíková, 2007), in which the average system
accessibility for users (average response time) is
minimized. The robust system design is formulated as
a min-max model bringing some difficulties into the
computational process (Kvet and Janáček, 2017b).
To formulate the mathematical model for robust
EMS design, we introduce the following notations..
Let symbol J denote the set of users’ locations and
let symbol I denote the set of possible service center
locations. Furthermore, let b
j
denote the number of
users sharing the location j. To solve the problem, p
locations from I must be chosen so that the maximal
scenario objective function value is to be minimized.
The objective function value of an individual scenario
is defined as a sum of users’ distances from the
location of the service center providing them with
service multiplied by b
j
. To incorporate system
robustness into the mathematical model, a set U of
possible failure scenarios is needed to be introduced.
This set contains also one specific scenario called
basic scenario, which represents standard conditions
in the associated transportation network. For the
purpose of conciseness, let U
0
denote the set of
scenarios without the basic one, i.e. U
0
= U – {basic
scenario}. The integer distance between locations i
and j under a specific scenario u∈U is denoted by d
iju
.
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
22

Even if the radial model is originally suggested for
integer distance or time values only, the used
principle enables us to adjust the model also for real
values without any big problems.
The decisions, which determine the structure of
the rescue service system, are modeled by decision
variables y
i
∈{0,1} modeling the decision on service
center location at the place i∈I by the value of 1 if a
service center is located at i and by the value of 0
otherwise. In the robust problem formulation, the
variable h denotes the upper bound of the objective
functions over the set U of scenarios. To formulate
the radial model, the integer range [0, v] of all
possible distances of the matrices {d
iju
} is partitioned
into zones according to (García et al., 2011, Janáček,
2008). The value of v is computed according to the
expression (1).
{
}
max : , , 1
iju
vdiIjJuU=∈∈∈− (1)
The radial formulation of the problem is based on
the idea of making a system of zones. The zone s
corresponds to the interval (s, s+1]. To complete the
radial model, auxiliary zero-one variables x
jus
for j∈J,
u∈U and s = 0 … v need to be introduced. The
variable x
jus
takes the value of 1, if the distance of the
user at j∈J under the scenario u∈U from the nearest
located center is greater than s and it takes the value
of 0 otherwise. Based on these assumptions, the
expression x
ju0
+ x
ju1
+ x
ju2
+ … + x
juv
constitutes the
distance d
ju*
from user location j to the nearest located
service center under scenario u∈U. Similarly to the
set covering problem, let us introduce a zero-one
constant a
iju
s
under scenario u∈U for each i∈I , j∈J,
s∈[0..v]. The constant a
iju
s
is equal to 1, if the
disutility d
iju
between the user location j and the
possible center location i is less than or equal to s,
otherwise a
iju
s
is equal to 0. Then the model of the
robust system design problem can be formulated as
follows.
M
inimize h
(2)
:1
,0,1 ,
s
jsu iju i
iI
Subject to x a y
f
or j J s , , v u U
∈
+≥
∈= ∈
(3)
i
iI
yp
∈
=
(4)
0
v
jjsu
jJ s
bx hforuU
∈=
≤∈
(5)
{0, 1}
i
y
for i I∈∈
(6)
{0, 1} , 0, 1 ,
jsu
x
for j J s , ,v u U∈∈=∈
( 7 )
0h ≥
(8)
The objective function (2) gives an upper bound
of all objective function values corresponding to the
scenarios. The constraints (3) ensure that the
variables
x
jus
are allowed to take the value of 0, if
there is at least one center located in radius
s from the
user location
j and constraint (4) limits the number of
located service centers by
p. The link-up constraints
(5) ensure that each perceived disutility (time or
distance) is less than or equal to the upper bound
h.
The obligatory constraints (6), (7) and (8) are
included to ensure the domain of the decision
variables
y
i
, x
jus
and h.
3 SERVICE SYSTEM
ROBUSTNESS EVALUATION
The main goal of robust service system design is to
make the system resistant to randomly occurring
failures on the associated transportation network. To
evaluate the gauges of robustness, we introduce the
following additional notations. As before, let
U
denote the set of all considered failure scenarios,
which contains also the
basic scenario. Let y denote
the vector of location variables
y
i
; i∈I. Let y
b
correspond to the basic system design, i.e. the
solution of a simple weighted
p-median problem, in
which only the
basic scenario is taken into account.
Let
f
b
(y) denote the associated objective function
value. Similarly, let
y
r
denote the solution of the
model (2)-(8), which brings the robust system design.
Finally, the objective function (2) will be denoted by
f
r
(y). The price of robustness (POR) expresses the
relative increment (additional cost) of the basic
scenario objective function, when
y
r
is applied instead
of the optimal solution
y
b
obtained for the basic
scenario. Its value is defined by (9).
() ()
()
100*
br bb
br
ff
POR
f
−
=
yy
y
(9)
Robust Emergency Medical System Design as a Multi-objective Goal Programming Problem
23

The price of robustness expresses the percentage
increase in cost in the basic scenario when the robust
system design is chosen, but it does not express what
we gain by applying the robust solution. Therefore,
we introduce also a coefficient called
gain of
robustness
(GOR) expressed by (10).
() ()
()
100*
rb rr
rr
ff
GOR
f
−
=
yy
y
(10)
This coefficient evaluates the profit following
from applying the robust solution instead of the
standard one in the worst case ignoring detrimental
scenarios.
4 MULTI-OBJECTIVE
APPROACHES
The main disadvantage of the standard approach to
robust service system design described by the model
(2)-(8) consists in minimizing only the worst possible
impact of detrimental scenarios on the resulting
system performance measured by average service
accessibility for system users (average response
time). It must be noted that the partial objective
functions corresponding to individual scenarios may
take different values and it is assumed that not only
the highest one should be considered. Therefore, three
different multi-objective-based approaches will be
introduced in the following subsections.
4.1 Function GetGoalMinMax
The first approach is based on minimization of the
objective function for the
basic scenario under the
condition that the objective functions corresponding
to the detrimental scenarios do not increase too much.
To achieve this goal, the following denotation must
be introduced and it will be used in the remaining
parts of this paper. If the index
u is set to the value of
zero, it means that the
basic scenario is concerned. In
other words, the matrix {
d
ij0
} corresponds to the basic
scenario
.
If all the scenario objective functions are to be
taken into account in the form of separate constraints,
the goal value
G(u) for each scenario u∈U
0
should be
computed. The expression (11) shows the weighted
p-median problem solved for each failure scenario.
Remember, that the symbol
U
0
denotes the set of
detrimental scenarios without the
basic scenario.
()
1
11
:,
min min
,
iju
j
jJ
diI
Gu b
I
II p
∈
∈
=
⊆=
(11)
Based on these preliminaries, a non-negative
parameter
ε can be introduced to limit the maximal
increase of the objective function
G(u) for scenario
u∈U
0
. The parameter ε can either take a given exact
value or it can be expressed as some percentage of the
objective function
G(u). Then, the model for robust
EMS design can be formulated by the expressions
(12)-(17).
0
0
v
j
js
jJ s
M
inimize b x
∈=
(12)
:1
,0,1 ,
s
jsu iju i
iI
Subject to x a y
f
or j J s , , v u U
∈
+≥
∈= ∈
(13)
i
iI
yp
∈
=
(14)
()
0
0
v
jjsu
jJ s
bx Gu foruU
ε
∈=
≤+ ∈
(15)
{0, 1}
i
y
for i I∈∈
(16)
{0, 1} , 0, 1 ,
jsu
x
for j J s , ,v u U∈∈=∈
( 1 7 )
Since the mathematical model (12)-(17) has very
similar structure as the original model (2)-(8), it is not
necessary to explain each constraint separately. There
are only two differences to be noted.
The first one is the objective function, which now
corresponds to the service accessibility of all users
under the
basic scenario.
The second difference consists in the link-up
constraints (15), in which the objective functions of
all scenarios are limited by their goal values instead
of their upper bound.
4.2 Function AdjGetGoalMinMax
The second suggested approach to robust EMS design
follows from the previous
GetGoalMinMax function
described by the model (12)-(17) and goal values
G(u) for all scenarios from the set U
0
.
The adjustment consists in replacing the link-up
constraints (15) of the former model by their adjusted
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
24

version (18), in which only the maximal goal is taken
into account.
0
0
v
jjsu
jJ s
bx MG foruU
ε
∈=
≤+ ∈
(18)
The maximal goal value
MG can be obtained by
the following expression (19). The individual goals
G(u) are defined by (11).
()
{
}
0
max :
M
GGuuU=∈ (19)
This way, the
AdjGetGoalMinMax strategy can be
described by minimizing the objective function (12)
under the constraints (13), (14), (16), (17) and (18).
4.3 Function GetGoalMinH
The last modeling strategy GetGoalMinH is based on
a different principle. Here, the robust service system
design is obtained in such a way that the goal
objective function value
G(0) for the basic scenario
is computed first. Then, the value of parameter
ε must
be given to limit the maximal possible increase of
mentioned goal value
G(0). The objective function
used in this approach minimizes possible increase
h
of the maximal goal
MG over the set of scenarios. The
associated mathematical model can be formulated in
the following way.
M
inimize h
(20)
:1
,0,1 ,
s
jsu iju i
iI
Subject to x a y
f
or j J s , , v u U
∈
+≥
∈= ∈
(21)
i
iI
yp
∈
=
(22)
0
0
v
jjsu
jJ s
bx MGhforuU
∈=
≤+ ∈
(23)
()
0
0
0
v
jjs
jJ s
bx G
ε
∈=
≤+
(24)
{0, 1}
i
y
for i I∈∈
(25)
{0, 1} , 0, 1 ,
jsu
x
for j J s , ,v u U∈∈=∈
( 2 6 )
0h ≥
(27)
The minimized objective function (20) expresses
the increase of the maximal goal value
MG over the
objective functions corresponding to individual
scenarios. The constraints (21) ensure that the
variables
x
jus
are allowed to take the value of 0, if
there is at least one center located in radius
s from the
user location
j and constraint (22) limits the number
of located centers by
p. The link-up constraints (23)
ensure that each perceived disutility (time or distance)
is less than or equal to the maximal goal value
MG
increased by
h. The constraint (24) does not allow to
exceed given value of the objective function for the
basic scenario G(0) by more than ε. Finally, the
obligatory constraints (25), (26) and (27) are included
to ensure the domain of the decision variables.
5 CASE STUDY
The main goal of the computational study reported in
this section was to study:
• robustness coefficients,
• computational time demands.
The first aspect consists in robustness coefficients
POR and GOR introduced in Section 3. Since each
approach minimizes different objective function, for
each resulting vector
y of location variables y
i
the
robust objective functions
f
b
and f
r
were computed in
order to evaluate
POR and GOR. The values of f
b
and
f
r
are defined by (28) and (29) respectively.
{
}
0
() min : 1
b
jiji
jJ
fbdy
∈
==
y
(28)
{
}
min : 1 :
() max
j iju i
r
jJ
bdy
f
uU
∈
=
=
∈
y (29)
The second studied characteristic of all suggested
modeling approaches consists in computational time.
All numerical experiments were performed using
the optimization software FICO Xpress 7.3. They
were run on a PC equipped with the Intel® Core™ i7
5500U processor with 2.4 GHz and 16 GB RAM.
The benchmarks were derived from the real
emergency health care system, which was originally
implemented in eight regions of Slovak Republic. For
each region (Bratislava (BA), Banská Bystrica (BB),
Košice (KE), Nitra (NR), Prešov (PO), Trenčín (TN),
Trnava (TT) and Žilina (ZA)), all cities and villages
with corresponding population
b
j
were taken into
account. The coefficients
b
j
were rounded to
hundreds. In the benchmarks, the set of communities
represents both the set
J of users’ locations and the set
Robust Emergency Medical System Design as a Multi-objective Goal Programming Problem
25
I of possible center locations as well. The cardinalities
of these sets are reported in the tables together with
the number
p of located centers. The network time -
distances from a user to the nearest located center
were derived from the real transportation network.
Due to the lack of scenario benchmarks for the
experiments, the problem instances used in the
computational study were created in the way used in
(Janáček and Kvet, 2016). There were selected one
quarter of matrix rows so that these rows
corresponded to the biggest cities concerning the
number of system users. Then same of them were
chosen randomly and the associated time distance
values were multiplied by the randomly chosen
constant from the numbers 2, 3 and 4. The rows,
which were not chosen by this random process, stay
unchanged. This way, 10 different scenarios were
generated for each self-governing region. These
benchmarks and generated scenarios were used also
in the research reported in (Janáček and Kvet, 2016,
Janáček and Kvet, 2017, Kvet and Janáček, 2017a,
Kvet and Janáček, 2017b).
The experiments were organized so that each of
suggested multi-objective-based approaches was
used to get the resulting robust EMS design for two
different values of parameter
ε. The obtained results
are reported in the following six tables. The left part
of all tables contains the sizes of used benchmarks.
The right part contains the obtained results reported
by four values:
• Let the symbol ObjF denote the particular
model objective function.
• Computational time in seconds is reported in
columns denoted by
CT.
• Finally, the coefficients POR and GOR are
reported in percentage.
The expressions (9) and (10) define their values.
In this short computational study, the values of
parameter
ε were set directly, i.e. they were not set to
any percentage of the scenario goals.
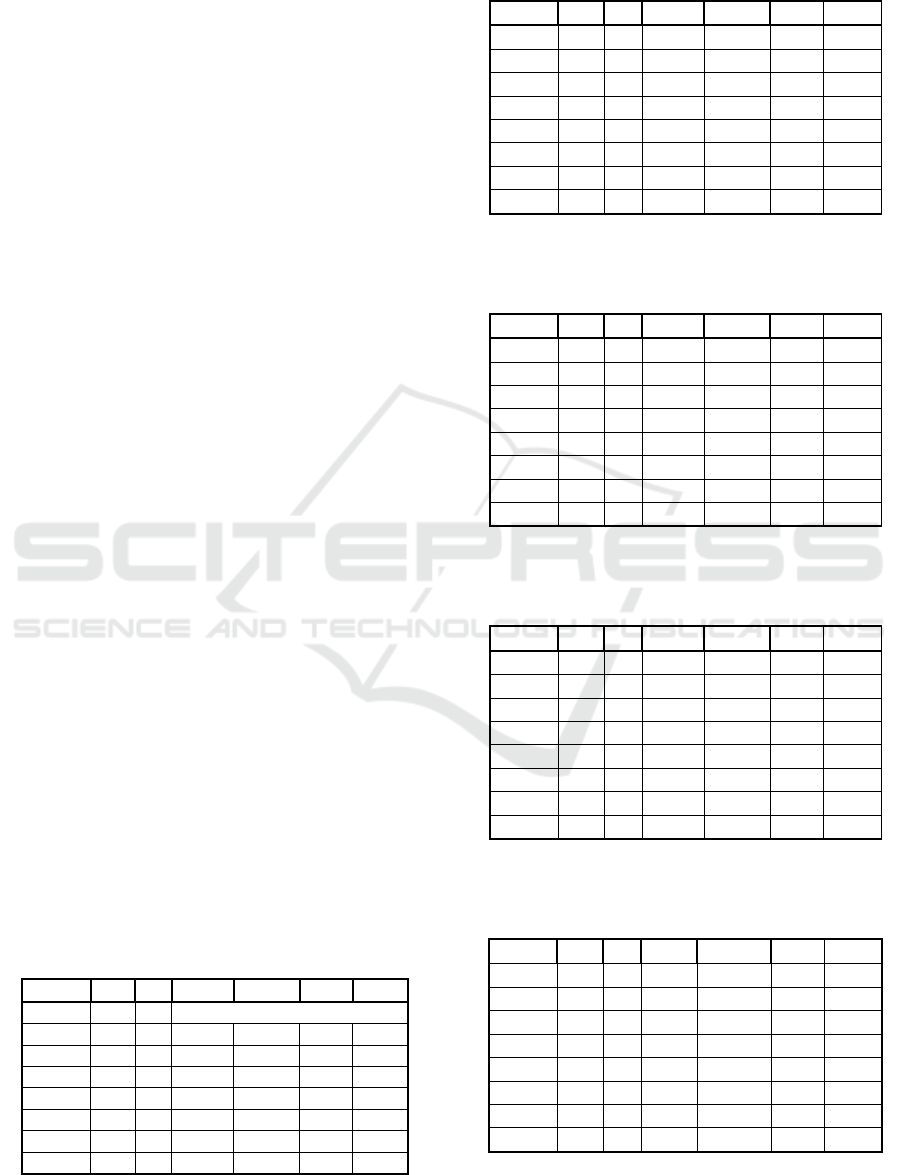
Table 1: Results of the GetGoalMinMax approach applied
on benchmarks derived from the self-governing regions of
Slovakia. The parameter ε was set to 1600.
Region |I| p ObjF CT POR GOR
BA 87 14 Problem infeasible
BB 515 52 17289 705.0 0.00 0.00
KE 460 46 20063 929.1 0.10 3.55
NR 350 35 22728 1299.7 0.34 2.24
PO 664 67 20025 1203.7 0.00 0.00
TN 276 28 15739 478.4 0.34 3.19
TT 249 25 18966 1422.9 0.49 3.55
ZA 315 32 21320 4593.6 1.55 8.53
Table 2: Results of the GetGoalMinMax approach applied
on benchmarks derived from the self-governing regions of
Slovakia. The parameter ε was set to 3000.
Region |I| p ObjF CT POR GOR
BA 87 14 21999 126.0 8.15 32.18
BB 515 52 17289 492.3 0.00 0.00
KE 460 46 20042 392.4 0.00 0.00
NR 350 35 22651 268.9 0.00 0.00
PO 664 67 20025 1111.3 0.00 0.00
TN 276 28 15686 75.9 0.00 0.00
TT 249 25 18873 133.7 0.00 0.00
ZA 315 32 21119 779.4 0.59 4.99
Table 3: Results of the AdjGetGoalMinMax approach
applied on benchmarks derived from the self-governing
regions of Slovakia. The parameter ε was set to 1600.
Region |I| p ObjF CT POR GOR
BA 87 14 22050 138.2 8.40 36.24
BB 515 52 17289 710.1 0.00 0.00
KE 460 46 20055 841.1 0.06 1.46
NR 350 35 22756 1132.7 0.46 3.76
PO 664 67 20025 1165.5 0.00 0.00
TN 276 28 15706 473.0 0.13 3.26
TT 249 25 18939 1011.5 0.35 1.72
ZA 315 32 21320 539.4 1.55 8.53
Table 4: Results of the AdjGetGoalMinMax approach
applied on benchmarks derived from the self-governing
regions of Slovakia. The parameter ε was set to 3000.
Region |I| p ObjF CT POR GOR
BA 87 14 21999 75.7 8.15 32.18
BB 515 52 17289 788.4 0.00 0.00
KE 460 46 20042 434.3 0.00 0.00
NR 350 35 22651 250.0 0.00 0.00
PO 664 67 20025 1284.7 0.00 0.00
TN 276 28 15686 188.8 0.00 0.00
TT 249 25 18873 134.2 0.00 0.00
ZA 315 32 21119 559.2 0.59 4.99
Table 5: Results of the GetGoalMinH approach applied on
benchmarks derived from the self-governing regions of
Slovakia. The parameter ε was set to 500.
Region |I| p ObjF CT POR GOR
BA 87 14 6871 83.7 1.70 10.98
BB 515 52 386 18380.0 2.61 2.73
KE 460 46 548 15768.5 2.16 6.29
NR 350 35 710 15775.4 2.14 6.84
PO 664 67 286 18419.1 2.00 5.48
TN 276 28 328 1522.6 3.16 9.85
TT 249 25 998 2226.6 2.08 4.61
ZA 315 32 601 2957.5 2.33 12.93
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
26
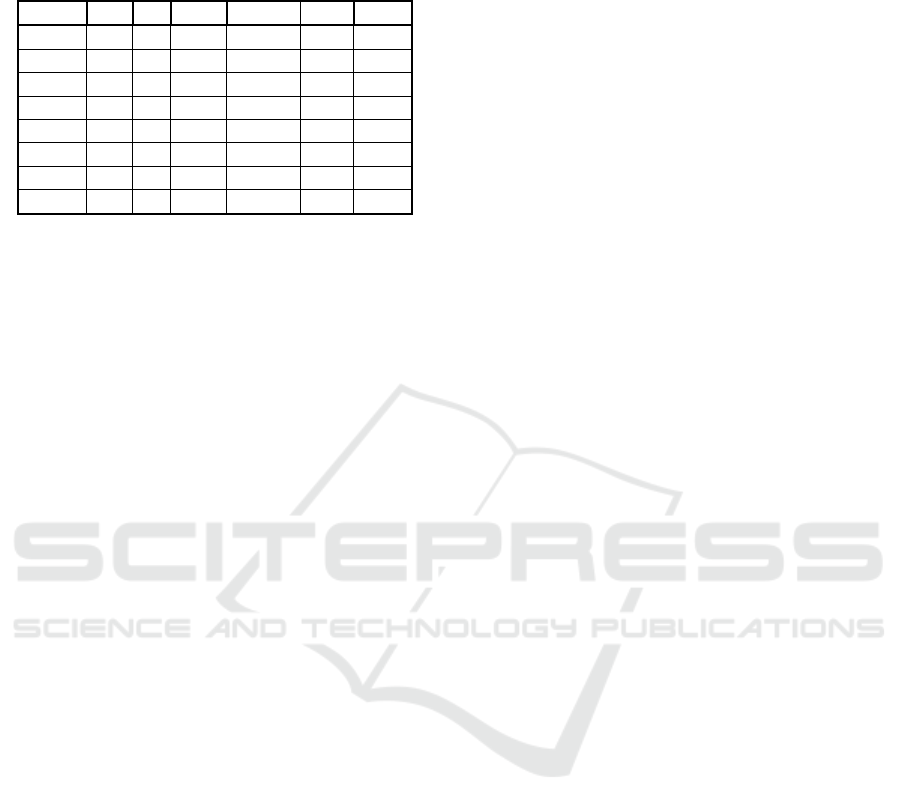
Table 6: Results of the GetGoalMinH approach applied on
benchmarks derived from the self-governing regions of
Slovakia. The parameter ε was set to 1500.
Region |I| p ObjF CT POR GOR
BA 87 14 3217 104.4 6.88 25.70
BB 515 52 386 18054.0 2.61 2.73
KE 460 46 548 23663.2 2.16 6.29
NR 350 35 657 13426.0 2.47 7.07
PO 664 67 286 19660.5 2.00 5.48
TN 276 28 284 2378.1 4.05 10.13
TT 249 25 788 2267.6 3.87 5.68
ZA 315 32 525 4196.0 3.75 13.31
Analyzing the results reported in Tables 1 - 6, the
expectations have been confirmed. As can be
observed, the quality of obtained resulting system
designs measured by the values of coefficients
POR
and
GOR depend on the parameter settings. As far as
the service system robustness is concerned, presented
approaches represent suitable contribution to the
state-of-the-art methods for robust system designing.
Focusing on computational time requirements, the
big difference between the first two approaches and
the third one can be explained by the model structure.
While the mathematical model used in the functions
GetGoalMinMax and AdjGetGoalMinMax uses a
min-sum optimization criterion, the model used in the
GetGoalMinH approach takes the form of a min-max
problem, which is generally harder to solve, leading
to longer computation times.
6 CONCLUSIONS
This paper was focused on robust emergency medical
service system design. The robustness follows the
idea, which aims to make the system resistant to
various randomly occurring detrimental events,
which may negatively affect system performance and
quality of the service provided. The main focus was
on the set of detrimental scenarios, which allows
forming an additional constraint to the model for each
element of the scenario set. In this paper, three
approaches were introduced and experimentally
compared.
It can be observed that the computational time
demands depend on the model structure. If we replace
a min-sum objective by a min-max optimization
criterion, then the model gets more complicated so it
requires a longer computation time.. Besides that,
quality of obtained results is very satisfactory.
The future research in this field could be aimed at
other approximate techniques, which will enable to
reach shorter computational time with acceptable
solution accuracy. Another future research goal could
be focused on mastering the presented problem with
a larger set of detrimental scenarios.
ACKNOWLEDGEMENT
This paper was supported by the research grant
VEGA 1/0689/19 “Optimal design and economically
efficient charging infrastructure deployment for
electric buses in public transportation of smart cities”.
This work was also supported by the Slovak Research
and Development Agency under the Contract no.
APVV-19-0441.
REFERENCES
Antunes, C., H. and Henriques, C. O. 2016 Multi-objective
optimization and multi-criteria analysis models and
methods for problems in the energy sector. Multiple
criteria decision analysis, Springer, 1071-1169.
Avella, P., Sassano, A., Vasil’ev, I., 2007. Computational
study of large scale p-median problems. In Mathematical
Programming, Vol. 109, No 1, pp. 89-114.
Correia, I. and Saldanha da Gama, F. 2015 Facility
locations under uncertainty. In Laporte, G. Nikel, S. and
Saldanha da Gama, F. (Eds). Location Science,
Heidelberg: Springer Verlag, pp. 177-203.
Current, J., Daskin, M., Schilling, D., 2002. Discrete
network location models. In Drezner Z. (ed) et al.
Facility location. Applications and theory, Berlin,
Springer, pp. 81-118.
Doerner, K. F. et al., 2005. Heuristic solution of an
extended double-coverage ambulance location problem
for Austria. In Central European Journal of Operations
Research, Vol. 13, No 4, pp. 325-340.
Elloumi, S., Labbé, M., Pochet, Y., 2004. A new
formulation and resolution method for the p-center
problem. INFORMS Journal on Computing 16, pp. 84-
94.
García, S., Labbé, M., Marín, A., 2011. Solving large p-
median problems with a radius formulation. INFORMS
Journal on Computing, Vol. 23, No 4, pp. 546-556.
Gendreau, M., Potvin, J. 2010. Handbook of
Metaheuristics, Springer Science & Business Media,
648 p.
Ingolfsson, A., Budge, S., Erkut, E., 2008. Optimal
ambulance location with random delays and travel
times, In Health Care Management Science, Vol. 11,
No 3, pp. 262-274.
Janáček, J., 2008. Approximate Covering Models of
Location Problems. In Lecture Notes in Management
Science: Proceedings of the 1st International
Conference ICAOR, Yerevan, Armenia, pp. 53-61.
Janáček, J. and Kvet, M. 2016. Designing a Robust
Emergency Service System by Lagrangean Relaxation.
Robust Emergency Medical System Design as a Multi-objective Goal Programming Problem
27

In Proceedings of the conference Mathematical
Methods in Economics, September 6th-9th 2016,
Liberec, Czech Republic, pp. 349-353.
Janáček, J. and Kvet, M. 2017. An Approach to Uncertainty
via Scenarios and Fuzzy Values. Croatian Operational
Research Review 8 (1), pp. 237-248.
Jánošíková, Ľ. 2007. Emergency Medical Service Planning.
Communications Scientific Letters of the University of
Žilina, 9(2), pp. 64-68.
Kvet, M. and Janáček, J. 2017a. Hill-Climbing Algorithm
for Robust Emergency System Design with Return
Preventing Constraints. In 9th International Conference
on Applied Economics: Contemporary Issues in
Economy, 2017, Toruń, Poland, pp. 156-165.
Kvet, M. and Janáček, J. 2017b. Struggle with curse of
dimensionality in robust emergency system design. In
Proceedings of the 35th international conference
Mathematical Methods in Economics MME 2017,
September 13th -15th 2017, Hradec Králové, Czech
Republic, pp. 396-401.
Kvet, M. and Janáček, J. 2018. Reengineering of the
Emergency Service System under Generalized
Disutility. In the7th International Conference on
Operations Research and Enterprise Systems ICORES
2018, Madeira, Portugal, pp. 85-93.
Pan, Y., Du, Y. and Wei, Z. 2014. Reliable facility system
design subject to edge failures. American Journal of
Operations Research 4, pp. 164-172.
Scaparra, M.P., Church, R.L. 2015. Location Problems
under Disaster Events. Location Science, eds. Laporte,
Nikel, Saldanha da Gama, pp. 623-642.
Snyder, L. V., Daskin, M. S., 2005. Reliability models for
facility location; The expected failure cost case. In
Transport Science, Vol. 39, No 3, pp. 400-416.
ICORES 2021 - 10th International Conference on Operations Research and Enterprise Systems
28
