ACO Algorithms to Solve an Electromagnetic Discrete Optimization

Problem

Anton Duca

and Ibrahim Hameed

Politehnica University of Bucharest, Faculty of Electrical Engineering, Bucharest, Romania

NTNU University, Faculty of Information Technology and Electrical Engineering, Alesund, Norway

Keywords: Ant Algorithms, Optimization, Non-Destructive Electromagnetic Testing (NDET), Inverse Problems.

Abstract: The paper proposes and studies the efficiency of the ant colony optimization (ACO) algorithms for solving

an inverse problem in non-destructive electromagnetic testing (NDET). The inverse problem, which consists

in finding the shape and parameters of cracks in conducting plates starting from the signal of an eddy

current testing (ECT) probe, is formulated as a discrete optimization problem. Two of the most widely

known ant algorithms are adapted and applied to solve the optimization problem. The influence over the

optimization algorithms performances of some problem specific local search strategies is also analyzed.

1 INTRODUCTION

Eddy Current Testing (ECT) is one of the most used

electromagnetic methods commonly employed in the

non-destructive evaluation of conductive materials

(Yusa et al., 2016). The ECT principle is based on

the interaction between induced eddy currents and

an examined conductive structure, interaction due to

the electromagnetic induction phenomena. The

method is applied in various application fields for

material thickness measurements, corrosion

evaluation, proximity measurements, and so on.

However, at the present time the most widely spread

area of application is the diagnosis and detection of

discontinuities in conductive materials. Real cracks

(such as stress corrosion cracks) usually appear in

steam generator tubes used in pressurized water

reactor of nuclear power plants (Yusa, 2017).

The Non-destructive Electromagnetic Testing

(NDET) inverse problem deals with the

identification of crack parameters using the ECT

measured signal (Yusa et al., 2016) (Yusa, 2017).

The optimization problem associated with the

inverse problem aims to minimize the difference

between the simulated signal corresponding to a

potential solution and the measured (real) signal.

Since deterministic methods can not be applied

because of multiple local minimum, heuristics based

methods, like genetic algorithms, tabu search,

particle swarm optimization, and so on, have

emerged as the standard techniques for solving these

non-convex and ill conditioned difficult inverse

problems.

The present paper proposes and deals with

studying and comparing the efficiency of ant

algorithms to solve the optimization problem

associated with the inverse NDET problem.

The first ant algorithm, the Ant System (AS),

was proposed by (Dorigo et al., 1996) and was

targeted towards hard non-determinist polynomial

(NP) combinatorial optimization problems such as

the Travelling Salesman Problem (TSP) (Stutzle,

Hoos, 1997) (Dorigo et al., 1999) (Ridge, Kudenko,

2007), Quadratic Assignment Problem (QAP)

(Stutzle, Hoos, 1997) (Dorigo et al., 1999) or

Multiple Knapsack Problem (MKP) (Fidanova,

2007) (Ke et al., 2013). The algorithm simulates the

behaviour of ants in real ant colonies when

searching for food. The ants are social insects which

communicate information about food sources using

a substance called pheromone, substance secreted

along their search path.

During time, to improve the performances of the

initial algorithm a significant number of solutions

have been proposed, the most notorious ant

algorithms being the Max-Min Ant System (MMAS)

(Stutzle, Hoos, 1997) and the Ant Colony

Optimization (ACO) (Dorigo et al., 1999). In the

same time several algorithms derived from ant

algorithms for combinatorial optimization have been

Duca, A. and Hameed, I.

ACO Algorithms to Solve an Electromagnetic Discrete Optimization Problem.

DOI: 10.5220/0009980001150122

In Proceedings of the 12th International Joint Conference on Computational Intelligence (IJCCI 2020), pages 115-122

ISBN: 978-989-758-475-6

115

proposed for continuous optimization problems

(ACOR) (Socha, Dorigo., 2008).

To solve the inverse NDET problem two

approaches will be studied: the first one is based on

an ant algorithm for continuous optimization

(ACOR) and the second is based on an algorithm

designated to combinatorial optimization (MMAS).

To speed up the optimization process and to

avoid getting trapped in local minimum points some

problem specific local search strategies are used to

enhance the ant algorithms when solving the inverse

NDET problem. The influence over the ant based

algorithms performances of the local search

frequency is also studied.

2 THE NDET PROBLEM

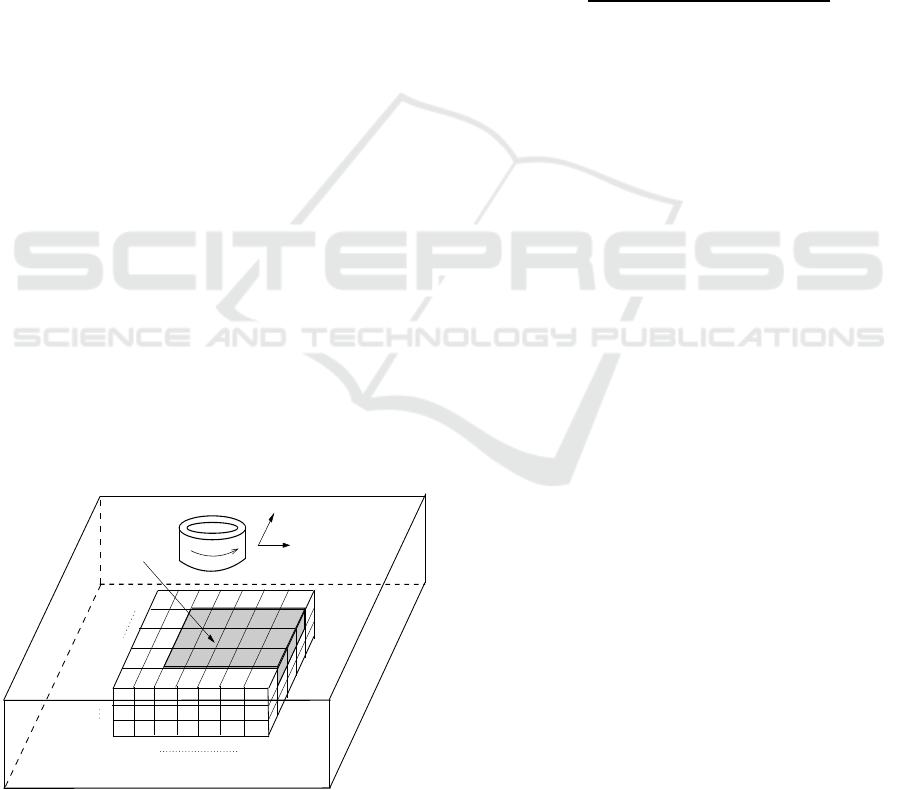
2.1 Tested Configuration

The problem used for testing is a slightly different

version of JSAEM (Japan Society for Applied

Electromagnetics) benchmark #2 similar with the

one in (Janousek et al., 2017). The non-magnetic

conductor (Ω

) surface is scanned using pancake coil

with a self-induction. The non-magnetic plate (40 x

40 x 1.25 mm

) has the conductivity =106 S/m and

contains one crack located in the region Ω

(10 x 1 x

1.25 mm

) divided uniformly in a grid of cells (13 x

5 x 10) (Figure 1). The cracks are cubes described

by 6 integer parameters, c=[ix

, ix

, iy

, iz, s], the

indices of the first / last cells along x [length] and y

[width], number of cell along z [depth iz], and

conductivity 

= s % . The crack is considered as

having a uniform conductivity, zero or a percentage

from the plate conductivity.

Figure 1: Conductor plate with a crack.

2.2 ECT Signal Simulation

For the simulation of the ECT signals a fast FEM-

BEM solver is used (Chen et al., 1999) (Rebican et

al., 2006). The simulated ECT signals use a database

generated in advance for cracks with different

widths (Yusa et al., 2003), (Chen et al., 2006). To

calculate the ECT signal for a crack with the FEM-

BEM a linear equations system of small dimension

needs to be solved, corresponding to the finite

elements composing the crack. This leads to a

significant computational time decrease.

The optimization problem associated to the

NDET inverse problem has the following objective

function:

















∆









∆

















(1)

where c is the vector containing the crack

parameters, N

is the scanning points number, and

Z

/ Z

true

are the simulated / measured coil

impedance variations in the i-th scanning point.

3 ACO ALGORITHMS

3.1 MMAS

The MMAS is an ant colony optimization algorithm

proposed by Stutzle and Hoos which proved its

efficiency on combinatorial optimization problem

such as TSP and QAP (Dorigo et al., 1999). As ACO

optimization algorithms, MMAS is based on the

natural phenomenon of ants forage for food. During

their search path ants create tours (graphs) on which

they deposit a substance called pheromone. An ant

movement along the edges of the graph is a

probabilistic decision based on the pheromone

information.

In practice MMAS is implemented as an iterative

stochastic algorithm with the next stages:

pheromone initialisation, tour (solution) construction

and evaluation, local search, pheromone

evaporation, pheromone deposit on the best global

route, pheromone limitation, and if necessary

pheromone reinitialization. The pseudocode of the

algorithm is as follows:

Scanning

Pancake coil

Crack

ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications

116

;initialize pheromones table

foreach ant of the colony

;construct solution

;evaluate solution

end for

;local search

;evaporate pheromones

;deposit pheromone for best ant

;apply correction to pheromones

foreach pheromone value

if pheromone <

τmin

pheromone = τmin

if pheromone > τmax

pheromone = τmax

end for

;reset pheromones if necessary

noIterations ++

while

(noIterations < maxNoIterations)

and

(optimal solution not found)

Pheromone Initialization. Each pheromone from the

pheromones table (graph) is assigned an initial value

which equals the maximum allowed value (

τmax).

This value is usually set to 1 / (ρ F

min) where ρ is the

evaporation rate and Fmin is the smallest value of the

objective function to be minimized.

Solution Construction. The ants construct an initial

solution starting from a random node. Starting from

a node an ant movement can be exploitative or

explorative. The decision is made using a random

number and an exploration threshold, which is a

parameter value of the algorithm. If the decision is

exploitation then the ant computes the probabilities

for choosing the next possible nodes in the graph

and choses the node with the highest probability.

The probability to choose a node j when starting

from a node i is:

= ([τ

]

[η

]

)/( ∑

[τ

]

[η

]

(2)

where τ

is the pheromone for the edge between the

nodes i and j, k is a node which can be selected from

the node i, and η is a heuristic information

representing the attractiveness of the move (in case

of TSP the length of the ij edge).

If the decision is exploration than the computed

probabilities are used as weights to choose the next

node using a probabilistic method such as wheel

selection.

Local Search. Local search is used to improve the

solution quality with neighbourhood strategies. Two

different approaches can be applied: a problem

independent heuristic (as tabu search), and secondly

some problem specific local search strategy.

Pheromone Evaporation. Each pheromone

corresponding to an edge of the graph is decreased

with the following formula:

= (1 – ρ) τ

, (3)

where ρ is the evaporation rate.

Trail Update. Pheromone is deposited on all edges

connecting the components of the solution for the

best ant. There are the following approaches: the

best overall solution, or the best solution at the

current iteration and the best overall solution. The

update formula is:

= 1/F + τ

, (4)

where F is the objective function value for the best

solution (in the case of TSP the length of the tour).

Pheromone Correction. In the case of MMAS, to

avoid the algorithm stagnation the pheromones are

limited to an interval [

τmin τmax]. The minimum and

maximum values of the pheromones are usually

chosen as:

min

= 1/2n, τ

max

= 1 / (ρ Fmin),

(5)

where F

min is smallesr objective function value

(smallest length of tour for TSP) and n is the

problem size (number of cities for TSP).

Reinitialise Pheromones. Pheromone table can be

reinitialised if the algorithm stagnates and does not

improve the overall best after an imposed number of

iteration. The pheromone values are set to their

initial values

τmax.

3.2 ACOR

Proposed in (Socha, Dorigo., 2008) the ACOR

algorithm is an extension of ant based optimization

algorithms for continuous optimization problems.

ACOR is a population based algorithm which

stores the pheromones table as a solutions archive

(6). The solutions are ordered using their fitness

values in ascending order (f(s

) < f(s

k+1

)), where f: R

–> R is the objective function to be minimized. Each

ACO Algorithms to Solve an Electromagnetic Discrete Optimization Problem

117

solution has an associated weight ω corresponding

to its fitness value (ω

> ω

k+1

(6)

Solution Construction. The construction of a new

solution starts from a solution l from the archive.

The lth solution can be chosen using a wheel

selection mechanism. The selection probability for

the lth solution is:

= ω

/ ∑

(7)

After choosing the start solution, an ant constructs a

new solution in n steps. At each step i the ant

calculates a value for the corresponding optimization

variable using only information about the ith

dimension.

The new solutions are constructed using the

solution archive by calculating the parameters of the

Gaussian kernels G

(the number of the Gaussian

kernels is equal with the number of variables of the

optimization problem n). More details about

calculating the parameters of the Gaussian kernels

can be found in (Socha, Dorigo., 2008).

After constructing a set of solutions the

algorithm evaluates them, add them to the solution

archive, sorts the solutions archive according to the

fitness values, calculates weights and Gaussian

kernels, and in the end removes the worst solutions

by keeping the solutions archive size to a specified

number.

3.3 Ant Algorithms Approach for the

NDET Inverse Problem

The ant algorithms used for the inversion process

have to be customized for this type of NDET

problems. The ACO for continuous domains, such as

ACOR, store their pheromone table as a solution

archive and can simply be adapted to the discrete

optimization problem by rounding the coordinates

values before the evaluation of the objective

function.

The ant algorithms for combinatorial

optimization, such as MMAS and ACO, need

specific design modification to be used for the

NDET inverse problem.

The first design issue is to map the inverse

problem on a graph. This paper proposes the use of a

layered graph. Each layer in a graph corresponds to

a variable of the optimization function (a parameter

of the crack) and its vertices (the nodes) are given by

the number of possible values of the discrete

variable. The edges (the arcs) between the nodes of

different layers have assigned pheromone levels and

represent a possibility of choice: for example, an

edge between a node i from a layer x and a node j

from another layer y means that when constructing a

candidate solution after the parameter x has been

assigned a value i the parameter y might receive a

value j.

The second design issue is related to the tour

construction (candidate solution). At each step, in

order to move from a vertex to another an ant has to

compute a probability distribution (2). If in the case

of TSP the attractiveness was represented by the

distance between the two cities in our case the

proposed solution is to be the best value of the

objective function which was previously obtained

with that combination of parameter values.

The maximum and minimum values for the

MMAS pheromone levels will include the best value

of the objective function obtained at the current step

(instead of the length of the tour) and the number of

vertices in the graph. To avoid extreme cases the

objective function will be normalized and have a

minimum non-zero value.

The last issue is the local search methodology.

The proposed local search methods are NDET

problem specific, and they aim to avoid local

minima and increase the speed of convergence of the

inversion algorithm.

4 LOCAL SEARCH STRATEGY

Initially proposed in (Duca et al., 2014) and used in

conjunction with PSO (Particle Swarm

Optimization) (Kennedy, Eberhart, 1995) based

algorithms, and also successfully applied in (Duca et

al., 2014, 2) in conjunction with advanced PSO

algorithms (Sun et al., 2004) (Clerc, 2012) (Altinoz

et al., 2015), the local search methods are applied

after a number of iterations performed by the

optimization procedure. The local search strategy

generates 16 potential solutions starting from the

solution with the best fitness. A test point is

generated changing one parameter of the starting

ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications

118

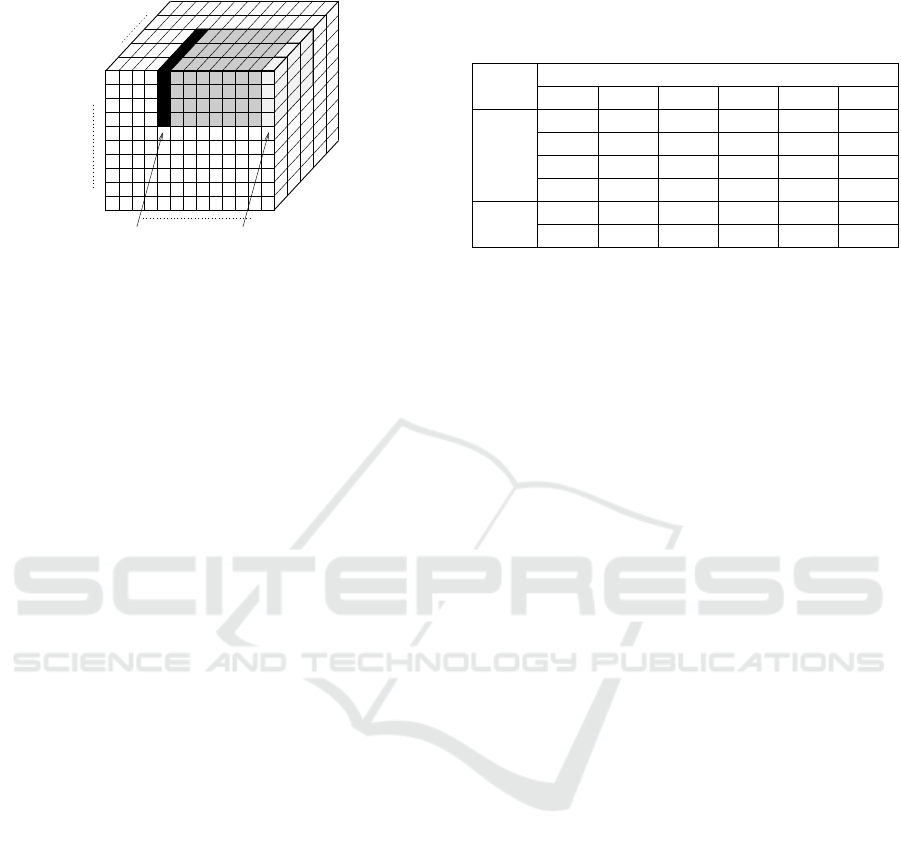
point using expansion, contraction or displacement.

Figure 2: Negative displacement on OX for the crack c =

[6, 13, 1, 3, 4, 3].

The contraction / expansion can be performed

along the length (OX), width (OY) or depth (OZ),

but also conductivity. The contraction / expansion

operations generate 12 testing points, because the

operations can be applied in two different ways for

the length and width, changing ix1/iy1 or ix2/iy2.

The displacement can be performed for OX or for

OY axis but not for OZ (the crack always starts from

the plate surface). The displacement operation

generates four new testing points. Figure 2 shows a

negative displacement on OX performed on a crack

described by the parameters [6, 13, 1, 3, 4, 3].

5 RESULTS

In this paper, the inverse NDET problem is solved

using six different schemes: three MMAS schemes

(MMAS, MMAS with high frequency local search

MMAS-LS-hf, MMAS with low frequency local

search MMAS-LS-lf) and three ACOR schemes

(ACOR, ACOR with high frequency local search

ACOR-LS-hf, ACOR with low frequency local

search ACOR-LS-lf). For the schemes with high

frequency the local search is applied on the best

solution after each iteration of the algorithm, while

for the schemes with low frequency the local search

is applied after 80 evaluations of the objective

function (equivalent with 16 iterations for the ACOR

and 40 iterations for MMAS).

To compare the efficiency of the employed

schemes six inner defects (ID, the crack is on the

same side with the coil) are considered: four with

zero conductivity (ID1-ID4) and two with non-zero

conductivity (ID5-ID6, crack conductivity is 3% and

2% of the plate conductivity). The values of the

crack parameters are given in Table 1. For example,

ID4 has the length of 5.39mm (7cells x 0.77mm),

the width of 0.4mm (2cells x 0.2mm), the depth of

40% from the plate thickness (iz=4), and zero

conductivity (s=0).

Table 1: Cracks used for testing.

Crack

Crack parameters

iz s

ID1

4 10 2 4 5 0

ID2

5 9 1 5 3 0

ID3

3 11 2 3 2 0

ID4

4 10 3 4 4 0

ID5

4 10 2 4 5 3

ID6

3 11 2 3 2 2

To make a relevant statistical study, 30

numerical simulations (tests) were performed for

each crack reconstruction. After a previous tuning

the most suitable ACOR parameters were: archive

size 40, number of ants 5, locality of the search

process 0.01, convergence speed 0.85. The MMAS

parameters were chosen as suggested in (Ridge,

Kudenko, 2007): number of ants 2, alpha pheromone

term 4, distance heuristic term beta 3, exploration /

exploitation threshold 0.75, pheromone update

frequency for best so far 1, random chosen start

variable for solution construction, limits of trail

pheromone 0.01 and 2, number of iterations without

improvement (which resets the pheromone table) 10.

The optimization algorithms were stopped when

the exact solution was found (the objective function

is zero) or the algorithm completed a maximum

number of 1000 objective function (OF) evaluations.

Table 2 (see Appendix) presents the numerical

results of the reconstructions as the minimum, the

maximum, the average value and the standard

deviation of the objective function for the best

solution for each of the 30 tests, and the number of

tests in which the exact parameters of the crack were

found (the exact fit).

The performances obtained with the ACOR

based algorithms outperform the ones with the

MMAS for all the six tested cracks. The local search

strategy improves the converge speed for both

algorithms. The inversion schemes when the local

search is applied with lower frequency performed

significantly better than the schemes with high

frequency, providing better average values and

higher number of exact findings. The exceptions are

in the case of ID6 and partially ID3 (for ACOR

algorithms) and ID3 (for the MMAS algorithms).

The improvements and superiority of the

algorithms with local search can also be seen from

mean-best evolution during the optimization process

(Figures 3-8). Besides the fact that statistical mean

values are smaller, the LS-lf algorithms are more

added cells eliminated cells

ACO Algorithms to Solve an Electromagnetic Discrete Optimization Problem

119

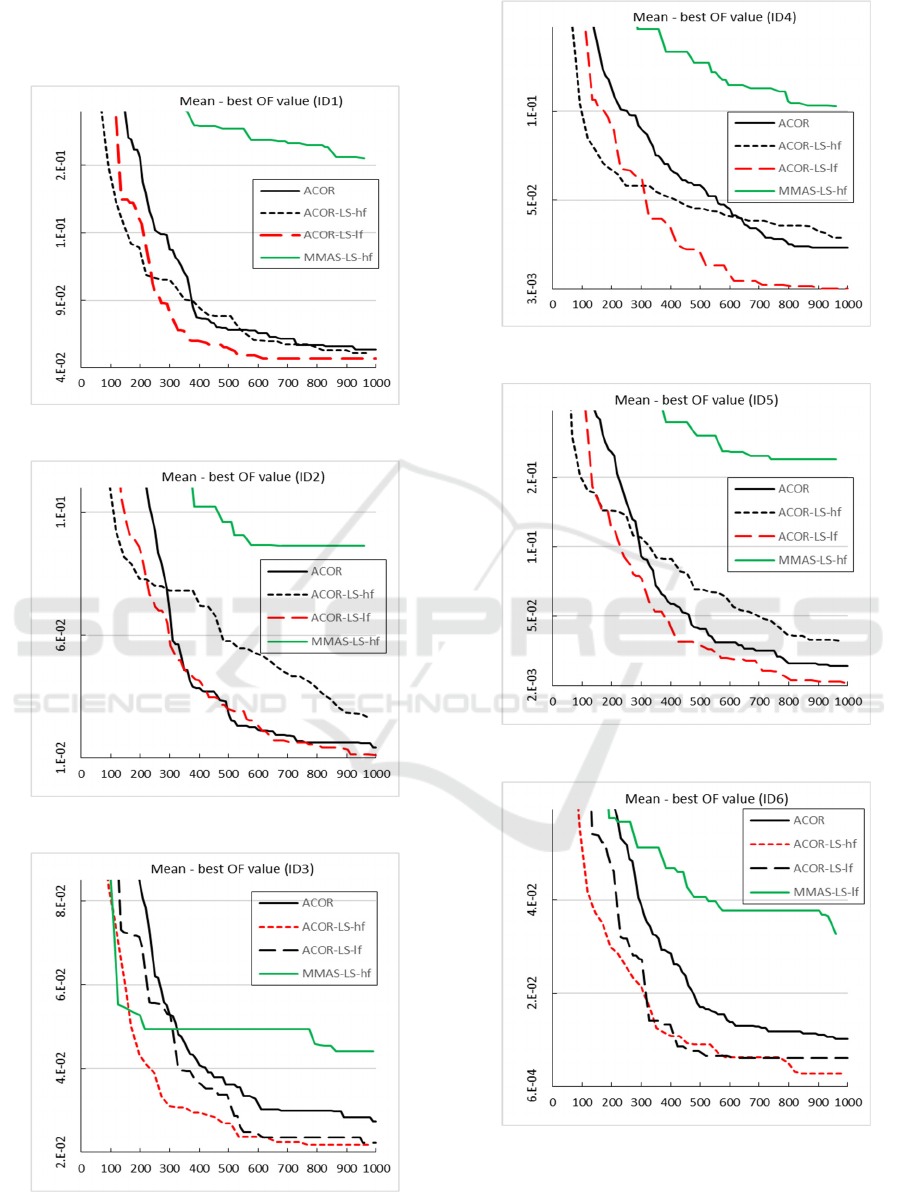
stable having a smoother evolution for the cracks ID

1/2/4/5, while the LS-hf algorithms perform better

for the cracks ID 3/6.

Figure 3: Mean-best OF value variation for test ID1.

Figure 4: Mean-best OF value variation for test ID2.

Figure 5: Mean-best OF value variation for test ID3.

Figure 6: Mean-best OF value variation for test ID4.

Figure 7: Mean-best OF value variation for test ID5.

Figure 8: Mean-best OF value variation for test ID6.

ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications

120

6 CONCLUSIONS

The paper studied the efficiency of ant based

algorithms used for the reconstruction of cracks

starting from the ECT signals supplied by a probe.

Two type of ant algorithms have been adapted and

analysed, ACOR for continuous domains and

MMAS for discrete optimization problems. The

paper also analysed the efficiency of the ant

algorithms in conjunction with some problem

specific local search methods aiming to enhance the

inversion process.

The schemes based on ACOR provide better

performances (higher number of exact findings and

smaller average and standard values for the objective

function) than the proposed MMAS schemes, for

both conductive and non-conductive cracks.

The ant algorithms enhanced with local search

strategies proved to be, by far, the best approach for

solving the inverse problem. The schemes enhanced

with local search significantly improve the

performances of both type of algorithms, ACOR and

MMAS, for cracks with zero or non-zero

conductivity. In terms of frequency, a lower

frequency use of the local search strategies seems to

be preferable to a high frequency, which seems to

lead to a premature convergence for most of the test

cases.

ACKNOWLEDGEMENTS

This paper was written in the frame of the EEA

Grants, project EEA-MG-RO-NO-2018-0069.

REFERENCES

Altinoz, O.T., Yilmaz, A.E., Duca, A. and Ciuprina, G.,

2015. Incorporating the avoidance behavior to the

standard particle swarm optimization 2011. Advances

in electrical and computer engineering, 15(2), pp.51-

59.

Chen, Z., Miya, K., Kurokawa, M., 1999. Rapid prediction

of eddy current testing signals using A-Φ method and

database. In NDT&E International, vol. 32, pp. 29-36.

Chen, Z., Rebican, M., Yusa, N., Miya, K., 2006, Fast

simulation of ECT signal due to a conductive crack of

arbitrary width. In IEEE Transactions on Magnetics,

vol. 42, pp. 683-686.

Clerc, M., 2012. Standard particle swarm optimization.

Open access archive HAL (http://clerc.maurice.

free.fr/pso/ SPSO_descriptions.pdf).

Dorigo, M., Maniezzo, V., Colorni, A. 1996. Ant system:

optimization by a colony of cooperating agents. In

IEEE Transactions on Systems, Man, and Cybernetics,

Part B (Cybernetics), 26(1), pp. 29-41.

Dorigo, M., Di Caro, G., 1999. Ant colony optimization: a

new meta-heuristic. In Proceedings of the Congress on

Evolutionary Computation, pp. 1470-1477.

Duca, A., Rebican, M., Janousek, L., Smetana, M.

Strapacova, T., 2014. PSO based techniques for NDT-

ECT inverse problems. In Electromagnetic

Nondestructive Evaluation (XVII), 39, pp.323-330.

Duca, A., Rebican, M., Duca, L., Janousek, L. and

Altinoz, T., 2014. Advanced PSO algorithms and local

search strategies for NDT-ECT inverse problems. In

International Symposium on Fundamentals of

Electrical Engineering (ISFEE), pp. 1-5.

Fidanova, S., 2007. Ant colony optimization and multiple

knapsack problem. In Handbook of Research on

Nature-Inspired Computing for Economics and

Management, pp. 498-509. IGI Global.

Janousek, L., Rebican, M., Smetana, M., Duca, A., 2017.

Diagnosis of real cracks from eddy current testing

signals using parallel computation. In Nondestructive

Testing and Evaluation, 32(4), pp. 435-443.

Ke, L., Zhang, Q., Battiti, R., 2013. MOEA/D-ACO: A

multiobjective evolutionary algorithm using

decomposition and antcolony. In IEEE transactions on

cybernetics 43, no. 6, pp. 1845-1859.

Kennedy, J., Eberhart, R., 1995. Particle swarm

optimization. Proceedings of IEEE International

Conference on Neural Networks, pp. 1942-1948.

Rebican, M., Chen, Z., Yusa, N., Janousek, L., Miya, K.,

2006. Shape reconstruction of multiple cracks from

ECT signals by means of a stochastic method In IEEE

Transactions on Magnetics, vol. 42, pp. 1079-1082.

Ridge, E., Kudenko, D., 2007. Tuning the performance of

the MMAS heuristic. In Engineering stochastic local

search algorithms. designing, implementing and

analyzing effective heuristics, pp. 46-60. Springer,

Berlin, Heidelberg.

Socha, K., Dorigo, M., 2008. Ant colony optimization for

continuous domains. In European journal of

operational research, 185(3), pp.1155-1173.

Stutzle, T., Hoos, H., 1997. MAX-MIN ant system and

local search for the traveling salesman problem. In

IEEE Evolutionary Computation, pp. 309-314.

Sun, J., Feng, B., Xu, W., 2004, Particle swarm

optimization with particles having quantum behavior,

in: IEEE Proceedings of Congress on Evolutionary

Computation, pp. 325–331.

Yusa, N., Chen, Z., Miya, K., Uchimoto, T., and Takagi,

T., 2003. Large-scale parallel computation for the

reconstruction of natural stress corrosion cracks from

eddy current testing signals. In NDT&E International,

vol. 36, pp. 449–459.

Yusa, N., Uchimoto, T, Kikuchi, H., (Eds.), 2016.

Electromagnetic Nondestructive Evaluation (XIX),

IOS Press.

Yusa, N., 2017. Probability of detection model for the

non-destructive inspection of steam generator tubes of

PWRs. In Journal of Physics: Conference Series, vol.

860, no. 1, p. 012032. IOP Publishing.

ACO Algorithms to Solve an Electromagnetic Discrete Optimization Problem

121

APPENDIX

Table 2: Objective function values and standard deviation for the NDET problem.

(Bold RED is the best algorithm option for a crack, bold GREEN is the best MMAS option for a crack)

Crack / Algorithm

Min-

est

OF value

(

× E-02

)

Exact fit

(OF=0)

Max -

est

OF value

(

×E-02

)

Mean -

est

OF value

(

× E-02

)

Standard

deviation

(

× E-02

)

ID1

ACOR 0 8 /30 10.87 5.35 3.57

ACOR-LS–hf 0 8 /30 10.87 5.11 3.37

ACOR-LS–lf 0 9 /30 13.41 4.71 3.39

MMAS 0 1 /30 45.31 24.68 10.95

MMAS-LS–hf 6.4 0 /30 49.08 22.56 10.29

MMAS-LS–lf 0 4 /30 49.08 19.51 11.43

ID2

ACOR 0 21 /30 6.22 1.40 2.36

ACOR-LS–hf 0 20 /30 15.40 2.62 4.45

ACOR-LS–lf 0 22 /30 5.35 1.12 2.16

MMAS 8.12 0 /30 25.62 17.96 5.00

MMAS-LS–hf 14.98 0 /30 36.89 18.88 6.42

MMAS-LS–lf 0 4 /30 19.43 9.64 6.28

ID3

ACOR 0 18 /30 7.23 2.25 2.99

ACOR-LS–hf 0 19 /30 7.22 1.68 2.39

ACOR-LS–lf 0 20 /30 7.22 1.73 2.64

MMAS 0 4 /30 11.43 7.36 3.28

MMAS-LS–hf 0 14 /30 16.09 3.92 4.17

MMAS-LS–lf 0 5 /30 9.64 5.50 2.78

ID4

ACOR 0 20 /30 10.40 2.65 4.01

ACOR-LS–hf 0 21 /30 16.16 3.19 5.09

ACOR-LS–lf 0 29 /30 10.39 0.35 1.90

MMAS 0 2 /30 25.02 15.84 5.83

MMAS-LS–hf 0 2 /30 29.51 15.00 5.96

MMAS-LS–lf 0 5 /30 19.57 10.56 5.93

ID5

ACOR 0 23 /30 10.64 1.63 3.09

ACOR-LS–hf 0 20 /30 19.25 3.41 5.54

ACOR-LS–lf 0 28 /30 7.46 0.34 1.43

MMAS 10.64 0 /30 43.22 21.62 6.80

MMAS-LS–hf 7.46 0 /30 24.09 21.57 3.37

MMAS-LS–lf 0 1 /30 24.09 16.49 6.55

ID6

ACOR 0 23 /30 5.08 1.08 2.06

ACOR-LS–hf 0 28 /30 5.10 0.34 1.29

ACOR-LS–lf 0 26 /30 5.05 0.67 1.74

MMAS 0 1 /30 13.08 8.02 3.34

MMAS-LS–hf 0 5 /30 12.08 6.26 4.03

MMAS-LS–lf 0 9 /30 5.10 3.34 2.35

ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications

122