Lyapunov Stability of a Nonlinear Bio-inspired System for the Control of
Humanoid Balance
Vittorio Lippi
a
and Fabio Molinari
b
Technische Universit
¨
at Berlin, Fachgebiet Regelungssysteme, Einsteinufer 17 D-10587, Berlin, Germany
Keywords:
Posture Control, Humanoid, Stability.
Abstract:
Human posture control models are used to analyse neurological experiments and control of humanoid robots.
This work focuses on a well-known nonlinear posture control model, the DEC (Disturbance estimate and
Compensation). In order to compensate disturbances, unlike other models, DEC feedbacks signals coming from
sensor fusion rather than raw sensory signals. In previous works, the DEC model is shown to predict human
behavior and to provide a control system for humanoids. In this work, the stability of the system in the sense of
Lyapunov is formally analysed. The theoretical findings are combined with simulation results, in which an
external perturbation of the support surface reproduces a typical scenario in posture control experiments.
1 INTRODUCTION
Mathematical models of human balance are used for
the analysis of neurological experiments (van der
Kooij et al., 2007; van der Kooij et al., 2005; van
Asseldonk et al., 2006; Goodworth and Peterka, 2018;
Mergner, 2010; Engelhart et al., 2014; Pasma et al.,
2014; Jeka et al., 2010; Boonstra et al., 2014), and
for the control of humanoid robots. Most of human
posture control studies exploit linear models such as
the independent channel model (Peterka, 2002), that
assumes a linear and time invariant behaviour (Engel-
hart et al., 2016). Linear models have the advantage of
being simple to analyse and relatively easy to be fit on
data. However, experiments reveal that human posture
control exhibits important non-linearities.
In this work, we study the stability of a non-linear
bio-inspired posture control system, the DEC, Distur-
bance estimate and Compensation (Mergner, 2010).
The DEC model consists of a servo control loop and
a compensation of external disturbances estimated
on the basis of sensory inputs. The control princi-
ple can be addressed as “feed forward disturbance
correction” (Luecke and McGuire, 1968; Roffel and
Betlem, 2007; Zhong et al., 2012) or, in German,
“St
¨
orgr
¨
oßenaufschaltung” (Bleisteiner and Mangoldt,
2013). Throughout this paper, the DEC is used to
model a scenario where the subject stands on a tilting
a
https://orcid.org/0000-0001-5520-8974
b
https://orcid.org/0000-0003-2617-962X
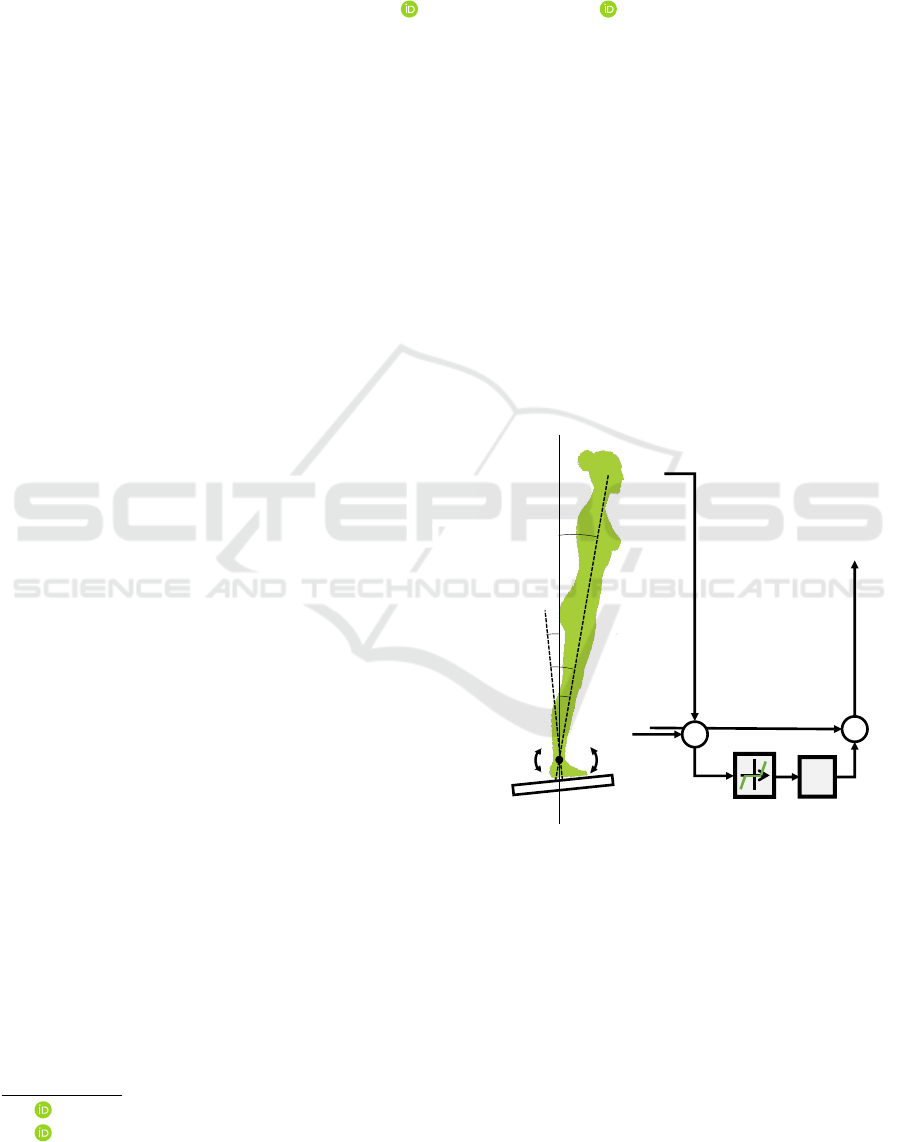
a
FS
a
BS
a
BS
Gravitational
Vertical
Vestibular
ሶ
𝜶
𝑩𝑺
signal
∫
-
+
r
()
Leaky integrator
Proprioception
ෝ
𝜶
𝑩𝑺
Signal, used
for control
ෝ
𝜶
𝑭𝑺
a
BF
=a
BS
-a
FS
Figure 1: Posture control model. On the left: illustration of
the scenario and definition of angles used in text. On the
right: schema of the bio-inspired sensor fusion.
surface. We analyse the effect of a dead-band nonlin-
earity that affects the sensory-based estimate of the
support surface tilt. Such nonlinearity, common in
literature, is assumed on the basis of the behaviour ob-
served in humans. The formal conditions for Lyapunov
stability are investigated.
The paper is organized as follows: in Section 2, the
control problem is introduced and the body mechanics
is described; Section 3 provides details about human-
inspired sensor fusion and actuation; the conditions
726
Lippi, V. and Molinari, F.
Lyapunov Stability of a Nonlinear Bio-inspired System for the Control of Humanoid Balance.
DOI: 10.5220/0009970307260733
In Proceedings of the 17th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2020), pages 726-733
ISBN: 978-989-758-442-8
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
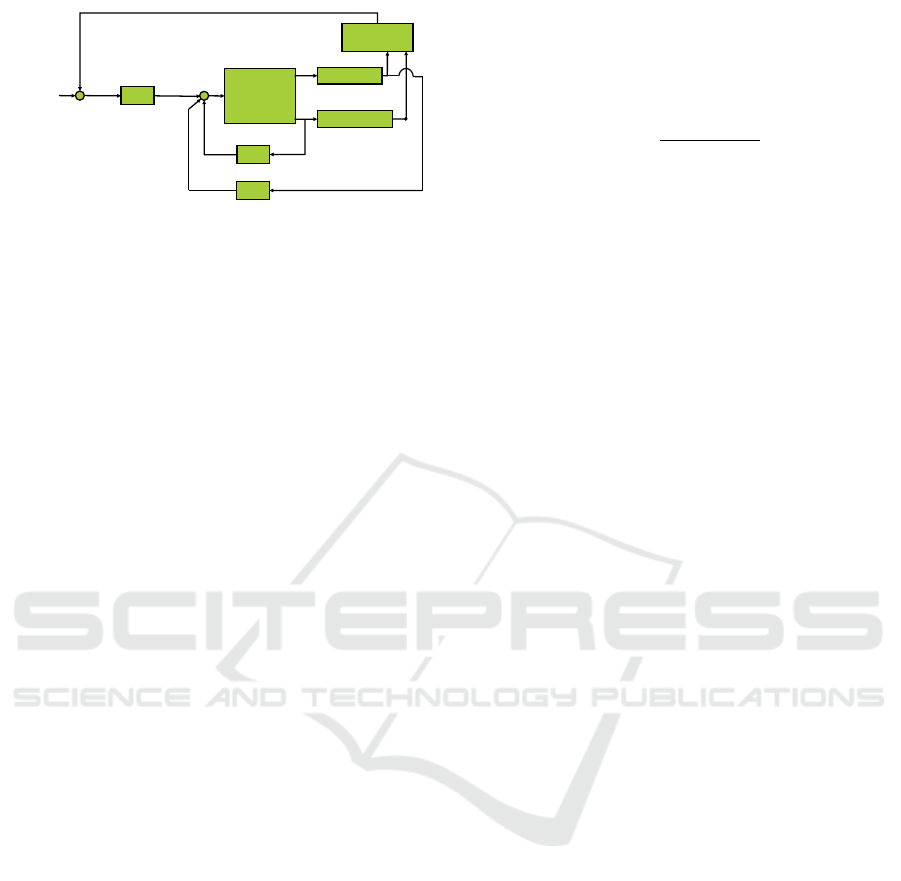
𝑷𝑫
Body
Dynamics
𝑷𝑫
Body sway
estimator
Passive
Desired Position
Neural
controller
-
-
-
Proprioception
Vestibular
𝜶
𝑩𝑭
𝑲
𝑮
-
Gravity compensation
𝜶
𝑩𝑺
ෝ
𝜶
𝑩𝑺
𝜶
𝒓𝒆𝒇
Figure 2: A scheme of a controller based on the DEC con-
cept. The sensory inputs are used to reconstruct the physical
disturbances acting on the body (in this scenario gravity and
support surface tilt). The system is controlled by a servo
controller, consisting of a PD regulator setting the desired
body position, and a direct compensation of the estimated
gravity disturbance.
for stability are obtained in Section 4, where evidence
is also provided; Section 5 presents simulations and a
qualitative discussion of the system behaviour; conclu-
sions and future work are presented in Section 6.
2 PROBLEM DESCRIPTION
Human posture dynamics in the sagittal plane is usu-
ally modelled as an inverted pendulum. Depending
on the scenario, the model can be a single inverted
pendulum (SIP), see, e.g., (Mergner et al., 2003; Jafari
et al., 2019), or a multiple inverted pendulum, see, e.g.,
(Alexandrov et al., 2017; Hettich et al., 2013; Lippi
et al., 2013; Lippi and Mergner, 2017; Abedi and
Shoushtari, 2012). The number of degrees of freedom
(DoF) representing the body dynamics is in general
linked to the intensity of external stimuli, see (Atkeson
and Stephens, 2007) for further details. In this work,
we consider a SIP model that is used to represent the
upright stance in presence of small disturbances. In
literature, models with 2 DoF have been used for mod-
elling balance in the frontal plane (Goodworth and
Peterka, 2010; Lippi et al., 2016).
In the remainder of this paper, we consider the fol-
lowing scenario: the subject is balancing on a tilting
platform whose inclination is controlled by an exter-
nal input. In order to keep the equilibrium despite
the tilting movement, the orientation in space of the
inverted pendulum is actively controlled by an ankle
movement.
Formally,
α
BS
∈ R
denotes the angle between the
body (pendulum axis) and the vertical (gravity axis).
α
BF
∈ R
denotes the angle between the body and the
axis normal to the tilting platform. The third consid-
ered angle is
α
FS
∈ R
that represents the angle of the
tilting platform with regards to the vertical axis. From
Figure 1, this three angles are linearly dependent, i.e.,
α
BF
= α
BS
− α
FS
. (1)
The torque provided by the ankle is
T
a
∈ R
, whereas
the one produced by the gravitational force is T
G
∈ R.
The pendulum dynamics is described by
¨
α
BS
=
T
a
+ T
p
+ T
G
J
B
, (2)
where
J
B
∈ R
>0
is the moment of inertia of the body
around the ankle joint and
T
p
∈ R
is the torque describ-
ing passive stiffness and damping, i.e.,
T
p
= K
p
p
α
BF
+ K
p
d
˙
α
BF
(3)
The passive stiffness, i..e,
K
p
p
, and damping, i.e.,
K
p
d
,
causes additional destabilisation. However, as in (Ott
et al., 2016), they have a role in stabilising the system
dynamics in presence of delays.
3 HUMAN-INSPIRED SENSORS
AND ACTUATION
3.1 Sensors’ Information
Signal
ˇ
α
BS
∈ R
provides the estimate of
α
BS
(body
sway) obtained by the vestibular system (or, for hu-
manoids, by the IMU). On the other hand, signal
ˇ
α
BF
∈ R
is the proprioceptive input measured at the an-
kle (for humanoids, given by an encoder). Both signals
are estimates of the corresponding physical quantities.
Their derivatives with respect to time are
˙
ˇ
α
BS
∈ R
,
sensed by the vestibular system, and
˙
ˇ
α
BF
∈ R
, sensed
by the proprioceptive system.
In what follows, we put a check symbol above all
measured variables (i.e.,
ˇx
). On the other hand, all
estimated variables have the ”hat” symbol above them
(i.e., ˆx).
3.2 Gravity Compensation
The gravity force is the largest effect acting on the
body, see (Zebenay et al., 2015). Formally, the torque
produced by this force is
T
G
= m
B
· g ·h
B
· sin (α
BS
),
where
g
is the gravity acceleration,
m
B
∈ R
>0
the body
mass, and
h
B
∈ R
>0
the height of the centre of mass.
Under the assumption of a small angle,
T
G
' m
B
· g · h
B
· α
BS
. (4)
The ankle torque, actively produced by the subject in
order to keep the body standing despite the tilting plat-
form, i.e.,
T
a
in (2), also compensates for this gravity
Lyapunov Stability of a Nonlinear Bio-inspired System for the Control of Humanoid Balance
727

Table 1: List of variables and their definition. The second column contains equation numbers, in parentheses, or section number
depending on where the variable is defined.
Variable Defined in Definition
α
BF
(1) Ankle joint angle
α
BS
(2) Body sway respect to the vertical
α
FS
§2 Support surface rotation
ˆ
α
FS
(8) Support surface rotation estimate based on sensor fusion (vestibular+proprioceptive)
ˆ
α
BS
(10) Body sway estimate based on sensory input (vestibular+proprioceptive)
ˇ
α
BS
§3.1 Body sway estimate based on vestibular input
disturbance. In fact, let
T
G
a
be the component of
T
a
compensating gravity, such that
T
a
= −T
G
a
+ T
a
a
, (5)
where
T
a
a
is the ankle torque’s component not due
to gravity compensation. Gravity is slightly under-
compensated in humans, see, e.g., (Mergner et al.,
2009; Hettich et al., 2014), thus, as in (Ott et al., 2016),
we assume an arbitrary gain, i.e.,
K
G
∈ R
>0
, for gravity
compensation. Thus,
T
G
a
= K
G
·
ˇ
α
BS
. (6)
3.3 Support Surface Tilt Compensation
In order to reproduce the behaviour observed in hu-
mans, see, e.g., (Mergner et al., 2009; Mergner et al.,
2003; Hettich et al., 2015; Hettich et al., 2014), the
control input
T
a
a
is not computed by directly using the
measured quantity
ˇ
α
BS
, but an estimate of
α
BS
, say
ˆ
α
BS
. To this end, first, the inspection of human be-
haviour suggests to use signal
˙
ˆ
α
FS
∈ R
, obtained by
using both vestibular and proprioceptive sensed val-
ues, to estimate the tilting platform’s angle. Denote
this estimate by
ˆ
α
FS
∈ R
. This value is then used for
computing
ˆ
α
BS
, which closes the control loop.
Formally, by (1), one has
˙
ˆ
α
FS
=
˙
ˇ
α
BS
−
˙
ˇ
α
BF
. (7)
The estimate of
ˆ
α
FS
simulates the human behaviour.
This is done by feeding
˙
ˆ
α
FS
into function
ρ(·)
, which
is then integrated through a leaky integrator, i.e.,
ˆ
α
FS
=
Z
t
0
ρ
˙
ˆ
α
FS
− c
L
ˆ
α
FS
dτ (8)
with c
L
∈ R
>0
and the threshold function defined as
ρ(α) :=
α + θ if α ≤ −θ
0 if − θ < α < θ
α − θ if θ ≤ α
, (9)
for θ ∈ R
>0
.
With this piece of information at hand, we compute
ˆ
α
BS
, the quantity used in T
a
a
, by employing (1), i.e.,
ˆ
α
BS
=
ˆ
α
FS
+
ˇ
α
BF
. (10)
3.4 Other Disturbances
In order to completely describe the effect of the envi-
ronment on the body, other disturbances should also
be taken into account. Field forces can be produced,
for example, by an horizontal translation of the sup-
port surface
x
f s
leading to a torque
T
trans
= ¨x
f s
·h
B
·m
B
and an external touch that can be estimated as
T
ext
=
¨
ˇ
α
BS
J
B
− T
a
. A robotic control applying also these dis-
turbances is described in (Zebenay et al., 2015). Cur-
rently, a model of human support surface translation
compensation is still object of research, and there are
no evidences yet of a direct compensation of such
disturbances. In this work only gravity will be consid-
ered.
3.5 Servo Control
As in (Ott et al., 2016), the system is controlled
through a
PD
controller with proportional coefficient,
respectively derivative coefficient, being
K
a
p
∈ R
, re-
spectively K
a
d
∈ R, i.e.,
T
a
a
= K
a
p
ε + K
a
d
dε
dt
, (11)
where the error variable ε is defined as
ε :=
ˆ
α
BS
− α
ref
, (12)
with the desired position being, in general,
α
ref
= 0
.
All delays involved into the processing of sensory in-
puts and the motor control are not considered in this
analysis. In neurology the concept was proposed in
(Merton, 1953) to explain the role of the muscle stretch
reflex for the control of posture and movements: a PD-
controller adjusts the force of the muscles so as to
produce the desired pose or movement.
Remark 1.
Gravity is compensated by directly using
the available measure
ˇ
α
BS
, whilst
T
a
a
uses the esti-
mated value
ˆ
α
BS
. This is due to the fact that the non-
linearity has been experimentally observed only on the
latter (Mergner et al., 2009; Mergner et al., 2003; Het-
tich et al., 2014). Qualitatively, the effect on the thresh-
old applied on
ˆ
α
BS
is that the slower the platform tilt-
ing is, the less it is compensated (gain nonlinearity).
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
728

For very slow platform movements (i.e.
˙
α
FS
< θ
), there
is even no compensation. A similar nonlinearity ap-
plied on the gravity compensation would produce a
paradoxical behaviour.
4 STABILITY ANALYSIS
Assumption 1.
As done in (Lippi and Mergner, 2017;
Lippi et al., 2013; Mergner, 2010), we assume the
direct measurements to be equal to the corresponding
variables, i.e.,
ˇ
α
BS
= α
BS
and
ˇ
α
BF
= α
BF
.
Let the input to the system be
u =
˙
α
FS
, (13)
i.e., the tilting speed of the platform. The state vector
is four-dimensional and equal to
x =
x
1
x
2
x
3
x
4
=
α
BS
˙
α
BS
ˆ
α
BS
α
FS
. (14)
Starting from (2), we derive a model for the system
at hand, by incorporating (4), (6), (8), (10), and (11).
This yields the following system:
˙x
1
= x
2
˙x
2
= a
1
x
1
+ a
2
x
2
+ a
3
x
3
+ a
4
x
4
+ f (u)
˙x
3
= bx
1
+ x
2
− bx
3
− bx
4
+ g(u)
˙x
4
= u
(15)
where
a
1
=
K
p
p
+ K
a
d
c
L
+ mgh
B
− K
G
J
B
, (16)
a
2
=
K
a
d
+ K
p
d
J
B
, (17)
a
3
=
K
a
p
− c
L
K
a
d
J
B
, (18)
a
4
=
K
p
p
− c
L
K
a
d
J
B
, (19)
b = C
L
, (20)
g(u) = ρ(u) − u , (21)
f (u) = K
a
d
g(u) − K
p
d
u. (22)
Note that the nonlinearity brought about by
ρ(·)
affects
the system only through input
u
. Figure 3 illustrates
f (u) and g(u).
System (15) can be also written in matrix form
1
,
i.e.,
˙
x(t) = Ax(t) + B(u(t)), (23)
1
In this case we explicitly report the dependence on time.
−θ θ
−θ
θ
g(u)
f
(
u
)
Figure 3: f (u) and g(u).
where
A :=
0 1 0 0
a
1
a
2
a
3
a
4
b 1 −b −b
0 0 0 0
(24)
and
B(u) :=
0
f (u(t))
g(u(t))
u(t)
. (25)
System (23) is a linear system, with nonlinearity on
the control input. The dynamics of the fourth state is
a simple integrator of input
u
, thus
0
is an eigenvalue
of the system’s dynamics. The remaining three eigen-
values can be determined by the choice of
K
p
a
and
K
d
a
,
our design parameters. In the following the stability
conditions are derived in an analytical way while in
previous work the stability of the DEC was demon-
strated empirically with simulations (Lippi et al., 2013)
and robot experiments (Hettich et al., 2014; Ott et al.,
2016; Zebenay et al., 2015).
Lemma 1. If K
a
p
and K
a
d
are chosen such that
K
a
d
< c
L
J
B
− K
p
d
, (26)
K
a
p
+ K
a
d
c
L
< K
G
− mgh
B
− K
p
p
− c
L
k
p
d
, (27)
K
a
p
< K
G
− mgh
B
− K
p
p
, (28)
then system (23) has three eigenvalue with negative
real part.
Proof.
By definition of eigenvalues, the spectrum of
A is
eig(A) = {0} ∪ eig(
˜
A),
where
˜
A :=
0 1 0
a
1
a
2
a
3
b 1 −b
.
The characteristic polynomial of
˜
A
, whose solutions
are
˜
A’s eigenvalues, is:
p
A
(λ) = λ
3
+(b−a
2
)λ
2
+(−a
3
−a
2
b − a
1
)λ− b(a
1
+a
3
).
Lyapunov Stability of a Nonlinear Bio-inspired System for the Control of Humanoid Balance
729

By the Descartes Rule of Signs, we can impose that all
eigenvalues of
˜
A have negative real part, by holding
b − a
2
> 0
−a
3
− a
2
b − a
1
> 0
−b(a
1
+ a
3
) > 0
.
This latter becomes a set of inequalities in
K
a
d
and
K
a
p
,
by incorporating (16)-(20). This yields (26)-(28), thus
concluding the proof.
Lemma 2. The solution to system (23) is
x(t) = e
At
x(0) +
Z
t
0
e
A(t−τ)
B(u(τ))dτ. (29)
Proof.
Let
u
1
(t) := f (u(t))
,
u
2
(t) := g(u(t))
, and
u
3
(t) := u(t). We have
˙
x(t) = Ax(t) +
˜
B
˜
u(t), (30)
with
˜
B
˜
u(t) = B(u(t)) (31)
where
˜
u(t) := [u
1
(t), u
2
(t), u
3
(t)]
0
and
˜
B :=
0 0 0
1 0 0
0 1 0
0 0 1
.
By (Skogestad and Postlethwaite, 2007, (4.7)),
x(t) = e
At
x(0) +
Z
t
0
e
A(t−τ)
˜
B
˜
u(τ)dτ,
which, by incorporating (31), yields (29), thus con-
cluding the proof.
In (29), the first addendum is the free response, and
the integral is referred to as forced response. By (29),
system’s stability is determined only by matrix
A
, thus
the nonlinearity acting on the input, i.e.,
B(u(t))
, does
not play any role for stability. The following two
definitions of stability are extracted from (Mellodge,
2015, Chapter 3) and (Bernstein and Bhat, 1995).
Definition 1
(Asymptotic Stability)
.
System (30) is
asymptotically stable if and only if all the eigenvalues
of A are in the left half of the complex plane.
Definition 2
(Lyapunov Stability)
.
System (30) is Lya-
punov stable if and only if no eigenvalues of A are in
the right half of the complex plane and all eigenvalues
on the imaginary axis are semisimple (i.e., they have
algebraic multiplicity equal to the geometric multiplic-
ity).
Theorem 1.
If
K
a
p
and
K
a
d
are chosen as in Lemma 1,
system (23) is Lyapunov stable, but not asymptotically
stable.
Proof.
Consider system (30) which is an equivalent
of (23). Clearly, system (30) is Lyapunov stable
(asymptotically stable) if and only if also (23) is Lya-
punov stable (asymptotically stable).
By Lemma 1, matrix
A
has three eigenvalues with neg-
ative real part and one eigenvalue (the integrator in
x
4
) which is on the imaginary axis and semisimple.
By Definition 2, system (30) is Lyapunov stable. By
Definition 2, system (30) is not asymptotically stable,
thus the proof is concluded.
The non-linear system can be stabilised by choos-
ing the appropriate pair of proportional and derivative
coefficients for the PD controller.
5 SIMULATION
The parameters, defined on the basis of human anthro-
pometrics (see (Winter, 2009)) and previous posture
control analysis (see (Mergner et al., 2009; Mergner
et al., 2003; Hettich et al., 2014)), are shown in Table 2.
With the specific set of parameters, and by (26)-(28),
Table 2: System parameters.
Parameter Value
J
B
71.55 Kg · m
2
K
g
0.8
K
p
p
157.31 N · m
K
p
d
39.32 N · m · s
c
L
0.0125 s
−1
θ 0.0028 rad
m 80 Kg
h 1.80 m
we design
K
a
p
= −1200 N · m
and
K
a
d
= −1000 N · m · s.
The behavior of the system is shown in regime of free
response with no support surface tilt velocity, and
forced response with a periodic input. Specifically the
following conditions are simulated:
Condition 1: free response with
x(0) = [π/10,0.1,π/10, 0]
T
.
The free response with no support surface tilt is the
characteristic one of a linear second-order system (see
Fig. 4). This happens because the nonlinearity affects
only the input
u(t)
. The leaky integrator used in the
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
730
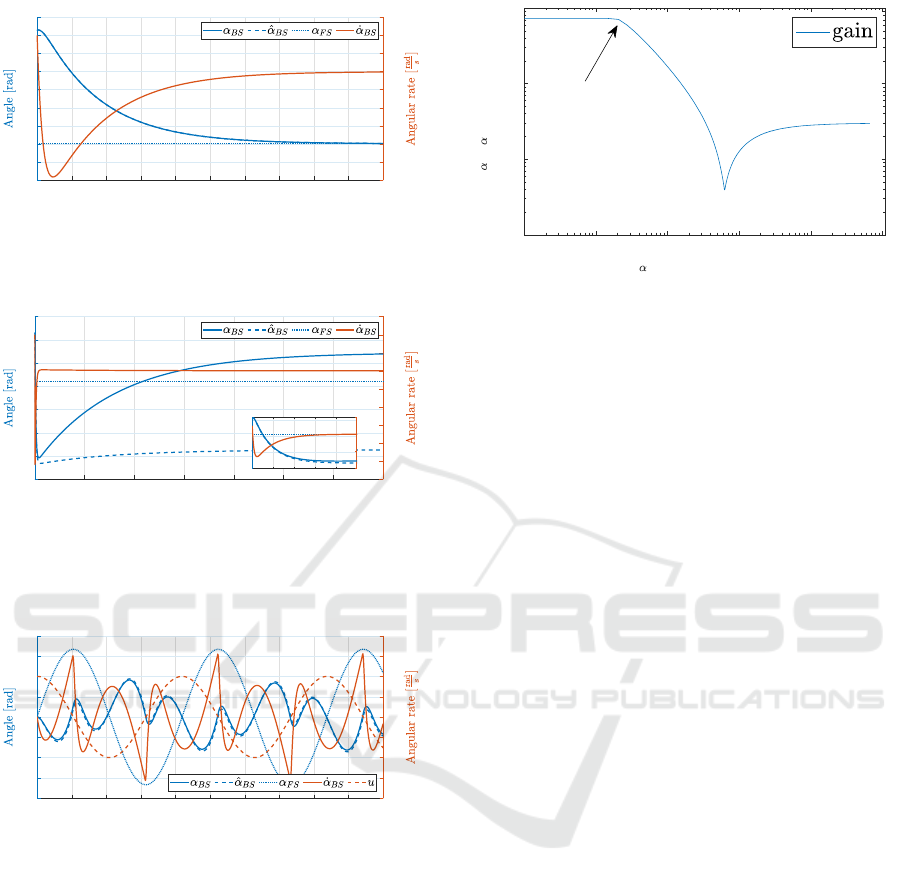
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time [s]
-0.1
-0.05
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
-0.3
-0.25
-0.2
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
Experiment 1. Free response
Figure 4: Free response with horizontal support surface and
initial conditions
x(0) = [π/10, 0.1,π/10,0]
T
.
The estimate
ˆ
α
BS
is equivalent to α
BS
when α
FS
= 0.
0 50 100 150 200 250 300 350
Time [s]
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
-0.3
-0.25
-0.2
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
Experiment 2. Free response
0 1 2 3 4 5
0
0.1
0.2
0.3
-0.4
-0.2
0
0.2
Figure 5: Free response with tilted, but not moving, support
surface and non-zero initial body sway velocity and body
lean, i.e.
x(0) = [π/10, 0.1,π/10, π/15]
T
.
The smaller plot
shows the transient during the first 5 seconds.
0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5
Time [s]
-0.04
-0.03
-0.02
-0.01
0
0.01
0.02
0.03
0.04
-0.2
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0.2
Experiment 3. Forced response
Figure 6: Forced response to sinusoidal support tilt with
initial conditions
x(0) = [0, 0,0, 0]
T
, and input
u(t) =
0.1cos(10t).
estimate of α
FS
is constantly at zero.
Condition 2: free response with
x(0) = [π/10,0.1,π/10, π/15]
T
.
The free response with a constant support surface tilt
is shown in Fig. 5. The response is again the char-
acteristic of a linear system, in which
x
4
behaves as
a constant signal affecting the dynamics of
x
2
and
x
3
.
There is a residual lean
α
BS
due to the error in body
sway estimate
ˆ
α
BS
.
Condition 3: forced response with
x(0) = [0,0,0, 0]
T
and
u(t) = 0.1cos(10t).
10
-4
10
-3
10
-2
10
-1
10
0
10
1
FS
p.p. Amplitude [rad]
10
-1
10
0
10
1
10
2
BS
/
FS
p.p. gain
peak velocity
reaches
the threshold
Figure 7: Support surface tilt to body sway gain with si-
nusoidal support tilt at different amplitude. The gain is
computed as the ratio between peak to peak amplitude for of
the input and the one of the output. Smaller support surface
tilt are associated with larger gains because they are under-
compensated due to the nonlinearity. The plateau on the left
is the zone of linear behavior that happens when the support
surface rotation speed is always under threshold
θ
. For larger
amplitudes the gain tends asymptotically to a constant gain,
i.e. linear behavior.
The forced response shows a partial rejection of the
external disturbance. The effect of the nonlinearity
is reflected in the difference between
α
BS
and its es-
timated value
ˆ
α
BS
. The simulations is repeated with
different amplitudes for the support surface tilt pro-
file, producing the results in Fig. 7. The gain, in this
context defined as the ratio between peak to peak am-
plitude for of the input and the output is plotted for
different amplitudes. Smaller support surface tilt are
associated with larger gains because they are under-
compensated due to the nonlinearity. Specifically the
plateau on the left is the zone of linear behavior that
happens when the support surface rotation speed is
always under threshold
θ
and the disturbance is not
compensated. For larger amplitudes the gain tends
asymptotically to a constant gain because the signal is
almost always above the threshold.
6 CONCLUSIONS AND FUTURE
WORK
The formal analysis of the system has provided a condi-
tion for the stability, specifically on the gains of the PD
controller, i.e.,
(26)
-
(28)
. This confirms the idea, sug-
gested by empirical experiments with human subjects
and robots, that the nonlinearity is benign in that it
does not endanger the stability of the system. There is
the hypothesis that such dead-band nonlinearity could
be useful in cutting out vestibular noise, especially
when the support surface is not moving (that is the
most common scenario in nature). In order to study
Lyapunov Stability of a Nonlinear Bio-inspired System for the Control of Humanoid Balance
731

the effect of the threshold on noise future work may in-
tegrate methods for the analysis of stochastic systems
(Han. et al., 2018; Bj
¨
ornsson. et al., 2018). Another
important aspect in posture control, that was not con-
sidered here, is the effect of delay. Delay imposes a
limitation on feedback gain that can be considered the
motivation for the feed-forward compensation of ex-
ternal disturbances (in this work, gravity). The effects
of delay have been studied formally in the linear case
(Antritter et al., 2014), but not yet with the nonlinear
system. As the DEC has also been applied to multi-
ple degrees of freedom scenarios (Lippi et al., 2019b;
Lippi and Mergner, 2017) the formal study may be ex-
tended to multiple inverted pendulum models. A way
to tackle the complexity of the multiple DoF problem
may require the use of numerical methods for the study
of the stability (Giesl. et al., 2018; Bj
¨
ornsson. and
Hafstein., 2018; Giesl. and Mohammed., 2018), this
will require a particular effort considering the number
of state variables required to represent the dynamics
of the mechanical degrees of freedom, the dynamics
of the sensory estimates (e.g. the leaky integrator in
the presented work) and the ones used to represent the
delays.
ACKNOWLEDGEMENTS
C
O
M
T
T
S
E
This work is supported by the project
COMTEST (Lippi et al., 2019a), a
sub-project of EUROBENCH (European
Robotic Framework for Bipedal Locomotion
Benchmarking, www.eurobench2020.eu)
funded by H2020 Topic ICT 27-2017 under
grant agreement number 779963.
REFERENCES
Abedi, P. and Shoushtari, A. L. (2012). Modelling and
simulation of human-like movements for humanoid
robots. In Proceedings of the 9th International Con-
ference on Informatics in Control, Automation and
Robotics - Volume 1: ICINCO, pages 342–346. IN-
STICC, SciTePress.
Alexandrov, A. V., Lippi, V., Mergner, T., Frolov, A. A.,
Hettich, G., and Husek, D. (2017). Human-inspired
eigenmovement concept provides coupling-free sen-
sorimotor control in humanoid robot. Frontiers in
neurorobotics, 11:22.
Antritter, F., Scholz, F., Hettich, G., and Mergner, T. (2014).
Stability analysis of human stance control from the
system theoretic point of view. In Control Conference
(ECC), 2014 European, pages 1849–1855. IEEE.
Atkeson, C. G. and Stephens, B. (2007). Multiple balance
strategies from one optimization criterion. In 2007
7th IEEE-RAS International Conference on Humanoid
Robots, pages 57–64. IEEE.
Bernstein, D. S. and Bhat, S. P. (1995). Lyapunov stabil-
ity, semistability, and asymptotic stability of matrix
second-order systems. Journal of mechanical design,
117(B):145–153.
Bj
¨
ornsson., H., Giesl., P., Gudmundsson., S., and Hafstein.,
S. (2018). Local lyapunov functions for nonlinear
stochastic differential equations by linearization. In
Proceedings of the 15th International Conference on
Informatics in Control, Automation and Robotics - Vol-
ume 2: CTDE, pages 579–586. INSTICC, SciTePress.
Bj
¨
ornsson., H. and Hafstein., S. (2018). Verification of a
numerical solution to a collocation problem. In Pro-
ceedings of the 15th International Conference on Infor-
matics in Control, Automation and Robotics - Volume
2: CTDE, pages 587–594. INSTICC, SciTePress.
Bleisteiner, G. and Mangoldt, W. (2013). Handbuch der
Regelungstechnik. Springer-Verlag.
Boonstra, T. A., van Vugt, J. P., van der Kooij, H., and Bloem,
B. R. (2014). Balance asymmetry in parkinson’s dis-
ease and its contribution to freezing of gait. PLoS One,
9(7):e102493.
Engelhart, D., Boonstra, T. A., Aarts, R. G., Schouten, A. C.,
and van der Kooij, H. (2016). Comparison of closed-
loop system identification techniques to quantify multi-
joint human balance control. Annual Reviews in Con-
trol, 41:58–70.
Engelhart, D., Pasma, J. H., Schouten, A. C., Meskers, C. G.,
Maier, A. B., Mergner, T., and van der Kooij, H. (2014).
Impaired standing balance in elderly: a new engineer-
ing method helps to unravel causes and effects. Jour-
nal of the American Medical Directors Association,
15(3):227–e1.
Giesl., P., Arg
´
aez., C., Hafstein., S., and Wendland., H.
(2018). Construction of a complete lyapunov func-
tion using quadratic programming. In Proceedings of
the 15th International Conference on Informatics in
Control, Automation and Robotics - Volume 2: CTDE,
pages 560–568. INSTICC, SciTePress.
Giesl., P. and Mohammed., N. (2018). Combination of refine-
ment and verification for the construction of lyapunov
functions using radial basis functions. In Proceedings
of the 15th International Conference on Informatics in
Control, Automation and Robotics - Volume 2: CTDE,
pages 569–578. INSTICC, SciTePress.
Goodworth, A. D. and Peterka, R. J. (2010). Influence of
stance width on frontal plane postural dynamics and
coordination in human balance control. Journal of
Neurophysiology, 104(2):1103–1118.
Goodworth, A. D. and Peterka, R. J. (2018). Identifying
mechanisms of stance control: a single stimulus multi-
ple output model-fit approach. Journal of Neuroscience
Methods, 296:44–56.
Han., H., Hamasaki., D., and Fu., J. (2018). State- and
uncertainty-observers-based controller for a class of t-s
fuzzy models. In Proceedings of the 15th International
Conference on Informatics in Control, Automation and
Robotics - Volume 2: CTDE, pages 551–559. INSTICC,
SciTePress.
Hettich, G., Assl
¨
ander, L., Gollhofer, A., and Mergner, T.
(2014). Human hip—ankle coordination emerging
ICINCO 2020 - 17th International Conference on Informatics in Control, Automation and Robotics
732

from multisensory feedback control. Human Movement
Science, 37:123–146.
Hettich, G., Lippi, V., and Mergner, T. (2013). Human-like
sensor fusion mechanisms in a postural control robot.
In Londral, A. E., Encarnacao, P., and Pons, J. L., ed-
itors, Proceedings of the International Congress on
Neurotechnology, Electronics and Informatics. Vilam-
oura, Portugal, pages 152–160.
Hettich, G., Lippi, V., and Mergner, T. (2015). Human-like
sensor fusion implemented in the posture control of a
bipedal robot. In Neurotechnology, Electronics, and
Informatics, pages 29–45. Springer.
Jafari, H., Nikolakopoulos, G., and Gustafsson, T. (2019).
Stabilization of an inverted pendulum via human brain
inspired controller design. In IEEE-RAS International
Conference on Humanoid Robots. IEEE.
Jeka, J. J., Allison, L. K., and Kiemel, T. (2010). The dynam-
ics of visual reweighting in healthy and fall-prone older
adults. Journal of motor behavior, 42(4):197–208.
Lippi, V. and Mergner, T. (2017). Human-derived distur-
bance estimation and compensation (dec) method lends
itself to a modular sensorimotor control in a humanoid
robot. Frontiers in neurorobotics, 11:49.
Lippi, V., Mergner, T., and Hettich, G. (2013). A bio-inspired
modular system for humanoid posture control. In:
Ugur, E., Oztop, E., Morimoto, J., and Ishii, S. (Eds)
Proceedings of IROS 2013 Workshop on Neuroscience
and Robotics ”Towards a robot-enabled, neuroscience-
guided healthy society”.
Lippi, V., Mergner, T., Seel, T., and Maurer, C. (2019a).
COMTEST project: A complete modular test stand
for human and humanoid posture control and balance.
In 2019 IEEE-RAS 19th International Conference on
Humanoid Robots (Humanoids) Toronto, Canada. Oc-
tober 15-17.
Lippi, V., Mergner, T., Szumowski, M., Zurawska, M. S.,
and Zieli
´
nska, T. (2016). Human-inspired humanoid
balancing and posture control in frontal plane. In
ROMANSY 21-Robot Design, Dynamics and Control:
Proceedings of the 21st CISM-IFToMM Symposium,
June 20-23, Udine, Italy, volume 569, pages 285–292.
Springer.
Lippi, V., Molinari, F., and Seel, T. (2019b). Distributed
bio-inspired humanoid posture control. In 2019 41st
Annual International Conference of the IEEE Engineer-
ing in Medicine and Biology Society (EMBC), pages
5360–5365. IEEE.
Luecke, R. H. and McGuire, M. (1968). Analysis of opti-
mal composite feedback-feedforward control. AIChE
Journal, 14(1):181–189.
Mellodge, P. (2015). A Practical Approach to Dynamical
Systems for Engineers. Woodhead Publishing.
Mergner, T. (2010). A neurological view on reactive human
stance control. Annual Reviews in Control, 34(2):77–
198.
Mergner, T., Maurer, C., and Peterka, R. J. (2003). A multi-
sensory posture control model of human upright stance.
Progress in Brain Research, 142:189–201.
Mergner, T., Schweigart, G., and Fennell, L. (2009). Vestibu-
lar humanoid postural control. Journal of Physiology -
Paris, 103:178–194.
Merton, P. (1953). Speculations on the servo-control of
movement. In Ciba Foundation Symposium-The Spinal
Cord, pages 247–260. Wiley Online Library.
Ott, C., Henze, B., Hettich, G., Seyde, T. N., Roa, M. A.,
Lippi, V., and Mergner, T. (2016). Good posture, good
balance: comparison of bioinspired and model-based
approaches for posture control of humanoid robots.
IEEE Robotics & Automation Magazine, 23(1):22–33.
Pasma, J., Engelhart, D., Schouten, A., Van der Kooij, H.,
Maier, A., and Meskers, C. (2014). Impaired standing
balance: the clinical need for closing the loop. Neuro-
science, 267:157–165.
Peterka, R. (2002). Sensorimotor integration in human pos-
tural control. Journal of neurophysiology, 88(3):1097–
1118.
Roffel, B. and Betlem, B. (2007). Process dynamics and
control: modeling for control and prediction. John
Wiley & Sons.
Skogestad, S. and Postlethwaite, I. (2007). Multivariable
feedback control: analysis and design, volume 2. Wi-
ley New York.
van Asseldonk, E. H., Buurke, J. H., Bloem, B. R., Ren-
zenbrink, G. J., Nene, A. V., van der Helm, F. C., and
van der Kooij, H. (2006). Disentangling the contri-
bution of the paretic and non-paretic ankle to balance
control in stroke patients. Experimental neurology,
201(2):441–451.
van der Kooij, H., van Asseldonk, E., and van der Helm, F. C.
(2005). Comparison of different methods to identify
and quantify balance control. Journal of neuroscience
methods, 145(1-2):175–203.
van der Kooij, H., van Asseldonk, E. H. F., Geelen, J., van
Vugt, J. P. P., and Bloem, B. R. (2007). Detecting
asymmetries in balance control with system identifica-
tion: first experimental results from parkinson patients.
Journal of Neural Transmission, 114(10):1333.
Winter, D. A. (2009). Biomechanics and motor control of
human movement. John Wiley & Sons.
Zebenay, M., Lippi, V., and Mergener, T. (2015). Human-
like humanoid robot posture control. In 2015 12th
International Conference on Informatics in Control,
Automation and Robotics (ICINCO), volume 2, pages
304–309. INSTICC, SciTePress.
Zhong, H., Pao, L., and de Callafon, R. (2012). Feedforward
control for disturbance rejection: Model matching and
other methods. In 2012 24th Chinese Control and De-
cision Conference (CCDC), pages 3528–3533. IEEE.
Lyapunov Stability of a Nonlinear Bio-inspired System for the Control of Humanoid Balance
733
