Address-bit Differential Power Analysis on Boolean Split Exponent

Counter-measure

Christophe Negre

1,2

DALI, Universit

e de Perpignan, France

LIRMM, Universit

e de Montpellier et CNRS, France

Keywords:

Side Channel Analysis, Address Bit Differential Power Analysis, Exponentiation, Randomization.

Abstract:

Current public key cryptographic algorithms (RSA, DSA, ECDSA) can be threaten by side channel analyses.

The main approach to counter-act such attacks consists in randomizing sensitive data and address bits used in

loads and stores of an exponentiation algorithm. In this paper we study a recent counter-measure ”Boolean

split exponent” (Tunstall et al. 2018) preventing differential power analysis on address bits. We show that one

of their proposed protections has a ﬂaw. We derive an attack exploiting this ﬂaw and we successfully apply it

on a simulated power consumption of an RSA modular exponentiation.

1 INTRODUCTION

Side channel analysis is a serious threat for devices

performing cryptographic computation. Speciﬁcally,

it can threaten exponentiation x

involved in cur-

rently used cryptosystems (RSA, DSA and ECDSA).

In 1996, in a seminal work (Kocher, 1996) Kocher

showed that a statistical analysis of the computation

time can leak out the secret key used in RSA cryp-

tosystem. Afterwards, it was shown that the power

consumption can be used to extract secret informa-

tion: with simple power analysis (SPA) (Kocher et al.,

1999) one can read on the power trace the sequence of

operations (squaring/multiplication) performed dur-

ing an exponentiation and then deduce the secret ex-

ponent. In (Kocher et al., 1999) the authors introduce

the differential power analysis (DPA) which computes

differences on the power traces to determine the bits

of the key.

To counter-act these side channel analyses, the ba-

sic approach is to randomly mask sensitive data: we

can blind the point x by multiplying it by a random

element (Coron, 1999) or use randomized represen-

tation (Clavier et al., 2010), and we can use addi-

tive or multiplicative mask of the exponent (Coron,

1999; Tunstall and Joye, 2010). But this is not al-

ways sufﬁcient, since it was shown (Itoh et al., 2003)

that the loads and stores performed during the expo-

nentiation induce a power consumption correlated to

the corresponding address bits. This can be exploited

to mount a differential power analysis on the address

bits (ADPA). Recently some strategies (Izumi et al.,

2010; Tunstall et al., 2018) were proposed to counter-

act this attack by randomizing the address bits used in

the loads and stores of the exponentiation algorithm.

Contribution. In this paper we analyse a poten-

tial ﬂaw in the signed version of the boolean exponent

splitting approach of (Tunstall et al., 2018). We show

that the sequence of operations (squarings and multi-

plications) are not fully regular: we show that if we

can distinguish a squaring from a multiplication we

can deduce the bit used to randomize the address bits.

Then a classical differential power analysis on the ad-

dress bits can be performed to determine the secret ex-

ponent. We validate this attack by simulating power

traces based on the Hamming weight model. We pro-

vide a method for distinguishing a squaring from a

multiplication which has a high level of conﬁdence.

Then we show that an ADPA attack can be performed

and successfully deduce the secret exponent with a

few thousand power traces.

Organization of the Paper. In Section 2 we review

power analyses on exponentiation algorithm and re-

lated counter-measures. In Section 3 we show that

there is a ﬂaw in the counter-measures “boolean split-

ting exponent” of (Tunstall et al., 2018). In Section 4

we present our approach for power consumption sim-

ulation of modular exponentiation, and we apply an

attack on the “boolean splitting exponent” exploiting

the ﬂaw shown in Section 3. We ends the paper in

Section 5, with a few concluding remarks.

632

Negre, C.

Address-bit Differential Power Analysis on Boolean Split Exponent Counter-measure.

DOI: 10.5220/0009891306320637

In Proceedings of the 17th International Joint Conference on e-Business and Telecommunications (ICETE 2020) - SECRYPT, pages 632-637

ISBN: 978-989-758-446-6

2 REVIEW OF POWER

ANALYSES

In currently used public key cryptosystems (e.g. RSA,

DSA, ECDSA), the sensitive operation is an exponen-

tiation x

for x ∈ G a ﬁnite group or ring and κ a

secret exponent. With the square-and-multiply algo-

rithm one can compute x

as a sequence of squarings

R ← R

followed by a multiplication g ← g × x when

the i-th bit κ

= 1. This basic approach is not secure

when considering side channel analysis. For exam-

ple, if we monitor the power consumption of an ex-

ponentiation, then, a simple power analysis (Kocher

et al., 1999) can identify on the trace the operations

performed (square or multiplication) on the device

and then deduce the secret exponent κ. To counter-

act this attack modiﬁed versions of the square-and-

multiply exponentiation are recommended for which

the sequence of computed operations is not related to

bits of the exponent κ. The most popular method is

the Montgomery ladder (Joye and Yen, 2002) which

involves two variables R

and R

, for which, during

the exponentiation, we always have R

= xR

and the

loop iteration is always a multiplication followed by

a squaring (cf. Algorithm 1).

Algorithm 1: Montgomery-ladder.

Require: x ∈ G, one n-bit integers κ =

∑

n−1

i=0

Ensure: x

1: R

← 1

; R

← x;

2: for i = n − 1 down to 0 do

3: R

1−κ

← R

· R

¬κ

;

4: R

← R

;

5: return R

The Montgomery ladder is a good protection

against SPA, but it is not robust against attack like dif-

ferential power analysis (DPA) (Kocher et al., 1999),

collision attack (Fouque and Valette, 2003; Yen et al.,

2006). Indeed these attacks guess one or several bits

of the key and they predict the power consumption

at some iteration of the exponentation. If this predic-

tion is correct this means that the guessed bits are also

correct otherwise one can try another guess. To coun-

teract such attacks at the algorithmic level, the best

approaches randomize data in order to render power

consumption unpredictable:

• Point blinding. The strategy here is to hide the

data x and R

by either multiplying x by a

random element (Coron, 1999), adding a ran-

dom mask or by randomizing the representation

of x (Clavier et al., 2010).

• Exponent masking. In this case we randomly

modify the exponent. (Coron, 1999) proposed to

add to κ a random mutiple r ×N where N is the or-

der of G. One can also (Tunstall and Joye, 2010)

randomize the exponent as κ

= β

−1

κ mod N and

compute x

as (x

)

Point blinding and Exponent masking counter-

measures induce an overhead which, for the later, is

important since the level of randomization have to be

larger than the longest run of 0 or 1 in κ (Smart et al.,

2008).

Point blinding approaches used alone are not suf-

ﬁcient to counter-act DPA attack on the address bits

(ADPA (Itoh et al., 2003)). Indeed guessing a few key

bits leads to a prediction of the address bits involved

in the loads and stores performed during the expo-

nentiation. Predicting these address bits, leads to pre-

dicting the behavior of the power consumption dur-

ing the loads or stores and performing a DPA on sev-

eral power traces validates the guessed key bit or not.

Since point blinding counter-measures do not modify

the sequence of operations done during the exponen-

tiation, they do not protect the implementation from

an ADPA.

Consequently, to counter-act such DPA on address

bits, the authors in (Izumi et al., 2010) proposed a ﬁrst

version of the Montgomery-ladder which randomizes

the loads and stores. This work was subsequently im-

proved in (Tunstall et al., 2018) which provides two

kinds of randomized Montgomery-ladder. In their

ﬁrst approach they use one random bit a

to split the

key bit κ

= a

⊕ b

and which decides the order of

loads R

and R

for the multiplication R

×R

in Step

3 of Algorithm 1. This bit a

is also used to randomly

store the results of the squaring in Step 4 and the mul-

tiplication in Step 3 of Algorithm 1 done in one itera-

tion of the Montgomery ladder. This requires a bit b

which memorizes how the value are stored in the two

registers R

and R

at the end of a loop iteration. This

approach is shown in Algorithm 2.

Algorithm 2: Montgomery-Ladder with XOR split exponent

I (Tunstall et al., 2018).

Require: x ∈ G, two n-bit integers A =

∑

n−1

i=0

and

B =

∑

n−1

i=0

Ensure: x

where κ = A ⊕ B

1: R

← 1

; R

← 1

; R

← 1

; b

←

{0,1};

¬b

← x;

2: for i = n − 1 down to 0 do

3: R

← R

· R

¬a

;

4: R

← R

⊕b

)⊕a

;

5: R

¬a

← R

;

6: b

← b

;

7: return R

Address-bit Differential Power Analysis on Boolean Split Exponent Counter-measure

633

The authors in (Tunstall et al., 2018) propose a

second approach (Algorithm 3) which randomizes the

signed version of the Montgomery ladder. This algo-

rithm perform the exponentiation as a sequence of two

multiplications one between R

and R

and between

and either U

= x or U

= x

−1

. In Algorithm 3 the

addresses used in the store instructions are ﬁxed and

then they are not correlated to the bits of the expo-

nent. The random bit a

(and thus b

= κ

⊕a

) is used

to randomize the load instructions in Step 4 and Step

5. The bit b

is used to memorize how the data are

placed in the registers R

and R

at the end of a loop

iteration.

Algorithm 3: Montgomery-Ladder with XOR split exponent

II (Tunstall et al., 2018).

Require: x ∈ G, two n-bit integers A =

∑

n−1

i=0

and

B =

∑

n−1

i=0

Ensure: x

where κ = A ⊕ B

1: R

← 1

; R

← 1

; R

← 1

; b

←

{0,1};

¬b

← x;

2: for i = n − 1 down to 0 do

3: R

← R

⊕b

· R

⊕b

)⊕a

;

4: R

← R

·U

;

5: b

← b

;

6: return R

3 WEAKNESSES OF BOOLEAN

SPLIT RANDOMIZATION

In (Tunstall et al., 2018) the authors claim that their

algorithm combined with a point blinding technique

has the same security level but with a lower cost as the

method based on randomizing the exponent (Coron,

1999; Tunstall and Joye, 2010). For Algorithm 2

and 3, this is not entirely true:

• Randomizing the exponent alone prevents from

the three attacks : DPA, collision and ADPA. This

approach ensure that the sequence of points R

0,i

and R

1,i

in G for i = n − 1, . . . , 0 computed dur-

ing the exponentiation are always different. This

renders impossible to predict the power consump-

tion of operation involving R

0,i

and R

1,i

and then

prevents DPA and collision attack. Randomizing

the exponent also randomly changes the bits of the

exponent, which implies that the stores and loads

are also randomized and thus unpredictable.

• Randomizing the loads and stores like it is done in

Algorithm 2 and 3 does not modify the sequence

of computed element R

0,i

and R

1,i

of G. So a cor-

rect guess of the bits of the exponent would lead

to a correct guess of R

and R

at the considered

iteration. So if we want to hide these values we

have to inject a high level of randomization oth-

erwise a small amount of leakage could be ex-

ploited and would lead to a successful DPA. The

only approach which produces a randomized and

unpredictable sequence of computed points R

0,i

and R

1,i

in the exponentiation is the point blinding

of (Coron, 1999) which multiplies x by a random

value.

The table below summarizes the strength of the

counter measures reviewed in Section 2 when they are

used alone. This table shows that exponent random-

izations are the most robust methods.

Table 1.

Counter-measure DPA and CA ADPA

Point blinding yes no

Exponent randomization yes yes

Address randomization no yes

Algorithm 3 has a more important ﬂaw. The main

problem of Algorithm 3 is that in Step 3, a multipli-

cation of two different data R

and R

is done when

= 1 but when a

= 0 this multiplication is either

× R

or R

× R

, which are squarings done us-

ing a multiplication routine. But distinguishig such a

squaring done with multiplication routine from a gen-

uine multiplication can be detected by power analysis.

In (Hanley et al., 2011) the authors showed that the

power consumption of these operations can be distin-

guished using template methodology.

If we successfully distinguish the power trace of

× R

from either R

× R

or R

× R

, for unknown

and R

, we can deduce the value of a

for i = n −

1,...,0. Then the randomization of loads and stores

is broken and DPA can be conducted on the address

bits of Algorithm 3.

4 EXPERIMENTATION

In this section we present experimental results of the

proposed attack on address randomization of Algo-

rithm 3. The attack is performed on a simulated power

traces using the hamming weight leakage model.

4.1 Simulation of Power Consumption

We target an RSA modular exponentiation with an

RSA modulus N of bit length 1024. We consider an

implementation of the modular exponentiation RSA

based on a word-level Montgomery modular multi-

plication algorithm (Bosselaers et al., 1993). Then

in order to simulate the power consumption of a full

SECRYPT 2020 - 17th International Conference on Security and Cryptography

634

FAFA

FA = Full Adder

FA FA

0, ..., 0, b

, ..., b

, . . . , r

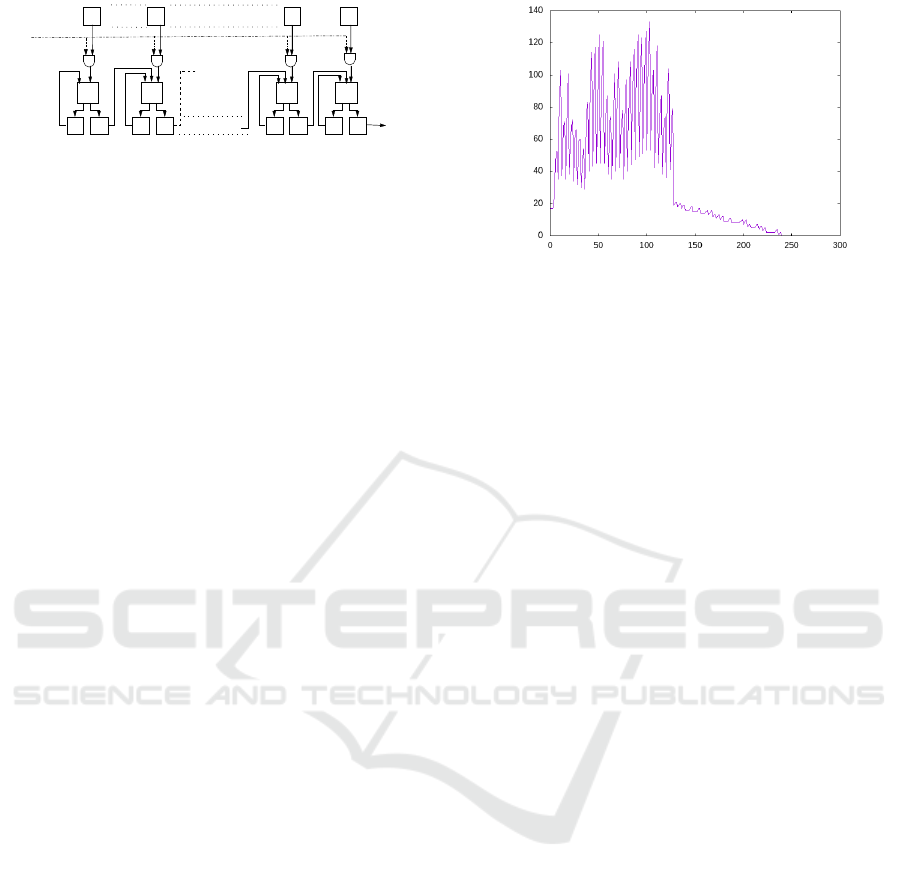
Figure 1: 32-Bit sequential multiplier.

modular multiplication we only need to generate the

power consumption of w-bit additions and multiplica-

tions.

32-bit multiplier and adder. We deﬁned a circuit per-

forming multiplication of 32-bit integers and a circuit

performing addition of 32-bit integers. The multi-

plier shown in Fig. 1 is a bit sequential multiplier.

It computes r = a × b where a = (a

,...,a

)

and

b = (b

,...,b

)

as shown in the following pseudo-

code:

for i = 0 to 32 do

r ← r + 2

× a)

The i-th bit r

is output after the i-th clock-cycle. The

additions in Fig. 1 are done through carry save adder

in order to reduce the critical path delay. This means

that the carries are not propagated and but are saved

in the ﬂip-ﬂops c

for i = 0,...,31. After the ﬁrst 32

iterations the ﬁrst 32 bits r

,...,r

of r are generated

and output. But it remains to perform 32 more itera-

tions, with input 0 in place of b

,to propate the carries

and generate r

,...,r

We do not provide the circuit of the 32-bit adder,

since it is a classical 32 bit adder, which can be easily

found in the literature.

To get the power consumption of one clock-cycle

of the multiplier we compute the hamming weight of

signal ﬂowing in the wires. We split the clock cycle

into four parts P

and P

. We assume that at be-

ginning of a cycle there are only 0 on all wires. Then

we propagate data from the ﬂip-ﬂop and deduce the

simulated consumption:

• Each wire containing a signal 1 and connecting

a ﬂip-ﬂop and a ﬁrst gate contributes to 1 on the

consumption of P

and P

• Each wire containing a 1 and connecting a ﬁrst

gate and a second gate contributes to to the con-

sumption of P

and P

• Each wire containing a 1 and connecting a second

gate and a third gate contributes to 1 to the con-

sumption of P

and P

• Each wire containing a 1 and connecting a third

gate and the ﬂip-ﬂop contributes to 1 to the con-

sumption of P

The above simulation of the consumption is highly

Figure 2: Power trace of a 32-bit multiplication.

simpliﬁed but we believe that it is sufﬁcient to vali-

date the potential threat of the proposed attack on Al-

gorithm 3. We show in Fig. 2 an example of the simu-

lated power consumption of one w-bit multiplication.

Word level Montgomery modular multiplication. For

a modular multiplication we use the word level

version (Bosselaers et al., 1993) of the Mont-

gomery modular multiplication with word size w.

Given two integers A and B consisting of s words

the modular multiplication are performed as fol-

lows

1: R ← (0,. . . , 0)

2: for i = 0 to s − 1 do

3: q ← (R + A[i] × B) × N

mod 2

4: R ← (R + q × N + A[i] × B)/2

Step 3 consists of two w-bit multiplications and

one w-bit addition. Step 4 involves two products of

a ws-bit integer by a w-bit integer and two additions

of two ws-bit integers. Each of these operations are

computed through a sequence of w-bit multiplications

and/or additions.

4.2 Distinguishing a Square from a

Multiplication

We would like to distinguish a multiplication (A × B)

mod N from a squaring (A × A) mod N. The main

idea to get such distinguisher is that during the mul-

tiplication of (A × A) mod N for each i 6= j the same

product is done twice as A[i] × A[ j] and in reverse

operand A[ j] × A[i] in Step 3 the word level Mont-

gomery multiplication. But since these multiplica-

tions involve the same data their power trace must be

correlated.

Then we tried to compute the covariance of the

power traces of the 32-bit multiplication in order to

determine if they are correlated or not. But this strat-

egy was not successful. Probably this is due to the

non symmetric form of the considered 32-bit multi-

plier. We tried another strategy where we evaluate the

Address-bit Differential Power Analysis on Boolean Split Exponent Counter-measure

635

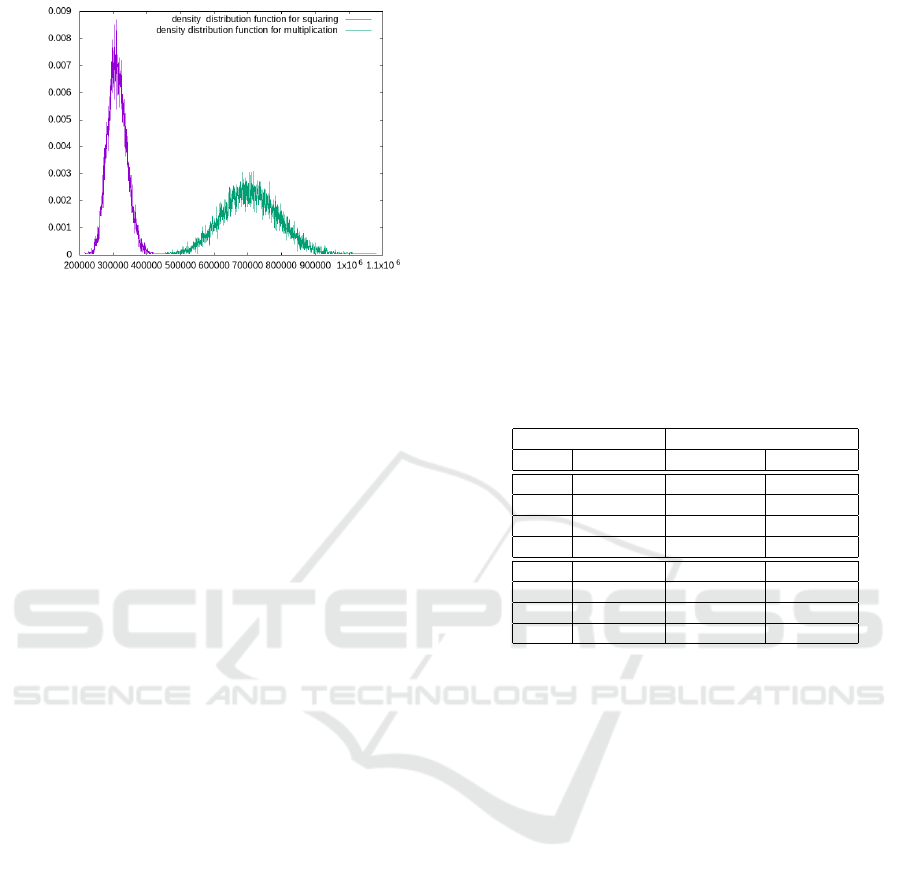
Figure 3: Square and non square repartition of power con-

sumption.

difference of the mean of the power traces:

i, j

(A,B)=

Tr(Mul(A[i], B[ j])

−

Tr(Mul(B[i], A[ j])

This computed value might be low if A = B,

since, in this case, many computed bits appearing

in the multiplication Mul(A[i],A[ j]) also appear in

Mul(A[ j],A[i]) and they cancel out in the difference

of σ

i, j

(A,A). If A 6= B these bits do not cancel out re-

sulting in a higher value for σ

i, j

(A,B). This effect is

ampliﬁed if we add up σ

i, j

(A,B) over all i < j:

σ(A,B) =

∑

0≤i< j≤s

i, j

(A,B).

In order to check this fact we performed the fol-

lowing experiment: for a sufﬁciently large number of

time (

∼

10000) we chose randomly A and B and com-

puted σ(A, B) and σ(A, A). We obtained the resulting

density distribution function shown in Fig. 3.

Fig. 3 clearly shows that we can easily distinguish

a squaring from a genuine multiplication. We esti-

mated the mean value m and the standard deviation d

for the two cases: squaring (S) and genuine multipli-

cation (M):

= 310000,d

= 28000

= 710038,d

= 82000

Given a power trace for a multiplication A × B

mod N, we compute σ(A,B) and we deduce that A =

B if σ(A,B) is close to m

and A 6= B if it is close to

. To a get an estimation of the probability of suc-

cess of this approach, we use the following inequal-

ity of Bienaym

e-Tchebychev for a random variable X

with mean m and standard deviation d:

P(|X −m| > kd) < 1/k

We chose k = 3 leading to a level of conﬁdence in

our distinguisher of 1 − 1/9.This is validated by an

experiment for 5000 samples for which we get 99.5%

of success.

4.3 Final Step: ADPA

Now, since we have a reliable distinguisher, we can

proceed to the next step: ﬁnding the bits of the expo-

nent with a DPA attack on the address bits. Given a

power trace of an exponentiation x

mod N we can

ﬁnd the random bit a

used in Algorithm 3 for all

i = 0,...,n − 1. Our goal now is to ﬁnd difference

of the power trace related to the address bits involved

in loads or stores. Let us analyze the loads and stores

in order to select interisting power traces and compute

a difference producing a peak if the guess is incorrect

and a ﬂat trace if the guess is correct.

The table below shows the relation between the

(i + 1)-th iteration and i-th iteration for the operation

done in Step 5 in Algorithm 3 depending on the value

of b

and a

Table 2.

(i + 1)-th iter. i-th iter.

bit Op. (Step 5) bits Op. (Step 4)

= 0 R

← R

= 0, a

= 0 R

← R

= 0 R

← R

= 0, a

= 1 R

← R

= 1 R

← R

= 0, a

= 0 R

← R

= 1 R

← R

= 0, a

= 1 R

← R

= 0 R

← R

= 1, a

= 0 R

← R

= 0 R

← R

= 1, a

= 1 R

← R

= 1 R

← R

= 1, a

= 0 R

← R

= 1 R

← R

= 1, a

= 1 R

← R

If we focus on the cases a

= 0 (the row in bold in

the table), we can notice that:

• Case 1: b

⊕ k

= 0. The operations in Step 5 of

the two iterations are the same. In particular the

address for U

is the same.

• Case 2. b

⊕ k

= 1. The operations in Step 5 of

the two iterations are different. In particular the

address bits for U

are different.

Consequently, we proceed by guessing the value of

g = k

⊕ k

i+1

. Then we select the power traces such

that a

= 0 and such that a

i+1

⊕ g = 0. If our guess is

correct we will have:

0 = a

i+1

⊕ g = a

i+1

⊕ k

i+1

⊕ k

= b

i+1

⊕ k

= b

⊕ k

This means that if the guess g is correct, then Case

1 applies, which means that computing the difference

of the power traces of loop i and i + 1 would lead to

a zero difference for the address of U

, and the differ-

ence will be ﬂat. If the guess is not correct, we are in

Case 2, and the difference would be equal to the con-

sumption of the address of U

minus the one for U

Adding a sufﬁcient number of such differences would

lead to a ﬂat difference if the guess is correct and a

peak if it is not correct.

SECRYPT 2020 - 17th International Conference on Security and Cryptography

636

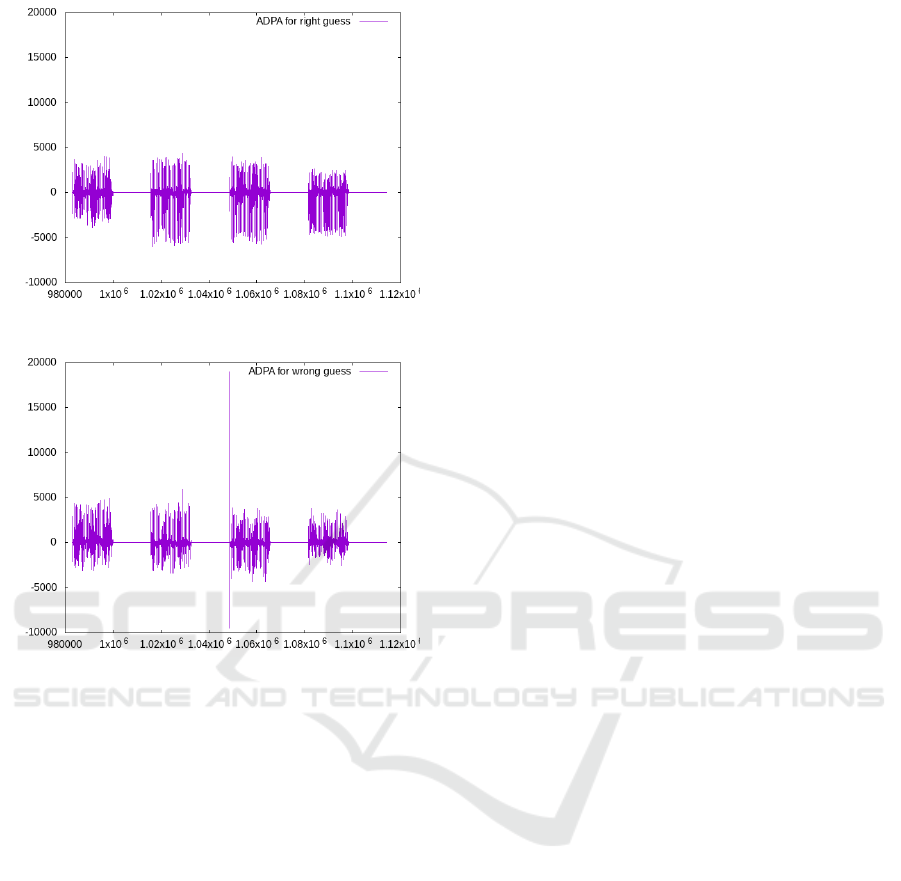
Figure 4: Difference for a correct guess on k

i+1

⊕ k

Figure 5: Difference for a wrong guess on k

i+1

⊕ k

In Fig. 4 and Fig. 5 we provide the ADPA obtained

for an RSA of size 1024 bits and using 4000 traces.

We can see the peak in Fig. 5 showing that the guess

g is not correct. There is no peak in Fig. 4 which

means that the guess is correct.

This experimentation shows that the proposed ap-

proach is effective to extract the whole key. This

means that Algorithm 3 does not provide the claimed

protection from ADPA. This attack works even if the

elements are blinded at the beginning of the expo-

nentiation, by either a randomized representation or

a multiplication with a random element.

5 CONCLUSION

In this paper we considered two exponentiation al-

gorithms (Algorithm 2 and 3) proposed in (Tunstall

et al., 2018) with randomized store and load in or-

der to counter-act address bit differential power anal-

ysis. We analyzed the security of these approaches,

and we showed that Algorithm 3 has a an important

ﬂaw. Indeed, the operation done in Step 3 of Algo-

rithm 3 is a square or multiplication depending on

the bit used for load and store randomization. With

a simulated power consumption we showed that we

can distinguish a square from a multiplication. This

means that the randomization of loads and stores in

Algorithm 3 is not effective anymore and an ADPA

can be conducted to recover the whole secret key with

a few thousand power traces.

REFERENCES

Bosselaers, A., Govaerts, R., and Vandewalle, J. (1993).

Comparison of Three Modular Reduction Functions.

In CRYPTO’93, volume 773 of LNCS, pages 175–186.

Clavier, C., Feix, B., Roussellet, M., and Verneuil, V.

(2010). Horizontal Correlation Analysis on Exponen-

tiation. In ICICS 2010, volume 6476 of LNCS, pages

46–61.

Coron, J.-S. (1999). Resistance against Differential Power

Analysis for Elliptic Curve Cryptosystems. In CHES

1999, pages 292–302.

Fouque, P. and Valette, F. (2003). The Doubling Attack –

Why Upwards Is Better than Downwards. In CHES

2003, pages 269–280.

Hanley, N., Tunstall, M., and Marnane, W. (2011). Using

templates to distinguish multiplications from squaring

operations. Int. J. Inf. Sec., 10(4):255–266.

Itoh, K., Izu, T., and Takenaka, M. (2003). Address-Bit Dif-

ferential Power Analysis of Cryptographic Schemes

OK-ECDH and OK-ECDSA. In CHES 2002, LNCS,

pages 129–143.

Izumi, M., Ikegami, J., Sakiyama, K., and Ohta, K. (2010).

Improved countermeasure against address-bit DPA for

ECC scalar multiplication. In DATE 2010, pages 981–

984.

Joye, M. and Yen, S. (2002). The Montgomery Powering

Ladder. In CHES 2002, volume 2523 of LNCS, pages

291–302.

Kocher, P. (1996). Timing Attacks on Implementations of

Difﬁe-Hellman, RSA, DSS, and Other Systems. In

CRYPTO ’96, volume 1109 of LNCS, pages 104–113.

Kocher, P. C., Jaffe, J., and Jun, B. (1999). Differential

Power Analysis. In CRYPTO’99, volume 1666 of

LNCS, pages 388–397.

Smart, N. P., Oswald, E., and Page, D. (2008). Randomised

representations. IET Inform. Security, 2(2):19–27.

Tunstall, M. and Joye, M. (2010). Coordinate Blinding over

Large Prime Fields. In CHES 2010, pages 443–455.

Tunstall, M., Papachristodoulou, L., and Papagiannopoulos,

K. (2018). Boolean Exponent Splitting. Technical

Report 2018/1226, IACR Cryptology ePrint Archive.

Yen, S., Ko, L., Moon, S., and Ha, J. (2006). Relative Dou-

bling Attack Against Montgomery Ladder. In ICISC

2005, LNCS, pages 117–128.

Address-bit Differential Power Analysis on Boolean Split Exponent Counter-measure

637