
Towards Large-scale Gaussian Process Models
for Efficient Bayesian Machine Learning
Fabian Berns
1
and Christian Beecks
1,2
1
Department of Computer Science, University of M
¨
unster, Germany
2
Fraunhofer Institute for Applied Information Technology FIT, Sankt Augustin, Germany
Keywords:
Bayesian Machine Learning, Gaussian Process, Statistical Data Modeling.
Abstract:
Gaussian Process Models (GPMs) are applicable for a large variety of different data analysis tasks, such as
time series interpolation, regression, and classification. Frequently, these models of bayesian machine learning
instantiate a Gaussian Process by a zero-mean function and the well-known Gaussian kernel. While these
default instantiations yield acceptable analytical quality for many use cases, GPM retrieval algorithms allow to
automatically search for an application-specific model suitable for a particular dataset. State-of-the-art GPM
retrieval algorithms have only been applied for small datasets, as their cubic runtime complexity impedes
analyzing datasets beyond a few thousand data records. Even though global approximations of Gaussian
Processes extend the applicability of those models to medium-sized datasets, sets of millions of data records
are still far beyond their reach. Therefore, we develop a new large-scale GPM structure, which incorporates
a divide-&-conquer-based paradigm and thus enables efficient GPM retrieval for large-scale data. We outline
challenges concerning this newly developed GPM structure regarding its algorithmic retrieval, its integration
with given data platforms and technologies, as well as cross-model comparability and interpretability.
1 INTRODUCTION
Gaussian Process Models (GPMs) describe concrete
instantiations of Gaussian Processes regarding their
main components – i.e. mean function and covariance
function – including data-specific hyperparameters.
These bayesian machine learning models have been
applied for various tasks of data analysis such as time
series interpolation (Roberts et al., 2013; Li and Mar-
lin, 2016), nearest neighbour analysis (Datta et al.,
2016), anomaly description (Beecks et al., 2019), re-
gression (Titsias, 2009; Duvenaud et al., 2013), and
classification (Li and Marlin, 2016; Hensman et al.,
2013). Due to their roots in bayesian inference, GPMs
enable uncertainty quantifications for their inferred
predictions in a mathematical tractable manner even
for small sets of training data (Rivera and Burnaev,
2017). As non-parametric models, GPMs are fre-
quently used for the aforementioned analytical tasks
(Lee et al., 2018; Hensman et al., 2013), in particular
if the underlying data is unreliable, noisy, or partially
missing and if the degree of sparsity or idiosyncrasy
is high.
In order to retrieve a GPM for a given dataset, dif-
ferent algorithms have been proposed, such as Com-
positional Kernel Search (CKS) (Duvenaud et al.,
2013) and Automatic Bayesian Covariance Discov-
ery (ABCD) (Lloyd et al., 2014). Rasmussen and
Williams (2006) and Lloyd et al. (2014) argue that
any combination of an arbitrary mean and covari-
ance function can be expressed by a another covari-
ance function and constant zero-mean. This modi-
fication allows the covariance function to act as the
sole data modeling entity of a GPM. Since among
other reasons GPM retrieval algorithms exhaustively
search the space of possible GPMs in terms of dif-
ferent covariance functions, they tend to be rather in-
efficient concerning increasing dataset size. Global
approximations, such as the Nystrm approximation
(Kim and Teh, 2018; Rasmussen and Williams, 2006),
optimize on the main bottleneck of these algorithms,
i.e. model evaluation and selection. The Nystrm ap-
proximation reduces their cubic runtime complexity
by a linear factor (Liu et al., 2018), which enables the
Scalable Kernel Composition (SKC) algorithm to re-
trieve GPMs for datasets comprising up to 100,000
data records (Kim and Teh, 2018).
Although SKC is currently the most efficient GPM
retrieval algorithm in terms of runtime, analyzing
more than 100,000 data records is still far beyond its
Berns, F. and Beecks, C.
Towards Large-scale Gaussian Process Models for Efficient Bayesian Machine Learning.
DOI: 10.5220/0009874702750282
In Proceedings of the 9th International Conference on Data Science, Technology and Applications (DATA 2020), pages 275-282
ISBN: 978-989-758-440-4
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
275

Data
Encoding via JSONComposite Kernel
Knowledge
SE + (PER x SE) | SE
(LINxPER)+(SExSE)
(LIN xPERxSE) + PER
"type": "ADD",
"child_nodes": [{
"type": "SE",
"hyper_param": […]
}, {
"type": "MUL",
"child_nodes": [{
"type": "PER",
Reoccuring patterns
Anomalies
etc.
Figure 1: Data Pipeline – Vision for GPM Retrieval.
scope (Kim and Teh, 2018). Thus, we further extend
upon given GPM retrieval algorithms by proposing a
new large-scale GPM structure enabling the analysis
of very large datasets. Our new structure facilitates to
dynamically build up a large-scale GPM from inde-
pendent sub-models describing local data partitions.
Their divide-&-conquer-based nature further reduces
computational complexity and thus increases perfor-
mance of corresponding GPM retrieval algorithms.
First preliminary experiments show that our proposal
outperforms the computation time of state-of-the-art
algorithms by several orders of magnitude. In partic-
ular, on a dataset of 10,000 records our proposal en-
ables to speed up GPM retrieval by a factor of 1,000.
Given the proposed GPM structure enabling auto-
matic and efficient GPM retrieval for large datasets,
we identified the following further challenges in the
field of Gaussian Processes:
Challenge 1: Algorithms for large-scale GPM
Challenge 2: Integration of that GPM retrieval algo-
rithm with state-of-the-art data platforms
Challenge 3: Techniques to support interpretability
and comparability of GPMs
Challenge 4: Domain-specifc adaptations of large-
scale GPM structures
Challenge 5: Application of bayesian machine
learning for data mining
Accomplishing those challenges enables on the one
hand to efficiently retrieve GPMs as well as on the
other hand to process and analyze big data by means
of GPMs in practice. Furthermore, techniques to al-
low for further comparability of those models broad-
ens their applicability in various domains of data anal-
ysis and contributes especially to the fourth and fifth
challenge. As the fields of data mining and data sci-
ence advance and bayesian machine learning gains
popularity, we consider the latter two challenges as
perpetual.
We aim to embed contributions related to those
challenges into our conclusive vision: a self-
contained data pipeline for GPM retrieval. Figure 1
illustrates the four main parts of such a data pipeline.
Starting with the raw data, the GPM retrieval algo-
rithm is used to determine the corresponding GPMs
by optimizing individual composite covariance func-
tions (cf. Duvenaud et al., 2013). These are trans-
lated into a machine-readable and -processable for-
mat, such as JavaScript Object Notation (JSON),
and made accessible via state-of-the-art data plat-
forms, such as MongoDB (Bradshaw et al., 2020) and
Apache Spark (Zaharia et al., 2016). Their querying
capabilities alongside the developed techniques allow
for interpretability and comparability of GPMs in or-
der to uncover repeating patterns, anomalies, motifs
as well as other (dis)similarity phenomena within and
across datasets.
The paper is structured as follows: Section 2
presents background information and related work.
The proposed large-scale GPM structure is introduced
in Section 3, while the challenges mentioned above
are explained in detail in Section 4. The results of
our preliminary performance evaluation are discussed
in Section 5, before we conclude our paper with an
outlook on future work in Section 6.
2 BACKGROUND AND RELATED
WORK
2.1 Gaussian Process
A Gaussian Process (Rasmussen and Williams,
2006) is a stochastic process over random variables
{ f (x)|x ∈ X }, indexed by a set X , where every sub-
set of random variables follows a multivariate normal
distribution. The distribution of a Gaussian Process is
the joint distribution of all of these random variables
and it is thus a probability distribution over the space
of functions in R
X
. We formalize a Gaussian Process
as follows:
f (·) ∼ GP
m(·), k(·, ·)
(1)
where the mean function m : X → R and the covari-
ance function k : X ×X → R are defined ∀x, x
0
∈ X as
follows:
m(x) = E[ f (x)] (2)
k(x, x
0
) = E[( f (x) −m(x)) · ( f (x
0
) − m(x
0
))] (3)
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
276
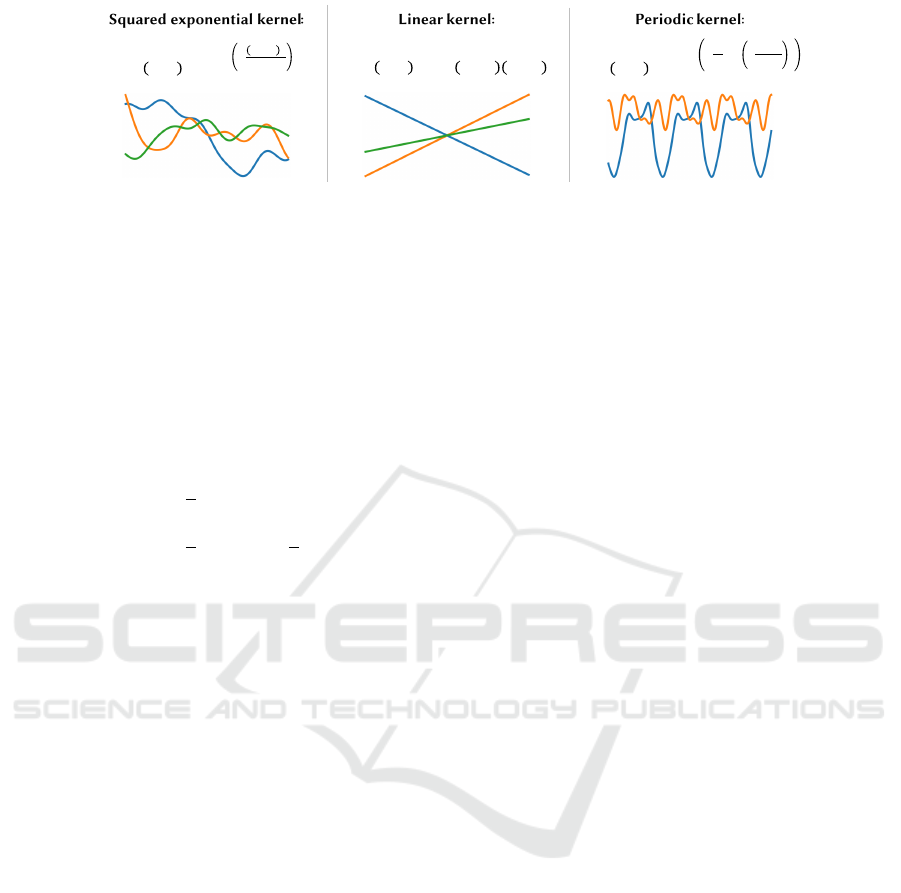
Figure 2: Definitions and illustrations of different kernel functions.
Given a finite dataset D = {X,Y } with X =
{x
i
|x
i
∈ X ∧1 ≤ i ≤ n} representing the underlying in-
dex values, such as timestamps, and Y = { f (x
i
)|x
i
∈
X } representing the target data values, e.g. tempera-
ture measurements, the hyperparameters of the mean
and covariance functions are determined by maxi-
mizing the log marginal likelihood (Rasmussen and
Williams, 2006; Duvenaud et al., 2013; Lloyd et al.,
2014; Kim and Teh, 2018) of the Gaussian Process,
which is defined as follows:
L(µ, K|y) = −
1
2
(y − µ)
T
K
−1
(y − µ)
−
1
2
log(|K|) −
n
2
log(2π)
(4)
As can be seen in Equation 4, the marginaliza-
tion of a Gaussian Process for a given dataset D of
n records results in a finite data vector y ∈ R
n
, mean
vector µ ∈ R
n
, and covariance matrix K ∈ R
n×n
which
are defined as y[i] = f (x
i
), µ[i] = m(x
i
), and K[i, j] =
k(x
i
, x
j
), respectively.
While the covariance matrix is frequently used
as major data modeling entity, it often lacks in de-
scribing individual statistical behaviors in a structured
way. To this end, Duvenaud et al. (Duvenaud et al.,
2013) propose to approximate and structure the co-
variance function via multiple compositional kernel
expressions. The corresponding GPM retrieval algo-
rithms are summarized in the following section.
2.2 Retrieval Algorithms
GPM retrieval algorithms, such as CKS (Duvenaud
et al., 2013), ABCD (Lloyd et al., 2014; Steinruecken
et al., 2019), and SKC (Kim and Teh, 2018), aim to
discover the statistical structure of a dataset D by de-
termining a covariance function k which maximizes
the log marginal likelihood L. For this purpose, the
mean function of the Gaussian Process is commonly
instantiated by a constant zero function (Duvenaud
et al., 2013; Rasmussen and Williams, 2006), so as to
correspond to an additional data normalization step.
The covariance function, as the sole data modeling
entity of these algorithms, is algorithmically com-
posed via operators implementing addition and mul-
tiplication among different (composed) base kernels.
Prominent base kernels include the linear kernel, pe-
riodic kernel, and the frequently used Gaussian kernel
(cf. Mohri et al. 2018), which are able to capture for
instance smooth, jagged, and periodic behavior (Du-
venaud et al., 2013). We illustrate datasets with differ-
ent statistical behaviors and their corresponding base
kernels in Figure 2.
The algorithms mentioned above apply an open-
ended, greedy search in the space of all feasible ker-
nel combinations in order to progressively compute a
GPM fitting the entire dataset D, respectively Y ∈ D.
The CKS algorithm (Duvenaud et al., 2013) follows
a simple grammar to expand kernel expressions, that
we call Basic Kernel Expansion Strategy (BES). This
strategy produces candidate kernel expressions within
every iteration of CKS according to the following
grammar (Duvenaud et al., 2013):
S
0
→S × b, b ∈ B
S
0
→S + b, b ∈ B
(5)
Starting with a set of base kernels b ∈ B, the can-
didates of every following iteration are generated via
expanding upon the best candidate of the previous it-
eration. More specifically, the underlying grammar
prescribes to create a new candidate kernel expres-
sions for every possible replacement S
0
of any subex-
pression S of the best kernel from the previous iter-
ation. Moreover, a new candidate is also generated
for every replacement of a base kernel b with another
one b
0
. ABCD extends that grammar with regards to
a change point operator | , in order to locally restrict
the effect of kernel expressions (Lloyd et al., 2014;
Steinruecken et al., 2019):
S
0
→ S |b ∈ B (6)
Even though the Basic Kernel Expansion Strat-
egy (BES) allows to rigorously generate candidates,
evaluating every expansion of every subexpression
poses a major bottleneck of state-of-the-art algo-
rithms. Moreover, the greedy search keeps only a
single candidate, i.e. the best performing one, per
iteration, neglecting all the other candidates. Thus,
reducing the set of candidates per iteration in order
to cover just the most promising candidate kernels
Towards Large-scale Gaussian Process Models for Efficient Bayesian Machine Learning
277

would improve on the performance of the respective
algorithms presumably without affecting model qual-
ity. Furthermore, assessing model quality in terms of
log marginal likelihood epitomizes another bottleneck
of current algorithms, which is intrinsic to the frame-
work of Gaussian Processes itself (Hensman et al.,
2013). The cubic runtime complexity of that basic
measure inhibits analysis of large-scale datasets (cf.
Kim and Teh, 2018).
To summarize, state-of-the-art GPM retrieval al-
gorithms are not suited for the analysis of large-scale
datasets due to their cubic computation time complex-
ity as well as unmanageable candidate quantity.
2.3 Approximations
As stated in the previous subsection, the computa-
tional complexity for evaluating and inferring from
Gaussian processes, which lies in O(n
3
), is a long-
standing obstacle for the application of Gaussian Pro-
cesses to analysis of large-scale data (Liu et al., 2018).
Liu et al. (2018) give a literature review of common
successful global and local approximations.
Global Approximations include na
¨
ıve subset-of-
data-approaches (Hayashi et al., 2019), where only
m n data points are used for training, reducing com-
plexity to O(m
3
), sparse kernel methods (Melkumyan
and Ramos, 2009), where the covariance between two
points x
i
, x
j
is set to 0 if |x
i
− x
j
| exceeds a thresh-
old, giving a complexity of O(αn
3
) where α ∈ (0, 1)
depends on the threshold, and sparse approximations
(Gittens and Mahoney, 2016). The latter include
the Nystrm-approximation (Rasmussen and Williams,
2006), a low-rank approximation of the covariance
matrix (O(nm
2
)) and constrained kernel methods
(Wilson and Nickisch, 2015), which assume or con-
struct additional constraints on data, such as an evenly
spaced grid of input values (up to O(n)). Those global
approximations are able to capture global patterns,
but lack capabilities to capture local patterns (Liu
et al., 2018).
Local approaches all work with local experts,
kernel expressions trained and evaluated on seg-
ments of data (Rivera and Burnaev, 2017). The
subclasses of local approaches are threefold: Na
¨
ıve
local approaches (Kim et al., 2005), which parti-
tion the input space into distinct segments that are
trained and predicted through the local expert by
completely disregarding nearby segments, mixture-of-
experts (MoE) approaches (Masoudnia and Ebrahim-
pour, 2014), which treat local experts as components
of a Gaussian mixture model and product-of-experts
(PoE) approaches (Hinton, 2002), which are similar
to MoE, but place stronger emphasis on agreement
between experts. Local expert approaches are called
inductive when the segmentation of the input space is
decided independently of the data and transductive if
the data informs the segmentation (Liu et al., 2018).
Based on the outlined taxonomy (Liu et al., 2018),
the proposed large-scale GPM structure (cf. Section
3) is classified as local approximation approach (cf.
Rivera and Burnaev, 2017). We omit MoE and PoE
based solutions due to scalability boundaries of non-
independent sub-models. Moreover, we do not utilize
global approximations, since they optimize for the in-
ner workings of Gaussian Processes, which remain
unaltered here. Subsequently, intertwining those to
approximation strategies can be used in future work
to further optimize performance of GPM retrieval, but
is not considered within this paper.
3 LARGE-SCALE GAUSSIAN
PROCESS MODELS
In this section, we describe the structural design for
large-scale GPMs. The structure is designed to re-
duce computational complexity of GPM evaluation as
well as to mitigate the amount of kernel expression
candidates, which need to be evaluated as part of the
respective retrieval algorithm. Since these two issues
are the main bottlenecks of current GPM retrieval al-
gorithms, respective solution strategies are separately
covered in the following two subsections.
3.1 Reduction of Computational
Complexity
Liu et al. (2018) as well as Rivera and Burnaev (2017)
highlight local approximations as a key possibility
to reduce complexity of common GPM evaluations
based on likelihood measures (cf. Equation 4). These
approximations do not extrapolate data’s inherent be-
havioral patterns based on a small subset of the given
data like low-rank matrix approximations. Instead
they build a holistic GPM constructed from locally-
specialized GPMs trained on non-overlapping seg-
ments of the data. Thus, the covariance matrix of
the holistic GPM is composed of the respective ma-
trices of its local sub-models. (Liu et al., 2018). This
divide-&-conquer approach fastens calculation of log
marginal likelihood, since the resulting covariance
matrix is a block diagonal matrix (Rivera and Bur-
naev, 2017), whose inversion and determinant compu-
tation time complexity is lower in contrast to regular
matrices (Park and Apley, 2018). Rivera and Burnaev
(2017) highlight, that local approximations allow to
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
278

”model rapidly-varying functions with small correla-
tions” in contrast to low-rank matrix approximations.
Embedding the concept of local approximations
into GPM retrieval algorithms requires the notion of
a change point operator for global data partitioning.
While change point operators in principle allow for
a global data partitioning, their nature of fading one
kernel expression into another (Lloyd et al., 2014;
Steinruecken et al., 2019) does neither produce clear
boundaries between sub-models nor enables indepen-
dence of these models. Therefore, we adapt the given
notion of a change point operator to utilize indica-
tor functions instead of sigmoid functions to separate
kernel expressions. The resulting large-scale GPM
K : X × X → R is defined as follows:
K (x, x
0
|{k
b
}
m
b=1
, {τ
b
}
m
b=0
) =
m
∑
b=1
k
b
(x, x
0
) · 1
{τ
b−1
<x≤τ
b
}
(x) · 1
{τ
b−1
<x
0
≤τ
b
}
(x
0
) (7)
The parameter m ∈ N defines the number of sub-
models k
b
: X ×X → R, where each sub-model k
b
can
be thought of as a local covariance function model-
ing the restricted domain [τ
b−1
, τ
b
] ⊆ X . In this way,
each sub-model k
b
is only responsible for a certain
coherent fraction of the data, which is delimited by
the change points τ
b−1
and τ
b
. The specific change
points τ
0
= x
1
and τ
m
= x
n
denote the start and end
of the data set D. One can show, that the usage of in-
dicator functions (thus having disjoint data segments)
produces a block diagonal covariance matrix (cf. Low
et al. 2015), which can be utilized for efficient GPM
evaluation.
3.2 Reduction of Candidate Quantity
In contrast to the previous section, which outlined
how we will reduce the complexity of evaluating
a single GPM via a divide-&-conquer-based ap-
proach, this section investigates measures to reduce
the amount of to-be-evaluated candidates per sub-
model covariance function k
b
. Kernel expansion
strategies define, how candidate kernel expressions
are generated based on an already existing one from
the previous iteration. Thus, optimizing on kernel ex-
pansion strategies is crucial for reducing candidate
quantity. Equation 5 illustrates the state-of-the-art
strategy used by CKS (Duvenaud et al., 2013), ABCD
(Lloyd et al., 2014) and SKC (Kim and Teh, 2018).
While this strategy allows to exhaustively search the
space of possible kernel expressions for the most ap-
propriate one, it entails to evaluate a lot of inferior
candidates as a by-product. Every sub-model k
b
of
a GPM K (cf. Equation 7) can be a composite co-
variance function. In principle, it may contain change
point operators, but we only consider additive and
multiplicative operators to ensure separation of con-
cerns between K and its sub-models k
b
.
Although state-of-the-art algorithms consider ev-
ery possible kernel expansion regardless of their
structure up to a certain depth (cf. Subsection 2.2),
they retroactively enforce a hierarchy, i.e. a Sum-
of-Products (SoP) hierarchy (Duvenaud et al. 2013;
Lloyd et al. 2014), among additive operators A : X ×
X → R and multiplicative operators M : X × X → R
(cf. Equation 8). Thus, these algorithms structure the
resulting kernel expressions to foster comprehensibil-
ity in hindsight. We incorporate that SoP form (cf.
Equation 8) into our kernel expansion strategy to pro-
hibit functionally redundant composite kernel expres-
sions, which result from different expressions produc-
ing the same SoP form.
A :=
t
∑
i=0
M
i
, M :=
a
∏
j=0
b, b ∈ B (8)
Based on the mathematically formalization of the
SoP form given in Equation 8, we illustrate the new
SoP Kernel Expansion Strategy (SES) by means of a
grammar as follows:
M
0
→M ×b, b ∈ B
A
0
→A + b, b ∈ B
(9)
Instead of allowing to replace every possible
subexpression with a base kernel b, additions A are
expanded via adding a further base kernel and mul-
tiplications M are handled analogously. To comply
with the SoP form, any base kernel b added to A is
treated as trivial multiplication M
i
=
∏
0
i=0
b. This
grammar ensures, that every resulting kernel expres-
sion complies to the SoP form. As with state-of-the-
art algorithms, base kernels are considered the initial
candidates of this strategy.
To sum up, we propose two approaches for re-
ducing the computational complexity and candidate
quantity when inferring large-scale GPMs in order to
apply GPM retrieval algorithms to very large datasets.
On the one hand, local approximations by means of
an indicator change point operator reduce computa-
tional complexity by partitioning a GPM into several
locally-specialized sub-models. On the other hand,
reducing the amount of candidate covariance func-
tions per sub-model k
b
by employing SES allows to
save on evaluative calculations for inferior models.
Towards Large-scale Gaussian Process Models for Efficient Bayesian Machine Learning
279

4 CHALLENGES
We regard the new structural design for GPMs de-
scribed in the previous section as a first step to-
wards large-scale GPMs for efficient bayesian ma-
chine learning. Subsequently, we define the following
challenges to further advance the broader application
of Gaussian Processes for big datasets:
Algorithms for Large-scale GPMs. Efficient and
scalable algorithms need to be developed to
retrieve GPMs based on uni- and multivariate
datasets. Such algorithms ought to be robust to-
wards different dataset sizes and dimensionalities
of the input data in order to be applicable for a
large amount of different scenarios, including
limited computing resources.
Integration with Data Platforms. Having large-
scale GPM retrieval algorithms in place, they
need to be integrated with state-of-the-art big
data and streaming platforms to allow for a
broader application of GPM retrieval. Big data
and streaming platforms such as MongoDB
(Bradshaw et al., 2020), Spark (Zaharia et al.,
2016), and Kafka (Le Noac’h et al., 2017) deliver
their own data processing frameworks, for which
GPM retrieval algorithms need to be adapted
especially in order to efficiently exploit their
distributed computation capabilities.
Interpretability of GPM. While a successfully re-
trieved GPM can be used for a large variety of
tasks such as regression and classification, the
model itself is exploitable, too. This model can
be used as a proxy to further explain the data, that
it is describing. It allows to interpret the com-
position of given data in terms of behavioral pat-
terns such as periodicities and linear trends. Fur-
thermore, motifs and anomalies within a dataset
can be retrieved by relating a GPM’s components,
e.g. its sub-models or used base kernels, to one
another and derive frequent as well as rarely oc-
curring patterns. In order to enable comparability
among GPMs for different datasets, the concept
of interpreting GPMs themselves is extended with
regards to multiple models. In this way, patterns
such as motifs and anomalies can be found across
datasets.
Domain-specific Adaptations. From a statistical
perspective, covariance and mean functions of a
Gaussian Process encapsulate prior knowledge
about the given data (Rasmussen and Williams,
2006). GPM retrieval algorithms circumvent the
need for prior knowledge by searching the realms
of those functions (usually only for the covariance
function). The given general-purpose large-scale
GPM structure does not incorporate any expert
knowledge due to its domain-agnostic nature.
Subsequently, integrating that prior knowledge
into the GPM structure further improves on GPM
retrieval, since it enables a more educated search.
Application for Data Mining. Finally, after having
successfully retrieved a GPM the question re-
mains, how to further utilize it for data mining
purposes. Performing data mining tasks such as
frequent pattern mining (Chee et al., 2019) and
clustering (Ghosal et al., 2020) using a GPM in-
stead of the actual data, is advantageous as the
model represents data’s inherent characteristics
and behavioral patterns in a more abstract, de-
noised and reliable way.
5 PRELIMINARY EXPERIMENTS
While the aforementioned challenges are important
for advancing large-scale GPM retrieval and analy-
sis algorithms in general, we have already addressed
the first particular challenge mentioned above by de-
veloping an initial prototype for large-scale GPM re-
trieval (Berns et al., 2019), which we refer to as Ef-
ficient GPM Retrieval (EGR) algorithm. In order
to compare the runtime performance of our proto-
type (EGR) to those of the state-of-the-art algorithms
CKS and ABCD, we make use of different benchmark
datasets made available by Duvenaud et al. (2013),
Lloyd et al. (2014), Zamora-Mart
´
ınez et al. (2014),
and T
¨
ufekci (2014). The results are summarized in
Table 1.
Table 1: GPM retrieval time of our prototype (EGR) in com-
parison to state-of-the-art algorithms.
Runtime
Dataset Size CKS ABCD EGR
Airline 144 00:00:09 00:00:12 00:00:05
Solar 391 00:00:10 00:00:13 00:00:05
Mauna 702 00:01:13 00:02:10 00:00:07
SML 4,137 08:27:46 09:27:32 00:00:33
Power 9,568 61:27:14 74:42:08 00:01:35
As can be seen in the table above, the EGR al-
gorithm is able to outperform both algorithms CKS
and ABCD in terms of runtime needed to retrieve a
large-scale GPM fitting the underlying dataset. While
CKS and ABCD need more than two days to finish
the computation of the resulting GPM for the Power
dataset, our prototype was able to finish the compu-
tation in less than two minutes. Despite this differ-
ence in runtime, the model quality in terms of MSE
for this dataset was only slightly better for both CKS
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
280

(0.0726) and ABCD (0.0726) than for our prototype
EGR (0.1017).
In addition, we applied the EGR algorithm to the
Household Electric Power Consumption dataset in-
troduced by Hebrail and Berard (2012) comprising
2,075,259 data records. While the EGR algorithm
was able to retrieve a large-scale GPM in less than
1.5 hours, we interrupted the computation of both al-
gorithms CKS and ABCD after 14 days, since they
were not able to complete the GPM computation.
We thus conclude, that the proposed large-scale
GPM structure enables the development of efficient
retrieval algorithms that scale to millions of data
records.
6 CONCLUSION
In this paper, we introduce a new structure for Gaus-
sian Process Models (GPMs) enabling the analysis
of large-scale datasets. This new structure utilizes
a concatenation of locally specialized models to re-
duce both kernel search complexity as well as compu-
tational effort required in the evaluative calculations.
Furthermore, we incorporate the given candidate for-
mat (i.e. sum of products form) directly into the can-
didate generation mechanism. This results in fewer
to-be-evaluated candidates and subsequently ought to
improve on future GPM retrieval algorithms as well.
Although we made a first step towards large-scale
GPM retrieval, several challenges in that field re-
main open issues. We outlined those challenges in
detail and backed our claims regarding the perfor-
mance implications of our new model. For this pur-
pose, we have implemented a first prototype for large-
scale GPM retrieval and investigated its performance
in comparison to the state of the art.
Apart from further developing this initial proto-
type, we plan to address the challenges mentioned in
this paper in our future work.
REFERENCES
Beecks, C., Schmidt, K. W., Berns, F., and Graß, A.
(2019). Gaussian processes for anomaly description
in production environments. In Proceedings of the
Workshops of the EDBT/ICDT 2019 Joint Conference,
EDBT/ICDT 2019, Lisbon, Portugal, March 26, 2019.
Berns, F., Schmidt, K., Grass, A., and Beecks, C. (2019). A
new approach for efficient structure discovery in IoT.
In 2019 IEEE International Conference on Big Data
(Big Data), pages 4152–4156. IEEE.
Bradshaw, S., Brazil, E., and Chodorow, K. (2020). Mon-
goDB: The defintive guide : powerful and scalable
data storage. O’Reilly Media Inc., 3rd revised edi-
tion.
Chee, C.-H., Jaafar, J., Aziz, I. A., Hasan, M. H., and
Yeoh, W. (2019). Algorithms for frequent itemset
mining: a literature review. Artificial Intelligence Re-
view, 52(4):2603–2621.
Datta, A., Banerjee, S., Finley, A. O., and Gelfand, A. E.
(2016). Hierarchical nearest-neighbor gaussian pro-
cess models for large geostatistical datasets. Journal
of the American Statistical Association, 111(514).
Duvenaud, D., Lloyd, J. R., Grosse, R., Tenenbaum, J. B.,
and Ghahramani, Z. (2013). Structure discovery in
nonparametric regression through compositional ker-
nel search. In Proceedings of the 30th International
Conference on International Conference on Machine
Learning, ICML’13, pages III–1166–III–1174.
Ghosal, A., Nandy, A., Das, A. K., Goswami, S., and Pan-
day, M. (2020). A short review on different clustering
techniques and their applications. In Mandal, J. K.
and Bhattacharya, D., editors, Emerging Technology
in Modelling and Graphics, volume 937 of Advances
in Intelligent Systems and Computing, pages 69–83.
Springer Singapore, Singapore.
Gittens, A. and Mahoney, M. W. (2016). Revisiting the
nystr
¨
om method for improved large-scale machine
learning. J. Mach. Learn. Res., 17(1):3977–4041.
Hayashi, K., Imaizumi, M., and Yoshida, Y. (2019). On
random subsampling of gaussian process regression:
A graphon-based analysis.
Hebrail, G. and Berard, A. (2012). Individual household
electric power consumption data set.
Hensman, J., Fusi, N., and Lawrence, N. D. (2013). Gaus-
sian processes for big data. In Proceedings of the
Twenty-Ninth Conference on Uncertainty in Artificial
Intelligence, UAI’13, pages 282–290, Arlington, Vir-
ginia, United States. AUAI Press.
Hinton, G. E. (2002). Training products of experts by
minimizing contrastive divergence. Neural Comput.,
14(8):1771–1800.
Kim, H. and Teh, Y. W. (2018). Scaling up the Automatic
Statistician: Scalable structure discovery using Gaus-
sian processes. In Proceedings of the 21st Interna-
tional Conference on Artificial Intelligence and Statis-
tics, volume 84 of Proceedings of Machine Learning
Research, pages 575–584. PLMR.
Kim, H.-M., Mallick, B. K., and Holmes, C. C. (2005).
Analyzing nonstationary spatial data using piecewise
gaussian processes. Journal of the American Statisti-
cal Association, 100(470):653–668.
Le Noac’h, P., Costan, A., and Bouge, L. (2017). A per-
formance evaluation of apache kafka in support of
big data streaming applications. In 2017 IEEE Inter-
national Conference on Big Data (Big Data), pages
4803–4806. IEEE.
Lee, J., Bahri, Y., Novak, R., Schoenholz, S. S., Penning-
ton, J., and Sohl-Dickstein, J. (2018). Deep neural
networks as gaussian processes. In 6th International
Conference on Learning Representations, ICLR 2018,
Vancouver, BC, Canada, April 30 - May 3, 2018, Con-
ference Track Proceedings. OpenReview.net.
Towards Large-scale Gaussian Process Models for Efficient Bayesian Machine Learning
281

Li, S. C.-X. and Marlin, B. M. (2016). A scalable end-to-
end gaussian process adapter for irregularly sampled
time series classification. In Lee, D. D., Sugiyama,
M., Luxburg, U. V., Guyon, I., and Garnett, R., edi-
tors, Advances in Neural Information Processing Sys-
tems 29, pages 1804–1812. Curran Associates, Inc.
Liu, H., Ong, Y.-S., Shen, X., and Cai, J. (2018). When
gaussian process meets big data: A review of scalable
gps.
Lloyd, J. R., Duvenaud, D., Grosse, R., Tenenbaum, J. B.,
and Ghahramani, Z. (2014). Automatic construction
and natural-language description of nonparametric re-
gression models. In Proceedings of the Twenty-Eighth
AAAI Conference on Artificial Intelligence, AAAI’14,
pages 1242–1250. AAAI Press.
Low, K. H., Yu, J., Chen, J., and Jaillet, P. (2015). Par-
allel gaussian process regression for big data: Low-
rank representation meets markov approximation. In
Proceedings of the Twenty-Ninth AAAI Conference on
Artificial Intelligence, AAAI’15, pages 2821–2827.
AAAI Press.
Masoudnia, S. and Ebrahimpour, R. (2014). Mixture of ex-
perts: a literature survey. Artificial Intelligence Re-
view, 42(2):275–293.
Melkumyan, A. and Ramos, F. (2009). A sparse covariance
function for exact gaussian process inference in large
datasets. In International Joint Conference on Artifi-
cial Intelligence.
Mohri, M., Rostamizadeh, A., and Talwalkar, A. (2018).
Foundations of machine learning. Adaptive compu-
tation and machine learning. The MIT Press, Cam-
bridge, Massachusetts, second edition edition.
Park, C. and Apley, D. (2018). Patchwork kriging for large-
scale gaussian process regression. Journal of Machine
Learning Research, 19(1):269–311.
Rasmussen, C. E. and Williams, C. K. I. (2006). Gaussian
Processes for Machine Learning (Adaptive Computa-
tion And Machine Learning). The MIT Press.
Rivera, R. and Burnaev, E. (2017). Forecasting of com-
mercial sales with large scale gaussian processes. In
2017 IEEE International Conference on Data Mining
Workshops (ICDMW), pages 625–634. IEEE.
Roberts, S., Osborne, M., Ebden, M., Reece, S., Gibson, N.,
and Aigrain, S. (2013). Gaussian processes for time-
series modelling. Philosophical transactions. Series
A, Mathematical, physical, and engineering sciences,
371(1984):20110550.
Steinruecken, C., Smith, E., Janz, D., Lloyd, J. R., and
Ghahramani, Z. (2019). The Automatic Statistician.
In Automated Machine Learning, Series on Chal-
lenges in Machine Learning. Springer.
Titsias, M. (2009). Variational learning of inducing vari-
ables in sparse gaussian processes. In van Dyk, D.
and Welling, M., editors, Proceedings of the Twelth
International Conference on Artificial Intelligence
and Statistics, volume 5 of Proceedings of Machine
Learning Research, pages 567–574, Hilton Clearwa-
ter Beach Resort, Clearwater Beach, Florida USA.
PMLR.
T
¨
ufekci, P. (2014). Prediction of full load electrical power
output of a base load operated combined cycle power
plant using machine learning methods. Interna-
tional Journal of Electrical Power & Energy Systems,
60:126–140.
Wilson, A. G. and Nickisch, H. (2015). Kernel interpolation
for scalable structured gaussian processes (kiss-gp). In
Proceedings of the 32Nd International Conference on
International Conference on Machine Learning - Vol-
ume 37, ICML’15, pages 1775–1784. JMLR.org.
Zaharia, M., Franklin, M. J., Ghodsi, A., Gonzalez, J.,
Shenker, S., Stoica, I., Xin, R. S., Wendell, P., Das,
T., Armbrust, M., Dave, A., Meng, X., Rosen, J., and
Venkataraman, S. (2016). Apache spark. Communi-
cations of the ACM, 59(11):56–65.
Zamora-Mart
´
ınez, F., Romeu, P., Botella-Rocamora, P., and
Pardo, J. (2014). On-line learning of indoor tempera-
ture forecasting models towards energy efficiency. En-
ergy and Buildings, 83:162–172.
DATA 2020 - 9th International Conference on Data Science, Technology and Applications
282
