A Gradient Descent based Heuristic for Solving Regression Clustering

Problems

Enis Kayıs¸

Industrial Engineering Department, Ozyegin University, Istanbul, Turkey

Keywords:

Regression Clustering, Heuristics, Gradient Descent.

Abstract:

Regression analysis is the method of quantifying the effects of a set of independent variables on a dependent

variable. In regression clustering problems, the data points with similar regression estimates are grouped into

the same cluster either due to a business need or to increase the statistical signiﬁcance of the resulting regres-

sion estimates. In this paper, we consider an extension of this problem where data points belonging to the same

level of another partitioning categorical variable should belong to the same partition. Due to the combinatorial

nature of this problem, an exact solution is computationally prohibitive. We provide an integer programming

formulation and offer gradient descent based heuristic to solve this problem. Through simulated datasets, we

analyze the performance of our heuristic across a variety of different settings. In our computational study, we

ﬁnd that our heuristic provides remarkably better solutions than the benchmark method within a reasonable

time. Albeit the slight decrease in the performance as the number of levels increase, our heuristic provides

good solutions when each of the true underlying partition has a similar number of levels.

1 INTRODUCTION

In many business applications, one is interested in the

effect of a set of independent variables over a partic-

ular response variable. Traditional statistical meth-

ods (e.g., ordinary least squares (OLS) regression),

and other advanced regression models, can provide

answers to this question. However, it may be mis-

leading to estimate a single regression equation for the

whole dataset and instead, it may be more meaningful

to identify the effect over smaller subsets of the data.

For example, ﬁnding the effect of price on the sales

volume over a set of products that show similar price

elasticity is very valuable for a decision-maker while

setting individual product prices, instead of measur-

ing price elasticity across all the products.

Clusterwise regression is a technique that clusters

data into groups with the same regression line (i.e.,

hyperplane). Charles (1977) introduced the problem

to the literature as ”r

egression typologique.” It has ap-

plications in a wide range of areas such as marketing

(e.g., Wedel and Kistemaker, 1989 and Brusco et al.

2003), environmental systems (e.g., He et al. 2008),

rainfall prediction (e.g., Bagirov et al. 2017), agri-

culture (e.g., Costanigro et al. 2009), transportation

https://orcid.org/0000-0001-8282-5572

(e.g., Luo and Yin 2008), and medicine (e.g., McClel-

land and Kronmal, 2002). Sp

ath (1979) provides an

exchange algorithm to ﬁnd hard cluster memberships

for each data point that minimizes the sum of squares

error (SSE). As an alternative to this hard clustering

method, Desarbo (1988) suggested a soft clustering

method in which they ﬁnd the probability of each data

point is in any one of the clusters in order to maximize

the log-likelihood function assuming the regression

errors come from a multinomial normal distribution.

Given a known number of clusters, ﬁnding the

optimal cluster memberships is a challenging prob-

lem due to its combinatorial nature. Lau et al.

(1999) provides a nonlinear mixed-integer program-

ming model to ﬁnd the optimal soft clustering of the

dataset into two clusters and uses expectation maxi-

mization heuristic to solve this model. Carbonneaou

et al. (2011) suggests to solve the problem using

a mixed logical-quadratic programming formulation,

instead of a traditional big-M formulation and ﬁnds

that the proposed formulation leads to numerically

stable and exact global optimal solutions in the ex-

perimental datasets. Carbonneaou et al. (2012) ex-

tends the previous work with an application of repet-

itive branch and bound algorithm to solve the mixed-

integer nature of the problem. Bagirov et al. (2013)

proposes an incremental algorithm to solve the clus-

102

Kayı¸s, E.

A Gradient Descent based Heuristic for Solving Regression Clustering Problems.

DOI: 10.5220/0009836701020108

In Proceedings of the 9th International Conference on Data Science, Technology and Applications (DATA 2020), pages 102-108

ISBN: 978-989-758-440-4

terwise regression problem which constructs initial

solutions at each iteration using results obtained at the

previous iteration. Based on tests on multiple regres-

sion datasets, they ﬁnd that the proposed algorithm

is very efﬁcient even in large datasets that are dense

and do not contain outliers. Joki et al. (2020) pro-

vides a support vector machine based formulation to

approximate the clusterwise regression problem with

an L

accuracy measure that is naturally more robust

to outliers. Part et al. (2017) uses a mixed-integer

quadratic programming formulation and designs and

compares the performance of several metaheuristic-

based algorithms (e.g., genetic algorithm, column

generation, two-stage approach) with synthetic data

and real-world retail sales data. Procedures to deter-

mine the optimal number of clusters, when this num-

ber is not known a priori, have also been suggested in

the literature (e.g., Shao and Wu 2005).

In this paper, we study an extension of the regres-

sion clustering problem. In our problem, data points

belong to some predeﬁned subgroups and thus data

points from the subgroup are constrained to be in the

same cluster after the regression clustering procedure

is applied. The optimality criteria is the minimiza-

tion of the total sum of squares error (SSE) in these

two subsets after two independent OLS regressions

are applied to them. Due to a large number of pos-

sible partitions, a complete enumeration approach is

computationally prohibitive. Instead, we provide gra-

dient descent based heuristics to solve this problem.

We propose to cycle through the partition vari-

ables at each iteration and consider all possible binary

splits based on each variable. The candidate split de-

pends on the type of the independent variable. For an

ordered or a continuous variable, we sort the distinct

values of the variable and place “cuts” between any

two adjacent values to form partitions. Hence for an

ordered variable with L distinct values, there are L −1

possible splits, which can be huge for a continuous

variable in large-scale data. Thus we specify a thresh-

old L

cont

(say 500, for instance), and only consider

splits at the L

cont

equally spaced quantiles of the vari-

able if the number of distinct values exceeds L

cont

+1.

An alternative way of speeding up the calculation is to

use an updating algorithm that “updates” the regres-

sion coefﬁcients as we change the split point, which

is computationally more efﬁcient than having to re-

calculate the regression every time. Here, we adopt

the former approach for its algorithmic simplicity.

Splitting on an unordered categorical variable is

quite challenging, especially when there are many

categories. Setting up a different OLS equation for

each level may lead to statistically insigniﬁcant re-

sults, especially if the number of observations for a

particular level is small. Instead, we would like to

ﬁnd a collection of these levels that have the same

regression equation. For a categorical variable with

L levels, the number of possible nonempty partitions

is equal to 2

L−1

− 1. When L > 20 levels, the num-

ber of feasible partitions is more than one million. In

this paper, we focus on this case due to its combina-

torially challenging nature. Since it is not possible to

search through all these solutions, we propose an in-

teger problem formulation to solve this problem. We

devise gradient descent based heuristic as an alterna-

tive.

The rest of the paper is organized as follows. Sec-

tion 2 presents the formulation of the problem and no-

tation used throughout the paper. We provide a list

of heuristics to solve the particular problem in Sec-

tion 3 and compare the performance of these heuris-

tics via simulated datasets in Section 4. Section 5

concludes the paper with a discussion on future work

that addresses limitations of the current method and

generated datasets and potential avenues for future re-

search.

2 PROBLEM FORMULATION

Consider the problem of splitting a node based on a

single categorical variable s ∈ R with L unique val-

ues which we will deﬁne as levels or categories. Let

y ∈ R be the response variable and x ∈ R

denote the

vector of linear predictors. The linear regression rela-

tionship between y and x varies under different values

of s. For the sake of our argument, we assume there to

be a single varying-coefﬁcient variable. The proposed

algorithm can be extended to cases with multiple par-

tition variables by either forming factors through the

combination of original factors or searching for opti-

mal partition variable-wise.

Let (x

) denote the measurements on subject

i, where i = 1, ·· · , n and s

∈ {1, 2,·· · , L} denotes a

categorical variable with L levels. The partitioned re-

gression model is:

∑

m=1

) + ε

, (1)

where w

) ∈ {0, 1} denotes whether the i-th obser-

vation belongs to the m-th group or not. We require

that

∑

m=1

(s) = 1 for any s ∈ {1,2, ··· , L}.

In this paper, we consider binary partitions,

namely M = 2, but multi-way partitions can be ex-

tended in a straightforward fashion. To simplify our

notation in binary partitioning, let w

:= w

) ∈

{0,1}, which is a mapping from {1, 2 ··· , L} to

{0,1}. Further, deﬁne atomic weights for each level

A Gradient Descent based Heuristic for Solving Regression Clustering Problems

103

as {τ

,· · · , τ

} ∈ {0, 1}

, where τ

= 1 indicates the

l-th level is in group “1”, otherwise in group “0”.

Then, we can write the observation-level weights as

∑

l=1

=l)

Let the level association vector τ

τ = (τ

,· · · , τ

)

W = diag{w

} and I − W = diag{1 − w

}, the re-

sponse vector y = (y

,· · · , y

)

, and the design matrix

X = (x

,· · · , x

)

. The standard linear regression

theory would then imply that, the total sum of squared

error (SSE) of the two splitted datasets can be stated

as follows:

Q(τ

τ) := SSE

+ SSE

:= ky − X(X

W X)

−1

W yk

(2)

+ ky − X{X

(I −W )X}

−1

(I −W )yk

:= Q

(τ

τ) + Q

(τ

τ), (3)

where the vector of atomic weights τ

τ is deﬁned on

the integer space {0, 1}

. The objective is to ﬁnd the

vector τ

τ that minimizes Q(τ

τ).

The combinatorial optimization problem deﬁned

above is a special case of the regression clustering

problem described in the Introduction section. In

the original problem, each data point can belong to

any particular partition. However, our formulation re-

quires each data point with the same level to belong to

the same partition. As there are no explicit solutions

for the original problem, our formulation is clearly

more challenging to solve.

2.1 Integer Programming Formulation

It is possible to rewrite the combinatorial optimization

problem deﬁned in the previous subsection as an inte-

ger programming formulation. For expositional sim-

plicity, we assume in this subsection that x ∈ R. For

each datapoint i, we need to decide whether it should

belong the left group, i.e., t

= 1, or the right group,

i.e., t

= 0. Hence the problem one needs to solve can

be formulated as:

min

,...,t

}

∑

i=1



− α

− β

)

+(1 − t

)(y

− α

− β

)



(4)

s.t.

∑

i=1

− β

(

t)x

∑

i=1

(5)

∑

i=1

−

∑

i=1

∑

i=1

∑

i=1

−

∑

i=1

∑

i=1

(6)

∑

i=1

− β

(

t)x

](1 − t

)

∑

i=1

(1 − t

)

(7)

∑

i=1

−

∑

i=1

(1−t

∑

i=1

(1−t

)

(1 − t

)

∑

i=1

−

∑

i=1

(1−t

∑

i=1

(1−t

)

(8)

−t

≤ M(s

− s

) ∀i, j ∈ {1, 2, ...,n} (9)

−t

≤ M(s

− s

) ∀i, j ∈ {1, 2, ...,n} (10)

1 ≤

∑

i=1

≤ n − 1 (11)

∈ {0, 1} ∀i ∈ {1, 2, ...,n} (12)

In this formulation, the objective function in (4) is

the total SSE as deﬁned in 3. Constraints (5)-(8) sim-

ply handles the simple linear regression coefﬁcient

equations for the left and right partitions. Constraints

(9) and (10) ensure that if two data points have the

same level (i.e., s

= s

), then they should belong to

the same partition (i.e., t

= t

). In these constraints,

M is a large positive number, though one could set

M = 1 as t

is a binary variable. Constraint (11) guar-

antees that each partition is nonempty. Lastly, binary

variables are stated by constraint (12).

The resulting integer programming formulation

has nonlinear parts in the objective function as well

as the constraints. When the number of data points, n,

is realistically large, it is computationally prohibitive

to solve this problem. Hence we resort to gradient

descent based heuristics which we describe next.

3 HEURISTICS

As the exact solution to the problem is not feasible,

we resort to heuristics to solve the problem. The sim-

plest heuristic to consider, which would provide an

exact solution, is an exhaustive search where one con-

siders all possible partitions of the factor levels into

two disjoint sets. For a categorical variable with L

levels, an exhaustive procedure will attempt 2

L−1

− 1

possible splits. Even though it is possible to run this

heuristic when L is very small, this approach becomes

computationally prohibitive when L is moderate or

large, which is the case in most real-life applications.

For example, a dataset with 21 categories requires a

search of 1,048,575 possible splits, which is compu-

tationally infeasible.

We consider a gradient descent based algorithm as

a heuristics to ﬁnd a solution to our problem. The al-

gorithm borrows the idea of gradient descent on an in-

teger space. In this algorithm, we start with a random

partition of the L levels into two nonempty and non-

overlapping groups, then cycle through all the levels

and sequentially ﬂip the group membership of each

level. The L group assignments resulting from ﬂip-

ping each individual category are compared in terms

DATA 2020 - 9th International Conference on Data Science, Technology and Applications

104

of the SSE criterion Q(τ

τ) deﬁned in (3). We then

choose the grouping that minimizes Q(τ

τ) as the cur-

rent assignment and iterate until the algorithm con-

verges. This algorithm performs a gradient descent

on the space of possible assignments, where any two

assignments are considered adjacent or reachable if

they differ only by one level. The gradient descent al-

gorithm is guaranteed to converge to a local optimum,

thus we can choose multiple random starting points in

the hope of reaching the global optimal. If the crite-

rion is locally convex near the initial assignment, then

this search algorithm has polynomial complexity in

the number of levels.

4 COMPUTATIONAL RESULTS

In order to assess the quality of the solutions gener-

ated by our gradient descent algorithm, we conduct

a computational study with simulated datasets. We

are interested in how the quality changes as the num-

ber of levels, number of data points, the magnitude of

the residuals vary. Whenever the optimal partitioning

is not known, we compare our heuristic to a random

search. The random search method simply generates

random partitions and returns the one with the small-

est total SSE as deﬁned in 3.

In our numerical study, we run the gradient search

algorithm 5 times, each time with a different ran-

domly generated initial solution, and report the best

solution out of 5 replications. In an alternative im-

plementation, which is called the descent search with

a ﬁxed initial method, we assign all the levels into a

single partition as the initial solution. The compari-

son between the results of these two versions enables

us to investigate whether varying the initial solution

and using multiple starting points change the solution

quality. The random search method searches through

max4000, 2

L−1

− 1 unique random partitions with 5

replications. We again report the best solution out

of these 5 replications. When L ∈ 8, 12, the random

search method gives the optimal partitioning with a

single replication. However, as the number of levels

increases the performance of this method should dete-

riorate quite rapidly as the search space is increasing

exponentially fast.

4.1 Dataset Generation

The simulated datasets have the following character-

istics. We assume that there is a single predictor, p,

and consider three different settings. In the ﬁrst two

settings, we model the case in which the optimal par-

tition is binary. In the ﬁrst partition, the underlying re-

gression equations are taken as y

= 10000−8∗ p

+ε

for the ﬁrst partition and y

= 5000 − p

+ ε

for the

second one. In the ﬁrst setting, we let even-numbered

levels to be in the ﬁrst partition and the old numbered

partitions to be in the second partition. In the second

setting, we let only two levels to be in the ﬁrst parti-

tion and the rest to be in the second partition. Varia-

tions between the results of these two settings help us

analyze the performance with respect to the unequal

number of elements in the optimal partitions. The

third setting is used to analyze cases in which multi-

way partition is optimal. We consider 8 partitions and

in each partition the underlying regression equation is

taken as y

= 10000 −(s

mod 8) −((s

mod 8) +1) ∗

+ ε

. In this last setting, the optimal number of par-

titions is 8, but since we are only interested in binary

partitions, the optimal binary partition depends on the

underlying dataset, hence it is not known unless one

could ﬁnd the exact solution to our problem. In all set-

tings, we randomly generated p

uniformly from the

interval [500,1000] and ε

from a normal distribution

with mean zero and variance σ

We generated 396 datasets in total. In each

dataset, we vary one of the following parameters: The

number of levels varied from 8 to 48 in increments

of 4. For each number of level L, we consider three

variations with respect to the number of data points:

30L,60L,90L. We let σ

to vary from 100 to 400 in

increments of 100. Thus we have a full factorial de-

sign with 11*3*4*3=396 different datasets. All com-

putations are carried out on a machine with Intel Core

i7-8565U CPU @ 1.80 GHz processor and 16 GB

RAM.

4.2 Numerical Analysis

In order to assess the quality of different methods, we

calculate the percentage gap between the total SSE of

the solution generated by the method at hand and that

of the best solution out of the three methods: descent

search, descent search with ﬁxed initial, and random

search. Table 1 presents the summary statistics of the

percentage gaps of the three methods across all the

generated datasets. Overall, the descent search gives

the best result with an average of 0.49% percentage

gap. However, notice that the percentage gap could be

as large as 39.81%. This shows that when the descent

search method gets stuck in a local minimum, there

could be a signiﬁcant performance loss. Our sec-

ond method, which is a variant of the descent search

method and uses the same initial solution, has a some-

what lower performance. Finally, the performance of

the random search is expectedly the worst by far in

all the summary statistics. It is possible to achieve

A Gradient Descent based Heuristic for Solving Regression Clustering Problems

105

0% percentage gap with this method when L ≤ 12

in which case the random search method becomes

an exhaustive search. However, this method easily

leads to signiﬁcantly low performances for some of

the datasets.

Table 1: Summary statistics about the percentage gaps of

the three methods across 396 datasets.

Descent

Descent Search

(Fixed Initial)

Random

Average 0.49% 4.85% 38.67%

Min 0.00% 0.00% 0.00%

h Perc. 0.00% 0.00% 0.00%

h Perc. 0.00% 0.00% 5.57%

Median 0.00% 0.00% 42.37%

h Perc. 0.00% 7.48% 59.35%

h Perc. 0.00% 25.51% 83.61%

Max 39.81% 50.70% 89.37%

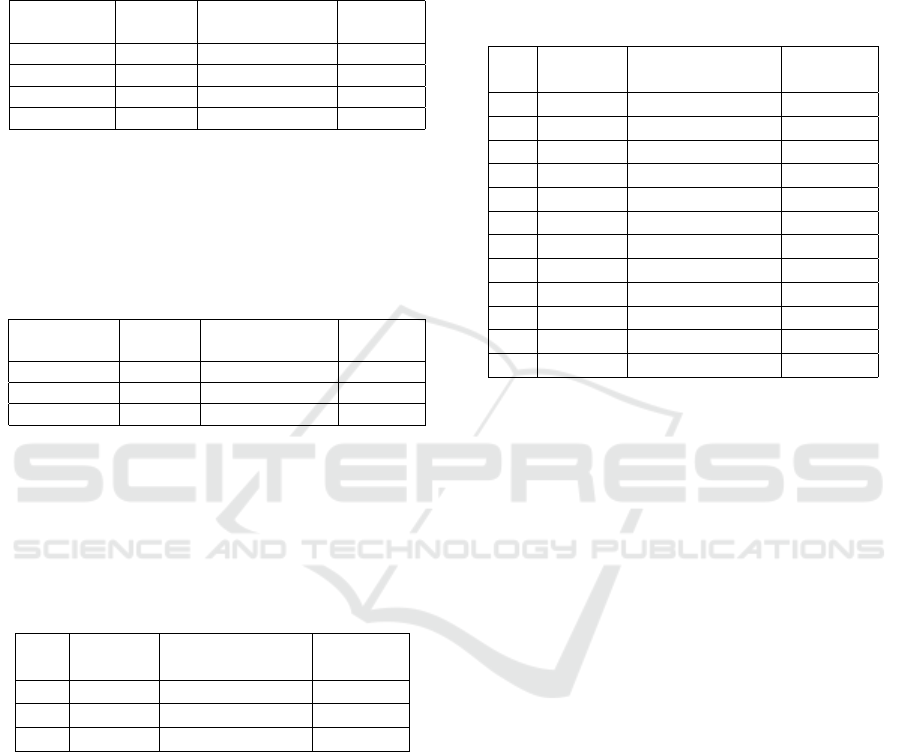
Figure 1 shows the gaps of three methods as the

number of levels varies. Notice that the performance

of the random search method decays quite fast as the

number of levels increases beyond 12. The perfor-

mance of the decent search method is more robust:

the decay in the solution quality is moderate with in-

creasing L. However, the initial solution has a signif-

icant effect on the performance especially if the num-

ber of levels is small: In these cases, the search space

is smaller, thus using different initial solutions is ef-

fective in overcoming the stacking to a local minimum

problem. Moreover, the comparative performance is

also worse for cases with L mod 8 = 0 due to our de-

sign of the computational experiments: In these cases,

there is an equal number of elements in each partition

which increases the comparative performance of de-

scent search with multiple initial solutions to increase.

10%

20%

30%

40%

50%

60%

70%

80%

10%

12%

14%

8 12 16 20 24 28 32 36 40 44 48

Gap (Random Search) (%)

Gap (Descent Search) (%)

Number of Levels

Descent Search Descent Search (Fixed Initial) Random Search

Figure 1: The average percentage gaps of the three methods.

In the ﬁrst two settings of our computational ex-

periments where there are two underlying regression

equations, the optimal partition is binary and known

given the level. For these experiments, we compute

the number of misclassiﬁed levels in each method.

Table 2 present the maximum number of misclassi-

ﬁed levels for each method across varying numbers

of levels. In line with our ﬁndings in Figure 1, the

descent search method has the lowest number of mis-

classiﬁcations, which tends to increase with the num-

ber of levels. However, in both implementations of

the descent search method, the maximum number of

misclassiﬁcations is only 1. With the random search

method, the number of misclassiﬁcations increases

rapidly with the number of levels. Notice that the

fraction of levels that is misclassiﬁed is also increas-

ing, which explains the underlying reason for the poor

performance if this method.

Table 2: The maximum number of misclassiﬁed levels for

the three methods.

Descent

Descent Search

(Fixed Initial)

Random

8 0 1 0

12 0 1 0

16 0 1 2

20 1 1 2

24 0 1 4

28 1 1 5

32 1 1 7

36 1 1 11

40 1 1 12

44 1 1 13

48 0 1 17

How does the underlying regression setting affect

the performance of our solution methods? Table 3

shows the average percentage gaps of each method

across three underlying regression settings. In the ﬁrst

setting with an equal number of levels in each parti-

tion, the descent search method performs the best ex-

cept two datasets for which descent search with the

ﬁxed initial solution gives the best solution. In the

second setting, which represents the case with an un-

even number of levels in each partition (i.e., 2 vs.

L − 2), the descent search with the ﬁxed initial so-

lution has the best solution. Since most of the levels

actually belong to the same group, starting with the

initial solution of assigning all the levels into a single

partition is very close to the optimal solution. In this

case, the descent search method could ﬁnd the optimal

solution after two iterations. As another support of

this claim, we observe that the computational times of

the descent search method with the ﬁxed initial solu-

tion for these cases are signiﬁcantly smaller. Finally,

the descent search method performs signiﬁcantly bet-

ter than the other two methods under the setting with

DATA 2020 - 9th International Conference on Data Science, Technology and Applications

106

8 underlying partitions. Neither starting with all lev-

els in the same partition nor a random search seems

like a good idea.

Table 3: The average percentage gaps of the three methods

across different regression settings.

Regression

Setting

Descent

Descent Search

(Fixed Initial)

Random

1 0.14% 7.96% 34.63%

2 1.31% 0.00% 53.16%

3 0.00% 6.81% 27.06%

All 0.48% 4.92% 38.28%

The effect of the number of data points (n) on the

performance of the three heuristics is quite small as

shown in Table 4. There is a slight decrease in the

performance of the descent search heuristic.

Table 4: The average percentage gaps of the three methods

across different number of data points.

Number of

Data Points

Descent

Descent Search

(Fixed Initial)

Random

30 ∗ L 0.09% 4.84% 38.23%

60 ∗ L 0.72% 3.92% 38.18%

90 ∗ L 0.64% 6.01% 38.44%

Table 5 displays the average percentage gaps of

each heuristic as the standard deviation of the residu-

als (σ) varies. We ﬁnd that the magnitude of the resid-

uals does not have a signiﬁcant effect on the perfor-

mance of our heuristics.

Table 5: The average percentage gaps of the three methods

across varying residual error standard deviation.

Descent

Descent Search

(Fixed Initial)

Random

100 0.28% 5.28% 39.20%

200 0.52% 5.16% 37.39%

300 0.82% 4.38% 38.33%

Average computation times (in seconds) are pre-

sented in Table 6 across a varying number of levels.

As expected, the descent search with the ﬁxed ini-

tial method is the fastest one and the descent search

method comes second. However, remember that the

descent search method runs with 5 different initial so-

lutions, yet the computation times are more than ﬁve-

fold as compared to using the ﬁxed initial solution

as the number of levels increases. This observation

suggests that the convergence rate with random ini-

tial points decreases with the number of levels. Also,

notice that the computation times with the random

search method is quite high. When L ≤ 12, with a

single replication it is possible to search the whole

feasible region hence the comparatively small com-

putational times. When L > 12, however, the random

search method evaluates the same number of solu-

tions, hence the slight increase in computational times

is due to increased data points.

Table 6: Average computational times (seconds) of the three

methods.

Descent

Descent Search

(Fixed Initial)

Random

8 0.20 0.04 0.16

12 0.52 0.09 2.97

16 0.79 0.13 26.43

20 1.35 0.22 27.80

24 1.95 0.31 28.67

28 3.12 0.48 32.82

32 3.67 0.55 29.94

36 4.76 0.72 30.49

40 6.32 0.93 32.89

44 7.49 1.13 31.95

48 9.21 1.38 32.93

All 3.58 0.54 25.19

5 CONCLUSIONS

We study an extension of the regression clustering

problem with the additional constraint that observa-

tions with the same value on a partitioning variable

should have the same regression ﬁt. This is a chal-

lenging problem to solve due to its combinatorial na-

ture. We provide an integer programming formulation

to solve this problem, which is unfortunately compu-

tationally prohibitive to solve. Alternatively, we of-

fer a gradient descent based heuristic which iterates

through solutions in order to ﬁnd the best binary parti-

tion to minimize the total SSE. In our numerical study

with 396 simulated datasets, we ﬁnd that the perfor-

mance of our heuristic is very good as compared to

the benchmark method (the random search), albeit a

slight decrease as the number of levels increases. The

performance is best when each of the true underlying

partitions has a similar number of levels.

There are a number of avenues for future research

to further investigate this research problem. First, de-

composition techniques such as Bender’s decompo-

sition could be developed to ﬁnd the exact solution

of the integer programming formulation provided in

the paper. It is also fruitful to develop and compare

other meta-heuristics to solve this problem. Finally,

an evaluation using real-life datasets would increase

our understanding of the problem and our solution

methodology.

A Gradient Descent based Heuristic for Solving Regression Clustering Problems

107

REFERENCES

Bagirov, A. M., Mahmood, A., and Barton, A. (2017). Pre-

diction of monthly rainfall in victoria, australia: Clus-

terwise linear regression approach. Atmospheric Re-

search, 188:20–29.

Bagirov, A. M., Ugon, J., and Mirzayeva, H. (2013). Non-

smooth nonconvex optimization approach to cluster-

wise linear regression problems. European Journal of

Operational Research, 229(1):132–142.

Brusco, M. J., Cradit, J. D., Steinley, D., and Fox, G. L.

(2008). Cautionary remarks on the use of cluster-

wise regression. Multivariate Behavioral Research,

43(1):29–49.

Brusco, M. J., Cradit, J. D., and Tashchian, A. (2003). Mul-

ticriterion clusterwise regression for joint segmenta-

tion settings: An application to customer value. Jour-

nal of Marketing Research, 40(2):225–234.

Carbonneau, R. A., Caporossi, G., and Hansen, P. (2011).

Globally optimal clusterwise regression by mixed

logical-quadratic programming. European Journal of

Operational Research, 212(1):213–222.

Carbonneau, R. A., Caporossi, G., and Hansen, P. (2012).

Extensions to the repetitive branch and bound al-

gorithm for globally optimal clusterwise regression.

Computers & Operations Research, 39(11):2748–

2762.

Charles, C. (1977). R

egression typologique et reconnais-

sance des formes. PhD thesis.

Costanigro, M., Mittelhammer, R. C., and McCluskey, J. J.

(2009). Estimating class-speciﬁc parametric models

under class uncertainty: local polynomial regression

clustering in an hedonic analysis of wine markets.

Journal of Applied Econometrics, 24(7):1117–1135.

DeSarbo, W. S. and Cron, W. L. (1988). A maximum like-

lihood methodology for clusterwise linear regression.

Journal of classiﬁcation, 5(2):249–282.

Fisher, W. D. (1958). On grouping for maximum homo-

geneity. Journal of the American statistical Associa-

tion, 53(284):789–798.

Hastie, T. J., Tibshirani, R. J., and Friedman, J. H. (2009).

The elements of statistical learning : data mining, in-

ference, and prediction. Springer series in statistics.

Springer, New York.

He, L., Huang, G., and Lu, H. (2008). Health-risk-

based groundwater remediation system optimization

through clusterwise linear regression. Environmental

science & technology, 42(24):9237–9243.

Joki, K., Bagirov, A. M., Karmitsa, N., M

akel

a, M. M., and

Taheri, S. (2020). Clusterwise support vector linear re-

gression. European Journal of Operational Research.

Lau, K.-N., Leung, P.-l., and Tse, K.-k. (1999). A mathe-

matical programming approach to clusterwise regres-

sion model and its extensions. European Journal of

Operational Research, 116(3):640–652.

Luo, Z. and Yin, H. (2008). Probabilistic analysis of pave-

ment distress ratings with the clusterwise regression

method. Transportation research record: Journal of

the Transportation Research Board, (2084):38–46.

McClelland, R. L. and Kronmal, R. (2002). Regression-

based variable clustering for data reduction. Statistics

in medicine, 21(6):921–941.

ath, H. (1979). Algorithm 39 clusterwise linear regres-

sion. Computing, 22(4):367–373.

Wedel, M. and Kistemaker, C. (1989). Consumer ben-

eﬁt segmentation using clusterwise linear regres-

sion. International Journal of Research in Marketing,

6(1):45–59.

DATA 2020 - 9th International Conference on Data Science, Technology and Applications

108