Accelerating Homomorphic Encryption using Approximate Computing

Techniques

Shabnam Khanna and Ciara Rafferty

Centre for Secure Information Technologies (CSIT), Queen’s University Belfast, U.K.

Keywords:

Homomorphic Encryption, Approximate Computing, Task Skipping, Depth Reduction, Loop Perforation.

Abstract:

This research proposes approximate computing techniques to accelerate homomorphic encryption (HE). In

particular, the CKKS encryption scheme for approximate numbers is targeted. There is a requirement for HE in

services dealing with conﬁdential data, however current constructions are not efﬁcient enough for real-time

applications. A homomorphic encryption scheme which uses approximate arithmetic (showing faster results

than previous HE schemes) already exists, the CKKS scheme, and this research applies a variation of the

approximate computing techniques of task skipping and depth reduction (derived from loop perforation) to

determine whether further approximating the functions evaluated using CKKS scheme can have a positive

impact on performance of homomorphic evaluation. This is demonstrated via the evaluation of the logistic

and exponential functions that this is possible, showing positive results. The speed up in running time for

HE with task skipping is between 12.1% and 45.5%, depth reduction gives 35-45.5% speed-up with a small

error difference than task skipping alone. The combination of both techniques corresponds to a halving of

the running time, at the cost of increased error. This novel approach to further approximate homomorphic

encryption shows that it is possible for certain functions, where running time is of paramount importance, that

further approximations can be made with a lower-impacting greater error.

1 INTRODUCTION

As an increasing amount of data is stored in the

cloud, data security and privacy is evermore important.

Currently, to be able to compute on encrypted data

stored on the cloud, data has to be downloaded and

decrypted, using a key the provider has access to,

before re-encrypting it and restoring on the cloud

(Gentry, 2010). Homomorphic encryption (HE)

removes the need for download and decryption, by

allowing operations to be performed directly on

encrypted data, thereby enabling safe computation and

reducing the risk of data privacy-loss. Using HE, data

on the cloud could be stored in ciphertext form, upon

which analysis can be performed. Applications include

machine learning algorithms to predict trends using

sensitive data, electronic voting and secure database

searches (Archer et al., 2017). The growing demand

for analysis on encrypted data has motivated interest

and activity towards standardisation of HE schemes

and parameters (Albrecht et al., 2018).

Currently, HE schemes are effective in terms of

evaluating functions in ciphertext form to a high level

of accuracy, as shown by numerous applications, one

being Secure Genome-Wide Association Studies (Blatt

et al., 2019), but are not currently efﬁcient enough

for real-time usage. For example, in research which

applied a logistic regression model homomorphically,

the training took up to a few days (Chen et al., 2018).

This research proposes the integration of approximate

computing techniques with HE schemes to achieve

improved HE evaluation runtimes.

One of the main motivations driving research into

approximate computing is to design energy-efﬁcient

technology for the future (Barua and Mondal, 2019).

One way to achieve this, is to trade-off between

accuracy and the energy and running time required

to compute algorithms. There are many applications

where this trade-off is acceptable such as machine

learning, signal processing, and big data analytics

(Barua and Mondal, 2019). To the best of the authors’

knowledge, evaluating the impact of approximate

computing to advance the practicality of HE has not

yet been conducted. This research provides an insight

as to whether using approximate computing is feasible

for approximate HE and the effect such techniques

have when applied to the CKKS encryption scheme

(Hee Cheon et al., 2017), currently the only HE scheme

based on approximate arithmetic.

In this research, two approximate computing

380

Khanna, S. and Rafferty, C.

Accelerating Homomorphic Encryption using Approximate Computing Techniques.

DOI: 10.5220/0009828803800387

In Proceedings of the 17th International Joint Conference on e-Business and Telecommunications (ICETE 2020) - SECRYPT, pages 380-387

ISBN: 978-989-758-446-6

techniques, task skipping and loop perforation,

are adapted to accelerate HE. To demonstrate the

efﬁciency of the proposed approximate computing

techniques, two target functions are considered for

HE evaluation: the logistic and exponential functions.

These are compared to the same operations without

approximate computing optimisations. Both are

implemented in Microsoft SEAL’s HE library (SEAL,

2019), and results are given, measuring performance

and average error with respect to the actual calculation.

2 RELATED WORKS

2.1 Homomorphic Encryption

Due to numerous data leaks and the increasing focus

on the privacy of public data, including who has access

to it and what is done with this data, being able to

efﬁciently compute with encrypted data would be

ideal for both the user and the company who wants to

continue analysing data. An example application of

HE, is e-voting (Chillotti et al., 2016). In 2009, the

ﬁrst fully homomorphic encryption (FHE) scheme was

proposed (Gentry, 2009) after over 30 years research

into ﬁnding the ﬁrst FHE scheme. Over the past

10 years there has been a large advancement in the

development of HE schemes. Further details on major

HE schemes can be found in the following subsection.

2.1.1 Homomorphic Encryption (HE) Schemes

An elementary deﬁnition of homomorphic encryption

is simply where computations can be performed on

the ciphertexts, which, when decrypted, give the

same result as if those same computations had been

performed on the plaintexts (Halevi, 2017). This can

be written as follows:

E(m

) ? E(m

) = E(m

? m

) ∀m

, m

∈ M,

where

is an encryption algorithm,

is the set of all

plaintexts and ? is an arbitrary operation.

Deﬁnition 1.

Homomorphic Encryption (Halevi,

2017), (Vaikuntanathan, 2011):

A homomorphic (public-key) encryption scheme

is deﬁned as a quadruple of four probabilistic

polynomial-time algorithms as follows:

• KeyGen:

An algorithm generating a public key

and a private key

from an input of a unary

representation of the security parameter λ, 1

• Encrypt:

An algorithm which takes as input the

public key

, and a single-bit message

µ ∈ {0, 1}

and outputs a ciphertext c.

• Decrypt:

An algorithm which takes as input the

secret key

, and a ciphertext

to output a

message µ

∈ {0, 1}.

• Evaluate:

An algorithm which inputs the public

key

, a function represented using boolean

circuits

BC ∈ {BC}

(consisting of gates such

as AND and XOR), the original ciphertext (

c =

Enc(x)) and outputs a new ciphertext c

A HE scheme is often denoted as

E = (KeyGen, Encrypt, Decrypt, Evaluate).

The difference between a standard encryption

scheme and a HE scheme is that the HE scheme

contains an Evaluation stage, where multiple

ciphertexts (usually represented as a vector of

ciphertexts) are inputs into the evaluation algorithm

(which evaluates a given function) and outputs a new

ciphertext. The choice of function to be evaluated

depends on the application requirements.

Since Gentry’s ﬁrst FHE scheme (Gentry, 2009), a

variety of HE schemes have been introduced. Several

are based on the Learning with Errors (LWE) problem

proposed by Regev (Regev, 2005), or its Ring variant

(RLWE) (Lyubashevsky et al., 2013), for example, the

BV Scheme (Brakerski and Vaikuntanathan, 2011), the

LTV scheme (Lyubashevsky et al., 2013), the BGV

scheme (Brakerski et al., 2012), the GSW scheme

(Gentry et al., 2013) and the CKKS encryption scheme

(Hee Cheon et al., 2017). There are other schemes

which derive from those named above and more

details (including the implementation libraries) can

be found at (Albrecht et al., 2018). Since the aim

of this research is to accelerate HE evaluation using

approximate computing techniques, the CKKS scheme

is best suited, since it enables approximate arithmetic

(Hee Cheon et al., 2017).

2.1.2 The CKKS Encryption Scheme

The CKKS HE scheme was introduced in 2017

(Hee Cheon et al., 2017), and uses the RLWE

assumption. However, unlike previous RLWE-based

HE schemes, it does not use exact arithmetic, instead

enabling approximate arithmetic. This approach

enables the calculation of the approximate value of the

plaintext after decryption, to a predetermined accuracy.

Before a text can be encrypted, it is scaled (by

multiplying a scaling factor to the message), ensuring

the size of the error (often considered as noise) does

not grow out of hand during evaluation. It must also

be encoded (and decoded after evaluation), where

the input vector is converted into a polynomial using

isometric ring isomorphisms, to ensure the size of the

error and plaintext remain the same. The encryption

of a message

, giving the ciphertext

satisﬁes

Accelerating Homomorphic Encryption using Approximate Computing Techniques

381

< c, sk >= m + e(modq)

where

is a small error,

is the ciphertext and

is the secret key, stating

that when the ciphertext,

, is decrypted using a

secret key,

, the result is the message,

with a

small error,

. The scheme has a batching technique

used to pack the plaintext messages into a number

of slots, which can be run simultaneously, improving

efﬁciency. Key switching techniques (similar to the

BGV scheme) are required for ciphertext operations

and whenever a ciphertext multiplication has occurred,

the new ciphertext must be rescaled to the chosen scale

before any further calculations are calculated. Once all

operations are evaluated the ﬁnal ciphertexts must be

decrypted and decoded. A detailed explanation of the

CKKS scheme is given in (Hee Cheon et al., 2017).

The Residual Number System (RNS) variant

(Cheon et al., 2019) has fast polynomial approximation

and can perform speedy multiplicative inverses and

Discrete Fourier Transforms (DFT), when compared

with the original CKKS scheme (Hee Cheon et al.,

2017). It allows for larger integers to be implemented

and for techniques based on RNS decomposition

and the Number Theoretic Transform (NTT). Further

information regarding the RNS-variant of the CKKS

scheme can be found in (Cheon et al., 2019).

The CKKS scheme has been proposed for use in

speciﬁc applications, e.g. logistic regression (Blatt

et al., 2019) and a multi-party version for use in Neural

Networks (Chen et al., 2019b). The HEAAN library

(HEAAN, 2018) and Microsoft’s HE library SEAL

(SEAL, 2019) are two of the many libraries which

implement the RNS variant of the CKKS scheme.

2.2 Approximate Computing

Due to the increasing demand of computing power

outpacing supply (Mittal, 2016), and the increasing

need for more ‘real-time’ computations, this has

motivated the research into approximate computing,

where a compromise is made between the quality

and efﬁciency of calculations. Mittal (2016) provides

a comprehensive survey of approximate computing

techniques, summarised in this section. Software

techniques include precision scaling, load value

approximation, loop perforation and task skipping,

memoization, multiple inexact program versions,

voltage scaling, reducing branch divergence in SIMD

architectures and speciﬁc neural network-focussed

approximate computing techniques. Hardware

techniques include using inexact or fault hardware,

approximating SRAM/eDRAM/DRAM/non-volatile

memories, using approximate computing techniques

for GPUs/FPGAs, using scalable effort design for

approximate computing and reducing error-correction

overhead using approximate computing. The

applications of these techniques has been shown in

areas such as machine learning, signal processing and

ﬁnancial analysis, to name a few (Mittal, 2016).

Since, to the best of the authors’ knowledge, this

is the ﬁrst research applying approximate computing

to HE, the techniques which the authors believe could

have a substantial impact on performance are targeted.

This research proposes and adapts deﬁnitions of task

skipping and loop perforation for acceleration of the

CKKS HE scheme.

2.2.1 Task Skipping

Task skipping is an approximate computing technique,

whereby a particular task, input or memory reference

is skipped according to a user-set condition (Mittal,

2016). This can be any condition, for example when

a particular variable hits a certain threshold, then a

particular task is skipped. The task skipping condition

is set so that, although a particular task is skipped when

that condition is met, the quality of the result is still

met. An example of task skipping in use can be seen

in (Goiri et al., 2015), where the authors apply (as well

as data input sampling) task skipping to MapReduce

programs and using these with various statistical

theories to reduce run times by approximately 38x

with an error of tolerance of 1% with 95% conﬁdence.

2.2.2 Loop Perforation

A basic deﬁnition of loop perforation is to skip certain

iterations of a loop to output a result which is accurate

to a certain (perhaps pre-deﬁned) level of accuracy

(Mittal, 2016), e.g. skipping every second term in the

addition of a sequence, yet still result in an answer

with only a 5% difference to the original solution.

Sidiroglou-Douskos et al. deﬁne a 2-step loop

perforation process; ﬁrstly to ﬁlter out loops which

cannot be perforated (‘critical loops’) and secondly

to ﬁnd loops which can be perforated for certain

inputs and a corresponding accuracy bound (‘greedy

exploration’) (Sidiroglou-Douskos et al., 2011). They

show performance improvements, whilst preserving

accuracy, to applications such as information retrieval,

machine-learning and Monte Carlo simulations. In

this research, the concept of loop perforation was ﬁrst

studied as an approximate computing technique to be

applied to the homomorphic evaluation of the selected

functions. However, with no immediately recognisable

loops in this process, using the multiplication approach

described in (Song, 2017), each depth of the

calculation is considered to be a loop. The question

then becomes whether it is possible to calculate the

evaluation with one depth reduced yet still output

SECRYPT 2020 - 17th International Conference on Security and Cryptography

382

an appropriately accurate answer. This leads to the

approach of replacing the higher depth terms with

the highest one of the depth below, and analysing

the effect this has on the

Evaluation

process. This

concept is a form of a known computing technique,

depth reduction.

2.2.3 Depth Reduction

By representing a polynomial in the form of an

arithmetic circuit, the number of gates (usually AND,

XOR) denotes the size of the circuit and the depth is

the longest path in the circuit (Tavenas, 2015), i.e. the

maximum number of steps required to calculate an

operation. For this research, this can be interpreted

as the amount of operations required to calculate the

term with the highest power of that polynomial. Much

research has been carried out into arithmetic sizes and

improving the corresponding depths, e.g. (Valiant and

Skyum, 1981), (Tavenas, 2015), (Allender et al., 1998).

These works do not take the same explicit approach of

replacing the terms requiring higher depth calculations

with those requiring lower depth calculations as in this

research, however the principle of reducing the depth

of a circuit to evaluate, for example, a polynomial, for

efﬁciency purposes is the same.

3 PROPOSED APPROXIMATION

TECHNIQUES FOR HE

3.1 Preliminaries

The security of this research aligns with the advised

parameter sets as deﬁned in the HE Community

Standard, (Albrecht et al., 2018); the bits for each

prime per level, the vector of inputs (must be a power

of 2) and therefore the polynomial modulus degree

are all aligned with the advised parameter sets. As

with previous work on the CKKS scheme, (Hee Cheon

et al., 2017), (Cheon et al., 2019), (Chen et al., 2019a),

all methods proposed in this research have at least

an 80-bit security level. The ring dimension is set as

N = 2

, resulting in

= 2

plaintext slots, which

means that that the functions can be evaluated for each

slot in parallel. The scale for this implementation is

set at

and the ciphertext modulus for the ﬁrst and

last level is set to 60-bit, with all intermediate moduli

set to 40-bit. The parameters used here, especially for

= 8192

input slots, can be considered conservative.

For further details on parameters see (Hee Cheon

et al., 2017) or (Cheon et al., 2019). The accuracy

of the deﬁned functions to be calculated (logistic

and exponential functions) is kept the same as in

(Hee Cheon et al., 2017) to ensure fair comparison.

Two sets of inputs have been used: The ﬁrst set is the

vector 0 to 1 split into

slots and the second set is

the vector 1 to 8192 split into

slots, increasing by

increments of 1.

The application of depth reduction and task

skipping techniques in this research are to the RNS

variant of the CKKS scheme, used to calculate

the logistic function and the exponential function,

using their Taylor Series approximations to orders

9 and 8 respectively as in (Hee Cheon et al., 2017).

These functions have been chosen because of their

usefulness: the logistic function is commonly used in

statistics, neural networks and machine learning and

the exponential function for being one of a typical

circuit to be evaluated (Hee Cheon et al., 2017).

The logistic function can be approximated by the

corresponding Taylor Series approximation:

f (x) =

1+e

−x

≈

x −

480

−

80640

1451520

+ O(x

)

(1)

The exponential function, can be approximated by

the corresponding Taylor Series approximation:

g(x) = e

≈ 1 + x +

120

720

5040

40320

(2)

3.2 Approximate HE via Task Skipping

In this research, it is proposed that instead of explicitly

setting a condition for when to skip a task, it is selected

on the basis that for a decimal number between 0 and

1, the more it is multiplied by itself the smaller it

becomes. This makes the largest powered term in each

polynomial negligible, and therefore has less impact

on the accuracy of the result if it is skipped. For any

other input greater than 1, the removal of the largest

powered term has the most impact on the accuracy so

cannot be removed. Hence, for inputs greater than 1,

the lowest two terms of the polynomials are skipped

as they have less impact on the accuracy of the result.

For approximate HE with task skipping, three

approaches are proposed and the approximated

polynomials deﬁned for the logistic and exponential

functions respectively:

Approach 1 - input vector 0 to 1, the largest

powered term in both polynomials is skipped.

f (x) ≈

x −

480

−

80640

(3)

g(x) ≈ 1 +x +

120

720

5040

(4)

Accelerating Homomorphic Encryption using Approximate Computing Techniques

383

Approach 2 - input vector 0 to 1, the lowest three

terms are skipped.

f (x) ≈

480

−

80640

1451520

(5)

g(x) ≈ 1 +

120

720

5040

40320

(6)

Approach 3 - input vector 1 to ‘number of slots’,

the lowest three terms are skipped.

f (x) ≈

480

−

80640

1451520

(7)

g(x) ≈ 1 +

120

720

5040

40320

(8)

3.3 Approximate HE via Depth

Reduction

In this proposed depth reduction approach, instead of

certain iterations in a loop being skipped, a certain

number of depths are skipped, (usually more than

one depth skipped is not plausible due to the large

error occurring as more terms are approximated by

the largest term in the maximum depth required).

Since the functions being evaluated are deﬁned to

orders of

, with results in depths of single-ﬁgures,

the approach in this research is a one-depth reduction.

The higher power terms which require the extra depth

are replaced with the highest powered term of a lower

depth. This replacement procedure aims to provide a

more accurate estimation than task skipping alone and

since performing an addition is less computationally

intensive than multiplication, this results in a more

accurate approximation with a lower computational

cost. If these terms were not replaced, this would

instead be a task skipping technique.

To further understand depth reduction (using the

multiplication approach in (Song, 2017), see the

following example: To calculate

homomorphically

is a depth 4 calculation, one can reduce this to a depth 3

calculation,

(where

is a constant). In general, this

can be the largest possible term calculated with one

lower level of depth, which can be found by deﬁning a

new level whenever a polynomial term equals a power

of 2. The novelty in this approach is to replace terms

of the polynomials resulting in depth 4 calculation

with the largest term requiring depth 3 calculations (as

opposed to removing the term completely as in Task

Skipping Approach 2). Focusing on the two functions

in this research, the logistic and exponential functions

with depth 4 are approximated by their Taylor Series’

requiring depth 3 calculations as follows:

• Logistic function:

f (x) ≈

x −

480

−

80640

−

80640

(9)

• Exponential Function:

g(x) ≈ 1 + x +

120

720

5040

(10)

The double negative, highest powered term in

equation (9) greatly impacts the accuracy of the

approximation, especially for larger input values.

To combat this, yet still to retain the beneﬁts

of approximating the logistic function using depth

reduction, this equation will be slightly modiﬁed; the

highest powered term(s) will be multiplied by

−1

be turned into positive terms, therefore to compensate

this change without altering the approximation in (9)

by a large amount, the

term is also multiplied by

−1

. This results in the depth reduced approximation

to be implemented as follows:

f (x) ≈

x −

−

480

80640

(11)

3.4 Approximate HE via Task Skipping

and Depth Reduction

The functions to be evaluated can be approximated

further by combining and applying together the two

previously proposed techniques. Applying depth

reduction to Task Skipping Approach 1 has been

computed in the form of the basic depth reduction

technique. However, depth reduction can be applied

to Task Skipping Approaches 2 and 3, resulting in the

following polynomials being evaluated for the inputs

deﬁned in Section 3.1:

• Logistic function:

f (x) ≈

480

−

80640

−

80640

(12)

• Exponential Function:

g(x) ≈ 1 +

120

720

5040

(13)

Due to the alternating signs in the approximation

of the logistic function, in addition to applying

task skipping and depth reduction techniques, the

resulting approximation gives a large error and thus

needs modiﬁcation to give a more accurate evaluation.

Hence, the non-constant terms in the approximation

deﬁned in equation (12) are multiplied by

−1

, giving

the following approximation to be implemented:

f (x) ≈

−

480

80640

(14)

SECRYPT 2020 - 17th International Conference on Security and Cryptography

384

By using equation 13 as the approximation of the

exponential function for this approach, the calculation

still satisﬁes task skipping and depth reduction

techniques, but gives a more accurate result with

an additional reduction in running time. All of the

approximate functions, as given in Equations (1-8),

(11), (13) and (14), are homomorphically evaluated.

3.5 State of the Art in Approximate HE

Table 1 shows the current state-of-the-art running times

of the homomorphic evaluation of the logistic and

exponential functions, as given in (Hee Cheon et al.,

2017)

, (Cheon et al., 2019)

. It also shows that the

RNS variant of the CKKS scheme provides a much

faster evaluation time for the logistic and exponential

functions. In this research the depths and polynomial

degree have been kept the same as is in Table 1 to

ensure fair comparisons. It is important to note that

the results presented in this research cannot directly

be compared to those in Table 1 due to differences in

implementation arising from different libraries used.

Table 1: State-of-the-art implementation results for the

evaluation of the logistic and exponential functions using the

HEAAN library.

Method Depth N log q log Q

Polynomial

Degree

Total

Time

Amortised

Time

Logistic Function

HEAAN

3 2

30 155 7 0.54 s 130 µs

HEAAN

4 2

30 185 9 0.78 s 90 µs

HEAAN-RNS

3 2

55 281 7 0.161 s 19 µs

Exponential Function

HEAAN

3 2

30 155 7 0.65 s 160 µs

HEAAN-RNS

3 2

55 281 7 0.164 ms 20 µs

4 RESULTS AND ANALYSIS

In this section, the proposed approximate techniques

(from Section 3) are implemented and compared

against implementations of the functions without

approximate techniques, both in the SEAL library

(SEAL, 2019). Table 2 displays the results. The

amortised running times (i.e. the running time per

individual ciphertext slot) are deﬁned in microseconds,

as the time taken for the algorithm to run from the

encoding step to the decoding stage. The approximate

computing techniques is applied to the

Evaluation

stage of the HE scheme, hence the

KeyGen

running

times are not included. The error terms are calculated

as absolute errors of the approximate evaluation

against the actual evaluation of the functions. The

calculation of the average error uses the absolute

values to work out an average error from all the input

values. The computations have been run on an Intel

Core i7-8700 CPU @3.20 GHz with 16GB RAM

using Microsoft’s SEAL library (Version 3.4) (SEAL,

2019). Table 2 shows running times, with and without

approximate optimisations, for homomorphically

evaluated logistic and exponential functions using

the inputs as described in Section 3.2. For each

optimisation the percentage speed-up is calculated

against the running time without optimisation and the

average error is calculated against the ‘actual’ input

evaluated in each function. In all cases the input vector

is of size 2

, i.e. 8192 slots.

Task Skipping Approach 3 and Depth Reduction

with Task Skipping Approach 3 are compared with

second row for each function in Table 2, for input

values 1-8192. All other approximate technique

approaches are compared with the ﬁrst row, where

input values range from 0 to 1. The results for ‘without

optimisations’ in Table 2 cannot be directly compared

with the results outlined in (Cheon et al., 2019), due

to differing underlying libraries used. It is also unfair

to compare the HEAAN and SEAL libraries directly.

Here SEAL is used to measure the effect the proposed

approximations have on homomorphic evaluations.

Further generic software optimisations could improve

performance. All approaches show a speedup of

12.1-45.5% for task skipping, 35-45.5% for depth

reduction and 53.3-57.6% for both techniques applied

together across all the functions evaluated.

For input values 0-1, as shown in Table 2, both

logistic and exponential functions beneﬁt from Task

Skipping Approach 1. It runs on average 40% faster

with a larger error for the logistic function and around

10% better approximation for the exponential function.

For depth reduction, the logistic function shows a

similar speed up compared to Task Skipping Approach

1 but with a larger error. The exponential function,

however, beneﬁts from an approximately 4x smaller

error than Task Skipping Approach 1, with a similar

speed-up. When applying both techniques together,

both functions run in around half the time compared to

when no optimisation is used, 53.3% (exponential) and

57.6% (logistic), with an expected larger error value

than when either technique applied on its own.

For the evaluations of the logistic and exponential

functions shown in Figure 1, Figures 1a and

1c (equations (3) and (11) respectively) show

the techniques which fare best for high accuracy

applications and Figures 1b and 1d (equations (14)

and (13) respectively) show the techniques for when

running time is most important. For Figures 1b, 1d and

Table 2, the approximations do not follow the general

trend of the outputs for the inputs 0-1. As shown in

Figures 1b and 1d, as the input value increases the error

value increases as well, i.e. unlike in Figures 1a and 1c

the trend of function approximation is not continuous.

Accelerating Homomorphic Encryption using Approximate Computing Techniques

385

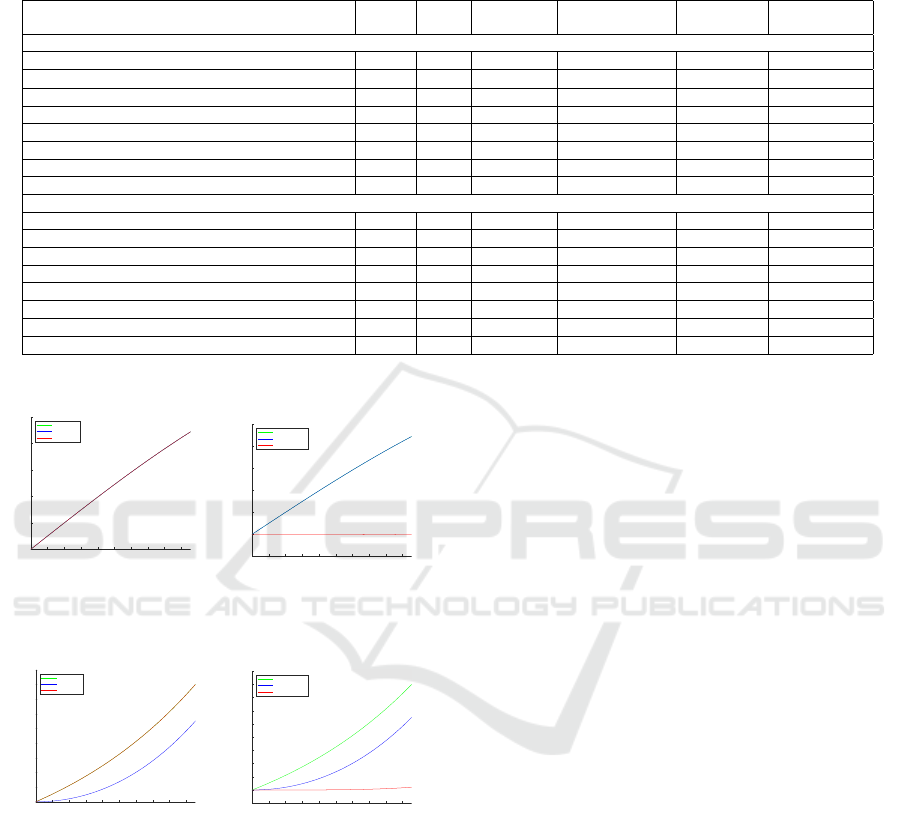
Table 2: Table showing results for homomorphic evaluation of approximated logistic and exponential functions respectively.

Three task skipping techniques (outlined in Section 3.2) and the depth reduction technique (outlined in Section 3.3) are

presented. Results are calculated using the RNS-CKKS scheme implemented in the SEAL library. The corresponding equation

numbers are shown in brackets. The rows with N/A in the speed-up column are the baseline results used for comparison.

Homomorphic Evaluation

of Function

Degree log Q

Total Time Amortized Time % speed-up

Average error

from actual

Logistic Function

Without Optimisation (1), inputs 0-1 9 280 0.274354 s 33 µs N/A 1.52 x 10

−7

Without Optimisation (1), inputs ≥ 1 9 280 0.275538 s 34 µs N/A 3.55 x 10

Task Skipping Approach 1 (3) 7 240 0.144749 s 18 µs 45.5 % 2.08 x 10

−6

Task Skipping Approach 2 (5) 9 280 0.234501 s 29 µs 12.1 % 0.11979

Task Skipping Approach 3 (7) 9 280 0.235498 s 29 µs 12.1 % 3.55 x 10

Depth Reduction (11) 7 240 0.145621 s 18 µs 45.5 % 6.18 x 10

−4

Task Skipping Approach 2 with Depth Reduction (14) 7 240 0.114206 s 14 µs 57.6 % 0.12041

Task Skipping Approach 3 with Depth Reduction (14) 7 240 0.114705 s 14 µs 57.6% 3.55 x 10

Exponential Function

Without Optimisation (2), inputs 0-1 8 280 0.495471 s 60 µs N/A 0.333321

Without Optimisation (2), inputs ≥ 1 9 280 0.495397 s 60 µs N/A 5.59 x 10

Task Skipping Approach 1 (4) 7 240 0.316672 s 39 µs 35 % 0.08334

Task Skipping Approach 2 (6) 8 280 0.38291 s 47 µs 21.6 % 0.70835

Task Skipping Approach 3 (8) 8 280 0.384384 s 47 µs 21.6 % 5.59 x 10

Depth Reduction (10) 7 240 0.318610 s 39 µs 35 % 2.42 x 10

−5

Task Skipping Approach 2 with Depth Reduction (13) 7 240 0.228299 s 28 µs 53.3 % 0.70833

Task Skipping Approach 3 with Depth Reduction (13) 7 240 0.227856 s 28 µs 53.3 % 5.59 x 10

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

Input

0.5

0.55

0.6

0.65

0.7

0.75

g(x)

xAct

xApprox

xApproxTS1

(a) Logistic Function Task

Skipping Approach 1,

equation (3)

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

Input

0.45

0.5

0.55

0.6

0.65

0.7

0.75

g(x)

xAct

xApprox

xApproxDRTS2

(b) Logistic Function Depth

Reduction with Task Skipping

Approach 2, equation (14)

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

Input

1.2

1.4

1.6

1.8

2.2

2.4

2.6

2.8

g(x)

xAct

xApprox

xApproxDR

Depth Reduction, equation

(11)

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

Input

0.8

1.2

1.4

1.6

1.8

2.2

2.4

2.6

2.8

g(x)

xAct

xApprox

xApproxDRTS2

(d) Exponential Function

Depth Reduction with

Task Skipping Approach 2,

equation (13)

Figure 1: Graphical representation of the approaches for both

functions where accuracy (1a, 1c) and improved running

time (1b, 1d) are the focus.

As shown by the large average error values in Table 2,

for large input vectors (inputs

≥ 1

) the average error

is much worse and thus for such inputs, the reduction

in accuracy caused by the proposed approximation

techniques in their current form is too costly to justify

the gain in terms of run time. This is considered upon

in the recommendations in Section 5.

5 CONCLUSIONS

This research shows the proposed approximate

computing techniques provide a decent run-time

speedup of homomorphic evaluation, from 12.1-45.5%

(task skipping), 35-45.5% (depth reduction) and

53.3-57.6% (the combination of techniques). The

SEAL library is used to indicatively show how

approximate computing for homomorphic evaluation

of the logistic and exponential functions affects

performance, targeting the CKKS scheme.

As shown in Table 2, the error values for when

these techniques are applied to inputs

≥ 1

are very

large, therefore, giving unreliable estimations, even

though there is a speed-up. Thus, these techniques in

their current form, are recommended for input values

in the range 0-1.

Based on this research’s results, for a balanced

trade-off between performance and accuracy, the

recommended approximate computing techniques for

the logistic and exponential functions respectively are

(for input values 0 to 1): Task Skipping Approach 1

and Depth Reduction.

REFERENCES

Albrecht, M., Chase, M., Chen, H., Ding, J., Goldwasser,

S., Gorbunov, S., Halevi, S., Hoffstein, J., Laine,

K., Lauter, K., Lokam, S., Micciancio, D., Moody,

D., Morrison, T., Sahai, A., and Vaikuntanathan, V.

(2018). Homomorphic Encryption Security Standard.

SECRYPT 2020 - 17th International Conference on Security and Cryptography

386

Technical report, HomomorphicEncryption.org,

Toronto, Canada.

Allender, E., Jiao, J., Mahajan, M., and Vinay, V. (1998).

Non-commutative arithmetic circuits: depth reduction

and size lower bounds. Theoretical Computer Science,

209(1):47 – 86.

Archer, D., Chen, L., Cheon, J. H., Gilad-Bachrach, R.,

Hallman, R. A., Huang, Z., Jiang, X., Kumaresan, R.,

Malin, B. A., Soﬁa, H., Song, Y., and Wang, S. (2017).

Applications of Homomorphic Encryption. Technical

report, HomomorphicEncryption.org, Redmond WA,

USA.

Barua, H. B. and Mondal, K. C. (2019). Approximate

Computing: A Survey of Recent Trends—Bringing

Greenness to Computing and Communication. Journal

of The Institution of Engineers (India): Series B.

Blatt, M., Gusev, A., Polyakov, Y., Rohloff, K., and

Vaikuntanathan, V. (2019). Optimized Homomorphic

Encryption Solution for Secure Genome-Wide

Association Studies. IACR Cryptology ePrint Archive,

2019:223.

Brakerski, Z., Gentry, C., and Vaikuntanathan, V. (2012).

(Leveled) Fully Homomorphic Encryption Without

Bootstrapping. In Proceedings of the 3rd Innovations

in Theoretical Computer Science Conference, ITCS

’12, pages 309–325, New York, NY, USA. ACM.

Brakerski, Z. and Vaikuntanathan, V. (2011). Efﬁcient

Fully Homomorphic Encryption from (Standard) LWE.

In Proceedings of the 2011 IEEE 52Nd Annual

Symposium on Foundations of Computer Science,

FOCS ’11, pages 97–106, Washington, DC, USA.

IEEE Computer Society.

Chen, H., Chillotti, I., and Song, Y. (2019a). Improved

Bootstrapping for Approximate Homomorphic

Encryption. In Ishai, Y. and Rijmen, V., editors,

Advances in Cryptology – EUROCRYPT 2019, pages

34–54, Cham. Springer International Publishing.

Chen, H., Dai, W., Kim, M., and Song, Y. (2019b). Efﬁcient

Multi-Key Homomorphic Encryption with Packed

Ciphertexts with Application to Oblivious Neural

Network Inference. Cryptology ePrint Archive, Report

2019/524. https://eprint.iacr.org/2019/524.

Chen, H., Gilad-Bachrach, R., Han, K., Huang, Z.,

Jalali, A., Laine, K., and Lauter, K. E. (2018).

Logistic regression over encrypted data from fully

homomorphic encryption. IACR Cryptology ePrint

Archive, 2018:462.

Cheon, J., Kyoohyung, H., Kim, A., Kim, M.,

and Song, Y. (2019). A Full RNS Variant

of Approximate Homomorphic Encryption: 25th

International Conference, Calgary, AB, Canada,

August 15–17, 2018, Revised Selected Papers, pages

347–368.

Chillotti, I., Gama, N., Georgieva, M., and Izabach

ene,

M. (2016). A Homomorphic LWE Based E-voting

Scheme. In Takagi, T., editor, Post-Quantum

Cryptography, pages 245–265, Cham. Springer

International Publishing.

Gentry, C. (2009). Fully homomorphic encryption using

ideal lattices. In STOC, pages 169–178.

Gentry, C. (2010). Computing Arbitrary Functions of

Encrypted Data. Commun. ACM, 53(3):97–105.

Gentry, C., Sahai, A., and Waters, B. (2013).

Homomorphic Encryption from Learning with

Errors: Conceptually-Simpler, Asymptotically-Faster,

Attribute-Based. In Canetti, R. and Garay, J. A.,

editors, Advances in Cryptology – CRYPTO 2013,

pages 75–92, Berlin, Heidelberg. Springer Berlin

Heidelberg.

Goiri, I., Bianchini, R., Nagarakatte, S., and Nguyen, T. D.

(2015). ApproxHadoop: Bringing Approximations

to MapReduce Frameworks. In Proceedings of the

Twentieth International Conference on Architectural

Support for Programming Languages and Operating

Systems, ASPLOS ’15, page 383–397, New York, NY,

USA. Association for Computing Machinery.

Halevi, S. (2017). Homomorphic Encryption, pages 219–276.

Springer International Publishing, Cham.

HEAAN (2018). HEAAN. https://github.com/snucrypto/

HEAAN.

Hee Cheon, J., Kim, A., Kim, M., and Song, Y.

(2017). Homomorphic Encryption for Arithmetic of

Approximate Numbers. pages 409–437.

Lyubashevsky, V., Peikert, C., and Regev, O. (2013). On

Ideal Lattices and Learning with Errors over Rings. J.

ACM, 60(6):43:1–43:35.

Mittal, S. (2016). A Survey of Techniques for Approximate

Computing. ACM Comput. Surv., 48(4):62:1–62:33.

Regev, O. (2005). On Lattices, Learning with Errors,

Random Linear Codes, and Cryptography. In

Proceedings of the Thirty-seventh Annual ACM

Symposium on Theory of Computing, STOC ’05, pages

84–93, New York, NY, USA. ACM.

SEAL (2019). Microsoft SEAL (release 3.4). https://github.

com/Microsoft/SEAL. Microsoft Research, Redmond,

WA.

Sidiroglou-Douskos, S., Misailovic, S., Hoffmann, H.,

and Rinard, M. (2011). Managing Performance

vs. Accuracy Trade-offs with Loop Perforation. In

Proceedings of the 19th ACM SIGSOFT Symposium

and the 13th European Conference on Foundations of

Software Engineering, ESEC/FSE ’11, pages 124–134,

New York, NY, USA. ACM.

Song, Y. (2017). Homomorphic Encryption for Arithmetic

of Approximate Numbers. Accessed at https://www.

microsoft.com/en-us/research/video/homomorphic-

encryption-arithmetic-approximate-numbers/.

Tavenas, S. (2015). Improved bounds for reduction to depth

4 and depth 3. Information and Computation, 240:2 –

11. MFCS 2013.

Vaikuntanathan, V. (2011). Computing Blindfolded: New

Developments in Fully Homomorphic Encryption. In

2011 IEEE 52nd Annual Symposium on Foundations

of Computer Science, pages 5–16.

Valiant, L. G. and Skyum, S. (1981). Fast parallel

computation of polynomials using few processors.

In Gruska, J. and Chytil, M., editors, Mathematical

Foundations of Computer Science 1981, pages

132–139, Berlin, Heidelberg. Springer Berlin

Heidelberg.

Accelerating Homomorphic Encryption using Approximate Computing Techniques

387